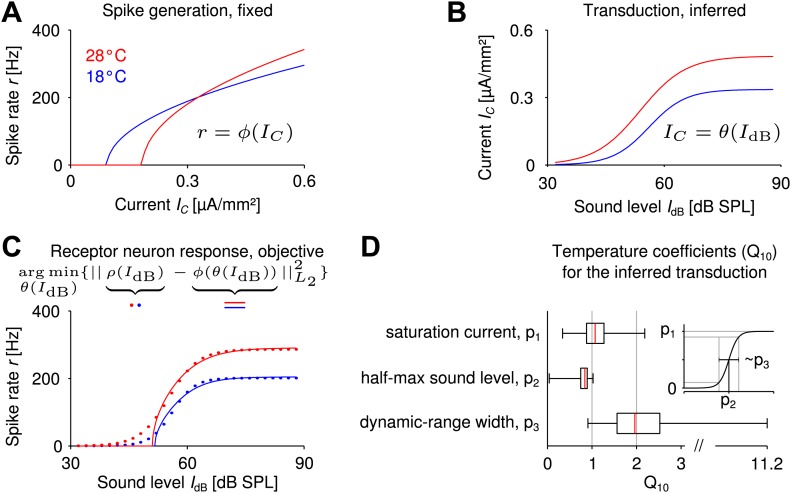
Figure 4. Reverse engineering mechanosensory transduction functions that favor temperature compensation of firing rate.

(A) Example of a model-based f-I curve, denoted $r=\varphi \left(I_C\right)$, at two temperatures. (B) Example of a sigmoidal transduction function converting sound intensity to current, $I_C=\theta \left(I_{\text{dB}}\right)$. (C) Representative receptor neuron responses, $r=\rho \left(I_{\text{dB}}\right)$, at two temperatures (dotted lines), as well as a receptor neuron response, $r=\varphi \left(\theta \left(I_{\text{dB}}\right)\right)$, ‘constructed’ from the f-I curve in A and the transduction function in B. For each model of spike generation, the optimal transduction function, $I_C=\theta \left(I_{\text{dB}}\right)$, minimizing the error between the corresponding ‘constructed’ receptor neuron response and the representative receptor neuron response (dotted line in C) was derived. (D) The statistics of temperature dependence of the optimal transduction functions, $I_C$, across all models. The width of the dynamic range depended most on temperature and increased with heating for nearly all optimized transduction functions. But the temperature dependence of the saturation current and the half-maximum sound intensity (mainly when decreasing with temperature) were also found to contribute to temperature compensation. Note that the ranges marked by the whiskers cover all data (including outliers) in this plot.

DOI: http://dx.doi.org/10.7554/eLife.02078.012