A simple epidemiological model for populations in the wild with Allee effects and disease-modified fitness

Abstract

The study of the dynamics of human infectious disease using deterministic models is typically carried out under the assumption that a critical mass of individuals is available and involved in the transmission process. However, in the study of animal disease dynamics where demographic considerations often play a significant role, this assumption must be weakened. Models of the dynamics of animal populations often naturally assume that the presence of a minimal number of individuals is essential to avoid extinction. In the ecological literature, this a priori requirement is commonly incorporated as an Allee effect. The focus here is on the study disease dynamics under the assumption that a critical mass of susceptible individuals is required to guarantee the population's survival. Specifically, the emphasis is on the study of the role of an Allee effect on a Susceptible-Infectious (SI) model where the possibility that susceptible and infected individuals reproduce, with the S-class the best fit. It is further assumed that infected individuals loose some of their ability to compete for resources, the cost imposed by the disease. These features are set in motion in as simple model as possible. They turn out to lead to a rich set of dynamical outcomes. This toy model supports the possibility of multi-stability (hysteresis), saddle node and Hopf bifurcations, and catastrophic events (disease-induced extinction). The analyses provide a full picture of the system under disease-free dynamics including disease-induced extinction and proceed to identify required conditions for disease persistence. We conclude that increases in (i) the maximum birth rate of a species, or (ii) in the relative reproductive ability of infected individuals, or (iii) in the competitive ability of a infected individuals at low density levels, or in (iv) the per-capita death rate (including disease-induced) of infected individuals, can stabilize the system (resulting in disease persistence). We further conclude that increases in (a) the Allee effect threshold, or (b) in disease transmission rates, or in (c) the competitive ability of infected individuals at high density levels, can destabilize the system, possibly leading to the eventual collapse of the population. The results obtained from the analyses of this toy model highlight the significant role that factors like an Allee effect may play on the survival and persistence of animal populations. Scientists involved in biological conservation and pest management or interested in finding sustainability solutions, may find these results of this study compelling enough to suggest additional focused research on the role of disease in the regulation and persistence of animal populations. The risk faced by endangered species may turn out to be a lot higher than initially thought.

1. Introduction

The use of mathematical models to study the dynamics of infectious diseases in animal populations, has been carried out, to some degree, under the implicit assumption, at least in the field of deterministic epidemiology, that disease patterns are inherently robust. This perspective has been ‘strengthened’ from the a priori selection of (i) classical deterministic epidemic model (that ignore critical demographic/ecological factors) and (ii) an emphasis (often a demand) that we must use tractable models. In fact, the identification, development, management and/or control of animal populations, we are told, can be effectively carried out with the aid of simple models that capture the essence of the population's dynamics. Specifically, in the context of classical disease dynamics, the quantification of management or general intervention measures is transferred to (or assumed to be captured by) the disease's basic reproduction number or R₀. This framework-dependent approach implicitly assumes the existence of tractable disease patterns (robustness), to the point, that we can ignore the details and focus the effectiveness of interventions on its impact on the basic reproduction number (R₀). The dimensionless ratio R₀ therefore provides a simplified and highly popular way of bringing in the power of models into the development of quantitatively-driven policies. R₀ is therefore indeed the ideal vehicle for designing, testing, and evaluating control and/or management strategies as long as we accept that the structure of classical contagion models is indeed representative of the processes that we wish to control. The effectiveness of intervention therefore reduces to their ability to bring the corresponding control reproductive number (R_c) below 1. Further, in general we deal with uncertainty through the use of sensitivity and uncertainty analyses on the parameters involved in R₀ or R_c (transmission, length of infectious period, and more, see Hethcote & Yorke 1984; Castillo-Chavez et al 1989a; Cintron-Arias et al 2009). Clearly, some of the inherent elements observed in the dynamics of non-domesticated animal populations are bypassed. The focus of this paper is on the study of the role of framework variations on disease dynamics in animal populations. We are interested in questions like: Is the model appropriate? Should some measures of fitness be incorporated? What would be the dynamics under non-classical circumstances? Will R₀ play a defining role under assumptions that incorporate some measure of population fitness?

Several studies have put emphasis among other factors on biological control (Feng et al 2000; Fagan et al 2002), evolution (e.g., myxomatosis, Dwyer et al 1990); conservation biology (e.g., survival of endangered species, Courchamp et al. 2000; Hilker et al. 2009; Thieme et al. 2009), renewable resources/sustainability (e.g., fisheries, Sherman and Duda 1999; Pauly et al 2002), or dispersal as a function of initial conditions (Castillo-Chavez & Yakubu 2001; Berezovskaya et al. 2010). These studies have highlighted the dramatic impact that differences in individuals’ fitness have on population-level dynamics and the resulting dynamics have turned out to be rather complex (Castillo-Chavez & Yakubu 2001; Berezovskaya et al. 2004). Therefore, it is not surprising to see that the research of some of the members of the scientific community interested in the development of sustainable management policies/strategies have often build their theoretical work on the shoulders of well-understood contagion frameworks, models with well understood pre-intervention dynamics. One of the aims of this research is to bring up the importance of some neglected factors. We bring these issues to the forefront with the aid of a simple minimal model, built under reasonable underlying assumptions, and yet capable of generating complex dynamics. We use this model to highlight the need to develop intervention strategies that do not entirely rely on R₀. The incorporation of Allee effects, disease-dependent reproduction, and disease's impact on the competitive ability of infected individuals, tends to support complex disease dynamics patterns. From the model's analyses, we conclude that the incorporation of fitness’ reduction factors naturally lead to outcomes that challenge the canonical use of standard modeling protocols in the study of disease dynamics in non-domestic animal populations and, consequently, on the development of intervention strategies that take into account at least superficially the role of natural selection.

Micro-parasitic and macro-parasitic infections are important drivers of host demographics (Anderson and May 1979; Hudson et al. 2001; Hilker et al. 2009) as well as key contributors to the decline of some species and even their extinction (Daszak et al. 1999; Harvell et al. 2002; Smith et al. 2006; Thieme et al. 2009). The impact of disease outbreaks can indeed be devastating, particularly in populations that face extinction at low population levels, the so-called Allee effect (Allee 1938; Stephens & Sutherland 1999; Stephens et al 1999; Courchamp et al 2009; Kang & Lanchier 2011). A number of mechanisms have been identified as responsible for “causing” Allee effects including failure to locate mates (Hopper & Roush 1993; Berec et al 2001), inbreeding depression (Lande 1998), failure to satiate predators (Gascoigne & Lipcius 2004), lack of cooperative feeding (Clark & Faeth 1997). In short, populations in the wild that maintain a minimal density do decrease the probability of (local or global) extinction (Hilker et al. 2009).

Infectious disease outbreaks are likely to enhance the defining role of Allee effects (e.g., the African wild dog (Burrows et al. 1995; Courchamp et al. 2000), the island fox (Clifford et al. 2006; Angulo et al. 2007), the noble crayfish and amphibian species like frogs, salamanders (Rachowicz et al. 2005&2006; Skerrat et al. 2007)) and therefore, an understanding of the interactions between disease dynamics and Allee effects is important. Biological conservation theory must assess the fragility of systems which depends on Allee effects that are often sensitive to the devastating role of disease outbreaks. In fact, Deredec & Courchamp (2006) and Hilker et al. (2005) have shown that the combination of parasitism and Allee effects increases the likelihood of extinction. Yakubu (2007) used a basic reproductive number approach to assess the likelihood of persistence or extinction of infected populations, exploring the relationship between demographic epidemic processes by using a discrete-time SIS model. Thieme et al. (2009) and Hilker et al. (2009) studied the role of density-dependent transmission on host populations and concluded that host extinction was a possible outcome. The models used can support complex dynamics, the kind that can be characterized by the existence of saddle node and Hopf bifurcations and tri-stability. The kind of dynamical transitions that can lead to the host population's abrupt extinction (Hilker 2010). Predator-prey and host-parasitoid models involving prey's or host's Allee effects have in fact been studied in both discrete and continuous time systems (e.g., Cushing 1994; Emmert & Allen 2004; Drew et al 2006; Jang & Diamond 2007; Berezovskaya et al. 2010; Kang & Armbruster 2011). In the context of epidemics, SI models incorporating disease-reduced infertility have been explored by various researchers (e.g., Diekmann & Kretzshmar 1991; Berezovskaya et al. 2004). Here, we introduce a generic SI model that incorporates the three features (I) the population's net reproduction rate incorporates an Allee effect; (II) infected individual experience reductions in their reproductive fitness; and (III) infectious individuals’ ability to compete for resources is diminished as a function of the disease and population size. The model introduced in this manuscript is used to address the following epidemiological questions: Under which conditions will the model lead to a disease-free state? Under what conditions will a disease drive a population to extinction? Under what conditions will this model support disease persistence? How do Allee thresholds, the reductions in reproductive ability of infected individuals, and disease-driven reductions in individuals’ competitiveness, change with population density?

The rest of this article is organized as follows: In Section 2, we introduce a simple SI model that incorporates Allee effects in its reproduction process, disease-induce reductions in fitness, and density-dependent disease-reduced competitive ability; In Section 3, we learn that the model can support a compact global attractor, and we also identify sufficient conditions that guarantee either disease-free dynamics or endemic persistence; Section 4 identifies the number of interior equilibrium and studies their stability and related bifurcation phenomena; Section 5 focuses on the study of the effect of changing parameter on the number of interior equilibrium and their stability with, particularly focus, on cases that lead to hysteresis; Section 6 summarizes the results in this manuscript and discusses some of the implications of the analytical results. The detailed proof of our theoretical results are provided in Appendix.

2. General SI model and its basic dynamical properties

We start from the assumptions that the population under consideration is facing a disease that can be captured with an SI (Susceptible-Infected) framework. This population is invaded by an infectious disease with the following characteristics: (a) the disease transmission is captured by the law of mass-action; (b) disease although not always fatal it is assumed to be always untreatable and so, excess deaths due to the disease are included; (c) the net reproduction rate is density-dependent regardless of epidemiological status, that is, it affects susceptible and infected individuals, an effect incorporated via a well-defined threshold (Allee effect threshold) that responds to population size; (d) infected individuals may experience reductions in reproduction ability; (e) infected individuals may experience reductions in competitive ability, which may also be altered by population density effects. The general SI model with an Allee effect, built in its net reproduction rate, is given by the following set of nonlinear differential equations:

$$\frac{dS}{dt}=f(S,I),$$ (1)

$$\frac{dI}{dt}=\beta SI-dI,$$ (2)

$$f(S,I)=\{\begin{array}{c}r(S+\rho I)(S+{\alpha }_{1}I-\theta )(I-S-{\alpha }_{2}I)-\beta SI\hfill \\ 0,\text{if}S=0\text{and}r\rho I({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)\le 0\hfill \end{array}\phantom{\}}.$$ (3)

S denotes the normalized susceptible population; I denotes the properly (see below) normalized infected population; all parameters are nonnegative; the parameter 0 ≤ ρ ≤ 1 describes the reduce reproductive ability of infected individuals (ρ = 0 means that infected individuals loose their reproducing ability while ρ = 1 indicates that they experience no reduction in reproductive fitness); the parameter 0 ≤ α_i ≤ 1, i = 1, 2 denote the competitive ability of infected individuals as a function of total population size; the parameter r denotes the maximum birth-rate of the species; d denotes the death rate of infected individuals, a parameter that includes additional disease-induced deaths; the parameter 0 < θ < 1 denotes the Allee threshold (normalized susceptible population); and β is the disease transmission rate.

The term r(S+ρI)(S+α₁I–θ)(1 – S – α₂I)in f(S, I) models the net reproduction rate of newborns, a term that accounts for reductions in fitness. Our model normalizes the susceptible population to be 1 in a disease-free environment and defines the infected population relative to this normalization. Thus, the carrying capacity of the whole population S + I is not defined by a constant, its size depends on the ability of individuals to use the resources (with the susceptible using a higher level of resources per individual than infected). The features outline above include factors not routinely considered in infectious-disease models. Allee effects are found in the epidemiological literature (see Thieme et al. 2009; Hilker et al. 2009) as well as in prey-predator interaction models (Berezovskaya et al. 2010). The model introduced here will be analyzed in the next sections. The analysis is used to discuss the implications of having incorporated fitness factors.

The study of the dynamics of System (1)-(2) requires the introduction of the following important sets:

$$\begin{array}{cc}X=\{(S,I)\in {\mathbb{R}}_{+}^2\},\hfill & X_x=\{(S,0)\in X\}\hfill \\ {\Omega }_{\theta }^{\alpha }=\{(S,I)\in X:0\le S+{\alpha }_{1}I\le \theta \},\hfill & {\Omega }_{\theta }=\{(S,I)\in X:0\le S+I\le \theta \},\hfill \\ {\Omega }_1=\{(S,I)\in X:0\le S+{\alpha }_{2}I\le 1\},\hfill & {\Omega }_1^S=\{(S,I)\in X:0\le S\le 1\},\hfill \end{array}$$

System (1)-(2) reduces to the following generic single species population model with an Allee effect in X_x:

$$\frac{dS}{dt}=rS(S-\theta )(1-S)$$ (4)

where the Allee threshold is denoted by θ. The population converges to 0 if initial conditions are below θ; converges to 1 if initial conditions are above θ. The first basic property of System (1)-(2) is stated in the following lemma:

Lemma 2.1. [Positively invariant sets] X, X_x, Ω_θ and ${\Omega }_1^S$ are positive invariant sets for System (1)-(2). Moreover, for any initial condition in X, we have that

$$\underset{t\to \infty }{\lim \sup }S\left(t\right)\le 1.$$

The detailed proof of Lemma 2.1 is provided in Appendix. Lemma 2.1 shows that Model (1)-(2)is well-defined biologically. The normalized susceptible population will not go beyond 1 but the infected (always assumed infectious) population does not have such property due its diminished disease-induced competitive ability. In fact, it may support populations above 1. Hence, the sets ${\Omega }_{\theta }^{\alpha }$ and Ω₁ may require additional conditions if we are to maintain positive invariance. The following lemma provides such conditions:

Lemma 2.2. [Positively invariant sets]Assume that ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ then both ${\Omega }_{\theta }^{\alpha }$ and Ω₁ are positively invariant. If in addition, 0 < ρ < 1 then for any initial condition in ${\Omega }_{\theta }^{\alpha }$ we have

$$\underset{t\to \infty }{\lim \sup }\max \{S\left(t\right),I\left(t\right)\}=0.$$

The detailed proof of Lemma 2.2 is provided in Appendix. The parameters α₁, α₂ model the competitive ability of infected individual when the total population is below or above the Allee threshold, respectively. The condition ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ corresponds to the situations when the carrying capacity of the total population S + α₂I is 1, that is, here we are referring to the situation when the overall competitive ability of infected individuals at high population densities times (that is, discounted) by the Allee threshold (α₂θ)is less than or equal to the overall competitive ability of infected individuals at low total population densities α₁. Lemma 2.2 suggests that ${\Omega }_{\theta }^{\alpha }$ is a reasonable approximation for the basin attraction of (0, 0). A direct corollary from Lemma 2.2 follows:

Corollary 2.1. [Boundedness] Assume that all parameters are strictly positive and ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ then for any initial condition in X, we have

$$\underset{t\to \infty }{\lim \sup }I\left(t\right)\le \frac{1}{{\alpha }_2}.$$

Proof. From the proof of Lemma 2.2, we see that for any initial condition with the property Z_α2 = S + α₂I > 1, we have

$$\frac{S}{\rho }+I>Z_{{\alpha }_2}>1\text{and}\frac{S}{\theta }+\frac{{\alpha }_{1}I}{\theta }>Z_{{\alpha }_2}.$$

Thus,

$$\frac{d{Z}_{{\alpha }_2}}{dt}<r\rho (\frac{S}{\rho }+1)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)<r\rho \theta (Z_{{\alpha }_2}-1)(1-Z_{{\alpha }_2})<0.$$

Therefore,

$$\underset{t\to \infty }{\lim \sup }{Z}_{{\alpha }_2}\left(t\right)\le 1\Rightarrow \underset{t\to \infty }{\lim \sup }I\left(t\right)\le \frac{1}{{\alpha }_2}.$$

Corollary 2.1 implies that the carrying capacity of the infected population is $\frac{1}{{\alpha }_2}$ whenever the inequalities ${\alpha }_2\le \frac{{\alpha }_1}{\theta },\rho >0$ hold. Combining this result with the results in Lemma 2.1, we conclude that System (1)-(2) has a compact global attractor A = {(S, I) ∈ X : S + α₂I ≤ 1}. An estimate of a compact global attractor for System (1)-(2) has been found (see Theorem 3.1) whenever the inequality ${\alpha }_2>\frac{{\alpha }_1}{\theta }$ holds.

3. Sufficient conditions for a disease-free or a disease-persistence system

Populations must be bounded. Thus, we first show that Model (1)-(2) has a compact global attractor:

Theorem 3.1. [Compact attractor]Assume that all parameters are strictly positive. Then System (1)-(2) has a compact global attractor. More precisely, if ${\alpha }_2>\frac{{\alpha }_1}{\theta }$ then the compact set $[0,1]\times [0,\frac{M+d}{d}]$ attracts all points in X where

$$M=\underset{0\le S\le 1,0\le I\le \frac{1}{{\alpha }_2}}{\max }\left\{r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)\right\}.$$

While if ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$, then the compact set $[0,1]\times [0,\frac{1}{{\alpha }_2}]$ attracts all points in X.

The detailed proof of Theorem 3.1 is provided in Appendix. Theorem 3.1 shows that System (1)-(2) is bounded whenever the parameters are strictly positive, a property that allows the identification of sufficient conditions guaranteeing a stable disease-free state and disease persistence (see Theorem 3.2 and Theorem 3.3). If some of the parameters in System (1)-(2) are zero then the statement in Theorem 3.1 does not hold. Establishing boundedness of the System (1)-(2) in this last case is still possible under a set of weakened assumptions (see Theorem 5.1 for results in some extreme case).

3.1. Sufficient conditions for a disease-free system

Theorem 3.2. [Sufficient conditions for a disease-free system] System (1)-(2) has disease-free dynamics, that is,

$$\underset{r\to \infty }{\lim \sup }I\left(t\right)=0,$$

if

1. β ≤ d or if

2. All parameters are strictly positive and

   $$1\le \frac{\beta \theta }{d}<\frac{\theta ({\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho })}{{\alpha }_1+{\alpha }_2\theta }andC=\frac{({\alpha }_1+{\alpha }_2+\rho ){\left(\frac{d}{\beta }\right)}^2+(\frac{d}{r}+\rho \theta )}{(\theta \rho +\rho +{\alpha }_1+{\alpha }_2\theta )\frac{d}{\beta }}>1.$$ (5)

   System (1)-(2) has only two attractors (0,0) and (1,0) whenever β ≤ d, with the equilibrium (0,0) globally stable whenever Condition (5) is satisfied.

The detailed proof of Theorem 3.2 is provided in Appendix. The effective reproductive ratio of an infectious disease (here referred to as just R), in the context of this manuscript is defined as the number of secondary infections produced by a single infected/infectious individual over his/her entire infectious period when the susceptible population is at a fixed demographic equilibrium (level S*). The case when S* equals the total population corresponds, to the situation when R equals R₀ (the basic reproduction number or ratio). For System (1)-(2), R is defined by the expression

$$R=\frac{\beta S^{\ast }}{d}$$ (6)

The numerator is the number of secondary infections βS* per unit of time while the denominator denotes the inverse of the average infectious period, that is, the inverse of the disease-enhanced per-capita mortality rate, d. Disease-free populations eventually settle to their local carrying capacity (here more or less equivalent to a demographic equilibrium) provided that, the initial population size is not below the Allee threshold (i.e., S(0) ≥ θ). Therefore, (6) gives the basic reproductive ratio, at either the demographic equilibrium S* = θ or S* = 1. Therefore, $R_0^{\theta }=\frac{\beta \theta }{d}$ denotes the low reproductive ratio at the Allee threshold while $R_0=\frac{\beta }{d}$ denotes the basic reproductive number at the locally asymptotically stable equilibrium 1.

R₀ (a dimensionless quantity) denotes the average number of secondary infections generated by a “typical” infective individual when introduced in a population of susceptible individuals at a demographic steady state (typically S* = 1). R₀ is intimately connected to bifurcation phenomena and, it is therefore, the bifurcation (biological) parameter of choice. Traditional epidemiological models namely, those of the SI, SIS, and SIR type, and a number generalizations (e.g., Kermack & McKendrick 1927; Lajmanovich & Yorke 1976; Hethcote & van Ark 1987), tend to be completely characterized by whether R₀ > 1 or R₀ < 1, generating the standard epidemic pattern (robust disease dynamics, see Brauer & Castillo-Chavez 2012). That is, a transcritical ‘forward’ bifurcation is the natural outcome as R₀ crosses 1. That is, either infected individuals will not successfully in invading a large susceptible population (R₀ < 1) and the disease will die out or, if R₀ > 1, a small number of infected individuals will always (deterministic world) succeed in invading a large susceptible population. Theorem 3.2 shows that System (1)-(2) does not support such transcritical bifurcation since, in fact, there may not be an outbreak when R₀ > 1. According to Theorem 3.2,when $R_0^{\theta }>1$, that is, when $R_0>\frac{1}{\theta }$ with the parameters exceeding a critical value C > 1 (C determined by the Allee threshold θ, the role of reduced reproduction ρ and the reductions on the competitive ability α_i, i = 1, 2 of infected individuals), would mean, in this case, that the disease will not become established. The condition $\frac{\beta }{d}>\theta$, i.e., $R_0^{\theta }>1$, $R_0>\frac{1}{\theta }$ indicates that the disease free equilibrium (1,0) is a saddle and (θ, 0) is a source. Hence, if r = 0.5, ρ = 0.1, θ = 0.2, α₁ = 0.1, α₂ = 1, β = 1, and d = 0.15, we have that

$$1\le R_0^{\theta }=\frac{4}{3}<\frac{\theta ({\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho })}{{\alpha }_1+{\alpha }_2\theta }=1.4\text{and}C=\frac{({\alpha }_1+{\alpha }_2+\rho ){\left(\frac{d}{\beta }\right)}^2+(\frac{d}{r}+\rho \theta )}{(\theta \rho +\rho +{\alpha }_1+{\alpha }_2\theta )\frac{d}{\beta }}=5.507>1.$$

Thus according to Theorem 3.2, System (1)-(2) is globally stable at (0, 0). In this case, the disease will drive the whole population to extinction. We observe that C as defined in Condition (5)must always be greater than 1 if d > r. A plausible explanation for this phenomena, is that even though the basic reproduction number R₀ is large, the maximum birth rate of the species r, is too small to sustain a susceptible population, in a system, with Allee effects. Thus, the susceptible population by decreasing to zero fast enough, guarantees that the infected population becomes eventually extinct (for a ‘paradoxical’ result see Berezovskaya et al. 2004)

Here, the reproductive ratio associated with the Allee threshold θ will be denoted by $R_0^{\theta }$. We will use the dimensionless quantity $R_0^{\theta }$ to classify the model dynamics in the next sections. System (1)-(2) does support complex dynamics, including ‘hysteresis’ ( multiple endemic states when $\theta <R_0^{\theta }<1$). The SI model can indeed support a stable disease-free equilibrium and two endemic locally stable equilibria, in certain parameter ranges, with the disease being able to re-establish itself with the aid of two “selective forces”, the Allee effect and disease-induce reductions in individuals’ competitive ability (also a function of total population size, see Theorem 4.1 and the bifurcation diagrams provided in Section 5).

3.2. Sufficient conditions for the persistent endemic

In this subsection, we identify sufficient conditions for disease persistent (endemicity) in System (1)-(2). We start with the following proposition:

Proposition 3.1. [Positively invariant sets] Assume that all parameters are strictly positive and ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$. Then if there exists some α such that the following inequalities hold

$$1\ge S\left(0\right)+{\alpha }_{2}I\left(0\right)>0and1\ge Z_{{\alpha }_1}\left(0\right)=S\left(0\right)+{\alpha }_{1}I\left(0\right)=\alpha >\theta$$

and

$$r\rho (\alpha -\theta )\left(1-\alpha (1+\mid 1-\frac{{\alpha }_2}{{\alpha }_1}\mid )\right)>\frac{\beta }{{\alpha }_1}+(d-\beta ).$$

Then the set

$${\Omega }_{\alpha }=\{(S,I)\in X:\alpha \le S+{\alpha }_{1}I\le 1andS+{\alpha }_{2}I\le 1\}$$

is positively invariant.

The detailed proof of Proposition 3.1 is provided in the Appendix. A direct application of Proposition 3.1 and the average Lyapunov Theorem (Hutson 1984) leads to the following theorem on the persistence of the disease:

Theorem 3.3. [Sufficient condition for endemicity] Assume that all conditions in Proposition 3.1 hold. If, in addition, $\frac{d}{\beta }<\alpha$, then there exists some ε > 0, such that for any initial condition taken in Ω_α, we have

$$\underset{t\to \infty }{\lim \inf }\min \{S\left(t\right),I\left(t\right)\}\ge ∊.$$

See the detailed proof of Theorem 3.3 in Appendix. Theorem 3.3 gives an approximation of the basins of attractions for System (1)-(2) under the conditions of the theorem. It further suggests that disease persistence requires two additional conditions: (A) The total population should be above the Allee threshold; and (B) a combination of large values of r and ρ combined with relative small values for $\frac{{\alpha }_2}{{\alpha }_1}$, $\frac{\beta }{{\alpha }_1}$, and $\frac{d}{\beta }$.

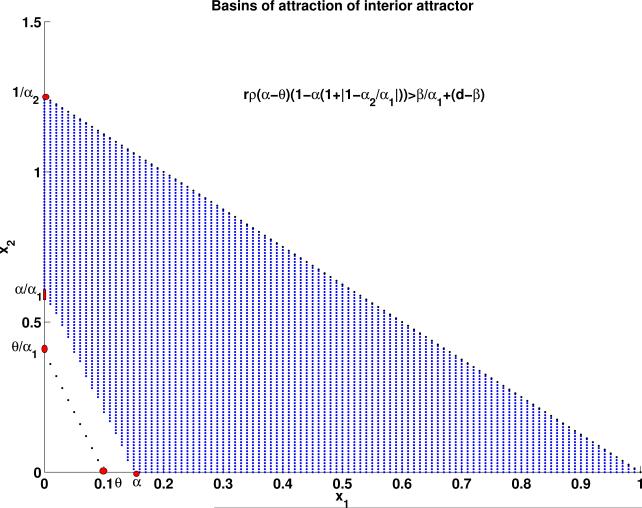
If the requirements of Theorem 3.3 are met then the basins of attraction of the interior attractor of System (1)-(2) can be approximated by Ω_α, the blue region shown in Figure 1.

Figure 1.

The blue region corresponds to the basin of attraction of the interior attractor of System (1)-(2)providedthe conditions of Theorem 3.3 are met. The black curves are S + α₁I = θ and S + α₂I = 1.

4. Multiple interior equilibria and possible bifurcations

The emphasis in this section is on the qualitative study of the solutions of System (1)-(2). From the proof of Theorem 3.2, we learned that interior equilibria (S*, I*) of System (1)-(2) must satisfy the following conditions:

$$S^{\ast }=\frac{d}{\beta }\text{and}{I}^{\ast }>0$$

where

$$f(S^{\ast },I^{\ast })=f(\frac{d}{\beta },I^{\ast })=r(\frac{d}{\beta }+\rho I^{\ast })(\frac{d}{\beta }+{\alpha }_1{I}^{\ast }-\theta )\left(1-\frac{d}{\beta }-{\alpha }_2{I}^{\ast }\right)-d{I}^{\ast }=0.$$

Thus, the number of positive roots of $f(\frac{d}{\beta },I^{\ast })=0$ determines the number of interior equilibrium of System (1)-(2). In order to identify the number of interior equilibria, we require the partial derivative of f(S, I) with respect to I at $S=\frac{d}{\beta }$, which is given by

$${\frac{\partial f(S,I)}{\partial I}\mid }_{S=\frac{d}{\beta }}=a{I}^2+bI+c$$ (7)

where $a=-3r\rho {\alpha }_1{\alpha }_2,b=2r\rho ({\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho })(\frac{{\alpha }_1+{\alpha }_2\theta }{{\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho }}-\frac{d}{\beta })$ and

$$c=-\frac{({\alpha }_1+{\alpha }_2+\rho )r{d}^2-(\theta \rho +\rho +{\alpha }_1+{\alpha }_2\theta )r\beta d+(d+r\rho \theta ){\beta }^2}{{\beta }^2}.$$

The equation ${\frac{\partial f(S,I)}{\partial I}\mid }_{S=\frac{d}{\beta }}=0$ has two real roots v_i, i = 1, 2 given by

$$v_1=\frac{-b-\sqrt{b^2-4ac}}{2a},v_2=\frac{-b+\sqrt{b^2-4ac}}{2a}.$$

where necessarily, we must have that b² > 4ac. The main features of the dynamics of System (1)-(2) can be summarized in the following results:

Theorem 4.1. [Dynamical properties of (1)-(2)] Under the assumption that all parameters of System (1)-(2) are strictly positive, that the system is positively invariant and bounded in X, and that it supports three boundary equilibria: (0, 0), (θ, 0), and (1, 0), with (0, 0) always locally asymptotically stable, it follows that: (θ, 0) is a saddle if $R_0^{\theta }<1$ and a source if $R_0^{\theta }>1$; (1, 0) is locally asymptotically stable if β ≤ d (i.e., R₀ < 1) and a saddle if β > d (i.e., R₀ > 1). Moreover, System (1)-(2) may have none, one, two or three interior equilibria, depending on parameter values. Sufficient conditions for the existence ofequilibria are summarized below under the assumption that all parameters are strictly positive.

• No interior equilibrium: If β ≤ d or if Condition (5) holds.

• One interior equilibrium: If $1<R_0^{\theta }<\max \{\frac{1}{\theta },\frac{\theta ({\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho })}{{\alpha }_1+{\alpha }_2\theta }\}$ and C < 1 with C defined in Condition (5).

• Two interior equilibria: If $R_0^{\theta }>1$ and $f(\frac{d}{\beta },v_2)>0$

• Three interior equilibria: If $R_0^{\theta }<1$, $f(\frac{d}{\beta },v_1)<0$ and $f(\frac{d}{\beta },v_2)>0$.

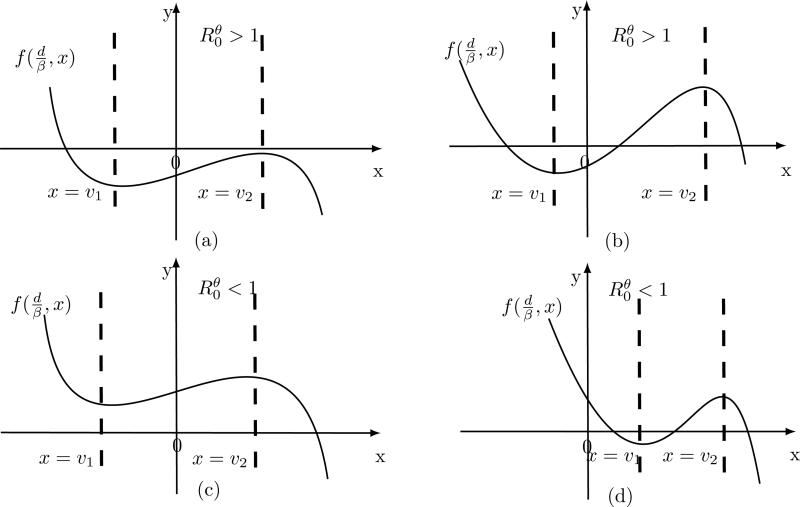
The schematic nullclines of System (1)-(2) are shown in Figure 2. Since a bifurcation in general, takes place at a set of parameter values where an equilibrium or fixed point of the system changes its stability and/or appears/disappears then from Theorem 4.1 we conclude that:

1. If $R_0^{\theta }>1(\frac{d}{\beta }>\theta )$ then System (1)-(2) has either none or two interior equilibrium, a saddle node and Hopf bifurcations are possible.

2. If $R_0^{\theta }<1(\frac{d}{\beta }<\theta )$ then System (1)-(2) has either one or three interior equilibria where backward and cusp bifurcations (hysteresis) can occur.

Figure 2.

Schematic nullclines of System (1)-(2)regarding thenumberof interior equilibria when all parameters are strictly positive. The positive x-intercepts represent interior equilibria of (1)-(2), that is, the positive roots of $f(\frac{d}{\beta },I)=0$

We are ready to settle the question of stability of interior equilibria:

Theorem 4.2. [Stability of interior equilibrium] We start by assuming that all parameters are strictly positive and let $(\frac{d}{\beta },I^{\ast })$ denote an interior equilibrium of system (1)-(2). If

$$\frac{({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )-\frac{\beta }{r}}{2({\alpha }_1+{\alpha }_2+\rho )}<\frac{d}{\beta }<\frac{1+\theta -\sqrt{{(\theta -1∕2)}^2+3∕4}}{3}or\max \{\frac{({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )-\frac{\beta }{r}}{2({\alpha }_1+{\alpha }_2+\rho )},\frac{1+\theta +\sqrt{{(\theta -1∕2)}^2+3∕4}}{3}\}<\frac{d}{\beta },$$ (8)

then $(\frac{d}{\beta },I^{\ast })$ is a locally asymptotically stable interior equilibrium in the following three cases:

• Case I: $(\frac{d}{\beta },I^{\ast })$ is the only interior equilibrium of System (1)-(2).

• Case II: $(\frac{d}{\beta },I^{\ast })$ is the largest interior equilibrium (that is, the second component of the equilibrium is the largest) of System (1)-(2) (the case when it has two interior equilibrium).

• Case III: $(\frac{d}{\beta },I^{\ast })$ is the largest or smallest interior equilibrium provided that System (1)-(2) has three interior equilibrium (we mean that the second component ofthe equilibrium is the largest or the smallest).

While $(\frac{d}{\beta },I^{\ast })$ is a saddle node in the following two cases:

• Case IV: $(\frac{d}{\beta },I^{\ast })$ is the smaller interior equilibrium when System (1)-(2) has two interior equilibrium, i.e., the second component of the equilibrium is smaller.

• Case V: $(\frac{d}{\beta },I^{\ast })$ is the middle interior equilibrium when System (1)-(2) has three interior equilibrium (the second component of the equilibrium is in the ‘middle’).

See Appendix for the detailed proof of Theorem 4.1 and Theorem 4.2. The results in these two theorems provide a sufficient condition so that System (1)-(2) can support two locally asymptotically stable interior equilibria. For instance, direct computations show that System (1)-(2) has three equilibria: (0.85, 0.82), (0.85, 1.645) and (0.85, 3.42) when

$$r=2.35;\rho =0.85;{\alpha }_1=1;{\alpha }_2=0.02;\theta =0.235;d=0.85;\beta =1.$$

Since

$$\max \{\frac{({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )-\frac{\beta }{r}}{2({\alpha }_1+{\alpha }_2+\rho )},\frac{1+\sqrt{{(\theta -1∕2)}^2+3∕4}}{3}\}=\max \{0.435,0.635\}<\frac{d}{\beta }=0.85,$$

thus (0.85, 0.82) and (0.85, 3.42) are locally asymptotically stable. Further, the results in Theorem 4.2 suggest that the interior equilibrium in Case I, II, III may go through a Hopf-bifurcation as parameters vary.

4.1. Hysteresis and possible bifurcations

Hysteresis is supported by System (1)-(2), a result that is evident from the schematic nullclines of System (1)-(2) (see Figure 2-3). A summary of the number of interior equilibria in different cases is collected in Table 1 as a function of values of $R_0^{\theta }$.

Figure 3.

Schematic nullclines for System (1)-(2) on the number of interior equilibria when one of ρ, α₁, α₂ is zero. The intercepts between the parabola $y=r(\frac{d}{\beta }+\rho x)(\frac{d}{\beta }+{\alpha }_{1}x-\theta )(1-\frac{d}{\beta }-{\alpha }_{2}x)$ and the straight line y = dx in the first quadrant represent interior equilibria of (1)-(2), i.e., the positive roots of $f(\frac{d}{\beta },I)=0$.

Table 1.

Summary of the number of interior equilibrium for System (1)-(2) when one or two or all of ρ, α₁, α₂ are zero.

Values of ρ, α1, α2	$R_0^{\theta }>1$	$\theta <R_0^{\theta }<1$	$R_0^{\theta }<\theta$
All three parameters are strictly positive
ρ > 0, α1 > 0, α2 > 0	0 or 2	1 or 3	0
One parameter is zero
ρ = 0, α1 > 0, α2 > 0	0 or 2	1	0
ρ > 0, α1 = 0, α2 > 0	1	1	0
ρ > 0, α1 > 0, α2 = 0	1	0	0
Two parameters are zero
ρ = 0, α1 = 0, α2 > 0	1 if $R_0^{\theta }>\frac{r\theta {\alpha }_2}{\rho \theta {\alpha }_2-\beta }$ but unstable	1	0
ρ = 0, α1 > 0, α2 = 0	1 if $R_0^{\theta }>\frac{r\theta {\alpha }_1}{r{\alpha }_1-\beta }$ but unstable	1	0
ρ > 0, α1 = 0, α2 = 0	1 if $R_0^{\theta }<1+\theta -\frac{rd\rho +{\beta }^2}{r\rho \beta }$ but unstable	1 if $R_0^{\theta }>1+\theta -\frac{rd\rho +{\beta }^2}{r\rho \beta }$	0
Three parameters are zero
ρ = 0, α1 = 0, α2 = 0	0	1	0

Hysteresis in the context of simple disease models has important qualitative implications. Hysteresis allows the possibility of multiple steady states with fixed parameters. Under hysteresis, small changes in model parameters can generate large changes in equilibrium levels (Hadeler & Van Den Driessche 1997; Dushoff et al 1998; Feng et al 2000; Castillo-Chavez & Song 2003; Song et al 2006). The use of Central Manifold Theory to identify the direction of the bifurcation can be found in Castillo-Chavez and Song (Theorem 4.1 & 4.2 and their Corollaries) in 2004 with a detailed account to applications to epidemiological models in Kribs-Zaleta (2001).

Hysteresis (often referred as (or including) backwards bifurcations) in disease models may be the result of asymmetrical transmission rates between groups (Castillo-Chavez, et al. 1989; Huang et al. 1990; Huang et al. 1992) or the impact of behavioral responses to disease levels (Hadeler & Castillo-Chavez 1995; Hadeler & Van Den Driessche 1998; Fenichel et al 2011). The increasing relevance of hysteresis in the study of disease dynamics, broadly understood to include the dynamics of socially-driven processes, where the role of R₀ is less prominent, can be seen from the growing number of results (see list below and references within these articles).

1. Behavior in individuals during or after recovery from a disease (Hethcote & Yorke 1984; Scalia-Tomba 1991; Dushoff et al 1998; Del Valle et al 2005).

2. Adaptive behavior of individuals to disease (Hadeler & Castillo-Chavez 1995; Huang et al 2002; Greenhalgh & Griffiths 2009; Fenichel et al 2011).

3. The effect of education and vaccination (Gupta et al 1991; Hadeler & Müfiller 1992; Hadeler & Castillo-Chavez 1995; Kribs-Zaleta et al. 2000; Brauer 2004).

4. Nonconcave transmission functions or a non-constant contact rates (Anderson & May 1978; Hadeler & K. Dietz 1983; van den Driessche & Watmough 2000).

5. Reduced fertility of infected individuals (Anderson & May 1978; Diekmann & Kretzschmar 1991).

6. Exogenous reinfection in tuberculosis (Feng et al 2000; Castillo-Chavez et al 2002; Song 2002; Wang 2005)

7. Adaptive behavior in contagion models for the dynamics of social processes (Gonzalez et al 2003; Song et al 2006; Castillo-Chavez & Song 2003; Sanchez et al 2007)

Model (1)-(2) exhibits hysteresis when $\theta <R_0^{\theta }<1$, a dimensionless ratio connected to competing fitness factors among infected population from reductions in reproductive ability or reductions in competitive ability (a function of total population density). System (1)-(2) can go through a saddle node bifurcation, Hopf bifurcation, and a catastrophic events, which occur when a stable limit cycles merges with the adjacent saddle, leading to the annihilation of both susceptible and infected population.

The saddle node bifurcation curves are embedded in the following two curves:

$$f(\frac{d}{\beta },v_1)=0\text{or}f(\frac{d}{\beta },v_2)=0$$

when v_i, i = 1, 2 are positive roots of

$${\frac{\partial f(S,I)}{\partial I}\mid }_{S=\frac{d}{\beta },I}=0.$$

Hopf bifurcation: stability of the bifurcating periodic orbits. A formula for the stability of the periodic orbits generated via a Hopf bifurcation is available for the case when the Jacobian matrix has the form $\left(\begin{array}{cc}\hfill 0\hfill & \hfill -R_0^{\theta }\hfill \\ \hfill R_0^{\theta }\hfill & \hfill 0\hfill \end{array}\right)$ with $R_0^{\theta }>0$. Through the change of variables

$$u=\frac{S}{\theta },v=\frac{I}{\theta },\tau =\frac{t}{d},$$

System (1)-(2)is rewritten when S > 0 as follows:

$$\frac{du}{d\tau }=F(u,v)=\gamma (u+\rho v)(u+{\alpha }_{1}v-1)\left(\frac{1}{\theta }-v-{\alpha }_{2}v\right)-R_0^{\theta }uv$$ (9)

$$\frac{dv}{d\tau }=G(u,v)=v(R_0^{\theta }u-1)$$ (10)

where $R_0^{\theta }=\frac{\beta \theta }{d}$ and $\gamma =\frac{r{\theta }^2}{d}$. The Jacobian matrix of System (9)-(10) at the interior equilibrium $(\frac{1}{R_0^{\theta }},v^{\ast })$ has the form $\left(\begin{array}{cc}\hfill F_u(\frac{1}{R_0^{\theta }},v^{\ast })\hfill & \hfill F_v(\frac{1}{R_0^{\theta }},v^{\ast })\hfill \\ \hfill R_0^{\theta },v^{\ast }\hfill & \hfill 0\hfill \end{array}\right)$. By properly choosing the values of γ, θ, ρ and α_i, i = 1, 2, we are able to make v* = 1, $F_u(\frac{1}{R_0^{\theta }},v^{\ast })=0$ and $F_v(\frac{1}{R_0^{\theta }},v^{\ast })=-R_0^{\theta }$. For example, letting

$$\gamma =\frac{\theta {\left(R_0^{\theta }\right)}^3}{(1+\rho R_0^{\theta })(R_0^{\theta }-{\alpha }_1{R}_0^{\theta }-1)(\theta +{\alpha }_2\theta R_0^{\theta }-R_0^{\theta })}$$

and

$$\theta =\frac{R_0^{\theta }(1+\rho {\left(R_0^{\theta }\right)}^2-\rho {\alpha }_1{\left(R_0^{\theta }\right)}^2)}{{\left(R_0^{\theta }\right)}^3\rho {\alpha }_2(1-{\alpha }_1)+R_0^{\theta }(\rho +{\alpha }_1+{\alpha }_2-1)+2},$$

we see from the form of the matrix that there is a Hopf bifurcation at $u=\frac{1}{R_0^{\theta }}$, v = 1. Using the Theorem 3.4.2 and the formula 3.4.11 (Guckenheimer & Holmes 1983), we conclude that the stability of the bifurcating periodic orbit is determined by the sign of the number h where

$$h=R_0^{\theta }(F_{uuu}+F_{vvv}+G_{uuu}+G_{vvv})+F_{uv}(F_{uu}+F_{vv})-G_{uv}(G_{uu}+G_{vv})-F_{uu}{F}_{uu}+F_{vv}{G}_{vv},$$

which can be given in the simplified form

$$h={R_0^{\theta }(F_{uuu}+F_{uvv})+F_{uv}(F_{uu}+F_{vv})\mid }_{u=\frac{1}{R_0^{\theta }},v=1}.$$

If h < 0 the bifurcating periodic orbits are asymptotically stable, a supercritical bifurcation, that is, the periodic orbits occur for those bifurcation parameters (close to the bifurcation value) for which the equilibrium is unstable. If h > 0 the bifurcating orbits are unstable, a subcritical bifurcation, that is, the (unstable) periodic orbits occur for those bifurcation parameters (close to the bifurcation value) for which the equilibrium is stable. We give two examples of expression for h:

1. When α₁ = α₂ = 1, the Hopf-bifurcation origination from System (9)-(10) at $(\frac{1}{R_0^{\theta }},1)$ is supercritical if h < 0 and subcritical if h > 0 where

   $$h=-\frac{2{\left(R_0^{\theta }\right)}^3(2\rho {\left(R_0^{\theta }\right)}^3({\rho }^2+\rho -2)+{\left(R_0^{\theta }\right)}^2(3{\rho }^3+4{\rho }^2-9\rho -4)+R_0^{\theta }(2{\rho }^2-4\rho +6)-4)}{{(2-R_0^{\theta }+\rho R_0^{\theta })}^2{(I+\rho R_0^{\theta })}^2}$$
2. When ρ = α₁ = 0 and α₂ = 1, the Hopf-bifurcation of System (9)-(10) at $(\frac{1}{R_0},1)$ is supercritical if h < 0 and subcritical if h > 0 where

   $$h=-\frac{{\left(R_0^{\theta }\right)}^3(6{\left(R_0^{\theta }\right)}^3-13{\left(R_0^{\theta }\right)}^3+8R_0^{\theta }-2)}{2{(1-R_0^{\theta })}^4}.$$

5. Disease dynamic patterns

We use numerically-generated bifurcation diagrams to investigate how changes in parameter values affect the patterns generated by System (1)-(2). We focus on the effect of the relative competitive ability (i.e., α_i, i = 1, 2) of the sub-population of infected individuals on the dynamics of System (1)-(2). We proceed by fixing the values of r, θ, β, d, and ρ and proceed to investigate the role of the remaining parameter with the aid of specific sub-models. Specifically, we scale away the parameter β by letting t → βt, $r\to \frac{r}{\beta }$ and $d\to \frac{d}{\beta }$. Thus, increasing the values of β corresponds to decreasing in the values of r and d. For convenience, we fix β = 1 in the bifurcation diagrams highlighted.

The values of α_i, i = 1, 2 describe the fitness (relative competitive ability of infected with respect to susceptible individuals) of the infected sub-population at low and high population levels. The set of factors considered in Model (1)-(2) include the maximum reproduction rate of infected individuals over their average infectious period, i.e., r/β (we use r in our bifurcation diagrams), the relative reproductive success of infected individuals (another measure of I-class’ fitness), ρ; the value of the Allee threshold θ, and the death rate of I-class, d, which includes disease-induced deaths. We explore how changes in α_i, i = 1, 2 affect the dynamics of System (1)-(2) using relevant one- and two-dimensional bifurcation diagrams, constructed under two scenarios: $R_0^{\theta }>1$ and $R_0^{\theta }<1$. The two-dimensional bifurcation diagrams in α₁ and α₂ space, provide information on the number of interior equilibria as α_i, i = 1, 2 are varied. One-dimensional bifurcation diagrams involving either α₁ or α₂ allow us to investigate the stability of these equilibria at different levels of the infected sub-population. For comparison purposes, we have chosen four sets of factors, which are typical and therefore manage to capture interesting dynamical outcomes.

• Set 1: r = 3.5, θ = 0.12, β = 0.2, β =1, d = 0.15 with $R_0^{\theta }=\frac{\beta \theta }{d}<1$.

• Set 2: r = 3.5, θ = 0.18, ρ = 0.2, β = 1, d = 0.15 with $R_0^{\theta }=\frac{\beta \theta }{d}<1$.

• Set 3: r = 2.35, θ = 0.2, ρ = 0.8, β = 1, d = 0.85 with $R_0^{\theta }=\frac{\beta \theta }{d}<1$.

• Set 4: r = 2.35, θ = 0.6, ρ = 0.8, β = 1, d = 0.25 with $R_0^{\theta }=\frac{\beta \theta }{d}>1$.

From Figure 4-5, we see that hysteresis occurs in sets linked to $R_0^{\theta }<1$ (Set 1 & 3). Saddle node bifurcation occurs in sets linked to $R_0^{\theta }>1$ (Set 2 & 4). The differential outcome in Set 1 and Set 3 come from the fact that Set 3 support more stable dynamics than Set 1; the smallest interior equilibrium is locally asymptotically stable, the result of larger value of ρ and d and lower value of r (see Theorem 4.2). The differential outcome in Set 2 and Set 4 come from the fact that Set 4 generates two disjoined saddle node bifurcations as the values of α_i, i = 1, 2 are varied (see Figure 5(d)-5(f)). These last outcomes may be the result of large value of ρ and the large difference in the values of d and θ. We summarize the effects of α_i, i = 1, 2 in Table 2 based on the four settings described above.

Figure 4.

First row includes two dimensional bifurcation diagrams (α₁ and α₂) for System (1)-(2) highlighting the number of interior equilibria. The black region represents no interior equilibrium; the white region corresponds to the case of one interior equilibrium; the blue region corresponds to the case of two interior equilibria; and the red region corresponds to the case of three interior equilibria. The second and third rows are bifurcation diagrams for the System (1)-(2)focusing on the number of interior equilibria and their stability. The red color represents source interior equilibria; the blue color represents sink interior equilibrium; the green color represents saddle interior equilibrium.

Figure 5.

First row corresponds the two dimensional bifurcation diagrams over α₁ and α₂ for System (1)-(2)focusing on the number of interior equilibria: The black region represents no interior equilibrium; the white region one interior equilibrium; blue region two interior equilibria; and the red region three interior equilibria. The second and third rows correspond to bifurcation diagrams for System (1)-(2) that highight the number of interior equilibria and their stability. The red color represents that source interior equilibrium; the blue color represents sink interior equilibrium; the green color represents saddle interior equilibrium.

Table 2.

Effects of α₁ and α₂ on dynamics.

Values of R 0		Effects when $R_0^{\theta }<1$	Effects when $R_0^{\theta }>1$
Intensity of values
Small values of	α 1	Either can keep the infected population in a low level or Destabilize the system then drive the whole population extinct through a catastrophic event.	Either exhibits disease-driven extinction (Theorem 3.2, condition C) or disease persists with large infected population (this may be caused by switching Allee thresholds).
	α 2	Disease persists with large infected population.	Disease persists with large infected population.
Intermedium values of	α 1	Hysteresis occurs	Either disease persists or exhibits disease-driven extinction.
	α 2	Hysteresis occurs	Either disease persists or exhibits disease-driven extinction.
Large values of	α 1	The infected population persists and is relatively large.	Disease persists.
	α 2	Either can keep the infected population in a low level or Destabilize the system then drive the whole population extinct through a catastrophic event.	Either exhibits disease-driven extinction (Theorem 3.2, condition C) or disease persists.

5.1. Four examples

System (1)-(2) has a total of 6 parameters after we scale away β. Hence, it is difficult to evaluate how each scenario affects the dynamics. Thus, 4 different cases are selected and the focus is directed to the study of the effect of ρ, d, r, and θ on the dynamics given that α_i, i = 1, 2 are kept fixed.

1. Model I: This model assumes that the infected sub-population does not have ability to reproduce, that is, ρ = 0; it also lacks the ability to compete when the total population density is low, that is, α₁ =0 but infected individuals are as competitive as susceptible provided that total population is above the Allee threshold, that is, α₂ = 1.

2. Model II: This model assumes that infected individuals have reduced reproductive ability, that is, 0 < ρ < 1; further, it assumes that their ability to compete for resource is equivalent to their reproduction ability, that is, α₁ = α₂ = ρ.

3. Model III: This model assumes that the infected sub-population has reduced reproductive ability, that is, 0 < ρ < 1; it also assumes that its competitive and reproductive ability are equivalent when the total population density is low, that is, α₁ = ρ and that, further, it has the same competitive ability as that of the members of the susceptible sub-population but just when the total population is above the Allee threshold, that is, α₂ = 1.

4. Model IV: This model assumes that the infected sub-population has reduced reproductive ability, that is, 0 < ρ < 1 and further, that it has the same competitive ability as that of the members of the susceptible sub-population, that is, α₁ = α₂ = 1.

We summarize the basic dynamic features associated with these special or extreme cases of the main model in Table 3 using the theoretical results established in previous sections.

Table 3.

Summary of the basic dynamics of four models.

Values of ρ, α1, α2	The global attractor	Number of interior equilibria
		$R_0^{\theta }>1$	$\theta <R_0^{\theta }<1$
ρ = 0, α1 = 0, α2 = 1	See Theorem 5.1	1 if $\frac{d}{\beta }+\frac{\beta }{r}<\theta$ but ustable	1
0 < α1 = α2 = ρ ≤ 1	$[0,1]\times [0,\frac{1}{\rho }]$	0 or 2	1 or 3
0 < α1 = ρ ≤ 1, α2 = 1	[0, 1] × [0, 1] if ρ ≥ θ	0 or 2	1 or 3
0 < ρ < 1, α1 = α2 = 1	[0, 1] × [0, 1]	0 or 2	1 or 3

Model I is an extreme cases of System (1)-(2) and the results stated in Theorem 3.1 do not apply. The basic dynamical outcomes associated with Model I are summarized as follows:

Theorem 5.1. [Dynamical properties of Model I] Assume that ρ = α₁ = 0 and α₂ = 1. Let $R_0^{\theta }=\frac{\theta \beta }{d}$.

• If β < d, then System (1)-(2) has $(0,0)\cup (1,0)$ as its global attractor.

• If $d>\frac{{\theta }^2}{4}$, then $\lim {\sup }_{t\to \infty }S\left(t\right)+I\left(t\right)<\frac{r(1+\frac{d}{r}-\theta )}{d-\frac{{\theta }^2}{4}}$.

• If d > rθ, then $\lim {\sup }_{t\to \infty }S\left(t\right)+I\left(t\right)<\frac{r(1+\frac{d}{r}-\theta )}{d-r^{\theta }}$.

• System (1)-(2) has at most one interior equilibrium $(S^{\ast },I^{\ast })=(\frac{d}{\beta },\frac{(\frac{1}{R_0^{\theta }}-1)(1-\frac{d}{\beta })}{\frac{1}{R_0^{\theta }}+\frac{\beta }{r^{\theta }}-1})$ in X, where I* < 1 if

  $$1<R_0^{\theta }<\mathrm{mim}\{\frac{1}{\theta },\frac{r\theta }{r\theta -\beta }\}$$

  and I* > 1 if

  $$\frac{r\theta }{r\theta -\beta }<R_0^{\theta }<\min \{1,\frac{rd\theta }{{\beta }^2-rd\theta }\}.$$

  In addition, (S*, I*) is a saddle in the case that $R_0^{\theta }>1$.

• If $\frac{d}{\beta }\le \theta <\frac{\beta }{r}$ or $\max \{\frac{\beta }{r},\frac{d}{\beta }\}<\theta <\frac{\beta }{r}+\frac{d}{\beta }$, then System (1)-(2) has no interior equilibrium in X. Thus, if System (1)-(2) is bounded then any trajectory with an initial condition in the interior of X converges to (0, 0).

The detailed proof of Theorem 5.1 is provided in Appendix. This theorem states that when ρ = α₁ = 0, α₂ = 1, as long as $R_0^{\theta }<1$, System (1)-(2) can only have an endemic equilibrium. Further, the dynamics of System (1)-(2) remain bounded in at least three cases: β < d, $d>\frac{{\theta }^2}{4}$, and d > rθ. The patterns of dynamics generated by Model I are relatively simple when compared to those of three additional specials models. The dynamics of Model II, III, IV are similar and thus, we focus primarily on the study of the dynamics of Model II. We also include one dimensional bifurcations diagram associated with Model III, IV involving different scenarios than those highlighted with Model II.

The effects of d and p are shown in Figure 6; the effects of r, θ, ρ are shown in Figure 7; and the effects of r and d are collected in Figure 8. We use these bifurcation diagrams, to summarize the effects of the selected factors, on the dynamics of the System (1)-(2), in Table 4 and in Table 5

Figure 6.

First row are two dimensional bifurcation diagrams of α₁ and α₂ for Model II regarding the number of interior equilibria: The black region represents no interior equilibrium; the white region represents one interior equilibrium; blue region represents two interior equilibria and the red region represents three interior equilibria. The second and third rows are bifurcation diagrams for system (1)-(2) regarding the number of interior equilibria and their stability. The red color represents that interior equilibrium is a source; the blue color represents that interior equilibrium is a sink; the green color represents that interior equilibrium is a saddle.

Figure 7.

First row are two dimensional bifurcation diagrams of ρ – θ and θ – r for Model II regarding the number of interior equilibria: The black region represents no interior equilibrium; the white region represents one interior equilibrium; blue region represents two interior equilibria and the red region represents three interior equilibria. The second and third rows are bifurcation diagrams for system (1)-(2) regarding the number of interior equilibria and their stability. The red color represents that interior equilibrium is a source; the blue color represents that interior equilibrium is a sink; the green color represents that interior equilibrium is a saddle.

Figure 8.

First one is a two dimensional bifurcation diagrams of ρ and d for Model II regarding the number of interior equilibria: The black region represents no interior equilibrium; the white region represents one interior equilibrium; blue region represents two interior equilibria and the red region represents three interior equilibria. The second and third rows are bifurcation diagrams for system (1)-(2) regarding the number of interior equilibria and their stability. The red color represents that interior equilibrium is a source; the blue color represents that interior equilibrium is a sink; the green color represents that interior equilibrium is a saddle.

Table 4.

Effects of r and ρ on dynamics.

Values of R 0		Effects when $R_0^{\theta }<1$	Effects when $R_0^{\theta }>1$
Intensity of values
Small values of	r	1.Disease persists at a low level if $\frac{d}{\beta }$ large enough (Theorem 4.2); 2.Destabilize the system and may drive the whole population extinct through a catastrophic event (Figure 6(c)).	1.Disease persists at a low level if $\frac{d}{\beta }$ small enough (Theorem 4.2); 2.Exhibit disease-driven extinction (Figure 6(d)).
	ρ	Destabilize the system and may drive the whole population extinct through a catastrophic event (Figure 6(e)).	Either disease persists with large infected population or exhibit disease-driven extinction (Figure 6(f)).
Intermedium values of	r	Hysteresis occurs.	Disease persists.
	ρ	Hysteresis occurs.	Disease persists.
Large values of	r	Disease persists at large infected population.	Disease persists at large infected population.
	ρ	Diseases persists at relatively large infected population.	Disease persists at low infected population.

Table 5.

Effects of θ and d on dynamics.

Intensity of values of parameters		Effects on dynamics
Small values of	θ	Disease persists at relatively large population levels.
	d	Disease persists at large population levels (Figure 8).
Intermedium values of	θ	Disease persists and hysteresis may occur (Figure 7(e)).
	d	Destabilize the system and exhibit multiple equilibria but not hysteresis (Figure 7(b)-7(f)).
Large values of	θ	1.Destabilize the system and drive the whole population extinct through a series of catastrophic event (Figure 7(f)); 2. Exhibit disease-driven extinction (Figure 7(e)).
	d	Disease persists at low population levels.

Thus, from Figure 6, 7, 8, 9, we conclude that in general, increases in the maximum birth rate of species, in the relative reproduction ability of infected populations, in the relative competitive ability of infected populations at low population level, and in disease induced death rate can stabilize the system, resulting in disease persistence. On the other hand, increases in the Allee effect threshold, disease transmission rates, and in the relative competitive ability of infected population at the higher population level can destabilize the system resulting in the eventual collapse of the whole population, a catastrophic (disease-induced) event.

Figure 9.

One dimensional bifurcation diagrams for Model III & IV regarding the number of interior equilibria and their stability. The red color represents that interior equilibrium is a source; the blue color represents that interior equilibrium is a sink; the green color represents that interior equilibrium is a saddle.

6. Discussion

Despite the relevance of natural selection in the study of disease dynamics and evolution, selective factors are not routinely incorporated in models for the transmission dynamics of populations in the wild (but see for example, Dwyer et al 1990). Furthermore, as one moves into issues of management and control, the complications involved in finding ‘optimal’ solutions have moved researchers to focus on the challenges posed by management and control, leaving the underlying dynamics in the “hands” of R₀, and therefore most often in a world where disease dynamics are “predictable” and “robust.” In this manuscript, we have made efforts to incorporate the role of selection by building a simple model that accounts for disease-induced reductions in reproductive ability, density dependent effects on fitness, and reductions in the fitness of infected individuals in the form of a diminished capacity to compete for resources. These features in the context of a SI model with an Allee effect lead to rich, interesting, and complex dynamics that include but are not limit to multi-stability (hysteresis), saddle node bifurcation, Hopf bifurcation and catastrophic events (those tied in to disease-induced extinction). We found that the dynamics of Model (1)-(2) can be characterized as follows:

1. Switching Allee thresholds: Switching is possible as the relevance of the relative competitive advantageous ability of infected individuals (α₂) increases (the total population is high, around 1) in contrast to the relative competitive ability of infectious individuals (α₁) when total population levels are low. Theorem 3.1 implies that the total population S + α₂I of System (1)-(2) can be above 1 provided that $\frac{{\alpha }_1}{\theta }<{\alpha }_2$. The total population of System (1)-(2) is always bounded by 1 when $\frac{{\alpha }_1}{\theta }\ge {\alpha }_2$. Letting N = S + α₂I and assuming that $\frac{{\alpha }_1}{\theta }<{\alpha }_2$ and S > 0, we have (System (1)-(2)):

   $$\begin{array}{cc}\hfill \frac{dN}{dt}=& r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_2)SI-dI\hfill \\ \hfill =& r\theta (S+\rho I)(\frac{S}{\theta }+\frac{{\alpha }_1}{\theta }I-1)(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_2)SI-dI.\hfill \end{array}$$ (11)

   It is possible for System (1)-(2) to have a locally asymptotically stable interior equilibrium with S* < θ, I* > 1, that is,

   $$\frac{S^{\ast }}{\theta }+\frac{{\alpha }_1}{\theta }{I}^{\ast }<1\text{and}{S}^{\ast }+{\alpha }_2{I}^{\ast }<1.$$

   For example, taking r = 2, ρ = 0.15, θ = 0.56, d = 0.1, β = 0.7692, α₁ = ρ = 0.56, α₂ = 1, we see that System (1)-(2) has a locally asymptotically stable interior equilibrium (0.13, 2.399). The infected population with less reproduction ability ρ < 1 and different competitive fitness as the total population level varies leads to an Allee threshold switch. Specifically, S + α₂I = 1 becomes the effective Allee threshold and $\frac{S}{\theta }+\frac{{\alpha }_1}{\theta }I=1$ the effective carrying capacity.

2. Disease-induced extinction: Theorem 3.2 clarifies the outcomes in two scenarios when System (1)-(2) has disease-free dynamics: 1. If β ≤ d, then System (1)-(2) has two global attractors, (0, 0) and (1, 0); 2. If $R_0^{\theta }>1$ and Condition (5) holds, then System (1)-(2) has (0,0) as its global attractor, that is, the population goes to extinct. The second case can be considered as a case of disease-induced extinction due to the interplay of three features incorporated in System (1)-(2) (reduced reproductive ability ρ, impact of competitive ability of infected population at low and hight population levels α_i, i = 1, 2), and the potentially low maximum reproductive rate, r. Both cases do not support interior equilibrium and the transition between the both scenarios is mediated by the emergence of an endemic equilibrium, which seems to undergo a Hopf bifurcation (simulations). These phenomena have been noted by Thieme et al (2009). From the bifurcation diagrams, we observe that for large values of the Allee effect threshold θ (see Figure 7(c)-7(f)), the competitive ability of infected individuals α₂ at high population levels (see Figure 5(e)), the lower reproductive ability ρ of infected population (see Figure 6(e)), and the lower value of the maximum reproductive rate r (see Figure 6(c)), can lead to disease-induced extinction of the population through a series of catastrophe events that occur when a stable limit cycles merges with the adjacent saddle, leading to the annihilation of susceptible and infected sub-populations.

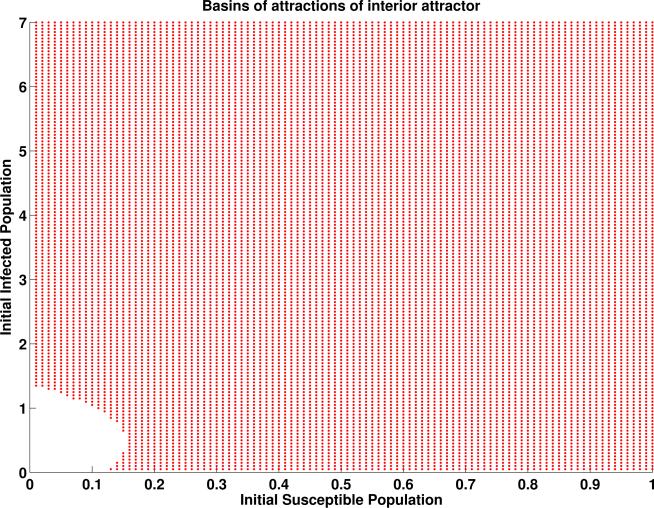
3. Basin of attraction of interior attractor: Theorem 3.3 provides an estimate of the basins of attractions of System (1)-(2) under some conditions. In order to have an idea of what happens when the conditions in Theorem 3.3 do not hold, we have carried out numerical simulations that suggest that System (1)-(2) seem have a relative large basins of attractions when the system supports three interior equilibria (e.g., hysteresis). For example, when r = 3.5, θ = 0.12, ρ = 0.2, β = 1, d = 0.15, α₁ = 0.15, α₂ = 0.1, System (1)-(2) has three interior equilibria (0.15, 0.3095), (0.15, 0.6226) and (0.15, 6.6180), with (0.15, 0.3095) a source; (0.15,0.6226) a saddle, and (0.15, 6.6180) a locally asymptotically stable sink. Simulations suggest that the trajectory converges to (0.15, 6.6180) whenever the initial infected population is larger than 1.3 (not very realistic) or the initial susceptible population is larger than 0.15 (see Figure 10).

4. Hysteresis: Theorem 4.1-4.2 shows that System (1)-(2) can support one or three interior equilibria $(\frac{d}{\beta },I^{\ast })$ when $R_0^{\theta }<1$, that is, when $\frac{d}{\beta }>\theta$. The medium interior equilibrium is always a saddle and the smallest interior equilibrium can be a sink or a source. For example, when r = 3.5, θ = 0.12, ρ = 0.2, β = 1, d = 0.15, α₁ = 0.15, α₂ = 0.1, System (1)-(2) has three interior equilibria with the smallest interior equilibrium a source. When r = 2.35; ρ = 0.85; α₁ = 1; α₂ = 0.02; θ = 0.235; d = 0.85; β = 1, System (1)-(2) also has three interior equilibria with the smallest interior equilibrium a sink (see Figures 4, 5, 6, 7 and 8, 9).

5. Stabilizer and destabilizer: Simulations suggest that increasing the values of d, r, ρ or α₁ can stabilize System (1)-(2), that is, the disease persists. On the other hand increasing the values of β, θ or α₂ can destabilize System (1)-(2) leading eventually to population collapse (see Figure 4, 5, 6, 7 and 8, 9 and Table 2, 4, 5).

Figure 10.

The red region is the basins attractions of interior attractor (i.e., the equilibrium (0.15, 6.6180)) of system (1)-(2) when r = 3.5, θ = 0.12, ρ = 0.2, β =1, d = 0.15, α₁ = 0.15, α₂ = 0.1.

To summed it up, the study carried out in this manuscript shows that the introduction of fitness factors and Allee effects, in the most rudimentary ways, can lead to a series of outcomes and questions that challenge standard protocols. Our analysis suggests that the basic reproduction number R₀ may be a deficient measure, in the sense that building, testing and evaluating control and/or management strategies must be carried out on frameworks that incorporate the impact of factors like disease on fitness. For example, from Figure 8(d) we see that within a certain range of R₀ values $(R_0=\frac{\beta }{d}\in$ (5.66.2)) there is no disease dynamics. However, we also see that there is no susceptible population either, the population has gone extinct. Thus, if decreasing the value of R₀ from 6.2 to a lower value under some control strategy may cause the extinction of the species. High disease rates may in some instances guarantee the survival of a population.

Appendix

In this appendix, we collect technical details associated with the proof of key results in this manuscript.

Proof of Lemma 2.1

Proof. Notice that f(S, I) is continuous in X and smooth when S > 0. It is easy to check that (0, 0) is a trivial equilibrium of System (1)-(2). Thus, for any point (S, I) ∈ X with S > 0, we have that

$${\frac{dS}{dt}\mid }_{S=0}=\{\begin{array}{c}r\rho I({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)\ge 0\hfill \\ 0,\text{if}r\rho I({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)<0\hfill \end{array}\phantom{\}}$$

and

$${\frac{dI}{dt}\mid }_{I=0}=0.$$

Therefore, X is a positively invariant set, just a continuity argument.

For any initial condition taken in X_x, System (1)-(2) reduces to (4), which is positively invariant in X_x, again a continuity argument.

Take an initial condition in ${\Omega }_1^S$ and observe that if S(0) = 1 at some time T then since X is positively invariant, we must have

$${\frac{dS}{dt}\mid }_{t=0}=r(1+\rho I)(1+{\alpha }_{1}I-\theta )(-{\alpha }_{2}I)-{\beta }_{1}I<0.$$

This indicates that S will start to decrease and proceed to drop below 1. Thus, any initial condition in ${\Omega }_1^S$ will not leave ${\Omega }_1^S$ for all future times, that is, ${\Omega }_1^S$ is positively invariant as well.

For any point in X with S > 1, we have that

$$\frac{dI}{dt}=r(R+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)\beta SI\le 0.$$

Thus,

$$\underset{t\to \infty }{\lim \sup }S\left(t\right)\le 1.$$

Take any initial condition in Ω_θ and observe that α_i ≤ 1, i = 1, 2 and thus we have that

$$S\left(0\right)+{\alpha }_{i}I\left(0\right)\le S\left(0\right)+I\left(0\right)\le \theta ,i=1,2\Rightarrow 1-S-{\alpha }_{2}I\ge 1-\theta >0.$$

Therefore, we must have that

$${\phantom{\mid }\frac{dS}{dt}+\frac{dI}{dt}\mid }_{t=0}=\{\begin{array}{c}r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-dI\le 0\hfill \\ 0,\text{if}S=0\text{and}r\rho I({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)\le 0.\hfill \end{array}\phantom{\}}$$

This implies that

$$S\left(t\right)+I\left(t\right)\le \theta \text{for all}t\ge 0.$$

Therefore, the set Ω_θ is positively invariant.

Proof of Lemma 2.2

Proof. For any initial condition in X, if S + α₁I ≤ θ and ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$, we have therefore that

$$S+{\alpha }_{2}I<\frac{S}{\theta }+\frac{{\alpha }_{1}I}{\theta }\le 1\Rightarrow 1-S-{\alpha }_{2}I>0.$$

While if S + α₂I > 1 and ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ then we also must have that

$$\frac{S}{\theta }+\frac{{\alpha }_{1}I}{\theta }>S+{\alpha }_{2}I\ge 1\Rightarrow S+{\alpha }_{1}I>\theta .$$

Let Z_α1 = S + α₁I and Z_α2 = S + α₂I and take any initial condition with S(0) > 0 then it must be that

$$\begin{array}{cc}\hfill \frac{d{Z}_{{\alpha }_1}}{dt}=& r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_1)SI-d{\alpha }_{1}I\hfill \\ \hfill \frac{d{Z}_{{\alpha }_2}}{dt}=& r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_2)SI-d{\alpha }_{2}I\hfill \end{array}$$ (12)

For any point in ${\Omega }_{\theta }^{\alpha }$ with S > 0, we have $\frac{d{Z}_{{\alpha }_1}}{dt}\le 0$. And for any point such that S > 0 and S + α₂I > 1, we must have that

$$\begin{array}{cc}\hfill \frac{s{Z}_{{\alpha }_2}}{dt}=& r\rho \theta (\frac{S}{\rho }+I)(\frac{S}{\theta }+\frac{{\alpha }_{1}I}{\theta }-1)(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_2)SI-d{\alpha }_{2}I\hfill \\ \hfill \le & r\rho \theta Z_{{\alpha }_2}(Z_{{\alpha }_2}-1)(1-Z_{{\alpha }_2})<0.\hfill \end{array}$$

This shows that S + α₂I ≤ 1 will hold at some future time. Since ${\frac{d{Z}_{{\alpha }_2}}{dt}\mid }_{S+{\alpha }_{2}I=1}\le 0$, we must have that S + α₂I ≤ 1 for all future time. Thus, both ${\Omega }_{\theta }^{\alpha }$ and Ω₁ are positively invariant if ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ holds.

Take any initial condition in ${\Omega }_{\theta }^{\alpha }$, if ${\alpha }_2<\frac{{\alpha }_1}{\theta }$ holds then from System (12) we conclude that:

$$\frac{d{Z}_{{\alpha }_1}}{dt}<r\rho (\frac{S}{\rho }+I)(S+{\alpha }_{1}I-\theta )(1-\theta )<r\rho (1-\theta )(S+{\alpha }_{1}I)(S+{\alpha }_{1}I-\theta )<0.$$

Thus,

$$\underset{t\to \infty }{\lim }{Z}_{{\alpha }_1}\left(t\right)=0\Rightarrow \underset{t\to \infty }{\lim \sup }\max \{S\left(t\right),I\left(t\right)\}=0.$$

Proof of Theorem 3.1

Proof. Define h(S, I)= r(S + ρI)(S + α₁I – θ)(1 – S – α₂I) and observe that if ${\alpha }_2>\frac{{\alpha }_1}{\theta }$, we must consider the following two cases when h is positive:

1. S + α₁I < θ but S + α₂I > 1. In this case, we require $0<I<\frac{\theta }{{\alpha }_1}<\frac{1}{{\alpha }_2}$.

2. S + α₁I > θ but S + α₂I < 1. In this case, we require $0<I<\frac{1}{{\alpha }_2}$.

If (S + α₁I < θ, S + α₂I < 1) or (S + α₁I > θ, S + α₂I > 1) then we have h ≤ 0. Now define

$$M=\underset{0\le S\le 1,0\le I\le \frac{1}{{\alpha }_2}}{\max }\left\{h(S,I)\right\}$$

then for strictly positive parameters, we have that

$$h(S,I)\le M\text{for all}(S,I)\in X.$$

Let N^T = S + I. We have that

$$\frac{d{N}^T}{dt}=\{\begin{array}{c}r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-dI\le M-dI\hfill \\ 0,\text{if}S=0\text{and}r\rho I({\alpha }_{1}I-\theta )(1-{\alpha }_{2}I)-dI\le 0\hfill \end{array}\phantom{\}}$$

Let ε > 0 be very small then according to Lemma 2.1, for some large enough t₁, we have that

$$S\left(t\right)<1+∊,\text{for all}t>T.$$

Thus,

$$\frac{d{N}^T}{dt}\le M-dI=M+dS-d{N}^T\le M+d(1+∊)-d{N}^T,\text{for all}t>t_1.$$

Hence, if ${\alpha }_2>\frac{{\alpha }_1}{\theta }$ we have

$$\underset{t\to \infty }{\lim \sup }{N}^T\left(t\right)\le \frac{M+d}{d}\Rightarrow \underset{t\to \infty }{\lim \sup }I\left(t\right)\le \frac{M+d}{d}.$$

While if ${\alpha }_2\le \frac{{\alpha }_1}{\theta }$ then making use of Lemma 2.2 and its corollary 2.1, we conclude that System (1)-(2) has $[0,1]\times [0,\frac{1}{{\alpha }_2}]$ as its compact global attractor. Therefore, System (1)-(2) is bounded, whenever all parameters are strictly positive.

Proof of Theorem 3.2

Proof. According to Theorem 3.1, we know that for any ε > 0 and any initial condition (S(0), I(0)) ∈ X, there exists some time t₁ such that

$$S\left(t\right)<1+∊\text{for all}t>t_1.$$

If β < d, then we can choose ε small enough such that β(1 + ε) – d = a < 0. This implies that for time t₁ large enough, we have

$$\frac{dI}{dt}\le I(\beta (1+∊)-d)\le -\alpha I<0$$

Therefore, lim_t→∞I(t)= 0.

Any interior equilibrium (S*, I*) of System (1)-(2) should satisfy the following equalities:

$$S^{\ast }=\frac{d}{\beta }\text{and}{I}^{\ast }>0$$

where

$$f(S^{\ast },I^{\ast })=f(\frac{d}{\beta },I^{\ast })=r(\frac{d}{\beta }+\rho I^{\ast })(\frac{d}{\beta }+\rho I^{\ast }-\theta )\left(1-\frac{d}{\beta }-I^{\ast }\right)-d{I}^{\ast }=0.$$

Thus, the number of positive roots of

$$f(\frac{d}{\beta },I^{\ast })=r(\frac{d}{\beta }+\rho I^{\ast })(\frac{d}{\beta }+{\alpha }_1{I}^{\ast }-\theta )\left(1-\frac{d}{\beta }-{\alpha }_2{I}^{\ast }\right)-d{I}^{\ast }=0$$

determines the number of interior equilibrium of System (1)-(2).

If β = d and I > 0, then

$$f(\frac{d}{\beta },I)=f(1,I)=r(1+\rho I)(1+{\alpha }_{1}I-\theta )(-{\alpha }_{2}I)-dI<0.$$

Thus, system (1)-(2) has no interior equilibrium in the case that β = d.

Now assume that β > d. The partial derivative of f(S, I) with respect to I at $S=\frac{d}{\beta }$ is

$${\phantom{\mid }\frac{\partial f(S,I)}{\partial I}\mid }_{S=\frac{d}{\beta }}=\alpha I^2+bI+c$$

where a = –3rρα₁α₂, $a=-3r\rho {\alpha }_1{\alpha }_2,b=2r\rho ({\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho })(\frac{{\alpha }_1+{\alpha }_2\theta }{{\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho }}-\frac{d}{\beta })$ and

$$c=-\frac{({\alpha }_1+{\alpha }_2+\rho )r{d}^2-(\theta \rho +\rho +{\alpha }_1+{\alpha }_2\theta )r\beta d+(d+r\rho \theta ){\beta }^2}{{\beta }^2}.$$

If $\frac{d}{\beta }\le \theta$ then $f(\frac{d}{\beta },0)\le 0$. If in addition, we have

$$\frac{d}{\beta }>\frac{{\alpha }_1+{\alpha }_2\theta }{{\alpha }_1+{\alpha }_2+\frac{{\alpha }_1{\alpha }_2}{\rho }}\text{and}\frac{r({\alpha }_1+{\alpha }_2+\rho ){\left(\frac{d}{\beta }\right)}^2+(d+r\rho \theta )}{(\theta \rho +\rho +{\alpha }_1+{\alpha }_2\theta )r\frac{d}{\beta }}>1,$$

then b < 0 and c < 0. This implies that $\frac{\partial f(S,I)}{\partial I}\mid {}_{S=\frac{d}{\beta }}<0$. Thus, $f(\frac{d}{\beta },I^{\ast })=0$ has no positive root, that is, System (1)-(2) has no interior equilibrium in ${\mathbb{R}}_{+}^2$.

Since all parameters are strictly positive then according to Theorem 3.1, System (1)-(2) has a compact global attractor. Thus, from an application of the Poincaré-Bendixson Theorem (Guckenheimer & Holmes 1983) we conclude that the trajectory starting at any initial condition living in X converges to one of three boundary equilibria when the System (1)-(2) has no interior equilibrium. Therefore,

$$\underset{t\to \infty }{\lim \sup }I\left(t\right)=0.$$

Simple algebraic calculations show that (0, 0), (θ, 0), and (1, 0) are three disease free equilibria of System (1)-(2), with (0,0) always locally asymptotically stable; (θ, 0) a saddle if $\frac{\theta \beta }{d}<1$ and a source if $\frac{\theta \beta }{d}>1$; (1, 0) is locally asymptotically stable if β ≤ d (i.e., R₀ < 1) and a saddle if β > d (i.e., R₀ > 1). Therefore, System (1)-(2) has only two attractors (0, 0) and (1, 0) if β ≤ d while System (1)-(2) has global stability at (0, 0) if Condition (5) is satisfied.

Proof of Proposition 3.1

Proof. From the proof of Theorem 3.1, we know that Ω₁ is a compact global attractor of System (1)-(2). Thus, we can restrict the study of the dynamics of System (1)-(2) to this compact set Ω₁. If we start at any initial condition in Ω₁, we have that:

$$\begin{array}{cc}\hfill \frac{d{Z}_{{\alpha }_1}}{dt}=& r(S+\rho I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{2}I)-\beta (1-{\alpha }_1)SI-d{\alpha }_{1}I\hfill \\ \hfill =& r\rho (\frac{S}{\rho }+I)(S+{\alpha }_{1}I-\theta )(1-S-{\alpha }_{1}I+({\alpha }_1-{\alpha }_2)I)-\beta (1-{\alpha }_1)SI-d{\alpha }_{1}I\hfill \end{array}$$

Let us choose some α such that

$$1\ge S\left(0\right)+{\alpha }_{2}I\left(0\right)>0\text{and}1\ge Z_{{\alpha }_1}\left(0\right)=S\left(0\right)+{\alpha }_{1}I\left(0\right)=\alpha >\theta .$$ (13)

Then we have

$$\begin{array}{cc}\hfill {\phantom{\mid }\frac{d{Z}_{{\alpha }_1}}{dt}\mid }_{t=0}\ge & r\rho Z_{{\alpha }_1}(Z_{{\alpha }_1}-\theta )(1-Z_{\alpha 1})-\beta (1-{\alpha }_1)I-d{\alpha }_{1}I-r\rho Z_{{\alpha }_1}(Z_{{\alpha }_1}-\theta )\mid {\alpha }_1-{\alpha }_2\mid I\hfill \\ \hfill \ge & r\rho \alpha (\alpha -\theta )(1-\alpha )-m\alpha \hfill \end{array}$$

where

$$m=\frac{\beta (1-{\alpha }_1)+d{\alpha }_1+r\rho \alpha (\alpha -\theta )\mid {\alpha }_1-{\alpha }_2\mid }{{\alpha }_1}.$$

Thus, we have ${\frac{d{Z}_{\rho }^{\ast }}{dt}\mid }_{t=0}>0$ if

$$r\rho (\alpha -\theta )\left(1-\alpha (1+\mid 1-\frac{{\alpha }_2}{{\alpha }_1}\mid )\right)>\frac{\beta }{{\alpha }_1}+(d-\beta ).$$ (14)

Therefore, if there exists α such that the Equalities (13)-(14) hold, then we have Z_α1 (t) > α for all t > 0. The set Ω_α a define below by

$${\Omega }_{\alpha }=\{(S,I)\in X:\alpha \le S+{\alpha }_{1}I\le I\text{and}S+{\alpha }_{2}I\le 1\}$$

is used to note that if ${\alpha }_2<\frac{{\alpha }_1}{\theta }$ then from Lemma 2.2 it follows that Ω₁ is positively invariant. Therefore, it follows that Ω_α is also positively invariant.

Proof of Theorem 3.3

Proof. From Proposition 3.1 we know that the set Ω_α is positively invariant. Define the average Lyapunov function V = I and note that since $\frac{d}{\beta }<\alpha$ then for any initial conditions in Ω_α, we have that

$$\frac{dV}{dt}=\frac{dI}{dt}=\beta I\left(S-\frac{d}{\beta }\right).$$

From Theorem 3.1 it follows that System (1)-(2) has a compact global attractor Ω₁. The family B_I = {(S, I) ∈ Ω_α : I = 0} are compact positively invariant sets. Take any initial condition in Ω_α then from its positive invariant property we see that

$${\phantom{\mid }\frac{dV}{Vdt}\mid }_{I=0}\ge \beta \left(\alpha -\frac{d}{\beta }\right)>0.$$

Hence, we can apply Theorem 2.5 of Hutson (1984) to guarantee the persistence of I. That is, there exists a ε > 0 such that for any initial condition in Ω_α, we have

$$\underset{t\to \infty }{\lim \inf }I\left(t\right)\ge ∊.$$

Proof of Theorem 4.1

Proof. The positive invariant and boundedness properties of System (1)-(2) can be directly derived from Lemma 2.1 and Theorem 3.1. It is easy to check that System (1)-(2) always has (0, 0), (θ, 0), and (1, 0) as its boundary equilibria. We conclude that (0, 0) is always locally asymptotically stable; (θ, 0) is a saddle if $R_0^{\theta }<1$ (i.e., $\frac{\beta \theta }{d}<1$) and it is a source if $R_0^{\theta }>1$ (i.e., $\frac{\beta \theta }{d}>1$); (1, 0) is a saddle when β > d (i.e., R₀ > 1) and locally asymptotically stable if β < d(i.e., R₀ < 1) by calculating the eigenvalues of Jacobian matrices of System (1)-(2) evaluated at these equilibria (see (15), (16) and (17)). The sufficient condition on no interior equilibrium can be derived from Theorem 3.3.

$$J_{(0,0)}=\left(\begin{array}{cc}\hfill -r\theta \hfill & \hfill -r\rho \theta \hfill \\ \hfill 0\hfill & \hfill -d\hfill \end{array}\right)$$ (15)

$$J_{(\theta ,0)}=\left(\begin{array}{cc}\hfill r\theta (1-\theta )\hfill & \hfill r\theta {\alpha }_1(1-\theta )-\beta \theta \hfill \\ \hfill 0\hfill & \hfill \beta \theta -d\hfill \end{array}\right)$$ (16)

$$J_{(1,0)}=\left(\begin{array}{cc}\hfill -r(1-\theta )\hfill & \hfill -r(1-\theta ){\alpha }_2-\beta \hfill \\ \hfill 0\hfill & \hfill \beta -d\hfill \end{array}\right)$$ (17)

Notice that $f(\frac{d}{\beta },0)>0$ when $\frac{d}{\beta }>\theta$. Thus, if $f(\frac{d}{\beta },v_1)<0$ and $f(\frac{d}{\beta },v_2)>0$ with v_i > 0, i = 1, 2, then $f(\frac{d}{\beta },v^{\ast })=0$ has three positive roots, that is, System (1)-(2) has two interior equilibria in X.

While if $\frac{d}{\beta }<\theta$, we have $f(\frac{d}{\beta },0)<0$. Thus, if in addition $f(\frac{d}{\beta },v_2)>0$ with v₂ > 0 then $f(\frac{d}{\beta },v^{\ast })=0$ has two positive roots. Therefore, in this case, System (1)-(2) has two interior equilibria in X.

Proof of Theorem 4.2

Proof. The Jacobian matrix of System (1)-(2) associated with the equilibrium $(\frac{d}{\beta },I^{\ast })$ is

$$J_{(\frac{d}{\beta },I^{\ast })}=\left(\begin{array}{cc}\hfill {\frac{\partial f}{\partial S}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}\hfill & \hfill {\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}\hfill \\ \hfill \beta I^{\ast }\hfill & \hfill 0\hfill \end{array}\right)$$ (18)

where ${\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}$ is defined in (7) and

$$\begin{array}{cc}\hfill {\frac{\partial f}{\partial S}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}=& -r({\alpha }_1{\alpha }_2+\rho {\alpha }_2+\rho {\alpha }_1){\left(I^{\ast }\right)}^2\hfill \\ \hfill & -2r({\alpha }_1+{\alpha }_2+\rho )\left(\frac{d}{\beta }+\frac{\frac{\beta }{r}-({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )}{2({\alpha }_1+{\alpha }_2+\rho )}\right)I^{\ast }\hfill \\ \hfill & -r\left(3{\left(\frac{d}{\beta }\right)}^2-2(\theta +1)\left(\frac{d}{\beta }\right)+\theta \right)\hfill \end{array}$$ (19)

Thus, we have ${\frac{\partial f}{\partial S}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}<0$ for all I* > 0 if

$$\frac{({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )-\frac{\beta }{r}}{2({\alpha }_1+{\alpha }_2+\rho )}<\frac{d}{\beta }<\frac{1+\theta -\sqrt{{(\theta -1∕2)}^2+3∕4}}{3}$$

or

$$\max \{\frac{({\alpha }_1+({\alpha }_2+\rho )\theta +\rho )-\frac{\beta }{r}}{2({\alpha }_1+{\alpha }_2+\rho )},\frac{1+\theta +\sqrt{{(\theta -1∕2)}^3+3∕4}}{3}\}<\frac{d}{\beta }.$$

According to the definition of ${\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}$ and making use of Figure 2, we conclude that

$${\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}<0$$

in the following cases:

1. $(\frac{d}{\beta },I^{\ast })$ is the only interior equilibrium of System (1)-(2).

2. $(\frac{d}{\beta },I^{\ast })$ is the largest interior equilibrium when System (1)-(2) has two interior equilibrium, that is, the second component of the equilibrium is the largest.

3. $(\frac{d}{\beta },I^{\ast })$ is the largest or smallest interior equilibrium when System (1)-(2) has three interior equilibrium, that is, the second component of the equilibrium is the largest or the smallest.

Similarly, we have

$${\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}>0$$

in the following cases

1. $(\frac{d}{\beta },I^{\ast })$ is the smaller interior equilibrium when System (1)-(2) has two interior equilibrium, that is, the second component of the equilibrium is smaller.

2. $(\frac{d}{\beta },I^{\ast })$ is the middle interior equilibrium when System (1)-(2) has three interior equilibrium, that is, the second component of the equilibrium is middle.

The trace and determinate of the Jacobian matrix (18) evaluated the equilibrium $(\frac{d}{\beta },I^{\ast })$ are

$$T=trace\left(J_{(\frac{d}{\beta },I^{\ast })}\right)={\frac{\partial f}{\partial S}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}\text{and}D=det\left({\frac{\partial f}{\partial S}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}\right)=-\beta I^{\ast }{\frac{\partial f}{\partial I}\mid }_{S=\frac{d}{\beta },I=I^{\ast }}.$$

Thus, if T < 0 and D > 0 then $(\frac{d}{\beta },I^{\ast })$ is locally asymptotically stable while if D < 0, then $(\frac{d}{\beta },I^{\ast })$, it is a saddle node.

We can conclude that the statement of Theorem 4.2 holds.

Proof of Theorem 5.1

Proof. If β < d, then according to Theorem 3.2, System (1)-(2) has disease free dynamics.

Let N = S + I. If $d>\frac{{\theta }^2}{4}$ then we have

$$\begin{array}{cc}\hfill \frac{dN}{dt}=& rS(S-\theta )(1-S-I)-dS=rS(S-\theta )-rS(S-\theta )N-d(N-S)\hfill \\ \hfill =& rS(S+\frac{d}{r}-\theta )-(d-\frac{{\theta }^2}{4})N\le r(1+\frac{d}{r}-\theta )-(d-\frac{{\theta }^2}{4})N\hfill \end{array}$$

Thus, $\lim {\sup }_{t\to \infty }S\left(t\right)+I\left(t\right)<\frac{r(1+\frac{d}{r}-\theta )}{d-\frac{{\theta }^2}{4}}$.

If d > rθ then

$$\begin{array}{cc}\hfill \frac{dN}{dt}=& rS(S-\theta )(1-S-1)-dS=rS(S-\theta )-r{S}^{2}N+rS\theta N-d(N-S)\hfill \\ \hfill =& rS(S+\frac{d}{r}-\theta )-(d-r\theta )N\le r(1+\frac{d}{r}-\theta )-(d-r\theta )N\hfill \end{array}$$

Thus, $\lim {\sup }_{t\to \infty }S\left(t\right)+I\left(t\right)<\frac{r(1+\frac{d}{r}-\theta )}{d-r^{\theta }}$.

It is easy to check that when System (1)-(2) has an interior equilibrium if ρ = α₁ = 0, α₂ = 1. The interior equilibrium should has the form as $(S^{\ast },I^{\ast })=(\frac{d}{\beta },\frac{(\frac{d}{\beta }-\theta )(1-\frac{d}{\beta })}{\frac{d}{\beta }+\frac{\beta }{r}-\theta })$. If $\theta <\frac{d}{\beta }<1$ and $\frac{d}{\beta }+\frac{\beta }{r}>\theta$, then

$$0<\frac{(\frac{d}{\beta }-\theta )(1-\frac{d}{\beta })}{\frac{d}{\beta }+\frac{\beta }{r}-\theta }<\frac{\frac{d}{\beta }-\theta }{\frac{d}{\beta }-\theta +\frac{\beta }{r}}<1.$$

If $\frac{d}{\beta }+\frac{\beta }{r}<\theta$ and $\frac{d}{\beta }(\theta -\frac{d}{\beta })<\frac{\beta }{r}$, then

$$0<\frac{(\frac{d}{\beta }-\theta )(1-\frac{d}{\beta })}{\frac{d}{\beta }+\frac{\beta }{r}-\theta }=\frac{\theta -\frac{d}{\beta }-\frac{d}{\beta }(\theta -\frac{d}{\beta })}{\theta -\frac{d}{\beta }-\frac{\beta }{r}}>1.$$

From the arguments above, we conclude that if $\frac{d}{\beta }\le \theta <\frac{\beta }{r}$ or $\max \{\frac{\beta }{r},\frac{d}{\beta }\}<\theta =\frac{\beta }{r}+\frac{d}{\beta }$ holds then System (1)-(2) has only boundary equilibria, that is, no interior equilibrium. Then according to the Poincaré-Bendixson Theorem (Guckenheimer & Holmes 1983), the trajectory starting with any initial conditions in X converges to one of three boundary equilibria when System (1)-(2) has a compact global attractor [0, 1] × [0, M]. Since $\frac{d}{\beta }\le \theta$ then we have

$$\beta \theta \ge d\text{and}\beta >d.$$

Hence, both (θ, 0) and (1, 0) are transversal unstable. Thus, for any initial condition taken in the interior of X, it is impossible for its trajectory to converge to (θ, 0) or (1, 0). Thus, the trajectory must converge to (0, 0).