An analysis of the use of hyperoxia for measuring venous cerebral blood volume: Comparison of the existing method with a new analysis approach

Abstract

Hyperoxia is known to cause an increase in the blood oxygenation level dependent (BOLD) signal that is primarily localised to the venous vasculature. This contrast mechanism has been proposed as a way to measure venous cerebral blood volume (CBVv) without the need for more invasive contrast media. In the existing method the analysis modelled the data as a dynamic contrast agent experiment, with the assumption that the BOLD signal of tissue was dominated by intravascular signal. The effects on the accuracy of the method due to extravascular BOLD signal changes, as well as signal modulation by intersubject differences in baseline physiology, such as haematocrit and oxygen extraction fraction, have so far been unexplored. In this study the effect of extravascular signal and intersubject physiological variability was investigated by simulating the hyperoxia CBVv experiment using a detailed BOLD signal model. This analysis revealed substantial uncertainty in the measurement of CBVv using the existing analysis based on dynamic contrast agent experiments. Instead, the modelling showed a simple and direct relationship between the BOLD signal change and CBVv, and an alternative analysis method with much reduced uncertainty was proposed based on this finding. Both methods were tested experimentally, with the new method producing results that are consistent with the limited literature in this area.

Introduction

Hyperoxia has previously been proposed as a tracer for measuring venous cerebral blood volume (CBVv) (Bulte et al., 2007). The subject is asked to breathe a hyperoxic gas mixture interleaved with periods of air breathing. Breathing a hyperoxic gas mixture produces an increase in venous haemoglobin saturation resulting in an increase in the blood oxygenation level dependent (BOLD) signal. In analogy with T₁-based contrast agent studies for measuring total cerebral blood volume (CBV), the measured BOLD signal from tissue is normalised by the signal from a 100% CBV voxel located in a large vein (Rempp et al., 1994; Newman et al., 2003). This analysis approach assumes that the signals measured in both cases are dominated by intravascular signal change. However, the tissue signal has a significant extravascular component that makes up around 70% of the total signal at 3.0 T (Uludağ et al., 2009). The magnitude of the BOLD response is also dependent on physiological differences between subjects (Blockley et al., 2012) potentially confounding the measurement of CBVv. However, quantitative measurements of CBVv have a number of potential uses. For example, the acquisition of normative data in the healthy brain would allow for a comparison with the diseased state. In addition, the dynamic range of the BOLD response is strongly influenced by CBVv (Blockley et al., 2012). Therefore measurements of CBVv may be useful when controlling for differences in the magnitude of the BOLD response across subjects and in disease.

In this work we performed simulations of the existing method of measuring CBVv using a detailed model of the BOLD signal and its response to a hyperoxic stimulus. These simulations enable the physiological confounds of this method to be considered in a way that experiments alone could not achieve. Specifically the effect of intersubject variations in baseline physiology and alterations in cerebral blood flow (CBF) and oxygen metabolism (CMRO₂) due to hyperoxia were considered. Following on from these simulations an alternative analysis method is proposed that has lower sensitivity to baseline physiological variability. Experiments were performed to establish the plausibility of the measurements produced by both methods with reference to literature values.

Theory and Simulations

Extravascular BOLD signal

Firstly we consider the effect of an increase in venous haemoglobin saturation on the BOLD signal when the brain is under baseline resting conditions. At 3.0 T the majority of the BOLD signal originates in the extravascular compartment and is caused by an enhancement of the tissue transverse relaxation rate, R₂*, by magnetic field gradients surrounding deoxygenated blood vessels. Theoretical and Monte Carlo numerical analyses have shown that the enhancement of extravascular R₂* (δR₂*) is a function of CBVv (V_v) and venous deoxyhaemoglobin concentration ([dHb]_v, g_dHb dl_blood⁻¹) (Ogawa et al., 1993; Yablonskiy and Haacke, 1994).

$$\delta R_2^{\ast }=k{V}_v{\left[\mathit{dHb}\right]}_v^{\beta }$$ (1)

Here κ reflects properties of the experiment including vessel geometry, field strength and the susceptibility of deoxyhaemoglobin. The exponent β is dependent on the blood vessel scale under examination due to diffusion of water protons around these vessels, with β=1 being used for larger vessels, such as venules and larger, and β=2 being used for capillaries. The aim of this study was to target CBVv and hence β=1 is most appropriate, leading to the following relation for the change in extravascular R₂* (ΔR₂*). Since the aim of these experiments was to measure resting baseline CBVv it is assumed to be unchanged in this simple model.

$$\Delta R_2^{\ast }=\kappa V_v\Delta {\left[\mathit{dHb}\right]}_v$$ (2)

Hyperoxia results in only small changes in ΔR₂* suggesting that a linear approximation is appropriate to describe the fractional change in BOLD signal (δS_tiss).

$$\delta S_{\text{tiss}}\approx \mathit{TE}\kappa V_v\Delta {\left[\mathit{dHb}\right]}_v$$ (3)

Therefore, for venous vessels the resting CBVv is a function of the BOLD signal change that results from the change in deoxyhaemoglobin concentration (Δ[dHb]_v) caused by a hyperoxic stimulus. This enables CBVv to be measured as long as Δ[dHb]_v can be accurately estimated. However, it is clear that this would not be the case for capillaries. In addition this model does not take account of intravascular signal change, which still represents a significant fraction of the total signal at 3.0 T. Therefore, detailed modelling of the BOLD signal, incorporating all of these effects, is required to test whether CBVv can be measured in this way.

Oxygen transport modelling

We now consider the underlying physiology that results in an increase in venous haemoglobin saturation during the administration of a hyperoxic stimulus. Oxygen is carried by the blood in two ways, bound to haemoglobin or dissolved in plasma. If we first consider the arterial blood, its saturation (SaO₂) is dependent on the oxygen partial pressure of the blood (PaO₂) in units of mmHg. This can be approximated by the following relation (Severinghaus, 1979).

$${\mathit{SaO}}_2=\frac{1}{\frac{23400}{{\left({\mathit{PaO}}_2\right)}^3+150{\mathit{PaO}}_2}+1}$$ (4)

The total oxygen content of the blood (CaO₂) is the sum of the haemoglobin (ϕ [Hb] SaO₂) and plasma (ε PaO₂) contributions.

$${\mathit{CaO}}_2=\varphi \left[\mathit{Hb}\right]{\mathit{SaO}}_2+\epsilon {\mathit{PaO}}_2$$ (5)

The constants ϕ, [Hb] and ε are the oxygen carrying capacity of haemoglobin (ϕ=1.34 mlO₂ g_Hb ⁻¹), the blood haemoglobin concentration ([Hb]=15 g_Hb dl_blood⁻¹, equivalent to a haematocrit of 0.45) and the solubility coefficient of oxygen in blood (ε=0.0031 mlO₂ dl_blood⁻¹ mmHg⁻¹), respectively (Chiarelli et al., 2007). This relation holds for venous blood, but the total oxygen content of venous blood (CvO₂) can also be defined in terms of CaO₂, where CmetO₂ is the oxygen extracted to serve oxidative metabolism.

$${\mathit{CvO}}_2={\mathit{CaO}}_2-{\text{CmetO}}_2$$ (6)

Rearranging, the venous haemoglobin saturation (SvO₂) can be written in the following way, where PvO₂ is the oxygen partial pressure of venous blood.

$${\mathit{SvO}}_2=\frac{{\mathit{CaO}}_2-{\text{CmetO}}_2-\epsilon {\mathit{PvO}}_2}{\varphi \left[\mathit{Hb}\right]}$$ (7)

Hence the resting [dHb]_v level can be evaluated given the following relation.

$${\left[\mathit{dHb}\right]}_v=\left[\mathit{Hb}\right](1-{\mathit{SvO}}_2)$$ (8)

It is fair to assume that PvO₂ is negligibly small as the oxygen in the venous plasma is in equilibrium with that bound to haemoglobin. Since the change in haemoglobin saturation due to hyperoxia is relatively small the change in PvO₂ will be even smaller, i.e. ΔPvO₂≈3 mmHg. For now, we will consider that CmetO₂ is not altered by hyperoxia. With these assumptions the change in venous deoxyhaemoglobin concentration, Δ[dHb]_v, can then be described by,

$$\Delta {\left[\mathit{dHb}\right]}_v=-\frac{\varphi \left[\mathit{Hb}\right]\Delta {\mathit{SaO}}_2+\epsilon \Delta {\mathit{PaO}}_2}{\varphi }.$$ (9)

Here ΔSaO₂ and ΔPaO₂ are the changes in SaO₂ and PaO₂ in response to hyperoxia, respectively. Unlike PvO₂, PaO₂ contributes significantly to Δ[dHb]_v as it can be easily three orders of magnitude greater than the venous effect, i.e. ΔPaO₂≈200 mmHg. Equation [9] predicts that changes in venous blood oxygen saturation will dominate during a hyperoxic stimulus. For example, when ΔPaO₂=200 mmHg and [Hb]=15 g_Hb dl_blood⁻¹, the change in arterial deoxyhaemoglobin content, Δ[dHb]_a, is approximately −0.24 g_dHb dl_blood⁻¹, whilst Δ[dHb]_v is approximately −0.70 g_dHb dl_blood⁻¹. This equates to a ~3 times larger change in [dHb] in venous vessels. Hence changes in the BOLD signal will be strongly weighted towards the venous vasculature. However, Eq. [9] assumes isometabolism and therefore detailed modelling of the BOLD signal is required to examine the results when this is not true.

Simulations

Simulations were performed to test the underlying principle of using hyperoxia to measure resting baseline CBVv and the sensitivity of this method to intersubject variations in physiology. Oxygen transport and the BOLD signal are dependent on properties of the blood, with the haematocrit and venous haemoglobin saturation being the most important. However, the value of these parameters does have substantial variation within the population. The PET literature defines a relatively broad range of OEF values from 0.35 to 0.55 (Marchal et al., 1992). Similarly haematocrit varies in the range 0.42-0.50 for males and 0.37-0.47 for females (McPhee and Hammer, 2009). These parameters, along with CBVv, determine the maximum BOLD signal amplitude. A detailed BOLD signal model (Griffeth and Buxton, 2011) was used to simulate the BOLD response to hyperoxia to investigate the effect of variability in baseline physiology. A summary of the salient features of the model and analysis approach will now be presented; see (Griffeth and Buxton, 2011) and (Blockley et al., 2012) for further detail. The detailed BOLD signal model includes intra- and extravascular signal contributions from three vascular compartments; arteries, capillaries and veins. Extravascular signals were modelled using the results of numerical simulations for two vessel scales to reflect the different signal characteristics of capillaries (β=2) compared with arteries and veins (β=1) (Ogawa et al., 1993). Intravascular signals were described using empirical measurements of blood R₂* as a function of oxygenation and haematocrit (Zhao et al., 2007; Griffeth and Buxton, 2011). Capillary blood haemoglobin saturation was described by a weighted average of the arterial and venous values (Griffeth and Buxton, 2011). Distribution of blood to the three compartments was achieved by assigning a value of total CBV and partitioning this volume into relative volume fractions, Ω, for each of the compartments (subscript a, c, v for the arterial, capillary and venous compartments, respectively). Relative volume fractions were initially set as Ω_a=0.2, Ω_c=0.4 and Ω_v=0.4. The effect of physiological variation was simulated by randomly selecting pairs of haematocrit and OEF values to sample the expected distribution of the population (Blockley et al., 2012). Values were selected in the ranges 0.37-0.50 and 0.35-0.55 for haematocrit and OEF, respectively. The baseline total CBV fraction was added as an additional randomly selected value meaning that each data point was defined by three parameters. Total CBV fraction was allowed to vary in the range 0 to 0.1 to bracket the experimentally observed value of 0.05 (Roland et al., 1987).

The following steps were followed to simulate the CBVv experiment. The BOLD signal change (δS=ΔS/S₀) resulting from breathing a hyperoxic gas mixture was simulated for tissue (tiss) and vein (vein) using the detailed BOLD signal model. One thousand values of δS_tiss and δS_vein were produced using a uniform random number generator to select values for haematocrit, OEF and CBVv in the ranges described above. The uncertainty introduced by this physiological variability was assessed by plotting the measured signals against the true CBVv to assess the scatter in this relationship. For the existing method the measured quantity is the tissue signal normalised by the signal from a vein measured at steady state, per Eq. [10] (Bulte et al., 2007). This equation is re-written in terms of percentage CBVv rather than ml g⁻¹ of tissue as in the original reference.

$${\mathit{CBV}}_v=h\frac{\ln (\delta S_{\text{tiss}}+1)}{\ln (\delta S_{\text{vein}}+1)}$$ (10)

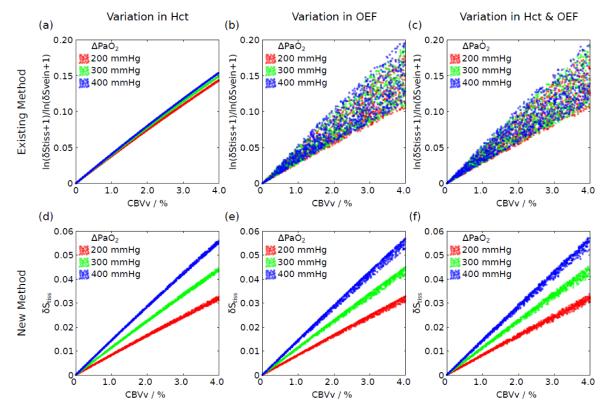
Scaling of the measured signals in terms of CBVv is provided by the constant h=(1-Hct)/(1-r Hct), where Hct is the haematocrit and r=0.85 corrects for differences between small and large vessel haematocrit. However, this scaling was neglected at this stage in order to test the fundamental relationship between the measured quantity and CBVv. Figure 1a-c plot the effect of intersubject physiological variation on this relationship for three different levels of hyperoxia: ΔPaO₂=200 mmHg, 300 mmHg and 400 mmHg. The effect of haematocrit and OEF alone, and in combination, reveals that OEF causes substantial variability in this relationship. Such variability will increase the uncertainty on the measurement of CBVv.

Figure 1.

Simulation of the relationship between the measured signal and true CBVv for the existing (Eq. [10]) and new methods (Eq. [11]). Three different hyperoxia levels were simulated described by the change in arterial PO₂ (ΔPaO₂). The effect of variations in haematocrit (a,d) and OEF (b,e) alone, and in combination (c,f), are considered. A large amount of uncertainty is observed for the existing method suggesting that it cannot accurately account for physiological variability. By plotting the unnormalised tissue BOLD signal response a much tighter and approximately linear response is revealed.

This result led us to consider an alternative analysis approach that does not require a measurement of the venous BOLD signal change (δS_vein). Figure 1d-f plots the unnormalised tissue BOLD signal, δS_tiss, against CBVv for the same hyperoxic levels to investigate the effect of haematocrit and OEF alone and in combination. A much tighter and approximately linear relationship is revealed that shows lower sensitivity to OEF. However, the slope of this relationship is dependent on the specific ΔPaO₂ experienced by the subject. Due to the linearity of the relationship between δS_tiss and CBVv a method for scaling the former in units of the latter is required. Figure 1d-f show that variations in haematocrit and OEF result in much less uncertainty in this relationship than was the case for the existing method. However this effect is relatively small, leading to a ±5% variation in the value of Δ[dHb]_v with respect to the mean value for ΔPaO₂=200 mmHg (typical of the experiments below) given the range of haematocrit expected in the population. This variation is similarly small for the OEF. Therefore, an empirical model, inspired by the form of Eq. [3], is proposed to calculate an appropriate scaling factor as a function of echo time (TE) and ΔPaO₂ alone. The error caused by not including the effects of variation in haematocrit and OEF are likely to be smaller than the typical precision of this experiment. This also results in a more practical method as further measurements of haematocrit and OEF are not required.

$${\mathit{CBV}}_v=\left(\frac{A}{\mathit{TE}}+B\right)\left(\frac{C}{\Delta {\mathit{PaO}}_2}+D\right)\delta S_{\text{tiss}}$$ (11)

Further simulations were performed (not shown) varying TE and ΔPaO₂ to estimate A, B, C and D yielding the following values: A=27.0 ms, B=0.2, C=245.1 mmHg, D=0.1.

Three potential confounds of this new method were identified. Firstly, the relative volume fractions (Ω) of the vascular compartments determines the proportion of the signal derived from the different extravascular regimes (static dephasing versus motional narrowing) with the potential to increase the uncertainty in the CBVv measurement. This effect was examined by setting the arterial volume fraction as Ω_a=0.2 and varying the venous fraction Ω_v between 0.4 and 0.6, whilst keeping the sum of Ω_v and, the capillary fraction, Ω_c constant. Figure 2a shows that this has only a weak effect on the relationship between δS_tiss and CBVv. Secondly, it has been observed that CBF decreases during hyperoxia, through the direct effect of oxygen (Bulte et al., 2007) and through an associated reduction in blood carbon dioxide (CO₂) levels (Iscoe and Fisher, 2005). This effect was investigated by simulating the effect of a 5% flow reduction during hyperoxia. The concomitant change in CBV was modeled as previously described (Griffeth and Buxton, 2011). Briefly, the change in total CBV at steady state was defined using Grubb’s relation: CBV=CBF^α where α=0.38. This change was then distributed across the vascular compartments using similar power law relations. For the venous compartment α was set to 0.2 (Chen and Pike, 2009) and for the capillary compartment a value α=0.1 was used, with the arterial compartment contributing the remainder of the volume change. Since these experiments were performed at steady state, the slow recovery of CBVv due to balloon effects was not considered. Figure 2b shows that this causes the relationship between δS_tiss and CBVv to shift and broaden. Finally, the effect of a change in CMRO₂ during hyperoxia was considered. However, it isn’t clear from the literature whether CMRO₂ increases (Rockswold et al., 2010), remains the same (Diringer et al., 2007) or decreases (Richards et al., 2007; Xu et al., 2012) during hyperoxia. Therefore, CMRO₂ changes of ±10% were simulated. Figure 2c shows that this causes the relationship between δS_tiss and CBVv to shift and broaden in a similar manner to Fig. 2b, but to a larger degree.

Figure 2.

Simulation of the relationship between the measured signal and true CBVv for the new method (Eq. [11]). (a) The effect caused by the distribution of vessel scales was examined by altering the fraction of the total CBV occupied by venous vessels (Ω_v), whilst keeping the combined capillary and venous fraction constant. (b) Hyperoxia has been shown to cause a reduction in CBF (ΔCBF), hence the effect of a 5% flow reduction was examined. (c) It has also been suggested that hyperoxia may alter resting CMRO₂. CMRO₂ changes of ±10% (ΔCMRO₂) were considered.

Experimental Methods and Results

Imaging

This study was approved by the National Research Ethics Service, Oxfordshire REC A. Informed consent was obtained from nine healthy subjects (6 male, mean age 28±4 years). Subjects were scanned at 3.0T on Siemens Trio (n=7) and Verio (n=2) scanners (Siemens Medical Solutions, Erlangen, Germany). Both systems were equipped with a transmit body coil and multi-channel head receive coils (Trio – 12 channel, Verio – 32 channel). Foam inserts were placed around the subject’s head to minimise motion. Gradient-echo echo planar images (EPI) were acquired with BOLD-weighting (TE=30 ms). Images were acquired with 3×3×3 mm³ spatial resolution using a 64×64 matrix over 53/44 (Trio/Verio) slices with a temporal resolution of 3.0/2.4 s. A high resolution structural MPRAGE scan (Mugler and Brookeman, 1990) was acquired to enable grey and white matter masks to be generated (TR/TE = 2040/4.7 ms, flip = 8°, 1 mm isotropic resolution).

The hyperoxic condition was achieved by presenting 100% oxygen to the subject via a two tube nasal cannula at 7 lpm, whilst simultaneously sampling inspired and expired gases. Due to mixing with room air, the inspired oxygen fraction was approximately 50%. Two 2 minute periods of hyperoxia were interleaved with 2 minutes of room air. End-tidal PO₂ (PetO₂) and PCO₂ (PetCO₂) were recorded throughout the experiment using a Biopac MP150 (Biopac Systems, Inc. Goleta, CA, USA) with oxygen and carbon dioxide gas analyser units (O2100C and CO2100C), at a sampling rate of 25 Hz. PCO₂ data were not analysed further due to a calibration error in some data sets.

Analysis

Two subjects were excluded from the analysis due to a ΔPetO₂ less than 100 mmHg. Images were pre-processed using FSL software tools for motion correction (Jenkinson et al., 2002) and brain extraction (Smith, 2002). High pass temporal filtering with a cut-off of 240 s and spatial smoothing with a Gaussian kernel with a full width half maximum of 5 mm was applied to the data. The BOLD signal response due to hyperoxia was analysed by fitting a general linear model of the expected time-course using FEAT (Woolrich et al., 2001). This model function was generated by convolving a 2 minute box-car with a Gamma-variate function (phase 0 s, standard deviation 30 s, mean lag 60 s) (Bulte et al., 2012). The PetO₂ time-course was not used as a regressor as this would require accurate synchronisation with the scanner, precise selection of the end-tidal PO₂ in the respiratory cycle and would lead to the inclusion of additional noise. The resulting parameter estimate for the hyperoxia challenge was converted to percent BOLD signal change by dividing by the mean signal intensity over time and multiplying by 100. Maps of percent BOLD signal change were then used to calculate CBVv in percent using Eq. [10] (existing method) and Eq. [11] (new method).

For the existing method, voxels within the sagittal sinus were selected in the following way. Firstly, the centre of the sagittal sinus was manually defined on 5 slices and a 3 dimensional spline fitted to these points. An 8×8 voxel region of interest was then placed at the vessel centre defined by the spline on a slice-by-slice basis to produce the final mask. The percent BOLD signal change map was then masked before thresholding at the 99^th percentile. Finally, the mean of the remaining voxels was used to define δS_vein in Eq. [10]. The new method (Eq. [11]) requires a measurement of the change in PaO₂ between the normoxic and hyperoxic states (ΔPaO₂). We infer this from measurements of PetO₂ under the assumption that the arterial blood is well equilibrated with the gas in the alveoli and that the alveolar-arterial oxygen gradient is not altered by hyperoxia. The hyperoxic PetO₂ was measured from the last 30 s of each 2 minute hyperoxia challenge, whilst the normoxic value was taken from a 1 minute window preceding the first hyperoxic block.

Functional data were also registered to the subject’s own structural image (Jenkinson et al., 2002). Automated segmentation of the structural image was performed using FAST to produce grey matter, white matter and CSF regions of interest (ROI) (Zhang et al., 2001). Grey and white matter ROIs were then transformed back into functional space and subsequently used to calculate the mean and standard deviation of CBVv for these tissue types. Figure 3 shows five example slices taken from approximately the same region of the brain in each of the subjects. Table 1 gives mean grey and white matter CBVv values.

Figure 3.

Maps of CBVv for the existing and new methods, calculated using Eq. [10] and [11] respectively, as a percentage of the total voxel volume. Note the difference in scaling between each of the methods; 0-16% versus 0-4%.

Table 1.

Mean grey and white matter percent CBVv for both methods. Regions of interest created by segmentation of a high resolution structural image.

Subject	Existing Method				New Method
	Grey Matter CBVv /%		White Matter CBVv /%		Grey Matter CBVv /%		White Matter CBVv /%		ΔPETO2 /mmHg
	Mean	S.D.	Mean	S.D.	Mean	S.D.	Mean	S.D.
1	9.77	9.53	6.69	5.07	2.38	2.70	1.64	1.33	198.4
2	8.16	9.20	4.21	2.91	2.68	3.31	1.37	0.97	201.6
3	9.14	8.04	5.41	2.94	2.75	2.79	1.60	0.88	161.5
4	6.53	7.31	3.90	3.26	1.76	2.19	1.06	0.98	147.3
5	8.68	8.61	4.64	4.41	2.03	2.15	1.08	1.08	149.1
6	8.42	7.81	4.74	3.38	1.88	2.29	1.11	0.83	197.0
7	7.01	6.35	4.62	2.79	1.81	2.04	1.24	0.80	222.9
Mean*	8.24	1.14	4.89	0.92	2.18	0.41	1.30	0.24	182.5

^*Intersubject mean and standard deviation calculated from individual subject mean values.

Discussion

Measuring the BOLD response to a hyperoxia challenge has the potential to provide the most sensitive measurement available of CBVv. The existing analysis approach essentially treated hyperoxia as a contrast agent that simply alters the venous blood signal, so that normalising the BOLD signal change in a tissue voxel to the signal change measured inside a large vein gives the fractional venous CBV in that voxel. Here we used a detailed model of the BOLD effect to show that a different physical picture of the effect of hyperoxia can provide a better foundation for determining CBVv. Specifically, we found that the BOLD signal change itself, without normalisation, has a simple and direct relationship with CBVv. The basic physical picture is that a given level of hyperoxia, in the absence of flow or metabolism changes, produces the same change in venous deoxyhemoglobin concentration Δ[dHb]_v in all venous vessels, regardless of the baseline oxygen extraction fraction. Because the BOLD signal change is primarily driven by a change in total deoxyhemoglobin (the product of CBVv and Δ[dHb]_v), CBVv can be determined directly from the BOLD signal change provided that Δ[dHb]_v is accurately estimated. Experimental data was analysed based on using both the new approach and the existing approach. The results differed by about a factor of four, with the results of the new approach in good agreement with literature values.

In addition, we examined the confounding effects of subject variability of haematocrit and baseline oxygen extraction fraction on the estimate of CBVv. If there is no accompanying change in CBF or CMRO₂ with hyperoxia, the new method is insensitive to variations in baseline OEF. However, if CBF or CMRO₂ changes with hyperoxia, this conclusion changes, and the sensitivity to baseline OEF grows. For this reason, maintaining constant CBF and minimising the potential for CMRO₂ change are important goals for these experiments. We also examined the effect of variability in haematocrit, which affects the estimation of the deoxyhaemoglobin change Δ[dHb]_v. Whilst this effect is small, accuracy can be improved by directly measuring haematocrit in each subject and including its effect in a model of the scaling factor. Knowledge of the subject’s OEF could also improve the accuracy of the new method and could be incorporated into the model, but is unlikely to be available in practice.

Simulations

An ideal method for measuring CBVv should produce a tight one-to-one relationship between the measured quantities and CBVv, regardless of differences in haematocrit and OEF across subjects. If these unknown variables broaden the distribution of possible measurement outcomes for a given CBVv increase, the uncertainty of the CBVv estimate grows. Figure 1a-c show that the existing measurement technique (Eq. [10]) gives a large uncertainty in CBVv. However, by plotting δS_tiss alone (Fig. 1d-f) a much lower uncertainty in the value of CBVv can be achieved. This perhaps paradoxical result can be explained by considering two elements of the signal change. Firstly, the change in BOLD signal due to hyperoxia is proportional to CBVv and Δ[dHb]_v, as suggested by the simplistic model described by Eq. [3]. Secondly, oxygen transport modelling reveals that when CMRO₂ is constant during hyperoxia Δ[dHb]_v is independent of OEF and only weakly dependent on haematocrit (Fig. 1d-f). Hence changes in tissue signal with hyperoxia should be proportional to CBVv. However, during an uncontrolled hyperoxic respiratory challenge it is likely that CBF may be reduced (Bulte et al., 2007), resulting in an altered relationship between δS_tiss and CBVv, and increased uncertainty (Fig. 2b). A reduction in CBF causes an increase in the OEF. Importantly the resultant decrease in venous oxygen saturation is dependent on baseline OEF, unlike isometabolic hyperoxia. Correction for this effect requires an unconfounded estimate of the change in CBF (see discussion below). There is still much debate as to whether CMRO₂ is altered during hyperoxia (Diringer et al., 2007; Richards et al., 2007; Rockswold et al., 2010; Xu et al., 2012). However, it is clear from Fig. 2c that, if changes in this parameter were present, they would cause a large degree of uncertainty in measurements made with the new method. In a similar manner to changes in CBF, changes in CMRO₂ introduce a dependency on the baseline OEF. Likewise a measurement of OEF is required for correction, which is not easily obtainable.

The weak dependence of this method on haematocrit was predicted to produce a ±5% variation in Δ[dHb]_v. Since the change in R₂* due to hyperoxia is proportional to the product of CBVv and Δ[dHb]_v, this results in a ±5% error in the estimation of CBVv. This error can be minimised by measuring haematocrit in each subject and including it in the model used to calculate the scaling factor (Eq. [11]). Alternatively this error can be reduced by increasing ΔPaO₂, resulting in an increased fraction of the total oxygen content to be carried by the plasma. Since the plasma content is independent of haematocrit the mean Δ[dHb]_v is increased, but the variability due to haematocrit is unchanged, diluting the effect of physiological variability. It must be noted that the parameters that define Eq. [11] are magnetic field dependent and hence the values presented here are only valid at 3.0 T. Similar simulations would be required to define these parameters at different magnetic field strengths.

The underlying cause of the uncertainty seen with the existing method can be explained by the differing relaxivity characteristics of the intravascular and extravascular signal. Figure 2a suggests that the extravascular signal is dominated by larger venous vessels, since altering the volume fraction occupied by small vessels (capillaries) has only a weak effect on the resulting BOLD signal. We might therefore consider the extravascular compartment to have linear relaxivity (Eq. [2]) (Ogawa et al., 1993; Yablonskiy and Haacke, 1994). However, the relaxivity of blood has been shown by theory and experiment to be quadratic (Thulborn et al., 1982; Jensen and Chandra, 2000; Silvennoinen et al., 2002; Gardener et al., 2010) meaning that the change in intravascular signal is dependent on the normoxic haemoglobin saturation of the blood. This introduces a dependency on OEF, that does not exist for the extravascular signal, resulting in the observed uncertainty.

It is also important to note that the interpretation of the hyperoxia BOLD signal presented here is incompatible with using hyperoxia to calibrate the BOLD response (Chiarelli et al., 2007). In hyperoxia calibrated BOLD a hyperoxic respiratory challenge is used to measure the BOLD scaling parameter M, which encompasses properties of the baseline physiological state including CBVv and [dHb]₀ (Chiarelli et al., 2007). However, we have recently shown that this approach is only valid when the correct values for haematocrit and OEF are assumed in the calculation of M (Blockley et al., 2012). Therefore suggesting that the hyperoxia BOLD signal is predominantly modulated by CBVv.

Experiments

Experimental measurements of CBVv using both methods produced very different mean values; 8.24% and 2.18% for grey matter for the existing and new methods respectively. There are currently few studies in the literature that quantitatively measure CBVv. Variants of the qBOLD sequence have been used in several studies with whole brain average CBVv estimates in the range 2.68% to 3.68% (An and Lin, 2002; An and Lin, 2002). One study presented grey and white matter specific CBVv values of 1.75% and 0.58% (He and Yablonskiy, 2007). The fact that the results of the new method are comparable with those derived from the qBOLD method lends credibility to the assumption that CBF and CMRO₂ changes are small or non-existent at the hyperoxic levels achieved in this study. However, confirmation of this assumption is still required and is the subject of ongoing work.

The consistency of the results of the new method with those from qBOLD is also not surprising, as measurements of CBVv made using hyperoxia and qBOLD share a common theoretical background. The qBOLD technique relies on the different characteristics of the extravascular transverse signal decay during short and long timescales following excitation or refocussing. In the short timescale the signal decay is quadratically exponential, but reverts to monoexponential in the long timescale. Each of these timescales is differently sensitive to CBVv and [dHb]_v enabling these parameters to be disentangled when data are acquired in both conditions. The hyperoxia CBVv method only acquires data in the long timescale, relying on the effects of hyperoxia to separate the CBVv effect from [dHb]_v, i.e. by modulating [dHb]_v whilst keeping CBVv constant.

Effects of hyperoxia

Changes in CBF during hyperoxia can theoretically be corrected by measuring this change using arterial spin labelling (ASL). However, oxygen is paramagnetic and is known to alter the T₁ of arterial blood (Silvennoinen et al., 2003). Accurate quantification of ASL data requires knowledge of the arterial blood T₁, confounding the estimation of CBF when the oxygen level changes during an experiment (Buxton et al., 1998). Recently this limitation has been overcome by measuring the T₁ of arterial blood in each experiment (Pilkinton et al., 2012). However, this technique is time consuming and has not yet been performed in humans.

Alternatively changes in CBF and CMRO₂ can be minimised by carefully controlling the respiratory stimulus. The major driver of changes in CBF during hyperoxia is the associated hypocapnic effect (Iscoe and Fisher, 2005). Similarly the effect of oxygen on CMRO₂ is proportional to the degree of hyperoxia induced (Xu et al., 2012). In the experiments performed in this study an uncontrolled hyperoxia challenge was employed. However, greater control can be achieved using automated respiratory control methods (Wise et al., 2007; Prisman et al., 2008). Such methods could be used to maintain isocapnia, whilst maintaining an oxygen level that minimises changes in CMRO₂. The ability to target specific changes in PaO₂ using these methods opens up a further interesting possibility. When TE=30 ms and ΔPaO₂=306 mmHg the scaling factor between CBVv and δS_tiss is 1. Therefore, the percentage BOLD signal change in response to hyperoxia is numerically equivalent to the percentage CBVv.

Conclusion

It was shown by simulation that the existing method for measuring CBVv using hyperoxic contrast has substantial sensitivity to variations in baseline physiology. This sensitivity is caused by the normalisation of the mostly extravascular tissue signal by intravascular blood signal. This knowledge enabled an alternative analysis with reduced sensitivity to be proposed. Experimental application of this new method produced results that were consistent with the limited results available in the literature.

Highlights.

The potential of hyperoxic contrast for measuring venous CBV was investigated.

Simulations were performed to examine sensitivity to physiological variability.

The existing method was found to be very sensitive to physiological variability.

A new method was proposed with much reduced sensitivity to physiological variability.

Measurements of venous CBV with the new method are in line with literature values.