Shape-Constrained Multi-Atlas Segmentation of Spleen in CT

Abstract

Spleen segmentation on clinically acquired CT data is a challenging problem given the complicity and variability of abdominal anatomy. Multi-atlas segmentation is a potential method for robust estimation of spleen segmentations, but can be negatively impacted by registration errors. Although labeled atlases explicitly capture information related to feasible organ shapes, multi-atlas methods have largely used this information implicitly through registration. We propose to integrate a level set shape model into the traditional label fusion framework to create a shape-constrained multi-atlas segmentation framework. Briefly, we (1) adapt two alternative atlas-to-target registrations to obtain the loose bounds on the inner and outer boundaries of the spleen shape, (2) project the fusion estimate to registered shape models, and (3) convert the projected shape into shape priors. With the constraint of the shape prior, our proposed method offers a statistically significant improvement in spleen labeling accuracy with an increase in DSC by 0.06, a decrease in symmetric mean surface distance by 4.01 mm, and a decrease in symmetric Hausdorff surface distance by 23.21 mm when compared to a locally weighted vote (LWV) method.

1. INTRODUCTION

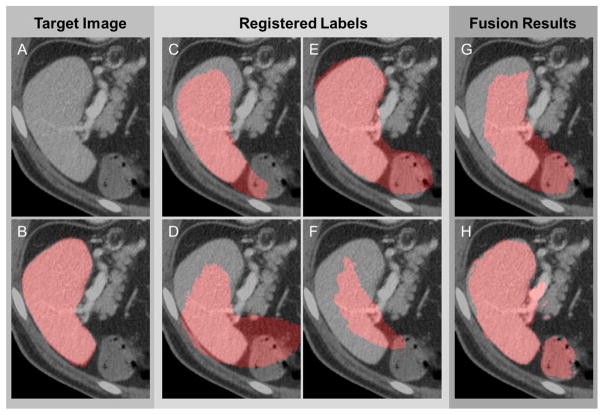
Automated spleen segmentation on clinical CT data is a challenging problem due to the complicity and the variability of abdominal anatomy across populations. Multi-atlas segmentation is a potential approach that can provide robust segmentation of the spleen. Voting (e.g., majority vote (MV [1]), locally weighted vote (LWV [2])) and statistical fusion (e.g., STAPLE [3]) algorithms have been developed to improve the efficacy of combing potentially conflicting labels from multiple atlases. However, registrations of abdominal CT images are problematic given large-scale difference in abdominal anatomy and similar intensities between organs. The atlas labels with problematic registrations may misalign with the target structure, and/or include various redundant structures, and thus substantially undermine the fusion results even when additional intensity information is considered (Fig. 1).

Figure 1.

Challenges of atlas-based spleen segmentation. (A) The intensity image of the target. (B) The manually labeled ground truth of the target. (C) – (F) The atlas labels registered to the target space. (G) The fusion estimate by majority vote. (H) The fusion estimate by locally weighted vote.

We posit that the integration of shape information into the label fusion framework can provide more accurate fusion in cases of problematic registrations between atlas and target images. Although extensively used, point-based shape models have practical limitations as they require manual annotation of corresponding landmarks. Alternatively, an implicit shape model [4–6] has been used to characterize shape variations by voxel-wise high dimensional signed distance function (SDF), where each volume with its all voxels (instead of several landmarks) is considered as a single observation for the shape training. The implicit shape model has been successfully applied to some level set approaches of anatomical structures to constrain the shape of the segmentation [6]. Herein, we propose a multi-atlas segmentation framework that integrates the implicit shape model to regularize the fusion results.

2. METHODS AND RESULTS

2.1 Spleen localization

In our previous spleen approach, we used a regression method, i.e., regression forests region recognition (RFRR [7]), to localize the spleen region with a bounding box and demonstrated that multi-atlas segmentation of spleen provides better estimate on the reduced region of interest. In this study, all intensity and label images referred below were cropped in terms of the identified bounding boxes. Here we omit the mechanism of RFRR for brevity.

2.2 Pose-free implicit shape model

All atlas label images are co-registered into the same space with 7 degrees of freedom (DOF). The binary labels are transformed into high dimensional SDF to implicitly represent the shape of spleen, and then collected in an M × N observation matrix A, where M is the number of observations, and N is the number of voxels. A Principle Component Analysis (PCA) procedure is used to extract the variability of spleen shape, where the mean shape Φ̄ is the voxel-wise average across observations,

$$\overline{\mathrm{\Phi }}=\frac{{\mathrm{\sum }}_m{A}_m.}{M}$$ (1)

and the modes of variation are provided by singular value decomposition (SVD) on the covariance of the centered observation matrix

$$U\mathrm{\sum }{U}^T=\frac{1}{M}{(A-\overline{\mathrm{\Phi }})}^T(A-\overline{\mathrm{\Phi }})$$ (2)

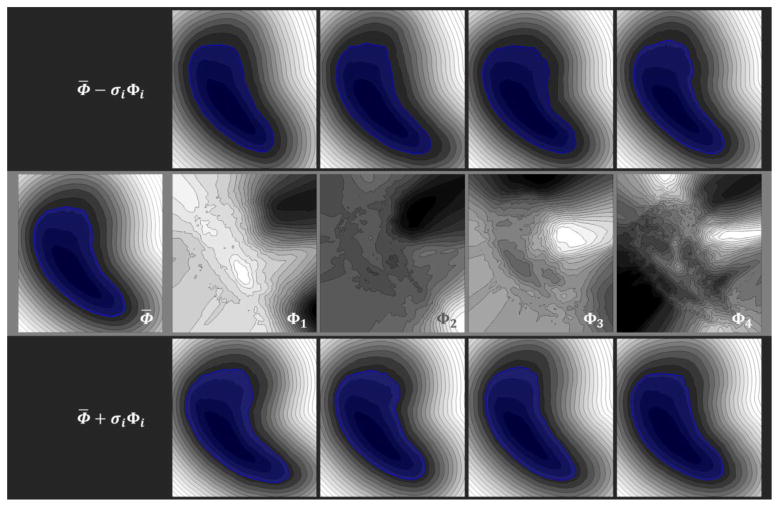
where Σ is a diagonal matrix with its diagonal values as the eigenvalues λ_i, and U denotes an eigenspace with each column as an eigenvector, i.e., one mode of variation Φ_i, associated with the corresponding eigenvalue λ_i (Fig 2). The value of the eigenvalue indicates the dominance of its associated mode of variation, while the modes with relatively small eigenvalues are usually ignored due to their limited variances provided.

Figure 2.

Pose-free implicit parametric shape model. The shape model is represented by signed distance function (SDF) of each voxel over the whole volume. The region within the zero level set (highlighted in blue) is considered as the binary shape representation. The second row illustrates the mean and the first four modes of variation of the shape model. The first and the third row present the specific shapes parameterized by the square root of the eigenvalues.

Given the implicit shape model, a specific shape can be then characterized by the combination of the modes of variations on the basis of the mean shape.

$$\mathrm{\Phi }\equiv \mathrm{\Phi }(\mathit{\omega })=\overline{\mathrm{\Phi }}+{\sum }_i{\omega }_i{\mathrm{\Phi }}_i$$ (3)

where ω_i denotes the shape parameter associated with its mode of variation.

2.3 Shape-constrained multi-atlas segmentation framework

2.3.1 Initiate Estimate

We initialize with a regular fusion of the registered atlas labels via locally weighted vote (LWV). In particular, we define the weight on voxel i between the jth registered atlas image S_j and the target image T in terms of intensity similarity in a 3 × 3 × 3 neighborhood Ω

$$w_{ij}=exp\left(-\frac{{\mathrm{\sum }}_{k\in \mathrm{\Omega }}{\Vert S_{kj}-T_k\Vert }^2}{\sigma }\right)$$ (4)

where σ is a parameter that controls the de-weighting degree in terms of the local dissimilarity. Comparing to MV, LWV tends to capture a more complete spleen volume even though some regions are not covered by the majority of atlas labels.

2.3.2 Shape Registration

The pose-free implicit shape model is then transformed into the target space based on the registration between the binary image of the mean shape and that of the current segmentation. We found that a single registration on binary images is practically error-prone due the existence of massive missing/redundant structures. Therefore, we apply two registrations between these binary images with two distinct effective ranges, i.e., (1) the whole volume of both image and (2) the mean shape region, of the similarity metric of registration, so that the two sets of registered mean shapes tend to capture the outer and inner boundary of the current estimate, respectively. The registrations use normalized correlation criterion as the similarity metric with 7 DOF.

2.3.3 Shape Projection

The segmentations can then be projected to the registered shape model based on the mean shape registration which effectively constrains the estimate within the shape model. In particular, based on each set of two registrations, the pose-free shape model is transformed into the target space. The current estimate of the spleen is converted into SDF, i.e., Φ_c, and projected to two registered shape models.

$$\widehat{\mathit{\omega }}=U({\mathrm{\Phi }}_c-\overline{\mathrm{\Phi }})$$ (5)

where ω̂ is the projected shape parameter, which is then used to reconstruct the projected shape,

$$\widehat{\mathrm{\Phi }}=U^T\widehat{\mathit{\omega }}+\overline{\mathrm{\Phi }}$$ (6)

In implementation, we restrict the absolute value of projected shape parameter to be no larger than the square root of its corresponding eigenvalue to preserve a reasonable reconstructed spleen shape.

2.3.4 Shape-Probability Conversion

The output of the shape projection can be considered as the representation of how far voxels are inside/outside the projected spleen shape, which can be converted into a shape prior of how likely the voxels represent the spleen via an exponential function.

$$\mathrm{P}=exp(-\alpha \widehat{\mathrm{\Phi }})$$ (7)

where α indicates the steepness of the conversion from SDF to probability.

2.3.5 Iterative Refinement

The shape probabilistic priors, along with the label probability provided by LWV, are used to generate a new estimate of the spleen, and the fusion estimate can be refined with iterative adjustment.

Please refer to Fig. 3 to the detailed flowchart of the proposed framework.

Figure 3.

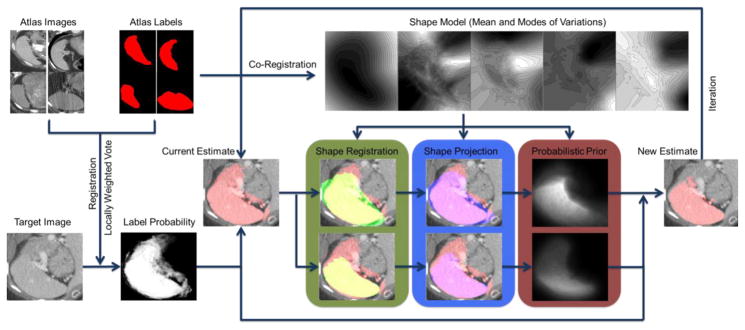
Flowchart of the proposed method. The atlas labels are co-registered to construct a pose-free implicit parametric shape model, including the mean and the modes of variation of the spleen shape. The atlas images are registered to the target image, based on which the atlas labels are propagated to the target space. The locally weighted vote yields the initial fusion result of the registered atlas labels weighted by the local intensity similarity between the registered atlas images and the target image in the form of a fuzzy estimate of label probability and a binary estimate of spleen segmentation. The binary image of the mean shape from the pre-constructed spleen shape model is registered to that of the current estimate with two distinct effective ranges, i.e., (1) the whole volume of both image and (2) the mean shape region, of the similarity metric of registration so that the pose-free shape model is transformed into the target space. The current estimate of the spleen is then projected to the two registered shape models. The shape projections are converted into probabilistic priors to adjust the label probability from locally weighted vote, and then generate a new estimate of the spleen. The estimate can be refined with iterative adjustment.

2.4 Data and Validation

Under an Institutional review board waiver, 25 portal venous phase contrast-enhanced CT abdomen scans were randomly selected from a larger ongoing colorectal cancer chemotherapy trial. Images were approximately 512 × 512 × 152 with a resolution of 0.7 × 0.7 × 3.0 mm. Scans with poor contrast bolus timing (i.e. not portal venous phase) or aberrant patient positioning were excluded, leaving 20 scans for analysis. Spleens were manually labeled by an experienced radiologist on a volumetric basis using the MIPAV software (NIH, Bethesda, MD [8]). All intensity and label images were cropped in terms of the bounding boxes around the localized spleen region as described in section 2.1.

All subjects are processed in a leave-one-out cross validation framework. Comparing to a baseline LWV method, our proposed shape-constrained method achieves significantly higher Dice similarity coefficient (DSC [9]) (Δ= 0.06, p < 0.01), significantly lower symmetric mean surface distance (Δ= −4.01 mm, p < 0.01), and significantly lower symmetric Hausdorff surface distance (Δ= −23.21 mm, p < 0.01) (Table 1) verified by Wilcoxon signed rank tests. Our shape-constrained method presents a substantial effect in correcting the spleen shape (Fig. 4).

Table 1.

Error metrics via different methods

Metrics	MV	LWV	Proposed method
Dice Similarity Coefficient	0.69±0.17	0.77±0.13	0.83±0.08
Symmetric Mean Surface Distance (mm)	8.01±6.12	7.49±7.66	3.48±1.88
Symmetric Hausdorff Surface Distance (mm)	33.81±19.00	45.88±27.84	22.67±8.23

Figure 4.

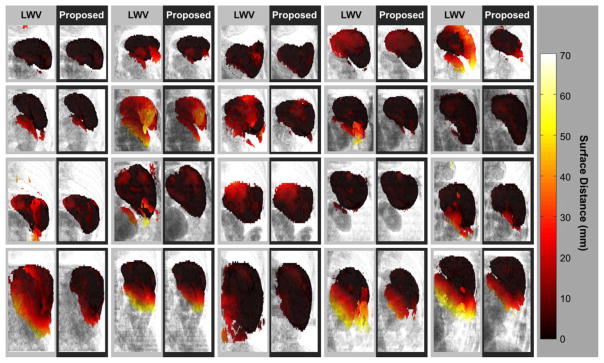
Fusion results by locally weighted vote and the proposed shape-constrained method on 20 subjects. The results of the two methods are placed side-by-side for each subject for comparison. The background rendering provides a reference of the surrounding anatomy (ribs, kidney, etc.). The rendering of the spleen segmentation is colored in terms of the surface distance from the estimate to the ground truth. Note that we use symmetric (the average of bi-directional) surface distance as the error metrics for validation in Table 1, but the one-way surface distance here for ease of visualization.

3. DISCUSSION

Spleen segmentation in CT images via multi-atlas segmentation can be detrimentally impacted by problematic registrations between atlases and target images. While the pose-free implicit shape model is not difficult to construct, challenges lie in the model-estimate alignment and shape-probability conversion. We used two sets of registrations with distinct effective ranges of similarity metric between the fusion estimate and the mean shape of shape model to provide the inner and outer boundary of the spleen shape to compensate for the uncertainty of the correct pose alignment. We project the fusion estimate to the registered shape model, which yields finer matchup with the fusion estimate under shape constraint. The projected shape represented in SDF is converted into the shape probabilistic prior through an exponential function, and thus regularizes the fusion estimate by shape information.

We note the pose-free implicit shape model can be built upon the atlas labels for label propagation with no additional data required. This presents opportunities to combine the proposed framework with the state-of-art label fusion methods (e.g., [10]) to yield shape-constrained fusion estimate. In addition, the usage of the shape information, beyond a simple probabilistic prior, requires further study.