Statistical label fusion with hierarchical performance models

Abstract

Label fusion is a critical step in many image segmentation frameworks (e.g., multi-atlas segmentation) as it provides a mechanism for generalizing a collection of labeled examples into a single estimate of the underlying segmentation. In the multi-label case, typical label fusion algorithms treat all labels equally – fully neglecting the known, yet complex, anatomical relationships exhibited in the data. To address this problem, we propose a generalized statistical fusion framework using hierarchical models of rater performance. Building on the seminal work in statistical fusion, we reformulate the traditional rater performance model from a multi-tiered hierarchical perspective. This new approach provides a natural framework for leveraging known anatomical relationships and accurately modeling the types of errors that raters (or atlases) make within a hierarchically consistent formulation. Herein, we describe several contributions. First, we derive a theoretical advancement to the statistical fusion framework that enables the simultaneous estimation of multiple (hierarchical) performance models within the statistical fusion context. Second, we demonstrate that the proposed hierarchical formulation is highly amenable to the state-of-the-art advancements that have been made to the statistical fusion framework. Lastly, in an empirical whole-brain segmentation task we demonstrate substantial qualitative and significant quantitative improvement in overall segmentation accuracy.

1. INTRODUCTION

Multi-atlas segmentation represents an extremely powerful generalize-from-example framework for image segmentation [1, 2]. In multi-atlas segmentation, multiple labeled examples (i.e., atlases) are registered to a previously unseen target-of-interest [3, 4], and the resulting voxelwise label conflicts are resolved using label fusion [5–10]. Herein, we focus on the problem of label fusion – a critical component of multi-atlas segmentation that has a substantial impact on segmentation accuracy.

Over the past decade, interest and research into the label fusion problem has exploded in popularity and significant improvement across an incredible range of applications has been shown. Broadly speaking, there are two primary perspectives on the problem of label fusion: (1) voting methods in which the underlying segmentation is modeled as some local, semi-local, or non-local weighted combination of the provided atlas information (e.g., [8–10]), and (2) statistical fusion methods in which the problem is cast from a Bayesian inference perspective and generative models of rater/atlas performance are maximized through an expectation-maximization (EM) [11] framework (e.g., [5–7, 12, 13]).

Regardless of the fusion approach, fusion algorithms typically treat all of the considered labels equally. As a result, the complex anatomical relationships that are often exhibited in multi-label segmentation problems are entirely neglected. To illustrate, consider a typical whole-brain segmentation problem in which there are often upwards of 100 unique labels that are estimated. Within those structures there are known anatomical and hierarchical relationships which could be leveraged – e.g., one such relationship might be medial frontal cortex → frontal cortex → cerebral cortex → cerebrum → brain (where “→” could be interpreted as “is part of”). While generalized hierarchical segmentation frameworks have been around for almost two decades (e.g., [14]) and recently considered for an application-specific voting fusion approach [15], a general hierarchical fusion framework has not been considered in the statistical fusion context.

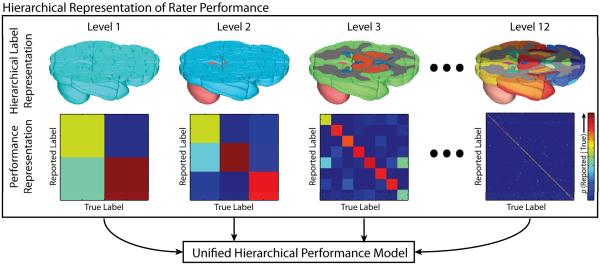
We propose a generalized statistical fusion framework using hierarchical models of rater performance. Building on the seminal Simultaneous Truth and Performance Level Estimation (STAPLE) [7] algorithm, we reformulate the rater performance model to utilize hierarchical relationships through a multi-tier performance model (Figure 1). The proposed model is built on the simple concept that the performance of a rater at the higher levels of the hierarchical model (e.g., brain vs. non-brain or cerebrum vs. cerebellum) should propagate to the lower levels of the hierarchy (i.e., the individual labels-of-interest) in an informed manner. This work (1) provides an important theoretical advancement to the underlying theory of statistical fusion, (2) demonstrates superior performance in both simulated and empirical whole-brain data, and (3) shows that the proposed framework is amenable to many of the current advancements in the statistical fusion family.

Figure 1.

Hierarchical representation of rater performance. A hierarchical model is developed for the brain, where, at each level, the performance of a rater is quantified. The overall quality of rater is then estimated through the unified hierarchical performance model.

This manuscript is organized in the following manner. First, the theory for the generalized hierarchical statistical fusion is derived. Second, we demonstrate superior performance on both simulated and empirical whole-brain segmentation data. Finally, we conclude with a brief discussion on the optimality of the approach and the potential for improvement.

2. THEORY

2.1 Problem Definition

Let T∈L ^N×1 be the latent representation of the true target segmentation, where L = {0, …, L – 1} is the set of possible labels that can be assigned to a given voxel. Consider a collection of R raters (or registered atlases) with associated la decisions, D∈L ^N×R. The goal of any statistical fusion algorithm is to estimate the latent segmentation, T, using the observed labels, D and the provided generative model of rater performance.

2.2 Hierarchical Performance Model

Consider a pre-defined hierarchical model with levels. At each level of the hierarchy, let ${\mathcal{S}}_m\in \mathcal{S}=\{{\mathcal{S}}_0,\cdots ,{\mathcal{S}}_{M-1}\}$ be a mapping vector that maps a label in the original collection of labels, s ∈ L, to the corresponding label at the be m^th level of the, hierarchy, ${\mathcal{S}}_{ms}\in {\mathit{L}}^m$ is the collection labels at the m^th level of the hierarchy. Additionally, let the performance of the raters at hierarchical level m be parameterized by ${\theta }^m\in {\mathbb{R}}^{R\times L^m\times L^m}$ (i.e., L^m × L^m confusion matrix for each rater). Specifically, ${\theta }_{j{\mathcal{S}}_{m{s}^{{\prime }^{{\mathcal{S}}_{ms}}}}}^m$ is the probability that rater j observes label s' given that the true label is m^th at the m^th level of the hierarchy. Thus, the generative model that must be defined is described by

$$f(D_{ij}=s^{\prime }\mid T_i=s,\mathcal{S},\{{\theta }^0,\dots ,{\theta }^{M-1}\left\}\right)$$ (1)

which can be directly interpreted as the probability that rater j observes label s' given the true label, hierarchical model, and the corresponding confusion matrices. To directly estimate this distribution we propose a formulation in which the complete model of hierarchical performance (Eq. 1) is unified through a constrained geometric mean across the multitier estimate of rater performance.

$$\begin{array}{cc}\hfill f(D_{ij}=s^{\prime }\mid T_i=s,\mathcal{S},\{{\theta }^0,\dots ,{\theta }^{M-1}\left\}\right)& ={\left(\prod _{m=0}^{M-1}f(D_{ij}={\mathcal{S}}_{m{s}^{\prime }}\mid T_i={\mathcal{S}}_{ms},{\theta }^m)\right)}^{{\alpha }_{js}}\hfill \\ \hfill & ={\left(\prod _{m=0}^{M-1}{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m\right)}^{{\alpha }_{js}}\hfill \end{array}$$ (2)

where, μ_js is an exponent that maintains the constraint that ${\Sigma }_{s^{\prime }}{\left({\Pi }_m{\theta }_{j{\mathcal{S}}_{m{s}^{{\prime }^{{\mathcal{S}}_{ms}}}}}^m\right)}^{{\alpha }_{js}}=1$. In other words, μ_js ensures that the model in Eq. 1 is valid discrete probability mass function. Note, given the constraints on each individual θ^m (i.e., a valid confusion matrix) a unique value for μ_js is guaranteed to exist and can easily be found using a standard searching algorithm (e.g., binary search, gradient descent). Given the model in Eq. 2, it is now possible to utilize the provided hierarchical model within the EM-based statistical fusion framework.

2.3 E-Step: Estimation of the Voxelwise Label Probabilities

Let $\mathit{W}\in {\mathbb{R}}^{L\times N}$ where ${\mathit{W}}_{si}^{\left(k\right)}$ represents the probability that the true label associated with voxel i is label s at iteration k of the algorithm given the provided information and model parameters

$$W_{si}^{\left(k\right)}\equiv f(T_i=s\mid \mathit{D},\mathcal{S},{\{{\theta }^0,\dots ,{\theta }^{M-1}\}}^{\left(k\right)}).$$ (3)

Using a Bayesian expansion and the assumed conditional independence between the registered atlas observations, Eq. 3 can be re-written as

$$W_{si}^{\left(k\right)}=\frac{f(T_i=s){\Pi }_{j}f(D_{ij}=s^{\prime }\mid T_i=s,\mathcal{S},{\{{\theta }^0,\dots ,{\theta }^{M-1}\}}^{\left(k\right)})}{{\Sigma }_{n}f(T_i=n){\Pi }_{j}f(D_{ij}=s^{\prime }\mid T_i=n,\mathcal{S},{\{{\theta }^0,\dots ,{\theta }^{M-1}\}}^{\left(k\right)})}$$ (4)

where f(Tⁱ = s) is a voxelwise a priori distribution of the underlying segmentation. Note that the denominator of Eq. 4 is simply the solution for the partition function that enables W to be a valid probability mass function (i.e., Σ_s W_si = 1). Using the simplified generative model in Eq. 2, the final form for the E-step of the EM algorithm can be written as

$$W_{si}^{\left(k\right)}=\frac{f(T_i=s){\Pi }_j{\left({\Pi }_m{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^{m,\left(k\right)}\right)}^{{\alpha }_{js}^{\left(k\right)}}}{{\Sigma }_{s^{″}}f(T_i=s^{″}){\Pi }_j{\left({\Pi }_m{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{m{s}^{″}}}^{m,\left(k\right)}\right)}^{{\alpha }_{j{s}^{″}}^{\left(k\right)}}}$$ (5)

2.4 M-Step: Estimation of the Hierarchical Performance Level Parameters

The estimate of the performance level parameters (M-step) is obtained by finding the parameters that maximize the expected value of the conditional log likelihood function (i.e., using the result in Eq. 5). Unlike the traditional STAPLE approach, however, the parameters for each level of the hierarchy are maximized independently.

$$\begin{array}{cc}\hfill {\theta }_j^{m,(k+1)}& =\underset{{\theta }_{\mathit{j}}^{\mathit{m}}}{\arg \max }\sum _{i}E\left[\text{ln}f\right(D_{ij}=s^{\prime }\mid T_i=s,\mathcal{S},\{{\theta }^0,\dots ,{\theta }^{M-1}\})\mid \mathit{D},\mathcal{S},{\{{\theta }^0,\dots ,{\theta }^{M-1}\}}^{\left(k\right)}]\hfill \\ \hfill & =\underset{{\theta }_{\mathit{j}}^{\mathit{m}}}{\arg \max }\sum _i\sum _s{W}_{si}^{\left(k\right)}\text{ln}f(D_{ij}=s^{\prime }\mid T_i=s,\mathcal{S},\{{\theta }^0,\dots ,{\theta }^{M-1}\left\}\right)\hfill \\ \hfill & =\underset{{\theta }_{\mathit{j}}^{\mathit{m}}}{\arg \max }\sum _i\sum _s{W}_{si}^{\left(k\right)}\text{ln}{\left(\prod _m{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m\right)}^{{\alpha }_{js}^{\left(k\right)}}\hfill \\ \hfill & =\underset{{\theta }_{\mathit{j}}^{\mathit{m}}}{\arg \max }\sum _i\sum _s{W}_{si}^{\left(k\right)}{\alpha }_{js}^{\left(k\right)}\sum _m\text{ln}{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m\hfill \end{array}$$ (6)

Noting the constraint that each row of the rater performance level parameters must sum to unity to be a valid probability mass function (i.e., ${\Sigma }_{s^{\prime }}{\theta }_{j{\mathcal{S}}_{m{s}^{{\prime }^{{\mathcal{S}}_{ms}}}}}^m=1$), we can maximize the performance level parameters at each level of the hierarchical model by differentiating with respect to each element and using a Lagrange Multiplier (λ) to formulate the constrained optimization problem. Following this procedure, we obtain

$$\begin{array}{cc}\hfill 0& =\frac{\partial }{\partial {\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m}\left[\sum _i\sum _s{W}_{si}^{\left(k\right)}{\alpha }_{js}^{\left(k\right)}\sum _m\text{ln}{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m+\lambda \sum _{s^{\prime }}{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^m\right]\hfill \\ \hfill -\lambda & =\frac{{\Sigma }_{i:{\mathcal{S}}_{m{D}_{ij}}={\mathcal{S}}_{m{s}^{\prime }}}{\Sigma }_{s^{″}:{\mathcal{S}}_{m{s}^{″}}={\mathcal{S}}_{ms}}{\alpha }_{j{s}^{″}}^{\left(k\right)}{W}_{s^{″}i}^{\left(k\right)}}{{\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^{m,(k+1)}}\hfill \\ \hfill {\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^{m,(k+1)}& =\frac{{\Sigma }_{i:{\mathcal{S}}_{m{D}_{ij}}={\mathcal{S}}_{m{s}^{\prime }}}{\Sigma }_{s^{″}:{\mathcal{S}}_{m{s}^{″}}={\mathcal{S}}_{ms}}{\alpha }_{j{s}^{″}}^{\left(k\right)}{W}_{s^{″}i}^{\left(k\right)}}{-\lambda }\hfill \\ \hfill {\theta }_{j{\mathcal{S}}_{m{s}^{\prime }}{\mathcal{S}}_{ms}}^{m,(k+1)}& =\frac{{\Sigma }_{i:{\mathcal{S}}_{m{D}_{ij}}={\mathcal{S}}_{m{s}^{\prime }}}{\Sigma }_{s^{″}:{\mathcal{S}}_{m{s}^{″}}={\mathcal{S}}_{ms}}{\alpha }_{j{s}^{″}}^{\left(k\right)}{W}_{s^{″}i}^{\left(k\right)}}{{\Sigma }_i{\Sigma }_{s^{″}:{{\mathcal{S}}_{ms}}^{″}={\mathcal{S}}_{ms}}{\alpha }_{j{s}^{″}}^{\left(k\right)}{W}_{s^{″}i}^{\left(k\right)}}\hfill \end{array}$$ (7)

where $s^{″}:{\mathcal{S}}_{m{s}^{″}}={\mathcal{S}}_{ms}$ is the collection of all labels that map to the true label of interest, ${\mathcal{S}}_{ms}$ and $i:{\mathcal{S}}_{m{D}_{ij}}={\mathcal{S}}_{m{s}^{\prime }}$ is the collection of all voxels in which the observed label, D_ij maps to the observed label of interest, ${\mathcal{S}}_{m{s}^{\prime }}$. At this point, it is important to note that (1) that performance model formulation in Eq. 2 allows for each level of the hierarchy to be maximized independently when maximizing the log-likelihood function, and (2) the result in Eq. 7 uses ${\alpha }_{js}^{\left(k\right)}$ which can then be updated following the constraint: ${\Sigma }_{s^{\prime }}{\left({\Pi }_m{\theta }_{j{\mathcal{S}}_{m{s}^{{\prime }^{{\mathcal{S}}_{ms}}}}}^{m,(k+1)}\right)}^{{\alpha }_{js}^{(k+1)}}=1$.

2.5 Initialization and Detection of Convergence

Given an a priori hierarchical model, there are no additional parameters in the proposed approach when compared to the original STAPLE algorithm. As a result, the algorithm can be initialized in exactly the same manner as described in [7]. With that said, the detection of convergence is slightly different, as we utilize all levels of the hierarchy. Thus, convergence is detected when the normalized trace between consecutive iterations falls below some arbitrary threshold (herein, ∈ = 10⁻⁴), where the normalized trace is given by

$$\frac{1}{\mathit{LRM}}\sum _j\sum _{m}tr\left({\theta }_j^m\right)$$ (8)

2.6 Application to state-of-the-art Statistical Fusion Approaches

Over the past decade, there have been several advancements to the statistical fusion framework, for instance (1) characterizing spatially varying performance – Spatial STAPLE [6], and (2) incorporation of non-local correspondence models – Non-Local STAPLE (NLS) [5]. In the interest of brevity, we only derive the hierarchical version of STAPLE in this manuscript. However, in the following experiments we demonstrate the amenability of the hierarchical approach to Spatial STAPLE, NLS, and the combination of the two Non-Local Spatial STAPLE (NLSS).

3. METHODS AND RESULTS

3.1 Motivating Simulation

Before assessing the empirical performance, we present a motivating simulation to demonstrate the manner in which hierarchical models can be integrated into the statistical fusion framework (Figure 2). Here, a single 2D slice model (300 × 300 voxels) was constructed to loosely approximate the types of relationships that are often exhibited in the brain. Given the provided truth model, a collection of 15 labeled observations were constructed by randomly applying boundary errors of varying strength (see Figure 2 for the best/worst observations). As baselines, the results of a majority vote, STAPLE, and Spatial STAPLE are presented. Additionally, we consider three different hierarchical models with depths ranging from 3 to 5. The presented simulation was performed with 20 Monte Carlo iterations in order to estimate the variance in the results. The results in Figure 2 demonstrate substantial qualitative and significant (p < 0.01, paired t – test) improvement exhibited by the hierarchical implementations of both STAPLE and Spatial STAPLE. The different hierarchical models provide important insight into the effect of differing perspectives on the hierarchical relationships exhibited in the data. Here, the 4-level model was statistically superior to both the 3-level model and the 5-level model. While the proposed formulation relies on an a priori hierarchical model, it is intriguing to quantify the impact of both neglecting the observed hierarchical relationships (i.e., the 3-level model) and over-modeling these relationships (i.e., the 5-level model).

Figure 2.

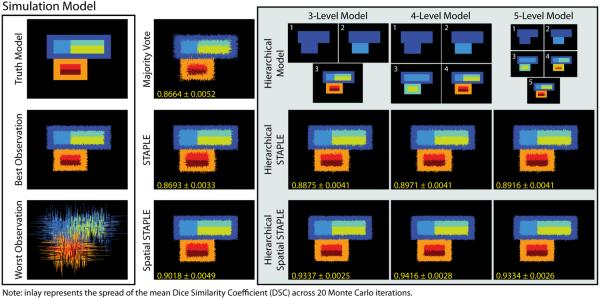
Results on the motivating simulation. A simulated truth model was constructed to loosely model the types of relationships exhibited in the brain. The hierarchical formulations of STAPLE and Spatial STAPLE provide significant increases in overall segmentation accuracy. Here, the 4-level model results in statistically superior performance when compared to the 3- and 5-level models.

3.2 Empirical Whole-Brain Data and Experimental Design

For the empirical whole-brain experiments, a collection of 45 MPRAGE images from unique subjects are considered as part of the Open Access Series of Imaging Studies (OASIS, http://www.oasis-brains.org) [16] with subjects ranging in age from 18 to 90. All images had a resolution of 1 × 1 × 1mm³. All images were labeled using the brainCOLOR protocol (http://www.braincolor.org/) [17] and provided by Neuromorphometrics, Inc. (Somerville, MA, www.neuromorphometrics.com). Each labeled image contained exactly 133 unique labels (including background). For the purposes of evaluation, 15 of these images were randomly selected as training data, and the remaining 30 were selected as testing data.

Herein, we consider two separate registration frameworks. First we consider an affine-only pairwise registration framework [3] (using “reg_aladin” as part of the “NiftyReg” package – http://sourceforge.net/projects/niftyreg/). Additionally, we consider a pairwise non-rigid registration framework in which the provided affine registrations are augmented with a non-rigid registration [4] (using the Advanced Normalization Tools (ANTs) package – http://stnava.github.io/ANTs/). For both registration frameworks, all 15 training atlases were independently registered to all 30 of the testing atlases – resulting in 450 registrations.

To evaluate fusion performance, we consider several algorithms. First, in order to provide a benchmark of algorithmic performance, we consider a majority vote and a locally weighted vote (as described in [8]). Additionally, we consider STAPLE, Spatial STAPLE, NLS, and NLSS as well as the hierarchical versions of each, referred to as Hierarchical STAPLE, Hierarchical Spatial STAPLE, Hierarchical NLS, and Hierarchical NLSS, respectively. For the hierarchical algorithms, we constructed a 12-level hierarchical model (manually constructed by an experienced neuroimaging analyst). Note, for clarity of presentation only NLSS and hierarchical NLSS are considered for the non-rigid registration approach.

3.3 Empirical Whole-Brain Results

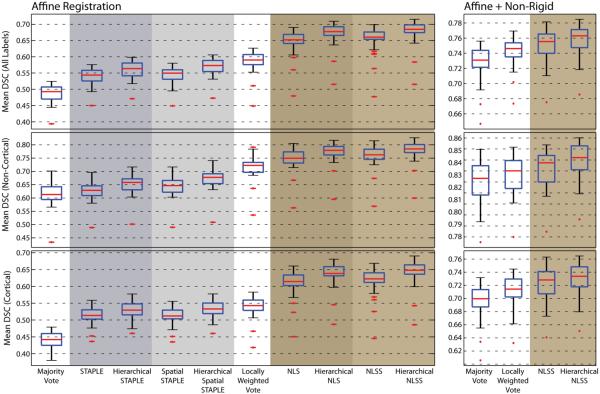
The quantitative results for the empirical whole-brain experiment (Figure 3) demonstrate consistent improvement by the hierarchical implementations of each of the considered statistical fusion algorithms. The quantitative results are broken up into 3 different categories (1) all labels, (2) non-cortical labels, and (3) cortical labels. As expected, the results for the cortical labels are considerably poorer than the results for the non-cortical labels. Regardless, the hierarchical implementations provide consistent improvement regardless of the differing label contexts. For the affine registration framework, the hierarchical implementations provided a mean improvement across the testing data of 0.0188, 0.0245, 0.0250, and 0.0237 for STAPLE, Spatial STAPLE, NLS, and NLSS, respectively. All improvements were statistically significant (p < 0.01, paired t – test). Note, the relatively poor performance by STAPLE and Spatial STAPLE are not surprising considering the fact that they do not utilize the atlas-target intensity differences when estimating the final segmentation.

Figure 3.

Quantitative results on the empirical whole-brain segmentation experiment. The hierarchical implementations of STAPLE, Spatial STAPLE, NLS, and NLSS provide statistically significant accuracy improvements across each of the considered label sets for the affine registration framework. Similarly, Hierarchical NLSS provides substantial accuracy improvements for the non-rigid registration framework.

For the non-rigid registration framework, Hierarchical NLSS provided a small, but significant mean improvement across the testing data of 0.0068 over NLSS. Despite this relatively small magnitude of improvement, Hierarchical NLSS provided statistically significant improvement (p < 0.01, paired t – test) over NLSS for labels (the remaining 54 were statistically indistinguishable).

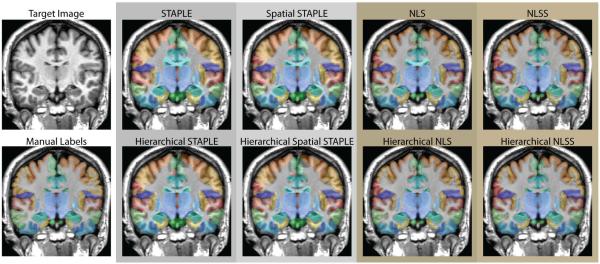
The qualitative results (Figure 4) support the quantitative improvement. Using the affine registration framework, all of the considered statistical fusion algorithms exhibit substantial visual improvement for many of the considered labels. In particular, there appears to be marked improvement in the quality of the lateral ventricle labels and many of the cortical labels.

Figure 4.

Qualitative improvement exhibited by several state-of-the-art statistical fusion algorithms with the reformulated hierarchical performance model for the affine registration framework. For each of the considered statistical fusion algorithms we see substantial visual improvement for many of the considered labels. In particular, there appears to be marked improvement in the quality of the lateral ventricle labels and many of the cortical labels.

4. DISCUSSION

Herein, we propose a novel statistical fusion framework using a reformulated hierarchical performance model. Given an a priori model of the hierarchical relationships for a given segmentation task, the proposed generative model of performance provides a straightforward mechanism for quantifying rater performance at each level of the hierarchy. The primary contributions of this manuscript are: (1) we have demonstrated statistically significant improvement on both simulated and empirical whole-brain data, (2) we have shown that the proposed hierarchical formulation is highly amenable to many of the state-of-the-art advancements that have been made to the statistical fusion framework, and (3) we have provided a theoretical advancement to the statistical fusion framework that enables the simultaneous estimation of multiple (hierarchical) confusion matrices for each rater.

There are several potential advancements to this framework that require future exploration. First, all of the presented experiments have relied upon an a priori model of the hierarchical relationships within the data. The ability to infer these hierarchical relationships directly from a provided training set would dramatically increase the potential applications for this type of framework, and provide an underlying foundation for estimating the optimal hierarchical formulation for a given application. Second, we have derived this approach from the perspective of hierarchical relationships between labels. However, the same (or very similar) estimation framework could potentially be used to estimate rater performance using multiple labeling protocols. For example, if one had a collection of datasets that were labeled using two separate protocols (either manually or automatically) it may be possible to (1) estimate the relationships between the protocols, and (2) simultaneously estimate rater performance in terms of both protocols. This type of framework is fascinating and certainly warrants further investigation.

We have presented a powerful theoretical framework for leveraging the complex inter-structure relationships within the statistical fusion context. While traditional fusion approaches treat all labels equally, the proposed rater model more accurately infers the types of errors that raters (or atlases) make within a hierarchically consistent formulation.