Factors affecting grip force: Anatomy, mechanics, and referent configurations

Abstract

The extrinsic digit muscles naturally couple wrist action and grip force in prehensile tasks. We explored the effects of wrist position on the steady-state grip force and grip-force change during imposed changes in the grip aperture (apparent stiffness). Subjects held an instrumented handle steady using a prismatic five-digit grip. The grip aperture was changed slowly, while the subjects were instructed not to react voluntarily to these changes. An increase in the aperture resulted in an increase in grip force and its contraction resulted in a proportional drop in grip force. The apparent stiffness values (between 4 and 6 N/cm) were consistent across a wide range of wrist positions. These values were larger when the subjects performed the task with eyes open as compared to eyes-closed trials. They were also larger for trials that started from a larger initial aperture. After a sequence of aperture increase and decrease to the initial width, grip force dropped by about 25% without the subjects being aware of this. We interpret the findings within the referent configuration hypothesis of grip force production. The results support the idea of back-coupling between the referent and actual digit coordinates. According to this idea, the central nervous system defines referent coordinates for the digit tips, and the difference between the referent and actual coordinates leads to force production. If actual coordinates are not allowed to move to referent ones, referent coordinates show a relatively slow drift towards the actual ones.

INTRODUCTION

Bernstein (1967) pointed out redundancy as a central feature of the human system for the production of voluntary movements. This means that, for typical tasks and different levels of analysis, there are fewer constraints than the number of variables (degrees-of-freedom). Grasping an object with the five digits is an example. Each digit exerts a six-dimensional wrench on the object. The five digits have in all 30 force/moment degrees-of-freedom, which must satisfy six constraints of statics (force and moment balance in the three-dimensional space).

The skeletal system is often modeled as a combination of serial and/or parallel chains. Redundancy can occur for (a) serial chains in kinematics, and (b) parallel chains in statics. Conversely, serial chains in statics and parallel chains in kinematics may face the problem of over-determinacy. This is another possibility arising when the number of constraints exceeds the number of variables (see Zatsiorsky 2002, Chapter 2). However, a serial chain can also be statically redundant if the task constraints define only a subset of the components of the six-dimensional force/moment vector at the endpoint (Xu et al. 2012).

We focus in this study on interactions between grip force production and wrist action. To hold an object vertical with the thumb and fingers in opposition in a prismatic grasp, the forces applied by the thumb and the four fingers normal to the contact surfaces must be balanced. These balanced forces are collectively called grip force (Murray et al. 1994). One aspect of the redundancy problem during static prehension is related to the fact that the balance of thumb and finger normal forces can be achieved for a variety of grip force values. Wrist action, for example keeping the wrist static or producing a net wrist moment of force, is also redundant because of the multiple muscles crossing the wrist. Thus, the task of ‘naturally’ gripping an object at a prescribed wrist location is redundant since both task variables are not uniquely defined.

The gripping and wrist actions share several muscles; flexor digitorum profundis (FDP) and flexor pollicis longus (FPL) contribute to wrist flexion and grip force production, while extensor digitorum communis (EDC) contributes to wrist extension and grip relaxation. The bellies of these muscles are located in the forearm, their tendons cross the wrist joint and insert at the base of the distal phalanges (Platzer 2004). Additionally, there are dedicated muscles for wrist flexion/extension that do not directly affect grip force, whereas the intrinsic muscles of the hand have no direct effect on wrist action but can contribute to grip force via the extensor mechanism. The presence of the multiple muscle groups with different actions on the wrist-grip system potentially allows for various muscle activation patterns compatible with any task; hence, the system is redundant at the muscle level.

This muscle architecture couples the grip force production and wrist action in nonobvious ways. In particular, we recently found asymmetric relations between isometric wrist flexion/extension and grip force in tasks that required only one of the two actions (Paclet et al. 2014). Furthermore, we manipulated the wrist flexion-extension angle thus changing the length of extrinsic muscles, and observed variations in the maximal grip strength according to the classic force-length curve (McMahon 1984). Rather unexpectedly, however, the submaximal, ‘natural’ grip force was independent of the wrist position (Ambike et al. 2013).

Grip force production has been commonly described and discussed at the level of digit force generation (Johansson and Westling 1984; Jaric et al. 2006; Parikh and Cole 2012). Within the referent-configuration (RC) hypothesis (Feldman and Levin 1996; Feldman 2011), external mechanical variables such as forces are results of neural processes that can be adequately described as shifts in referent values for salient body coordinates. With respect to grip force production, the central controller has been assumed to specify a referent aperture that is smaller than the actual aperture defined by the object shape (Pilon et al. 2007). Grip forces emerge as the muscles are activated in proportion to the difference between the referent and actual coordinates of the digit tips. The relation between the force generated by a finger and the discrepancy between its actual and referent coordinates depends on a stiffness-like property of the grasp termed “apparent stiffness” (see Latash and Zatsiorsky 1993).

Here, we investigate the apparent stiffness (AS) of the grip defined as the force change produced by a small change in the grip aperture. AS is a gross property of the grip that depends on many factors including the current length of the various flexor and extensor muscles and their tonic stretch reflex characteristics (Latash et al. 2010). Since the lengths of FDP, FPL, and EDC muscles changes with wrist flexion-extension, we hypothesized that grip AS would also vary with wrist flexion-extension to account for the unchanged grip force over the wrist range of motion (Hypothesis-1).

Grip AS is also expected to vary with initial grip aperture width due to the change in the length of the primary grip flexors. Since the slope of the tonic-stretch-reflex curve increases with muscle length within a typical physiological range (Matthews 1959; Feldman 1966; Feldman & Orlovsky 1972), we expected grip AS to increase with the initial aperture size (Hypothesis-2).

Another factor manipulated in the study was the presence/absence of visual feedback. We used eyes-open and eyes-closed conditions to alter feedback on the hand-held object orientation. In the former, the subjects were asked to maintain the vertical orientation of the handle by watching a bull-eye level. In the latter, the subjects were asked to ‘not change their command to the hand’. No feedback on grip force was provided in either condition. The study of the effects of visual feedback of handle orientation was exploratory. Furthermore, it has been known that the force produced in isometric conditions drops if no visual force feedback is provided, even when subjects try to maintain its magnitude (Slifkin et al. 2000; Vaillancourt and Russell 2002; Baweja et al. 2009). Based on these reports, we expected the grip force to drop after a transient change in the grip aperture (Hypothesis-3).

METHODS

Subjects

Three female and seven male subjects (age 25.8 ± 6.7 years, height 1.69 ± 0.1 m, mass 70.7 ± 12.4 kg, hand length 18.2 ± 1.1 cm, hand width 8.7 ± 0.4 cm) voluntarily participated in the study. All the subjects were right-handed based on self-reported hand use during writing and eating. The subjects had no history of neuropathy or upper limb trauma. All subjects gave informed consent according to the procedures approved by the Office for Research Protections of the Pennsylvania State University.

Equipment

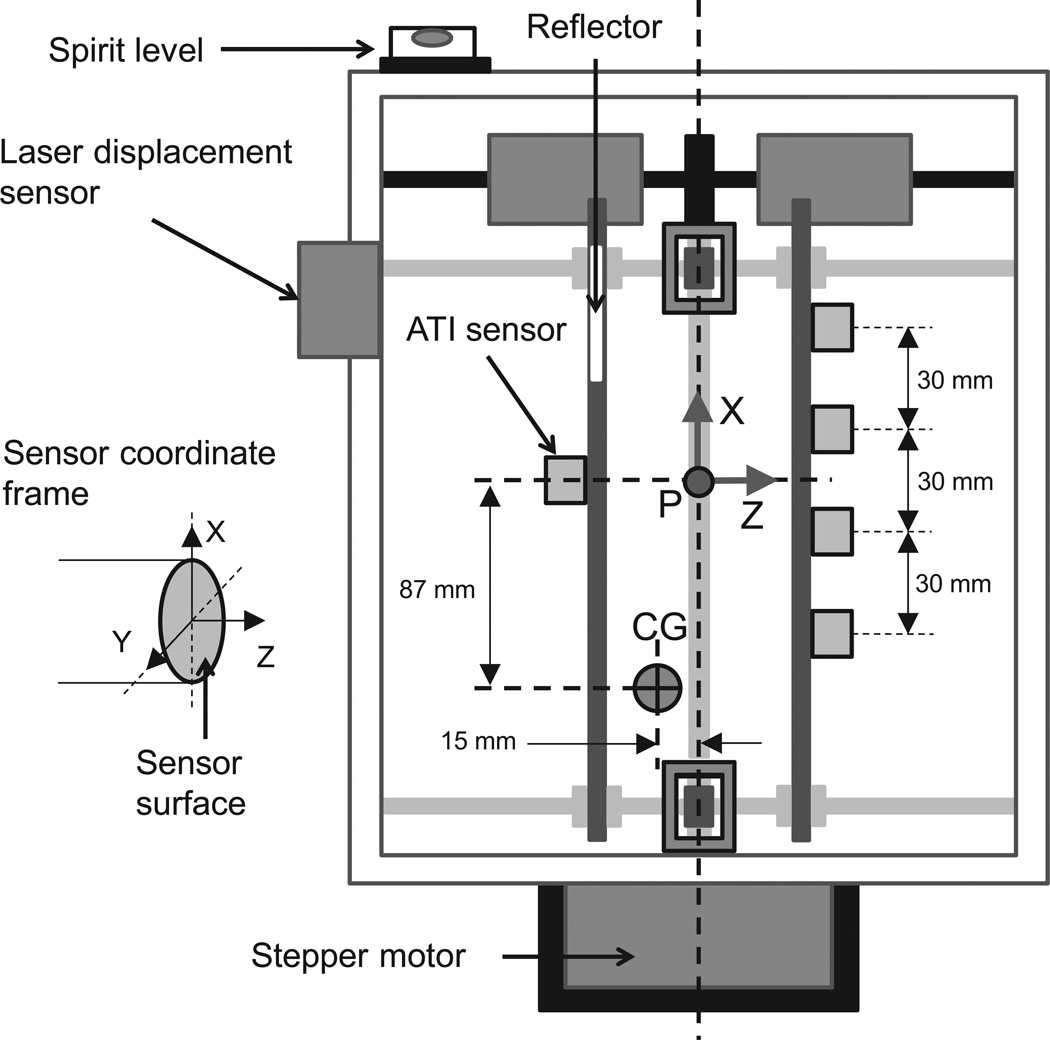
A metallic expanding handle, shown in Figure 1, was used to adjust grip aperture. Five 6-component (three force and three moment components) transducers (Nano 17, ATI Industrial Automation, Garner, NC) were mounted on the expanding handle. The sensors were aligned in the handle-fixed X–Z coordinate plane. An electric motor attached to a worm-and-screw arrangement was used to adjust the distance between the thumb and the finger sensors. This distance is defined as the aperture. The aperture changed symmetrically about the vertical axis of the handle. A laser displacement sensor (resolution, 0.015 mm; AR200-50M, Schmitt Measurement Systems, Portland OR) mounted on the handle measured the aperture width. A spirit level was placed on top of the handle. The entire assembly mass was 0.515 kg. The center of gravity (CG) of the assembly was 15 mm towards the thumb sensor from the midline of the handle and 87 mm below the line of attachment of the thumb sensor (data not shown). This CG location was estimated for an aperture of 8.5 cm.

Figure 1.

Schematic diagram of the expanding handle. The motor attached at the bottom changed the aperture width, i.e. the horizontal distance between the thumb and the finger sensor surfaces, symmetrically about the vertical axis. A handle-fixed coordinate frame is located at point P on the vertical symmetry axis of the handle and on a line passing through the center of the thumb sensor. The center of gravity (CG) of the assembly is towards the thumb sensor and displaced downward from point P. Each sensor measured digit forces and moments in a local coordinate frame shown.

Sandpaper (100-grit) was placed on the contact surface of each sensor to increase the friction between the digits and sensors. The digit pad–sandpaper static friction coefficient was about 1.4–1.5 (previously measured by Savescu et al. 2008). A wooden frame was constructed to support the subject’s forearm. A lever, attached to the frame via a hinge joint, supported the subject’s hand to prevent ulnar abduction. A potentiometer to measure the wrist flexion–extension (FE) angle was housed along the axis of the hinge.

Thirty analog signals from the sensors (5 sensors × 6 components) were routed to an analog–digital converter (PCI-6031, National Instruments, Austin, TX). The signal from the potentiometer, the laser and a trigger signal were sent to a serial port at the same time. The trigger signal indicated the instants when the motor on the handle was turned on or off. A customized LabVIEW program was used for data acquisition at 100 Hz with 16-bit resolution and subject feedback.

Experimental procedure

Subjects sat comfortably in a chair and rested their right forearm on the frame such that the shoulder was abducted at 45° and flexed at 0°, the elbow was flexed at 90°, and the palm faced medially. The forearm was strapped to the frame to prevent involuntary movement. The bottom of the hand rested on the lever. The hand was positioned so that the wrist flexion-extension axis was aligned with the hinge axis when the forearm and the hand were aligned (zero wrist flexion angle). The subjects gripped the instrumented handle with the digit tips and maintained its vertical orientation by watching the level.

Prior to testing, an orientation session acquainted the subjects to the experimental apparatus. The subjects were instructed to hold the handle with ‘natural’ grip force and to not intervene with possible force changes during changes of the grip aperture (Zatsiorsky et al. 2006). That is, subjects were told, “do not adjust your commands to your hand as the aperture changes”. Additionally, they were instructed to maintain the vertical orientation of the handle during the eyes-open conditions. They were required to ask for rest any time they felt tired.

The experiment consisted of two parts. In Part I, the subject held the expanding handle stationary in the right hand fingertips with the wrist in either the fully flexed or the fully extended position for 5 s. The aperture width was set to the maximum that the subject would experience over the course of the experiment (10.5 cm, see below). Four trials (2 flexions, 2 extensions) were performed in random order. The subject’s range of motion (ROM) was computed by selecting the smaller of the two extension and two flexion angles. The smaller angles were selected to avoid discomfort when the handle aperture increased during Part II of the experiment.

In Part II of the experiment, subjects held the handle with the right hand digits at five discrete wrist angles equally spaced over the subject’s ROM. At the start of each trial, the current wrist position (the potentiometer signal) and the desired wrist position were displayed on a computer screen. The subject aligned their wrist angle to match the specified wrist angle, leveled the handle using the spirit level, closed his/her eyes (for the eyes-closed conditions) and said ‘OK’ to indicate preparedness to the experimenter. At this time, the wrist-position feedback disappeared from the screen and then data collection commenced. During each individual trial, initial steady-state data were collected for about 10 s. Then the motor was turned on and the aperture started to increase. The laser signal was used to display the aperture width on another computer screen, visible to the experimenter only. The motor was stopped when the aperture increased by 1 cm and its direction reversed till the aperture returned to its initial width. Data were collected for an additional 10 s. The average motor speed was ~1.8 mm/s, so the expansion and the contraction phases lasted about 5.5 s each, and the entire trial lasted about 35 s. Each subject performed 60 trials: three repetitions at five wrist locations with two eye conditions (open and closed), and two initial aperture conditions (8.5 cm and 9.5 cm). The four conditions (eye conditions × initial aperture conditions) were blocked. The blocks with eyes closed were conducted first so that the subject’s performance during this condition could not be affected by her/his experience in the eyes-open condition. The blocks were randomized for initial aperture width across subjects, and the wrist positions were randomized within each block. There was a break of at least 10 s between the trials and a break of 10 minutes after the first two blocks to avoid fatigue. The total duration of the experiment was ~1.5 h.

Data analysis

MATLAB programs were written for data analysis. All data were low-pass filtered at a cutoff frequency of 10 Hz using a fourth-order, zero-lag Butterworth filter. In the sensor-fixed, local reference frame, the forces normal to the sensor surface correspond to the Z direction, and the X direction corresponds to the vertical, see Figure 1. Another reference frame is attached to the handle at point P such that the X-axes of the sensor-fixed and the handle-fixed reference frames are parallel, and the Z-axis of this frame points away from the thumb.

Grip mechanics

The analysis in this paper is limited to the grip plane defined as the handle-fixed X–Z plane in Figure 1. Grip force is the internal force exerted by the digits on the object. In the grip plane, the forces of the thumb (TH) and the virtual finger (VF) normal to the contact surfaces, i.e. F_Z^TH and F_Z^VF, respectively, must be balanced in static conditions. However, the hand-handle system is not necessarily static during aperture modulation in this study. Therefore, grip force F_G is defined as min(F_Z^TH, F_Z^VF) during the aperture modulation phases. During the static phases, since F_Z^TH = F_Z^VF, F_Z^TH is used as F_G. The net unbalanced force, called the manipulation force (Kerr and Roth 1986; Yoshikawa and Nagai 1991), leads to object motion. We quantified both the grip force and the manipulation force (see below), although the manipulation force was expected to be close to zero.

Similar to internal and manipulation forces, there may also exist an internal moment that causes no disturbance of the object’s rotational equilibrium, and a manipulation moment that tends to rotate the object. Analysis restricted to the grip plane includes moments about the handle-fixed Y-axis (Figure 1). Since our hypotheses primarily concern the grip force, we do not analyze the internal moment in this study. We only computed the net digit moment to quantify the external torque acting on the handle.

Determination of Apparent Stiffness

The term stiffness is often misused in human science literature (for a discussion, see Latash and Zatsiorsky 1993; Zatsiorsky 2002). Stiffness refers to the change in force per unit of quasi-static change in position while the system’s parameters remain invariant, an essential condition not always controlled in stiffness studies. We employ the term apparent stiffness defined as the change in force per unit change in aperture.

A perturbation of the aperture is represented as a vector Δw = [Δw₁ Δw₂ Δw₃ Δw₄ Δw₅]^T, where Δw_i is the perturbation in digit i, and T indicates vector transpose. For the analysis in the grip plane, the effect of the above perturbation on the digit forces and moments can be described by a (15 × 5) stiffness matrix [S] such that

$$\left[\begin{array}{c}\mathrm{\Delta }{f}^n\hfill \\ \mathrm{\Delta }{f}^t\hfill \\ \mathrm{\Delta }m\hfill \end{array}\right]=[\mathbf{S}][\mathrm{\Delta }w]$$

where Δfⁿ, Δf^t and Δm are the changes in (5 × 1) vectors of the forces F_Z, F_X, and moment M_Y, respectively, as measured in the sensor coordinate frames. To maintain handle equilibrium, the vector [Δfⁿ Δf^t Δm]^T must be in the null-space of the (6 × 15) so called grip matrix [G]:

$$[\mathbf{G}]\left[\begin{array}{c}\mathrm{\Delta }{f}^n\hfill \\ \mathrm{\Delta }{f}^t\hfill \\ \mathrm{\Delta }m\hfill \end{array}\right]=[\mathbf{0}]$$

The grip matrix allows us to determine the digit forces and moments required to exert a desired net force and moment on the grasped object (Mason and Salisbury 1985; Murray et al. 1994). Therefore, the above equation represents a constraint on the variations of the digit forces and moments for maintaining object equilibrium.

The analysis in the present study is performed in the grip plane and at the level of the thumb and the VF rather than that of the individual digits. Therefore, the grip stiffness value of interest is computed in the handle-fixed reference frame. In general, a grip stiffness matrix [S₀] can be obtained from the matrix [S] by applying rigid-body transformations. Such a matrix [S₀] is 3 × 3 for the planar case, in which the diagonal terms describe the change in the internal forces F_Z, F_X, and internal moment M_Y due to small changes in the corresponding kinematic variables. The off-diagonal terms describe the changes in the forces and moment due to changes in other kinematic variables (e.g., change in force F_Z due to perturbation along the X axis). In the ensuing analysis, only the AS along the handle-fixed Z-axis is computed: AS = δ(F_G)/δ(aperture).

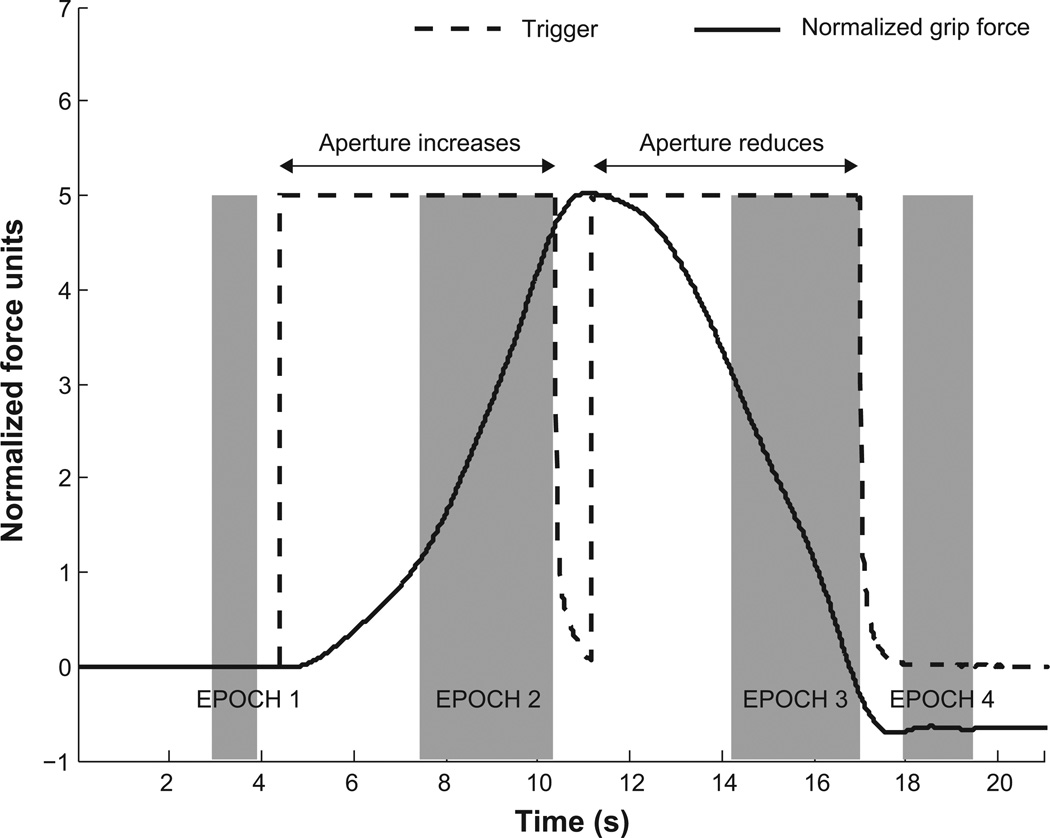
All forces and moments measured in the local sensor frames were transformed into the common handle-fixed reference frame located at point P. For each trial in Part II of the study, the trigger signal provided four time points: two indicating the starting of the motor (in two directions), and two indicating its stopping. These time points were used to segment the data for that trial into four epochs. Figure 2 illustrates the four epochs for a typical trial. It shows the trigger signal (dashed black trace) and the normalized grip force (thick black trace) against time. The first epoch was the initial steady state lasting between 1.5 and 0.5 s before the first trigger (motor turned ON). The motor speed rose from zero to the prescribed speed over 2.5 s (duration previously measured by Zatsiorsky et al. 2006), and therefore, the second epoch – the opening of the aperture – started 3 s after the first trigger and lasted up to the second trigger (motor turning OFF). Similarly, the third epoch was the closing of the aperture, and it started 3 s after the third trigger (motor turning ON) and lasted up to the fourth trigger (motor turning OFF). This provided a window of 6.6 ± 0.8 mm and 6.3 ± 0.9 mm (mean ± SD) for the second (aperture opening) and third (aperture closing) epochs, respectively, for obtaining estimates of AS. The total duration of the perturbation from the first to the fourth trigger signal was 12.4 ± 0.4 s (averages are across all trials). In previous studies, the window size used was up to 6.5 mm (Zatsiorsky et al. 2006) and ≤ 7 mm (Van Doren, 1998). The final epoch was the steady state starting 0.5 s after the last trigger and lasted 1.5 s.

Figure 2.

Typical subject response. The normalized grip force (thick black trace) and the trigger signal (dashed black trace) are plotted against time. The initial value of the normalized force at time 0 s is arbitrarily set to zero. Grip force increases as the aperture increases and decreases as the aperture reduces. The data is partitioned into four epochs associated with the initial steady state, aperture opening, aperture closing, and the final steady state. These are indicated as shaded bands.

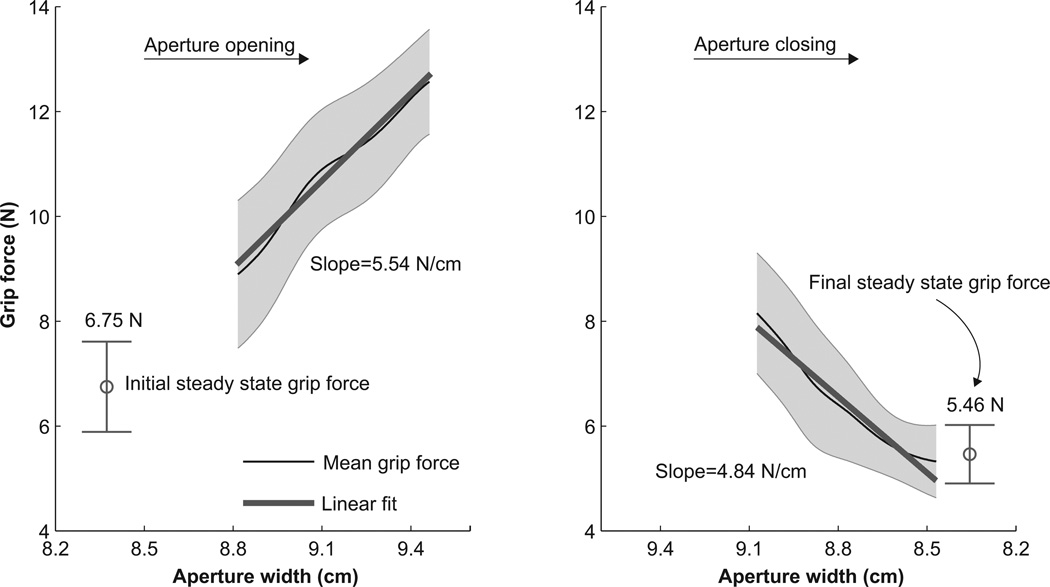
Following the segmentation, data from the three repetitions for each condition were averaged and used to compute the AS during epochs two and three and the steady state grip force during epochs one and four. Figure 3 shows representative data from one subject. The three repetitions for a particular wrist position, eye condition, and initial aperture size were averaged to obtain the mean grip force traces during the opening and closing of the aperture shown in the left and right panels of Figure 3, respectively (epochs two and three). The AS is the slope of the linear fits to these mean traces. The mean of the data from epochs one and four pooled across all repetitions of the task provide the initial and final steady state grip forces, respectively. These are also shown in Figure 3. Linear fits to the plots “grip force vs. aperture width” yielded good estimates of the AS. The median of the coefficients of determination for all fits was 0.9847 and its interquartile range was 0.0307.

Figure 3.

Computation of grip force and apparent stiffness (AS) for a representative subject. Data averages are across three repetitions for a particular wrist position, eye condition, and initial aperture size. Left panel shows the initial steady-state grip force (mean and SD) and the mean (black line) and SD (black band) of the grip force as the aperture increases from left to right. The right panel shows the mean (black line) and SD (black band) of the grip force as the aperture decreases from left to right and the final steady state grip force (mean and SD). The thick black line in each panel are the linear regression lines to the mean grip forces. The slopes of these linear fits are the AS.

Unbalanced digit forces and moments

The components of the handle assembly move during the aperture-manipulation phase of the experiment. This might lead to unbalanced forces and moments on the handle, which implies movement of the handle. The net digit force, after adjusting for handle weight was small indicating that the handle was stationary during the trials. The mean and standard deviation (SD) of the magnitude of the sum of all finger forces and handle weight (the manipulation force on the handle) was 0.63 ± 0.7 N with a maximum value of 1.6 N. These unbalanced forces are considered small.

The net digit moment magnitude and the net digit moment along the handle-fixed Y-axis M_Y (wrist pronation-supination) were analyzed in detail. A consistent, non-zero moment was applied by the digits on the handle to counter the unbalanced external torque. Possible sources of this external torque are the handle weight, since the handle CG is not located at point P (Figure 1), and cables of the sensors and the laser. In particular, the digits apply a consistent supination moment (M_Y) of about 50 Nmm on the handle. The detailed analysis is provided in Appendix A.

Statistics

Most data are presented as means and standard deviations (SD). The AS values were analyzed with a 4-way repeated measures ANOVA with factors Ramp (aperture opening and aperture closing), Eye-condition (open and closed), Initial-aperture (small and large), and Wrist-position (5 levels). Similarly, the steady-state grip force values were analyzed with four-way repeated-measures ANOVA with factors Perturbation (before and after), Eye-condition, Initial-aperture, and Wrist-position. All data were pooled across subjects. All statistics were performed using an α-level of 0.05. Mauchly’s sphericity tests were performed to verify the validity of using repeated-measures ANOVA. The Greenhouse-Geisser adjustment to the degrees-of-freedom was applied whenever departure from sphericity was observed. Significant effects of ANOVA were further explored using pairwise comparisons with Bonferroni corrections. All possible pairwise contrasts were conducted. All statistics were performed with SPSS statistical software.

The 4-way ANOVA for AS revealed a significant 4-way interaction effect (p < 0.05). Instead of interpreting this interaction, we pooled the data across the Ramp factor, which failed to show a significant main effect (p = 0.429), by taking the arithmetic mean of the AS values in the aperture opening and closing conditions. A 3-way repeated-measures ANOVA was then performed on the pooled AS data with the remaining three factors. The results of the 3-way ANOVA are reported below.

RESULTS

Apparent grip stiffness

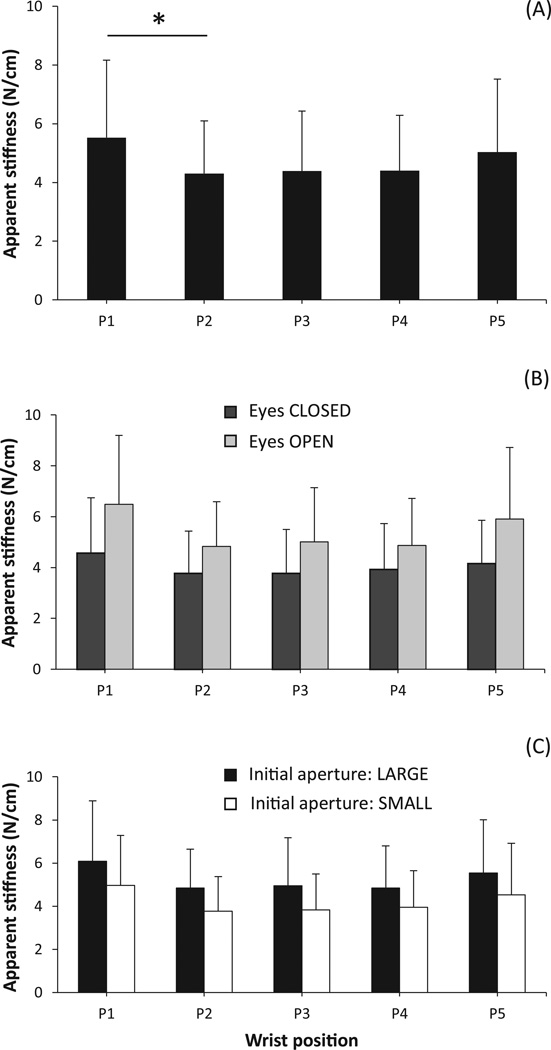
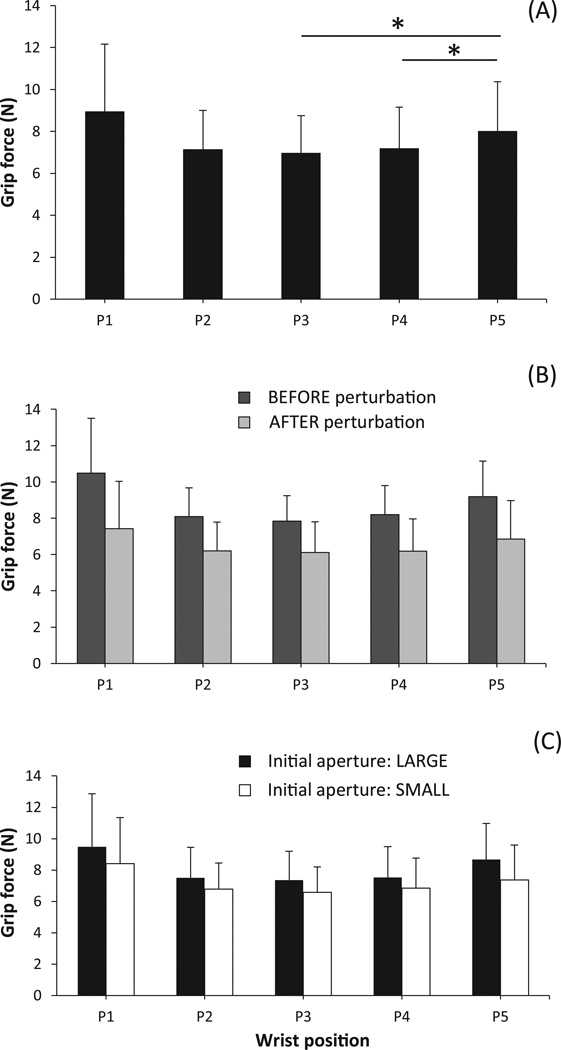
Changes in the grip aperture produced by the motor led to grip force (F_G) modulation. An increase in the aperture width led to an increase in F_G, whereas a decrease in the aperture width led to a drop in F_G (illustrated in Fig. 3). The apparent stiffness (AS) computed as the slope of the F_G dependence on aperture width showed a weak dependence on wrist position: While the effect of Wrist-position was significant (F_(1.84,16.63) = 7.69; p < 0.01), pairwise contrasts confirmed only a significant difference between the most flexed wrist position and the neighboring position (5.5±2.7 N/cm vs. 4.3±1.8 N/cm for positions P1 and P2 in Fig. 4 (A)). No significant differences across the four wrist positions from P2 to P5 were observed.

Figure 4.

Apparent stiffness mean and SD across various conditions. Wrist positions are labeled from P1 to P5 ranging from flexion to extension in that order. Significant differences are indicated with a star (*).

Performance of the task with eyes closed was associated with deviations of the handle from the vertical (on average, 10° ± 8°), while the handle was sufficiently close to the vertical within the error margin provided by the spirit level (2° ± 0.8°) in the eyes-open condition (repeated measures t-test: t₍₉₎ = 11.151; p < 0.01). When the subjects performed the task with eyes open the AS was larger than with eyes closed (5.4±2.4 N/cm vs. 4.0±1.8 N/cm, F_(1,9) = 12.22; p < 0.01). AS also depended on the initial aperture: It was larger for the wider aperture as compared to the smaller one (5.3±2.3 N/cm vs. 4.2±2.0 N/cm, F_(1,9) = 36.19; p < 0.01). The last two effects were uniform across all wrist positions, as seen in Figures 4(B) and (C).

Steady-state grip force

The ordered increase-decrease change in the grip aperture led to a change in F_G: The steady-state F_G value was significantly greater before the perturbation than after (8.7±2.2 N vs. 6.6±2.0 N; F_(1,9) = 31.64; p < 0.01). This effect was uniform across all wrist position (Fig. 5(B)). The subjects applied higher F_G in conditions with the larger grip aperture as compared to those with the smaller aperture (8.1±2.5 N vs. 7.2±2.2 N; F_(1,9) = 113.72; p < 0.01); see Fig. 5(C). They also had a tendency to apply stronger F_G when wrist position was close to one of the limits of the wrist range of motion (F_{(1.259,11.327)} = 6.963; p < 0.05). Pairwise contrasts confirmed significantly larger grip force at the extreme extension posture (P5 in Fig. 5 (A)) compared to its neighboring postures (8.0±2.3 N at P5 compared to 7.2±1.9 N at P4 and 6.9±1.7 N at P3). At the extreme flexion posture (P1), F_G was higher than at the neighboring postures (P2 and P3, see Fig. 5 (A)), but these differences did not reach statistical significance. Finally, F_G for the eyes-closed condition was smaller than that for the eyes-open condition (7.4±2.3 N vs. 7.9±2.5 N), but this difference did not reach statistical significance (F_(1,9) = 3.376; p = 0.099).

Figure 5.

The steady state grip force mean and SD for various conditions. Wrist positions are labeled from P1 to P5 ranging from flexion to extension in that order. Significant differences are indicated with a star (*).

There were also significant two-way interactions: Initial-aperture × Perturbation (F_(1,9) = 9.89; p < 0.05), Eye-condition × Initial-aperture (F_(1,9) = 7.99; p < 0.05), Perturbation × Wrist-position (F_(2.21,19.89) = 6.41; p < 0.01), and Eye-condition × Wrist-position (F_(4,36) = 3.96; p < 0.01). The first interaction results from the fact that the drop in F_G after the perturbation was larger for the large initial aperture size. The second interaction effect appears because the effect of eye condition on grip force (higher F_G for the eyes-open condition) was evident only for the small initial aperture. The third interaction reflects the fact that F_G was more uniform across wrist positions after perturbation than before the perturbation. Finally, Eye-condition had minimal effect on F_G only in wrist position P2; this yielded the last interaction effect.

It is well-known that a slow drop in isometric force occurs when the subject’s visual feedback of that force is removed, even as the subjects try to keep the force constant (Slifkin et al. 2000; Vaillancourt and Russell 2002; Baweja et al. 2009). In the present study, F_G was not expected to drop, for example to avoid slippage of the object. To test this, two subjects performed a control trial where they held the handle for 35 s while no change in grip aperture took place. Across all wrist positions and aperture sizes, the subjects showed, on average, a net drop in F_G of 0.6 N and 0.4 N, which is substantially lower than the average drop in F_G across the main experimental series: 2.2 ± 1.2 N.

DISCUSSION

The first hypothesis formulated in the Introduction – grip apparent stiffness (AS) would vary with wrist position – received partial support. While AS varied, this variation was limited to postures in a close proximity to the fully flexed wrist position. This observation is consistent with our earlier study (Ambike et al. 2013) wherein the “natural grip force” for the extreme wrist flexion was higher than for all other wrist positions. Other wrist positions had no effect on AS; so, for those positions Hypothesis-1 is rejected by the data.

Hypothesis-2 –AS increases with initial aperture size – is supported by the data. The larger initial grip aperture resulted in larger AS values. This result is in contrast to the findings of (Van Doren 1998) who reported only slight changes in AS with aperture size. This may be explained by the fact that the initial apertures used in this work were larger than those used by Van Doren, 8.5 and 9.5 cm compared to the maximum aperture of 6.5 cm in Van Doren’s study.

Hypothesis-3 is also supported by the data. Absence of visual feedback on the grip force during steady-state trials with no changes in the grip geometry resulted in some drop in grip force (Δ(F_G) < 1 N, control trials). However, we observed a consistent and larger drop in grip force after the cycle of handle expansion-contraction of similar duration (average Δ(F_G): 2.1 N). These results are consistent with earlier reports on a drop in the force produced in isometric accurate force production tasks after visual feedback had been turned off (Slifkin et al. 2000; Vaillancourt and Russell 2002; Baweja et al. 2009). While in the cited studies, force level was instructed but served no ecological purpose, in the current study F_G had to be above a certain value to prevent object slip. The potentially dangerous drop in F_G suggests that the underlying mechanism is powerful and can override, at least partly, safety constraints imposed by the friction conditions at the digit-object interface.

With respect to the exploratory goal, we observed that AS increased in conditions when the subjects were required to maintain handle orientation. The possible role of visual feedback is discussed below.

Grip force via referent aperture control

One of the least expected results of the current study is the relative independence of AS of the length of extrinsic hand muscles. Wrist joint rotation over most of its range produced little change in AS despite the large changes in the length of the extrinsic digit flexors (FDP and FPL). The estimated FDP tendon excursions over ± 50° wrist flexion-extension from the nominal position (the palm aligned with the forearm) ranges from 2.39 cm for the little finger to 2.18 cm for the middle finger (Lemay and Crago 1996; Brand and Hollister 1999; Paclet 2010). These observations are congruent with the constancy of “natural F_G” over the range of wrist flexion-extension positions (Ambike et al. 2013). Both groups of observations are in contrast to the strong modulation of the maximal F_G throughout the same range of wrist positions (Ambike et al. 2013), which is in line with the classic muscle force-length curve (McMahon 1984).

We analyze these results within the referent-configuration (RC) hypothesis (Feldman and Levin 1996; Feldman 2011) which is an extension of the classical equilibrium point hypothesis (Feldman 1986) to multi-effector actions. The RC hypothesis assumes that the central nervous system uses changes in neural variables that, given the external force field, produce changes in the body (effector) RC. Referent configurations are commonly not accessible to the effector because of anatomical and external constraints. As a result, equilibrium states are observed with non-zero muscle activations and active forces produced on the environment.

According to the RC hypothesis (Pilon et al. 2007), grip forces emerge as muscles are activated in proportion to the difference between the referent coordinates for the digit tips and their actual coordinates. Assuming that the resultant force acting normal to the digit-handle contact surface is zero, the two referent coordinates – for the thumb and for the four fingers combined – may be united into a single variable, the referent aperture (however, see discussion below). In a linear approximation, F_G magnitude is related to the difference between the referent and actual apertures by the AS. Assume now that, at a control level, a certain referent aperture is specified in the handle-fixed reference frame. Since the actual aperture does not depend on wrist angle, over the range of wrist flexion-extension, AS defines F_G unambiguously. Our results of constant AS throughout most of wrist range of motion and higher AS at the extreme wrist flexion correspond well to the earlier report on constant F_G throughout the wrist motion with somewhat higher F_G at the extreme wrist flexion (Ambike et al. 2013).

Specifying referent values for the task-relevant variables in an object-fixed reference frame may simplify object manipulation. An intuitive analogy is as follows. Imagine a fiddler playing music with the fiddle in various configurations relative to the body, e.g., over the shoulder or even behind the back. The claim here is that the fiddler’s central nervous system learned to control the task using referent coordinates of various fingers in a reference frame fixed to the fiddle rather than to the body or to the external world. Then, the position of the fiddle relative to the body becomes irrelevant for the successful execution of the task.

How many variables define the referent configuration?

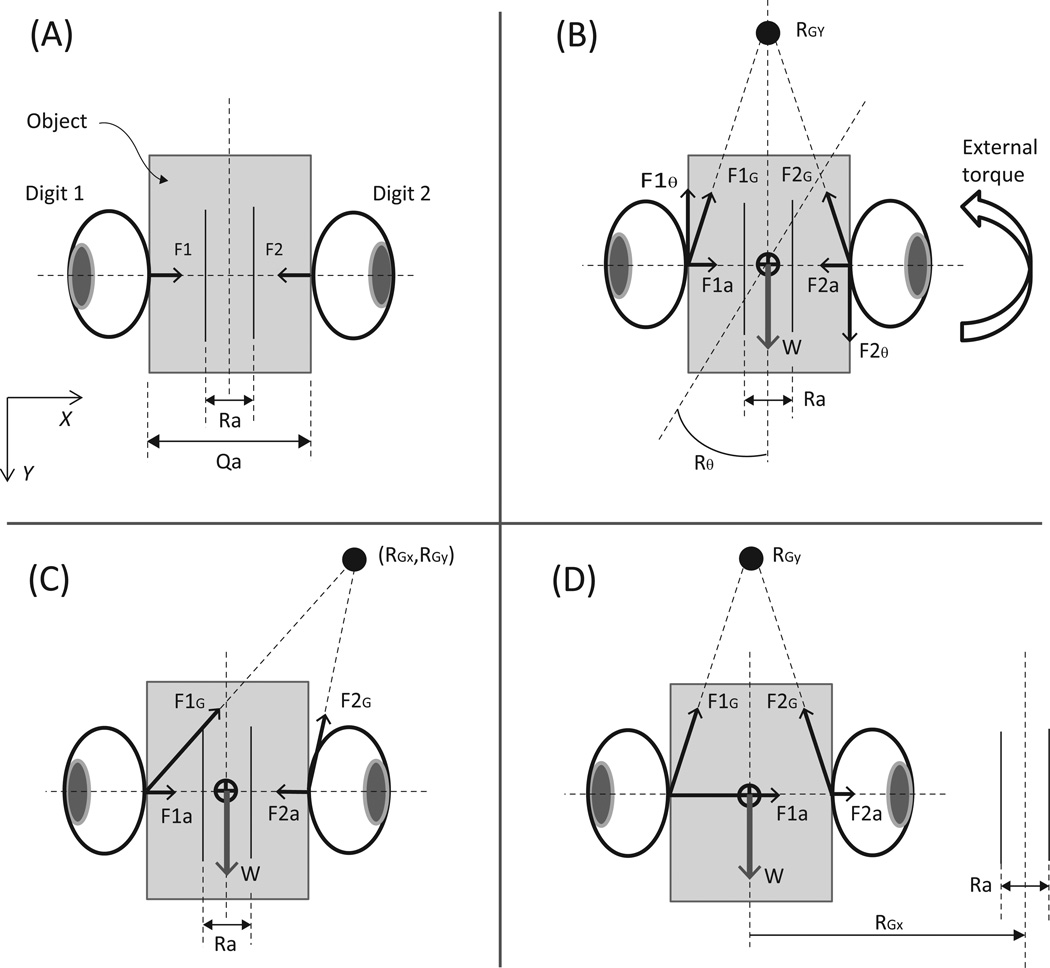
For static prehension tasks, the referent aperture may be visualized as shown in Figure 6(A). If the digits rest on parallel surfaces, the aperture is viewed as two lines parallel to the digit-object contact surfaces, displaced by equal amounts from those surfaces. The magnitudes of the forces at the contact surfaces are equal and are given by F₁ = −F₂ = AS(Qa-Ra)/2, where Qa is the object-defined actual aperture, and Ra is the central-nervous-system-specified referent aperture. Such schemes are implied or explicitly depicted in literature (Pilon et al. 2007; Latash et al. 2010). This picture suggests that: (a) the relation between the generated force and the differences between the current and referent positions is the same for the opposing digits, (b) the AS of the opposing digits is the same, and (c) a single variable Ra is sufficient for specifying F_G.

Figure 6.

Referent apertures and the mechanism of grip force generation. Figure 6(A) depicts the simplest case wherein two digits statically balance the object without applying any moment. Figure 6(B) depicts a possible way in which the referent coordinates can be modulated to counter object weight w and external torque acting on the object. Figures (C) and (D) depict two possible ways in which changes in four referent coordinates can produce movement of the object to the right. In all cases, the forces measured at the digit-object interface are the vector sum of the digit forces resulting from the prescribed values for all four referent coordinates. Assume zero external torque for simplicity. So, R_θ = 0.

In this study, we found that (1) symmetrical changes in actual configurations of the thumb and VF induced symmetrical changes in their respective forces (since unbalanced forces were small), and (2) these changes were linearly related to changes in the aperture produced by the motor. This suggests that the statements (a) and (b) above are reasonable. However, in the case of multi-finger prismatic grasp, Zatsiorsky et al. (2006) showed that, although the AS values for the thumb and VF were similar, those for individual digits were different. Therefore, the AS of the VF may be viewed as associated with four ‘digit-springs’ acting in parallel: AS_TH = AS_VF = ΣAS_i, where i = {index, middle, ring, little}, when the gripping surface is a plane. It is possible that the preferred distribution of the referent coordinate for the VF across the four actual fingers (see Latash et al. 2010) reflects the different AS values for the fingers.

There is some debate regarding the number of variables that define object gripping. For example, Smeets & Brenner (1999) suggest that gripping is akin to two independent pointing actions of opposing digits rather than a single change in hand aperture. On the other hand, Latash et al. (2010) suggest a more complete set of referent coordinates (Fig 6 (B)) for static object grasping in a gravity field and in the presence of external torques. In this scheme, hand control in a planar task may be described with referent values for three variables, referent aperture (Ra), referent vertical coordinate (R_GY), and referent angle (R_θ) with respect to the vertical (Y axis in Fig. 6). The force of digit i is the vector sum of forces arising due to (a) the difference between the referent and actual apertures (F_ia) along the X axis, (b) the difference between the referent and actual vertical coordinates (load resisting force F_iG), and (c) the difference between the vertical orientation of the object and its referent orientation (external torque-resisting moment of force via vertical forces F_iθ). This depiction assumes point contacts (Mason and Salisbury 1985).

During object manipulation, however, it is evident that digit forces are unequal so that the resultant manipulation force creates object motion. Slota et al. (2011) show that the unequal thumb and VF normal forces can be predicted from the object’s acceleration; a non-trivial result since only the unbalanced normal force is mechanically related to object acceleration. Two plausible ways of extending the referent coordinate idea to incorporate object manipulation are illustrated in Figures 6 (C) and (D). First, object manipulation in the vertical direction and object rotation is achieved by manipulating the referent coordinates R_GY and R_θ, respectively. Manipulation in the horizontal direction (more generally, in the direction of the digit normal forces) can be achieved by introducing another referent variable. In the first scenario, the referent aperture remains stationary relative the object, and the referent coordinate R_GY shifts while maintaining its vertical distance from the actual object center of gravity (CG). The additional reference coordinate is R_GX, and it generates oblique digit forces as shown in Figure 6(C). The second possibility is that the referent coordinate R_GY is unchanged relative to the object, and the referent aperture center shifts to a new location defined by R_GX. Note that here, digit 1 pushes against the object, and the object pushes against digit 2, so the normal forces measured at both the digit-object interfaces can point into the object. Since static equilibrium is a special case of object-grasp mechanics, it is reasonable to assume that at least four referent variables are necessary to describe planar object-grasp mechanics. Whether these speculations, or another set of four referent coordinates explain the findings of Slota et al. (2011), remains to be seen. Note that the actual RC dimensionality may be higher because it may include parameters that define muscle co-activation which have no or little effect on the net values of the mechanical variables.

Violations of equifinality of grip force

The significant drop in F_G after an “expansion-contraction” cycle of the grip aperture has been an unexpected finding. Ensuring adequate safety margin has frequently been viewed as one of the most powerful criteria that define F_G across conditions (Johansson and Westling 1984; Flanagan and Wing 1993; Flanagan and Tresilian 1994). In our experiment, a single 12-s cycle of the aperture width change led to a 25% drop in F_G. The safety margin for digit i (SM_i) is defined as SM_i = (F_N − F_T/μ)/F_N, where F_N and F_T are the normal and the vertical tangential forces of digit i, respectively, and μ is the friction coefficient (Westling and Johansson 1984; Burstedt et al. 1999; Zhang et al. 2011). The safety margin (SM) for the grip is min(SM_i), where i = {thumb, index, middle, ring, little}. During our study, the SM dropped from 59% to 52% due to the aperture perturbation (median values). There must be a powerful factor that led to such a major reduction of the safety margin.

Fatigue was unlikely to be such a factor. First, each trial lasted for about 30 s and involved modest grip forces (typically < 15 N). Earlier studies of fatigue (Singh et al. 2012) suggest that much higher forces are needed to produce measurable fatigue of flexor muscles that contribute to the grip force. Besides, control trials on two subjects showed a much lower drop in F_G over the same time period when no change in the aperture occurred.

A drop in F_G at the final state with the same aperture suggests that the referent aperture changed despite (or perhaps because of) the instruction to the subjects “not to interfere”. This could happen due to the hypothetical back-coupling between referent and actual configurations proposed in the model of (Martin et al. 2009). Within that model, RC attracts the actual body configuration resulting in non-zero force production if motion of the actual configuration is impeded. However, if actual configuration stays far from RC for a long time interval, RC starts to be attracted to the current actual configuration.

This phenomenon can account for the earlier reports of a relatively slow force drop in isometric force production tasks when visual control is unavailable (Slifkin et al. 2000; Vaillancourt and Russell 2002; Baweja et al. 2009). It can also account for the drop in F_G in the current study. Indeed, the aperture expansion and contraction were relatively slow. During that time interval, RC could move towards the actual configuration. This RC motion was safe since the difference between RC and the actual configuration remained large. However, when the actual configuration returned to its initial value, the RC change was reflected in the rather large drop in F_G. It is feasible that the strength of the back-coupling depends on the difference between the actual configuration and RC. In this case, the increase in the actual aperture with the handle expansion accelerated the process of RC drift and led to much larger drop in F_G as compared to the control trials.

There is also a possibility that the changes in the handle width were accompanied by changes in the RC component affecting muscle co-contraction. Note that changes in this so-called co-activation command can lead to changes in net forces if the external load is not zero (Feldman 1986; Latash 1992). The current data set does not allow distinction between the sources of changes in the grip force following the transient change in the handle width.

The RC drift suggests that the subject was unable ‘not to intervene’ as required by the instruction. This factor may be viewed as a limitation of the study or as its important feature. We studied the natural behavior of the hand under the instruction to the subjects ‘not to intervene voluntarily’. The inability of the subjects to follow this instruction could be partly due to the mentioned back-coupling between the actual and referent configurations and partly to the implicit constraint of not moving and not dropping the hand-held object during handle size changes.

Effects of vision on grip force and its changes

The results obtained in trials with eyes open and eyes closed were qualitatively similar, however, the changes in grip force were significantly larger when the subjects could watch the handle. It is possible that higher AS values were due to small adjustments in grip force to keep the handle orientation vertical during the imposed changes in grip aperture. Since the handle was not perfectly symmetrical and there was a residual digit moment (see Appendix A), changes in the normal forces could lead to violation of the handle orientation requirement, in particular because of the changes in the lever arms for the vertical tangential forces. Earlier studies have shown so-called chain effects (Gao et al. 2005; Aoki et al. 2007; Zatsiorsky and Latash 2008) when a change in only a subset of digit forces and/or other features of the task (such as handle geometry and friction conditions) lead to changes in many other variables caused by the static constraints.

In our experiment, the unbalanced moments were small and the subjects showed relatively minor handle deviations from the vertical, even in the closed-eyes trials. However, when they watched the handle, these small deviations were visible on the spirit level, and the subjects could introduce corrections that could, in particular, involve changes in the normal grip forces.

There are two main conclusions of this study. First, the results allow for a rather simple analysis of the control of object manipulation using the language of RCs, despite the complex anatomical structure of the hand. The seeming robustness of the grip apparent stiffness to substantial changes in wrist position and extrinsic hand muscle lengths may allow for some decoupling in the control of the wrist action from grip force production. A few referent variables can plausibly account for hand-object statics as well as dynamics. Secondly, this study suggests the presence of an underlying process functioning at a distinct time scale. The relatively slow drift of the referent configuration towards the actual one was invoked to explain the steady-state grip force characteristics. Indeed, it remains to be seen if such processes are present in other movements and body segments, and what purposes they could serve.

APPENDIX A

Statistical analysis of the unbalanced digit moments

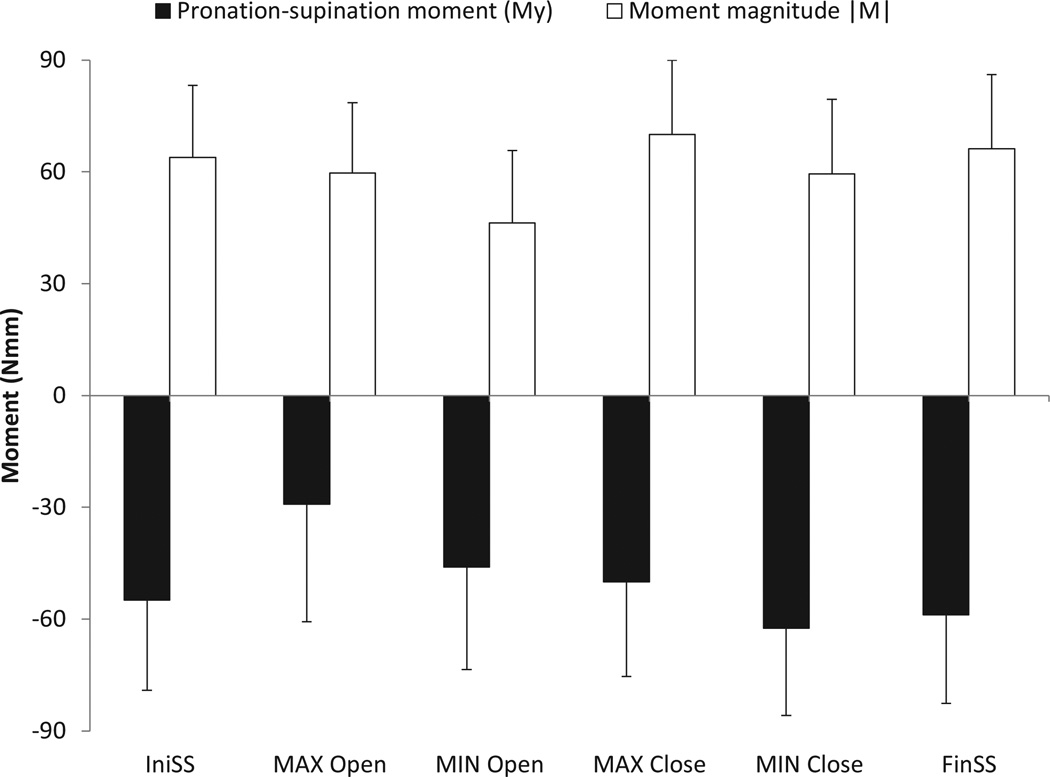
For each trial the resultant moment of all digits was computed in the handle-fixed reference frame located at point P (Figure 1). The moment profiles were averaged across the three repetitions for each condition. We analyzed the moment in the grasp plane (M_Y) and the magnitude of the moment vector (|M|). From the averaged moment trajectory for each condition, the following six M_Y and |M| values were selected: (1) initial steady-state values (IniSS), (2) the maximum value during the aperture opening phase (Max-Open), (3) the minimum value during the aperture opening phase (Min-Open), (4) the maximum value during the aperture closing phase (Max-Close), (5) the minimum value during the aperture closing phase (Min-Close), and (6) the final steady-state value (FinSS). Data were pooled across subjects and conditions (wrist position, eyes open/closed, initial aperture size) and subjected to a one-way ANOVA with the factor Epoch (6 levels). Pair-wise comparisons were done using Bonferroni corrections.

The results are shown in Figure 7. The ANOVA showed a significant effect of Epoch for both M_Y (F_(5,1094) = 37.104, p < 0.01) and |M| (F_(5,1094) = 31.395; p < 0.01), and several pair-wise comparisons were significant. We summarize the main observations below.

1. The initial and final steady-states values were the same for both variables.

2. The moments dropped during the aperture-opening epoch from their initial steady-state values.

3. The moments recovered during the aperture-closing epoch.

4. These changes, although significant, were small. The largest differences between the marginal means for any pair were: −33.26 Nmm for M_Y and 19.9 Nmm for |M|.

5. The overall means (SD) for the two variables were: −50.23 ± 28.2 Nmm for M_Y and 60.91 ± 20.9 Nmm for |M|.

Figure 7.

The mean and SD for the unbalanced moment about the handle-fixed Y axis M_Y (black bars) and the magnitude of the net unbalanced moment |M| (white bars) are shown. The following six moments are analyzed: (1) initial steady-state (IniSS), (2) the maximum during the aperture opening phase (Max Open), (3) the minimum during the aperture opening phase (Min Open), (4) the maximum during the aperture closing phase (Max Close), (5) the minimum during the aperture closing phase (Min Close), and (6) the final steady-state (FinSS).

We conclude that a consistent, non-zero moment was applied by the digits on the handle to counter the unbalanced external torque. Possible sources of this external torque are the handle weight, since the handle CG is not located at point P (Figure 1), and cables of the sensors and the laser. In particular, the digits applied a consistent supination moment of about 50 Nmm on the handle.