Methods for comparing center-specific survival outcomes using direct standardization

Abstract

The evaluation of center-specific outcomes is often through survival analysis methods. Such evaluations must account for differences in the distribution of patient characteristics across centers. In the context of censored event times, it is also important that the measure chosen to evaluate centers not be influenced by imbalances in the center-specific censoring distributions. The practice of using center indicators in a hazard regression model is often invalid, inconvenient, or undesirable to carry out. We propose a semiparametric version of the standardized rate ratio (SRR) useful for the evaluation of centers with respect to a right-censored event time. The SRR for center j can be interpreted as the ratio of the expected number of deaths in the total population (if the total population were in fact subject to the center j mortality hazard), to the observed number of events. The proposed measure is not affected by differences in center-specific covariate or censoring distributions. Asymptotic properties of the proposed estimators are derived, with finite-sample properties examined through simulation studies. The proposed methods are applied to national kidney transplant data.

1. Introduction

In many situations, interest lies in the comparison of survival outcomes by center (e.g., treatment facility, hospital, or other entity serving as health care provider). Center-specific evaluations can be carried out on a regular basis (e.g., annually) to identity centers with poor performance. Alternatively, a retrospective evaluation over a longer period could be used to identify centers with exceptionally good results, with the goal of specifying best practices. In other cases, comparisons across centers may be an interesting secondary analysis; for example, in a multi-center study to evaluate the impact of a specific treatment on mortality. An accurate comparison of center-specific survival outcomes needs to account for imbalances in risk factor distributions among centers. For instance, the inclusion of high-risk patients by a given center can make that center’s survival appear substandard. In addition, in the context of survival times subject to censoring, the same phenomenon can occur due to differences in center-specific censoring distributions.

In this report, we propose a semiparametric version of direct standardization, suitable for mortality comparisons by center. The proposed approach involves first fitting a Cox [1] regression model, stratified by center. The regression model is not used to directly estimate center effects, but rather to ensure that adjustment covariate effects are not confounded by center (which could occur in the absence of adjustment for center). For each center, j, the standardized rate ratio (SRR_j) is then computed as the ratio of expected to observed numbers of deaths; where ‘observed’ refers to the total number of deaths across all centers (j = 1, …, J) and ‘expected’ represents the number of total deaths estimated to occur if in fact all centers had mortality hazard equal to that of center j. Due to the use of direct standardization, the {SRR₁, SRR₂, …, SRR_J } can be compared (and validly ordered) since the same covariate and censoring distribution is applied to each; i.e., the total study population serves as the standard. This is in contrast to indirectly standardized measures, such as the Standardized Mortality Ratio (SMR).

The motivating example for this study involves the evaluation of center-specific post-transplant mortality for kidney transplant patients. Examples of factors known to strongly affect the post-transplant mortality hazard include age, primary renal diagnosis and pre-transplant time on dialysis; each of which may differ in distribution by center. Centers with mortality significantly greater than the national average may be subject to various degrees of intervention, including site visits and perhaps de-accreditation. Given the high stakes of such evaluations, it is important that the statistical methods used for identifying outlying centers be accurate.

A commonly used measure for evaluating center-specific survival is the standardized mortality ratio (SMR), defined as the ratio of the observed number of deaths at a given center, to the number expected if the center had mortality equal to the population average. The SMR is a tool familiar to fields such as epidemiology; for example, [2, 3, 4, 5]. The comparison of observed and expected outcomes is also commonly used for health care regulation; for example, [6, 7]. In the context of renal research, Wolfe et al. [8] and Wolfe [9] calculated SMRs among kidney transplant patients using mortality tables published by the United States Renal Data Systems. To relax the assumption of known standard mortality rates, Dickinson et al. [10] studied a semiparametric SMR based on Cox regression. Limitations of the SMR include its use of indirect standardization; each center’s SMR is essentially adjusted to a different (center-specific) covariate and censoring distribution. Centers cannot be rank-ordered based on indirect standardization, since two centers with equal covariate-specific mortality hazards could have different SMRs, merely due to differences in their respective covariate or censoring distributions. Therefore, although SMRs are potentially useful for internal evaluation (e.g., for centers to evaluate themselves or for a governing body to evaluate this center’s mortality comparing to that expected at the national level), they are less useful in the work of external evaluation (e.g., for surgeons and patients to compare center-specific results in the same region), since comparisons of center-specific results would play at least some role. We provide additional commentary on the SMR in Section 5.

Above, we note limitations in the SMR approaches. Naturally, this technique has its role in analysis contrasting centers. However, Noting room for improvement, we propose semiparametric version of direct standardization useful for survival analysis of centers. Direct standardization is also a commonly used approach in comparisons of mortality, usually through a measure termed the Standardized Rate Ratio (SRR) or Comparative Mortality Figure (CMF). One can express the SRR as the ratio of expected to observed numbers of deaths in the whole study population; the numerator of the SRR represents the expected number of deaths if all patients were treated at the given center, while the denominator equals the total observed number of deaths in the study population. [3, 4] compared the SRR with SMR in the framework of person-year methods. In particular, the main drawback of SMR (with respect to comparisons across centers) is not inherent to the SRR, since the same standard population is applied to all centers. Hence, center-specific SRRs are directly comparable.

The SRR has a long history in fields such as epidemiology, and there are many settings in which direct standardization is appropriate. The Cox model has dominated applications involving regression analysis of censored data since its development. Thus, the use of Cox regression to estimate directly standardized center effects is a natural choice. The main contribution of this report is to formalize procedures for the Cox regression-based SRR; including rigorous derivation of asymptotic properties, simulation studies and detailed comparisons to alternative approaches.

2. METHODS

First, we provide the notation to be used in this article. Let T_i and C_i represent the survival and censoring time, respectively, for the i’th patient, where i = 1, …, n. Let J be the number of centers. The total number of subjects is denoted by $n={\sum }_{j=1}^J{n}_j$, where n_j is the number of subjects in center j. Observation times are denoted by X_i = T_i ∧ C_i, with at-risk indicator Y_i(t) = I(X_i ≥ t), where a ∧ b = min{a, b} and I(A) is an indicator function taking the value 1 when condition A holds and 0 otherwise. The observed death indicators are denoted by Δ_i = I(T_i ≤ C_i), and the death counting process is defined as N_i(t) = Δ_iI(X_i ≤ t). Let G_i denote the center for subject i and set G_ij = I(G_i = j). Correspondingly, we set Y_ij(t) = Y_i(t)G_ij and N_ij(t) = N_i(t)G_ij. The observed data consist of n independent vectors, (X_i, Δ_i, G_i, Z_i), where Z_i is a vector of adjustment covariates.

The assumed center-stratified Cox model can be formulated as,

$${\lambda }_{ij}(t)\equiv \lambda (t\mid Z_i,G_i=j)={\lambda }_{0j}(t)exp\{{\beta }_0^T{Z}_i\},$$ (1)

where λ_0j(t) is an unspecified center-specific baseline hazard function and β₀ is a parameter vector. The partial likelihood estimator [11] of β₀ is denoted by β̂ and is given by the solution to U(β) = 0 where

$$U(\beta )=\sum _{j=1}^J\sum _{i=1}^n{\int }_0^{\tau }\{Z_{ij}-{\overline{Z}}_j(u;\beta )\}{dN}_{ij}(u)$$

with ${\overline{Z}}_j(u;\beta )=S_j^{(0)}{(u;\beta )}^{-1}{S}_j^{(1)}(u;\beta )$ and $S_j^{(d)}(u;\beta )=n^{-1}{\sum }_{i=1}^n{Y}_{ij}(u)Z_i^{\otimes d}exp\{{\beta }^T{Z}_i\}$ for d = 0, 1, 2. The Breslow estimator [12] of ${\mathrm{\Lambda }}_{0j}(t)={\int }_0^t{\lambda }_{0j}(u)du$ is then given by Λ̂_0j(t; β), where

$${\widehat{\mathrm{\Lambda }}}_{0j}(t;\beta )=\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{dN}_{ij}(u)}{S_j^{(0)}(u;\beta )}.$$

2.1. Indirect Standardization: Standardized Mortality Ratio (SMR)

We begin by introducing an alternative to the proposed measure. The standardized mortality ratio for center j is calculated as the ratio of observed to expected numbers of events,

$${\widehat{\mathit{SMR}}}_j(t)=\frac{O_j(t)}{E_j(t)},$$ (2)

where the numerator is given by $O_j(t)={\sum }_{i=1}^n{N}_{ij}(t)$ and the expected number of events is computed as

$$E_j(t)=\sum _{i=1}^n{\int }_0^t{Y}_{ij}(u)exp\{{\widehat{\beta }}^T{Z}_i\}d{\widehat{\mathrm{\Lambda }}}_0(u;\widehat{\beta }),$$

with Λ̂₀(t; β̂) representing an estimator of the average cumulative baseline hazard,

$${\widehat{\mathrm{\Lambda }}}_0(t;\widehat{\beta })=\frac{1}{n}\sum _{i=1}^n{\int }_0^t\frac{{dN}_i(u)}{S^{(0)}(u;\widehat{\beta })}$$ (3)

and β̂ is based on model (1). The estimator given in (2) was developed in [13], where part of the innovation was the proposed use of the center-stratified model to estimate β₀. Intuition would suggest computing E_j(t) using an unstratified model. However, estimation of β₀ in the absence of adjustment for center effects may produce a substantially biased estimate of due to confounding by center; or merely due to center affecting the hazard function, with or without confounding (i.e., due to the non-linear link function).

The calculation of ${\widehat{\mathit{SMR}}}_j(t)$ involves two stages. A stratified Cox model (Model 1) is fitted in the first stage, with the population average cumulative baseline hazard, Λ̂₀(t; β̂), then computed in the second stage (e.g., through a unstratified Cox model with no covariates) using β̂′Z_i as an offset. At the second stage, O_j(t), E_j(t) are calculated.

2.2. Direct Standardization: Standardized Rate Ratio (SRR)

Based on a form of indirect standardization, the SMR described in Section 2.1 can be viewed as a weighted ratio of center-specific cumulative hazards, with weight functions based on center-specific $S_j^{(0)}(t;\beta )$. These weight functions have an obvious disadvantage: they involve center-specific censoring and covariate distributions, which can differ considerably across centers. To rule out the possibility that differences among centers are due merely to different censoring and/or covariate distributions, the weight function should be specified such that differences among centers with respect to the resulting measure are a function only of corresponding differences in center-specific hazards. Motivated by such considerations, we propose an alternative method, referred to as the Standardized Rate Ratio (SRR), which can be interpreted as a semiparametric version of direct standardization. The proposed SRR is computed, for center j, as

$${\widehat{\mathit{SRR}}}_j(t)=\frac{{\mathcal{E}}_j(t)}{O(t)},$$ (4)

with $O(t)={\sum }_{j=1}^J{O}_j(t)$ being the total observed number of deaths across all centers, and

$${\mathcal{E}}_j(t)=\sum _{\ell =1}^J\sum _{i=1}^n{\int }_0^t{Y}_{i\ell }(u)exp\{{\widehat{\beta }}^T{Z}_i\}d{\widehat{\mathrm{\Lambda }}}_{0j}(u)$$ (5)

representing the expected number of total deaths if all centers had mortality hazard equal to that of center j. Similar to the SMR, the SRR is easily interpreted and is well understood by clinical investigators. The SRR also involves a ratio of observed and expected numbers of deaths. However, the ‘expected’ component is in the SRR’s numerator, while the ‘observed’ count is in the denominator. With respect to interpretation, SRR_j > 1 indicates that center j has a greater mortality rate than the overall average. Note that, although SRR_j(t) also involves the censoring and covariate distributions, the same weight function is applied across all centers; thus factoring out the impact of imbalances in center-specific censoring and covariate distributions. The proposed measures are desirable in this light, since their center-specific limiting values would differ only due to corresponding differences in center-specific hazards.

2.3. Asymptotic Properties

We summarize the asymptotic properties of the proposed SRR with the following theorem; we outline the proof in Appendix A.

THEOREM 1

Under the regularity conditions listed in Appendix A, ${\widehat{\mathit{SRR}}}_j(t)$ converges in probability to SRR_j(t) uniformly in t ∈ [0, τ], where

$${\mathit{SRR}}_j(t)=\frac{{\sum }_{\ell =1}^J{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)}{{\sum }_{\ell =1}^J{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)}$$

and $n^{\frac{1}{2}}\{{\widehat{\mathit{SRR}}}_j(t)-{\mathit{SRR}}_j(t)\}$ converges weakly to a zero-mean Gaussian process with variance function σ_j(t) = E[ξ_ij(t; β₀)²], where

$${\xi }_{ij}(t;\beta )=w(t;\beta ){\int }_0^t\frac{s^{(0)}(u;\beta )}{s_j^{(0)}(u;\beta )}{dM}_{ij}(u;\beta )+w(t;\beta ){\int }_0^t\left\{Y_i(u)exp({\beta }^T{Z}_i)-s^{(0)}(u;\beta )\right\}d{\mathrm{\Lambda }}_{0j}(u)$$ (6)

$$-w{(t;\beta )}^2{\int }_0^t{s}^{(0)}(u;\beta )d{\mathrm{\Lambda }}_{0j}(u)\sum _{\ell =1}^J{\int }_0^t\left\{{dN}_{i\ell }(u)-s_{\ell }^{(0)}(u;\beta )d{\mathrm{\Lambda }}_{0\ell }(u)\right\}$$ (7)

$$+w(t;\beta ){\int }_0^t{r}_j^T(u;\beta )d{\mathrm{\Lambda }}_{0j}(u)\mathrm{\Omega }{(\beta )}^{-1}{\int }_0^{\tau }\{Z_{i\ell }-{\overline{z}}_{\ell }(u;\beta )\}{dM}_{ij}(u;\beta )$$ (8)

with

$$\begin{array}{l}w(t;\beta )={\left\{\sum _{\ell =1}^J{\int }_0^t{s}_{\ell }^{(0)}(u;\beta )d{\mathrm{\Lambda }}_{0\ell }(u)\right\}}^{-1}\\ r_j(u;\beta )=s^{(1)}(u;\beta )-s^{(0)}(u;\beta ){\overline{z}}_j(u;\beta ).\end{array}$$

The variance function can be consistently estimated by ${\widehat{\sigma }}_j^2(t;\widehat{\beta })=n^{-1}{\sum }_{i=1}^n{\widehat{\xi }}_{ij}{(t;\widehat{\beta })}^2$, with ξ̂_ij(t; β̂) obtained by replacing limiting values in ξ_ij(t; β) with their empirical counterparts. With respect to this variance formula, a potentially time-saving strategy it is to treat the estimators of β₀ as constants, and hence ignore their variability. A justification for such simplification applies when the total study population is very large, such that β̂ has little variability. The resulting variance estimator is given by

$${\xi }_{ij}^R(t;\beta )=w(t;\beta ){\int }_0^t\frac{s^{(0)}(u;\beta )}{s_j^{(0)}(u;\beta )}{dM}_{ij}(u;\beta )+w(t;\beta ){\int }_0^t\left\{Y_i(u)exp({\beta }^T{Z}_i)-s^{(0)}(u;\beta )\right\}d{\mathrm{\Lambda }}_{0j}(u)$$ (9)

$$-w{(t;\beta )}^2{\int }_0^t{s}^{(0)}(u;\beta )d{\mathrm{\Lambda }}_{0j}(u)\sum _{\ell =1}^J{\int }_0^t\left\{{dN}_{i\ell }(u)-s_{\ell }^{(0)}(u;\beta )d{\mathrm{\Lambda }}_{0\ell }(u)\right\},$$ (10)

obtained by removing the line (8) in the formula of ξ_ij(t; β). The quantity ${\widehat{\xi }}_{ij}^R(t;\widehat{\beta })$ is obtained by replacing limiting values in ${\xi }_{ij}^R(t;\beta )$ with their empirical counterparts.

3. SIMULATION

We evaluate the finite-sample properties of the estimators described in Section 2 through a series of simulation studies. Death times were generated from the Weibull model, λ_ij(t) = α_jγjt^γ_j−1 exp(β^T Z_i) for i = 1, …, n_j and j = 1, …, 10, where Z_i = (Z_i1, Z_i2, Z_i3)^T. We set ${\mathit{\beta }}_0^T=({\beta }_1,{\beta }_2,{\beta }_3)=(0.02,-0.5,0.2)$. There are J = 10 centers. The number of subjects within each center varied under different scenarios. Censoring times were generated from either a Uniform distribution or an exponential distribution. In order to compare direct standardization with indirect standardization in the framework of semiparametric models, SMR and SRR were calculated at t = 1, t = 2 and t = 3. Each data configuration was replicated 1000 times.

3.1. Setting 1: Center-independent hazards

The first simulation setting considered the case where the hazard functions are equal across centers for all t ∈ [0, τ]. The censoring and covariate distributions were chosen to be center-independent. Specifically, censoring times were generated from an Uniform (0.5, 10) distribution; Z_i1 followed a Bernoulli (0.5) distribution; Z_i2 followed a logistic distribution with probability dependent on Z_i1, and Z_i3 came from a Normal distribution with constant variance 25 and mean dependent on Z_i1 and Z_i2 (e.g., E[Z_i3|Z_i1, Z_i2] = 50 + 0.2 Z_i1 − 0.5 Z_i2). Under this setting, the hazard functions are equal across centers, such that the limiting values of SRR equal 1 for each center. Results at time t = 3 are displayed in Table 1. For all centers, the average estimated SRR was very close to 1. The average asymptotic standard errors (ASE) were generally close to the empirical standard deviations (ESD), while the empirical coverage probabilities (CP) were generally consistent with the nominal value. This held for both the variance estimator derived in Theorem 1 (with corresponding asymptotic expansion given by (6), (7) and (8) and its approximation given by (9) and (10). In fact, the two sets of ASEs are virtually indistinguishable. Results were generally consistent across the observation time distribution (data not shown).

Table 1.

Simulation Setting 1: ${\widehat{\mathit{SRR}}}_j(t)$; center-independent hazards, covariate and censoring distributions; t=3

Center	(γj, αj)	TRUE	BIAS	ESD	Thm 1 (6), (7), (8)		Thm 1 (approx) (9), (10)
					ASE	CP	ASE	CP
1	(1, 0.2)	1.000	0.001	0.154	0.153	0.96	0.153	0.96
2	(1, 0.2)	1.000	0.004	0.160	0.154	0.94	0.153	0.94
3	(1, 0.2)	1.000	−0.000	0.151	0.153	0.95	0.153	0.95
4	(1, 0.2)	1.000	−0.006	0.163	0.153	0.93	0.153	0.93
5	(1, 0.2)	1.000	−0.007	0.149	0.153	0.95	0.153	0.95
6	(1, 0.2)	1.000	−0.003	0.155	0.153	0.94	0.153	0.94
7	(1, 0.2)	1.000	0.007	0.162	0.154	0.93	0.154	0.93
8	(1, 0.2)	1.000	−0.001	0.152	0.153	0.95	0.153	0.95
9	(1, 0.2)	1.000	0.002	0.158	0.154	0.95	0.152	0.95
10	(1, 0.2)	1.000	0.002	0.157	0.153	0.94	0.153	0.94

It is worth noting that whether or not the covariate or censoring distributions were center-dependent has no influence on the results in this setting. Correspondingly, similar results were found for the case of center-dependent covariate and censoring distribution.

3.2. Setting 2: Center-dependent hazards; Center-independent covariate and censoring distributions

For the second set of simulations, different values of α_j and γ_j were used, such that the hazard functions increased with increasing center number (j = 1, …, 10). The covariate distributions were chosen to be center-independent, and were generated from the same distributions from Setting 1. Results are provided in Table 2 for various sample sizes and censoring percentages. The proposed SRR appears to be approximately unbiased, with coverage probability close to 0.95 for both the standard error based on Theorem 1 and that based on the approximation. When the center-specific sample size is small (e.g., 25), the empirical CPs were slightly underestimated. Such results suggest that center-specific sample sizes play an important role in the proposed methods. In particular, the minimum sample size (across centers) needs to be reasonably large. Given this concern, centers of size less than 20 were eliminated from the real data analysis in Section 4. Collectively, simulation results from Setting 1 and Setting 2 indicate that the proposed method is quite accurate at and away from the null.

Table 2.

Simulation Setting 2: ${\widehat{\mathit{SRR}}}_j(t)$; center dependent hazards; center-independent covariate and censoring distributions; t=3.

nj	Censoring	Center	(γj, αj)	TRUE	BIAS	ESD	Thm 1 (6), (7), (8)		Thm 1 (approx) (9), (10)
							ASE	CP	ASE	CP
100	20%	2	(0.85, 0.08)	0.406	0.004	0.096	0.093	0.94	0.093	0.94
		4	(0.95, 0.16)	0.797	0.003	0.132	0.134	0.95	0.134	0.95
		6	(1.05, 0.24)	1.180	0.001	0.174	0.169	0.94	0.169	0.94
		8	(1.15, 0.32)	1.549	0.006	0.206	0.204	0.95	0.203	0.95
		10	(1.25, 0.4)	1.912	0.005	0.230	0.238	0.96	0.237	0.96
50	20%	2	(0.85, 0.08)	0.406	0.002	0.135	0.130	0.93	0.130	0.93
		4	(0.95, 0.16)	0.797	−.008	0.183	0.187	0.95	0.186	0.95
		6	(1.05, 0.24)	1.180	0.007	0.252	0.238	0.94	0.238	0.94
		8	(1.15, 0.32)	1.549	0.001	0.290	0.285	0.95	0.284	0.95
		10	(1.25, 0.4)	1.912	0.026	0.344	0.338	0.95	0.337	0.94
100	40%	2	(0.85, 0.08)	0.406	0.008	0.097	0.097	0.94	0.097	0.94
		4	(0.95, 0.16)	0.797	0.003	0.139	0.138	0.95	0.138	0.95
		6	(1.05, 0.24)	1.180	0.007	0.172	0.174	0.95	0.173	0.95
		8	(1.15, 0.32)	1.549	0.014	0.214	0.208	0.94	0.208	0.94
		10	(1.25, 0.4)	1.912	0.029	0.243	0.244	0.95	0.243	0.95
50	40%	2	(0.85, 0.08)	0.406	0.009	0.137	0.136	0.94	0.135	0.94
		4	(0.95, 0.16)	0.797	0.011	0.204	0.195	0.94	0.195	0.94
		6	(1.05, 0.24)	1.180	−0.007	0.249	0.242	0.94	0.241	0.94
		8	(1.15, 0.32)	1.549	0.019	0.302	0.294	0.94	0.294	0.94
		10	(1.25, 0.4)	1.912	0.043	0.357	0.345	0.95	0.344	0.95
125	20%	2	(0.85, 0.08)	0.529	0.006	0.110	0.106	0.94	0.106	0.94
100		4	(0.95, 0.16)	1.043	−0.004	0.169	0.171	0.95	0.171	0.95
75		6	(1.05, 0.24)	1.550	−0.002	0.256	0.255	0.95	0.255	0.95
50		8	(1.15, 0.32)	2.025	−0.015	0.384	0.381	0.93	0.380	0.93
25		10	(1.25, 0.4)	2.535	−0.004	0.651	0.632	0.93	0.630	0.92
125	40%	2	(0.85, 0.08)	0.601	0.001	0.122	0.118	0.94	0.118	0.94
100		4	(0.95, 0.16)	1.118	0.007	0.190	0.192	0.96	0.192	0.96
50		6	(1.05, 0.24)	1.773	−0.001	0.375	0.359	0.93	0.358	0.93
25		8	(1.15, 0.32)	2.324	0.045	0.636	0.621	0.93	0.619	0.93
15		10	(1.25, 0.4)	2.900	−0.062	1.034	0.914	0.91	0.910	0.90

3.3. Setting 3: Center-dependent hazards, Center-dependent censoring distribution

As mentioned previously, estimators based on indirect standardization may be misleading if either the censoring or covariate distributions are center-dependent. To illustrate this point, we performed simulations with the following three conditions: (i) the hazard functions were center-dependent, while center 2j − 1 had exactly the same hazard function as that of center 2j for j = 1, ···, 5; (ii) the censoring distributions for center 2j − 1 and 2j were substantially different. For center 2j − 1, the censoring times were generated from a uniform distribution such that the censoring mainly occurred in the later stages, while for center 2j the censoring times were generated from a uniform distribution for which the censoring tended to occur in the early stages; (iii) the covariate distributions (reused from Setting 2) were center-independent.

We compared the SRR and SMR in Table 3 for Setting 3. With respect to the true values, the limiting values of ${\widehat{\mathit{SRR}}}_{2j}(t)$ and ${\widehat{\mathit{SRR}}}_{2j-1}(t)$ are equal, as one would hope. This is not the case for ${\widehat{\mathit{SMR}}}_{2j}(t)$ and ${\widehat{\mathit{SMR}}}_{2j-1}(t)$, the differences being due to differences in the censoring distributions. With respect to the estimators themselves, both ${\widehat{\mathit{SRR}}}_j(t)$ and ${\widehat{\mathit{SMR}}}_j(t)$ are approximately unbiased. Note that the bias of ${\widehat{\mathit{SMR}}}_j(t)$ was calculated as the difference between it and its own limiting value.

Table 3.

Simulation Setting 3: centers 2j and 2j − 1 have equal hazards, but different censoring distributions; t=3.

Measure	Center	(γj, αj)	TRUE	BIAS	ESD
SMRj(t)	1	(0.8, 0.04)	0.227	−0.003	0.089
	2	(0.8, 0.04)	0.211	−0.002	0.068
	3	(0.9, 0.12)	0.658	0.001	0.162
	4	(0.9, 0.12)	0.637	0.003	0.121
	5	(1, 0.2)	1.050	0.003	0.208
	6	(1, 0.2)	1.051	−0.000	0.157
	7	(1.1, 0.3)	1.500	0.002	0.239
	8	(1.1, 0.3)	1.547	0.004	0.201
	9	(1.25, 0.4)	1.881	−0.002	0.279
	10	(1.25, 0.4)	2.003	−0.008	0.219
SRRj(t)	1	(0.8, 0.04)	0.221	−0.003	0.088
	2	(0.8, 0.04)	0.221	−0.002	0.073
	3	(0.9, 0.12)	0.645	0.002	0.162
	4	(0.9, 0.12)	0.645	0.004	0.124
	5	(1, 0.2)	1.044	0.002	0.216
	6	(1, 0.2)	1.044	−0.002	0.158
	7	(1.1, 0.3)	1.530	0.001	0.277
	8	(1.1, 0.3)	1.530	0.004	0.202
	9	(1.25, 0.4)	1.996	−0.004	0.351
	10	(1.25, 0.4)	1.996	−0.008	0.230

3.4. Setting 4: Center-dependent hazards; Center-dependent covariate distributions

We also performed simulations under a setting in which the distribution of the covariate vector differed by center. The set up for hazard functions and censoring distribution were the same as in Setting 2, while center 2j and 2j − 1 had substantially different covariate distributions. In center 2j − 1, the covariate Z_i1 followed a Bernoulli (0.2) distribution, Z_i2 followed a Bernoulli (0.8) distribution and Z_i3 came from a Normal distribution with mean 30 and standard deviation 10. In center 2j, Z_i1 followed a Bernoulli (0.8) distribution, Z_i2 followed a Bernoulli (0.2) distribution, and Z_i3 was derived from a Normal distribution with mean 50 and standard deviation 10.

Results based on Setting 4 are given in Table 4. Trends are similar to those from Setting 3, but much more pronounced. The limiting values of ${\widehat{\mathit{SRR}}}_{2j}(t)$ are equal to those of ${\widehat{\mathit{SRR}}}_{2j-1}(t)$, as one would expect. Conversely, the true values of ${\widehat{\mathit{SMR}}}_{2j}(t)$ and ${\widehat{\mathit{SMR}}}_{2j-1}(t)$ are different; with the differences being quite pronounced for j = 3, j = 4 and j = 5. Moreover, it appears that SMR₇(t) > SMR₁₀(t), which is misleading in the sense that SRR₇(t) < SRR₁₀(t).

Table 4.

Simulation Setting 4: centers 2j and 2j − 1 have equal hazards, but different covariate distributions; t=3.

Measure	Center	(γj, αj)	TRUE	BIAS	ESD
SMRj(t)	1	(0.8, 0.04)	0.319	−0.003	0.089
	2	(0.8, 0.04)	0.331	−0.002	0.068
	3	(0.9, 0.12)	0.931	0.001	0.162
	4	(0.9, 0.12)	0.919	0.003	0.121
	5	(1, 0.2)	1.484	0.003	0.208
	6	(1, 0.2)	1.307	−0.000	0.157
	7	(1.1, 0.3)	2.070	0.002	0.239
	8	(1.1, 0.3)	1.602	0.004	0.201
	9	(1.25, 0.4)	2.551	−0.002	0.279
	10	(1.25, 0.4)	1.725	−0.008	0.219
SRRj(t)	1	(0.8, 0.04)	0.345	−0.002	0.120
	2	(0.8, 0.04)	0.345	−0.000	0.041
	3	(0.9, 0.12)	0.929	0.005	0.212
	4	(0.9, 0.12)	0.929	0.003	0.105
	5	(1, 0.2)	1.386	−0.007	0.272
	6	(1, 0.2)	1.386	−0.000	0.186
	7	(1.1, 0.3)	1.908	−0.007	0.344
	8	(1.1, 0.3)	1.908	0.013	0.330
	9	(1.25, 0.4)	2.329	−0.006	0.412
	10	(1.25, 0.4)	2.329	−0.001	0.455

4. APPLICATION

We applied the proposed methods to investigate the performance of transplant centers with respect to post kidney transplant survival. Data were obtained from the Scientific Registry of Transplant Recipients (SRTR) and submitted by members of the Organ Procurement and Transplantation Network (OPTN). The SRTR database contains information on all wait-listed candidates, transplant recipients and organ donors in the United States. Included in the analysis were adult patients (≥ 18 years of age at transplant) who underwent deceased donor kidney transplantation between January 2000 and December 2008. Adjustment covariates in this study included age, race, gender, diagnosis, donation after cardiac death (DCD), Expanded Criteria Donor (ECD), BMI, dialysis time, indicator of previous kidney transplant and cold ischemia time. These variables have face validity from a clinical perspective and are based on a list of covariates used in SRTR. Transplant centers with sample size ≤ 20 and patients who received a living-donor transplant were eliminated from additional analysis. The final sample size was then n = 74, 088 from J = 217 centers across the United States. Failure time (recorded in years) was defined as the time from transplantation to graft failure or death, whichever occurred first. Graft failure was considered to occur when the transplanted kidney ceased to function.

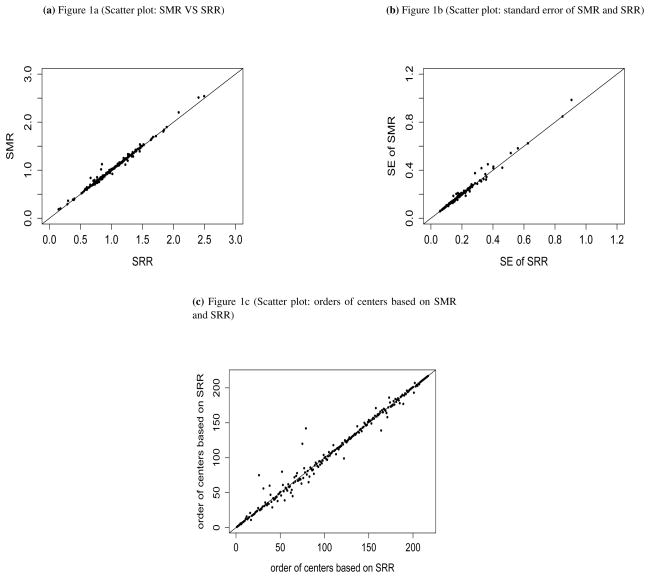
Stratified Cox regression was employed to model the hazard function. The indirectly standardized estimator, ${\widehat{\mathit{SMR}}}_j$, was calculated using SAS PROC PHREG with an offset. The proposed directly standardized estimator, ${\widehat{\mathit{SRR}}}_j$, was computed using SAS IML. Figure 1a represents the pairwise comparisons of the SMRs and SRRs. Figure 1b shows the standard error of these two measures. Figure 1c compares the orders of centers based on SRRs and SMRs. As shown, there are some discrepancies between these two measures. We applied bootstrapped techniques to evaluate whether the change in center-specific orderings (SMR versus SRR) exceeded that attributable to only sampling variation. Specially, we calculated the distribution of center-specific SMR orderings from 100 bootstrapped samples. We then calculated the 95% confidence intervals (CI) of these orders. Based on the bootstrapped resamples, for 20 out of 217 centers, the 95% confidence intervals (CI) based on SMR does not cover the order based on SRR from the original dataset. Among these 20 centers, 10 had SRR significantly different from the national average.

Figure 1.

Evaluation of J=217 kidney transplant centers

Using the asymptotic normality of the proposed estimators, we constructed the point-wise confidence intervals for SRR at t = 5 years (Figure 2). Center numbers are re-ordered by values of SRR. A total of 38 centers had observed number of events significantly lower than the expected calculating based on the national average hazards, while 28 centers were significantly above the expected. It is clear that the hazard functions varied among centers. Tables 5 presents the pairwise comparison of the numbers and percentages of “outlier” centers identified by p-values corresponding to their SMRs and SRRs (using tests of H₀: SMR_j = 1 and H₀: SRR_j = 1, respectively). A total of 6 centers changed “memberships” based on these two measures. Specifically, 2 centers were flagged to be significant based on SMR but flagged to be normal based on SRR; on the other hand, 4 centers were flagged to be significant based on SRR but flagged to be normal based on SMR. Through fitting a sequence of logistic regression models (rotating the center indicators as the response variates), it was revealed that, for these 6 centers, approximately half of the adjustment covariates had distributions significantly different from the remaining centers. In addition, through fitting a Cox model using censored as the event, 3 of the 6 centers in question were significantly predictive of the censoring hazard. In summary, we do observe some differences when comparing center effects estimated through direct versus indirect standardization, and the strongest examples of such discrepancies appear to be due to differences in the center-specific covariate and censoring distributions; consistent with the concepts described earlier in this report.

Figure 2.

Evaluation of J=217 kidney transplant centers: Point estimates and 95% confidence interval of ${\widehat{\mathit{SRR}}}_j$ at t = 5 years.

Table 5.

Number and percentage of centers giving significant results under SMR and SRR

SMR	SRR
	Non-significant	Significant	Row-sum
Non-significant	147 (67.8%)	4 (1.8%)	151 (69.6%)
Significant	2 (0.9%)	64 (29.5%)	66 (30.4 %)
Column-sum	149 (68.7%)	68 (31.3%)	217 (100%)

5. DISCUSSION

We propose semiparametric methods for estimating standardized rate ratios, as a means of evaluating center-specific mortality through direct standardization. Large-sample properties are derived and shown through simulation to be appropriate in finite samples. A computationally faster variance estimator is proposed for the SRR, and is shown to work practically as well as the full version. Application of the methods demonstrates several significant differences among kidney transplant centers in the United States.

There is some judgement required in deciding when to use indirect standardization and when to use direct standardization. Indirectly standardized estimators, such as SMR, provides a valid approach to evaluate how does a center’s mortality compare to that predicted at the population level for the kinds of patients at this center. However, it is important to emphasize that center-specific SMRs should not be compared with one another (a caution that applies to all indirectly standardized rates). The SRR, a directly standardized measure, does not share this drawback. The SRRs for two given centers will be unequal only because the center-specific mortality hazards differ; direct standardization accounts for imbalance with respect to center-specific covariate and censoring distributions. The proposed SRR shares the SMR’s ease of interpretation, but rectifies its key disadvantages and, hence, is a more appropriate choice in settings where mortality comparisons across centers are an objective.

The degree to which the SMR and SRR are different will depend on the application. In some settings, the two may not agree well, while in others they may be quite similar. The only way to know with certainty if SMR and SRR are equal would be to calculate both measures, which would not be a desirable option in many cases. In settings where, for a particular center, the SMR and SRR were unequal, it would be very difficult to claim that the SMR was correct; for the several reasons documented previously. Given the high stakes of evaluations by regulatory bodies, and the fact that the credibility of such organizations depends in part on the accuracy of their evaluations, it would appear the preferred analysis is the one that is most likely to be accurate.

The proposed SRR is computed using a stratified Cox model, which makes no assumptions about the functional form of the impact of center on the hazard function. The stratification by center plays a major role. For instance, the expected number of deaths considers each patient’s covariate vector, such that the regression parameter must be estimated consistently. Unless the death hazard is conditionally independent of center given the covariates, covariate effect estimates will generally be biased if based on a model with a non-linear link function and no accounting for center. This is an issue for the SMR as well, particularly since the Cox version of the SMR has historically been computed using a common-baseline (i.e., unstratified) model. He [13] proposed modifying the SMR through stratification, leading to the quantity we denoted by SMR and used in simulations (Section 3) for comparisons with the SRR. Such properties were demonstrated empirically by [13]; the magnitude of the bias (in the case of unstratified Cox models) increases when covariates are also center-dependent.

Random effects models are an option for contrasting centers. Moreover, a Bayesian formulation may be an attractive approach for center effect studies. The advantage for random effects model is that this approach would allow for the inclusion of even very small centers. In contrast, when the number of events for a center is small, the estimated center parameter from a fixed effect model may be unstable. However, Kalbfleish and Wolfe [14] compared the properties of a fixed effect model (FEM) and a random effect model (REM) for the purpose of profiling kidney dialysis facilities under various conditions. Essentially, the REM estimates are shrunk toward overall mean, and hence reduce the reported variation of facility performance. Second, the FEM method has the highest statistical power to identify exceptional facilities, for a given false positive rate; and identifying such extreme facilities is usually a main objective of center evaluations. Another issue for REM is the potential confounding effects when the patient risks are correlated with center effects. These findings suggest that a simple REM method may not be good enough and more sophisticated approaches are necessary. Further discussion of such issues is provided by Ohlssen et al. [15], who develop a more flexible random effects model using Bayesian nonparametric methods, in order to remedy the influence of outlying centers to which basic random effects models are susceptible.

The direct standardization methods derived in this report could be extended in several useful directions. Perhaps most notably, it is often of interest to evaluate center effects in settings where the event of interest is recurrent (e.g., hospitalizations, infections). Furthermore, it would also be useful to develop methods based on direct standardization that can accommodate competing risks or dependent censoring. Direct standardization could also be applied to compare center-specific survival probability and restricted mean lifetime.

APPENDIX A

To derive the large-sample properties for the SRR, we impose the following regularity conditions under the stratified Cox model:

1. (X_i, Δ_i, G_i, Z_i) are independent and identically distributed random vectors.

2. P(X_i ≥ τ) > 0 where τ is a pre-specified time point.

3. Z_ik have bounded total variation, i.e., |Z_ik| < κ for all i = 1, …n and k = 1, …, p, where κ is a constant and Z_ik is the kth component of Z_i.

4. ${\int }_0^{\tau }{\lambda }_{0j}(t)dt<\infty$.

5. Continuity of the following functions:

   $$s_j^{(1)}(t;\beta )=\frac{\partial }{\partial \beta }{s}_j^{(0)}(t;\beta ),s_j^{(2)}(t;\beta )=\frac{{\partial }^2}{\partial \beta \partial {\beta }^T}{s}_j^{(0)}(t;\beta )$$

   and $s_j^{(0)}(t;\beta )$, where $s_j^{(d)}(t;\beta )$ is the limiting value of $S_j^{(d)}(t;\beta )$ for d = 0, 1, 2, with $s_j^{(1)}(t;\beta )$ and $s_j^{(2)}(t;\beta )$ bounded and $s_j^{(0)}(t;\beta )$ bounded away from 0 for t ∈ [0, τ].

6. Positive-definiteness of the matrix Ω_j(β):

   $$\begin{array}{c}{\mathrm{\Omega }}_j(\beta )={\int }_0^{\tau }{v}_j(t;\beta )s_j^{(0)}(t;\beta ){\lambda }_{0j}(t)dt,\\ v_j(t;\beta )=\frac{s_j^{(2)}(t;\beta )}{s_j^{(0)}(t;\beta )}-{\overline{z}}_j{(t;\beta )}^{\otimes 2},\end{array}$$

   where ${\overline{z}}_j(t;\beta )=s_j^{(0)}{(t;\beta )}^{-1}{s}_j^{(1)}(t;\beta )$ is the limiting value of Z̄_j(t; β).

7. P(G_ij = 1|Z_i) > 0.

Condition (a) is employed in the derivation of the weak convergence. Condition (b) is a standard identifiability requirement. Condition (c) leads to the boundedness of several quantities and is applicable in most practical applications. Conditions (d) and (e) are not essential but simplify our proofs. With respect to condition (g), the selection probability given covariates is non-zero for all centers. This condition guarantees that the sample size n_j of each center goes to ∞ as the total sample size n goes to ∞.

We first show that ${\widehat{\mathit{SRR}}}_j(t)\stackrel{P}{\to }{\mathit{SRR}}_j(t)$ uniformly for t ∈ [0, τ]. The triangle inequality leads to

$$\Vert {\int }_0^t{S}_{\ell }^{(0)}(u;\widehat{\beta })d{\widehat{\mathrm{\Lambda }}}_{0j}(u;\widehat{\beta })-{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)\Vert \le \Vert {\int }_0^t{S}_{\ell }^{(0)}(u;\widehat{\beta })d{\widehat{\mathrm{\Lambda }}}_{0j}(u;\widehat{\beta })-{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0j}(u;\widehat{\beta })\Vert$$ (A.1)

$$+\Vert {\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0j}(u;\widehat{\beta })-{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)\Vert$$ (A.2)

To show that $(A.1)\stackrel{P}{\to }0$ uniformly in t, recall that $S_{\ell }^{(0)}(t;\beta )=n^{-1}{\sum }_{i=1}^n{Y}_{i\ell }(t)exp({\beta }^T{Z}_i)={\mathbb{P}}_n[I(X\ge t)I(G=\ell )exp({\beta }^{T}Z)]$, where is the empirical measure; i.e., ${\mathbb{P}}_n[I(X\ge t)I(G=\ell )exp({\beta }^{T}Z)]=n^{-1}{\sum }_{i=1}^n{Y}_{i\ell }(t)exp({\beta }^{T}Z)$. The collection of all cells, [t, ∞), in the real line is a VC class of index 2 and, hence, satisfies the entropy conditions for the Glivenko-Cantelli Theorem [16]. The boundedness conditions ensures that {I(X ≥ t)I(G = ℓ)exp(β^TZ), t ∈ [0, τ]} belong to some Glivenko-Cantelli class; i.e., $S_{\ell }^{(0)}(t;\widehat{\beta })\stackrel{a.s.}{\to }{s}_{\ell }^{(0)}(u;\widehat{\beta })$ uniformly in t ∈ [0, τ]. Next, for β, such that $\widehat{\beta }\stackrel{P}{\to }{\beta }_0$ (e.g, [17, 18]), the bounded condition of {Λ̂₀(t), t ∈ [0, τ]} and an application of the Dominant Convergence Theorem entails that $(A.1)\stackrel{P}{\to }0$ uniformly in t. Similarly, $(A.2)\stackrel{P}{\to }0$ uniformly in t. We already demonstrate that ${\int }_0^t{S}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0j}(u)\stackrel{P}{\to }{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)$ uniformly for t ∈ [0, τ]. Similarly, ${\int }_0^t{S}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0\ell }(u)\stackrel{P}{\to }{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)$ uniformly for t ∈ [0, τ]. The monotonicity and boundedness conditions ensure that ${\{{\int }_0^t{S}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0\ell }(u)\}}^{-1}\stackrel{P}{\to }{\{{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)\}}^{-1}$ uniformly for t ∈ [0, τ]. Therefore, we have that ${\widehat{\mathit{SRR}}}_j(t)\stackrel{P}{\to }{\mathit{SRR}}_j(t)$ uniformly for t ∈ [0, τ].

To prove weak convergence, we use the following decomposition,

$$n^{\frac{1}{2}}\left\{{\widehat{\mathit{SRR}}}_j(t)-{\mathit{SRR}}_j(t)\right\}=n^{\frac{1}{2}}\left\{\frac{{\int }_0^t{S}_{\ell }^{(0)}(u;\widehat{\beta })d{\widehat{\mathrm{\Lambda }}}_{0j}(u;\widehat{\beta })}{{\int }_0^t{S}_{\ell }^{(0)}(u;\widehat{\beta })d{\widehat{\mathrm{\Lambda }}}_{0\ell }(u)}-\frac{{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u;\widehat{\beta })}{{\int }_0^t{S}_{\ell }^{(0)}(u;{\beta }_0)d{\widehat{\mathrm{\Lambda }}}_{0\ell }(u;\widehat{\beta })}\right\}$$ (A.3)

$$+n^{\frac{1}{2}}\left\{\frac{{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)}{{\int }_0^t{S}_{\ell }^{(0)}(u;\widehat{\beta })d{\widehat{\mathrm{\Lambda }}}_{0\ell }(u;\widehat{\beta })}-\frac{{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)}{{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)}\right\}.$$ (A.4)

First, we have that

$$\begin{array}{l}(A.3)=w(t,{\beta }_0)n^{\frac{1}{2}}\left\{{\int }_0^t{S}^{(0)}(u;\widehat{\beta })\frac{{\sum }_{i=1}^n{dN}_{ij}(u)}{{nS}_j^{(0)}(u;\widehat{\beta })}-{\int }_0^t{s}^{(0)}(u;{\beta }_0)\frac{s_{\ell }^{(0)}(u;{\beta }_0)}{s^{(0)}(u;{\beta }_0)}d{\mathrm{\Lambda }}_{0\ell }(u)\right\}+o_p(1)\\ =w(t;{\beta }_0)\left[n^{-\frac{1}{2}}\sum _{i=1}^n{\int }_0^t\frac{s^{(0)}(u;{\beta }_0)}{s_j^{(0)}(u;{\beta }_0)}\left\{{dN}_{ij}(u;{\beta }_0)-s_j^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)\right\}+{\int }_0^t{r}_j^T(u;\beta )d{\mathrm{\Lambda }}_{0j}(u)n^{-\frac{1}{2}}(\widehat{\beta }-\beta )\right\}+o_p(1),\end{array}$$

where w(t; β) and r_j(u; β) are defined in Section 2. Note that the second equality of the argument above is obtained through the Functional Delta Method and Lemma 19.24 of [19]. Based on previously established empirical process theory for the Cox model (e.g., [17]), we have that

$$\begin{array}{l}{n}^{\frac{1}{2}}(\widehat{\beta }-{\beta }_0)=\left\{\sum _{\ell =1}^J{\mathrm{\Omega }}_{\ell }{({\beta }_0)}^{-1}\right\}{G}_n[\sum _{\ell =1}^J\{\{Z-{\overline{z}}_{\ell }(X;{\beta }_0)\}\mathrm{\Delta }I(G=\ell )\\ -{\int }_0^{\tau }\{Z-{\overline{z}}_{\ell }(u;{\beta }_0)\}exp({\beta }_0^{T}Z)I(X\ge u)I(G=\ell )d{\mathrm{\Lambda }}_{0\ell }(u)]+o_p(1),\end{array}$$

where the o_p(1) is uniform in t and is the empirical process defined by ${\mathbb{G}}_{n}f=\sqrt{n}({\mathbb{P}}_n-\mathbb{P})f$ . Through the Functional Delta Method,

$$(A.4)=-\frac{{\int }_0^t{s}^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)}{{\{{\sum }_{\ell =1}^J{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)\}}^2}\sum _{\ell =1}^J{G}_n[N_{\ell }(t)]+o_p(1).$$

Combining (A.3) and (A.4),

$$\begin{array}{l}{n}^{\frac{1}{2}}\left\{{\widehat{\mathit{SRR}}}_j(t)-{\mathit{SRR}}_j(t)\right\}\\ =G_n[w(t;{\beta }_0)\{{\int }_0^t\frac{s^{(0)}(u;{\beta }_0)}{s_j^{(0)}(u;{\beta }_0)}{dN}_j(u)+{\int }_0^t{r}_j^T(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)\left\{\sum _{\ell =1}^J{\mathrm{\Omega }}_{\ell }{({\beta }_0)}^{-1}\right\}\\ \sum _{\ell =1}^J\left\{\{Z-{\overline{z}}_{\ell }(X;{\beta }_0)\}\mathrm{\Delta }I(G=\ell )-{\int }_0^{\tau }\{Z-{\overline{z}}_{\ell }(u;{\beta }_0)\}exp({\beta }_0^{T}Z)I(X\ge u)I(G=\ell )d{\mathrm{\Lambda }}_{0\ell }(u)\right\}\}\\ -\frac{{\int }_0^t{s}^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0j}(u)}{{\{{\sum }_{\ell =1}^J{\int }_0^t{s}_{\ell }^{(0)}(u;{\beta }_0)d{\mathrm{\Lambda }}_{0\ell }(u)\}}^2}\mathrm{\Delta }I(X\le t)]+o_p(1);\end{array}$$

Since the VC classes with finite index satisfy the entropy conditions for the Donsker theorem [16], {I(X ≥ t), t ∈ [0, τ]} and {I(X ≤ t), t ∈ [0, τ]} belong to some Donsker classes. The same holds for the bounded monotone stochastic process {N(t), t ∈ [0, τ]}. Finally, the class of functions of Lipschitz transformations of Donsker classes is Donsker. Therefore, with the various bounded conditions and apply the Donsker theorem, Theorem 1 follows.