A Score-type Test for Heterogeneity in Zero-inflated Models in a Stratified Population

Abstract

We propose a score-type statistic to evaluate heterogeneity in zero-inflated models for count data in a stratified population, where heterogeneity is defined as instances in which the zero counts are generated from two sources. Evaluating heterogeneity in this class of models has attracted considerable attention in the literature, but existing testing procedures have primarily relied on the constancy assumption under the alternative hypothesis. In this paper, we extend the literature by describing a score-type test to evaluate homogeneity against general alternatives that do not neglect the stratification information under the alternative hypothesis. The limiting null distribution of the proposed test statistic is a mixture of chi-squared distributions which can be well approximated by a simple parametric bootstrap procedure. Our numerical simulation studies show that the proposed test can greatly improve efficiency over tests of heterogeneity that ignore the stratification information. An empirical application to dental caries data in early childhood further shows the importance and practical utility of the methodology in using the stratification profile to detect heterogeneity in the population.

1. Introduction

In many epidemiological and biomedical studies, the primary outcomes of interest take the form of counts which can be well represented by standard distributions such as the binomial, negative binomial and Poisson models. In practice, however, some count data exhibit a higher incidence of zeros which can not be accommodated by these standard distributions. For such data, it is a common practice to use zero-inflated models to characterize the population. These are two-component mixture models that combine a degenerate distribution at zero with a parametric non-degenerate distribution 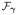known up to a finite dimensional parameter γ ∈ Γ. Specifically, the mixture distribution is defined as follows,

$$P(y=y_i)=\{\begin{array}{ll}{\pi }_i(\mathit{\omega })+(1-{\pi }_i(\mathit{\omega }))f(y_i;\mathit{\gamma }),\hfill & y_i=0\hfill \\ (1-{\pi }_i(\mathit{\omega }))f(y_i;\mathit{\gamma }),\hfill & y_i>0.\hfill \end{array}$$ (1)

where y denotes the random count variable and y_i its observed version for the ith observation, i = 1, …, n, and π_i(ω), 0 ≤ π_i(ω) ≤ 1, with ω being an unknown parameter, represents the unknown mixing probability, f (y_i; γ), with γ being a π × 1 vector of unknown parameters, represents the probability mass function of y under the homogeneous distribution. In essence, the density f(y_i; γ) is a positive smooth function that decays rapidly at infinity with some degree of uniformity. A good example of such functions is the exponential family density function, for which the associated mixture model has been extensively studied in statistical research [1, 2, 3, 4]. A non member of the exponential family such as the two-parameter negative binomial distribution also constitutes an example of this family [5, 6, 7, 8].

Under the mixture model in (1), zero counts are generated from two sources and the parameter π_i(ω) measures the extent of this heterogeneity in the population. In real life applications of this mixture model, one is interested in evaluating whether this heterogeneity is consistent with observed data. This question has been examined by many authors in a variety of settings [1, 9, 10, 11]. But existing methodologies often rely on restrictive formulations of the working mixing weight model. One general limitation is that the mixing weights are often assumed constant under the alternative hypothesis. Although important, such an approach may fail to reject homogeneity against alternatives that allow the mixing weight to depend on covariates. In recent papers, Jansakul and Hinde [10] and Todem et al. [11] have shown, using two-sided alternatives, that incorporating covariates into the mixing weights can greatly improve the test efficiency. By allowing potentially negative mixing weights under the alternative, the tests developed by these authors are only valid under the marginal representation of the mixture model which ignores its hierarchical representation. This is another limitation as zero-inflated models which maintain their hierarchical representation are usually fit in practice [12].

In this paper, we suggest an extension of existing homogeneity testing procedures to covariates with a focus on alternatives that are consistent with real applications of zero-inflated regression models. Specifically, we consider the situation where the mixing weight depends on a stratification variable with few strata under the alternative model. A complication, however, is that the implied hypotheses may not be typical and standard regularity conditions to conduct the test may not hold. There are hypothesized parameters under the null that lie on the boundary of the parameter space and one-sided composite hypotheses under the alternatives. We develop a score-type test of homogeneity that can accommodate these complications. Technically, the test statistic is similar in spirit to that of Silvapulle and Silvapulle [13] in detecting general alternatives and has the well known advantage of only requiring model estimation under the null hypothesis. Using numerical simulations and a real life example, the test statistic that can detect varying heterogeneity under the alternative is found to be relatively more powerful than the test that assumes constant heterogeneity under alternative, when the underlying heterogeneity varies with the stratification profile.

The rest of this article is organized as follows. In Section 2, we develop a one-sided score test for homogeneity of zeros against alternatives from the mixture models with stratum dependent mixing probabilities. In Section 3, we conduct numerical studies to evaluate the finite sample properties of the proposed testing procedure and illustrate its practical utility using a real life example in early childhood dental caries research. Some remaining issues are discussed in Section 4.

2. A score test of homogeneity in a stratified population

Suppose we are interested in evaluating the hypothesis of zero mixing weights against the alternative that the sample y_i, i = 1, · · ·, n, is obtained from model in (1). Under the null hypothesis H₀ : π_i(ω) = 0, the mixture model in (1) reduces to the homogeneous model with probability mass function f(y_i; γ). A popular approach for assessing this hypothesis consists of assuming a constant mixing weight under alternatives to homogeneity [9]. Such an approach may suffer from reduced power if the underlying true mixing weight depends on covariates. In this paper, we construct a test statistic that allows the mixing probability π_i(ω) to depend upon a categorical covariate such as a stratification variable under the alternative. Suppose that the population under study consists of K known distinct strata and that each stratum k has its own mixing weight ϖ_k, with 0 = ϖ_k ≤ 1. Let δ_ik be a non random binary variable which takes value 1 if subject i belongs to stratum k, 1 ≤ k ≤ K and 0 otherwise, with ${\sum }_{k=1}^K{\delta }_{ik}=1$. The mixing probability for subject i can be written as ${\pi }_i(\mathit{\omega })={\prod }_{k=1}^K{\varpi }_k^{{\delta }_{ik}}$ with ϖ_k = ω_k/(1 + ω_k), ω_k ≥ 0, and ω = (ω₁, ω₂, · · ·, ω_K)′. In other words, ϖ_k represents the proportion of extra zeros in Stratum k, k = 1, · · · K. To evaluate the homogeneity hypothesis, one is typically interested in the one-sided alternative,

$${\mathrm{H}}_0:{\omega }_k^{\ast }=0\text{for}\text{all}k\text{vs}.{\mathrm{H}}_1:{\omega }_k^{\ast }>0\text{for}\text{some}k,$$ (2)

where ${\omega }_k^{\ast }$ represents the true value of ω_k, k = 1, 2, · · · K.

Let δ_i = {δ_i1, · · ·, δ_iK} represent the stratification information for unit i and by x_i any potential covariates observed alongside y_i. We assume that observed data ${\{y_i\}}_{i=1}^n$ are random independent copies of y. Given data ${\{y_i,{\delta }_i,x_i\}}_{i=1}^n$ and setting θ = (ω′, γ′)′, we denote by ℓ_n(θ) the log likelihood function associated with parameter vector θ and by U_n(θ) = ∂ℓ_n(θ)/∂θ the corresponding first-order derivative with respect to parameter vector θ. Let θ^* = (ω^*′, γ^*′)′ be the true value of θ with E{U_n(θ^*)} = 0, to construct the score-based test statistic we assume the existence of a nonsingular matrix G(θ^*) and the following conditions:

• A1All strata share a common subset of θ.
• A2n^−1/2U_n(θ^*) →^d N (0, G(θ^*)) as n → ∞.
• A3For any α > 0, sup_||η||≤α ||n^−1/2{U_n(θ^* + n^−1/2η) − U_n(θ^*)} + G(θ^*)η|| = o_p(1), where o_p(1) represents the convergence to 0 in probability as n → ∞.

The discussion of these conditions and related technical details are provided in the Appendix. Let θ̂₀ = (0′, γ̂′)′, where γ̂ is an estimator of γ^* obtained under the null hypothesis. Because of the one-sided constraints ω_k ≥ 0, k = 1, · · ·, K, we consider the likelihood ratio test statistic for H₀ against H₁ based on the asymptotic normality of the ‘single’ observation S_n(θ₀) = n^−1/2U_nω(θ̂₀) to derive the general score statistic,

$$T_n=S_n{({\widehat{\mathit{\theta }}}_0)}^{\prime }{G}^{\mathit{\omega \omega }}({\widehat{\mathit{\theta }}}_0)S_n({\widehat{\mathit{\theta }}}_0)-\underset{\stackrel{\sim }{\mathit{\omega }}\ge 0}{inf}\left\{{\left(S_n({\widehat{\mathit{\theta }}}_0)-\stackrel{\sim }{\mathit{\omega }}\right)}^{\prime }{G}^{\mathit{\omega \omega }}({\widehat{\mathit{\theta }}}_0)\left(S_n({\widehat{\mathit{\theta }}}_0)-\stackrel{\sim }{\mathit{\omega }}\right)\right\},$$ (3)

where ω̃ ≥ 0 with ω̃ = (ω̃₁, ω̃₂, · · ·, ω̃_K)′ is interpreted coordinatewise, that is ω̃_k ≥ 0, for all k = 1, 2, · · ·, K. In practice, the quadratic function of ω̃ can be easily minimized by using available optimization subroutines such as optim in the statistical software R. When K = 1, ω = ω₁ ≡ ω is a scalar and the test statistic simply reduces to T_n = S_n(θ̂₀)′G^ωω(θ̂₀)S_n(θ̂₀)I{S_n(θ̂₀) > 0}, where I{.} represents the indicator function. The null hypothesis is then rejected for large values of T_n. Statistic T_n has the limiting distribution $\mathcal{T}=Z^{\prime }{G}^{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast })Z-{inf}_{\stackrel{\sim }{\mathit{\omega }}\ge 0}\{{(Z-\stackrel{\sim }{\mathit{\omega }})}^{\prime }{G}^{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast })(Z-\stackrel{\sim }{\mathit{\omega }})\}$ with $Z~N\left(\mathbf{0},G^{\mathit{\omega \omega }}{({\mathit{\theta }}_0^{\ast })}^{-1}\right)$ for large values of n [14]. When K = 1, this limiting distribution is a mixture of chi-squared distributions ${\chi }_0^2$ (a degenerate distribution with probability point mass at 0) and ${\chi }_1^2$, each with weight 0.5. For K > 1, the large sample distribution of the statistic T_n remains a mixture of chi-squared distributions but the mixing weights are quite complicated and are often approximated only through numerical methods [13].

When ${\mathit{\theta }}_0^{\ast }$ is known such as in simulation experiments for the study of the test empirical size, 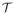the limiting null distribution of T_n can be approximated by generating for example one million points from a centered multivariate normal distribution with covariance matrix $G^{\mathit{\omega \omega }}{({\mathit{\theta }}_0^{\ast })}^{-1}$. However, when ${\mathit{\theta }}_0^{\ast }$ is unknown such as in real data analysis and simulation studies for the study of the test empirical power, a simple parametric bootstrap procedure can be used to approximate the distribution of 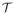. The bootstrap resampling method was introduced by Efron [15] and has become a routine method for approximating distributions that are difficult to obtain analytically. Its validity follows automatically from arguments given in Efron and Tibshirani [16]. From a parametric point of view, the bootstrap methodology consists of three simple steps: i) an estimation step under which the parameters of the null model are estimated from observed data, ii) a Monte Carlo step to generate B pseudo-data sets from the fitted model and calculate the associated test statistics; and finally iii) construction of the bootstrap distribution for a sufficiently large value of B. We give below the details of this procedure to obtain the large sample distribution of the proposed score test T_n.

1. Estimation step: Given observed data ${\{y_i,{\delta }_i,x_i\}}_{i=1}^n$, compute the estimator γ̂ of γ̇^* under the null model with probability mass function f(y_i; γ).

2. Monte Carlo step: For each b, generate the Monte Carlo sample ${\{y_i^{(b)}\}}_{i=1}^n$ from the null model with γ fixed at γ̂ and assign the generated data point $y_i^{(b)}$ to δ_i and x_i. For each Monte Carlo sample { $y_i^{(b)}$, δ_i, x_i}, i = 1, · · ·, n, calculate the statistic

   $$T_n^{(b)}=S_n{({\widehat{\mathit{\theta }}}_0^{(b)})}^{\prime }{G}^{\mathit{\omega \omega }}({\widehat{\mathit{\theta }}}_0^{(b)})S_n({\widehat{\mathit{\theta }}}_0^{(b)})-\underset{\stackrel{\sim }{\mathit{\omega }}\ge 0}{inf}\left\{{\left(S_n({\widehat{\mathit{\theta }}}_0^{(b)})-\stackrel{\sim }{\mathit{\omega }}\right)}^{\prime }{G}^{\mathit{\omega \omega }}({\widehat{\mathit{\theta }}}_0^{(b)})\left(S_n({\widehat{\mathit{\theta }}}_0^{(b)})-\stackrel{\sim }{\mathit{\omega }}\right)\right\}.$$

   where ${\widehat{\mathit{\theta }}}_0^{(b)}={({\mathbf{0}}^{\prime },{{\widehat{\mathit{\gamma }}}^{(b)}}^{\prime })}^{\prime }$ with γ̂^(b) being an estimate of γ̂ under the null hypothesis using the pseudo data { $y_i^{(b)}$, δ_i, x_i}, i = 1, · · ·, n.

3. Repeat Step 2 for b = 1, 2, · · ·, B.

By the Glivenko-Cantelli Theorem, when B is large, an approximate p-value of the test is $B^{-1}{\sum }_{b=1}^{B}I(T_n^{(b)}\ge t_n)$, the proportion of these artificial statistics which exceed t_n, the observed value of T_n. In our numerical applications, B is set to 1000.

3. Numerical Studies

We illustrate the use of the proposed score-type statistic to evaluate homogeneity against heterogeneity for the class of zero-inflated models for stratified discrete data. For the real data analysis, the zero-inflated negative binomial model will be used. The zero-inflated Poisson regression model will be utilized for the numerical experiment to reduce the computational burden. These two popular models verify all the smoothness and regularity conditions A2 and A3. Condition A1, however, will be discussed in regard to each working model specification. Derivations of the basic quantities required to construct the proposed test statistics for these models are relegated to the Appendix.

3.1. Dental Caries Data

Our motivating example comes from a longitudinal (three-wave) study designed to collect oral health information on inner-city low-income African American populations of Detroit, Michigan. Targeted participants were African American children under the age of 6 and their main caregivers of at least 14 years of age living in Detroit households with income below 250% of the 2000 federal poverty level. Study participants (index children and their caregivers) were randomly selected according to a two-stage probability sample design. At the first stage, census blocks were sampled with probabilities proportional to their size. Housing units were sampled at the second stage with probabilities inversely proportional to their size. From this sampling scheme, 1,021 families (children and their caregivers) were drawn and eventually examined. For selected participants, the oral examinations involved assessments of dental caries, periodontal disease, oral cancer and oral hygiene status. A set of questionnaires about demographics, social factors of oral health behaviors and practices including social support and depressive symptoms (measured by the Center of Epidemiologic Studies Scale CESD) among others, and biological characteristics was also administered. A food frequency questionnaire was administered to caregivers to collect information (such as the amount of sugar intake) on their own dietary practices and those of the child.

In this paper, we focus on a mouth-level index which represents the overall experience of dental caries for each surveyed child. This index counts the number of decayed surfaces (ds) which are surfaces with signs of clinically detectable enamel lesions comprising both noncavitated and cavitated lesions. Although this type of mouth-level indices has well documented limitations regarding its ability to measure dental caries, it continues to be instrumental in evaluating and comparing the risks of dental caries across population groups. Most importantly, it remains popular in dental caries research because it enables one to conduct historical comparisons in population-based studies [17]. A more detailed description of the study can be found elsewhere [18, 19, 20].

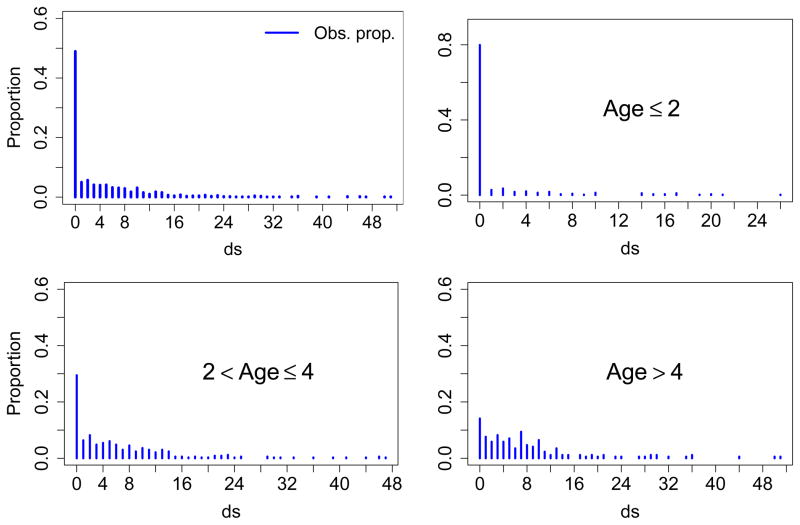
Our numerical computations ignore aspects of the multi-stage sampling design and are based on cross-sectional data obtained in the first wave of examinations and interviews completed between 2002–2003. Covariates considered in our analysis include the child’s age group (0 year ≤ Age ≤ 2 years; 2 years < Age ≤ 4 years; and Age > 4 years) and the child’s sugar intake or consumption (SI) measured in grams per day, variables that have been shown to be associated with dental caries [21, 22]. The children’s age group serves as the stratification variable in this paper (0 year ≤ Age ≤ 2 years for Stratum 1; 2 years < Age ≤ 4 years for Stratum 2; and Age > 4 years for Stratum 3). As a preliminary analysis, bar chart plots of relative frequencies for the overall sample and for each age-specific stratum are constructed and presented in Figure 1. From these plots, a sizeable proportion (about 50%) of children in the sample do not have dental caries. More importantly, zeros frequencies are more prominent in the youngest age group, with about 80% of these children having no tooth surfaces with signs of clinically detectable enamel lesions. This result is consistent with the fact that younger children do not have all their teeth erupted and therefore are less likely to have dental caries.

Figure 1.

Observed proportions of the number of decayed surfaces (ds) for the overall sample and for each age group.

Following earlier analyses of dental caries indices in these African American children, a negative binomial model is used to accommodate overdispersion due to sizeable frequencies of children with large caries counts [11]. Specifically, we consider a negative binomial regression model with mean ${\lambda }_i=exp\left\{{\sum }_{k=1}^3{\delta }_{ik}({\beta }_{0k}+{\beta }_{1k}\times {SI}_i)\right\}$ and an overdispersion parameter κ > 0. All parameters of the mean λ_i are stratum-specific but the overdispersion parameter κ is common across all strata to ensure that condition A1 is satisfied. This condition will be evaluated against data in a subsequent analysis. For this homogeneous model, parameter vector γ = (β′, κ)′ with β = (β₀₁, β₁₁, · · ·, β₀₃, β₁₃)′, and variable δ_ik represents the binary indicator for Stratum k, k = 1, 2, 3. This basic starting model is then evaluated against the associated zero-inflated model with a constant mixing probability π_i(ω) = ω/(1 + ω) ≡ ϖ₁ = ϖ₂ = ϖ₃, ω ≥ 0. For the caries index considered, the homogeneity hypothesis ω^* = 0 (no need for zero-inflation) fails to be rejected at 5% significance level against the zero-inflated model that neglects the mixing weight stratification (observed statistic = 0.158 with a p-value of 0.346 or 0.401, using respectively a mixture of ${\chi }_0^2$ and ${\chi }_1^2$ distributions, each with weight 0.5 and the proposed parametric bootstrap resampling scheme).

We then consider the proposed test that accommodates the stratification of mixing weights under the alternative hypothesis. Specifically, we assume a working zero-inflated negative binomial model with mixing probability ${\pi }_i(\mathit{\omega })={\prod }_{k=1}^3{\varpi }_k^{{\delta }_{ik}}$, where ϖ_k = ω_k/(1 + ω_k), ω_k ≥ 0, represents the proportion of extra zeros in Stratum k, k = 1, 2, 3, and ω = (ω₁, ω₂, ω₃)′. Under this working model, the homogeneity hypothesis is clearly rejected at 10⁻³ significance level (observed statistic t_n = 101.304, p-value < 0.001 obtained from a parametric bootstrap resampling scheme), therefore providing a strong evidence of heterogeneity in this population. Table 1 gives the parameter estimates and their standard errors, and summary statistics of the homogeneous (null) model and the heterogeneous models with a constant mixing weight and stratum-specific mixing weights. The AIC and BIC statistics provide another evidence that the zero-inflated negative binomial model coupled with stratum-specific mixing weights provides a better fit to these data compared to the homogeneous model and the zero-inflated negative binomial model with a constant mixing weight. Results from fitting the stratum-specific mixing weight model indicate that there is no inflation of zeros in Stratum 3 representing the oldest age group (ϖ̃₃ = 0.0478, se(ϖ̃₃) = 0.0358) in contrast to the two younger age groups (ϖ̃₁ = 0.7667, se(ϖ̃₁) = 0.0243, and ϖ̃₂ = 0.2119, se(ϖ̃₂) = 0.0329). Hence by averaging over the strata information, the test statistic based on the constant mixing weight approach loses power in detecting heterogeneity in these data. This example clearly illustrates the importance of formulating less restrictive alternative hypotheses when evaluating a null model. Given that the true underlying parametric model that provides the best representation of the data is often unknown, entertaining less restrictive formulations appears to be the most conservative strategy.

Table 1.

The fitted homogeneous (null) model and heterogeneous models with constant mixing weight and stratum-specific mixing weight to dental caries index ds

	No mixing weight (null) model		Constant mixing weight model		Stratum-specific mixing weight model
Vector θ	Estimates	Std. Errors	Estimates	Std. Errors	Estimates	Std. Errors
β01	0.2675	0.1795	0.3846	0.2605	1.6342	0.2147
β11	0.0009	0.0026	0.0010	0.0026	0.0025	0.0032
β02	1.6561	0.2015	1.7376	0.2317	1.9541	0.1450
β12	0.0011	0.0010	0.0010	0.0010	0.0008	0.0007
β03	2.2924	0.2599	2.3211	0.2503	2.3369	0.1651
β13	−0.0010	0.0012	−0.0009	0.0012	−0.0010	0.0008
κ	2.8603	0.1905	2.4527	0.6249	0.9601	0.1107
ϖ1	-	-	0.0811	0.1218	0.7667	0.0243
ϖ2	-	-	0.0811	0.1218	0.2119	0.0329
ϖ3	-	-	0.0811	0.1218	0.0478	0.0358
−2LogLik.	4030.5		4030.2		3791.4
AIC	4044.5		4046.2		3811.4
BIC	4078.1		4084.6		3859.4

−2LogLik.= −2ℓ_n(θ̃), AIC= −2ℓ_n(θ̃) + 2q, BIC= −2ℓ_n(θ̃) + q log(n), where θ̃ is the maximum likelihood estimate of θ^*, q = # model parameters.

As a final analysis, the non-separability condition A1 was examined by evaluating whether the overdispersion parameter κ was constant across all strata in the zero-inflated negative binomial model with stratum-specific mixing weights. A two degrees of freedom Wald test performed to this effect yielded an observed value of 0.88 (p-value=0.6461), suggesting no evidence from data to reject the constancy of the overdispersion parameter κ over the strata. This result was also consistent with the likelihood ratio test (observed statistic=1.30 and p-value=0.4780) and other summary statistics such as the AIC and the BIC (see Table 2). We noticed however that even when the overdispersion parameter is allowed to depend on the stratification variable, the constant mixing weight test remains insensitive in detecting the varying heterogeneity of the mixing weight under the alternative, in contrast to the proposed test.

Table 2.

Summary statistics comparing models that assume constant and stratum-specific overdispersion parameters

Summary Statistics	Constant overdispersion parameter κ	Stratum-dependent overdispersion parameter κ
AIC	3811.4	3816.7
BIC	3859.4	3874.3
−2LogLik.§	3791.4	3792.7

^§−2LogLik.= −2×Log-Likelihood value at θ̃, where θ̃ is the maximum likelihood estimate of θ^*. Δ(−2LogLik.) = 1.3 is the difference in −2×Log-Likelihood values between the constant and the stratum-dependent overdispersion parameter models. The p-value associated with Δ(−2LogLik.) is 0.4780 which is computed from a ${\chi }_2^2$ distribution.

3.2. Simulations

In this section, we conduct a numerical study to evaluate the finite sample performances of the proposed score test statistic T_n which are in turn compared to those of the constant mixing weight score test statistic. Similarly to the real data example, we consider a stratified population made of three strata. But to keep the simulation scheme simple, we restrict the true non-degenerate model 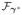to a Poisson process with covariate-dependent mean ${\lambda }_i^{\ast }=exp\{{\sum }_{k=1}^3{\gamma }_k^{\ast }{\delta }_{ik}+{\gamma }_4^{\ast }{v}_i\}$, where covariate v_i is generated from a uniform random variable on the interval [0, 1] and the membership indicators δ_i1, δ_i2 and δ_i3 are generated from a multinomial distribution with membership probabilities p₁ = 0.3, p₂ = 0.3, p₃ = 0.4, respectively. The stratum-specific intercept term, represented by the vector ( ${\gamma }_1^{\ast },{\gamma }_2^{\ast },{\gamma }_3^{\ast }$), takes values in the set {(−0.05, −0.10, −0.15), (0.05, 0.10, 0.15)} and the slope ${\gamma }_4^{\ast }$ associated with v_i is set to 0.5. In this simulation study, these intercept terms are used to capture the separation between the mean of the true homogeneous model 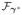and 0. Indeed, large values of ${\gamma }_k^{\ast }$, k = 1, 2, 3, shift the mean of the true non-degenerate model further away from 0, therefore making the two components of the mixture model easily detectable. For data generated under the associated zero-inflated model, the true mixing weight is ${\pi }_i^{\ast }({\mathit{\omega }}^{\ast })={\prod }_{k=1}^K{\varpi }_k^{\ast {\delta }_{ik}}$, with ${\varpi }_k^{\ast }={\omega }_k^{\ast }/(1+{\omega }_k^{\ast })$ being the true mixing weight in stratum k, k = 1, 2, 3 and ${\mathit{\omega }}^{\ast }={({\omega }_1^{\ast },{\omega }_2^{\ast },{\omega }_3^{\ast })}^{\prime }$.

Throughout the simulations, we assume the working mixing weight model ${\pi }_i(\mathit{\omega })={\prod }_{k=1}^K{\varpi }_k^{{\delta }_{ik}}$ with ϖ_k= ω_k/(1 + ω_k) under the alternative hypothesis. Conversely under the constant mixing weight alternative, the working mixing weight model is π_i(ω) = ω/(1 + ω). The maximum likelihood estimate γ̂ of ${\stackrel{.}{\mathit{\gamma }}}^{\ast }-({\stackrel{.}{\gamma }}_1^{\ast },{\stackrel{.}{\gamma }}_2^{\ast },{\stackrel{.}{\gamma }}_3^{\ast },{\stackrel{.}{\gamma }}_4^{\ast })$ under the null are obtained from the homogeneous Poisson model with the working mean model ${\lambda }_i=exp\{{\sum }_{k=1}^3{\gamma }_k{\delta }_{ik}+{\gamma }_4{v}_i\}$. Note here that the parameter γ₄ is constant across all strata in this working model to ensure that condition A1 is satisfied. Finally, all simulations were replicated 1,000 times and for sample sizes n from 50 to 400.

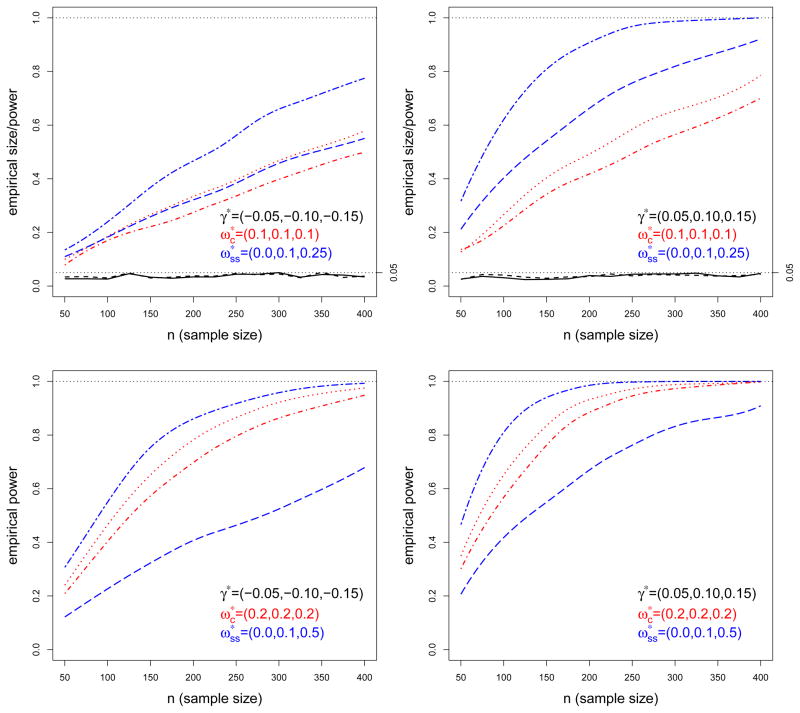
To investigate the empirical type I error rate of the proposed tests, we generate data from the homogeneous Poisson model ( ${\omega }_k^{\ast }=0$, k = 1, 2, 3) with the true mean ${\lambda }_i^{\ast }$ specified above. In Figure 2, as expected, the constant mixing weight and the proposed test statistics maintain their sizes at 5% nominal level regardless of the degree of separation between the homogeneous model and the degenerate distribution. We further investigate the empirical power of the tests when the true mixing weight is constant across the three strata by setting ${\mathit{\omega }}^{\ast }={\mathit{\omega }}_c^{\ast }$, where ${\mathit{\omega }}_c^{\ast }$ takes values from the set {(0.1, 0.1, 0.1), (0.2, 0.2, 0.2)}. Overall, larger sample sizes and increasing values of ${\omega }_k^{\ast }$, k = 1, 2, 3, improve the power of detecting the alternatives under consideration for the two tests. Moreover, the power also increases with increasing values of the intercept ${\gamma }_k^{\ast }$. The constant mixing weight test appears to perform slightly better than the stratum-adjusted test when the true mixing weight is constant. But this loss of power of the stratum-adjusted test appears to be minimal.

Figure 2.

Empirical size and power of constant mixing weight and stratum-specific mixing weight tests at 5% significance level, homogeneous model is Poisson. The black lines represent the data generated under the null model ( ${\mathit{\omega }}_c^{\ast }={\mathit{\omega }}_{ss}^{\ast }=0$). The red and blue lines represent the data generated under the constant ( ${\mathit{\omega }}_c^{\ast }$) and the stratum-specific ( ${\mathit{\omega }}_{ss}^{\ast }$) mixing weight model, respectively:

True mixing weight is zero (size): ——— stratum-specific mixing weight test; – – – constant mixing weight test

True mixing weight is constant (power): stratum-specific mixing weight test; constant mixing weight test

True mixing weight is stratum-specific (power): stratum-specific mixing weight test; constant mixing weight test.

We finally conduct a study to evaluate the performances of T_n when the constancy assumption under heterogeneity is violated. Figure 2 also presents the results of this study for ${\mathit{\omega }}^{\ast }={\mathit{\omega }}_{ss}^{\ast }$, where ${\mathit{\omega }}_{ss}^{\ast }$ takes values from the set {(0, 0.1, 0.25), (0, 0.1, 0.5)}. As expected, larger sample sizes and increasing values of one component of ω^* while maintaining the remaining components fixed, improve the power of detecting the alternatives under consideration for all tests. Moreover, the power also increases when the two components of the mixture distribution are well separated, occurring when ${\gamma }_k^{\ast }$, k = 1, 2, 3, are large. The stratum-adjusted test clearly outperforms the constant mixing weight test. And the maximum gain of efficiency of the stratum-adjusted test is achieved when one stratum-specific mixing probability is large while the remaining ones are negligible. Thus by averaging over the stratification variable, the stratum-unadjusted test may have weaker power to capture heterogeneity in the population. Findings from the dental caries data analysis are very consistent to this simulation conjecture. Indeed, the estimates from the alternative model show heterogeneous mixing weights across the three age groups, with the youngest children exhibiting a significantly higher mixing weight. This heterogeneity of mixing weights across the three age groups adversely affects power of the test statistic based on the constant mixing weight in detecting zero-inflation. Our simulations and real data analysis are reassuring and lend credence to the need to formulate more elaborate zero-inflated parametric models under alternative in evaluating zero-inflation.

4. Discussion

Whenever the inference for the mixing weight in zero-inflated regression models is of interest, existing testing methodologies have relied essentially on restrictive assumptions under heterogeneity. Typically, score tests that restrict the mixing weights to be constant under alternatives to homogeneity are often advocated. Our real life example and simulation studies have shown that testing procedures that rely on such restrictions may adversely affect statistical power in detecting heterogeneity. Using the general theory from Silvapulle and Silvapulle [13], we have extended the literature by developing a testing procedure to evaluate homogeneity in two-component mixture models, which explicitly takes into account the presence of stratification under heterogeneity. This procedure is shown to have satisfactory statistical power even when the true mixing weight is constant under heterogeneity.

One may argue that the test of zero inflation that assumes constancy of the mixing probability under the alternative can simply be performed within each stratum. This approach is in principle feasible but not necessarily optimal. Indeed, if there are parameters that are shared by some strata, a joint estimation requiring information across all these strata is unavoidable. In the dental caries example, the working regression model for the mean of the non-degenerate distribution is stratum specific but the three strata share the same overdispersion parameter κ. Likewise in our numerical studies, although the intercept of the working mean model of the non-degenerate distribution is stratum specific, the slope of the covariate v_i is stratum-independent and therefore requires information across all strata for its estimation.

To perform the test in practice, a parametric bootstrap is proposed to approximate the limiting distribution of the test statistic T_n under the null hypothesis. This parametric bootstrap requires the null model to be fitted for each simulated Monte Carlo sample, which can be computationally very cumbersome in some practical settings. Alternatively, a more efficient resampling procedure that perturbs the influence function using normal random variates to approximate the true distribution of the test statistics T_n can be used. This technique requires the null model to be fitted only once and has been extensively used in the literature when the desired limiting distribution is difficult or even impossible to derive analytically [23, 24, 25, 26].

The proposed test can be extended to refine the model specification. For example when the null hypothesis is rejected, it may be of interest to identify subgroups of the population that have nonzero mixing probabilities. We did not discuss how to identify these components, but our results can be used for this purpose. Inference regarding significance of each stratum mixing weight can be conducted taking into account that multiple tests are performed, which necessitates an adjustment of the type I error. Our testing procedure also assumes that the mixing weight under heterogeneity depends only on the stratification variable, which is essentially a categorical variable. In practice however, a two-component mixing weight model with a more general specification of the mixing weight is often considered. A good and popular example is the situation where the mixing weight under heterogeneity is also related to some continuous covariates in addition to the stratification variable. For such working mixing weight models, it is unclear how to construct a test of homogeneity against heterogeneity. These issues and other generalizations of the methodology are out of the scope of this work and are the subject of further research.

Appendix

Appendix 1. The technical details of regularity conditions

Condition A1 is the non-separability criterion that requires all strata to share a common subset of θ. It prevents the test of zero-inflation that assumes constancy of the mixing probability under the alternative to be simply performed within each stratum. Although our methodology remains valid even when the distributions of data across strata do not have some parameters in common, its efficiency however can be compromised. Conditions A2 and A3 essentially ensure that the asymptotic normality, the smoothness and regularity requirements of the score function are met.

We partition U_n as $U_n={\left(U_{n\mathit{\omega }}^{\prime },U_{n\mathit{\gamma }}^{\prime }\right)}^{\prime }$ to conform with the partition (ω′, γ′)′ of θ and we denote by G_ωω (θ), G_ωγ (θ), and G_γγ (θ) the corresponding blocks in G(θ). The estimator γ̂ is consistent for γ^* only when the null hypothesis is true. However, when the null is not true, γ̂ converges to γ̇^*, which is not necessarily γ^*. In other words, θ̂₀ = (0′, γ̂′)′ converges to ${\mathit{\theta }}_0^{\ast }={({\mathbf{0}}^{\prime },{{\stackrel{.}{\mathit{\gamma }}}^{\ast }}^{\prime })}^{\prime }$ with θ^*–probability 1, where ${\mathit{\theta }}_0^{\ast }$ satisfies the null hypothesis. Conditions A2 and A3 ensure that n^−1/2U_nω (θ̂₀) under H₀ converges in distribution to a centered normal model with asymptotic variance-covariance matrix $G^{\mathit{\omega \omega }}{({\mathit{\theta }}_0^{\ast })}^{-1}=G_{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast })=G_{\mathit{\omega }\mathit{\gamma }}({\mathit{\theta }}_0^{\ast })G_{\mathit{\gamma \gamma }}^{-1}({\mathit{\theta }}_0^{\ast })G_{\mathit{\gamma }\mathit{\omega }}({\mathit{\theta }}_0^{\ast })$.

Appendix 2. Detailed calculations for the zero-inflated negative model

Consider the zero-inflated negative binomial (ZINB) model for which the probability mass function of the homogeneous distribution is,

$$f(y_i;\mathit{\gamma })=\frac{\mathrm{\Gamma }({\kappa }^{-1}+y_i)}{\mathrm{\Gamma }({\kappa }^{-1})y_i!}{\left(\frac{\kappa {\lambda }_i}{1+\kappa {\lambda }_i}\right)}^{y_i}{\left(\frac{1}{1+\kappa {\lambda }_i}\right)}^{{\kappa }^{-1}},y_i=0,1,\cdots ,$$

where λ_i and κ > 0 represent the mean and the overdispersion parameter, respectively. We consider the working mean model ${\lambda }_i=exp\{{\mathbf{x}}_i^{\prime }\mathit{\beta }\}$ where β is a regression parameter vector of dimension (p − 1) × 1 associated with covariate x_i = (x_1i, · · ·, x_p−1i), i = 1, 2, · · ·, n. For this model, θ = (ω′, γ′)′ with ω = (ω₁, ω₂, · · ·, ω_K) and γ = (β′, κ)′. Let β̂ and κ̂ be the maximum likelihood estimates of β̇^* and κ̇^*, the values of β and κ under the null hypothesis that satisfy the condition $\mathrm{E}\{U_n({\mathit{\theta }}_0^{\ast })\}=0$, where ${\mathit{\theta }}_0^{\ast }={({\mathbf{0}}^{\prime },{{\stackrel{.}{\mathit{\gamma }}}^{\ast }}^{\prime })}^{\prime }$ with γ̇^* = (β̇^*′, κ̇^*′)′.

The score vector for the ZINB model evaluated at θ = θ̂₀ is $U_{n\mathit{\omega }}({\widehat{\mathit{\theta }}}_0)={\frac{\partial {\ell }_n(\mathit{\theta })}{\partial \mathit{\omega }}\mid }_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}$ with

$${\frac{\partial {\ell }_n(\mathit{\theta })}{\partial {\omega }_k}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}=\sum _{i=1}^n\left\{I(y_i=0){\left(1+\widehat{\kappa }{\widehat{\lambda }}_i\right)}^{1/\widehat{\kappa }}-1\right\}{\delta }_{ik},$$

where ${\widehat{\lambda }}_i=exp\{{\mathbf{x}}_i^{\prime }\widehat{\mathit{\beta }}\}$.

Matrices $G_{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast }),G_{\mathit{\omega }\mathit{\gamma }}({\mathit{\theta }}_0^{\ast })$ and $G_{\mathit{\gamma \gamma }}({\mathit{\theta }}_0^{\ast })$ are given as follows:

$$G_{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast })=\text{diag}{\left\{-E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k^2}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}\right)\right\}}_{k=1}^K$$

with

$$\begin{array}{l}E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k^2}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n\left(1-{\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)}^{1/{\stackrel{.}{\kappa }}^{\ast }}\right){\delta }_{ik},{\stackrel{.}{\lambda }}_i^{\ast }=exp\{{\mathbf{x}}_i^{\prime }{\stackrel{.}{\mathit{\beta }}}^{\ast }\},\\ G_{\mathit{\omega }\mathit{\gamma }}({\mathit{\theta }}_0^{\ast })=\left({\left\{-E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k\partial {\beta }_j}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{(j,k)=(1,1)}^{(p-1,K)},{\left\{-E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k\partial \kappa }|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{k=1}^K\right)\text{with}\\ E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k\partial {\beta }_j}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n{x}_{ji}{\stackrel{.}{\lambda }}_i^{\ast }{\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)}^{-1}{\delta }_{ik},k=1,2,\cdots ,K;j=1,2,\cdots ,p-1\end{array}$$

and

$$E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k\partial \kappa }|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n\left\{-\frac{1}{{\stackrel{.}{\kappa }}^{\ast 2}}log\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)+\frac{{\stackrel{.}{\lambda }}_i^{\ast }}{{\stackrel{.}{\kappa }}^{\ast }\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)}\right\}{\delta }_{ik},k=1,2,\cdots ,K,$$

and $G_{\mathit{\gamma \gamma }}({\mathit{\theta }}_0^{\ast })=\left(\begin{array}{cc}{\left\{-E\left({\frac{{\partial }^2{\ell }_n({\mathit{\theta }}_0^{\ast })}{\partial {\beta }_j\partial {\beta }_t}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{(j,l)=(1,1)}^{(p-1,p-1)}& \mathbf{0}\\ {\mathbf{0}}^{\prime }& -E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\kappa }^2}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\end{array}\right)$ with

$$E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\beta }_j\partial {\beta }_l}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n\frac{{\stackrel{.}{\lambda }}_i^{\ast }}{{\stackrel{.}{\kappa }}^{\ast }\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)}{x}_{ji}{x}_{li},j,l=1,2,\cdots ,p-1$$

and

$$\begin{array}{l}E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\kappa }^2}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n\{-\frac{2}{{\stackrel{.}{\kappa }}^{\ast 3}}log\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)+\frac{{\stackrel{.}{\lambda }}_i^{\ast }}{{\stackrel{.}{\kappa }}^{\ast 2}\left(1+{\stackrel{.}{\kappa }}^{\ast }{\stackrel{.}{\lambda }}_i^{\ast }\right)}\\ +E[\frac{2}{{\stackrel{.}{\kappa }}^{\ast 3}}(\text{ddg}(y_i+{\stackrel{.}{\kappa }}^{\ast -1})-\text{ddg}({\stackrel{.}{\kappa }}^{\ast -1}))+\frac{1}{{\stackrel{.}{\kappa }}^{\ast 4}}(\text{dtg}(y_i+{\stackrel{.}{\kappa }}^{\ast -1})-\text{dtg}({\stackrel{.}{\kappa }}^{\ast -1}))]\},\end{array}$$

where ddg (·) and dtg (·) are di-gamma and tri-gamma functions respectively.

Appendix 3. Detailed calculations for the zero-inflated Poisson model

Consider the zero-inflated Poisson (ZIP) model for which the probability mass function of the homogeneous distribution is,

$$f(y_i;\mathit{\gamma })=\frac{e^{-{\lambda }_i}{\lambda }_i^{y_i}}{y_i!},y_i=0,1,\cdots ,$$

where λ_i represents the mean parameter. We consider the working mean model ${\lambda }_i=exp\{{\mathbf{x}}_i^{\prime }\mathit{\beta }\}$ where β is a regression parameter vector of dimension p × 1 associated with covariate x_i = (x_1i, · · ·, x_pi), i = 1, 2, · · ·, n. For this model, γ = β. Let β̂ be the maximum likelihood estimate of β̇^*, the true value of β under the null hypothesis.

The score vector for the ZIP model evaluated at θ = θ̂₀ $U_{n\mathit{\omega }}({\widehat{\mathit{\theta }}}_0)={\frac{\partial {\ell }_n(\mathit{\theta })}{\partial \mathit{\omega }}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}$ with

$${\frac{\partial {\ell }_n(\mathit{\theta })}{\partial {\omega }_k}|}_{\mathit{\theta }={\widehat{\mathit{\theta }}}_0}=\sum _{i=1}^n\left\{I\{y_i=0\}{e}^{{\widehat{\lambda }}_i}-1\right\}{\delta }_{ik},$$

where ${\widehat{\lambda }}_i=exp\{{\mathbf{x}}_i^{\prime }\widehat{\mathit{\beta }}\}$.

Matrices $G_{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast }),G_{\mathit{\omega }\mathit{\gamma }}({\mathit{\theta }}_0^{\ast })$ and $G_{\mathit{\gamma \gamma }}({\mathit{\theta }}_0^{\ast })$ are given as follows:

$$G_{\mathit{\omega \omega }}({\mathit{\theta }}_0^{\ast })=\text{diag}{\left\{-E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k^2}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{k=1}^K$$

with

$$\begin{array}{c}E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k^2}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n\left(1-e^{{\stackrel{.}{\lambda }}_i^{\ast }}\right){\delta }_{ik},{\stackrel{.}{\lambda }}_i^{\ast }=exp\{{\mathbf{x}}_i^{\prime }{\stackrel{.}{\mathit{\beta }}}^{\ast }\}\\ G_{\mathit{\omega }\mathit{\gamma }}({\mathit{\theta }}_0^{\ast })={\left\{-E\left({\frac{{\partial }^2{\ell }_n}{\partial {\omega }_k\partial {\beta }_j}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{(j,k)=(1,1)}^{(p,K)}\end{array}$$

with

$$E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\omega }_k\partial {\beta }_j}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n{x}_{ji}{\stackrel{.}{\lambda }}_i^{\ast }{\delta }_{ik},k=1,\dots ,K;j=1,\cdots ,p$$

and

$$G_{\mathit{\gamma \gamma }}({\mathit{\theta }}_0^{\ast })={\left\{-E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\beta }_j\partial {\beta }_l}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)\right\}}_{(j,l)=(1,1)}^{(p,p)}$$

with

$$E\left({\frac{{\partial }^2{\ell }_n(\mathit{\theta })}{\partial {\beta }_j\partial {\beta }_l}|}_{\mathit{\theta }={\mathit{\theta }}_0^{\ast }}\right)=\sum _{i=1}^n{\stackrel{.}{\lambda }}_i^{\ast }{x}_{ji}{x}_{li},j,l=1,2,\dots ,p.$$