Analytic Methods for Individually Randomized Group Treatment Trials and Group-Randomized Trials When Subjects Belong to Multiple Groups

Abstract

Participants in trials may be randomized either individually or in groups, and may receive their treatment either entirely individually, entirely in groups, or partially individually and partially in groups. This paper concerns cases in which participants receive their treatment either entirely or partially in groups, regardless of how they were randomized. Participants in Group-Randomized Trials (GRTs) are randomized in groups and participants in Individually Randomized Group Treatment (IRGT) trials are individually randomized, but participants in both types of trials receive part or all of their treatment in groups or through common change agents. Participants who receive part or all of their treatment in a group are expected to have positively correlated outcome measurements. This paper addresses a situation that occurs in GRTs and IRGT trials – participants receive treatment through more than one group. As motivation, we consider trials in The Childhood Obesity Prevention and Treatment Research Consortium (COPTR), in which each child participant receives treatment in at least two groups. In simulation studies we considered several possible analytic approaches over a variety of possible group structures. A mixed model with random effects for both groups provided the only consistent protection against inflated type I error rates and did so at the cost of only moderate loss of power when intraclass correlations were not large. We recommend constraining variance estimates to be positive and using the Kenward-Roger adjustment for degrees of freedom; this combination provided additional power but maintained type I error rates at the nominal level.

1. Introduction

1.1. Background

Participants in trials may be randomized either individually or in groups, and may receive their treatment either entirely individually, entirely in groups, or partially individually and partially in groups. This paper concerns cases in which participants receive their treatment either entirely or partially in groups, regardless of how they were randomized. Participants in Group-Randomized Trials (GRTs) are randomized in groups and receive part or all of their treatment in groups or through common change agents. Participants in Individually Randomized Group Treatment (IRGT) trials are individually randomized but receive part or all of their treatment in groups or through common change agents. Participants who receive part or all of their treatment in a group are expected to have positively correlated outcome measurements.

Group-Randomized Trials (GRTs) are widely used for comparative studies when randomization at the individual level is not possible without substantial risk of contamination [1]. In a GRT, groups of subjects (e.g., schools, clinics, communities) are randomized to study groups, while outcomes are measured at the individual level. Groups may be small (e.g., classrooms) or large (e.g., counties). Group members have generally interacted prior to the intervention and continue to interact during and after the intervention [2, 3]. Components of the intervention may be delivered in these identifiable groups or to additional groupings created by the research team.

Individually Randomized Group Treatment (IRGT) trials are used for comparative effectiveness research, clinical trials, and especially community-based research. In an IRGT trial, individuals are randomized to treatments, but each participant receives some of their treatment in a group or through a common change agent. There is interaction among members of the same group or with the common change agent [4]. The groups may be created by the research team for the purposes of delivering components of the intervention or the groups may be naturally occurring groups that are used for that purpose [4].

Both GRTs and IRGT trials are commonly used study designs for intervention research and are employed across a range of disciplines [1, 4, 5]. There is a vast literature on the design and analysis of GRTs [2, 3], while there are far fewer publications on the methodologic challenges of IRGT trials [e.g., 6, 7, 8, 9]. Previous authors have recommended that analysts model or otherwise account for the positive intraclass correlation expected in GRTs and IRGT trials. Failure to do so will inflate the type I error rate [2, 3, 4]. These sources presented formulae that can be used to plan IRGT trials and GRTs so as to have sufficient power while maintaining the nominal type I error rate. However, the focus of previous publications has been limited to the simplest situation in which each participant belongs to a single group that does not change over time. In this paper we consider the case where participants in GRTs or IRGT trials may belong to more than one group, creating a more complex clustering structure among participants. We know that clustering will be present, but what is not clear is what modeling strategies will be most effective for this design.

1.2. A Motivating Example: The COPTR Consortium

The Childhood Obesity Prevention and Treatment Research Consortium (COPTR) was funded by the National Heart Lung and Blood Institute to support four trials aimed either at prevention or treatment of childhood obesity (http://public.nhlbi.nih.gov/newsroom/home/GetPressRelease.aspx?id=2725). COPTR is a set of four independent trials each operating in a different part of the country (CA, MN, TN, OH). Each of the four trials has its own intervention and evaluation protocol, and each is powered and will be analyzed separately. The four trials are funded under the same collaborative agreement by NHLBI and the staffs of the four studies meet periodically to share information and experiences. One of the authors (DMM) was chair of the design and analysis working group for the COPTR consortium from July 2010 through mid September 2012 and was supported in part by a subcontract to the COPTR Research Coordinating Unit at the University of North Carolina, Chapel Hill.

Although the four COPTR trials differ considerably in the structure and the number of groups that will be involved, they present an important variation on the prototypical IGRT design: each participant will belong to more than one group. In the designs we consider, each type of group is linked to the intervention, i.e., component(s) of the intervention are delivered through these groups. Such groups may be pre-existing (“naturally occurring”) groups such as schools or community centers, or in groups created specifically for the study.

In one COPTR study (COPTR1), participants will belong to two groups. They will belong to a small group created by study investigators in which they will receive one of three behavioral interventions. They will also belong to a larger naturally occurring group, their school community, which will also receive a related intervention or control program. Thus, participants in COPTR1 will belong to both a small intervention group and a larger, second group (their school community). In another COPTR trial (COPTR2), children will be randomized to participate in team sports or standard activities at a small number of community centers, and children will also have an intervention administered via a physician, who may see more than one child in the study. Thus, participants in COPTR2 will belong to both a recreation center group (large group) and a group defined by sharing the same physician (small group). These two designs also highlight the fact that sometimes groups may be crossed (like the small group intervention crossed with the school intervention in COPTR1) or only partly crossed (like the community centers and physicians in COPTR2). In other cases, the groups may be completely hierarchical (nested). The key feature is that participants will belong to two separate groups, and correlation may exist between members of each group.

1.3. Overview of the Paper

Though our motivating example is based on the four IRGT trials that comprise COPTR, it is easy to identify other IRGT trials and GRTs where participants may belong to more than one group. Consider, for example, any school-based GRT in which students may attend one school during the day, but may attend another school (or community center) for after school care. As another example, consider an IRGT trial for weight loss in which participants attend a group therapy class scheduled for a particular evening and participants may simultaneously also regularly attend exercise classes on different days and at different locations. Investigators have generally ignored groups secondary to those used for primary intervention delivery; the issue has generally been considered so minor that it is not even mentioned in papers reporting the results of these studies.

The lack of reporting and discussion of membership in more than one group in GRTs or IRGT trials does not mean that the issue is not common; instead it likely means that no one has considered implications for analysis. Indeed there has been no discussion on the implications of membership in multiple groups on type I error rate or power in the statistical literature. One recent paper [10] studied multiple sources of post-randomization clustering in trials where subjects were randomized individually and found several cases where participants belonged to multiple clusters, such as clusters based on surgeon and rehabilitation class.

Motivated by the four COPTR trials, in which we knew in advance that each participant would be involved in at least two different groups, we sought to identify the appropriate analytic model for any IRGT trial or GRT where participants belong to more than one group. For the purpose of this paper, we consider only posttest data from a single trial with intervention and control arms. Participants in both arms of the trial belong to two groups; through these groups participants receive part or all of their assigned treatment. We conducted a simulation study to compare the performance of various analytic model specifications under various underlying group structures.

2. Simulation Study

2.1. Description of the Population

We use “condition” to refer to treatment condition (e.g., treatment, control). We use “group” to refer to a group of participants who receive all or part of their treatment together (e.g., Tuesday night group, Saturday afternoon group). We assume that each participant belongs to two groups, such as a large community center and a small mentoring group, where there may be clustering within each group. We label the “large” groups (with a larger number of participants, e.g., the school community) as “A” groups, and the “small” groups (with a smaller number of participants, e.g., small intervention groups) as “B” groups. Thus, there will always be fewer total A groups than B groups except in the limiting case where there are equal numbers of A and B groups. In our simulations, each participant belongs to only one condition, but belongs to two groups, one A group and one B group.

The number of A groups was fixed at n_A = 6 (3 levels per condition), and the number of B groups varied. For each participant k in group A = i and B = j, we generated the outcome Y from y_ijk = βx_i + a_i + b_j + e_ijk where x_i is the treatment indicator (1 = treatment, 0 = control), a_i ~ N(0, ρ_A) is the group A-level error, b_j ~ N(0, ρ_B) is the group B-level error, and e_ijk ~ N(0, 1 − ρ_A − ρ_B) is the subject-level error. All random effects were independent, resulting in an ICC due to A groups of ρ_A and an ICC due to B groups of ρ_B. The treatment effect β was set to zero for analysis of type I error rates, and to 0.7 for analysis of power.

We initially fixed the sample size at N = 216 participants total, with 108 participants in each condition (treatment, control). Later simulations considered a larger total sample size. Four parameters were varied in generating the data: the total number of B groups, n_B = (6, 18, 24, 72), the group A ICC, ρ_A = (0, 0.001, 0.01, 0.1), the group B ICC, ρ_B = (0, 0.001, 0.01, 0.1), and the overlap in membership in the two group types (nested, uneven, crossed). Table 1 illustrates these three different types of overlap for n_B = 18. For simplicity the table shows only one condition, with groups A = (1, 2, 3) and B = (1, 2, …, 9). In the nested design, B groups were nested within A groups, while in the crossed design B groups were completely crossed. The uneven design fell in-between these two extremes, such that participants from all B groups in a condition were assigned unevenly to the A groups in that condition, such that P(B = j|A = i) was larger for some (i, j) combinations and smaller for others, although in all cases the number of participants in each A/B combination was fixed. Never did a participant belong to a treatment group A but a control group B or vice-versa.

Table 1.

Distribution of participants into small groups for the case of n_B = 18 B groups, for one condition only.

		Group B — Balanced									Group B — Unbalanced
	Group A	1	2	3	4	5	6	7	8	9	1	2	3	4	5	6	7	8	9
Nested	1	12	12	12	0	0	0	0	0	0	13	10	13	0	0	0	0	0	0
	2	0	0	0	12	12	12	0	0	0	0	0	0	13	6	17	0	0	0
	3	0	0	0	0	0	0	12	12	12	0	0	0	0	0	0	11	8	17
Uneven	1	6	6	6	4	4	4	2	2	2	1	4	4	5	7	3	4	5	3
	2	2	2	2	6	6	6	4	4	4	10	1	4	1	6	6	2	2	4
	3	4	4	4	2	2	2	6	6	6	4	5	4	4	2	3	6	5	3
Crossed	1	4	4	4	4	4	4	4	4	4	4	4	7	7	2	0	3	7	2
	2	4	4	4	4	4	4	4	4	4	2	1	2	8	4	4	4	6	5
	3	4	4	4	4	4	4	4	4	4	5	2	7	1	1	5	5	5	5

Varying these four parameters resulted in a 4 × 4 × 4 × 3 factorial experiment. However, the combinations with n_B = 6 and a nested design were not run, since with n_A = 6 this scenario had identical A and B groups. This resulted in 176 parameter combinations.

Sizes of the ICCs were chosen to reflect the range of values commonly seen in GRTs [11], with a slightly higher maximum to reflect the somewhat larger ICCs reported in IRGT trials [4]. Group sizes were chosen to reflect the designs of the COPTR trials. For each parameter combination, the data generation process was repeated 1000 times and results were averaged over the 1000 replicates.

The overlap scenarios described above produced balanced data, in the sense that the size of each A group and each B group was constant (although sizes of A/B combinations varied). We introduced imbalance into the simulation study by considering unequal sized B groups, keeping balance within the A groups by holding constant the number of participants in each A group at 36. To allow for imbalance in the number of participants in each B group, participants in each A group were randomly assigned to B groups with probabilities corresponding to those in the balanced case. For example, in the crossed design, participants in each A group had a probability of 1/9 of being assigned to each B group, but in the nested and uneven design these probabilities varied by the A group. To eliminate any variability due to differences in the distribution of participants to the B groups between simulation replicates, we drew sample sizes for the unbalanced scenario one time for each design (nested, uneven, crossed) and used this distribution of participants in groups for all simulation replicates. Table 1 shows the distribution of subjects to groups for the unbalanced design with n_B = 18 (for one condition only). The entire 4 × 4 × 4 × 3 factorial experiment (176 combinations total) was repeated with the unbalanced design. Throughout the rest of this paper we refer to the two scenarios as “balanced” and “unbalanced,” but in each case A is balanced and the label is with respect to B.

Although our initial simulations were designed to approximate conditions in COPTR studies, we also examined the effect of total sample size on our conclusions by quadrupling the original design to a total sample size of N = 864 (432 in each arm). High computational burden prohibited the entire experiment from being repeated, so we focused attention on the parameter combinations that showed the largest differences between the methods with the smaller sample size. Only balanced data (with respect to B groups) was considered for this larger sample size, since results for balanced and unbalanced data were similar for the smaller sample size. For power simulations with the larger sample size, the treatment effect β was taken to be half the treatment effect for the smaller sample size (β = 0.35).

2.2. Analytic Models

We compared the performance of seven analytic models: two models that modeled both A and B groups, two models that modeled A only, two models that modeled B only, and one model that did not account for clustering by either group (Table 2). Models also varied by restrictions on the variance components (constrained to be positive or no restriction), method of variance estimation (REML, ML, or empirical), and the method for estimating the degrees of freedom for testing the treatment effect (based on the number of groups in the model or the Kenward-Roger method [12]).

Table 2.

Analytic models used in simulation study.

	Groups	Degrees of Freedom	Restriction on	Variance
Model	Modeled	for Treatment Effect	Variance Comp.	Estimation
AB(KR nobound)	A and B	Kenward-Roger	Unbounded	REML
AB(KR bound)	A and B	Kenward-Roger	Bounded ≥ 0	REML
A(KR nobound)	A	Kenward-Roger*	Unbounded	REML
A(emp)	A	Based on A (DF = 4)	Unbounded	Robust
B(KR nobound)	B	Kenward-Roger**	Unbounded	REML
B(emp)	B	Based on B (DF = nB − 2)	Unbounded	Robust
IND	none	Based on # of participants (DF = 214)	n/a	ML

REML = Restricted Maximum Likelihood

^*Always equal to DF based on A groups, i.e., DF = 4

^**For balanced data, equal to DF based on B groups, i.e., DF = n_B − 2

All simulations were performed using SAS software, version 9.3 [13], and all models were estimated using PROC GLIMMIX with identity link and normal error distribution. When included, A and B were modeled as independent random effects. Unbounded variance components were allowed through use of the NOBOUND option and robust variance estimation was obtained through use of the EMPIRICAL option.

Due to small ICCs, some models failed to converge on a small fraction of the replicate data sets. Results are summarized only for replicates where all seven models produced estimates. Higher rates of convergence were noted using PROC GLIMMIX instead of PROC MIXED in early simulation runs, hence all analyses reported here used PROC GLIMMIX. In the subset of the simulation study run with both procedures, using PROC GLIMMIX we got a minimum of 97.4% convergence for the most complex model with balanced data, compared to a convergence rate of 94.6% using PROC MIXED.

Performance of the seven analytic models was summarized through calculation of the empirical type I error rate and power. When data were generated with no treatment effect (β = 0) we calculated the empirical type I error rate by calculating the percent of times that the null hypothesis of no treatment effect was rejected. When data were generated with a moderate-sized treatment effect (β = 0.7 for N = 216; β = 0.35 for N = 864) we calculated the empirical power similarly.

3. Results

3.1. Type I Error

Table 3 summarizes the overall results for type I error for balanced data with N = 216, by tabulating the number and percent of cells in the simulation experiment that the empirical type I error rate was lower than or higher than the lower or upper simulation error bounds around the nominal 5% level. Results are summarized by n_B values; there were 176 cells in the simulation experiment, with 32 cells for n_B = 6 and 48 cells for each of the other n_B values. The range of the observed type I error rates is also included.

Table 3.

Summary of Type I error simulation with N = 216 and balanced allocation of subjects to B groups. Results are displayed as the number (%) of cells in simulation experiment where type I error was significantly below or above the nominal 5% based on simulation error bounds, and the range of observed type I error rates.

	Model	Below	Above	Type I Error Range
nB = 6	AB (KR nobound)	13 (41%)	16 (50%)	1.8–13.1
	AB (KR bound)	25 (78%)	0 (0%)	1.4–4.5
	A (KR nobound)	1 (3%)	13 (41%)	3.5–27.0
	A (emp)	0 (0%)	31 (97%)	6.3–36.5
	B (KR nobound)	1 (3%)	14 (44%)	3.6–27.5
	B (emp)	0 (0%)	32 (100%)	6.9–36.3
	IND	0 (0%)	24 (75%)	4.6–53.3
nB = 18	AB (KR nobound)	17 (35%)	0 (0%)	2.7–6.1
	AB (KR bound)	30 (63%)	1 (2%)	1.4–6.4
	A (KR nobound)	0 (0%)	9 (19%)	4.0–15.2
	A (emp)	0 (0%)	48 (100%)	6.5–22.0
	B (KR nobound)	1 (2%)	24 (50%)	3.5–35.5
	B (emp)	0 (0%)	32 (67%)	5.2–38.5
	IND	0 (0%)	33 (69%)	4.6–42.7
nB = 36	AB (KR nobound)	17 (35%)	2 (4%)	2.3–6.5
	AB (KR bound)	27 (56%)	1 (2%)	1.5–6.5
	A (KR nobound)	1 (2%)	10 (21%)	3.3–12.3
	A (emp)	0 (0%)	48 (100%)	7.0–18.1
	B (KR nobound)	1 (2%)	25 (52%)	3.5–38.1
	B (emp)	0 (0%)	28 (58%)	4.3–39.4
	IND	0 (0%)	33 (69%)	4.5–39.9
nB = 72	AB (KR nobound)	18 (38%)	1 (2%)	2.2–6.7
	AB (KR bound)	23 (48%)	1 (2%)	1.9–7.0
	A (KR nobound)	1 (2%)	6 (13%)	3.6–7.6
	A (emp)	0 (0%)	48 (100%)	6.5–12.2
	B (KR nobound)	0 (0%)	25 (52%)	3.7–39.7
	B (emp)	0 (0%)	25 (52%)	4.0–40.1
	IND	0 (0%)	31 (65%)	4.1–38.7

Both AB models were somewhat conservative, with lower than 5% type I error in 37%-60% of cells in the balanced simulation study. Even so, the AB models were not dramatically conservative as the type I error rate was never lower than 1.4%.

The most conservative model was the AB(KR bound) model, that modeled both groups using the default non-negativity constraint on variance components. This model resulted in lower than nominal type I error rate in 60% of all cells across the balanced and unbalanced simulation studies. Suppression of the type I error rate was greater for a smaller number of B clusters, with 78% of cells with n_B = 6 having reduced type I error, compared to 48% of cells with n_B = 72. The model was also more conservative for smaller values of ρ_A. Type I error rate did not appear to be strongly related to ρ_B or the group overlap design (nested, uneven, crossed). Type I error rate was inflated in only three cells; the inflation was small (6–7%) and the frequency of this event was within the range of expected simulation type I error.

The AB(KR nobound) model that modeled both groups but allowed variance components to be negative was also conservative across many scenarios, with lower than 5% type I error in 37% of all simulation cells. The amount of suppression of the type I error rate was associated with the overlap between groups, which was not seen for the AB(KR bound) model. The largest reduction in type I error was for the crossed design (58% of cells) and the uneven design (44%), compared to the nested design which never produced reduced type I error. Suppression of the type I error was not strongly associated with either ICC (ρ_A, ρ_B) or the number of B groups.

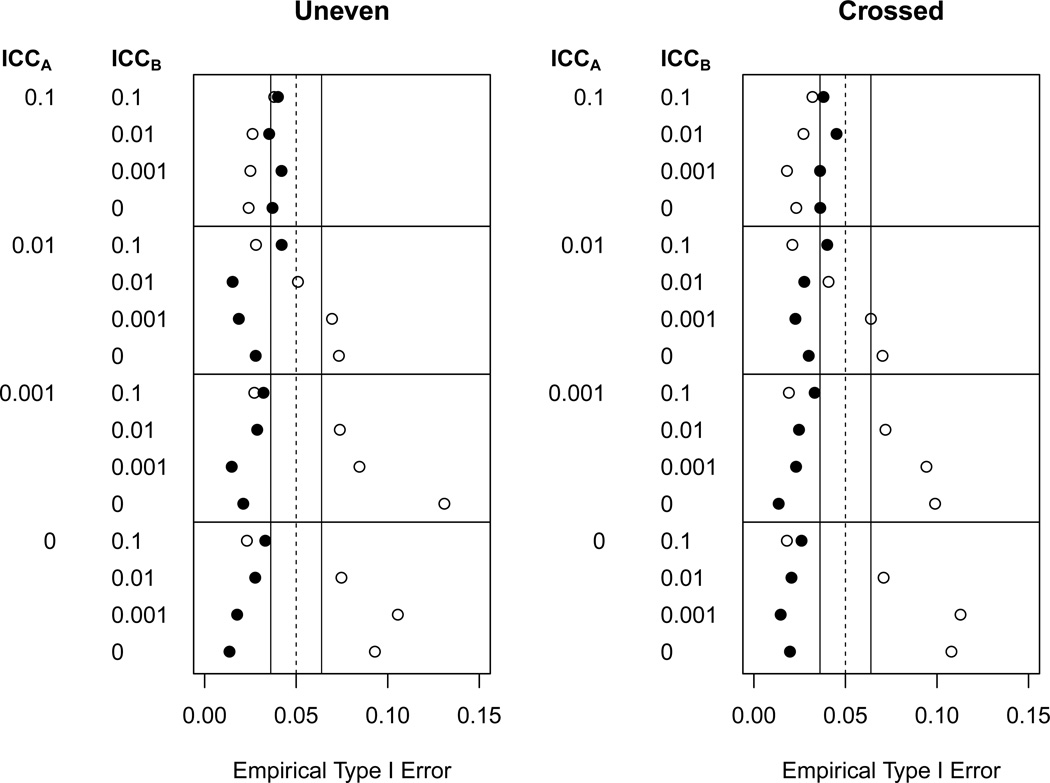
However, unlike the bound AB model, the unbound AB model produced inflated type I error in 11% of cells, which was more often than could be attributed to simulation error. Closer examination revealed that this inflation primarily occurred when the number of B groups was smallest and equal to the number of A groups (n_B = n_A = 6). Results from these simulations are displayed in Figure 1. In these 32 scenarios the AB(KR nobound) model resulted in inflated type I error an astonishing 50% of the time. In replications where the AB(KR nobound) model rejected, variance components were negative and standard error estimates were shrunken to near zero. The Kenward-Roger adjustment reduced the degrees of freedom to one in these cases, but this was not enough deflation to counterbalance the huge inflation of test statistics, leading to greater than nominal type I error.

Figure 1.

Empirical type I error when n_B = 6 (number of B groups equal to number of A groups) for analytic models AB(KR bound) (●), AB(KR nobound) (○).

To investigate whether the poorer performance of the AB(KR nobound) model was related to sample size, the portion of the simulation experiment with n_B = n_A = 6 was repeated with the larger sample size (N = 864). Overall, the pattern of results was similar, though the various inflations and reductions in type I error were slightly less extreme. As with the smaller sample size, the AB(KR nobound) model produced inflated type I error rates, though this was seen in fewer of the simulation cells (25%, compared to 50% for the smaller sample size). The main difference was when ρ_B = 0.01 (and ρ_A = {0, 0.001}), which resulted in marginally inflated type I error with the smaller sample size but not with the larger sample size. This inflation occurred in the scenarios with the smallest ρ_A and ρ_B, as was seen with the smaller sample size. In contrast, the AB(KR bound) model never produced inflated type I error, but did produce lower than nominal type I error in 56% of cells (compared to 78% for the smaller sample size). Detailed results with N=864 are available online as Supplementary Table 1 and Supplementary Figure 1.

Modeling only the A group (the A(KR nobound) model) resulted in type I error at nominal levels when the ICC for B was small. For instance, with ρ_B ≤ 0.01, the type I error rate was inflated in only 7% of the cells, and the maximum type I error was 8.8%. However, when ρ_B = 0.1 the performance of the A(KR nobound) model was poor. Design effects due to ρ_B = 0.1 were 1.2, 1.5, 2.1, and 4.5 for balanced data where group B sizes were 3, 6, 12, and 36 respectively. Ignoring the B groups in these cases therefore led to inflated type I error. The only scenarios when the A(KR nobound) model had nominal type I error with ρ_B = 0.1 was for the nested design (across all n_B and ρ_A values).

The remaining models, A(emp), B(emp), B(KR nobound), and IND, all had substantially inflated type I error rates. For these models, 50% to 100% of the cells had an observed type I error rate above the upper simulation error bound. Results for the larger sample size were similar, and in most cases were even worse, due to the larger design effect produced by the larger sample size.

Results for unbalanced data were similar to those for balanced data, with only a few small differences. The main difference was one of convergence; convergence was more of a problem for unbalanced data. Convergence was particularly problematic for the AB(KR nobound) model when the number of B groups was small. When convergence rates were similar, models had similar performance for both balanced and unbalanced data.

3.2. Power

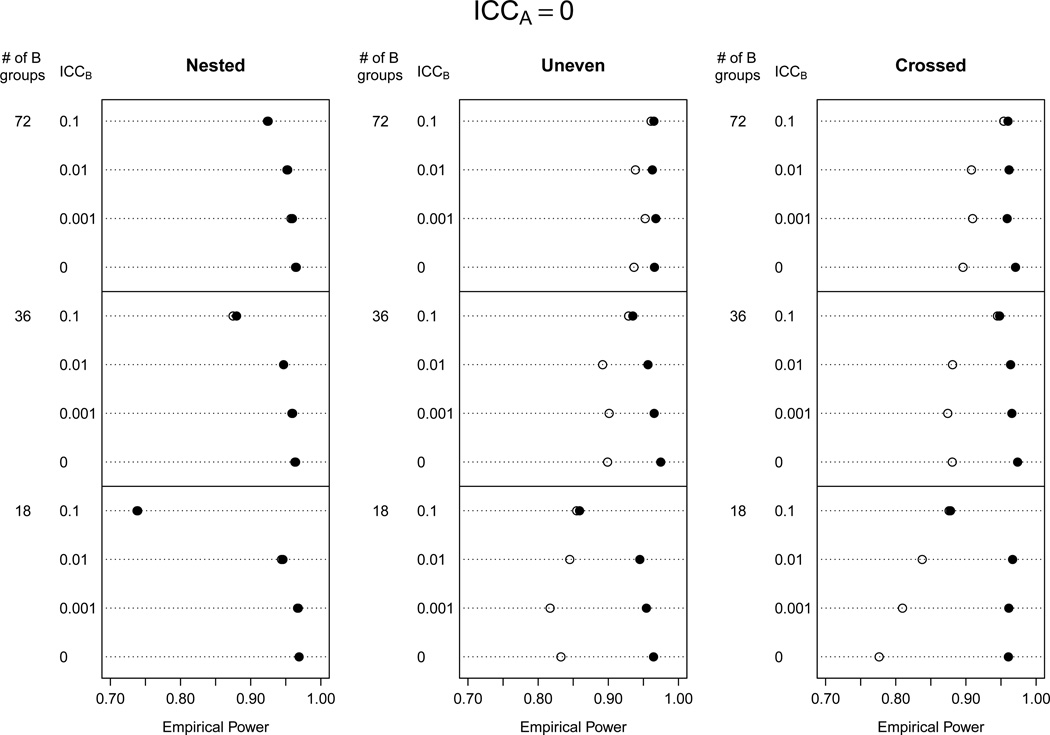
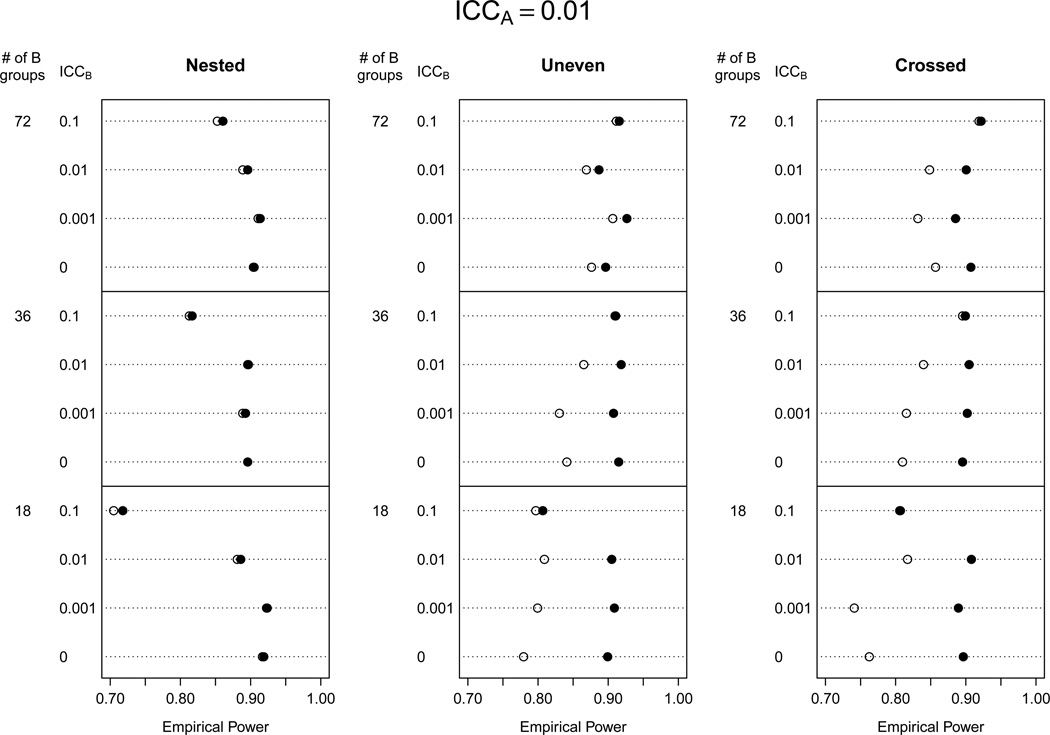
We investigated differences in power for both AB models, which had type I error rates at or below the nominal level for the majority of the 176 scenarios. We excluded in our power study the scenarios with n_B = 6 because the AB(KR nobound) model had an inflated type I error rate, especially for low ICC values. Figures 2–3 show empirical power for the AB models with and without the non-negativity constraint for ρ_A = 0 and ρ_A = 0.01. When ρ_A = 0.001, power results were similar to ρ_A = 0, and when ρ_A = 0.1, power was reduced for all models but comparisons between models were similar (results not shown).We also investigated power for the A (KR nobound) model for populations with ρ_B ≤ 0.01, which was where type I error rates were maintained at nominal levels. In these scenarios, power for the A(KR nobound) was essentially identical to the AB(KR bound) model, so results are not shown.

Figure 2.

Empirical power when ρ_A = 0 (no ICC due to A groups) for analytic models AB(KR bound) (●), AB(KR nobound) (○).

Figure 3.

Empirical power when ρ_A = 0.01 for analytic models AB(KR bound) (●), AB(KR nobound) (○).

Power was equivalent for the AB(KR bound) and AB(KR nobound) models for all ρ_A values when B groups were nested within A groups. Power was higher for the AB(KR bound) model when B was unevenly distributed in A or crossed with A, and the gains in power were quite substantial in some cases (e.g., 96% versus 78% for the crossed design with ρ_A = ρ_B = 0 and 18 B groups). Smaller ICC values for B groups caused larger decreases in power for the AB(KR nobound) model, while the AB(KR bound) model maintained high power in these scenarios.

Power results for the larger sample size (N = 864) were nearly identical to those for the smaller sample size, with the AB(KR nobound) model having reduced power for smaller values of ρ_B. Results for ρ_A = 0 are shown in online materials in Supplementary Figure 2. Power was drastically reduced for both models when ρ_B = 0.1, which is where the increase in design effect due to the larger sample size was the greatest.

One concern about the AB models is that when there truly is no intraclass correlation (i.e., ρ_A = ρ_B = 0), power will be reduced compared to the independence model. There is some indication of this in Figures 2 and 3, especially for the AB(KR nobound) model, but the impact is difficult to see because the intervention effect was large, and thus power was high for all models. To investigate the possible reduction in power, we evaluated this scenario (ρ_A = ρ_B = 0) with a treatment effect of β = 0.383, corresponding to 80% power for the independence model given the sample size of N = 216. Only analytic models with a type I error rate at or below the nominal level for this scenario were evaluated, which included both AB models, A(KR nobound), B(KR nobound), and the independence model. Results are shown in Table 4. Note that because the ICCs were zero, the design labels (nested, uneven, crossed) and the number of participants indicated for B groups denote how the groups were (incorrectly) specified in the mixed models, as there were not any true groups.

Table 4.

Summary of empirical power in the simulation when there is no intraclass correlation (ρ_A = ρ_B = 0) and the treatment effect is β = 0.383, corresponding to 80% power under the (true) independence model.

		Design
# B groups	Model	Nested	Uneven	Crossed
18	AB (KR nobound)	57	30	28
	AB (KR bound)	57	54	54
	A (KR nobound)	57	56	58
	B (KR nobound)	74	75	76
	IND	80	80	79
36	AB (KR nobound)	58	39	39
	AB (KR bound)	60	55	58
	A (KR nobound)	58	57	58
	B (KR nobound)	78	77	79
	IND	80	79	81
72	AB (KR nobound)	55	45	38
	AB (KR bound)	57	55	54
	A (KR nobound)	55	54	54
	B (KR nobound)	79	78	80
	IND	80	78	81

Several patterns emerge from these results when the ICC was zero for all groups. All mixed models maintained the nominal type I error rate, but suffered from a reduction in power relative to the independence model in at least some scenarios. The worst performance was for the AB(KR nobound) model, with power as low as 28% for the scenario with the smallest number of B groups and a crossed design. The overlap of the misspecified groups (nested, uneven, crossed) did not substantially affect power for any models except for AB(KR nobound); for this model, misspecifying nested groups resulted in similar power as the AB(KR bound) model, but for uneven or crossed groups power was greatly reduced. Another pattern from these results was that the penalty in power was smaller when a larger number of smaller groups were incorrectly specified. Thus, the B(KR nobound) model had higher power than the A(KR nobound) model since there were more B groups specified than A groups. With 36 or 72 B groups, the power for the B(KR nobound) model was essentially identical to the independence model. When this experiment was repeated with the larger sample size (N = 864) and corresponding smaller effect size (β = 0.191), results were strikingly similar (results not shown). Empirical power was nearly identical to the power for the smaller sample size, suggesting that the number of (incorrectly) specified groups was driving the reduction in power, not the size of these groups.

4. Discussion

Increasingly, randomized trials involve participants receiving treatments either entirely or partially in groups. We cannot document how common it is for participants to belong to more than one group in an IRGT trial or a GRT because authors do not report such information in their papers. Even so, one of the authors (DMM) has more than 30 years experience conducting and reviewing GRTs and 5 years experience studying IRGT trials. That experience suggests that participants belonging to multiple groups is not uncommon. Examples include (1) weight loss trials with both exercise and support group small groups, (2) smoking cessation interventions that involve both community-based interventions (e.g., billboards, etc.) and a physician who treats multiple patients, (3) substance abuse interventions with support group meetings and individual counseling by a provider. Other studies, such as each of the four COPTR trials, may deliberately plan or anticipate participants belonging to multiple groups over the course of the trial.

Positive intraclass correlation is expected whenever participants interact with one another in a group, whether it is a naturally occurring group or a group created by the investigator for purposes of delivering components of the intervention. Previous work has shown that ignoring the intraclass correlation associated with only one group per participant can and does inflate the type I error rate, even with small ICCs [2, 3, 10]. Our work in these simulations shows that failing to account for multiple group membership may similarly inflate type I error rates, unless the ICC in all but the modeled group is very small, i.e., < 0.01. Because it is impossible to know in advance what the ICC will be in each type of group, the prudent course for most trials would be to plan the design and analysis to account for multiple group membership.

These simulation studies support several conclusions and recommendations for future studies. First, the AB(KR bound) model performed well, both in terms of type I error rate and power, in simulations run to mimic conditions expected in an IRGT trial or GRT design, with both the smaller sample size (N = 216) and the larger sample size (N = 864). The AB(KR bound) model is well-suited for situations in which two types of groups are identifiable. Although the type I error rate was sometimes below the nominal 5% level (rates often in the 2–4% range), it was maintained at or below the expected level in all circumstances. Despite the reduction in type I error rate, power was reasonable across a range of circumstances. If only one group is identifiable, a model that only accounts for this primary group (i.e., the A(KR nobound) model) will only carry the nominal type I error rate when the non-identifiable group has a small ICC (ρ_B < 0.1). These results suggest that investigators who employ an IRGT trial or GRT design should identify all groups in which participants receive some of their treatments, record group membership for each participant, and model all group memberships in their primary analysis. Failure to do so could result in catastrophic inflation of type I error rate if ICCs are moderate; importantly, modeling all groups does not appear to carry a large reduction in power even when the ICCs are quite small.

Second, we found poor performance for both the A and B models when run using robust standard errors. We found no set of circumstances in which the A model with robust standard errors provided a type I error rate that was consistently within the 95% simulation error bounds around 5%: fully 99% of the cells exceeded that range for A(emp). The situation was only slightly better for the B model with robust standard errors, as 71% exceeded that range for B(emp). The B(emp) model performed well only when both ρ_A and ρ_B were 0.001 or smaller. Because investigators cannot be certain in advance that their ICCs will be that small, we cannot recommend that IRGT trials or GRTs model one group while ignoring another using empirical sandwich estimation for standard errors when the degrees of freedom are limited, as they were in these simulations. The uniformly poor performance of the A(emp) model, which used robust standard errors, can largely be attributed to the fact that there were only six A groups, well below the recommended threshold of 30–40 groups for use of the sandwich variance estimator [14, 15, 16]. We did not explore small-sample corrections to the robust standard error [e.g., 16, 17, 18], leaving that to future studies.

Third, we found that the independence model maintained the nominal type I error rate only when both ρ_A and ρ_B were 0.001 or smaller. As noted above, because investigators cannot be certain in advance that their ICCs will be that small, we cannot recommend that IRGT trials or GRTs employ an independence model. This recommendation is consistent with standard recommendations for GRTs [2, 3] and with prior recommendations for IRGT trials [4].

Fourth, we found that using mixed models led to a reduction in power compared to the independence model if there was no intraclass correlation in truth, especially if the treatment effect was small and the degrees of freedom for the test of interest were limited. This pattern is well-established in GRTs [2, 3], and we are not surprised to observe the same results in our simulations. The message for IRGT trials is the same as for GRTs: investigators should identify the smallest intervention effect they want to find and plan the study to have sufficient degrees of freedom and power for that effect given the ICCs they expect to have [2, 3]. It is our opinion that investigators should model groups where any positive correlation is expected; the loss of power from modeling the groups if the true ICC is zero is a reasonable price to pay to maintain the nominal type I error rate.

The final lesson from these simulations is that the Kenward-Roger adjustment appears to provide a solution to a problem noted previously when conducting an analysis that employs the default non-negativity constraint (bounded models). As reported earlier [19], the AB(KR bound) model was conservative compared to the AB(KR nobound) model when ICCs were very low (ρ_A or ρ_B = 0.001). Without the non-negativity constraint (AB(KR nobound)), estimates of ρ_A and ρ_B were unbiased, even for very low values of the ICC (ρ_A or ρ_B = 0.001). However, with the non-negativity constraint (AB (KR bound)), negative values of variance components were reset to zero, inflating the average ICC; when ρ = 0.001 the mean estimated ICC was often 8–30 times larger, and when ρ = 0.01 the estimated mean ICC was often 2–3 times larger. Only at ρ = 0.1 were mean ICC estimates relatively unbiased. An inflated ICC estimate leads to a deflated type I error rate, and a more conservative result. An interesting finding from these simulations is that type I error rate for the bounded model was not as extremely conservative as seen previously; the minimum empirical type I error rate we observed for the AB(KR bound) model was 0.014 compared to <0.001 in [19]. We believe this improvement is the result of using the Kenward-Roger adjustment, which was not available to the earlier study.

When ρ_A was small, the AB(KR bound) model had greater power than the AB(KR nobound) model, despite the AB(KR bound) model having a lower type I error rate. This advantage for the bound model is also likely related to the Kenward-Roger method for degrees of freedom. When both A and B variance components were estimated to be zero, the Kenward-Roger degrees of freedom for the test of condition were based on participants (df = N − 2). When only one variance component was set to zero, degrees of freedom were based on the other group. This recalculation of the degrees of freedom is in contrast to the unbound model, which always had substantially reduced degrees of freedom (sometimes as low as 1). Using a bound on variance components along with the Kenward-Roger degrees of freedom offered protection against reductions in power in the situation when there really was no intraclass correlation. These results are quite different from those reported in an earlier paper, published before the Kenward-Roger adjustment was developed [19], which found that both power and type I error rate were severely suppressed when the ICC was small and the analysis employed the default non-negativity constraint. However, these results are similar to a growing body of literature that suggests that the Kenward-Roger adjustment is superior to other methods for estimating the degrees of freedom in mixed models [20, 21].

It is important that IRGT trials and GRTs use appropriate analytic methods to account for correlation among participants in the same groups, whether those groups occur naturally or are created by the investigator. We have considered the case in which two possible groups for each participant might exist. Additional work is needed to investigate more complicated situations, such as when individuals might belong to different groups over time or to two different small treatment groups (so n_A and n_B would both be relatively large relative to total sample size). We also considered only designs with groups in both arms of the study, which may be the worst-case IRGT trial design. In this variation, IRGT trials experience similar challenges to GRTs, where groups always exist in both arms. For these trials, our findings suggest that investigators should make every effort to model all group structures in their data to protect the type I error rate. Our findings also suggest that investigators should employ the Kenward-Roger method for degrees of freedom, combined with the default non-negativity constraint, to protect power if ICCs are very small.

The sample sizes we considered are typical of IRGT trials and of school- or clinic-based GRTs, and results were similar for both a small design (N = 216) and a larger design (N = 864). Simulation results would be similar for even larger GRTs with sample sizes in the many thousands. Gurka et al. [22] provided the asymptotic theory and illustrative simulations needed to support our claim. Gurka et al. documented substantial type I error rate inflation for the mixed model Wald test when the covariance model is incorrectly specified. The problem is not an inaccurate approximation based on large sample theory. Instead, the problem is an incorrect and insufficient specification of the covariance model. As sample size increases to infinity, the estimated covariance model converges to a constant, but to the wrong constant, one that is too small. Hence ignoring the impact on the variance components of membership in multiple groups will always bias the test results, no matter how large the sample size.

All of our work has considered the scenario in which groups are associated with both the treatment and the outcome and the analysis is “intent to treat” (ITT). In an ITT analysis, data are analyzed strictly based on randomization assignment regardless of treatment actually received. In our simulations, groups were always nested within treatment assignment and individuals always belonged to groups in the same treatment assignment. No individuals ever belonged to groups outside of their randomized treatment assignment.

An ITT analysis is designed to estimate the effect of recommending one treatment over another, regardless of treatment that participants actually receive (e.g., due to dropout or non-adherence). Thus it might at first appear that such an analysis should account only for the originally randomized groups in a GRT or IRGT but not any additional small groups that might form between participants after randomization. However, the key question in whether or not it is statistically necessary to account for such groups is not whether the analysis is ITT, but rather whether or not groups are associated with both the treatment and the outcome. If participants belong to groups that are not associated with both the treatment and the outcome, such clustering is “ignorable” [10, 23], because failing to account for the clustering will not adversely affect either the treatment estimate or the type I error rate. If groups are associated with both treatment assignment and the outcome regardless of when the groups were formed failing to account for such clustering will adversely affect the type I error rate and so is not “ignorable”.

As an example, consider a hypothetical depression study in which all participants (regardless of treatment assignment) receive talk therapy as standard of care. There is likely an association between the outcome and groups based on the therapist, since some therapists are likely better than others, but such clustering is ignorable if randomization is independent of therapist. That is, if the therapist is equally likely to treat patients from both arms of the trial, the type I error rate will be maintained even if these groups are ignored. However, if therapists are more likely to treat patients from one arm of the study (perhaps due to geography), or worst case, if therapists are nested within treatment arms, then ignoring these clusters may lead to inflated type I error [10] and the clustering must be accounted for. In this case, as in ours, an ITT analysis is not enough to ensure a valid analysis.

One additional caveat is what may happen if participants in one arm of a GRT or IRGT trial start to cluster together post-randomization. Imagine a hypothetical GRT in which hospitals are randomized to receive either a hospital-wide intervention targeting improved mental health among patients with chronic illnesses (e.g., posters, promotional materials, staff education) or no intervention (control). If patients from a treatment hospital were more likely to join a support group outside of the hospital, then clustering by support group may be non-ignorable as it is associated with treatment arm and the outcome (mental health of the patient with a chronic disease). Although such support groups should be considered as part of the “intervention effect” (the intervention made individuals more likely to join a support group), our simulations show that failing to account for correlation due to some support groups being more effective than others may inflate the type I error.