Abstract
Spatial analytical techniques and models are often used in epidemiology to identify spatial anomalies (hotspots) in disease regions. These analytical approaches can be used to identify not only the location of such hotspots, but also their spatial patterns. We used spatial autocorrelation methodologies, including Global Moran's I and Local Getis-Ord statistics, to describe and map spatial clusters and areas in which nine malignant neoplasms are situated in Taiwan. In addition, we used a logistic regression model to test the characteristics of similarity and dissimilarity between males and females and to formulate the common spatial risk. The mean found by local spatial autocorrelation analysis was used to identify spatial cluster patterns. We found a significant relationship between the leading malignant neoplasms and well-documented spatial risk factors. For instance, in Taiwan, the geographic distribution of clusters where oral cavity cancer in males is prevalent was closely correspond to the locations in central Taiwan with serious metal pollution. In females, clusters of oral cavity cancer were closely related with aboriginal townships in eastern Taiwan, where cigarette smoking, alcohol drinking, and betel nut chewing are commonplace. The difference between males and females in the spatial distributions was stark. Furthermore, areas with a high morbidity of gastric cancer were clustered in aboriginal townships where the occurrence of Helicobacter pylori is frequent. Our results revealed a similarity between both males and females in spatial pattern. Cluster mapping clarified the spatial aspects of both internal and external correlations for the nine malignant neoplasms. In addition, using a method of logistic regression also enabled us to find differentiation between gender-specific spatial patterns.
Keywords: Spatial autocorrelation calculations, logistic regression, age-adjusted rate, malignant neoplasm, Taiwan
The study of spatially related objects or features involves first describing the regional characteristics that differentiate areas from one another before proceeding with an analysis of spatial interrelations[1]. Common spatial techniques used in health research include disease mapping, clustering techniques, diffusion studies, identification of risk factors through map comparisons, and regression analysis[2]. Spatial clustering techniques are essential for statistical consideration and form the starting approach in the development of models for predicting disease risk sites. Disease risk sites are areas located near one another, with a tendency to share similar disease risk factors because they apportion similar environments and are also often connected by the spread of communicable diseases via vectors or host dispersal[3].
Cuzick et al.[4] proposed three general criteria that can be utilized for cluster detection: (1) cell counts, (2) autocorrelative adjacencies of cells with high counts, and (3) distance between events. Numerical methods have been adopted extensively for spatial cluster detection in health research and epidemiology, especially for processing areal data. The analytical approaches include the following: join-count statistics[5], Ohno statistics[6], Poisson statistics[7], Global Geary's C[8]–[10], Global Moran's I[8]–[11], General Getis-Ord's G[12], Local Moran's I[13], and Local Gi(d) and Gi*(d)[11]–[14]. Spatial autocorrelation statistics, such as Moran's I and Geary's C methods, are global in the sense that they estimate the overall degree of spatial autocorrelation in a dataset. The possibility of spatial heterogeneity suggests that the estimated degree of autocorrelation may vary across geographical space significantly. Local spatial autocorrelation statistics provide estimates disaggregated to the level of the spatial analysis units, allowing assessment of dependency relationships in different areas. Local Gi(d) and Gi*(d) statistics can be used to conduct autocorrelation comparisons in different neighborhoods. A global average is used to help identify local regions of strong autocorrelation. A local version of the Moran's I and Geary's C statistics is also available.
This study applies spatial autocorrelation methods to medical care data collected by Taiwan National Health Insurance to determine the spatial clustering associated with nine malignant neoplasms and compare the similarity of local clusters between males and females. Furthermore, potential spatial risks that contribute to these healthcare events and redefine epidemiological and spatially referenced data are also investigated.
Objects and Methods
Study areas
The study areas included the mainland of Taiwan only (excluding all islets), which in 2000 comprised more than 22 million inhabitants living in an area of 36 000 km2. A total of 349 local administrative government areas included five main urban areas, two secondary urban areas, 162 rural townships, and 54 plain and aboriginal mountain townships (Figure 1). According to a bulletin issued in 2002 from the Ministry of the Interior, urban areas were regions that possess at least one metropolitan center and included neighboring cities and townships that share socioeconomic activities. Main urban areas were defined as those with a population larger than one million, specifically, Taipei-Keelung, Kaohsiung, Taichung-Changhua, Jhongli-Taoyuan, and Tainan. Secondary urban areas were defined as those with a residential population ranging from 0.3 to 1 million (such as Hsinchu and Chiayi).
Figure 1. Map of urban areas and aboriginal townships in the study areas.
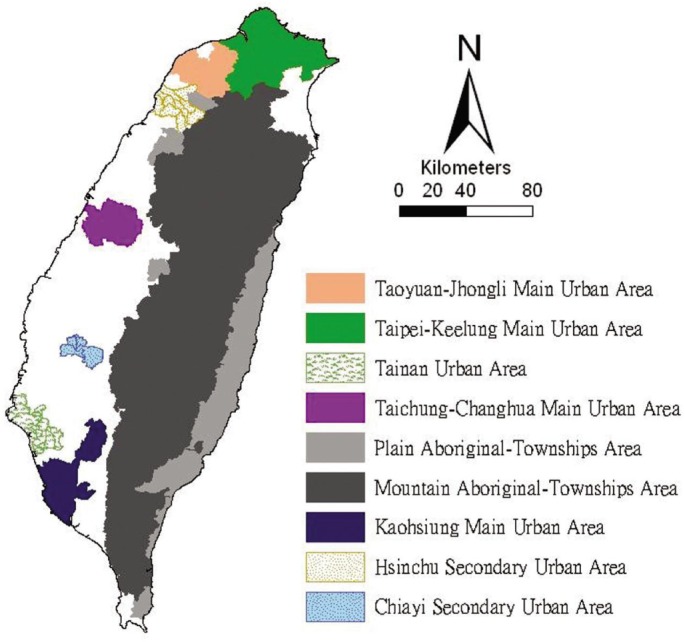
Map of the study areas was divided into 349 administrative districts, including seven urban areas and an integrated area of 54 plain and aboriginal mountain townships.
Data collection and management
The Taiwan National Health Insurance (NHI) program was implemented in 1995. The coverage rate of the program increased from 92.41% of the Taiwanese residential population in 1995 to more than 96.16% in 2000. Coverage further increased to 98% after the inclusion of active military in 2001. The average population in 2005–2009 numbered more than 22.9 million[15].
Once the NHI medical care data were properly collected and analyzed, a complete picture of population behaviors according to disease could be drawn for reference in the calculation of prevalence and incidence of various diseases. At the beginning of 2004, NHI data related to medical care, such as the leading causes of death, were reclassified and reprocessed in relation to smaller units or areas (e.g., precincts or townships rather than the country as a whole). NHI publicly announced regional data from the statistical analysis system (SAS) program in regular annual reports (e.g., NHI, 2005–2009)[16]–[20]. These reports are an accurate and reliable data source to help investigators examine healthcare issues in Taiwan.
The data were collected from contractual medical care institutions, which in this study are institutions where NHI covers prescription medicinal costs and treatment at outpatient clinics. Such facilities accumulate detailed databases of medical costs for inpatient care. The number of outpatient cases was classified in relation to disease codes, as defined in the 1975 edition of The International Classification of Diseases, Ninth Revision, Clinical Modification (hereafter, ICD 9 CM). Criteria for refining the data were first established. However, for calculating medical costs and number of visits, the disease code of the first group (main diagnosis code) was used as the cause of disease. Certain data were not included in the final statistical data set, for instance, in cases where patients suffered from diseases that defied code classification or in cases with mismatched ID numbers. Disease codes were classified according to gender and age. Cases sharing the same ID numbers though referencing different diseases were counted as separate instances[16]–[20].
Medical care data, such as the number of the cause of disease, obtained from the NHI reports between 2005–2009 were examined, and the prevalence rates of the nine malignant neoplasms were calculated. Disease classifications were compiled according to the ICD 9 CM and are indicated in parentheses. They include the following: tracheal, bronchial, and lung cancer (ICD 162); liver and intrahepatic bile duct cancer (ICD 155); colon and rectal cancer (ICD 153, 154); stomach cancer (ICD 151); oral cavity cancer (ICD 140, 141, 143–146, 148, 149); esophageal cancer (ICD 150); pancreatic cancer (ICD 157); non-Hodgkin's lymphoma (ICD 200, 202, 203); and leukemia (ICD 204–208). The Ministry of the Interior provided the mid-year population of each township for demographic background[15]. The smallest administrative units coded for this study were precincts and townships. The age-adjusted standard prevalence rates were calculated with a direct adjustment using the world population in 2000 as the standard population[21]. The age-adjusted standard prevalence rates during 2005–2009 were calculated according to which five-year prevalence rates were weighted by persons each year. The results showed the leading malignant neoplasms for males and females in both the whole of Taiwan and each township in the study area and were consequently applied to the calculation of spatial autocorrelation.
Determining spatial weights/connectivity matrices
The spatial weights matrix is a simple approach for representing similarities between location and attribute values in a region of contiguous areal objects. Autocorrelation was identified by the presence of neighboring cells or zones that take the same (binary) attribute value. Comparing neighboring values of spatial attributes by defining a weights matrix W in which each element wij measures the locational similarity of i and j (i identifies the row and j the column of the matrix) was a common practice. A simple measure of contiguity was used, coding wij = 1 if regions i and j were contiguous and wij = 0 otherwise. wij was set equal to 0 for all i[22].
The spatial weights matrix effectuated developing measures of spatial autocorrelation using four of the attribute types (nominal, ordinal, interval, and ratio). Any measure of spatial autocorrelation sought to compare a set of locational similarities wij (contained in a weights matrix) with a corresponding set of attribute similarities cij, combining them into a single index in the form of a cross-product: ∑i∑jCijWij.
This expression was the total obtained by multiplying every cell in the W matrix with its corresponding entry in the C matrix before summing.
Several approaches were used to measure cij as the nominal, ordinal, interval, and ratio scale. For nominal data, the typical approach involved setting cij to 1 if i and j took the same attribute value and 0 otherwise. For ordinal data, similarity was based on comparing the ranks of i and j. For interval and ratio data, the attribute of interest was denoted xi, and the product (Xi–u)(xj–u) was calculated, where u denoted the average of us[22].
In this study, spatial contiguity for polygons was the property of sharing a common boundary or vertex. Contiguity analysis was a significant method for assessing unusual features in the connectivity distribution[9],[23]. The queen's measure of contiguity was utilized to make up for spatial contiguity by incorporating both the rook and bishop relationships into a single measure[23]. The administrative districts considered in this study were highly irregular in both shape and size. Tsai et al.[11] showed that the most appropriate approach was the first order queen polygon contiguity method for quantifying the spatial weights matrix for connectivity analysis. The spatial weights/connectivity matrices were utilized in the Global Moran's I and Local G*(d) calculations described hereafter. The spatial weights matrix files were automatically produced by ArcMap 9.3.
Global Moran's I statistic
The global spatial autocorrelation statistical method was used to measure the correlation between neighboring observations to find the patterns and the levels of spatial clustering among neighboring districts[24]. The Moran's I statistic, similar to the Pearson correlation coefficient[25], was calculated by the following formulae:
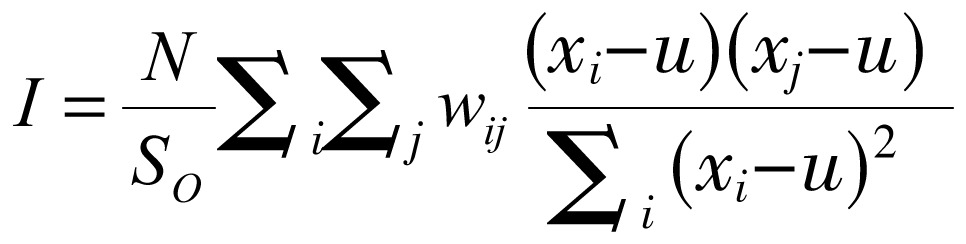 |
(1) |
where N is the number of districts; wij is the element in the spatial weight matrix corresponding to the observation pair i, j; xi and xj are observations for areas i and j with mean u; and
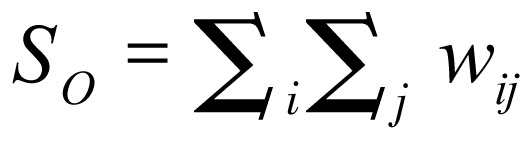 |
(2) |
Because the weights were row-standardized ∑ wij = 1, to sum the row totals in the weights matrix to 1, the first step in the spatial autocorrelation analysis required constructing a spatial weight matrix that contained information regarding the neighborhood structure for each location. Adjacency was defined as directly neighboring administrative districts inclusive of the district itself. Non-neighboring administrative districts were given a weight of 0.
Local Gi*(d) statistic
The local Gi*(d) statistic (local G-statistic) was used to test the statistical significance of local clusters as related to the nine malignant neoplasms and to determine the spatial extent of these clusters[12],[14]. The local G-statistic, which was useful for identifying individual members of local clusters by determining the spatial dependence and relative magnitude between an observation and neighboring observations[26], could be written as follows[12],[27],[28]:
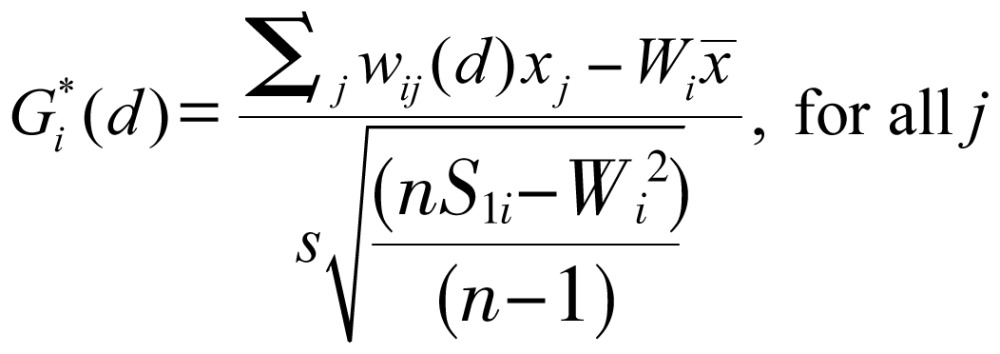 |
(3) |
where x is a measure of the prevalence rate of each leading malignant neoplasm within a given polygon, such as each administrative district; wij is a spatial weight that defines neighboring administrative districts j to i; and Wi is the sum of the weights wij, 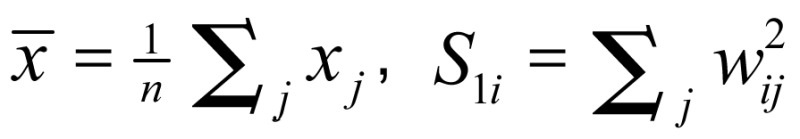 ,
, 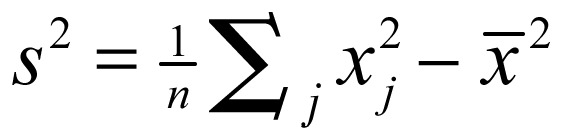 . Developing the spatial weights wij was the first step for calculating Gi*(d). The spatial weight matrix included wij = 1. The adjacency was defined by using a first order queen polygon continuity weight file that was constructed based on districts sharing common boundaries and vertices.
. Developing the spatial weights wij was the first step for calculating Gi*(d). The spatial weight matrix included wij = 1. The adjacency was defined by using a first order queen polygon continuity weight file that was constructed based on districts sharing common boundaries and vertices.
Non-neighboring administrative districts were given a weight of 0. The neighbors of an administrative district were defined as those that share a boundary with the administrative district. A simple 0/1 matrix was formed, where 1 indicates that the municipalities share common border or vertex and 0 indicates the contrary[27],[29].
The local G-statistic included the value in the calculation at i. Assuming that Gi*(d) is approximately normally distributed[12], the output of Gi*(d) can be calculated as a standard normal variant with an associated probability from the z-score distribution[30]. Clusters with a 95% significance level from a two-tailed normal distribution indicate significant spatial clustering, though only positively significant clusters (with a z-score value greater than +1.96) are mapped.
Logistic regression analysis
Similarities between spatial distribution patterns for males and females were displayed. In addition to mapping, logistic regression was performed. The binary response indicates whether a significant autocorrelation exists between administrative districts or areas. A higher correlation is present if the absolute value of the z-score of the local G-statistics is larger than 1.96, and a lower correlation otherwise. Gender was considered an explanatory variable in the logistic regression model. Thus, the model was expressed as:
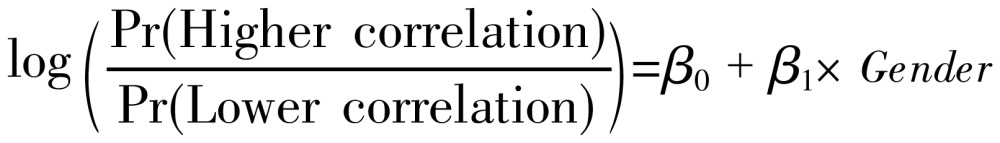 |
(4) |
where β0 and β0 are the logistic regression coefficients of the model. Pr (Higher correlation) and Pr (Lower correlation) denote the “Higher” and “Lower” correlation probabilities, respectively[11].
Global Moran's I statistic and the local Gi*(d) statistic were employed and mapped using ArcMap 9.3. Modeling of the logistic regression was performed using SPSS 12.0.
Results
The results of the prevalence rates for the nine malignant neoplasms between 2005 and 2009 in Taiwan were summarized in Table 1. The results showed that all prevalence rates related to the leading malignant neoplasm for males were higher than those for females. Gender ratios, defined as the ratio of males to females, generally ranged from 1 to 2, though they were occasionally even higher than 6, e.g., for oral cavity cancer and esophageal cancer.
Table 1. Association between Ubc9 expression and clinicopathologic features of breast cancer.
| Leading malignant neoplasms (ICD code) | Malea | Femalea | Ratio (male: female) |
| Tracheal, bronchial, and lung cancer (ICD 162) | 145.32 | 94.49 | 1.54 |
| Liver and intrahepatic bile duct cancer (ICD 155) | 241.78 | 122.88 | 1.97 |
| Colon and rectal cancer (ICD 153, 154) | 260.49 | 212.00 | 1.23 |
| Stomach cancer (ICD 151) | 77.96 | 49.68 | 1.57 |
| Oral cavity cancer (ICD 140, 141, 143–146, 148, 149) | 169.83 | 23.24 | 7.31 |
| Esophageal cancer (ICD 150) | 35.42 | 5.35 | 6.62 |
| Pancreatic cancer (ICD 157) | 21.08 | 18.02 | 1.17 |
| Non-Hodgkin's lymphoma (ICD 200, 202, 203) | 56.31 | 45.31 | 1.24 |
| Leukemia (ICD 204–208) | 36.85 | 31.09 | 1.19 |
Data were collected between 2005 and 2009.a indicates age-adjusted prevalence rates per 100 000 people.
The calculated global autocorrelation statistics for the nine malignant neoplasms in males and females in Taiwan were summarized in Table 2. The results of the Global Moran's tests for most of the cases related to the leading malignant neoplasms were statistically significant (z-scores greater than 1.96) and indicated spatial heterogeneity. However, opposing results (z-scores lower than 1.96) emerged in two cases of non-Hodgkin's lymphoma for females and leukemia for males, respectively.
Table 2. Global autocorrelation analysis of data for the nine malignant neoplasms In Taiwan according to gender.
| Leading malignant neoplasms (ICD code) | Male |
Female |
||
| Moran's index | Z(I) | Moran's index | Z(I) | |
| Tracheal, bronchial, and lung cancer (ICD 162) | 0.51 | 15.95* | 0.21 | 6.55* |
| Liver and intrahepatic bile duct cancer (ICD 155) | 0.56 | 17.60* | 0.40 | 12.77* |
| Colon and rectal cancer (ICD 153, 154) | 0.55 | 17.31* | 0.47 | 15.39* |
| Stomach cancer (ICD 151) | 0.43 | 13.86* | 0.35 | 11.16* |
| Oral cavity cancer (ICD 140, 141, 143–146, 148, 149) | 0.68 | 21.09* | 0.58 | 18.41* |
| Esophageal cancer (ICD 150) | 0.27 | 8.45* | 0.23 | 7.51 * |
| Pancreatic cancer (ICD 157) | 0.22 | 6.92* | 0.23 | 7.31* |
| Non-Hodgkin's lymphoma (ICD 200, 202, 203) | 0.07 | 2.29* | 0.02 | 0.75 |
| Leukemia (ICD 204–208) | 0.05 | 1.74 | 0.10 | 3.55* |
Data were collected between 2005 and 2009. A value In Z(I) greater than 1.96 Is statistically significant and Is Indicated by an asterisk (*).
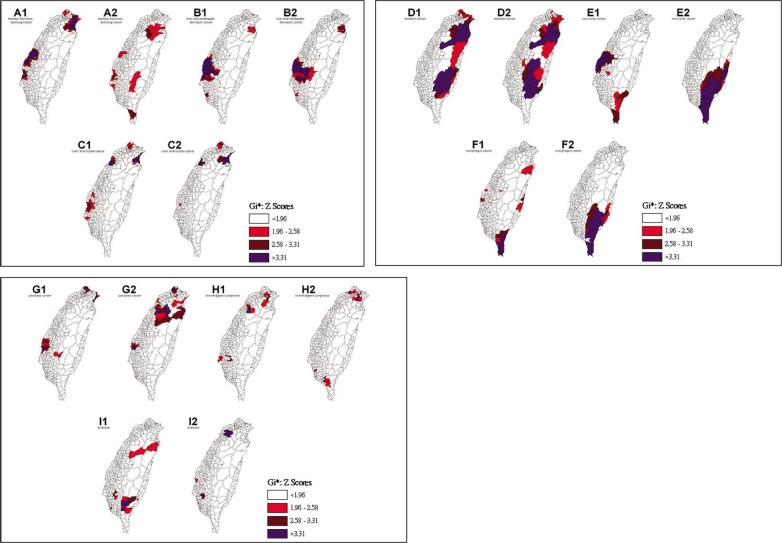
The spatial clusters (hot spots) obtained from the local Gi*(d) statistic for the nine malignant neoplasms for both males and females in Taiwan between 2005–2009 are shown in Figure 2. The z-score outcomes calculated by the Gi*(d) statistic were categorized as clusters or non-clusters at a 5% significance level. The nine malignant neoplasms in males and females were compared and the results were summarized in Table 3. No statistically significant dissimilarity (P > 0.05) was observed between the spatial distribution patterns for males and females for four of the nine spatial clusters. Dissimilarities were found in malignant neoplasms for tracheal, bronchial and lung cancer, colon and rectal cancer, oral cavity cancer, esophageal cancer, and non-Hodgkin's lymphoma.
Figure 2. Spatial clusters (hot spots) of the nine malignant neoplasms in Taiwan.
Maps show the spatial clusters of the nine malignant neoplasms in Taiwan: tracheal, bronchial, and lung cancer are designated by A; liver and intrahepatic bile duct cancer by B; colon and rectal cancer by C; stomach cancer is designated by D; oral cavity cancer by E; and esophageal cancer by F; pancreatic cancer is designated by G; non-Hodgkin's lymphoma by H; and leukemia by I. Gender is indicated by a number, where male is 1 and female is 2.
Table 3. Logistic regression model comparisons of the nine malignant neoplasms in Taiwan between 2005 and 2009.
| Leading malignant neoplasms (ICD code) | P | Description |
| Tracheal, bronchial, and lung cancer (ICD 162) | <0.001 | Dissimilaritya |
| Liver and intrahepatic bile duct cancer (ICD 155) | 0.253 | Similaritya |
| Colon and rectal cancer (ICD 153, 154) | 0.027 | Dissimilaritya |
| Stomach cancer (ICD 151) | 0.197 | Similaritya |
| Oral cavity cancer (ICD 140, 141, 143–146, 148, 149) | <0.001 | Dissimilaritya |
| Esophageal cancer (ICD 150) | <0.001 | Dissimilaritya |
| Pancreatic cancer (ICD 157) | 0.217 | Similaritya |
| Non-Hodgkin's lymphoma (ICD 200, 202, 203) | 0.009 | Dissimilarity |
| Leukemia (ICD 204–208) | 0.760 | Similarity |
a indicates that both compared sides must be Moran's tested clusters.
Discussion
Close locations are likely to share similar attributes. In other words, all variables are related, and nearby variables are more closely related than distant variables[31]. In epidemiology, a cluster becomes apparent when a number of health events that are situated in close proximity in space and/or time occur. The evaluation of spatial distributions as a measure of disease risk may provide etiological insights[32]. Spatial autocorrelation is defined as the relationship between the values of a single variable. This relationship is attributable to the geographical arrangement of areal units on a map and can be used to identify the degree of spatial clustering[33],[34]. In the present study, we used the local G-statistic to measure the degree of spatial clustering and to map the geographical patterns of areal units. Spatial clustering of the leading cause of death (also called a hot spot) was defined as a z-score value larger than 1.96. In epidemiology, hot spots are appealing because of their correlation to etiology. For this reason, the hot spots of nine malignant neoplasms, as obtained from the analysis, were indicated, and their spatial locations were identified. Information regarding spatial location is useful for detecting risk factors from a spatial viewpoint. A more detailed survey of these identified hot spots may reveal significant indications to the risk factors of these diseases.
The modifiable areal unit problem (MAUP) is a phenomenon in which different results are obtained from an analysis of the same data grouped into different sets of areal units. Studies of the MAUP based on empirical data provided only limited insight into the inability to control relationships between multiple spatial variables. Data simulation is necessary to control various properties of individual level data. Simulation studies, such as those conducted by Swift et al.[35], have demonstrated that the spatial support of variables can affect the magnitude of the ecological bias caused by spatial data aggregation. Manley et al.[36] concluded that MAUP is not an actual problem, but rather, a resource. Data at different scales can help identify processes operating at different scales. Defining an ideal single census geography that captures all the processes for all variables is evidently impossible[36]. Furthermore, the internal composition of the areal units may not be homogeneous, particularly for disease distribution. Matisziw et al.[37] suggested that downscaling the spatial structure of polygonal units should provide valuable information pertaining to the spatial distribution of diseases.
The z-scores for the local G-statistic were calculated using the logistic regression model. The results for various leading malignant neoplasms and for males and females were compared. However, the constraint condition for a spatial clustering comparison, e.g., defined as Moran's tested clusters on both sides, should be satisfied before testing the logistic regression for a comparison. Based on this constraint condition, the results of the comparison showed statistically significant differences for tracheal, bronchial and lung cancer, colon and rectal cancer, oral cavity cancer, and esophageal cancer. However, a further three cases comparing cancers of the liver, intrahepatic bile ducts, and stomach as well as the pancreas were not significantly different. In other words, the null hypothesis is accepted. The accepted null hypothesis results indicate that the common spatial factor(s) may interact with both males and females.
Previous ecological studies related to malignant neoplasms and their correlation to risk factors in Taiwan are scant, although oral cancer and stomach cancer have been documented and are discussed below in brief. This study of the spatial clustering of Taiwan's leading malignant neoplasms can act as a reference in the study of spatial epidemiology.
Areas showing an elevated mortality rate from oral cavity cancer for females were clustered in the aboriginal townships in eastern Taiwan. Aboriginal women in eastern Taiwan had a much higher prevalence of cigarette smoking, alcohol drinking, and betel nut chewing compared to women in other areas [38],[39]. In addition, Chiang et al.[40] suggested that high-risk areas of oral cancer incidence in males closely coincide with the spatial distribution of serious metal (e.g., chromium and nickel) pollution in soils in central Taiwan. Oral cavity cancer clusters according to gender were calculated in this study using the local G-statistic. The results show clear spatial clustering in central (males) and eastern Taiwanese aboriginal townships (females). The observations thus support the results of previous studies. Furthermore, males with oral cavity cancer show another spatial clustering in southern Taiwan. Spatial risks might have similar causes to previous studies in females, e.g., cigarette smoking, alcohol drinking, and betel nut chewing, but further studies are required.
Several meta-analyses have shown a strong and consistent association between Helicobacter pylori infection and non-cardiac gastric cancer[41]–[44]. The ecological study in Taiwan suggests an association between Helicobacter pylori infection and gastric cancer. Helicobacter pylori infection in early childhood may be a key issue, and a long induction time is seemingly required for gastric Carcinogenesis. High gastric cancer mortality areas were clustered in the aboriginal townships where Helicobacter pylori infection was prevalent[38],[45]. The results of this study are similar to those of previous studies. Stomach cancer clusters for males and females showed clustering in Taiwanese aboriginal townships and also revealed new carcinogen clustering in the northern coastal region of Taiwan. This significant finding warrants further investigation.
Conclusions
A spatial autocorrelation calculation is useful for cluster mapping regional malignant neoplasms. Cluster mapping helps clarify issues such as the spatial aspects of both internal and external correlations of leading malignant neoplasms and spatial pattern differences. This method enables planners to assess spatial risk factors and to ascertain the most advantageous types of healthcare policies for planning and implementing healthcare services. These issues can greatly affect the performance and effectiveness of healthcare services. Therefore, cluster mapping is a clear approach to enhance the understanding of the results.
Acknowledgments
The author thanks Taiwan's Department of Health for access to the National Health Insurance database.
References
- 1.Douven W, Scho Iten HJ. Spatial analysis in health research [M] In: De Lepper MJC, Scholten HJ, Stern RM, editors. The added value of geographical information systems in public and environmental health. Boston, MA: Kluwer Academic Press; 1995. pp. 117–134. [Google Scholar]
- 2.Gesler W. The uses of spatial analysis in medical geography: a review [J] Soc Sci Med. 1986;23(10):963–973. doi: 10.1016/0277-9536(86)90253-4. [DOI] [PubMed] [Google Scholar]
- 3.Waller LA, Gotway CA. Hoboken, NJ: John Wiley and Sons; 2004. Applied spatial statistics for public health data [M] [Google Scholar]
- 4.Cuzick J, Edwards R. Spatial clustering for inhomogeneous populations [J] J R Stat Soc (Ser B) 1990;52:73–104. [Google Scholar]
- 5.Upton G, Fingleton B. New York: Wiley; 1985. Spatial data analysis by example, volume 1: point pattern and quantitative data [M] [Google Scholar]
- 6.Ohno Y, Aoki K, Aoki N. A test of significance for geographic clusters of disease [J] Int J Epidemiol. 1979;8(3):273–280. doi: 10.1093/ije/8.3.273. [DOI] [PubMed] [Google Scholar]
- 7.Miyawaki N, Chen SC. A statistical consideration on the mapping of mortality [J] Soc Sci Med Med Geogr. 1981;15D(1):93–101. doi: 10.1016/0160-8002(81)90019-8. [DOI] [PubMed] [Google Scholar]
- 8.Cressie NAC. New York: Wiley; 1993. Statistics for spatial data [M] [Google Scholar]
- 9.Legendre P, Legendre L. Amsterdam: Elsevier; 1998. Numerical ecology (2nd English edition) [M] [Google Scholar]
- 10.Fortin MJ. Spatial statistics in landscape ecology [M] In: Klopatek JM, Gardner RH, editors. Landscape ecological analysis: issues and applications. New York: Springer-Verlag; 1999. pp. 253–279. [Google Scholar]
- 11.Tsai PJ, Lin ML, Chu CM, et al. Spatial autocorrelation analysis of health care hotspots in Taiwan in 2006 [J] BMC Public Health. 2009;9:464. doi: 10.1186/1471-2458-9-464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Getis A, Ord JK. The analysis of spatial association by use of distance statistics [J] Geographical Analysis. 1992;24(3):189–206. [Google Scholar]
- 13.Anselin L. The local indicators of spatial association––LISA [J] Geogr Anal. 1995;27(2):93–115. [Google Scholar]
- 14.Ord JK, Getis A. Local spatial autocorrelation statistics: distributional issues and an application [J] Geogr Anal. 1995;27(4):286–306. [Google Scholar]
- 15.Demographic data in 2005–2009 was purchased from Ministry of Interior, Republic of China (Taiwan)
- 16.National Health Insurance . Statistical annual report of medical care 2005 [M] Taipei: National Health Insurance; 2007. [Google Scholar]
- 17.National Health Insurance . Statistical annual report of medical care 2006 [M] Taipei: National Health Insurance; 2008. [Google Scholar]
- 18.National Health Insurance . Statistical annual report of medical care 2007 [M] Taipei: National Health Insurance; 2009. [Google Scholar]
- 19.National Health Insurance . Statistical annual report of medical care 2008 [M] Taipei: National Health Insurance; 2010. [Google Scholar]
- 20.National Health Insurance . Statistical annual report of medical care 2009 [M] Taipei: National Health Insurance; 2011. Available at http://www.doh.gov.tw/. [Google Scholar]
- 21.Ahmad OE, Boschi-Pinto C, Lopez AD, et al. Age standardization of rates: A new WHO standard (GPE discussion paper series, No. 31) [M] Geneva: World Health Organization; 2000. [Google Scholar]
- 22.Longley PA, Goodchild MF, Maguire DJ, et al. Geographic information systems and science (2nd edition) [M] UK: John Willey & Sons Limited; 2005. pp. 85–108. [Google Scholar]
- 23.Grubesic TH. Zip codes and spatial analysis: problems and prospects [J] Socioecon Plann Sci. 2008;42(2):129–149. [Google Scholar]
- 24.Boots BN, Getis A. Point pattern analysis (scientific geography series, volume 8) [M] Newbury Park, CA: Sage Publications; 1998. [Google Scholar]
- 25.Cliff AC, Ord JK. Spatial autocorrelation [M] London: Pion Limited; 1973. [Google Scholar]
- 26.Getis A, Morrison AC, Gray K, et al. Characteristics of the spatial pattern of the dengue vector, Aedes aegypti, in Iquitos, Peru [J] Am J Trop Med Hyg. 2003;69(5):494–505. [PubMed] [Google Scholar]
- 27.Wu J, Wang J, Meng B, et al. Exploratory spatial data analysis for the identification of risk factors to birth defects [J] BMC Public Health. 2004;4:23. doi: 10.1186/1471-2458-4-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Feser E, Sweeney S, Renski H. A descriptive analysis of discrete U.S. industrial complexes [J] J Reg Sci. 2005;45(2):395–419. [Google Scholar]
- 29.Ceccato V, Persson LO. Dynamics of rural areas: an assessment of clusters of employment in Sweden [J] J Rural Stud. 2002;18(1):49–63. [Google Scholar]
- 30.MacKellar FL. Early mortality data: sources and difficulties of interpretation [M] In: Kiple KF, editor. The Cambridge world history of human disease. Cambridge: Cambridge University Press; 1993. pp. 209–213. [Google Scholar]
- 31.Tobler W. Cellular geography [M] In: Gale S, Olsson G, editors. Philosophy in geography. Dordrecht: D. Reidel Publishing Company; 1979. pp. 379–386. [Google Scholar]
- 32.Moore DA, Carpenter TE. Spatial analytical methods and geographic information systems: use in health research and epidemiology [J] Epidemiol Rev. 1999;21(2):143–161. doi: 10.1093/oxfordjournals.epirev.a017993. [DOI] [PubMed] [Google Scholar]
- 33.Griffith DA, Arnrhein CG. Statistical analysis for geographers [M] Englewood Cliffs, NJ: Prentice Hall; 1991. [Google Scholar]
- 34.Kitron U, Kazmierczak JJ. Spatial analysis of the distribution of Lyme disease in Wisconsin [J] Am J Epidemiol. 1997;145(6):558–566. doi: 10.1093/oxfordjournals.aje.a009145. [DOI] [PubMed] [Google Scholar]
- 35.Swift A, Liu L, Uber J. Reducing MAUP bias of correlation statistics between water quality and GI illness [J] Comput Environ Urban Syst. 2008;32(2):134–148. [Google Scholar]
- 36.Manley D, Flowerdew R, Steel D. Scales, levels and processes: studying spatial patterns of British census variables [J] Comput Environ Urban Syst. 2006;30(2):143–160. [Google Scholar]
- 37.Matisziw TC, Grubesic TH, Wei H. Downscaling spatial structure for the analysis of epidemiological data [J] Comput Environ Urban Syst. 2008;32(1):81–93. [Google Scholar]
- 38.Lin JT, Wang LY, Wang JT, et al. Ecological study of association between Helicobacter pylori infection and gastric cancer in Taiwan [J] Dig Dis Sci. 1995;40(2):385–388. doi: 10.1007/BF02065425. [DOI] [PubMed] [Google Scholar]
- 39.Yang YH, Lee HY, Tnug S, et al. Epidemiological survey of oral submucous fibrosis and leukoplakia in aborigines of Taiwan [J] J Oral Pathol Med. 2001;30(4):213–219. doi: 10.1034/j.1600-0714.2001.300404.x. [DOI] [PubMed] [Google Scholar]
- 40.Chiang CT, Hwang YH, Su CC, et al. Elucidating the underlying causes of oral cancer through spatial clustering in high-risk areas of Taiwan with a distinct gender ratio of incidence [J] Geospatial Health. 2010;4(2):231–242. doi: 10.4081/gh.2010.203. [DOI] [PubMed] [Google Scholar]
- 41.Huang JQ, Sridhar S, Chen Y, et al. Meta-analysis of the relationship between Helicobacter pylori seropositivity and gastric cancer [J] Gastroenterology. 1998;114(6):1169–1179. doi: 10.1016/s0016-5085(98)70422-6. [DOI] [PubMed] [Google Scholar]
- 42.Eslick GD, Lim LL, Byles J. Association of Helicobacter pylori infection with gastric carcinoma: a meta-analysis [J] Am J Gastroenterol. 1999;94(9):2373–2379. doi: 10.1111/j.1572-0241.1999.01360.x. [DOI] [PubMed] [Google Scholar]
- 43.Xue FB, Xu YY, Wan Y. Association of Helicobacter pylori infection with gastric carcinoma: a meta-analysis [J] World J Gastroenterol. 2001;7(6):801–804. doi: 10.3748/wjg.v7.i6.801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang C, Yuan Y, Hunt RH. The association between Helicobacter pylori infection and early gastric cancer: a metaanalysis [J] Am J Gastroenterol. 2007;102(8):1789–1798. doi: 10.1111/j.1572-0241.2007.01335.x. [DOI] [PubMed] [Google Scholar]
- 45.Teh BH, Lin JT, Pan WH, et al. Seroprevalence and associated risk factors of Helicobacter pylori infection in Taiwan [J] Anticancer Res. 1994;14(3B):1389–1392. [PubMed] [Google Scholar]