Abstract
Inhibition of return (IOR) as an indicator of attentional control is characterized by an eccentricity effect, that is, the more peripheral visual field shows a stronger IOR magnitude relative to the perifoveal visual field. However, it could be argued that this eccentricity effect may not be an attention effect, but due to cortical magnification. To test this possibility, we examined this eccentricity effect in two conditions: the same-size condition in which identical stimuli were used at different eccentricities, and the size-scaling condition in which stimuli were scaled according to the cortical magnification factor (M-scaling), thus stimuli being larger at the more peripheral locations. The results showed that the magnitude of IOR was significantly stronger in the peripheral relative to the perifoveal visual field, and this eccentricity effect was independent of the manipulation of stimulus size (same-size or size-scaling). These results suggest a robust eccentricity effect of IOR which cannot be eliminated by M-scaling. Underlying neural mechanisms of the eccentricity effect of IOR are discussed with respect to both cortical and subcortical structures mediating attentional control in the perifoveal and peripheral visual field.
Keywords: visual attention, inhibition of return, eccentricity effect, cortical magnification, visual field
Effects of visual orienting can be demonstrated by various cueing paradigms. When attention is directed toward a peripheral location by an endogenous cue such as an arrow or a word that predicts where the target would most likely appear, facilitation is typically observed, that is, faster RT for detecting a target at the cued location relative to the uncued location. However, when using an exogenous cue such as a sudden flash of an outline box at a peripheral location, biphasic effects of attentional capture are frequently reported: When the cue-target interval is very brief, observers respond faster to a target at the cued location as compared to an uncued location. When the interval becomes longer, facilitation is reversed to inhibition, that is, observers respond slower to a subsequent target at the cued location. This latter inhibitory effect is typically known as “inhibition of return” (IOR) and has been independently discovered in the mid-1980s by Posner and Cohen (1984) and Tassinari, Aglioti, Chelazzi, Marzi, and Berlucchi (1987). It has been generally assumed that IOR has ecological significance for improving visual search efficiencies: By giving priority to novel locations rather than to those previously attended, visual search efficiency can be greatly improved.
Since the initial discovery of IOR, an increasing amount of research has been dedicated to this phenomenon (Berlucchi, 2006; Klein, 2000; Lupianez, Klein, & Bartolomeo, 2006). Typically, two types of cue-target procedures are employed for its investigation (Bao, Zhou, & Fu, 2004). One is a single-cue procedure, in which a peripheral cue is followed by a target stimulus appearing at either the previously cued location or an opposite, uncued location. The other is a double-cue procedure in which a second cue is added following the peripheral cue so as to reorient attention to the central fixation point before the onset of a following target. Independent of these procedures, IOR has been found to be a very robust phenomenon that can be observed in various situations. It occurs not only in detection tasks but also in discrimination tasks (e.g., Lupianez, Milan, Tornay, Madrid, & Tuleda, 1997; Pratt & Castel, 2001), not only with manual responses but also with eye movement responses (Abrams & Dobkin, 1994), not only in static stimulus displays but also in a dynamic environment (Tipper, Weaver, Jerreat, & Burak, 1994), and not only in normal young adults but also in other age groups and in patients (Bao et al., 2004; Langley et al., 2007; Larrison-Faucher, Briand, & Sereno, 2002; MacPherson, Klein, & Moore, 2003).
Given the role that IOR might play in the visual search process, it is important to know how IOR is spatially distributed in the visual field. Studies with a method of cueing one peripheral location and measuring the response time (RT) to targets at multiple locations in the visual field suggest that IOR not only dwells at the originally cued location, but also spreads to nearby locations (Maylor & Hockey, 1985) or even to the entire hemi-field with the vertical meridian as a boundary (Berlucchi, Tassinari, Marzi, & Stefano, 1989; Collie, Maruff, Yucel, Danckert, & Currie, 2000; Tassinari et al., 1987). In testing an attentional-momentum hypothesis with a paradigm of using multiple stimulus locations around a fixation, Pratt and colleagues obtained a different result (Pratt, Adam, & McAuliffe, 1998; Pratt, Spalek, & Bradshaw, 1999). Although the slowest detection RT was found at the originally cued location, and the fastest RT at the uncued opposite location, RTs at other locations did not suggest the vertical or horizontal meridian as a spatial boundary; the results rather implied a gradient of IOR where responses became slower as the distance between cue and target decreased. In a subsequent high spatial-resolution study that tested 441 target locations following a peripheral cue, indeed a gradient effect throughout the visual field was observed. Specifically, inhibition in the cued quadrant gradually gave way to facilitation in the opposite quadrant (Bennett & Pratt, 2001). This observation obscured the possible role of the vertical and horizontal meridians in the spatial distribution of IOR and implied a radial symmetry of attentional control in the visual field with the fixation point as the center.
Although these previous studies explored the spatial characteristics of IOR, they focused on IOR only in a limited area of the visual field. In fact, in most IOR studies only stimuli up to 12° eccentricities were examined. In a few studies more peripheral locations such as 18° (Collie et al., 2000) and 30° (Berlucchi et al., 1989; Tassinari et al. 1987) eccentricities were included, however, these studies did not examine directly the eccentricity effect of IOR since this was not their question of interest. Therefore, little is known about IOR in the more peripheral visual field. To find out whether IOR is homogeneously distributed in the visual field, a potential eccentricity effect of IOR has been recently addressed. By systematically manipulating stimulus eccentricity with a double-cue IOR paradigm, Bao and Pöppel (2007) observed a functional dissociation of attention control in the visual field. Specifically, the magnitude of IOR was found to be much stronger in the peripheral visual field relative to the foveal and perifoveal regions (up to approximately 15° eccentricity). This eccentricity effect of IOR is shown to be a robust phenomenon lasting approximately 3 s (Bao et al., 2013) and being resistant to subjects’ practice (Bao et al., 2011). To further investigate the generality of this functional subdivision of attentional control in the visual field, Bao and colleagues (Bao, Wang, & Pöppel, 2012) further measured the IOR effects with a single-cue paradigm and applied a very short cue-target interval typically being anticipated not to observe any inhibitory effect at all. Consistent with this expectation, no IOR effects were observed within the perifoveal region up to 15° eccentricity, whereas beyond 15° there were significant IOR effects. This eccentricity effect not only revealed an early onset of IOR in the periphery, but verified again a functional dissociation of attentional control in the visual field.
The concept of a functional dissociation of attentional control across the visual field may be related to the inhomogeneity of the visual field as suggested by psychophysical, neuropsychological, and neuroanatomical observations (for review see Strasburger, Rentschler, & Jüttner, 2011). Under photopic adaptation conditions, a central cone of high sensitivity in the performance plane of light-difference thresholds across the visual field is surrounded by a plateau of constant sensitivity in the near periphery (extending from 10° up to 20° vertically and 35° horizontally; Pöppel & Harvey, 1973; cf. Strasburger et al., 2011, Fig. 8). Consistent with this sensitivity difference, the modes of oculomotor programming are also different for targets that appear in these two regions. While perifoveal targets are usually reached by a single saccade, peripheral targets require at least two saccades: one bringing the visual axis close to the target, and a second – the corrective saccade – which aligns the visual axis with the target (Frost & Pöppel, 1976). This observation implies that the oculomotor system can accurately program one saccadic eye movement for perifoveal targets but not for targets that appear more peripherally in the visual field. In a study with patients who had suffered cerebral injuries of the central visual field with some perifoveal and peripheral vision left intact, a slowdown of temporal processing as measured by flicker fusion was observed for the perifoveal visual field, but not beyond (Pöppel, Cramon, & Backmund, 1975). In another study on residual vision (Pöppel, Held, & Frost, 1973), it was observed that the location of a target within the scotoma could still be discriminated by oculomotor responses if the targets were presented beyond approximately 10° eccentricity but not when they appeared within the perifovea. Thus, a functional subdivision of the visual field is supported presumably due to the different anatomical central projections: one emphasizing the geniculo-striate pathway and the other the colliculo-extrastriate pathway (Wilson & Toyne, 1970).
Although the human visual field has been shown to be inhomogeneous in many respects, the proposal of a functional dissociation of attentional control in the visual field as demonstrated by the eccentricity effect of IOR faces one important challenge, namely whether simply cortical magnification in early visual areas is responsible for this phenomenon. The concepts of cortical magnification and M-scaling have been studied for many years (Cowey & Rolls, 1974; Daniel & Whitteridge, 1961; Popovic & Sjöstrand, 2001; Rovamo & Virsu, 1979; Strasburger, Rentschler, & Harvey, 1994; Schiefer et al., 2001; for review see Strasburger et al., 2011). It is well known that the cortical representation of a unit area in the visual field decreases with its eccentricity. Since same-size stimuli had been used at different eccentricities in previous studies that demonstrated the eccentricity effect of IOR (Bao & Pöppel, 2007; Bao et al., 2011, 2012, 2013), their cortical representation was smaller when presented in the periphery than in the perifovea. Therefore, the eccentricity effect of IOR might just reflect cortical magnification, and might not be a valid indicator of a functional dissociation of attentional control in the visual field.
The present study aimed to clarify this possibility by comparing IOR effects at two stimulus eccentricities (7° and 21°) in a spatial cueing paradigm comparing two critical conditions: one being a same-size condition in which identical stimuli were used for both eccentricities, the other being a size-scaling condition in which the stimuli were scaled according to an estimate of the magnification factor. Stimuli were thus larger at 21° than at 7° eccentricity in the latter condition. If cortical magnification is responsible for the eccentricity effect of IOR, then the manipulation of stimulus size (same-size vs. size-scaling condition) should influence whether the eccentricity effect of IOR is observed. Specifically, a larger IOR magnitude at 21° relative to 7° eccentricity would only be expected in the same-size condition and not in the size-scaling condition since in the latter the cortical representations of both 7° and 21° targets would be approximately the same.
Methods
Participants
Sixteen university students (10 male and 6 female with an age range of 19–24 years) participated in the experiment. All participants were right-handed and had normal or corrected-to-normal vision. They were all naïve to the purpose of the experiment and were paid after the experiment.
Materials and Procedure
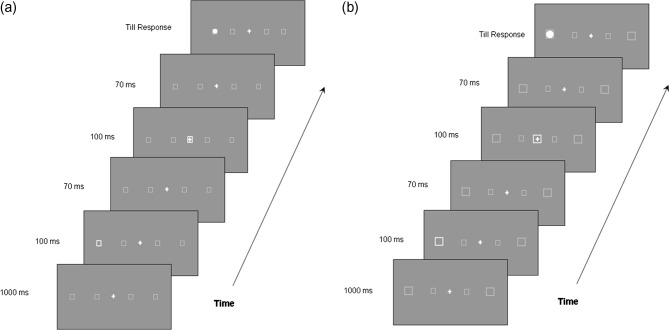
The experiment was conducted in a dimly illuminated room. Subjects were seated at 36.5 cm distance from a 19 in. CRT monitor with their heads resting on a chin rest. The spatial resolution of the CRT monitor was 1024 × 768 pixels and the refresh rate was set at 75 Hz. All stimuli were generated by a PC running Matlab software. Each trial started with a white fixation cross (1° × 1°) centered on the dark computer screen. After 1,000 ms, a white outline box serving as a peripheral cue appeared for 100 ms at one of the four peripheral locations (indicated by dash-line boxes in Figure 1) with equal probability. Two of the peripheral locations had an eccentricity of 7° (left, right) and the other two an eccentricity of 21° (left, right) (Figure 1). At 70 ms after the offset of the peripheral cue an outline box appeared at the fixation location for 100 ms, reorienting the subject’s attention back to the center. Another 70 ms later, a white disk serving as the target appeared at either the same or the symmetric opposite location of the peripheral cue, with equal probability. The target remained present until the participant responded, that is, pressed the space bar with the right index finger. Responding was instructed to be as quickly and as accurately as possible. During each trial, subjects were instructed to maintain their fixation at the central cross without shifting their gaze to the peripheral locations. This requirement was particularly checked by the experimenter during the practice session, and all subjects could follow this instruction successfully before the main test started. An intertrial interval of 1,000 ms with a blank screen was inserted after the subject responded.
Figure 1. Sample trial sequence of a double-cue IOR paradigm. A valid trial at 21° eccentricity is demonstrated for both the same-size condition (a) and the size-scaling condition (b).
The sizes of the cues and targets for different stimulus eccentricities were manipulated as follows: In the same-size condition the cue subtended 1° × 1° and the target 0.6° × 0.6° for both stimulus eccentricities (7° and 21°); In the size-scaling condition, the peripheral cue at 7° was kept at 1° × 1° size while, at 21°, it was magnified to 2.8° × 2.8°; the peripheral target at 7° was kept at 0.6° × 0.6° size while, at 21°, it was magnified to 1.68°, using a formula for calculating cortical magnification as suggested by Rovamo and Virsu (1979).
The experimental session consisted of 560 trials which were divided into 8 blocks. Four blocks were trials of the same-size condition and 4 blocks were trials of the size-scaling condition. There were 80 catch trials in which no targets were presented and the participants had to withhold their responses. Ten catch trials were randomly mixed with 60 target trials in each block. The number of trials for targets appearing in the left or right visual field, at 7° or 21° eccentricity, and at a cued or uncued location, was balanced in both the same-size and the size-scaling conditions. One half of the participants performed four blocks of the same-size condition first, and the other half performed four blocks of the size-scaling condition first. A practice block with 20 trials of the same-size condition and 20 trials of the size-scaling condition were tested before the main experiment. A short break of approximately 2 min between the experimental blocks was inserted. The entire experimental session lasted approximately 45 min.
Data Preparation
The total error rate for each subject was lower than 1% and therefore was not further analyzed. Response times for the correct trials of each subject were first submitted to a descriptive analysis. Those RTs outside of 3 standard deviations (±3 SD) from the mean were considered as outliers and were excluded from the RT data. A lower limit of 120 ms and a higher limit of 800 ms were further applied to double check whether there remained RTs that were physiologically impossible (too short RTs – less than 120 ms) or were due to reduced concentration (too long RTs – longer than 800 ms). Mean RTs for all experimental conditions are shown in Table 1 .
Table 1. Mean RTs (with Standard Error) for each experimental condition (ms).
| 7° Eccentricity | 21° Eccentricity | |||||
|---|---|---|---|---|---|---|
| Stimulus size | Valid | Invalid | IOR | Valid | Invalid | IOR |
| Same-size | 305 (9.4) | 282 (10.4) | 23 (4.0) | 324 (9.9) | 287 (10.7) | 37 (3.8) |
| Size-scaling | 316 (8.5) | 295 (9.3) | 21 (5.6) | 320 (8.7) | 290 (10.4) | 30 (5.9) |
Results
Mean RTs were analyzed with a 2 × 2 × 2 repeated-measure ANOVA, with Stimulus Size (same-size and size-scaling), Stimulus Eccentricity (7° and 21°), and cue-target Validity (valid and invalid) as within-subject variables.
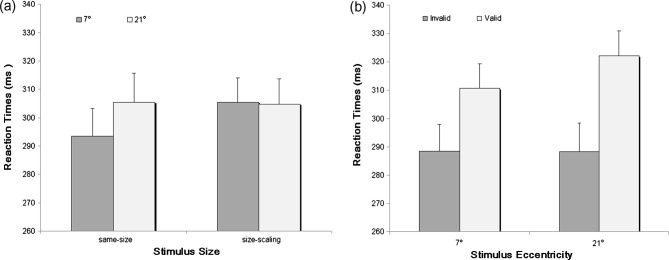
The results of the three-factorial ANOVA showed significant main effects of Stimulus Eccentricity, F(1, 15) = 11.308, p < .01, ηp2 = .430, and cue-target Validity, F(1, 15) = 48.153, p < .001, ηp2 = .762, but no main effect of Stimulus Size, F(1, 15) = 1.492, p > .05, ηp2 = .090. However, Stimulus Size significantly interacted with Stimulus Eccentricity, F(1, 15) = 31.961, p < .001, ηp2 = .681. Further analysis of this interaction using paired t-tests with Bonferroni correction showed a slower RT for 21° versus 7° stimuli, but only in the same-size condition (305 ms vs. 294 ms, p < .05), not in the size-scaling condition (305 ms vs. 306 ms, p = .875) (Figure 2a), as expected from the effect of cortical magnification. Consistent with previous observations (Bao & Pöppel, 2007; Bao et al., 2011, 2012, 2013), the interaction between Stimulus Eccentricity and cue-target Validity was also significant, F(1, 15) = 33.445, p < .001, ηp2 = .690. A further paired t-test on the magnitude of IOR (i.e., the RT difference between valid and invalid trials) for the two stimulus eccentricities revealed a stronger IOR magnitude for 21° versus 7° stimuli (34 ms vs. 22 ms, t(15) = −5.783, p < .001), showing an eccentricity effect of IOR (Figure 2b). More importantly, no three-way interaction between Stimulus Size, Stimulus Eccentricity, and cue-target Validity was observed, F(1, 15) = 1.069, p = .318, ηp2 = .067. This indicated that the eccentricity effect of IOR was not affected by the manipulation of stimulus size. In other words, a result pattern of stronger IOR at 21° versus 7° eccentricity stayed the same in both the same-size condition (37 ms vs. 23 ms) and the size-scaling condition (30 ms vs. 21 ms). No other effects were observed.
Figure 2. Data illustrating the observed two types of interactions. (a) Interaction between Stimulus Size and Stimulus Eccentricity. The RT for 21° eccentricity is significantly slower than that for 7° eccentricity in the same-size condition, whereas there is no such difference in the size-scaling condition. (b) Interaction between Stimulus Eccentricity and cue-target Validity. A larger IOR magnitude (i.e., RT difference between valid and invalid trials) for 21° versus 7° eccentricity is observed, that is, an eccentricity effect of inhibition of return. Standard errors are indicated by error bars.
Discussion
The present study examined whether the difference in cortical projection of the IOR stimuli (as inferred from the cortical magnification factor) is responsible for the eccentricity effect of IOR. By measuring the IOR magnitude at two different stimulus eccentricities (7° and 21°) in a same-size and a size-scaling condition, we observed a robust eccentricity effect of IOR – stronger IOR magnitude for 21° relative to 7° stimuli – independent of the manipulation of stimulus size. Since in the size-scaling condition, both the cue and the target at the more peripheral location (21°) were M-scaled simultaneously, we were concerned with a potential confounding of the effects of cue size and target size. Therefore, we further conducted a supplementary experiment with 10 subjects using similar experimental design and procedures, but having only the peripheral target magnified while keeping the peripheral cue size unchanged. Again, we observed a significant eccentricity effect of IOR (i.e., a larger IOR effect for 21° (41 ms) versus 7° (28 ms) eccentricity) which was unaffected by the manipulation of target size.
The main result of this study indicates that cortical magnification is not responsible for the eccentricity effect of IOR, since the critical manipulation in the study – Stimulus Size scaling – did not change the eccentricity effect of IOR. RT was influenced by stimulus size as expected, but IOR, i.e., RT difference, was not. Stimulus size exerts its influence on RT likely by spatial summation of luminous flux up to the size of receptive fields at the respective visual field location (Riccò’s Law; Strasburger et al., 2011). The latter can be estimated by a psychophysical procedure known as Westheimer’s paradigm (Oehler, 1985). Table 2 shows a comparison of the stimulus sizes used in the present study and estimated mean receptive field sizes at the same location. Stimulus size was just above mean receptive field size at 7° eccentricity, but was below it at 21° in the unscaled condition and above it in the scaled condition. So stimulus sizes compare to summation areas as intended and are thus chosen appropriately.
Table 2. Comparison between stimulus size in the present study and mean receptive field size at the two eccentricities used. Mean receptive field sizes are estimated from Equation 18 in Strasburger et al., 2011, based on Oehler (1985).
| Eccentricity | Target size unsealed | Target size scaled | Receptive field size |
|---|---|---|---|
| 7° | 0.6° | 0.6° | 0.42° |
| 21° | 0.6° | 1.68° | 0.90° |
The observation of a significant two-way interaction between Stimulus Eccentricity and cue-target Validity in the present study, together with other previous evidence (Bao & Pöppel, 2007; Bao et al., 2011, 2012, 2013), support the notion that the distribution of attention in the human visual field is not homogeneous but can be characterized by (at least) two attentional systems (see also Pöppel & Bao, 2012), one extending from the fovea to approximately 10° to 15° eccentricity along the horizontal meridian and the other beyond this perifoveal region up to the far periphery.
Although previous studies suggest that IOR is associated with a distributed neural network including the right parietal lobe, superior and middle temporal gyrus, frontal eye field, orbitofrontal cortex, and some subcortical structures including superior colliculus and cerebellum (Lepsien & Pollmann, 2002; Mayer, Seidenberg, Dorflinger, & Rao, 2004; Ro, Farne, & Chang, 2003; Sapir, Soroker, Berger, & Henik, 1999; Vivas, Humphreys, & Fuentes, 2003), it is still too early to specify the neural mechanisms underlying the eccentricity of IOR, since all these previous studies exploring the neural correlates of IOR have only examined the IOR effects in a limited range of stimulus eccentricity, typically within the perifoveal visual field. A direct comparison between IOR in the perifoveal and the peripheral regions of the visual field with fMRI technology comes however from a recent study by Lei and colleagues (2012). Consistent with previous studies, a stronger activation of the dorsal fronto-parietal network was evidenced for the perifoveal IOR, whereas the peripheral IOR was significantly associated with a stronger activation of the prefrontal cortex which indicates that different cortical mechanisms underlie the eccentricity effect of IOR. Due to the limited sensitivity of fMRI in their study, Lei and colleagues could not detect any potential subcortical contributions to the eccentricity effect of IOR.
In a structural model of attentional control (Bao & Pöppel, 2007) it has been argued that different anatomical pathways might be responsible for this functional dissociation. It has been well established that the more peripheral regions of the visual field show a stronger projection to the superior colliculus of the midbrain and from there to extrastriate regions, compared to the foveal and perifoveal regions which possess a strong geniculo-striate projection. Thus, the eccentricity effect of IOR might reflect different attentional control mechanisms which, on the one hand, are dominated by cortical and on the other hand by subcortical processes. In more general terms this functional dissociation of attentional control would highlight the importance of subcortical processing in attention as has been pointed out already some decades ago (Singer, Zihl, & Pöppel, 1977; for review see, e.g., LaBerge, 1995; Sommer & Wurtz, 2004).
Although the eccentricity effect of IOR in the visual field cannot be explained by cortical magnification, stimulus size and eccentricity certainly have an influence on visual processing. If reaction times at 7° and 21° eccentricities were compared for the same-size and the size-scaling conditions, a clear difference was observed. In the same-size condition the more peripheral targets (21°) resulted in significantly longer reaction times compared to the perifoveal targets (7°) as also observed in a previous study (Zhou, Bao, Sander, Trahms, & Pöppel, 2010). This difference was no longer present in the size-scaling condition indicating that, indeed, the extent of cortical representation being equalized for the two conditions is relevant for the speed of processing. The fact that the reaction times, after adjusting the size of the stimuli, were similar further strengthens the hypothesis for the eccentricity effect of IOR as not being due to speed differences in perifoveal and peripheral processing. There remains, however, an interesting paradox with respect to the interaction between stimulus size and eccentricity: One might have expected that reaction times for targets at 7° and 21° eccentricities under the size-scaling condition would correspond to the reaction time observed for 7° eccentricity for the same-size condition, but this was not the case; they were the same, but on a higher level corresponding to the slower reaction time under the same-size condition for 21° eccentricity. This result might indicate an instationarity within the experimental conditions as often observed in experiments using reaction time as critical indicator (Pöppel, Schill, Steinbüchel, 1990; Steinbach, Dreden, & Pöppel, 1991). Possibly, when a peripheral target of larger size is used, the overall saliency for all stimuli is increased, resulting in a lower level of general activation which then leads to slower response times. However, whatever may be the case this effect did not compromise the key observation of the eccentricity effect of IOR being independent of the magnification factor. This supports the basic notion of a robust phenomenon of different attentional control in the visual field.
Acknowledgments
This research was supported by the National Natural Science Foundation of China (No. 30670703; No. 91120004).
Footnotes
The first two authors contributed equally to this study.
References
- Abrams R. A., & Dobkin R. S. (1994). Inhibition of return: Effects of attentional cuing on eye movement latencies. Journal of Experimental Psychology: Human Perception and Performance, 20, 467–477. [DOI] [PubMed] [Google Scholar]
- Bao Y., & Pöppel E. (2007). Two spatially separated attention systems in the visual field: Evidence from inhibition of return. Cognitive Processing, 8, 37–44. [DOI] [PubMed] [Google Scholar]
- Bao Y., Sander T., Trahms L., Pöppel E., Lei Q., & Zhou B. (2011). The eccentricity effect of inhibition of return is resistant to practice. Neuroscience Letters, 500, 47–51. [DOI] [PubMed] [Google Scholar]
- Bao Y., Wang Y., & Pöppel E. (2012). Spatial orienting in the visual field: A unified perceptual space? Cognitive Processing, 13(Suppl 1), 93–96. [DOI] [PubMed] [Google Scholar]
- Bao Y., Wang Z., Liang W., Wang Y., Pöppel E., & Li H. (2013). Inhibition of return at different eccentricities in the visual field share the same temporal window. Neuroscience Letters, 534, 7–11. [DOI] [PubMed] [Google Scholar]
- Bao Y., Zhou J., & Fu L. (2004). Aging and the time course of inhibition of return in a static environment. Acta Neurobiologiae Experimentalis, 64, 403–414. [DOI] [PubMed] [Google Scholar]
- Bennett P. J., & Pratt J. (2001). The spatial distribution of inhibition of return. Psychological Science, 12, 76–80. [DOI] [PubMed] [Google Scholar]
- Berlucchi G. (2006). Inhibition of return: a phenomenon in search of a mechanism and a better name. Cognitive Neuropsychology, 23, 1065–1074. [DOI] [PubMed] [Google Scholar]
- Berlucchi G., Tassinari G., Marzi C. A., & Stefano M. D. (1989). Spatial distribution of the inhibitory effect of peripheral non-informative cues on simple reaction time to non-fixated visual targets. Neuropsychologia, 27, 201–221. [DOI] [PubMed] [Google Scholar]
- Collie A., Maruff P., Yucel M., Danckert J., & Currie J. (2000). Spatiotemporal distribution of facilitation and inhibitory of return arising from the reflexive orienting of covert attention. Journal of Experimental Psychology: Human Perception and Performance, 26, 1733–1745. [DOI] [PubMed] [Google Scholar]
- Cowey A., & Rolls E. T. (1974). Human cortical magnification factor and its relation to visual acuity. Experimental Brain Research, 21, 447–454. [DOI] [PubMed] [Google Scholar]
- Daniel P. M., & Whitteridge D. (1961). The representation of the visual field on the cerebral cortex in monkeys. Journal of Physiology, 159, 203–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frost D., & Pöppel E. (1976). Different programming modes of human saccadic eye movements as a function of stimulus eccentricity: Indications of a functional subdivision of the visual field. Biological Cybernetics, 23, 39–48. [DOI] [PubMed] [Google Scholar]
- Klein R. M. (2000). Inhibition of return. Trends in Cognitive Science, 4, 138–147. [DOI] [PubMed] [Google Scholar]
- LaBerge D. (1995). Computational and anatomical models of selective attention in object identification. In Gazzaniga M. S. (Ed.), The cognitive neurosciences (1st ed.). (pp. 649–663). Cambridge, MA: MIT Press. [Google Scholar]
- Langley L. K., Fuentes L. J., Vivas A. B., & Saville A. L. (2007). Aging and temporal patterns of inhibition of return. Journal of Gerontology, Series B: Psychological Sciences and Social Sciences, 62, 71–77. [DOI] [PubMed] [Google Scholar]
- Larrison-Faucher A., Briand K. A., & Sereno A. B. (2002). Delayed onset of inhibition of return in schizophrenia. Progress in Neuropsychopharmacology & Biological Psychiatry, 26, 505–512. [DOI] [PubMed] [Google Scholar]
- Lei Q., Bao Y., Wang B., & Gutyrchik E. (2012). fMRI correlates of inhibition of return in perifoveal and peripheral visual field. Cognitive Processing, 13(Suppl 1), 223–227. [DOI] [PubMed] [Google Scholar]
- Lepsien J., & Pollmann S. (2002). Covert reorienting and inhibition of return: an event-related fMRI study. Journal of Cognitive Neuroscience, 14, 127–144. [DOI] [PubMed] [Google Scholar]
- Lupianez J., Milan E. G., Tornay F. J., Madrid E., & Tuleda P. (1997). Does IOR occur in discrimination tasks? Yes it does, but later. Perception & Psychophysics, 59, 1241–1254. [DOI] [PubMed] [Google Scholar]
- Lupianez J., Klein R. M., & Bartolomeo P. (2006). Inhibition of return: Twenty years after. Cognitive Neuropsychology, 23, 1003–1014. [DOI] [PubMed] [Google Scholar]
- MacPherson A. C., Klein R. M., & Moore C. (2003). Inhibition of return in children and adolescents. Journal of Experimental Child Psychology, 85, 337–351. [DOI] [PubMed] [Google Scholar]
- Mayer A. R., Seidenberg M., Dorflinger J. M., & Rao S. M. (2004). An event-related fMRI study of exogenous orienting: Supporting evidence for the cortical basis of inhibition of return? Journal of Cognitive Neuroscience, 16, 1262–1271. [DOI] [PubMed] [Google Scholar]
- Maylor E. A., & Hockey R. (1985). Inhibitory component of externally controlled covert orienting in visual space. Journal of Experimental Psychology: Human Perception and Performance, 11, 777–787. [DOI] [PubMed] [Google Scholar]
- Oehler R. (1985). Spatial interactions in the rhesus monkey retina: A behavioural study using the Westheimer paradigm. Experimental Brain Research, 59, 217–225. [DOI] [PubMed] [Google Scholar]
- Popovic Z., & Sjöstrand J. (2001). Resolution, separation of retinal ganglion cells, and cortical magnification in humans. Vision Research, 41, 1313–1319. [DOI] [PubMed] [Google Scholar]
- Pöppel E., & Bao Y. (2012). The visual field paradox: A theoretical account on the reafference principle providing a common frame for the homogeneity and inhomogeneity of visual representation. Cognitive Processing, 13(Suppl 1), 285–287. [DOI] [PubMed] [Google Scholar]
- Pöppel E., Cramon D. v., & Backmund H. (1975). Eccentricity specific dissociation of visual functions in patients with lesions of the central visual pathways. Nature, 256, 489–490. [DOI] [PubMed] [Google Scholar]
- Pöppel E., & Harvey L. O. Jr. (1973). Light-difference threshold and subjective brightness in the periphery of the visual field. Psychologische Forschung, 34, 145–161. [DOI] [PubMed] [Google Scholar]
- Pöppel E., Held R., & Frost D. (1973). Residual visual function after brain wounds involving the central visual pathways in man. Nature, 243, 295–296. [DOI] [PubMed] [Google Scholar]
- Pöppel E., Schill K., & Steinbüchel N. v. (1990). Multistable states in intrahemispheric learning of a sensorimotor task. NeuroReport, 1, 69–72. [DOI] [PubMed] [Google Scholar]
- Posner M. I., & Cohen Y. (1984). Components of visual orienting. In Bouma H., & Bouwhuis D. G. (Eds.), Attention and performance X: Control of language processes (pp. 531–556). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Pratt J., Adam J. J., & McAuliffe J. (1998). The spatial relationship between cues and targets mediates inhibition of return. Canadian Journal of Experimental Psychology, 52, 213–216. [Google Scholar]
- Pratt J., & Castel A. D. (2001). Responding to feature or location: A re-examination of inhibition of return and facilitation of return. Vision Research, 41, 3903–3908. [DOI] [PubMed] [Google Scholar]
- Pratt J., Spalek T. M., & Bradshaw F. (1999). The time to detect targets at inhibited and noninhibited locations: Preliminary evidience for attentional momentum. Journal of Experimental Psychology: Human Perception and Performance, 25, 730–746. [Google Scholar]
- Ro T., Farne A., & Chang E. (2003). Inhibition of return and the human frontal eye fields. Experimental Brain Research, 150, 290–296. [DOI] [PubMed] [Google Scholar]
- Rovamo J., & Virsu V. (1979). An estimation and application of the human cortical magnification factor. Experimental Brain Research, 37, 495–510. [DOI] [PubMed] [Google Scholar]
- Sapir A., Soroker N., Berger A., & Henik A. (1999). Inhibition of return in spatial attention: Direct evidence for collicular generation. Nature Neuroscience, 2, 1053–1054. [DOI] [PubMed] [Google Scholar]
- Schiefer U., Strasburger H., Becker S. T., Vonthein R., Schiller J., Dietrich T. J., & Hart W. (2001). Reaction time in automated kinetic perimetry: Effects of stimulus luminance, eccentricity, and movement direction. Vision Research, 41, 2157–2164. [DOI] [PubMed] [Google Scholar]
- Singer W., Zihl J., & Pöppel E. (1977). Subcortical control of visual thresholds in humans: Evidence for modality-specific and retinotopically organized mechanisms of selective attention. Experimental Brain Research, 29, 173–190. [DOI] [PubMed] [Google Scholar]
- Sommer M. A., & Wurtz R. H. (2004). The dialogue between cerebral cortex and superior colliculus: Implications for saccadic target selection and corollary discharge. In Chalupa L. M., & Werner J. S. (Eds.), The visual neurosciences, Vol 2, (pp. 1466–1484). Cambridge/MA, London: MIT Press. [Google Scholar]
- Steinbach T., Dreden G. v., & Pöppel E. (1991). Long-term training in a choice reaction time task reveals different learning characteristics for the visual and auditory system. Naturwissenschaften, 78, 185–187. [DOI] [PubMed] [Google Scholar]
- Strasburger H., Rentschler I., & Harvey L. O. Jr. (1994). Cortical magnification theory fails to predict visual recognition. European Journal of Neuroscience, 6, 1583–1588. [DOI] [PubMed] [Google Scholar]
- Strasburger H., Rentschler I., & Jüttner M. (2011). Peripheral vision and pattern recognition: A review. Journal of Vision, 11, 1–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tassinari G., Aglioti S., Chelazzi L., Marzi C. A., & Berlucchi G. (1987). Distribution in the visual field of the costs of voluntarily allocated attention and of the inhibitory after-effects of covert orienting. Neuropsychologia, 25, 55–71. [DOI] [PubMed] [Google Scholar]
- Tipper S. P., Weaver B., Jerreat L. M., & Burak A. L. (1994). Object-based and environment-based inhibition of return of visual attention. Journal of Experimental Psychology: Human Perception and Performance, 20, 478–499. [PubMed] [Google Scholar]
- Vivas A. B., Humphreys G. W., & Fuentes L. J. (2003). Inhibitory processing following damage to the parietal lobe. Neuropsychologia, 41, 1531–1540. [DOI] [PubMed] [Google Scholar]
- Wilson M. E., & Toyne M. J. (1970). Retino-tectal and cortical-tectal projections in Macaca mulatta. Brain Research, 24, 395–406. [DOI] [PubMed] [Google Scholar]
- Zhou B., Bao Y., Sander T., Trahms T., & Pöppel E. (2010). Dissociation of summation and peak latencies in visual processing: An MEG study on stimulus eccentricity. Neuroscience Letters, 483, 101–104. [DOI] [PubMed] [Google Scholar]