Diamonds in the rough: a strong case for the inclusion of weak-intensity X-ray diffraction data

Here, new evidence is provided to show that the inclusion of weak-intensity, high-resolution X-ray diffraction data helps to improve the quality of experimental phases by imposing proper constraints on electron-density models during noncrystallographic symmetry averaging.

Abstract

Overwhelming evidence exists to show that the inclusion of weak-intensity, high-resolution X-ray diffraction data helps improve the refinement of atomic models by imposing strong constraints on individual and overall temperature B factors and thus the quality of crystal structures. Some researchers consider these data to be of little value and opt to discard them during data processing, particularly at medium and low resolution, at which individual B factors of atomic models cannot be refined. Here, new evidence is provided to show that the inclusion of these data helps to improve the quality of experimental phases by imposing proper constraints on electron-density models during noncrystallographic symmetry (NCS) averaging. Using electron-density correlation coefficients as criteria, the resolution of data has successfully been extended from 3.1 to 2.5 Å resolution with redundancy-independent merging R factors from below 100% to about 310%. It is further demonstrated that phase information can be fully extracted from observed amplitudes through de novo NCS averaging. Averaging starts with uniform density inside double-shelled spherical masks and NCS matrices that are derived from bound heavy-atom clusters at the vertices of cuboctahedrally symmetric protein particles.

1. Introduction  

An intensity-distribution analysis of the X-ray diffraction data of the Escherichia coli chaperonin GroEL structure over a decade ago showed that two-thirds of the reflections had measurable nonzero intensities in the highest resolution shell, with an average I/σ(I) of 0.58, including a substantial fraction of reflections over 3σ (Wang & Boisvert, 2003 ▶). Based on this observation, we suggested that these reflections should be included in structure refinement to improve the atomic models. Furthermore, we also suggested that they should be included in density-modification procedures to improve the electron-density maps (Wang & Boisvert, 2003 ▶; Wang, 2010 ▶). These data provide strong constraints for both atomic models and electron-density maps to confine back-Fourier transformed structure factors to match all observed weak-intensity reflections. Karplus and Diederichs recently confirmed our observation that the quality of atomic models can be improved when weak-intensity, high-resolution reflections are included in structure refinement (Karplus & Diederichs, 2012 ▶). Thus, the inclusion of weak-intensity high-resolution X-ray data should be general practice during structure determination.

The crystallographic community as a whole must overcome some inertia to adopt this recommendation. The pervasive exclusion of weak-intensity, high-resolution data is particularly evident in many recent publications of high-profile structures. The majority of previously reported structures in the PDB were determined after excluding those data that were poorly measured with the highest merging R factors and often the worst refinement statistics. By excluding them, the statistics of both data processing and atomic structure refinement can be improved, thereby somewhat reassuring structural biologists that the quality of the derived structures will be acceptable for publication. Their quality is comparable to those structures already in the PDB in which resolution is reported conservatively at a lower resolution of the data than the actual value. This is to avoid being chastized by peers for claiming that the resolution of the data is higher than it really is. Nevertheless, the community is gradually shifting towards the new practice of including weak-intensity, high-resolution data in structure determination (Evans & Murshudov, 2013 ▶; Larivière et al., 2012 ▶; Bunker et al., 2013 ▶).

Besides the statistics discussed above, there are admittedly a number of other reasons that argue against the inclusion of these data. Weak-intensity reflections often have large errors in their near-zero figures of merit for experimentally determined phases. Because of their very small amplitudes, these reflections contribute very little to the direct Fourier synthesis of experimental maps. However, they can still provide constraints in density-modification procedures as well as in noncrystallographic symmetry (NCS) averaging.

It is also possible that a sufficiently experienced structural biologist could easily construct atomic models of appropriate quality without using these data. New advancements in computational methods for structure refinement in the past decade have indeed helped to improve the quality of re-refined models. For example, some errors in protein models can be minimized when preferred conformations can be accurately predicted from sequence information. In fact, recent innovations in computational predictions of protein folding have provided a new avenue for fitting structures more accurately into maps calculated from low-resolution X-ray diffraction data (DiMaio et al., 2009 ▶; Adams et al., 2013 ▶). Therefore, the necessity of including weak-intensity high-resolution reflections in structure determination for producing high-quality models remains not so apparent.

Despite these valid reasons for choosing to omit weak data, we demonstrate in this study that the inclusion of these data results in a substantial improvement in both the visual characteristics of maps and the quality of the resulting atomic models. Further, we hope that by demonstrating these improvements we can smooth the community’s transition to adopting this emerging approach as a standard technique. Finally, we accept that the omission of weak data will apparently improve some statistics. However, the inclusion of these data is worthwhile because doing so allows a substantial improvement in map quality, which can reveal additional pertinent structural features that may otherwise be difficult to visualize.

2. Cuboctahedral symmetry of a 24-subunit YfbU particle and NCS averaging  

The E. coli protein YfbU, a protein of unknown function, was purified and crystallized in the cubic space group P23 (unit-cell parameters a = b = c = 230.08, α = β = γ = 90°) with 16 independent subunits in the asymmetric unit (see Supporting Information1). The Matthews coefficient of the crystal is 3.32 ų Da⁻¹, with a corresponding solvent content of 63% (Matthews, 1968 ▶). The crystals were derivatized with a phospotungstate W₁₂ cluster. When native Patterson maps were calculated at 5.0 Å resolution using the data collected from each of two W₁₂-derivative crystals, each of the eight bound W₁₂ clusters showed up as outstanding peaks in Harker sections, from which their locations were directly determined. In the W₁₂ cluster, the 12 W atoms are arranged in a small, slightly distorted symmetric octahedron having six square and eight triangular faces and 12 corners. Each W₁₂ cluster binds at each side of six independent dyads of the particle, shared by two subunits. The 12 W₁₂ clusters, including those related by threefold crystallographic symmetry, per 24-subunit particle form a symmetric cuboctahedron. The knowledge of this geometry provided the initial NCS matrices for 16-fold NCS averaging using well established procedures (Wang et al., 1997 ▶, 1998 ▶; Kleywegt & Jones, 1999 ▶). After the determination of our structure, we found that this structure had also been independently solved by Otwinowski and coworkers at 2.0 Å resolution (PDB entry 1wpb; Midwest Center for Structural Genomics, unpublished work).

YfbU forms a 24-subunit particle that sits on the crystallographic threefold axis with an empty cavity that is about 55 Å in diameter (Fig. 1 ▶). Each particle occupies about one-eighth of the unit-cell volume, with a diameter of about 115 Å. Within each particle there are eight independent subunits forming a 422 octamer, and there are two such particles in the asymmetric unit. For each particle, we imposed ideal P432 cuboctahedral symmetry (i.e. all fourfold and twofold NCS axes intercepting with the crystallographic threefold axis at its centre) using a global envelope encompassing the entire particle as was performed previously for the 72 symmetry of the ClpP particle (Wang et al., 1997 ▶, 1998 ▶). Because both the twofold and threefold interfaces are made of extensive hydrophilic residues and only the fourfold interfaces are made of extensive hydrophobic residues, we can also consider the particle to be made of six tetramers (or 2 × 2 tetramers per asymmetric unit). In fact, fourfold symmetric parallel four-helix bundles helped us to recognize the NCS. Within a large radius of the W₁₂ cluster binding sites, the correct boundaries and features of the particles were not recognizable in the initial isomorphous replacement experimental maps owing to strong ripple effects from the clusters.

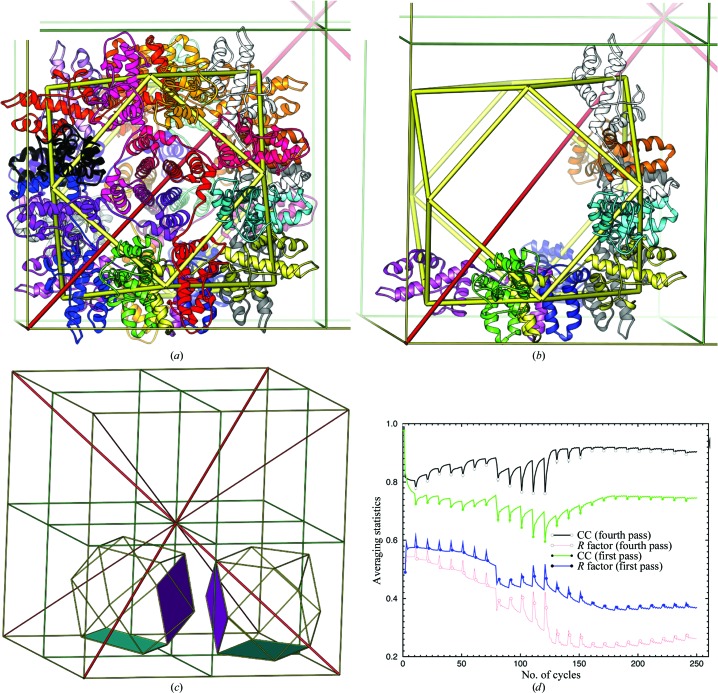
Figure 1.

Cuboctahedron of the 24-subunit YfbU particle and noncrystallographic symmetry averaging. (a) YfbU forms a 24-subunit particle with cuboctahedral P432 point symmetry and the particle sits on the crystallographic threefold axis. The vertices represent the binding sites for the W₁₂ cluster at the twofold-related interface of two subunits from which we derived initial NCS matrices. (b) Two tetramers within each particle are independent subunits in the half asymmetric unit. (c) Two particles in the asymmetric unit with four independent tetramers (shaded planes). Unit-cell edges are shown as thin yellow sticks, crystallographic dyads in green, crystallographic threefold axes in red and cuboctahedron symmetry as thick yellow sticks. (d) Noncrystallographic symmetry real-space electron-density averaging statistics in the first (filled) and fourth pass (open) after mask editing with the highest resolutions from 10 to 2.5 Å resolution in 20 steps with ten cycles of refinement at each resolution. Both R factors (black and green) and electron-density correlation coefficients (red and blue) are plotted.

Each set of NCS matrices has only two variables: a rotation of the particle around the threefold crystallographic axis and a translation along this axis away from (1/4, 1/4, 1/4) by 6.5° and 6.85 Å for one particle and by 11.7° and by 7.09 Å for the other. When these deviations are reduced to zero, the NCS would become crystallo­graphic symmetry. These two particles in the unit cell are also related by pseudo-translational NCS (tNCS) with a vector of approximate (1/2, 1/2, 1/2). However, this tNCS rapidly breaks down beyond 5 Å resolution owing to different rotations of the particles around the threefold axis (Fig. 2 ▶). Initial maps were calculated at 10 Å resolution using experimental phases derived from isomorphous replacement with the W₁₂ cluster. Our approach differed from conventional NCS averaging in that the starting experimental phases were abandoned in the next cycles without a phase-combination step after initial map calculation. New phases, α_ave, were calculated from the inverse Fourier transformation of averaged maps and were not constrained by the starting values (Wang et al., 1997 ▶, 1998 ▶; Kleywegt & Jones, 1999 ▶). In the next cycle, an unweighted 2F _obs − F _ave map was calculated and the process was repeated with gradually increasing resolution, where F _obs are observed amplitudes and F _ave are calculated amplitudes from the inverse Fourier transformation of averaged maps. The rotational and translational offsets were iteratively refined through matrix refinement, and the particle boundary was then redetermined using the improved NCS matrices through a powerful process of two times eightfold mask-less averaging (Fig. 1 ▶ d).

Figure 2.

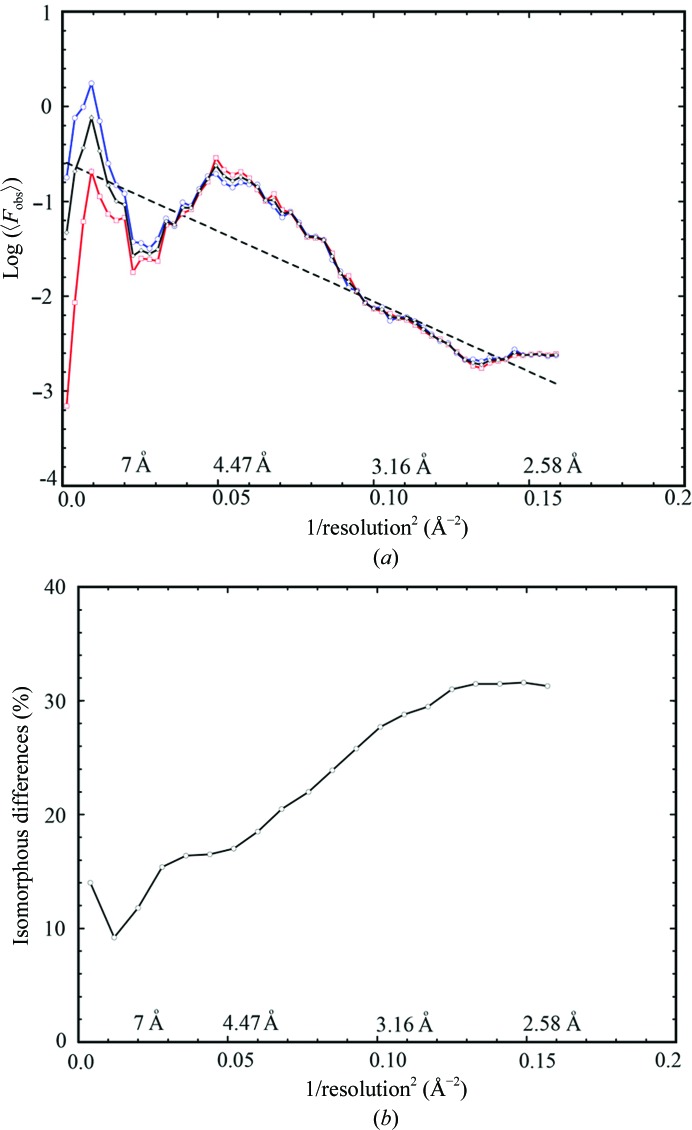
Wilson plots and quality of the experimental data. (a) Wilson plots for reflections with (h + k + l = 2n) in blue, reflections with (h + k + l = 2n + 1) in red and all reflections in black. Linear fitting (dotted line) for three sectors of data resulted in a single line. (b) Isomorphous differences between the two data sets processed from two different crystals as a function of reciprocal resolution squared.

Given the known final NCS matrices and particle masks, we gradually reduced the resolution of the initial experimental phases from 10 to 20, 30 and 40 Å resolution; finally, we used only five and then two lowest-resolution reflections with experimental phases for initial map calculation in retrospective test runs. The averaging process was repeated with an extra step of ten cycles for the added lowest resolution shell. Averaging statistics and phases from the new procedures were identical to those in the original averaging scheme (Supplementary Fig. S3). These calculations suggest that the success of the NCS averaging for the determination of this structure does not depend on the initial experimental phases. Similar calculations have previously been carried out (Wang et al., 1998 ▶; Braig et al., 1994 ▶). Finally, we have also succeeded in conducting NCS averaging starting with a double-shelled spherical mask for the particle.

3. Visual evidence in support of the inclusion of weak data  

Using 16-fold NCS averaging, we extended the phases for all data to a resolution of 2.5 Å [I/σ(I) of 0.46; Table 1 ▶]. At 2.5 Å resolution, the maps unambiguously reveal the positions of polypeptide backbone carbonyl O atoms for nearly all residues (Fig. 3 ▶). When the maps were recalculated after excluding the data beyond 2.8 Å and then 3.1 Å resolution these features were gradually lost, and when these data were excluded from the NCS averaging process the corresponding maps looked much worse. With the 2.5 Å resolution averaged maps we readily built a model with mostly correct conformations using the automated structural interpretation algorithm within Coot and refined it to a free R factor of 24.5% (Emsley et al., 2010 ▶; Murshudov et al., 1997 ▶), with minimal effort expended on model rebuilding (Table 1 ▶).

Table 1. Crystallographic statistics: data processing and structure refinement.

(a).

Data-processing statistics using the XDS program.

Resolution (Å)	No. of reflections	Multiplicity	Completeness (%)	I/σ(I)	R meas (%)	CC1/2 (%)
10.0	2273	6.6	96.4	32.55	4.3	99.9
7.0	4262	6.6	99.0	25.47	6.5	99.8
5.0	11215	6.8	99.8	14.20	14.1	99.1
4.5	6547	6.9	99.9	16.18	12.1	99.3
4.0	10196	6.9	99.9	15.49	12.7	99.2
3.8	5644	6.4	99.7	11.43	17.2	98.6
3.6	7006	6.9	99.9	9.45	22.6	98.0
3.4	8747	7.0	99.9	7.07	31.8	95.9
3.2	11028	6.7	99.9	4.40	50.6	91.0
3.0	14176	6.8	99.9	2.86	81.3	79.5
2.8	18514	6.9	100.0	1.97	117.6	67.3
2.6	24398	4.8	99.4	0.89	209.8	31.9
2.5	14552	3.3	94.5	0.46	312.1	13.5
Total	138551	6.1	99.1	6.87	29.2	98.5

(b).

Structure-refinement statistics. Values in parentheses are for the highest shell.

Resolution (Å)	56–2.5 (2.565–2.500)
No. of reflections	13249 (9055)
No. of atoms	22670 [16 × 164 residues]
Observation-to-parameter ratio†	1.45
R work (%)	21.0 (39.7)
R free (%)	24.7 (40.0)
R.m.s.d., bonds (Å)	0.0066
R.m.s.d., angles (°)	1.39
Ramachandran plot (%)
Most preferred areas	97.2
Most preferred plus allowed areas	99.9
Preferred side-chain rotamers	99.7
PDB code	4lr3

^†The observation-to-parameter ratio is calculated from the number of independent observations divided by four (x, y, z and B) times the number of atoms. With such a modest ratio, we found that the removal of NCS restraints in the refinement led to large differences between working and free R factors, so we kept them until the very last two cycles of refinement. Because the amplitude differences between fourfold NCS-rotated indexes differed by 51–55% owing to the misalignment of NCS axes with respect to the crystallographic axis, the cross-validation set was chosen randomly.

Figure 3.

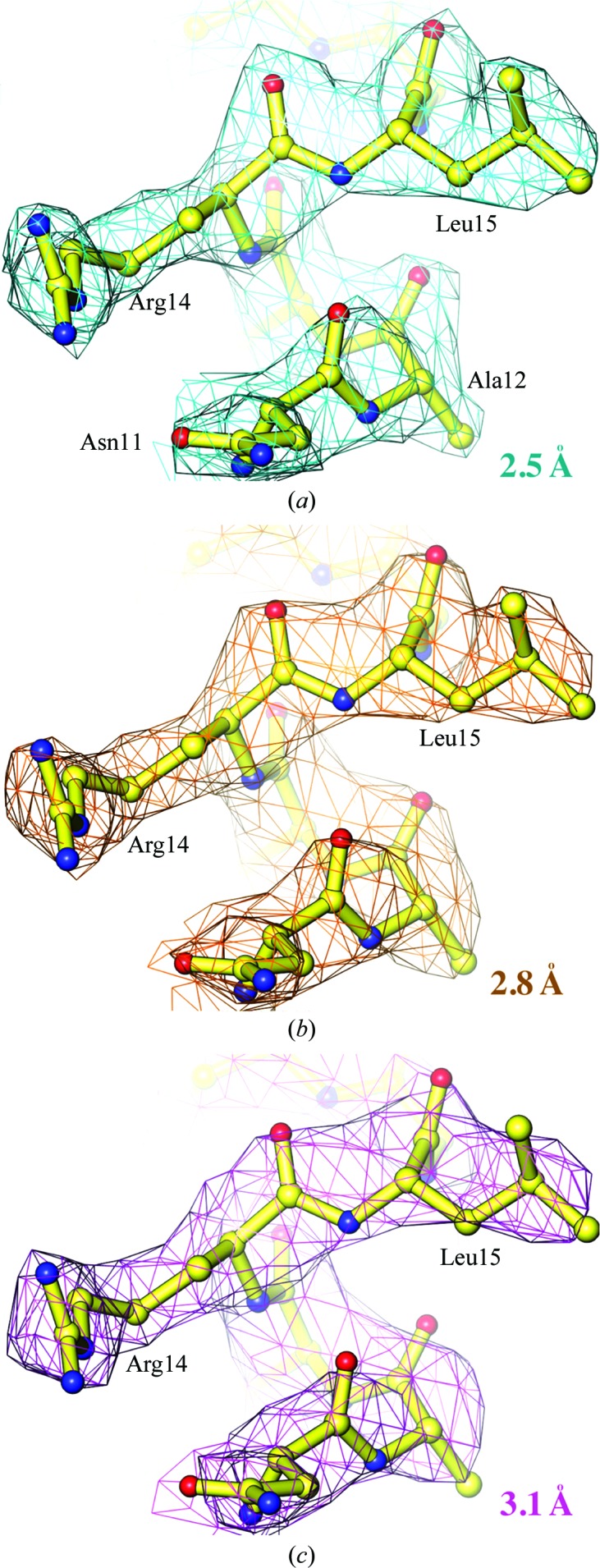
NCS-averaged experimental maps contoured at a level of 1σ superimposed on the refined model at 2.5, 2.8 and 3.1 Å resolution in (a), (b) and (c), respectively.

We noted that several long-side-chain residues such as Arg and Lys residues were rotameric outliers in each subunit in the automatically built model after structure refinement. Some of these outliers were in part owing to multiple rotameric conformations that were partially resolved in the electron-density maps at 2.5 Å resolution. An analysis of the cosine phase differences between the experimental phases and the model-derived phases further supports a deviation from the strict NCS restraints (Fig. 3 ▶), which would partially affect the quality of the experimental phases derived from NCS averaging. We observed a decrease of about 5% in the free R factor during refinement at the point when the NCS restraints were lowered from strong to weak. Deviation from NCS at high resolution is a common feature in structures of macromolecules owing to asymmetric packing environments in the crystal lattice (Wang & Boisvert, 2003 ▶). In all of these cases tight NCS restraints helped refinement to converge rapidly. At the same time, however, they also prevented refinement from further improving the structure when the coordinate errors were limited by errors of tight, incorrect NCS restraints.

Major initial errors in structures of proteins (or nucleic acids and their complexes) typically result from incorrect conformational assignments for backbone and side chains because of ambiguous electron density at relatively low resolution. For example, when protein backbone carbonyl O atoms are not discernible in experimental maps, one has to guess the polarity of polypeptide chains in α-helices and β-strands, and the location of C^α atoms in connecting loops, and given a crudely built protein backbone the side-chain rotamers as well. With the NCS-averaged experimental maps truncated at 3.1 Å resolution (Fig. 3 ▶), only an approximate model with a guessed sequence could be built, and unless extensive efforts were made at rebuilding the model, refinement stalled at a free R factor of about 35%.

In the highest 2.5 Å resolution shell of our data collected at the edge of the Pilatus detectors, the average signal-to-noise ratio or 〈I/σ(I)〉 is 0.46 and the half-split Pearson correlation coefficient or CC_1/2 is 0.14, as recommended by us and by Karplus and Diederichs, respectively (Wang & Boisvert, 2003 ▶; Wang, 2010 ▶; Karplus & Diederichs, 2012 ▶; Table 1 ▶). The merging R factor or redundancy-independent R _meas as defined by XDS (Diederichs & Karplus, 1997 ▶; Kabsch, 2010 ▶) in the highest resolution shell is 302%, which would be considered by many researchers to mean that these data were of little value. In the 3.1 Å resolution shell, 〈I/σ(I)〉, CC_1/2 and R _meas are about 3.5, 0.85 and 77%, respectively, which are statistics that might be considered to be more acceptable by the majority of the structural biology community. Given the very high overall merging statistic (29.2%) and poor statistics in the high-resolution shells (>100% after 3.1 Å resolution; Table 1 ▶), we tested the possibility of whether the threefold crystallographic symmetry was actually NCS symmetry by reprocessing the data in the lower symmetry group P222. We did not observe an improvement in merging statistics up to 3.5 Å resolution, although small variations existed between 3.1 and 2.5 Å resolution. If a small fraction of an individual crystal obeyed P222 symmetry and this lower symmetry portion of the crystal was responsible for the data beyond 3.1 Å resolution, then the random orientation of this fraction of the P222 crystals would make them indistinguishable from P23 symmetry. Moreover, twinning statistical tests did not support a possible twinning conversion of lower symmetry to P23. Thus, the symmetry of the crystals was indeed P23.

4. Electron-density correlation coefficients and other evidence  

In addition to the quality of the experimental maps (Fig. 3 ▶), other lines of evidence also exist to support that weak-intensity, high-resolution reflections do contain useful structural information. The first line of evidence is the contribution of weak data to experimental maps with and without them, which is measured by electron-density correlation coefficients, CC_ED, or electron-density differences as estimated using 1 − CC_ED (Table 2 ▶). In contrast to conventional NCS averaging, these experimental maps are unweighted 2F _obs − F _ave maps without inclusion of the figure-of-merit term, which can be zero for some weak intensity reflections. In order to avoid interpolation errors for CC_ED calculations, all maps were recalculated using fixed grids of 300 × 300 × 300. In the original averaging, we carried out matrix refinement and mask redetermination at 3.1 Å and then at 2.5 Å resolution. A comparison of the two maps recalculated both at 3.1 Å resolution with NCS matrices and masks determined at 3.1 and 2.5 Å resolution, respectively, shows that the two maps differ by 31.1%, suggesting an important contribution from data beyond 3.1 Å resolution (Table 2 ▶). When the same matrices and mask determined at 2.5 Å resolution were used for NCS averaging, addition of data between 3.1 and 2.5 Å resolution, between 3.1 and 2.8 Å resolution and between 2.8 and 2.5 Å resolution changes the experimental map by 8.7, 5.8 and 6.4%, respectively (Table 2 ▶). These statistics suggest that weak data do indeed contribute to experimental maps.

Table 2. Electron-density map correlation coefficients.

Electron-density maps were recalculated using fixed 300 × 300 × 300 grids for the calculation of correlation coefficients to avoid interpolation errors. We re-ran noncrystallographic symmetry averaging using matrices and masks derived at 3.1 Å resolution as well as using matrices and masks derived at 2.5 Å resolution. The experimental maps are calculated using unweighted 2F _obs − F _ave as coefficients and phases derived from averaged maps.

		Correlation coefficient (%)
3.1 Å experimental versus 2.5 Å experimental phases
3.1 Å map	3.1 Å map	68.9
3.1 Å map	2.8 Å map	66.1
3.1 Å map	2.5 Å map	64.5
2.5 Å experimental versus 2.5 Å experimental phases
3.1 Å map	2.8 Å map	94.2
3.1 Å map	2.5 Å map	91.3
2.8 Å map	2.5 Å map	93.6
2.5 Å experimental versus 2.5 Å calculated phases†
2.5 Å map	2.5 Å map	76.8
3.1 Å map	3.1 Å map	74.8
3.1 Å map	2.5 Å map	78.7

^†Amplitudes and phases for weighted 2F _obc − F _calc maps were prepared by the refinement program REFMAC, where F _calc are the calculated structure factors from final refined atomic model.

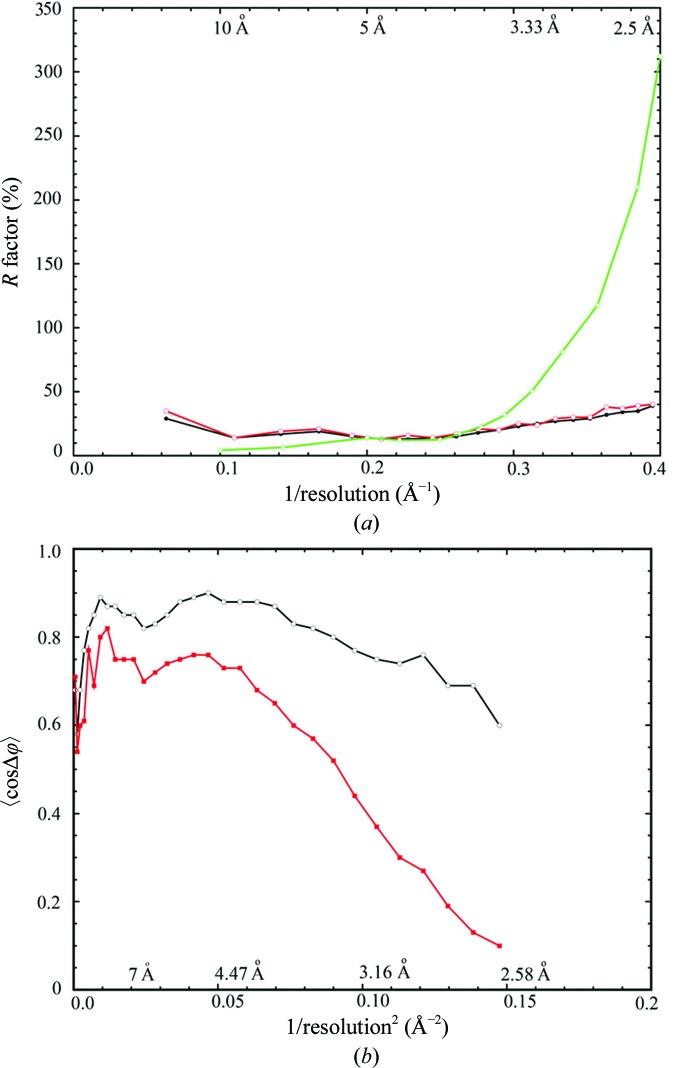
If we approximate the atomic-derived phases as the correct phases, given the relatively small free R-factor values (Fig. 4 ▶ a), cosine differences between NCS-averaging derived phases and atomic model derived phases show a rapid decrease after 3.1 Å resolution (Fig. 4 ▶ b). This is likely to be owing to breakdown of the strict NCS symmetry that was used for NCS averaging. Comparison of the calculated final maps with proper weighting factors at 2.5 Å resolution and the unweighted 2F _obs − F _ave experimental maps at 3.1 Å resolution shows the highest CC_ED of 78.7%, which is higher than the value of pairwise comparison both at 2.5 Å resolution (Table 2 ▶). This suggests that the experimental phases for data between 3.1 and 2.5 Å resolution were not as accurate as for the lower resolution data owing to both deviations of NCS matrices and accuracy of weak data. Thus, actual visual effects for inclusion of weak-intensity, high-resolution data might be stronger if more actual experimental phases could be derived for these reflections than we have presented here.

Figure 4.

Refinement and data-processing statistics. (a) Plots of crystallographic working (black) and free (red) R factor on amplitude as well as merging R factor (green, on intensity) as a function of reciprocal resolution. (b) Plots of average cosine of phase-angle differences between NCS-averaging-derived experimental and model-derived phases (red) as well as the cosine values of the estimated phase errors from differences (black) between observed and calculated amplitudes as a function of reciprocal resolution squared.

In addition, the natural logarithm of averaged intensity by resolution shell continues to decrease linearly when plotted versus the reciprocal resolution squared (the Wilson plot) until 2.75 Å, implying that these data are not random noise (Fig. 2 ▶ a). Moreover, when we processed data collected from two individual crystals at 2.5 Å resolution and compared them, we found that the isomorphous differences between them in the highest resolution shell were only 32% (Fig. 2 ▶ b). This is much smaller than what are considered to be differences caused by random noise. Lastly, the crystallographic and free R factors in the highest shell of 2.5 Å resolution are 38.7 and 40.0%, respectively (Table 1 ▶, Fig. 3 ▶), which are also smaller than the expected 42% for random noise (Evans & Murshudov, 2013 ▶). All of these collectively suggest that weak data do contain useful structural information.

Another important fact that has to be considered when attempting to include weak-intensity, high-resolution X-ray data is that the measurable intensities do not just precipitously drop to below unmeasurable and that they instead drop gradually with a long tail in asymmetric intensity distribution. The number of reflections between zones of measurable and unmeasurable intensities is often very large because it is proportional to the cube of reciprocal resolution. For example, in our initial analysis (Wang & Boisvert, 2003 ▶), extending the resolution with an I/σ(I) cutoff of 1 to an I/σ(I) cutoff of 0.58, we increased the amount of data by 40%. In this study, when we extended the cutoff to include data from 3.1 to 2.5 Å resolution, the observation-to-parameter ratio is nearly doubled from a system that has more parameters (four parameters per atom for x, y, z and B) than the number of independent observations to a system that now has more observations than parameters, not counting 16-fold NCS redundancy (Table 2 ▶). The inclusion of these additional data made refinement more robust. By not including these reflections in this analysis, we would have discarded 50% of the measured data. At 2.5 Å resolution, the average I/σ(I) = 0.46 (in the 2.5–2.6 Å resolution shell), which was our initial recommendation for deciding at what resolution it was appropriate to cut off the data (Wang & Boisvert, 2003 ▶).

5. Concluding remarks  

Based on new evidence presented here along with previous evidence, weak-intensity, high-resolution X-ray diffraction data do, without a doubt, contain valuable structural information. We recommend that the structural biology community should include data with an average I/σ(I) = 0.5 in the highest resolution shell of data processing and structure determination or follow the suggestions made by Karplus and Diederichs to use a CC_1/2 of over 10% (Karplus & Diederichs, 2012 ▶). However, we should be cautious about using the mean I/σ(I) value as a general criterion because it can be affected by an error scale factor which depends on the quality of crystals and the wavelength. Moreover, both criteria can be affected by the chosen width of the highest resolution shell. As an alternative option, authors may carry out structure determination in two steps, first using the existing criteria and then using the new criteria to justify resolution extension. In addition to the abbreviated statistics presented in publications, we also recommend the reporting of detailed data-processing statistics as a function of resolution, as in Table 1 ▶, as part of the supporting information. This will help to provide a smooth transition for the crystallographic community from the existing practice to the new practice, help the reader to see the correctness of crystallographic symmetry even when merging statistics may appear to be very high (in our case, 29.2%) and judge the effective resolution of the reported structures.

Supplementary Material

PDB reference: YfbU, 4lr3