Skip to main content
PMC home page
Journal of Radiation Research logoLink to Journal of Radiation Research
. 2013 Dec 17;55(3):451–454. doi: 10.1093/jrr/rrt138

Applicability of the linear–quadratic model to single and fractionated radiotherapy schedules: an experimental study

Akifumi Miyakawa 1,*, Yuta Shibamoto 1, Shinya Otsuka 1, Hiromitsu Iwata 2
PMCID: PMC4014161  PMID: 24351457

Abstract

The aim of this study was to examine the applicability of the linear-quadratic (LQ) model to single and fractionated irradiation in EMT6 cells. First, the α/β ratio of the cells was determined from single-dose experiments, and a biologically effective dose (BED) for 20 Gy in 10 fractions (fr) was calculated. Fractional doses yielding the same BED were calculated for 1-, 2-, 3-, 4-, 5-, 7-, 15- and 20-fraction irradiation using LQ formalism, and then irradiation with these schedules was actually given. Cell survival was determined by a standard colony assay. Differences in cell survival between pairs of groups were compared by t-test. The α/β ratio of the cells was 3.18 Gy, and 20 Gy in 10 fr corresponded to a BED3.18 of 32.6 Gy. The effects of 7-, 15- and 20-fraction irradiation with a BED3.18 of 32.6 Gy were similar to those of the 10-fraction irradiation, while the effects of 1- to 5-fraction irradiation were lower. In this cell line, the LQ model was considered applicable to 7- to 20-fraction irradiation or doses per fraction of 2.57 Gy or smaller. The LQ model might be applicable in the dose range below the α/β ratio.

Keywords: linear–quadratic model, biologically effective dose, hypofractionation, stereotactic radiotherapy, LQ model

INTRODUCTION

With the development of stereotactic irradiation, various fractionation regimens, including single-fraction and hypofractionated regimens, are now used in clinics. Therefore, comparing the biological effectiveness of various fractionation regimens is necessary to evaluate the outcome of treatment. While the linear–quadratic (LQ) model (n2d2/n1d1 = (1 + d1/[α/β])/(1 + d2/[α/β]), where d1 and d2 are fractional doses and n1 and n2 are fraction numbers) and the biologically effective dose (BED) concept derived from the LQ model (BED = D(1 + d/[α/β]), where D is the total dose and d is the fractional dose, are very useful for comparison among conventionally fractionated regimens [1–3], it has been pointed out that the LQ model does not fit well to single-fraction and hypofractionated regimens or to high-dose-per-fraction radiotherapy [1, 4–6]. More appropriate models for use in hypofractionated regimens are therefore currently being investigated by several groups [7–10]. At present, however, no new model has been proven to fit perfectly to high-dose-per-fraction irradiation.

While attempts should be made to establish better dose calculation models, a practical issue in clinics might be to determine the fractional dose levels to which the LQ model is applicable. Mathematical calculations and model estimations have been attempted to resolve this issue [11, 12] but, to our knowledge, no experiment has been conducted to address this issue directly. In this study, therefore, we carried out experiments to compare various fractionation schedules directly, and to evaluate the applicability of the LQ model and BED concept to 1- to 20-fraction irradiation.

MATERIALS AND METHODS

Cell line

The EMT6 mouse mammary sarcoma line was used. Characteristics of this cell line were described in detail previously [13]. The cells were cultured in Eagle's minimum essential medium containing 12.5% fetal bovine serum. The cells were always kept in an exponentially growing phase and were subcultured on the day before experiments.

Experimental design and procedures

It was planned to compare the effects of 1-, 2-, 3-, 4-, 5-, 7-, 10-, 15- and 20-fraction irradiation. First, the α/β ratio of the cell line was determined from four sets of single-dose experiments. Using the ratio, a BED for 20 Gy in 10 fractions was calculated, and fractional doses yielding the same BED were calculated using the LQ formula. Appropriate numbers of exponentially growing EMT6 cells were plated on 6-cm culture dishes in triplicate. Then, all of the fractionated irradiation schedules were carried out, and their effects on cell surviving fractions were compared. All irradiations were carried out using an X-ray machine (210 kVp, 10 mA, 2-mm Al filter) at room temperature, as described in detail previously [14]. The dose was calibrated using a RAMTEC 1000 dosimeter (Toyo Medic, Tokyo, Japan). The dose rate was 2 Gy per min. Control (0 Gy) groups received sham irradiation.

Regarding the interfraction interval, it was assumed that 24 h for this cell line would correspond to 1 week in humans, because the cell cycle time of this cell line was 11 h in vitro [15]. The potential doubling time for the EMT6 tumor cells in vivo was 1.5 days [16], while the potential doubling time for most human tumors is in the range of 4–12 days [17–19]. Our previous experiment showed that sublethal damage repair (SLDR) was completed within 2 h in this cell line [14], so an interfraction interval of 3 h 25 min (= 24/7 h) was considered to be sufficient to allow full SLDR. Therefore, irradiation was started at 8:00 a.m. and repeated at an interval of 3 h 25 min. The fractionated irradiation stopped at 9:40 p.m. every day; the interval between 9:40 p.m. and 8:00 a.m. the next day was regarded as corresponding to the weekend break in humans.

Cell survival assay

The effects of radiation were determined by the standard colony assay. Colonies were fixed and stained after 7 d for the control group. For irradiated groups, colonies were fixed after 7–10 d of culture depending on the radiation schedules, because fractionated radiation took 4 d at most. After irradiation, colony sizes were visually evaluated, and they were fixed when the mean colony sizes were approximately 1.5 mm, similar to those of the control group.

Statistical analysis

The LQ model fitting was performed using statistical software Mathematica (Wolfram Research, Inc., Champaign, IL, USA) as described previously [10]. All experiments were repeated four times, and differences in cell surviving fractions between pairs of fractionation groups were compared by t-test.

RESULTS

Figure 1 shows a dose-survival curve for EMT6 cells. The curve was fitted by the LQ model. The equation of the LQ model for the dose-survival curve was S = exp(−0.1411D − 0.0444D2). Therefore, the α/β ratio was 3.18 Gy (95% CI: 0.33–6.03 Gy). The BED for 20 Gy in 10 fractions was 32.6 Gy.

Fig. 1.

Fig. 1.

Open in a new tab

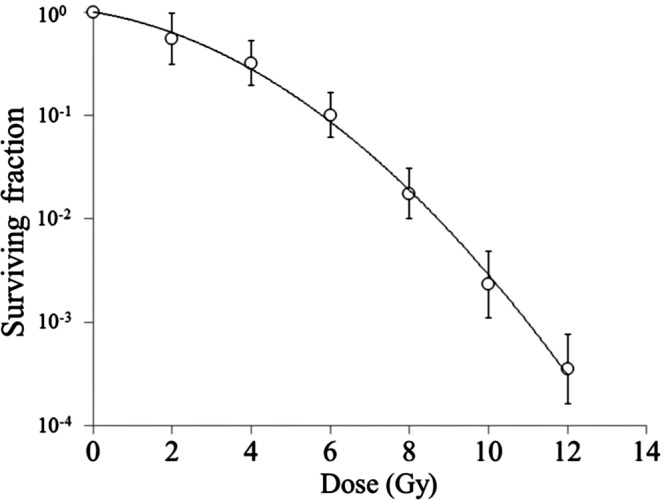
Dose–survival curve for EMT6 single cells. Bars represent standard deviation.

On the basis of the α/β ratio of 3.18 Gy, 1- to 20-fraction irradiation to yield a BED3.18 of 32.6 Gy, as shown in Fig. 2, was performed. Figure 3 shows the cell surviving fractions after 1- to 20-fraction irradiation. Surviving fractions after 7-, 15- and 20-fraction irradiation did not differ significantly from the surviving fraction after 20 Gy in 10 fractions. On the other hand, surviving fractions after 1- to 5-fraction irradiation were higher than those after 10-fraction irradiation, and the discrepancy became greater with the decrease in the fraction number.

Fig. 2.

Fig. 2.

Open in a new tab

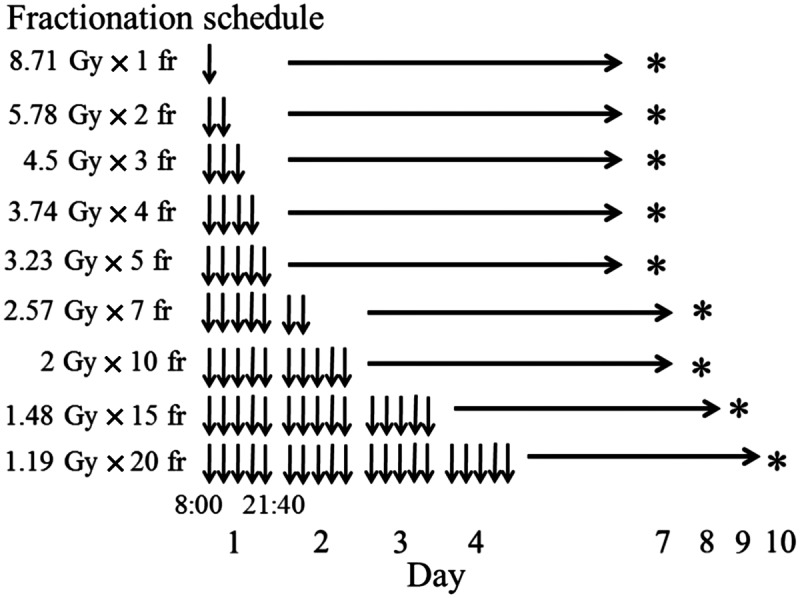
Radiation schedule. Irradiation was started at 8:00 a.m. and repeated at an interval of 3 h 25 min. Daily irradiation stopped at 9:40 p.m. *Colony staining.

Fig. 3.

Fig. 3.

Open in a new tab

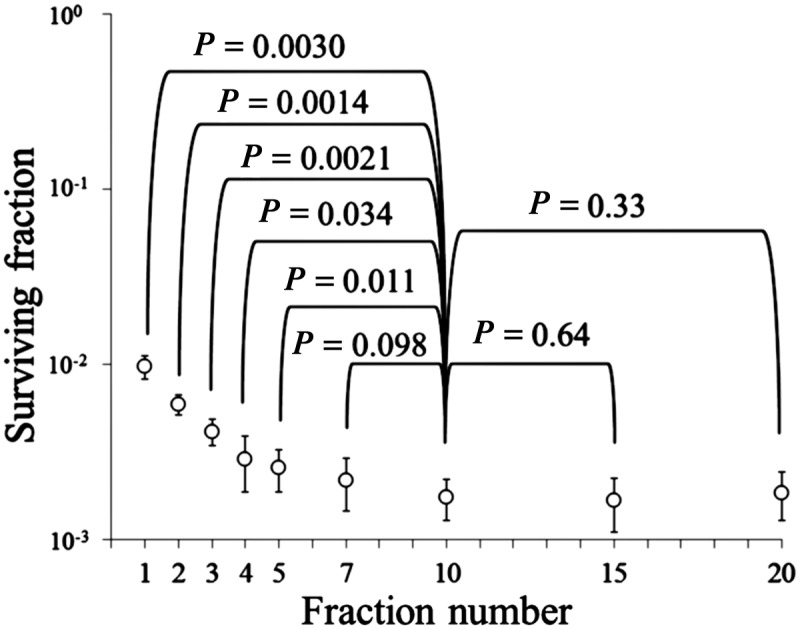
Surviving fractions of EMT6 single cells after single or fractionated irradiation with a biologically effective dose of 32.6 Gy for an α/β ratio of 3.18 Gy. Bars represent standard deviation.

DISCUSSION

In this study, the α/β ratio of EMT6 cells was experimentally determined to be 3.18 Gy, and 1- to 20-fraction irradiation to give a BED3.18 of 32.6 Gy was delivered to the cells. Despite the same BED, 1- to 5-fraction irradiation produced much higher cell surviving fractions than 10-fraction irradiation. Thus, it seems clear that the BED and LQ model are not applicable to single and hypofractionated irradiation in this cell line. On the other hand, they appear to be applicable to fractions of 7 or more.

To determine the applicable range of LQ formalism, it should be more pertinent to discuss the issue based on the dose per fraction rather than the fraction number. In this study, LQ formalism was applicable to 1.19–2.57 Gy per fraction. In a recent review, Shibamoto et al. [5] stated that the LQ model might be applicable up to a fractional dose approximately twofold the α/β ratio. The basis for this statement was as follows. Since the α/β ratio represents the dose at which cell killing from linear (α) and quadratic (β) components of the LQ formula is equal, the LQ model holds around the dose level of the α/β ratio. However, with an increase in the dose, the β cell kill component dominates in the LQ model, from which actual data have been shown to deviate. For this reason, it was considered that a fractional dose approximately twofold the α/β ratio might be a reasonable upper limit for the use of LQ formalism. However, our experimental results suggest that the LQ model is only applicable in the dose range below the α/β ratio. What are the reasons for the incompatibility of the model in the 1–5 fractions or at fractional doses of 3 Gy or higher?

When looking at the single-dose cell survival curve (Fig. 1), the LQ model appears to fit the data well. However, the surviving fraction at 2 Gy is slightly below the curve, while the surviving fractions at 4 and 6 Gy are slightly above the curve. This may partly explain the discrepancy between 2- to 5-fraction irradiation (i.e. 3.23–5.78 Gy/fraction) and 7 fractions or more (≤ 2.57 Gy/fraction). However, the dissociation of the single fraction (8.71 Gy) data cannot be explained. Another explanation may be the possibility of incomplete repair [1]. Wada et al. [20] recently reported that when the effects of potentially lethal damage repair (PLDR) and SLDR were taken into account in the LQ model, the cell survival response to carbon ion irradiation was well reproduced. However, PLDR may not be an important factor in the present study because we used exponentially growing cells. With respect to SLDR, we used an interfraction interval of 3 h 25 min. This was based on a previous experiment in which SLDR in this cell line was completed within 2 h [14]. On the other hand, completion of SLDR might take a longer time in other cell lines [21, 22]. Therefore, if it is assumed that the SLDR in our cell lines was not 100% complete within the interfraction interval of 3 h 25 min (although the magnitude was so small that this could not be proven experimentally), the effects of fractionated irradiation would become greater with an increase in the fraction number. However, the assumption of incomplete repair does not explain the similar cell survival fractions after 10-, 15- and 20-fraction irradiation in the present study. Another possible reason may be the cell cycle redistribution during fractionation. A longer cell cycle arrest is expected after a high dose than after a low dose, so a larger increase in radiosensitivity due to cell cycle redistribution may be expected when smaller doses per fraction are used [23]. There may be other problems intrinsic to the use of the LQ model in single and very hypofractionated irradiation, and this should be clarified in future studies.

If one dares to use the LQ model for single or hypofractionated irradiation, how large an error would be expected? The mean surviving fraction after a single 8.71-Gy dose in the fractionation experiment was 9.7 × 10−3 (log − 2.01). On the basis of the LQ equation, it is calculated to be 1.00 × 10−2, and the small difference would be within the range of experimental error. On the other hand, the mean surviving fractions after 7- to 20-fraction irradiation were 1.7–2.2 × 10−3 (log − 2.66 to − 2.78), and these surviving fractions correspond to those after a single dose of 10.3–10.5 Gy on the survival curve in Fig. 1. Therefore, the use of LQ formalism might lead to about 15–20% underestimation of the equivalent single dose. With an increase in fraction number, the discrepancy would decrease. Many clinicians still use the LQ model in hypofractionated radiotherapy without knowing the incorrectness of the model, and when one looks at such papers one should realize the magnitude of errors associated with the use of the LQ model from the above considerations.

CONCLUSION

In conclusion, the LQ model is not applicable to single-fraction and hypofractionated irradiation. In the cell line investigated, the LQ model was considered applicable to 7- to 20-fraction irradiation or doses per fraction of 2.57 Gy or smaller. These results suggest that the LQ model conversion may be correct in the dose range below the α/β ratio. Further investigation of appropriate dose conversion models or methods in single and hypofractionated (five fractions or less) radiotherapy is encouraged.

CONFLICT OF INTEREST

The authors declare that there are no conflicts of interest.

FUNDING

This work was supported in part by a research grant from the Japanese Ministry of Education, Culture, Sports, Science and Technology.

REFERENCES

  • 1.Joiner MC, Bentzen SM. Fractionation: the linear-quadratic approach. In: Joiner M-C, van der Kogel A-J, editors. Basic Clinical Radiobiology. 4th edn. London: Hodder Arnold; 2010. pp. 102–19. [Google Scholar]
  • 2.Bentzen SM, Joiner MC. The linear-quadratic approach in clinical practice. In: Joiner M-C, van der Kogel A-J, editors. Basic Clinical Radiobiology. 4th edn. London: Hodder Arnold; 2010. pp. 120–34. [Google Scholar]
  • 3.Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62:679–94. doi: 10.1259/0007-1285-62-740-679. [DOI] [PubMed] [Google Scholar]
  • 4.Iwata H, Shibamoto Y, Murata R, et al. Estimation of errors associated with use of linear-quadratic formalism for evaluation of biologic equivalence between single and hypofractionated radiation doses: an in vitro study. Int J Radiat Oncol Biol Phys. 2009;75:482–8. doi: 10.1016/j.ijrobp.2008.12.093. [DOI] [PubMed] [Google Scholar]
  • 5.Otsuka S, Shibamoto Y, Iwata H, et al. Compatibility of the linear–quadratic formalism and biologically effective dose concept to high-dose-per-fraction irradiation in a murine tumor. Int J Radiat Oncol Biol Phys. 2011;81:1538–43. doi: 10.1016/j.ijrobp.2011.05.034. [DOI] [PubMed] [Google Scholar]
  • 6.Shibamoto Y, Otsuka S, Iwata H, et al. Radiobiological evaluation of the radiation dose as used in high-precision radiotherapy: effect of prolonged delivery time and applicability of the linear–quadratic model. J Radiat Res. 2012;53:1–9. doi: 10.1269/jrr.11095. [DOI] [PubMed] [Google Scholar]
  • 7.Park C, Papiez L, Zhang S, et al. Universal survival curve and single fraction equivalent dose: useful tools in understanding potency of ablative radiotherapy. Int J Radiat Oncol Biol Phys. 2008;70:847–52. doi: 10.1016/j.ijrobp.2007.10.059. [DOI] [PubMed] [Google Scholar]
  • 8.Guerrero M, Carlone M. Mechanistic formulation of a linear–quadratic–linear (LQL) model: split-dose experiments and exponentially decaying sources. Med Phys. 2010;37:4173–81. doi: 10.1118/1.3456927. [DOI] [PubMed] [Google Scholar]
  • 9.Huang Z, Mayr NA, Lo SS, et al. A generalized linear–quadratic model incorporating reciprocal time pattern of radiation damage repair. Med Phys. 2012;39:224–30. doi: 10.1118/1.3666760. [DOI] [PubMed] [Google Scholar]
  • 10.Iwata H, Matsufuji N, Toshito T, et al. Compatibility of the repairable-conditionally repairable, multi-target, and linear–quadratic models in converting hypofractionated radiation doses to single doses. J Radiat Res. 2013;54:367–73. doi: 10.1093/jrr/rrs089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Fowler JF, Tomé WA, Fenwick JD, et al. A challenge to traditional radiation oncology. Int J Radiat Oncol Biol Phys. 2004;60:1241–56. doi: 10.1016/j.ijrobp.2004.07.691. [DOI] [PubMed] [Google Scholar]
  • 12.Garcia LM, Leblanc J, Wilkins D, et al. Fitting the linear–quadratic model to detailed data sets for different dose ranges. Phys Med Biol. 2006;51:2813–23. doi: 10.1088/0031-9155/51/11/009. [DOI] [PubMed] [Google Scholar]
  • 13.Shibamoto Y, Streffer C, Fuhrmann C, et al. Tumor radiosensitivity prediction by the cytokinesis-block micronucleus assay. Radiat Res. 1991;128:293–300. [PubMed] [Google Scholar]
  • 14.Shibamoto Y, Ito M, Sugie C, et al. Recovery from sublethal damage during intermittent exposures in cultured tumor cells: implications for dose modification in radiosurgery and IMRT. Int J Radiat Oncol Biol Phys. 2004;59:1484–90. doi: 10.1016/j.ijrobp.2004.04.039. [DOI] [PubMed] [Google Scholar]
  • 15.Shibamoto Y, Mimasu Y, Tachi Y, et al. Comparison of 5-fluorouracil and 5-fluoro-2′-deoxyuridine as an effector in radiation-activated prodrug. J Chemother. 2002;14:390–6. doi: 10.1179/joc.2002.14.4.390. [DOI] [PubMed] [Google Scholar]
  • 16.Shibamoto Y, Streffer C. Estimation of the dividing fraction and potential doubling time of tumors using cytochalasin B. Cancer Res. 1991;51:5134–8. [PubMed] [Google Scholar]
  • 17.Shibamoto Y, Shibata T, Miyatake S, et al. Assessment of the proliferative activity and radiosensitivity of human tumours using the cytokinesis-block micronucleus assay. Br J Cancer. 1994;70:67–71. doi: 10.1038/bjc.1994.251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Bourhis J, Dendale R, Hill C, et al. Potential doubling time and clinical outcome in head and neck squamous cell carcinoma treated with 70 Gy in 7 weeks. Int J Radiat Oncol Biol Phys. 1996;35:471–6. doi: 10.1016/s0360-3016(96)80008-3. [DOI] [PubMed] [Google Scholar]
  • 19.Shibamoto Y, Ike O, Mizuno H, et al. Proliferative activity and micronucleus frequency after radiation of lung cancer cells as assessed by the cytokinesis-block method and their relationship to clinical outcome. Clin Cancer Res. 1998;4:677–82. [PubMed] [Google Scholar]
  • 20.Wada M, Suzuki M, Liu C, et al. Modeling the biological response of normal human cells, including repair processes, to fractionated carbon beam irradiation. J Radiat Res. 2013;54:798–807. doi: 10.1093/jrr/rrt012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Leith JT, Vayer AV, Jr, De Wyngaert JK, et al. In vitro sublethal damage repair in tumour subpopulations from a heterogeneous human colon tumor. Br J Cancer Suppl. 1984;6:207–11. [PMC free article] [PubMed] [Google Scholar]
  • 22.Schwachöfer JH, Crooijmans RP, van Gasteren JJ, et al. Repair of sublethal damage in two human tumor cell lines grown as multicellular spheroids. Int J Radiat Oncol Biol Phys. 1989;17:591–5. doi: 10.1016/0360-3016(89)90111-9. [DOI] [PubMed] [Google Scholar]
  • 23.Withers HR. Cell cycle redistribution as a factor in multifraction irradiation. Radiology. 1975;114:199–202. doi: 10.1148/114.1.199. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Radiation Research are provided here courtesy of Oxford University Press

RESOURCES