Abstract
Prior studies of head direction (HD) cells indicate strong landmark control over the preferred firing direction of these cells, with few studies exhibiting shifts away from local reference frames over time. We recorded spiking activity of grid and HD cells in the medial entorhinal cortex of rats, testing correlations of local environmental cues with the spatial tuning curves of these cells' firing fields as animals performed continuous spatial alternation on a T-maze that shared the boundaries of an open-field arena. The environment was rotated into configurations the animal had either seen or not seen in the past recording week. Tuning curves of both cell types demonstrated commensurate shifts of tuning with T-maze rotations during less recent rotations, more so than recent rotations. This strongly suggests that animals are shifting their reference frame away from the local environmental cues over time, learning to use a different reference frame more likely reliant on distal or idiothetic cues. In addition, grid fields demonstrated varying levels of “fragmentation” on the T-maze. The propensity for fragmentation does not depend on grid spacing and grid score, nor animal trajectory, indicating the cognitive treatment of environmental subcompartments is likely driven by task demands.
Keywords: entorhinal cortex, experience, fragmentation, grid cells, head direction cells
Introduction
The medial entorhinal cortex (mEC) of rats contains grid cells (Fyhn et al. 2004; Hafting et al. 2005; Sargolini et al. 2006) and head direction (HD) cells (Sargolini et al. 2006; Brandon et al. 2011). These 2 cell populations in conjunction with hippocampal place cells (O'Keefe and Dostrovsky 1971) are thought to form the neural basis for spatial orientation in animals. Grid cells fire action potentials at specific, regular locations in space that fall on the vertices of repeating equilateral triangles (Hafting et al. 2005), and HD cells fire to specific headings in the animal's azimuth forming a “neural compass” (Taube et al. 1990a, 1990b). As spatial correlates with fixed metrics for a given environment, they presumably are essential for updating position information when other external sensory cues are absent in a process termed path integration (Gothard, Skaggs, McNaughton 1996; McNaughton et al. 1996).
Many studies have shown that both grid (Hafting et al. 2005) and HD cells (Taube et al. 1990a, 1990b) rotate with salient allocentric cues as animals forage for food. Dudchenko and Zinyuk (2005) tested animals performing spatial alternation on a T-maze while rotating the maze 90°. Rotated sessions were recorded separately in adjacent featureless rooms with the results indicating a commensurate rotation in the heading of HD cells from the thalamic anterodorsal nucleus (ADN). This finding suggests a strong influence of local cues and geometry over HD cells. That study is further supported by evidence from ADN HD cells that are more strongly influenced by rotations in arenas with asymmetric (trapezoid) geometry compared with symmetric (square) geometry (Clark et al. 2012). In the latter arena, HD cells appeared fixed to a cue card in the distal environment rather than the local arena geometry (Clark et al. 2012).
Arena geometry does not appear to affect the heading of HD cells from nondisoriented animals as much as disoriented animals, however (Knight et al. 2011). Graham et al. (2006) trained rats to swim to an escape platform in a kite-shaped pool where the platform was always at one of the right-angled corners. Walls surrounding the platform were all white, all black, or black and white. Given a constant wall color surrounding the platform, animals performed poorly in escaping from the geometrically unambiguous location of the platform. However, when the wall colors were black and white, animals performed much better on the task. This study has led others to pose that visual-guided navigation may provide enough geometric feature extraction without requiring explicit knowledge of the environment geometry to perform such guided tasks (Cheung et al. 2008; Sturzl et al. 2008).
Our project was initially motivated by an interest in the influence of task movement demands on HD and grid cell orientation. Previously, grid cells have been shown to be trajectory-dependent during spatial alternation (Lipton et al. 2007), they can perform a “look-ahead” computation on cued choice tasks (Gupta et al. 2012), and they can “fragment” to represent subcompartments of a hairpin maze task (Derdikman et al. 2009). Grid cells are also known to scale with environmental boundaries (Barry et al. 2007). Such rescaling may only be possible if the environment is relatively novel (Barry et al. 2007; Knierim and Hamilton, 2011) as effects are weak for rescaling between familiar enclosures (Hafting et al. 2005; Barry et al. 2007). Grid cell firing, through largely influenced by environmental boundaries, can be influenced by task and recency (Barry et al. 2012).
We tested the effect of recency on both grid and HD cells by varying the rotation of a T-maze environment. The recency of an experience in an environment may be one of the reasons that can mitigate recent questions surrounding the use of local cues and geometry to perform goal-directed tasks. Taube and Burton (1995) found that as rats move from familiar to novel environments rats retain their HD tuning, which was subsequently shown to depend on self-motion information (Stackman et al. 2003). This agrees with Dudchenko and Zinyuk (2005) who showed that when rats walk from a novel enclosure to a familiar one some ADN HD cells retain their tuning, but orient to landmarks in the familiar enclosure when the animal is carried into the arena. The fact that HD tuning can vary in the same space led us to ask whether nondisoriented rats could also tune their spatial cells differently in the same space over time.
We trained animals to perform spatial alternation on a modified T-maze in a single enclosure where the T-maze was rotated into configurations the animal had recently or not recently seen. We report a primary and secondary effect in our data with regard to spatial tuning curve rotations and grid field fragmentation, respectively. First, we observed that less recent rotations, more so than very recent rotations, induced commensurate shifts in grid fields and HD tuning. Secondly, grid cells appeared to fragment on T-maze recording sessions with respect to their corresponding open-field firing rate maps. We characterized this fragmentation and correlated it to relevant grid metrics finding none of them significant.
Materials and Methods
Subjects
Four male Long-Evans rats, weighing between 400 and 500 g, at the beginning of the experiment served as subjects (Charles River Laboratories, Wilmington, MA, USA). Each animal was housed individually in plexiglass cages under a 24-h light/dark cycle with free access to water, but food restricted to maintain approximately 85% ad libitum body weight. Animal habituation to experimenters and testing environment took place at 2 different times—1 week postarrival from the vendor and 1 week postsurgery. All subjects were pre-exposed to an open field (125 cm × 125 cm), where they were trained to forage for both Froot Loop Cereal (Kellogg Company, Battle Creek, MI, USA) and Sucrose Precision Pellets (Bio-Serv, Frenchtown, NJ, USA). Twenty-min open-field sessions later served as controls for same-day T-maze recordings of spatially modulated neurons.
Implant
Rats were implanted with a movable tetrode assembly consisting of 16 tetrodes, each insulated with 75 μm polyimide tubing (PolyMicro Technologies, Pheonix, AZ, USA) inside 30-gauge steel cannulae (Small Parts, Inc., Seattle, WA, USA). Each tetrode, composed of 4 equal length electrodes of 12-μm diameter nichrome wire (Kanthal, Palm Coast, FL, USA), is independently vertically driven, exiting the implant in a bundle with other channels encased in a 15-gauge steel cannula. The angle of the bundle with respect to the drive's vertical axis was about 25°.
Surgery
Surgical procedures are outlined below and follow the same techniques previously reported (Gupta et al. 2012). Subjects were given atropine (0.04 mg/kg) 20–30 min prior to the induction of general anesthesia using inhalation of isoflurane followed by an injection of a ketamine cocktail (ketamine 12.92 mg/mL, acepromazine 0.1 mg/mL, and xylazine 1.31 mg/mL). Ten to 12 skull screws were inserted along skull boundaries. Bone tissue was removed over the cerebellum where underlying dura was exposed to a single skull screw serving as an electrical ground. The implant site grazed against the left bone ridge between parietal and postparietal skull bones (approximately AP −8.0, ML −4.6 from bregma). After dura removal, and upon lowering the implant bundle on to the brain, the implant was initially secured with Kwik-Sil (World Precision Instruments, Sarasota, FL, USA) followed by several layers of dental acrylic. Tetrodes were lowered into the brain at the bundle angle to a depth of 2.8 mm below the dorsal surface. Postsurgical pain management included 0.1 mL buprenorphine IP and 4 mL of children's ibuprofen PO. Infection control was managed with cephalexin via water delivery at 168 mg/100 mL each day for 4 days postoperatively, and by daily cage changes for 7 days during animal recovery. All surgical procedures followed the National Institute of Health guidelines, and the protocol approved by the Boston University Institutional Animal Care and Use Committee.
Neural Recordings
Animals were tested daily with unit recordings during behavior in an open field and in a recessed T-maze (i.e., a T-maze with walls). Postrecording, tetrodes were turned at least 70 μm and no more than 100 μm per day. The tetrodes were connected to analog unit gain preamplifiers on the head stage. Recorded signals were linked via the head stage to digital amplifiers augmenting the signal 5000–20 000 times. All signals were sampled at 32.556 kHz and digitally bandpass-filtered from 1 Hz to 2 kHz by the 64-channel Cheetah Digital Lynx acquisition system (Neuralynx Corp., Bozeman, MT, USA). Units crossing each electrode's threshold were recorded for offline cluster cutting. Position and head direction data were calculated based on a green rostral diode and a red caudal diode video sampled at 30 Hz. Continuously sampled channels for the recording of local field potential were referenced to the animal's ground or a reference cortical electrode (the reference electrode was chosen to have no apparent theta-modulated signal that would interfere with theta detection at the recording site).
Histology
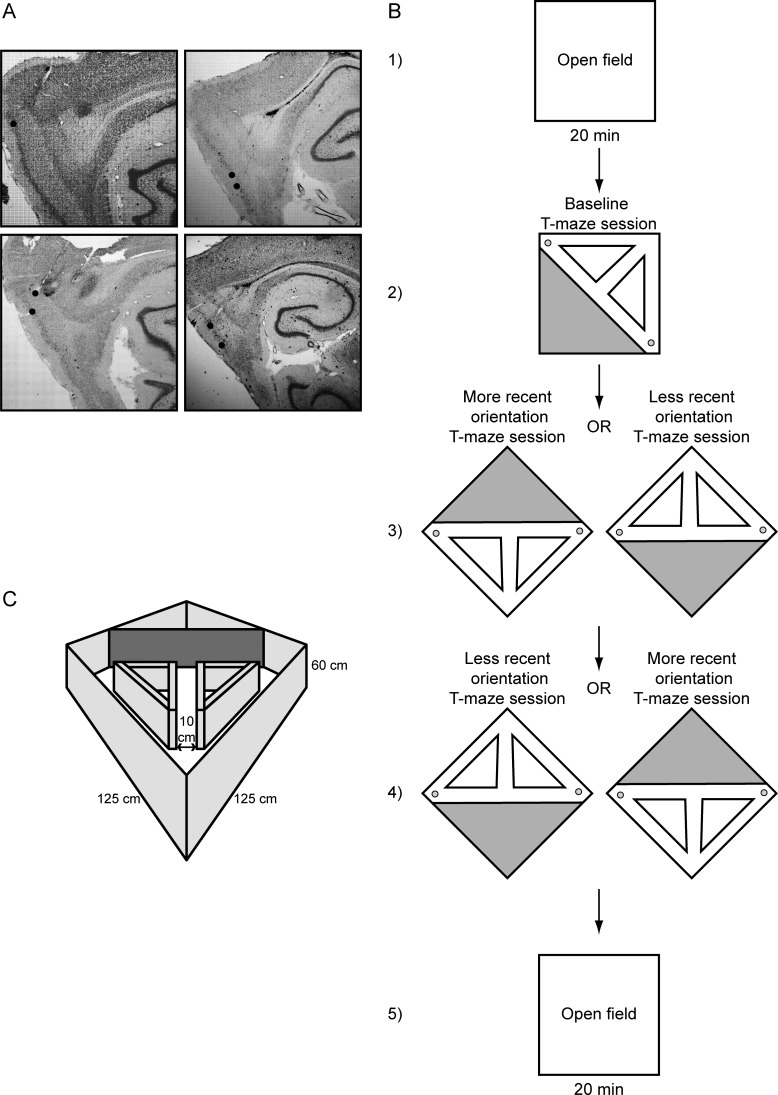
Tetrodes were not moved after the final recording session. Tetrode positions were confirmed by passing 25 μA current for 20 s through each tetrode 1 day prior to perfusion, creating a lesion visible after Nissl staining (Komorowski et al. 2009). Animals were overdosed with isoflurane and were perfused intracardially with saline followed by 4% formaldehyde. Brains were extracted and were stored in 4% formaldehyde at 6°C at least 24 h. Seventy hours prior to slicing, brains were transferred into a 30% sucrose solution. The brain was sectioned along a sagittal plane (to visualize tetrode tracks) into 35 μm slices. Sections were mounted on glass slides and stained with a neutral red Nissl stain. All tetrode tip lesions were confirmed to be localized within the mEC, as shown in Figure 1A.
Figure 1.
(A) Nissl-stained sagittal sections showing tetrode tracks going through layers II–V of the mEC in 4 different rats. (B) The testing protocol shows an initial 20-min open-field session followed by 3 subsequent T-maze sessions and a final 20-min open-field session. (C) The testing environment showing the square open field with prisms and blocking wall generating the T-maze.
Open-Field and T-Maze Sessions
Animals ran at least 5 sessions per recording day. The recording room had black curtains surrounding the environment with no discernible markings or cues visible except for the curtain separation, which was a fixed distal cue to the environment. Prior to recording a session, the animal was plugged into tethered preamplifiers while resting on a podium sitting outside the curtained enclosure entry way. After plugging in the animals, they were hand-lifted into the arena where recording commenced.
The first and final sessions were 20-min open-field recordings where animals randomly foraged for Froot Loop reward. Between all recording sessions, animals were given access to water and housed in a separate room from the recording room, while the environment was cleaned and altered. The environment was cleaned with lemon-scent Mr. Clean (Procter and Gamble, Cincinnati, OH, USA) before and after each of the 5 recording sessions. Animals were brought in from the outside podium through the curtain separation to the base of the T-maze. The first T-maze recording of the day was considered the baseline session and lasted until the animal achieved at least 30 correct laps, a criterion applied to all T-maze recordings. There was no rotation of the outer walls between the first open-field session and the first T-maze session, therefore these sessions required no post hoc alignment. After the first T-maze session, the T-maze environment was rotated (along with the outer boundary walls) into either a “more recent” orientation (an orientation the animal had experienced in the previous 1 week) or a “less recent” orientation (an orientation the animal had not experienced within the previous 1 week). In the third T-maze session, the rats ran the maze in an opposite orientation condition (more recent or less recent) from the previous T-maze recording (Fig. 1B). Mean performance results during spatial alternation and orientation type are shown in Figure 2. Presentation order of the more recent or less recent condition was pseudorandomized. After the final T-maze session, a last 20-min open-field recording completed the session.
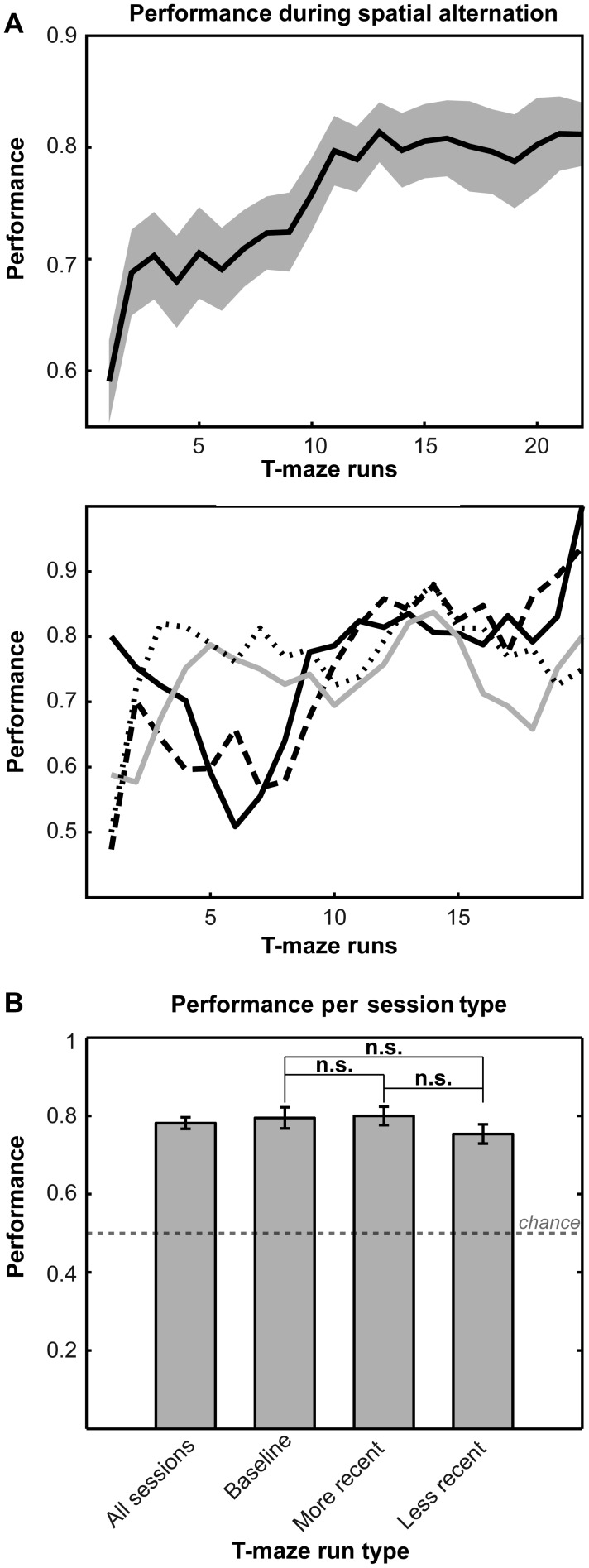
Figure 2.
Performance. (A) Top: Mean performance displayed for all 4 animals showing improvement from 59% to 83% across T-maze runs. Bottom: Individual performance across 20 T-maze runs for rats AC (black), P3 (long black dash), P5 (gray), and P9 (short black dash). (B) Performance does not vary significantly by T-maze run type [(baseline − more recent, P = 0.89); (baseline − less recent, P = 0.48), (more recent − less recent, P = 0.48), 2-sample t-tests with Holm–Bonferroni correction]. Note that more recent (experienced within the last 7 days) and less recent rotations (experienced beyond the last 7 days) are meant to occur on the same testing day in pseudorandomized order (Fig. 1).
Sometimes rats would fatigue or satiate early during the fourth recording session of the day making it difficult to reach criterion (at least 30 correct laps), and these particular sessions were removed from further analysis. As with other sessions, T-maze orientations used in these sessions were still considered “more recent” if used again for further recordings during the subsequent week. We instituted a resting period between recording the second and third T-maze sessions, lasting no longer than 1 h, to help with fatigue and satiation. Occasionally, we recorded an additional T-maze session (classified as more recent) prior to running the final open field with animals running the T-maze in either the more recent or less recent orientation they experienced earlier in the day.
Rotation Selection
T-maze rotations were conducted at quantiles of 45°, providing 8 possible orientations per T-maze session. Rotation distributions for both more recent (Supplementary Fig. 1A) and less recent (Supplementary Fig. 1B) sessions were not significantly different (P = 0.26, Kuiper's test). Because of the limitation of 8 possible rotations, we selected 1 week or 7 days as a cutoff between more and less recent sessions. When recording daily, this definition provides at least 1 orientation that the animal had not seen in the prior week. If more than 1 orientation for less recent or more recent rotations was available, the orientation was pseudorandomly selected, resulting in a counterbalanced distribution of more and less recent rotations (Supplementary Fig. 1C).
Spatial Alternation Task
The rats performed the task on a recessed T-maze sharing the boundaries of the open-field arena (Fig. 1C). Both T-maze and open-field arenas had outer perimeter walls with height of 60 cm, and the environment floor was covered with a TirePlast rubber mat (TAP Plastics, San Francisco, CA, USA), which provided a waterproof, nonadsorbent textured surface with high-spatial frequency preventing the floor from acting as a geographic cue during recording sessions. To create the T-maze task, prism-shaped walls were inserted into the open field with walls that measured 51 cm in height, and a blocking wall across the arena diagonal measured 60 cm in height. The prisms and blocking wall produced a T-maze with stem length of 88 cm, width across both reward arms of 176 cm, and track width of 10 cm. Diagonal return arms allowed rats to run from the reward sites at the end of each reward arm to the base of the stem. Rats always entered the T-maze from the base and roamed for no more than 2 min prior to recording. Though overhead lights were turned off during recording, the tracking diodes on the head stage provided some illumination around the animal. If the animal could fix to cues outside the recording environment, the most likely cue would have been the curtain separation of the outer environment. In addition, dull noise from air passing through ventilation ducts 7 m from the recording enclosure provided an auditory distal cue to the environment.
A precision pellet dropper (Med-Associates, St. Albans, VT, USA) delivering two 45 mg sucrose pellets (Bio-Serv, Frenchtown, NJ, USA) for correct turns was attached at each reward site. Reward delivery was manually controlled via scripts written in Matlab R2010A (Mathworks, Natick, MA, USA) with each output timestamped to the Neuralynx Digital Acquisition System. The experimenter always stood behind the base of the T-maze stem to view the rat in order to remotely trigger reward presentation.
Three animals were trained prior to surgery for 1–2 weeks in two 1-h sessions daily on the T-maze in relative darkness oriented in a standard 0° position with respect to the distal cues of the environment and the open field. During each session on training day 1, animals ran a sequence of 35 rightward turns, followed by a sequence of 35 leftward turns, during the blockade of the opposite half of the maze. Animals were blocked from retracing their steps should they turn around. On training day 2, the choice point blockade was manually switched between laps to force animals to alternate between reward sites every lap. This procedure continued for training days 2–3. By day 4, the choice point blockade was phased out, and animals were rewarded for correctly alternating between reward sites as they traversed the T-maze in a forward direction (Wood et al. 2000; Lipton et al. 2007). Postsurgery, animals received 1 day of training prior to test recording sessions, again in the standard 0° T-maze orientation.
One animal did not undergo the training procedure till after surgical implantation. In this rat, training proceeded following the prescribed training protocol described above until behavior reached at least 70% after which recording sessions resumed.
Data Analysis Methods
Cluster Cutting and Alignment Across Recording Sessions
Single units were cut manually “offline” after each recording session. Neurons were discriminated by peak amplitude and principal components measures for each waveform (Offline Sorter, Plexon, Dallas, TX, USA). Units with biologically realistic interspike intervals and characteristic spike time autocorrelations were retained (Brandon et al. 2011; Gupta et al. 2012). Waveform stability across T-maze and open-field sessions was confirmed by consistent cluster position and waveform profile during comparison on each electrode as shown in the examples in Figures 3 and 4.
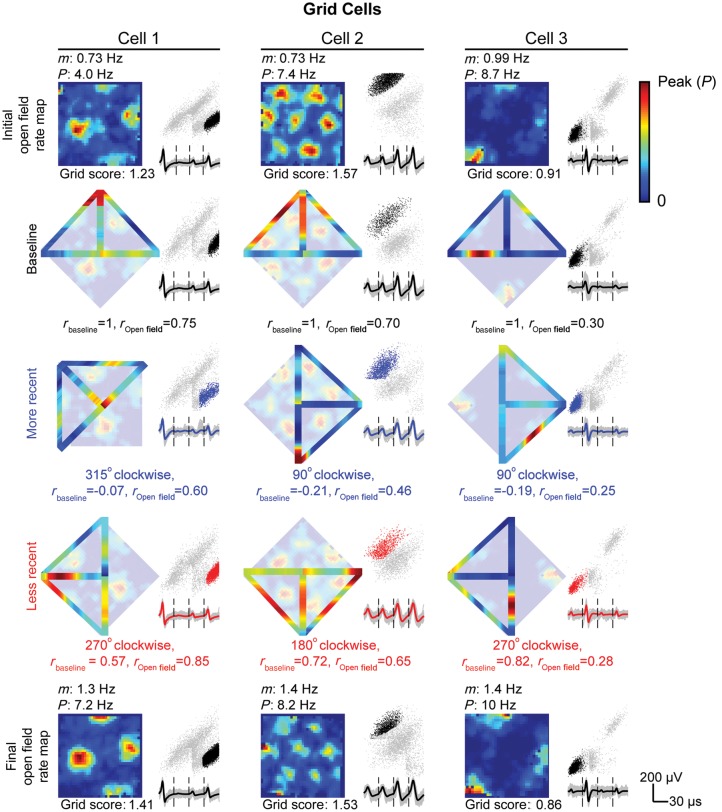
Figure 3.
Example grid cells on the open field and T-maze. Three grid cells are displayed in each column for every open-field and T-maze session conducted. All plots include cluster locations (black dots = open field or baseline T-maze recording, blue dots = more recent T-maze recording, and red dots = less recent T-maze recording) against uncut clusters (gray dots) for peak voltage from electrode 3 versus electrode 2. Beneath each cluster display, mean waveforms from electrodes 1 to 4 (from left to right) are shown. (Rows 1 and 5) Spatial rate map of grid cell firing during the initial (row 1) and final (row 5) 20-min open-field recording with mean (m) and peak (P) firing rate listed above and gridness score listed below. (Rows 2–4) Reconstructed spatial rate map from linearized baseline (row 2), more recent (row 3), or less recent (row 4) T-maze session overlaying initial open-field rate map with absolute rotation, linearized rate map correlation to baseline rate map, rbaseline, and open-field rate map, rOpen field, listed below. The baseline T-maze session is shown in a reference position with the base of the maze pointing north, although no rotation of the outer walls of the environment was performed between initial open-field and baseline T-maze sessions.
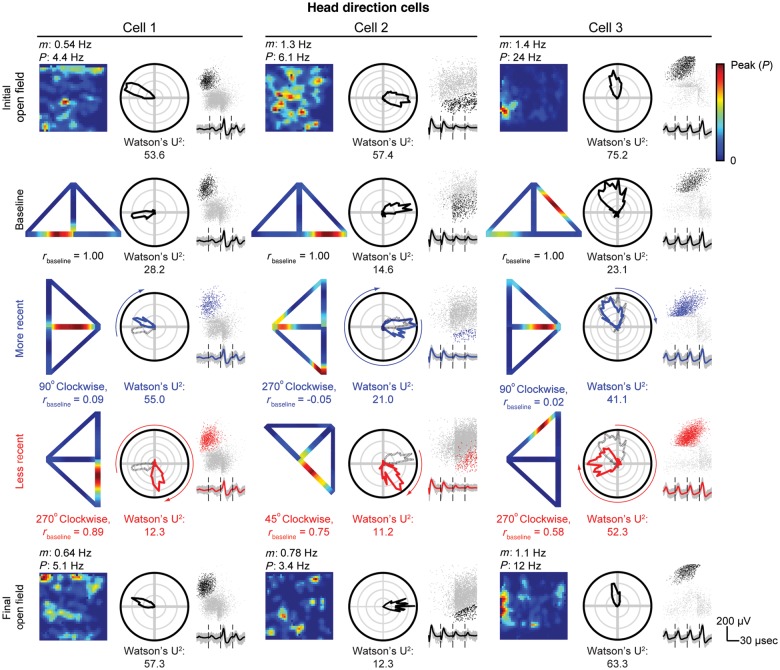
Figure 4.
Example HD cells on the open field and T-maze. Three HD cells are displayed in each column for every open-field and T-maze session conducted. All plots include cluster locations (black dots = open field or baseline T-maze recording, blue dots = more recent T-maze recording, and red dots = less recent T-maze recording) against uncut clusters (gray dots) for peak voltage from electrode 3 versus 2. Beneath each cluster display, mean waveforms from electrodes 1 to 4 (from left to right) are shown. Each panel also includes a polar histogram of PFD. For more recent and less recent T-maze recordings, the baseline preferred direction (gray dashed line) is overlaid with an arrow on the outside of the plot indicating the rotation of the T-maze with respect to the baseline session. (Rows 1 and 5) Spatial rate map of grid cell firing during the initial (row 1) and final (row 5) 20-min open-field recordings with mean (m) and peak (P) firing rate listed above and gridness score listed below. (Rows 2–4) Reconstructed spatial rate map from linearized baseline (row 2), more recent (row 3), or less recent (row 4) T-maze session with linearized rate map correlations to baseline, rbaseline, and the open field, rOpen field, listed below. The baseline T-maze session is shown in a reference position with the base of the maze pointing north, although no rotation of the outer walls of the environment was performed between initial open-field and baseline T-maze sessions.
Position, Direction, and Speed Estimation
The head stage for the unit recording preamplifier has a rostral green light-emitting diode situated 12 cm from a caudal red diode. An animal position was calculated as the centroid of the lit tracking diodes with no other visible light present. Up to 5 lost samples due to shadow effects or reflections near environment boundaries were replaced by linear interpolation and directional data. To quantify the degree of spatial selectivity, rate maps were constructed by calculating the occupancy-normalized firing rate for 3 cm × 3 cm bins of position data followed by smoothing with a pseudo-Gaussian kernel with a 3-cm standard deviation (Figs 3 and 4). Spatial autocorrelations of the smoothed rate map were generated to view spatial periodicity of grid fields using Pearson's product moment correlation coefficient (Sargolini et al. 2006; Brandon et al. 2011; Gupta et al. 2012). The autocorrelations were then used to produce a gridness score using gridness measure 3 from Brandon et al. (2011). This gridness score applies an eccentricity to the traditionally circular ring (Hafting et al. 2005; Sargolini et al. 2006) enclosing up to 6 peaks closest to the center peak of the spatial autocorrelation. The semi-major and semi-minor axes of the returned elliptical ring were subsequently used as metrics of grid field spacing. Running speed was calculated as the difference between computed positions over time.
HD was calculated as the angle between the rostral and caudal diodes. As an analog to spatial rate maps, heading occupancy-normalized polar histograms of the firing rate binned every 6° were produced to screen for the dependence of spiking on the animal's HD. Firing rate histograms were smoothed with a smoothing kernel of 3°. The degree of selectivity was determined via the Watson U2 statistic (Brandon et al. 2011; Gupta et al. 2012). The preferred firing direction (PFD) was taken as the angle of the mean resultant vector of the heading distribution (Taube et al. 1990a, 1990b; Knight et al. 2011; Brandon et al. 2012) calculated using the CircStat Toolbox for Matlab (Berens 2009).
Cell Selection
We categorized each neuron as a “grid cell” or “HD cell.” Neurons with a gridness score greater than zero were considered grid cells. Neurons with negative gridness scores, but with Watson U2 scores greater than 5 were classified as HDs cells (Brandon et al. 2011; Gupta et al. 2012). Analysis of our sample showed that it did not include any cells that show significance for both gridness and HD, that is, conjunctive grid-by-head direction cells (Sargolini et al. 2006).
Linearization
The T-maze was linearized to a 300-cm track covering the full trajectory for each lap of the T-maze. Position zero of this 300-cm track was the beginning and ending at the base of the maze, followed by the central stem (appearing separately for both the left and right turn trials), followed by traversal of the reward arms and return arms. Tracking positions acquired during maze running were all mapped to the nearest pixel of an idealized linear maze template of 1 cm2 bins as previously described (Gupta et al. 2012). For every session, the template was overlaid on the tracking data by identifying the peak in the 2-dimensional cross correlation between the ideal track bitmap and the binary matrix representing bins visited by the animal during that session. Since the cross correlation is only useful for detecting translations of the maze under the camera, the orientation and resolution of the session was manually indicated. Laps were disambiguated into temporal epochs between a rat's departure from the T-maze base (linearized position: 0–8 cm) to the rat's subsequent return at the base.
The sign of the linear position was changed to match the direction of each lap (Huang et al. 2009). Left-reward bound laps are indicated by the negative linear position, and right-reward bound laps are indicated by the positive linear position.
Spatial Correlation Between Baseline and Nonbaseline T-Maze Sessions
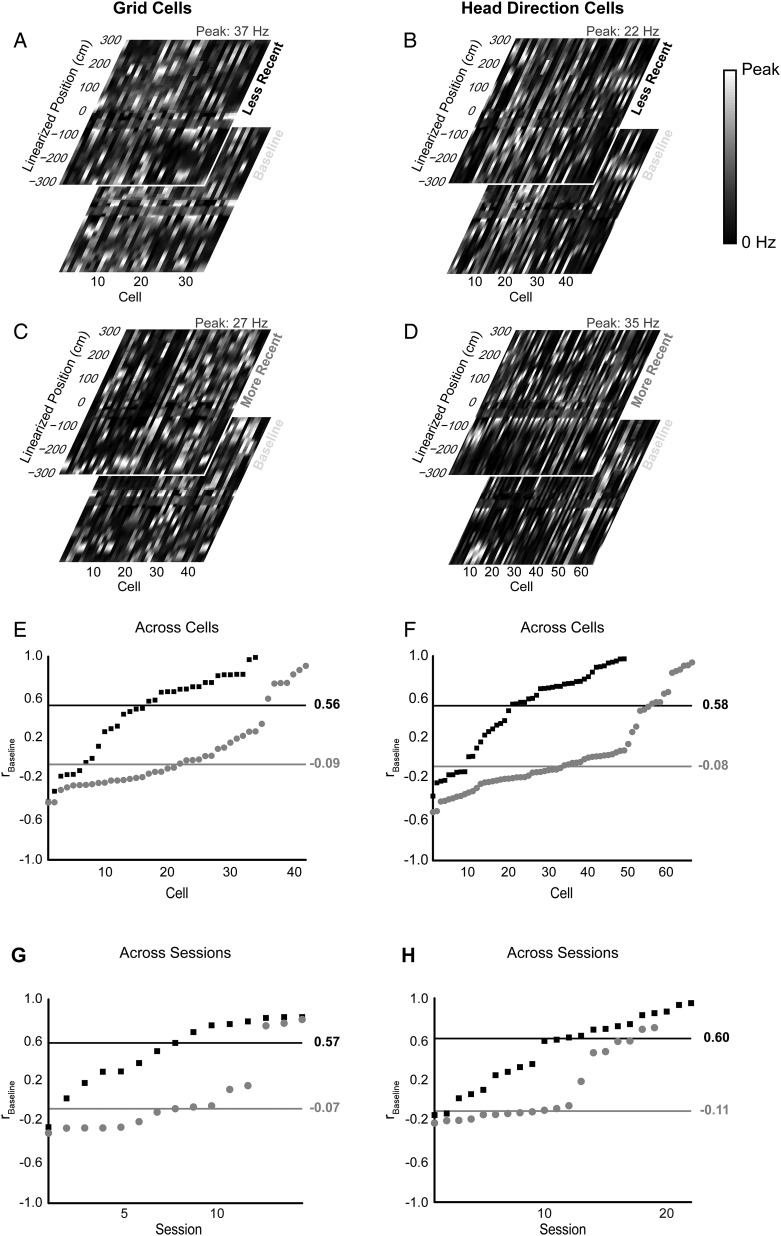
Occupancy-normalized rate maps were generated for all grid and HD cells across the linearized T-maze (Figs 3–5) smoothed with a boxcar window of 3 adjacent bins (2 cm). Rate map positions at positive and negative coordinates were smoothed separately. Special care was taken to smooth positions at the base of the stem at −300 cm (smoothed over −300, −299, and 0 cm), 0 cm (smoothed over −300, 0, and 300 cm), and 300 cm (smoothed over 0, 299, 300 cm) over appropriate windows. These rate maps yielded reconstructed T-maze plots shown in Figures 3 and 4. In Figure 5, linearized rate maps form a vector of firing rates at different linearized positions for baseline T-maze sessions and for less recent or more recent T-maze sessions (Fig. 5A–D). Pearson's correlation coefficient, rbaseline, was evaluated for each baseline vector to its respective more recent or less recent counterpart vector. The resulting distributions of rbaseline are plotted in Figure 5E,F. Because HD cells coherently rotate in a given animal (Taube et al. 1990a, 1990b; Knierim et al. 1995; Hargreaves et al. 2007), the distributions of rbaseline across sessions, instead of across cells, are shown in Figure 5G,H. A 2-sample Kolmogorov–Smirnov test (KS-test) was used to evaluate the significance between more recent and less recent rbaseline values for both grid and HD cells for individual cells and ensembles.
Figure 5.
Linearized rate map correlations for grid and HD cells. Population vectors of linearized rate maps for conditional (less recent and more recent) and baseline T-maze sessions are shown for (A and C) grid cells and (B and D) HD cells. Correlation coefficients between baseline and conditional T-maze sessions, rbaseline, for (E) grid cells and (F) HD cells show significantly higher correlations for the less recent orientation (black rectangles) versus the more recent (gray dots) orientation across all cells (grid cells: P = 3.7 × 10−5, KS-Statistic = 0.521; HD cells: P = 2.5 × 10−7, with KS-Statistic = 0.518; 2-sample KS test). Black and gray horizontal lines indicate a median rbaseline value for less recent and more recent distributions, respectively. Similar profiles are seen when looking at distributions of mean correlations across sessions of simultaneously recorded (G) grid cells and (H) HD cells (grid cells: P = 0.0011, KS-Statistic = 0.667; HD cells: P = 0.0015; KS-Statistic = 0.576; 2-sample KS test). Data ordered by value of rbaseline.
Cluster Quality
Isolation distance and L-ratio (Schmitzer-Torbert et al. 2005) were calculated for every cluster cut during a T-maze session along 12 feature quantities (4 tetrode channels × 3 principal component coefficients). Briefly, isolation distance utilizes the statistical quantity of Mahalanobis distance, D, which more accurately describes distances between clusters in higher-dimensional space compared with Euclidean distance. Isolation distance is the D2 value of the nth closest noise spike for a given cluster with n spikes. L-ratio assumes that cluster spike distributions are multivariate normal resulting in χ2 distributions of D2. For spiking outside a given cluster C, the quantity L(C) is the sum over probabilities for the ith spike not in C to fall outside the distribution of D2. L-ratio is L(C) divided by the number of spikes in C (Schmitzer-Torbert et al. 2005). Supplementary Figure 2 shows isolation distance and L-ratio distributions for clusters reported during baseline and nonbaseline T-maze sessions plotted against rbaseline.
T-Maze Rotation Measure
For computation of T-maze rotation, prior to each T-maze session, a presession video was recorded where 1 of 4 lights would flash on and off for 1 s starting at the base, then the left-reward boundary wall, then the choice point boundary wall, and finally the right-reward boundary wall of the T-maze. Each light was composed of two 660 nm, light-emitting diodes (RadioShack Corp., Fort Worth, TX, USA). The coordinates of the light at the T-maze base were considered the origin. From this origin to the centroid of the 3 remaining light coordinates, a vector for each T-maze session was established, whereby the angle between this and the baseline T-maze session vector established the absolute rotation.
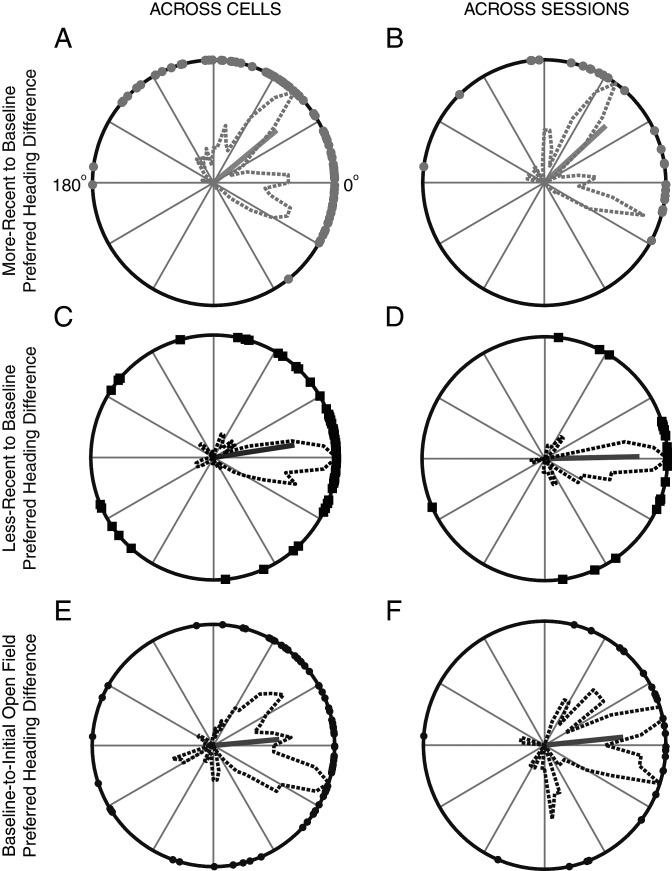
Preferred Heading Difference
The PFD of a HD cell for a given condition (more recent or less recent) was rotated back by an amount equal to the absolute rotation between the baseline T-maze session and the given conditional T-maze session. The difference between this adjusted PFD and the PFD recorded for the same cell during the baseline T-maze session constitutes the preferred heading difference (PHD) for both more recent (Fig. 6A) and less recent (Fig. 6C) conditions. Ninety-five percent confidence intervals for the mean PHD resultant vector angle were calculated for each condition via a circular 1-sample t-test (Berens 2009; Knight et al. 2011). Differences in PHD distributions for more recent and less recent conditions were tested with Kuiper's test (Berens 2009). The mean PHD for simultaneously recorded HD cells across both more recent and less recent T-maze sessions is shown in Figure 6B,D, respectively. Additionally, the PFD of a given HD cell recorded in the baseline T-maze session was compared with its PFD in the initial open field. As the initial open-field and baseline T-maze sessions were not rotated against each other, there was no need to adjust the PFD of an HD cell from either recording session. The distribution of these PFD differences was calculated across cells (Fig. 6E) and across sessions of simultaneously recorded ensembles (Fig. 6F).
Figure 6.
Preferred heading difference. The PHD between the adjusted PFD of a HD cell and the absolute rotation angle relative to the baseline session is plotted for all HD cells recorded during the (A) more recent (mean PHD: 39.3°, 95% confidence interval: [28.6°, 50.1°], mean resultant: 0.67) and (C) less recent (mean PHD: 8.8°, 95% confidence interval: [−4.0°, 21.5°], mean resultant: 0.66) T-maze orientations. Distributions from A and C significantly differ with P = 1.5 × 10−4 (Kuiper's test). Similar plots for mean PHD from ensembles of simultaneously recorded cells across sessions are shown again for the (B) more recent (mean PHD: 42.5°, 95% confidence interval: [21.3°, 63.6°], mean resultant: 0.69) and (D) less recent (mean PHD: 1.2°, 95% confidence interval: [−16.0°, 18.4°], mean resultant: 0.77) conditions. Distributions in B and D significantly differ with P = 0.0026 (Kuiper's test). Distributions of PHD between the baseline T-maze session and the initial open field are also shown (E) across cells (mean error: 5.4°, 95% confidence interval: [−10.8°, 21.5°], mean resultant: 0.55) and (F) across sessions (mean PHD: 5.7°, 95% confidence interval: [−17.0°, 28.4°], mean resultant: 0.65).
Grid Fragmentation Correlation Coefficient
The degree of correlation of a T-maze session to the initial open-field recording was used to indicate the degree of grid cell fragmentation (Derdikman et al. 2009; Whitlock and Derdikman 2012). Baseline T-maze sessions shared the same orientation and alignment of the initial open field and required no further rotation or translation. Alignment of nonbaseline sessions proceeded by rotating these sessions back to the same orientation of the baseline recording. The resulting rotated T-maze session's origin was translated to the origin of the baseline recording aligning the sessions. Regions of no occupancy for spatial rate maps of both the T-maze session and open field were excluded, and the remaining rate map was correlated using Pearson's correlation for 2-dimensional arrays. The resulting correlation coefficient, rOpen field, indicates a lower degree of fragmentation as its value approaches 1.
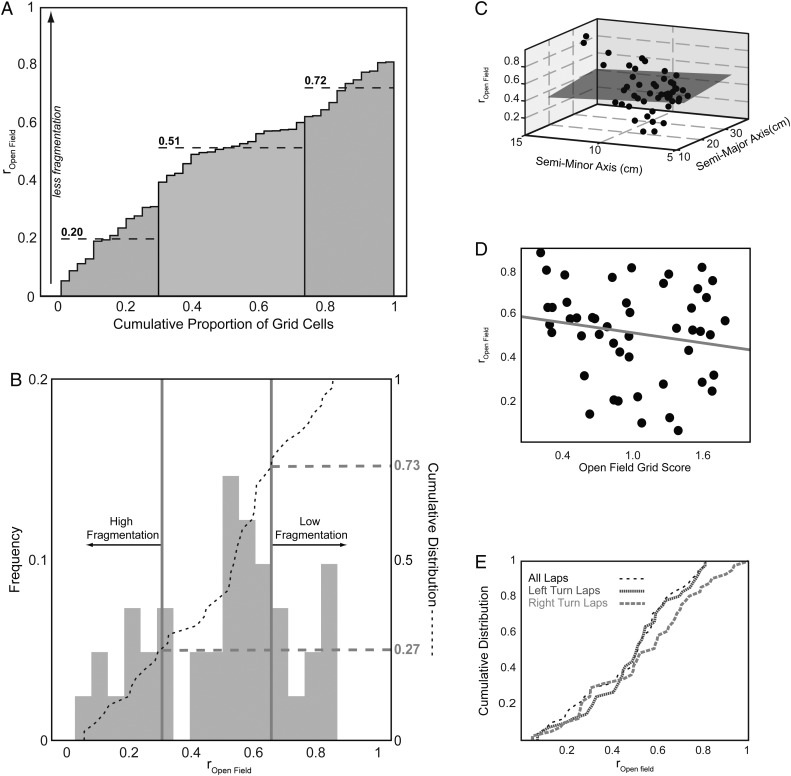
Grid Fragmentation Boundaries and Covariates
The fragmentation metric, rOpen field, follows from Derdikman et al. (2009). However, in that study, the hairpin maze and open-field sessions had nearly 100% overlap, whereas the T-maze sessions used in this study have considerably less. This makes rOpen field vulnerable particularly to undersampled environmental overlap and to grid field realignment. To measure grid field realignment with our T-maze studies, we attempted to identify the proportion of our cells that exhibited the highest propensity to fragment. To determine thresholds to consider grid fields as displaying “high”, “low,” or “intermediate” fragmentation, 2 separate analyses were performed for rOpen field between baseline T-maze and open-field sessions. In Figure 7A, the distribution of rOpen field was clustered into 3 partitions using iterative k-means partitioning, which minimized the squared Euclidean distance to the calculated centroid of each cluster. In Figure 7B, we bootstrapped over 10 000 trials to yield the distribution of each trial's median. A 99% confidence interval was generated by this distribution's empirical cumulative distribution yielding thresholds visible as gray vertical lines in Figure 7B.
Figure 7.
Grid cell fragmentation. (A) Correlation coefficient of grid cells between overlapping baseline T-maze and initial open-field rate maps, rOpen field, clustered via k-means analysis into 3 groups: Low (22% of cells, right group with centroid at 0.72), intermediate (49% of cells, middle group with centroid at 0.51), and high fragmentation groups (29% of cells, left group with centroid at 0.20). (B) Histogram (light gray bars) and cumulative distribution (black dashed line) of rOpen field thresholded into high (27% of cells, rOpen Field < 0.31) and low (27% of cells, rOpen Field > 0.62) fragmentation groups with thresholds (gray vertical lines) determined by a 99% confidence interval of medians bootstrapped over 10 000 trials. rOpen field does not significantly depend on (C) grid spacing measured by semi-major or semi-minor axes (gray plane: R2 = 0.002, P = 0.95) and (D) gridness score (gray line: R2 = 0.03, P = 0.23). (E) Cumulative distribution of rOpen Field for all laps (black, low-frequency dashed line), left turn laps (dark gray, high-frequency dashed line), or right turn laps (light gray, intermediate-frequency dashed line) indicates no significant trajectory dependence for the propensity of grid cells to fragment (all laps − left laps: P = 0.90; all laps − right laps: P = 0.73; left laps − right laps: P = 0.75; KS test with Holm–Bonferroni correction).
More recent and less recent T-maze sessions were excluded from these analyses because reduced overlap between a T-maze and its rotated open field may be confounded by other recency-related effects. Other covariates like grid spacing (as measured by semi-major and semi-minor axes retrieved during gridness score calculation, Fig. 7C), gridness score (Fig. 7D), and left- or right-reward bound trajectories were also considered (Fig. 7E).
Turning Point Analysis
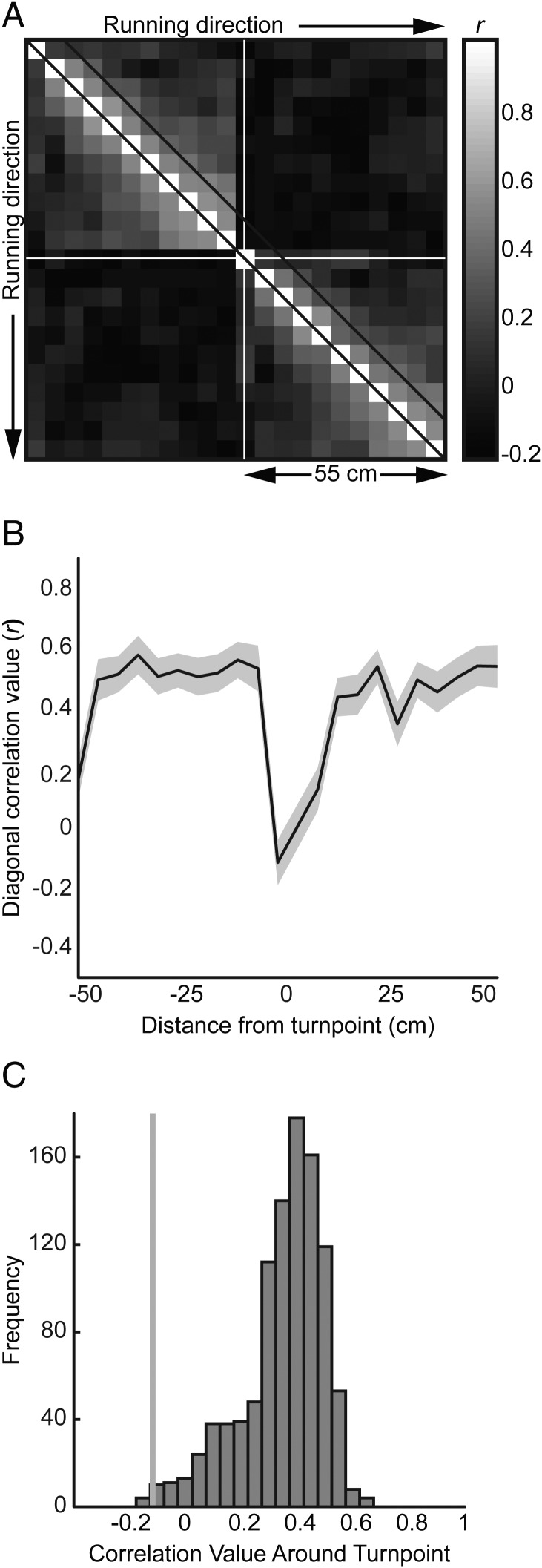
A spatial correlation matrix of firing rate population vectors was generated to see whether we could reproduce the turning point effect observed in Derdikman et al. (2009). Each population vector was centered at a turning point (position = 0) on the T-maze extending 55 cm around this point in 5-cm bins. The turning point was determined as the point of maximum curvature (k) calculated as:
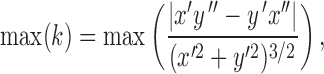 |
where x and y are the path segment coordinates (Derdikman et al. 2009). This point of maximum curvature was then mapped to its corresponding linearized coordinate. The occupancy-normalized firing rate was calculated for each bin of the population vector triggered on the turning point separately for both the left- and right-reward bound laps. Each population vector was normalized to the median firing rate. For each grid cell, a correlation matrix was generated taking the Pearson correlation of firing rates for every pair of spatial bins. The mean correlation for each pairwise combination of bins is plotted in Figure 8A across all grid cells, with the diagonal of the matrix plotted in Figure 8B (standard error of the mean shaded around the mean diagonal). We also repeated the shuffling Monte Carlo procedure of Derdikman et al. (2009). Correlation matrices were constructed by correlating each rate vector triggered at a specific position to a rate vector triggered at another position. These positions were randomly selected to be within 40 cm of an actual turning point. This procedure was repeated 1000 times yielding the distribution of correlation coefficients (r) at the trigger point shown in Figure 8C.
Figure 8.
Turning point analysis. (A) Spatial correlation matrix of firing rate population vectors centered at the turning point (white cross-hairs) in 5 cm bins, 55 cm around the turning point across all grid cells. Diagonal lines represent boundaries of first adjacent bin to each linear position. This diagonal is plotted in (B) with standard error of the mean (SEM) shaded in gray and minimal correlation just before 0 cm (the turning point). (C) Monte Carlo distribution of 1000 correlation coefficients between a trigger point (randomly chosen to within 40 cm of an actual maze turning point) and its adjacent bin. The gray line shows the minimum correlation (r = −0.12) with P < 0.007 with respect to the distribution.
Results
Behavioral Accuracy
All animals (n = 4) were trained on the spatial alternation task (Fig. 1B,C) prior to testing, which allowed them to start above chance (chance = 50%) on the first testing T-maze run. In Figure 2A (top), the mean accuracy (correct alternating laps/total laps) improved from a minimum of 59% to a maximum of 83% among 4 rats similar to Lipton et al. (2007). Individual rat performance reached 100% for some testing T-maze runs (Fig. 2A, bottom). Across T-maze recency conditions (Fig. 2B), there were no significant differences in mean performance between baseline and more recent T-maze trials (P = 0.89), baseline and less recent T-maze trials (P = 0.48), and more recent and less recent T-maze trials (P = 0.48) using 2-sample t-tests with Holm–Bonferroni correction. All rats performed at approximately the same level.
Cell Type
We recorded a total of 124 cells in the mEC (Fig. 1A) from 4 animals comprised of 42 grid cells and 82 HD cells. Figures 3 and 4 show examples of grid and HD cells, respectively, from the animals performing alternation. Spatial tuning properties of both cell types from this population remained consistent comparing between initial and final open-field sessions (Supplementary Fig. 3). Two-dimensional Pearson's correlation coefficients between initial and final open-field sessions for grid cells are above r = 0.56 (Supplementary Fig. 3A). HD cells do not vary their PFD by more than 10° between open-field sessions (Supplementary Fig. 3B).
Correlations Between T-Maze Sessions
In Figure 3, linearized firing rate maps are reconstructed into T-mazes to show the spatial firing rate of grid cells relative to the firing patterns in initial open-field recording. For illustration, we focus on cell 1 in Figure 3, which tends to fire maximally at the base of the T-maze and near the choice point. After a more recent 315° clockwise rotation, the grid cell no longer fires maximally at the base of the maze resulting in rbaseline = 0.07, a low correlation between the more recent and baseline linearized rate map. Rotating the T-maze into a less recent 270° clockwise position, rotates the peak firing rate back to the base of the maze and near the choice point yielding rbaseline = 0.57. Linearized firing rate maps of grid and HD cells recorded on the T-maze are shown in Figure 5A–D as population vectors for baseline, less recent, and more recent T-maze orientations. Correlating pairwise population vectors (e.g., baseline − less recent or baseline − more recent) results in 2 distributions of rbaseline for both grid (Fig. 5E) and HD cells (Fig. 5F). These distributions differ significantly for both cell types based on recency condition of the T-maze with a median less recent rbaseline = 0.56 and more recent rbaseline = −0.09 for grid cells (P = 3.7 × 10−5, 2-sample KS-test), and a median less recent rbaseline = 0.58 and more recent rbaseline = −0.08 for HD cells (P = 2.5 × 10−7, 2-sample KS-test). Across recording sessions, the distributions for the mean correlation coefficient for grid cells (Fig. 5G, 15 more recent sessions in gray and 15 less recent sessions in black) and HD cells (Fig. 5H, 19 more recent sessions in gray and 22 less recent sessions in black) are also significantly different with similar profiles to Figure 5E,F, respectively (grid cells: P = 0.0011 and HD cells: P = 0.0015, 2-sample KS-test).
Preferred Heading Difference
Reconstructed T-maze rate maps were generated for HD cells in Figure 4. As shown in cell 1, the polar HD plots reveal an incomplete rotation for this HD cell given a more recent 90° clockwise rotation of the T-maze. However, in the less recent 270° clockwise rotation, the PFD of the HD cell rotates with the T-maze. By adjusting the PFD of the more recent or less recent T-maze session back by the angle of rotation with respect to the baseline session, the PHDs for cell 1 in the more recent and less recent rotations were computed as 37.2° and 1.5°, respectively. This metric was applied across all HD cells (Fig. 6A,C) and across all simultaneously recorded ensembles of HD cells (Fig. 6B,D). The polar histograms across cells and cell ensembles are similar, with more recent rotations (Fig. 6A,B) generating a bimodal distribution of PHD with a mean of 39.3–42.5°, significantly differing from 0° across cells (95% confidence interval: [28.6°, 50.1°]) and sessions (95% confidence interval: [21.3°, 63.6°]). For less recent rotations, PHD distributions (mean of 1.2–8.8°) do not significantly differ from 0° across cells (95% confidence interval: [−4.0°, 21.5°], Fig. 6C) and sessions (95% confidence interval: [−16.0°, 18.4°], Fig. 6D). More and less recent rotation distributions significantly differ from each other across all cells (P = 1.5 × 10−4, Kuiper's test) and cell ensembles (P = 0.0026, Kuiper's test). These distributions are visible across cells for each animal individually as shown in Supplementary Figure 4.
We also looked at heading differences in PFD of HD cells between the initial open field and baseline T-maze recordings, again across cells (Fig. 6E) and sessions (Fig. 6F). Both distributions show a mean of 5.4–5.7°, which does not significantly differ from 0° across cells (95% confidence interval: [−10.8°, 21.5°]), and across sessions (95% confidence interval: [−17.0°, 28.4°]).
Grid Cell Fragmentation
Because grid cells have previously been noted to fragment in multicompartment environments (Derdikman et al. 2009), we sought to quantify the proportion of our grid cells that exhibited such fragmentation behavior. Grid cell firing rate maps (see Fig. 3 and Supplementary Fig. 5) recorded on the open-field and the baseline T-maze sessions were correlated generating a distribution of rOpen field. When rOpen field = 1, the open-field firing rate map and the baseline T-maze session rate map match perfectly indicating no fragmentation. When rOpen field = 0, there is no overlap in the rate maps between the open-field and baseline T-maze sessions indicating very high fragmentation. Using a k-means clustering algorithm (Fig. 7A), cells were clustered into 1 of the 3 groups: “Low” (22% of cells, rOpen field ≥ 0.59), “intermediate” (49% of cells, 0.34 < rOpen field < 0.59), and “high” (29% of cells, rOpen field ≤ 0.34) fragmentation. These proportions were similar to proportions generated via a bootstrapping procedure where 27%, 46%, and 27% of trial medians fell into low (rOpen field > 0.62), intermediate (0.31 ≤ rOpen field ≤ 0.62), or high (rOpen field < 0.31) fragmentation groups (Fig. 7B), respectively.
Covariates of grid spacing (as measured by semi-major and semi-minor axes of grid autocorrelation, see Materials and Methods) and gridness score were selected as possible predictors for rOpen field. Linear regression fits for grid spacing (Fig. 7C) and gridness score (Fig. 7D), however, show nonsignificant, weak correlations (grid spacing: R2 = 0.002, P = 0.95 and gridness score: R2 = 0.03, P = 0.23).
As in Derdikman et al. (2009) where trajectories from East-to-West and West-to-East were distinguished, we differentiated firing rate maps based on the trajectory of left- or right-reward bound turns. The empirical cumulative distribution function of rOpen field for all laps, left turn laps, and right turn laps do not significantly differ (Fig. 7E; all laps − left laps: P = 0.90; all laps − right laps: P = 0.73; left laps − right laps: P = 0.75; KS-test with Holm–Bonferroni correction). This suggests that the tendency to fragment is independent of trajectory.
Turning Point Analysis
As suggested by Derdikman et al. (2009), if rats tend to maintain separate maze arm representations via fragmentation, then adjacent bin positions should be highly correlated except at the boundary between maze compartments. In Figure 8A, a spatial correlation matrix of population rate vectors across 5 cm spatial bins extending 55 cm in each direction from a turning point is shown. The white diagonal lines show the correlations of adjacent bins. Typically, the mean correlation falls within 0.2–0.6 (Fig. 8B). However, the turning point (position = 0 cm) shows the minimum correlation with r = −0.12 (P < 0.007 with respect to the distribution in Fig. 8C). Therefore, this result would corroborate previous analysis, suggesting that turning points are candidate locations for resetting compartment representation.
Discussion
The current experiment tests animals as they perform a goal-directed, spatial alternation task in a T-maze that shares the physical space and overlapping features with the open-field arena. All sessions were recorded in the same curtain-enclosed space in relative darkness. During more recent rotations, both grid fields and HD tuning did not rotate with the T-maze as often as they rotated with the maze during less recent rotations. In addition to spatial rotations of the tuning curves of both HD and grid cells, the grid fields of grid cells showed varying degrees of fragmentation on the T-maze relative to firing patterns seen during open-field recordings. We characterized the proportion of our cells that fragmented and looked at covariates of grid spacing, gridness score, and trajectory specificity, but found that these measures ultimately did not predict a cell's propensity to fragment. These findings are discussed further below.
Implications of Recency for Spatial Tuning
The results suggest a strong influence after T-maze rotations to less recent orientations of the local T-maze cues on the PFD of HD cells and on grid cell firing fields. Figure 5E–H show stronger spatial rate map correlations of less recent rotations to baseline T-maze orientations for both grid and HD cells. Similarly, the PHD of HD cells in the less recent condition shows a tight tuning curve around 0° in Figure 6C,D, indicating that these cells stay in register with the local cues of the T-maze when the maze rotates to these less recent orientations. This matches findings from Hargreaves et al. (2007) where sorting session number across rats foraging in open arenas suggests that low-numbered sessions (“less recent”) showed tuning curves for CA1 place cells and parahippocampal spatial cells in register with the proximal environment before and after rotating the environment. Higher-numbered sessions (“more recent”) appeared more likely to yield spatial tuning curves in register with a bucket controlling idiothetic cues or unmanaged background (distal) cues. Our results also match findings from Dudchenko and Zinyuk (2005), where 90° rotations of a T-maze elicited commensurate shifts in the PFDs of ADN thalamic HD cells. Salience of the local T-maze cues during less recent rotations may be expected given the nature of the environment. For either recency condition, the animal was subject to high boundary walls, near complete darkness, and floors scrubbed clean between recording sessions. During less recent T-maze rotations, the animal may focus more on the task-relevant local cues like the pellet droppers and geometry of the T-maze turn locations. Over time, the influence of these cues may wane in favor of idiothetic cues or distal cues (e.g., the curtain separation through which the rat enters). This follows from the previous studies of hippocampal place cells (Brown and Skaggs 2002; Renaudineau et al. 2007) where rotating salient local cues could dominate over distal cues in rotating place fields. Studies of HD cells from the thalamus and postsubiculum have also shown the dominance of local cues if the maze is directionally polarizing (Dudchenko and Davidson 2002) or geometrically asymmetric (Clark et al. 2012) and if distal cues appear lacking (Dudchenko and Davidson 2002), criteria likely achieved during the less recent maze conditions.
More recent rotations typically elicited incomplete rotations of grid firing fields and HD PFDs. Figure 5E–H show weak spatial rate map correlations between more recent rotations and baseline T-maze orientations for both grid and HD cells. The lack of correlation exhibited by the HD cells tracks the bimodal distribution of PHD with 2 lobes centered at 52° and −18° (Fig. 6A,B). The lack of complete rotation during more recent rotations indicates a possible changed “reference frame” over repeated exposures in which the animal updates its initial sense of direction either from the distal cues in the room or from path integration rather than from the local cues of the rotated maze (Gothard, Skaggs, Moore, et al. 1996; Touretzky and Redish 1996; Nitz 2009). In the recording environment, the most salient visual distal cue could be the curtain separation through which every animal passed before entering the T-maze. Other distal cues include auditory noise from air ventilation ducts in the building. The salience of extramaze cues, or path integration of idiothetic cues, may increase over multiple experiences of the same rotation via increased learning of distal landmark control (Knierim et al. 1995; Taube and Burton 1995). Anchoring to a landmark outside the maze is more typical for thalamic HD cells (Zugaro et al. 2001, 2004).
With regard to grid cells, it is difficult to determine whether the change in firing patterns during more recent T-maze rotation sessions is either global remapping or an incomplete rotation. This is reminiscent of Skaggs and McNaughton (1998) who showed that CA1 place fields can be maintained or remap in different, but visually similar, environments. An alternative hypothesis for our observations is that learning reference frame instability is enhanced by more recent rotation experiences. As suggested in Skaggs and McNaughton (1998), partial remapping of place cells may be caused by incomplete orthogonalization of 2 cognitive maps due to translating an animal between 2 visually identical environments. Because the particular rotations we produced occur more closely and packed together in time during more recent T-maze rotation sessions, the stability of the reference frame will become more salient. Unlike Skaggs and McNaughton (1998), however, this hypothesis would also suggest that a decrease in learned reference stability should result in significant decreases in navigation-based performance, which, as measured by behavioral accuracy, was not seen.
Bimodal Distribution of PHD in More Recent Rotations
More recent rotations showed 2 distributions of PHD centered at 52° and −18° (Fig. 6A,B). The −18° lobe may represent minor errors the animals make staying in register with the local maze cues in a few sessions. The 52° lobe, however, could indicate errors in the animals' perception. This error varies across animals and within animals ranging from 38° to 115° and centering between 40° and 60° (Supplementary Fig. 4). We reasoned that this difference in error might stem from dissimilar rotation sequences between recency conditions, and possibly to unbalanced changes in rotation angle between conditions. However, Supplementary Figure 1 demonstrates that rotation sequence distribution is both counter-balanced and not significantly different based on recency condition. Because rotations were performed in quantiles of 45°, if there is learned instability in the animals' reference frame, they may incorrectly judge a rotation by a fixed amount like 45°. Though for this to occur, the animal would need to expect a 45° shift, which is unlikely as animal's faced pseudorandom selections of rotation angles.
The cue conflict between distal and local cues during more recent rotation sessions may explain the bimodal distribution seen in Figure 6A,B. Distal and local cue controls have been seen in hippocampal CA1 place cells where double rotation of distal extramaze and local intramaze cues revealed a subset of recorded place cells that fix either with distal or local cues (Shapiro et al. 1997; Knierim 2002; Yoganarasimha et al. 2006). Presumably distal cues provide orientation information that may enter the mEC and hippocampus from visual inputs that integrate with postsubiculum HD signal (Goodridge and Taube 1997; Yoganarasimha et al. 2006). Local cues may act more like object/item inputs entering the hippocampus via the lateral entorhinal cortex (Yoganarasimha et al. 2006). Proximal cues control CA3 cells much more coherently (Lee et al. 2004), whereas distal cues dominate in control over thalamic HD cells in double-rotation cue-conflict studies (Knierim 2002; Yoganarasimha et al. 2006). The dependence on distal cues in these upstream HD cells to set the initial orientation of the cognitive map is independent of feedback from the mEC (Clark and Taube 2011) and hippocampus (Golob and Taube 1997). It is possible for downstream HD cells, and co-localized grid cells, to have split cue-conflict representations like CA1 place cells.
The relative importance of the local reference frame may also be more prominent in goal-directed behavior rather than during random foraging (Young et al. 1994; Shapiro et al. 1997). As cue conflict grows with repeated exposure to more recent rotations, task demands and cue perception dictate which of either local or distal cues anchors the reference frame (Taube and Burton 1995). Fenton et al. (2010) have demonstrated that spike rate variability as animals pass through place fields switches back and forth from distal and local cue controls on the order of seconds. This suggests that the animal's moment-to-moment attention processes are constantly deciphering the relevant cues. With more recent experience to a particular T-maze rotation, the surrounding environment or path integration of idiothetic cues may have increased influence.
Grid Field Fragmentation
As reported by Derdikman et al. (2009), grid cells in the mEC will fragment their grid fields as rats run a hairpin maze that shares the boundaries of the open-field recordings. We also saw similar grid field fragmentation and used the correlation of the baseline T-maze recording to the initial open-field sessions as a fragmentation metric. This comparison did not require any realignment or rotation as the 2 sessions' outer boundary walls did not change between these 2 recordings. Figure 7A,B indicate that 27–29% of grid cells exhibited “high” fragmentation. The propensity to fragment was independent of grid spacing (Fig. 7C) and gridness score (Fig. 7D), suggesting a mechanism that induces fragmentation that does not depend on the intrinsic properties of the neuron. In addition, the propensity to fragment did not differ for left-turn or right-turn laps similar to the East-to-West and West-to-East laps in Derdikman et al. (2009). The fragmentation phenomenon strongly suggests that adjacent maze compartments should act more like interconnected submaps. These submaps should have spatial bins that are highly correlated to adjacent bins, except at the ends of these submaps where turning points are encountered. This resetting hypothesis, first suggested in the hairpin task (Derdikman et al. 2009), is also suggested in the continuous spatial alternation T-maze task as seen in Figure 8A–C.
A major difference between the hairpin maze and the T-maze, however, is the amount of overlap to the underlying open field. The hairpin maze's increased overlap gives it better sampling of the overall environmental similarity, allowing for better a test of correlation. Notwithstanding, fragmentation can still be seen in T-maze environments, but must be qualified along a continuum to isolate those grid cells that strongly fragment as opposed to those that do not. It is encouraging, even with our limited overlap between T-maze and open field, that we see the same turning point behavior as previously demonstrated (Derdikman et al. 2009).
The interconnected submaps generated by the fragmented compartments may serve as a metric for path equivalency in each compartment. This could allow solution of behavioral tasks via path integration that calculates distances to sequential turning points (Derdikman et al. 2009; Whitlock and Derdikman 2012) and requires inputs to grid cells that convey environment geometry. Within the mEC and subiculum are boundary vector cells (BVCs) that fire action potentials as a function of environmental boundaries (Solstad et al. 2008; Lever et al. 2009). BVCs can convey boundary information to grid cells as models have demonstrated (Burgess and O'Keefe 2011).
Interestingly, we also find that mEC HD cells remain stable between open-field and baseline T-maze recordings (Fig. 6E,F) corroborating Whitlock and Derdikman (2012). The potential for HD cell firing without entorhinal grid cell firing has previously been shown in studies using lesions of entorhinal cortex (Clark and Taube 2011), inactivation of medial septum (Brandon et al. 2011; Koenig et al. 2011), and recordings during development showing full maturation of HD cells prior to adult grid cell development (Langston et al. 2010; Wills et al. 2010). In a goal-directed paradigm, maze subcompartments may store discrete metrics of maze segments with varying levels of fragmentation potentially based on distance-to-goal, possibly using look-ahead strategies suggested by decoding analysis from Gupta et al. (2012). The conjunction of an invariant landmark-based HD signal (Taube and Burton 1995) with these compartmental metrics may more efficiently reduce errors accumulated via update from idiothetic cues, limiting the number of resets required with a path integration strategy.
Cell Categorization
We report 42 grid cells and 82 HD cells in this study. None of the other spatial cell types seen in the mEC like “conjunctive” grid by HD cells (Sargolini et al. 2006) are reported, and this may simply reflect a different anatomical distribution of recording sites compared with previous recordings. Unlike Sargolini et al. (2006), our tetrode positions may be more superficial. As the histology shows, most of our tetrodes reach layer II from where many of our grid cell recordings originate. It is telling that as we turn tetrodes from deeper layers to superficial layers, we record fewer HD cells and more “pure” grid cells, in line with previous observations. We observed spike clusters from conjunctive grid cells, but like clusters from other cell types, we were not necessarily able to retain those clusters across intraday recording sessions, and they were therefore excluded from the analyses.
Supplementary Material
Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.
Funding
This work was supported by the NIH R01 MH61492, R01 MH60013, and the ONR MURI N00014-10-1-0936.
Supplementary Material
Notes
We thank Andrew Bogaard for programming assistance, Tyler Ware for technical assistance, and Dr Sung Eun Yang for helping to construct environments. We also thank Dr Eric A. Zilli for constructive comments on the text. Conflict of Interest: None declared.
References
- Barry C, Ginzberg LL, O'Keefe J, Burgess N. Grid cell firing patterns signal environmental novelty by expansion. Proc Natl Acad Sci USA. 2012;109:17687–92. doi: 10.1073/pnas.1209918109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barry C, Hayman R, Burgess N, Jeffery KJ. Experience-dependent rescaling of entorhinal grids. Nat Neurosci. 2007;10:682–684. doi: 10.1038/nn1905. [DOI] [PubMed] [Google Scholar]
- Berens P. CircStat: a MATLAB toolbox for circular statistics. J Stat Softw. 2009;31:1–21. [Google Scholar]
- Brandon MP, Bogaard AR, Andrews CM, Hasselmo ME. Head direction cells in the postsubiculum do not show replay of prior waking sequences during sleep. Hippocampus. 2012;22:604–618. doi: 10.1002/hipo.20924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science. 2011;332:595–599. doi: 10.1126/science.1201652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JE, Skaggs WE. Concordant and discordant coding of spatial location in populations of hippocampal CA1 pyramidal cells. J Neurophysiol. 2002;88:1605–1613. doi: 10.1152/jn.2002.88.4.1605. [DOI] [PubMed] [Google Scholar]
- Burgess N, O'Keefe J. Models of place and grid cell firing and theta rhythmicity. Curr Opin Neurobiol. 2011;21:734–744. doi: 10.1016/j.conb.2011.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung A, Sturzl W, Zeil J, Cheng K. The information content of panoramic images II: view-based navigation in nonrectangular experimental arenas. J Exp Psychol Anim Behav Process. 2008;34:15–30. doi: 10.1037/0097-7403.34.1.15. [DOI] [PubMed] [Google Scholar]
- Clark BJ, Harris MJ, Taube JS. Control of anterodorsal thalamic head direction cells by environmental boundaries: comparison with conflicting distal landmarks. Hippocampus. 2012;22:172–187. doi: 10.1002/hipo.20880. [DOI] [PubMed] [Google Scholar]
- Clark BJ, Taube JS. Intact landmark control and angular path integration by head direction cells in the anterodorsal thalamus after lesions of the medial entorhinal cortex. Hippocampus. 2011;21:767–782. doi: 10.1002/hipo.20874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derdikman D, Whitlock JR, Tsao A, Fyhn M, Hafting T, Moser MB, Moser EI. Fragmentation of grid cell maps in a multicompartment environment. Nat Neurosci. 2009;12:1325–1332. doi: 10.1038/nn.2396. [DOI] [PubMed] [Google Scholar]
- Dudchenko PA, Davidson M. Rats use a sense of direction to alternate on T-mazes located in adjacent rooms. Anim Cogn. 2002;5:115–118. doi: 10.1007/s10071-002-0134-y. [DOI] [PubMed] [Google Scholar]
- Dudchenko PA, Zinyuk LE. The formation of cognitive maps of adjacent environments: evidence from the head direction cell system. Behav Neurosci. 2005;119:1511–1523. doi: 10.1037/0735-7044.119.6.1511. [DOI] [PubMed] [Google Scholar]
- Fenton AA, Lytton WW, Barry JM, Lenck-Santini PP, Zinyuk LE, Kubik S, Bures J, Poucet B, Muller RU, Olypher AV. Attention-like modulation of hippocampus place cell discharge. J Neurosci. 2010;30:4613–4625. doi: 10.1523/JNEUROSCI.5576-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Witter MP, Moser EI, Moser MB. Spatial representation in the entorhinal cortex. Science. 2004;305:1258–1264. doi: 10.1126/science.1099901. [DOI] [PubMed] [Google Scholar]
- Golob EJ, Taube JS. Head direction cells and episodic spatial information in rats without a hippocampus. Proc Natl Acad Sci USA. 1997;94:7645–7650. doi: 10.1073/pnas.94.14.7645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodridge JP, Taube JS. Interaction between the postsubiculum and anterior thalamus in the generation of head direction cell activity. J Neurosci. 1997;17:9315–9330. doi: 10.1523/JNEUROSCI.17-23-09315.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gothard KM, Skaggs WE, McNaughton BL. Dynamics of mismatch correction in the hippocampal ensemble code for space: interaction between path integration and environmental cues. J Neurosci. 1996;16:8027–8040. doi: 10.1523/JNEUROSCI.16-24-08027.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gothard KM, Skaggs WE, Moore KM, McNaughton BL. Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J Neurosci. 1996;16:823–835. doi: 10.1523/JNEUROSCI.16-02-00823.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham M, Good MA, McGregor A, Pearce JM. Spatial learning based on the shape of the environment is influenced by properties of the objects forming the shape. J Exp Psychol Anim Behav Process. 2006;32:44–59. doi: 10.1037/0097-7403.32.1.44. [DOI] [PubMed] [Google Scholar]
- Gupta K, Keller LA, Hasselmo ME. Reduced spiking in entorhinal cortex during the delay period of a cued spatial response task. Learn Mem. 2012;19:219–230. doi: 10.1101/lm.025866.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hargreaves EL, Yoganarasimha D, Knierim JJ. Cohesiveness of spatial and directional representations recorded from neural ensembles in the anterior thalamus, parasubiculum, medial entorhinal cortex, and hippocampus. Hippocampus. 2007;17:826–841. doi: 10.1002/hipo.20316. [DOI] [PubMed] [Google Scholar]
- Huang Y, Brandon MP, Griffin AL, Hasselmo ME, Eden UT. Decoding movement trajectories through a T-maze using point process filters applied to place field data from rat hippocampal region CA1. Neural Comput. 2009;21:3305–3334. doi: 10.1162/neco.2009.10-08-893. [DOI] [PubMed] [Google Scholar]
- Knierim JJ. Dynamic interactions between local surface cues, distal landmarks, and intrinsic circuitry in hippocampal place cells. J Neurosci. 2002;22:6254–6264. doi: 10.1523/JNEUROSCI.22-14-06254.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knierim JJ, Hamilton DA. Framing spatial cognition: neural representations of proximal and distal frames of reference and their roles in navigation. Physiol Rev. 2011;91:1245–1279. doi: 10.1152/physrev.00021.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knierim JJ, Kudrimoti HS, McNaughton BL. Place cells, head direction cells, and the learning of landmark stability. J Neurosci. 1995;15:1648–1659. doi: 10.1523/JNEUROSCI.15-03-01648.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight R, Hayman R, Lin Ginzberg L, Jeffery K. Geometric cues influence head direction cells only weakly in nondisoriented rats. J Neurosci. 2011;31:15681–15692. doi: 10.1523/JNEUROSCI.2257-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig J, Linder AN, Leutgeb JK, Leutgeb S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science. 2011;332:592–595. doi: 10.1126/science.1201685. [DOI] [PubMed] [Google Scholar]
- Komorowski RW, Manns JR, Eichenbaum H. Robust conjunctive item-place coding by hippocampal neurons parallels learning what happens where. J Neurosci. 2009;29:9918–9929. doi: 10.1523/JNEUROSCI.1378-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, Moser MB. Development of the spatial representation system in the rat. Science. 2010;328:1576–1580. doi: 10.1126/science.1188210. [DOI] [PubMed] [Google Scholar]
- Lee I, Yoganarasimha D, Rao G, Knierim JJ. Comparison of population coherence of place cells in hippocampal subfields CA1 and CA3. Nature. 2004;430:456–459. doi: 10.1038/nature02739. [DOI] [PubMed] [Google Scholar]
- Lever C, Burton S, Jeewajee A, O'Keefe J, Burgess N. Boundary vector cells in the subiculum of the hippocampal formation. J Neurosci. 2009;29:9771–9777. doi: 10.1523/JNEUROSCI.1319-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton PA, White JA, Eichenbaum H. Disambiguation of overlapping experiences by neurons in the medial entorhinal cortex. J Neurosci. 2007;27:5787–5795. doi: 10.1523/JNEUROSCI.1063-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNaughton BL, Barnes CA, Gerrard JL, Gothard K, Jung MW, Knierim JJ, Kudrimoti H, Qin Y, Skaggs WE, Suster M, et al. Deciphering the hippocampal polyglot: the hippocampus as a path integration system. J Exp Biol. 1996;199:173–185. doi: 10.1242/jeb.199.1.173. [DOI] [PubMed] [Google Scholar]
- Nitz D. Parietal cortex, navigation, and the construction of arbitrary reference frames for spatial information. Neurobiol Learn Mem. 2009;91:179–185. doi: 10.1016/j.nlm.2008.08.007. [DOI] [PubMed] [Google Scholar]
- O'Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- Renaudineau S, Poucet B, Save E. Flexible use of proximal objects and distal cues by hippocampal place cells. Hippocampus. 2007;17:381–395. doi: 10.1002/hipo.20277. [DOI] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, Redish AD. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience. 2005;131:1–11. doi: 10.1016/j.neuroscience.2004.09.066. [DOI] [PubMed] [Google Scholar]
- Shapiro ML, Tanila H, Eichenbaum H. Cues that hippocampal place cells encode: dynamic and hierarchical representation of local and distal stimuli. Hippocampus. 1997;7:624–642. doi: 10.1002/(SICI)1098-1063(1997)7:6&lt;624::AID-HIPO5&gt;3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL. Spatial firing properties of hippocampal CA1 populations in an environment containing two visually identical regions. J Neurosci. 1998;18:8455–8466. doi: 10.1523/JNEUROSCI.18-20-08455.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
- Stackman RW, Golob EJ, Bassett JP, Taube JS. Passive transport disrupts directional path integration by rat head direction cells. J Neurophysiol. 2003;90:2862–2874. doi: 10.1152/jn.00346.2003. [DOI] [PubMed] [Google Scholar]
- Sturzl W, Cheung A, Cheng K, Zeil J. The information content of panoramic images I: the rotational errors and the similarity of views in rectangular experimental arenas. J Exp Psychol Anim Behav Process. 2008;34:1–14. doi: 10.1037/0097-7403.34.1.1. [DOI] [PubMed] [Google Scholar]
- Taube JS, Burton HL. Head direction cell activity monitored in a novel environment and during a cue conflict situation. J Neurophysiol. 1995;74:1953–1971. doi: 10.1152/jn.1995.74.5.1953. [DOI] [PubMed] [Google Scholar]
- Taube JS, Muller RU, Ranck JB., Jr Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. J Neurosci. 1990a;10:420–435. doi: 10.1523/JNEUROSCI.10-02-00420.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taube JS, Muller RU, Ranck JB., Jr Head-direction cells recorded from the postsubiculum in freely moving rats. II. Effects of environmental manipulations. J Neurosci. 1990b;10:436–447. doi: 10.1523/JNEUROSCI.10-02-00436.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touretzky DS, Redish AD. Theory of rodent navigation based on interacting representations of space. Hippocampus. 1996;6:247–270. doi: 10.1002/(SICI)1098-1063(1996)6:3&lt;247::AID-HIPO4&gt;3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- Whitlock JR, Derdikman D. Head direction maps remain stable despite grid map fragmentation. Front Neural Circuits. 2012;6:9. doi: 10.3389/fncir.2012.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wills TJ, Cacucci F, Burgess N, O'Keefe J. Development of the hippocampal cognitive map in preweanling rats. Science. 2010;328:1573–1576. doi: 10.1126/science.1188224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood ER, Dudchenko PA, Robitsek RJ, Eichenbaum H. Hippocampal neurons encode information about different types of memory episodes occurring in the same location. Neuron. 2000;27:623–633. doi: 10.1016/S0896-6273(00)00071-4. [DOI] [PubMed] [Google Scholar]
- Yoganarasimha D, Yu X, Knierim JJ. Head direction cell representations maintain internal coherence during conflicting proximal and distal cue rotations: comparison with hippocampal place cells. J Neurosci. 2006;26:622–631. doi: 10.1523/JNEUROSCI.3885-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young BJ, Fox GD, Eichenbaum H. Correlates of hippocampal complex-spike cell activity in rats performing a nonspatial radial maze task. J Neurosci. 1994;14:6553–6563. doi: 10.1523/JNEUROSCI.14-11-06553.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zugaro MB, Arleo A, Dejean C, Burguiere E, Khamassi M, Wiener SI. Rat anterodorsal thalamic head direction neurons depend upon dynamic visual signals to select anchoring landmark cues. Eur J Neurosci. 2004;20:530–536. doi: 10.1111/j.1460-9568.2004.03512.x. [DOI] [PubMed] [Google Scholar]
- Zugaro MB, Berthoz A, Wiener SI. Background, but not foreground, spatial cues are taken as references for head direction responses by rat anterodorsal thalamus neurons. J Neurosci. 2001;21:RC154. doi: 10.1523/JNEUROSCI.21-14-j0001.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.