Predicting the Dynamics of Protein Abundance

Abstract

Protein synthesis is finely regulated across all organisms, from bacteria to humans, and its integrity underpins many important processes. Emerging evidence suggests that the dynamic range of protein abundance is greater than that observed at the transcript level. Technological breakthroughs now mean that sequencing-based measurement of mRNA levels is routine, but protocols for measuring protein abundance remain both complex and expensive. This paper introduces a Bayesian network that integrates transcriptomic and proteomic data to predict protein abundance and to model the effects of its determinants. We aim to use this model to follow a molecular response over time, from condition-specific data, in order to understand adaptation during processes such as the cell cycle. With microarray data now available for many conditions, the general utility of a protein abundance predictor is broad.

Whereas most quantitative proteomics studies have focused on higher organisms, we developed a predictive model of protein abundance for both Saccharomyces cerevisiae and Schizosaccharomyces pombe to explore the latitude at the protein level. Our predictor primarily relies on mRNA level, mRNA–protein interaction, mRNA folding energy and half-life, and tRNA adaptation. The combination of key features, allowing for the low certainty and uneven coverage of experimental observations, gives comparatively minor but robust prediction accuracy. The model substantially improved the analysis of protein regulation during the cell cycle: predicted protein abundance identified twice as many cell-cycle-associated proteins as experimental mRNA levels. Predicted protein abundance was more dynamic than observed mRNA expression, agreeing with experimental protein abundance from a human cell line. We illustrate how the same model can be used to predict the folding energy of mRNA when protein abundance is available, lending credence to the emerging view that mRNA folding affects translation efficiency. The software and data used in this research are available at http://bioinf.scmb.uq.edu.au/proteinabundance/.

Proteins are complex molecules with many cellular functions, including signaling, amplification and transduction, control of gene expression, and molecular transport. The integrity of these processes depends on protein synthesis, which is finely regulated across all organisms, from bacteria to humans. Protein synthesis, including the processing, degradation, and folding of mRNA, is mediated by the transcriptional machinery. Translation of proteins from mRNA is followed by localization, modification, and degradation. We define protein abundance as the number of copies of a protein molecule in a cell, which is a result of the dynamic balance among the aforementioned processes.

There is a growing range of technologies that contribute toward the measurement of mRNA and protein expression. mRNA levels can be measured using microarrays and RNA sequencing. Modern protein assays include conventional two-dimensional electrophoresis, mass spectrometry (MS)-based shotgun proteomics experiments, and high-throughput cell imaging (1–5). Although sequencing-based measurement of mRNA levels has become a routine task, current protocols for measuring protein expression are less routine and remain both complex and expensive. Because of the relative difficulty of obtaining protein abundance measurements, it is not unusual to use expression levels of mRNA as a stopgap for quantifying protein abundance. This implicitly assumes that mRNA abundance is the sole determinant of protein abundance (6–8). An expectation of a linear relationship between mRNA expression and protein abundance is inaccurate in general (9).

Proteome-wide abundance illustrates the dynamic range of cellular activity during important processes such as the cell cycle (10) or in response to stress (11). The cell cycle is the series of stages that drives the division and replication of a cell. The regulation of gene expression and protein abundance is coordinated to ensure the integrity of the progression through each of these stages (12). Defects can lead to catastrophic events, such as cell death and cancer. These events involve hundreds of molecules, and understanding them on the basis of mRNA expression levels alone is inadequate.

In order to predict (and ultimately model the determinants of) protein abundance under various conditions, we need methods that can integrate mRNA expression and complementary information on events and factors that modulate the rate of protein synthesis. Such methods would allow us to follow a molecular response over time, from condition-specific data, to understand the cellular behavior and what regulates it. With microarray data widely available, for many conditions, the utility of a protein abundance predictor is appreciable. With quantitative proteomics still in its infancy, and with emerging evidence in human pointing to the importance of understanding cellular dynamics at the protein level, this paper explores the extent to which protein abundance is more informative than transcript expression level in simpler eukaryotes. We specifically investigate the dynamic range of predicted protein abundance during the yeast cell cycle, for which there are currently no experimental data available.

To understand how abundance changes as a result of transcriptional and translational activities, we need to integrate transcriptomic and proteomic data (i.e. features that shed light on the pre- and post-translational states of genes). Obvious candidates include the expressed level of a transcript, its specific RNA sequence, its potential to fold into secondary structures, its codon usage, the availability of required tRNA, and its potential for interaction with relevant proteins, such as RNA binding proteins (RBPs).¹ Several studies have explored correlations between protein abundance and a multitude of transcript features, including molecular weight, codon adaption (also tRNA adaptation), half-life, folding energy, and various sequence features (6, 13–15).

The tRNA adaptation index (tAI) (16) represents the adaptation of a coding sequence relative to the tRNA pool of an organism. It is used to capture the effects of tRNA abundance and mRNA sequence on the translation rate (6, 16). The folding of the mRNA transcript can influence protein translation (14). For instance, it has been noted that the mRNA folding energy influences the rate of viral protein translation (17). It is known that interactions between mRNA and RBPs mediate post-transcriptional levels of regulation, such as transcript turnover and translational control (18, 19). Protein half-life captures the degradation side of the abundance equation. Its incorporation into a simple quantitative model for protein production has been shown to improve the prediction of steady-state protein abundance (20). The half-life of a protein is in turn dictated by numerous factors and events that can be used as input to a separate protein “stability” model (21).

A number of methods currently exist that can be used to predict protein abundance. Most methods make use of protein abundance and/or the protein translation rate inside the cell using mRNA expression levels as the principal predictive feature (7, 15, 22). Tuller and colleagues (6) used linear regression to integrate mRNA expression, tAI, and the evolutionary rate (ER) of the transcripts. (The evolutionary rate refers to the rate at which the mRNA sequence evolves (23).) The prediction accuracy of these tools is encouraging but leaves ample room for improvement, as outlined below.

The development of models of protein abundance from data faces several challenges. Firstly, real biological data have missing values, mostly because of technological shortcomings and constraints on experimental design. Most datasets are limited in coverage; this problem is especially true for protein abundance, which is typically measured at subcellular scales. Because of the restrictions of the many data-driven analyses, computational methods fail to interrogate and cross-reference datasets that are incomplete and that are not perfectly overlapping. Currently available models and studies on protein abundance prediction (6, 13–15) do not incorporate data with missing values; instead they are trained on the intersection of the datasets, which diminishes as the number of sources increases. Secondly, existing methods fall short in terms of transparency or interpretability; there are many factors that influence protein abundance that are not taken into account. In order to understand how protein translation is influenced by post-transcriptional and pre-translational events, we need a model that explains its predictions in terms of relevant features, or cellular events.

It has become clear that probabilistic methods, such Bayesian networks, can address realities of biological data, in terms of both their (uncertain) integration and their (incomplete) coverage (24, 25). To make the most of current transcriptomic and proteomic data, we developed a Bayesian network model that links transcriptional, post-transcriptional, and pre- and post-translational factors and events to predict protein abundance even in the absence of complete data. To understand how various factors influence protein abundance, we integrated mRNA–RBP interactions with mRNA sequence and expression levels and studied their effect on predictions. To investigate how accurate the model is, we collected and evaluated its predictions for large-scale datasets from Saccharomyces cerevisiae and Schizosaccharomyces pombe. In Bayesian networks, all predictions can be explained in terms of the features represented in the model, even when they are not observed. By predicting mRNA folding energy using the same model, we illustrate the flexibility that probabilistic inference affords.

To understand how proteome-wide abundance changes in specific conditions, we made use of microarray data collected across the cell cycle and predicted the abundance of proteins at each cell cycle stage. We aim to show that, compared with actual mRNA expression levels, predicted protein abundance more faithfully represents the extent of change we expect to see during the yeast cell cycle. We aim to demonstrate that abundance plays the same important role observed previously for human (10).

EXPERIMENTAL PROCEDURES

Model Training and Inference

Bayesian networks are probabilistic graphical models in which nodes represent (random) variables and their conditional dependences are indicated by directed arcs from “parent” to “child” nodes. Each node represents a feature of the model and can be considered as either an input or an output of the model. Variables are either discrete or continuous (real-valued). A node for a variable with discrete parents is a conditional probability table, in which each entry is a multinomial distribution (a discrete child node) or a Gaussian density (a continuous child node). A node for a continuous variable with continuous parents is a Gaussian density whose mean is a linear function of its parents' variables. Multiple continuous parents can be grouped into a single vector-valued node, representing a linear function of the multiple variables.

The full joint probability distribution for all of the variables Y₁ = y₁,Y₂ = y₂, …, Y_n = y_n can be calculated by taking the product of the conditional probabilities of the random variables in the network; P(y₁,y₂, …, y_n) = ${\displaystyle \prod _{i=1}^N\left(P\left(y_i|pa\left(Y_i\right)\right)\right)}$ where pa(Y_i) is the set of “parents” of Y_i (as indicated by the direction of edges, parent to child). From the joint probability, using marginalization, it is possible to determine any conditional probability that involves a subset of the variables (including latent variables). We use the variable x to (interchangeably) represent a single gene, transcript, ORF, or protein (as they are identified in a variety of datasets). To predict the protein abundance (PA), we infer the probability of PA(x)|e, where e is the available evidence for the query transcript or ORF x (i.e. a set of instantiated variables that represent the features). Similarly, to predict the mRNA folding energy (mF) given e, we infer the probability of mF(x)|e.

The parameters of the conditional probabilities are learned from data using Expectation-Maximization (26).

Features and Datasets

All of the features identified and discussed below are incorporated as nodes into our Bayesian network.

Protein Abundance PA(x)

We explored the prediction of protein abundance for two yeast species, S. cerevisiae and S. pombe. For S. cerevisiae, we used multiple sources of protein abundance data based on four large-scale experimental sets, hereinafter referred to as G2003 (27), N2006-YEPD (for yeast grown in rich media), N2006-SD (grown in minimal media) (5), and L2011 (28).

Tuller and colleagues observed that the translational efficiency (measured as the ratio of protein abundance to mRNA level) stayed constant in different growth conditions for budding yeast (6). They therefore suggested that data from different growth conditions can be combined after normalization. To determine the value assigned to PA(x), we first used an approach similar to that of Zur and Tuller and determined the average protein abundance across sources, renormalized across proteins and log-transformed (initially including only proteins for which we had data from at least three sources).

For S. pombe, we used protein abundance data from a study by Marguerat and colleagues (29) collected for proliferating and quiescent cells, hereinafter referred to as M2012-P and M2012-Q, respectively. These data were normalized in the same way as those for S. cerevisiae.

mRNA Expression: mRNA(x)

Two datasets, from research by Ingolia and colleagues (29, 30) and Wang and colleagues (31), contain mRNA expression levels for S. cerevisiae. Like Zur and Tuller, we initially discarded the transcripts for which we did not have data from both of these resources (14). We then normalized each dataset (dividing by its mean) and averaged the expression levels of both datasets. The final data were the log-transformed averaged expression levels taken from 4778 transcripts.

For S. pombe, we used the large-scale mRNA expression datasets constructed by Marguerat and colleagues (matching the protein abundance data above) (29). Following the procedure for S. cerevisiae, we normalized and log-transformed 6856 and 6943 transcript levels in cellular proliferation and quiescence states, respectively.

tRNA Adaptation Index tAI(x)

For a transcript x, tAI is defined based on its codon usage, as given in Equation 1 (13).

where lx is the total number of codons in transcript x and w_ik is the “relative adaptiveness” value (see Ref. 13) of the codon defined by the kth trinucleotide in transcript x.

Protein and mRNA Half-life: pHL(x) and mHL(x)

The half-life values of 5177 S. cerevisiae mRNAs were taken from a study by Shalem and colleagues (32). The half-life values of 3751 proteins were taken from a study by Belle and colleagues (20). For S. pombe, the half-life values of 4775 transcripts were taken from work by Marguerat and colleagues (29). Using InParanoid (33), we identified 2856 S. pombe orthologs of S. cerevisiae proteins from the study by Belle and colleagues. Half-life measurements were log-transformed for both species.

mRNA Fold Energy: mF(x)

Kertesz and colleagues (34) developed a strategy referred to as Parallel Analysis of RNA Structure (PARS), in which fragments of RNAs were treated with structure-specific ribonucleases. RNases S1 and V1 were used to determine whether a nucleotide was in a single- or double-stranded conformation, respectively. Specifically, Kertesz and colleagues used the ratio of the scores derived from the two conformationally exclusive ribonucleases. Similar to Zur and Tuller, we averaged the PARS scores of all of the nucleotides in S. cerevisiae transcripts to calculate mF(x) (14). For S. pombe, we identified the orthologs of S. cerevisiae transcripts using InParanoid (33) (accessed September 2012) and transferred PARS scores accordingly.

mRNA–RBP Interaction: RBP(x)

In order to study the relationship between mRNA and RBPs, we experimentally determined the interaction of 40 RBPs with budding yeast (S. cerevisiae) transcripts (35). Many mRNAs interact with multiple RBPs, and ∼70% of the yeast transcripts interact with RBPs. We note that there are 13,264 interactions in the datasets, with a single mRNA having a maximum of 14 RBP interactions.

To define the RBP(x) feature, we first divided the mRNAs into four classes based on the interaction data. Class 1 represented transcripts with no evidence of RBP interaction. Class 2 represented transcripts with evidence of one or two interactions. Class 3 represented transcripts with a minimum of three and a maximum of four interactions. Class 4 included transcripts with evidence of more than four interactions. We defined RBP(x) ∈ {class1,class2,class3,class4}. We note that the numbers of S. cerevisiae transcripts were 2220, 2069, 1663, and 765 for classes 1 through 4, respectively.

For evidence of mRNA–RBP interactions in S. pombe, we identified orthologous transcripts that interact with RBPs in S. cerevisiae. We used all 2856 S. pombe and S. cerevisiae ortholog pairs in InParanoid (33) (accessed September 2012).

Analysis of Cell Cycle Data

To investigate the enrichment of properties in cell cycle data (actual mRNA and predicted protein abundance), we used the expression values provided by Cyclebase, referred to as Pramila-38. These data were initially log₂–transformed and then centered at zero (the mean was subtracted from all time points) and adjusted so that the standard deviation was 1 across the entire experiment.

We used the yeast proteome, redundancy reduced to contain less than 90% sequence similarity (36). We divided the resulting ∼5600 proteins into two groups based on the predicted abundance fold change (FC) across the cell cycle: “positive” if FC > 4 and “negative” if FC ≤ 4. FC = abs[(PA(x)_max−PA(x)_min)/PA(x)_min] represents the maximum and minimum predicted abundance over a complete cycle. Similarly, as a reference, we divided the ∼5600 proteins into two groups based on fold change for the protein's mRNA across the cell cycle. We adjusted the mRNA expression fold-change threshold to keep the same proportions of positive versus negative: positive if FC > 2.84 and negative if FC ≤ 2.84.

We performed a statistical analysis using YeastMine (37) on both mRNA fold change and abundance fold change sets as follows. We counted the number of proteins in the positive and negative groups, distinguishing proteins that had a specific Gene Ontology term from those that did not. The null hypothesis was that proteins in both groups (stated above) do not differ in terms of their assigned properties. We used the hypergeometric test to establish the p value, the total probability of observing data as extreme or more extreme, given that the null hypothesis is true. We also determined the E-value by performing a Bonferroni multiple test correction.

RESULTS

A Bayesian Network Model of Protein Abundance

Our Bayesian network model (shown in Fig. 1) integrates features that are derived from multiple sources: nucleic acid sequence, mRNA expression, protein expression, interaction between mRNA and RNA binding proteins, mRNA fold, and mRNA and protein half-life. Thus, the inputs (and outputs) of the model are a combination of discrete and continuous-valued features. They are also a combination of features that are condition-invariant and depend only on sequence, such as the tAI, or condition-variant, including mRNA expression level and protein abundance.

Fig. 1.

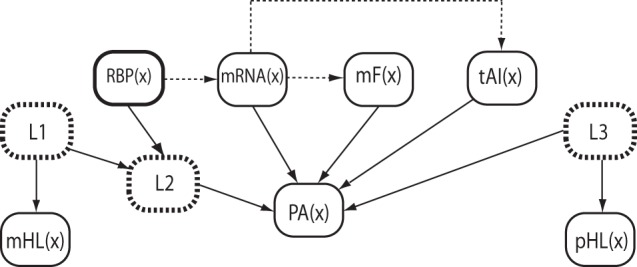
The Bayesian network model of protein abundance. The nodes are shown as rounded rectangles with arrows representing causal relationships from parent to child (dotted arrows are effectively excluded once the value of the child is specified). The main random variable is PA(x), representing protein abundance for a transcript or ORF x. Latent nodes are shown with dashed outlines, and discrete nodes have thicker outlines than continuous nodes. Each observable (nonlatent) node is also labeled with its data source.

PA(x) is a continuous-valued node that represents protein abundance, which we are interested in making predictions about. To do so, the model incorporates the level of expression (mRNA(x)), the relative tRNA abundance (tAI(x)), mRNA half-life (mHL(x)), and the folding energy (mF(x)) of a transcript x. In addition, the model includes RBP(x), which represents interaction with RBPs, and the half-life of the resulting protein pHL(x).

A major advantage of Bayesian networks is that we can incorporate biological knowledge about dependences among the features by virtue of how nodes are connected. We can also include nodes for latent (unobserved) features that capture putative events in the system we are modeling (for which no measurements are available). For example, it has been shown that mRNA expression (and also its folding) and tAI correlate with protein abundance (14). In our model, we linked mRNA(x) with PA(x) and mF(x) by expecting that a strong fold of a transcript would influence (improve) its expression and/or facilitate translation (14). We also added a direct influence between PA(x) and mF(x) and tAI(x), linking transcription with protein translation. Protein abundance is modulated by the interaction of mRNA with RBPs. Therefore, we added an indirect relationship between RBP(x) and PA(x) via a latent Boolean variable (shown with a dotted outline in Fig. 1) to represent two distinct labeled modes of interaction. The modes were determined during training with Expectation-Maximization.

To improve our ability to predict steady-state protein abundance, we added the protein and mRNA half-life nodes (pHL(x) and mHL(x), respectively). These nodes have latent Boolean parents connected to the PA(x) node, indicating an indirect relationship between mRNA/protein degradation and protein translation.

Bayesian networks are capable of inferring missing values given variables that are observed. We added edges (dotted in Fig. 1) to enforce the complementarity between the variables when some of the features are unknown. Because the mRNA sequence determines the adaptation of tRNAs, we added a link between mRNA(x) and tAI(x). We added a link between RBP(x) and mRNA(x) to model the post-transcriptional events. We note that if the data for all of the features are known, then the additional dotted relations (see Fig. 1) do not affect the PA(x) node. We can also infer mRNA(x) and mF(x) if their values are not observed.

Accuracy of Abundance Prediction

We first trained the Bayesian network and tested it in terms of the accuracy of predicted protein abundance. In this section, we report all results using 6-fold cross-validation for evaluating the model: the dataset is split into six subsets, with one subset kept aside for testing and the remaining five used for training. To evaluate the accuracy of predictions of protein abundance (and also folding energy), we relied on the Spearman rank correlation coefficient ρ. We wish to emphasize that correlation is not an ideal indicator of an ability to model the “dynamics” of protein abundance, but it helps to evaluate the influence of individual features in simple, single-condition scenarios. Indeed, we expect both condition-invariant features such as tAI and condition-variant features such as mRNA level to weakly correlate with protein abundance, but we also expect that these features contribute in qualitatively different and potentially complementary ways. Spearman correlation will not be able to distinguish between those ways. Later tests aim to resolve this.

We tested our model on the S. cerevisiae (G2003, N2006-YEPD, N2006-SD, and L2011) and S. pombe datasets (M2012-P and M2012-Q) both in combined form and separately. When combined, the cross-validated Spearman correlation coefficients for protein abundance were ρ = 0.77 and 0.74 for S. cerevisiae and S. pombe, respectively. We then tested our model on the separate sets for S. cerevisiae, keeping the other features in the model the same. The cross-validated Spearman correlation coefficients for predicting protein abundance were ρ = 0.61, 0.67, 0.66, and 0.70 for G2003, N2006-YEPD, N2006-SD, and L2011, respectively.

For reference, Tuller and colleagues proposed two linear predictors (hereinafter referred to as Tuller-1 and Tuller-2 (6)), shown in Equations 2 and 3.

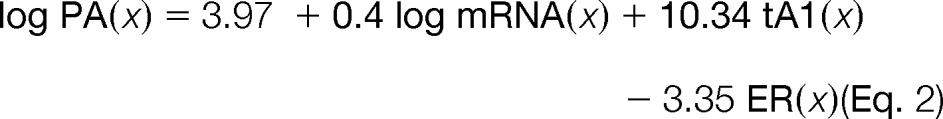On the combined protein abundance data (for which measurements were averaged across conditions), Tuller-1 achieved ρ = 0.74 and 0.75 for S. cerevisiae and S. pombe, respectively. On the same data, Tuller-2 achieved ρ = 0.73 and 0.73 for S. cerevisiae and S. pombe, respectively.

When Tuller-1 was tested on all four datasets separately, we obtained ρ values of 0.64, 0.67, 0.65, and 0.69 for G2003, N2006-YEPD, N2006-SD, and L2011, respectively. Similarly, when we tested Tuller-2, ρ equaled 0.63, 0.65, 0.64, and 0.69, respectively. (It is worth noting that coefficients in Tuller-1 and Tuller-2 as shown in Equations 2 and 3 were optimized on the same protein abundance data as used for testing. The only exception was the dataset from Lee and colleagues (28), which was added to the test by us.)

Yeast proteins are expressed at different rates under different physiological conditions, such as proliferating and quiescent states (29). It is thus enlightening to investigate predicted protein abundance under such conditions. We tested our model (trained on the proliferating state; M2012-P) on the quiescent-state mRNA expression data of S. pombe (all other features remained constant under the two conditions), comparing predictions with observations in M2012-Q. Nodes without observed values were left unspecified, and we inferred PA(x). The model predicted the protein abundance of the quiescent cell with ρ = 0.63, which indicates that our model behaved accurately in a condition for which it was not trained.

Determinants of Abundance

In practice, because of the technical limitations and constraints on the experimental design, all of the features are not always available for each transcript. We first trained our Bayesian network model on datasets for which we had data for all features. We then explored the impact and contribution of different features on the prediction of protein abundance. In Table I we show the accuracies of the model trained on the combined data for S. cerevisiae but using only a subset of the input features (as indicated).

Table I. Spearman rank correlation of predicted PA(x) with varying inclusion of features. All tests were performed using 6-fold cross validation.

Features used in model	S. cerevisiae data					S. pombe data M2012
	Combined	G2003	N2006-YEPD	N2006-SD	L2011
tAI(x)	0.71 ± 0.03	0.59 ± 0.04	0.61 ± 0.05	0.61 ± 0.03	0.68 ± 0.03	0.66 ± 0.11
mRNA(x)	0.61 ± 0.03	0.50 ± 0.03	0.59 ± 0.05	0.52 ± 0.09	0.53 ± 0.04	0.71 ± 0.10
mF(x)	0.63 ± 0.02	0.49 ± 0.03	0.59 ± 0.01	0.56 ± 0.06	0.57 ± 0.03	0.53 ± 0.09
tAI(x), mRNA(x)	0.75 ± 0.03	0.60 ± 0.03	0.66 ± 0.03	0.64 ± 0.04	0.67 ± 0.04	0.73 ± 0.10
tAI(x), mRNA(x), mF(x)	0.77 ± 0.03	0.61 ± 0.03	0.67 ± 0.03	0.62 ± 0.04	0.69 ± 0.02	0.74 ± 0.09
tAI(x), mRNA(x), mF(x), RBP(x)	0.77 ± 0.03	0.61 ± 0.03	0.67 ± 0.03	0.62 ± 0.04	0.69 ± 0.02	0.74 ± 0.09
tAI(x), mRNA(x), mF(x), RBP(x), mHL(x), pHL(x)	0.77 ± 0.03	0.61 ± 0.04	0.67 ± 0.03	0.61 ± 0.04	0.69 ± 0.02	0.74 ± 0.09
tAI(x), RBP(x), mHL(x), pHL(x)	0.71 ± 0.04	0.59 ± 0.05	0.61 ± 0.05	0.59 ± 0.04	0.68 ± 0.02	0.62 ± 0.11
tAI(x), mRNA(x), RBP(x)	0.75 ± 0.03	0.60 ± 0.03	0.66 ± 0.03	0.64 ± 0.04	0.67 ± 0.03	0.73 ± 0.10
mF(x), tAI(x)	0.76 ± 0.03	0.60 ± 0.03	0.67 ± 0.03	0.66 ± 0.04	0.70 ± 0.04	0.67 ± 0.09
mF(x), RBP(x)	0.64 ± 0.03	0.49 ± 0.04	0.58 ± 0.02	0.56 ± 0.06	0.56 ± 0.04	0.51 ± 0.11
mF(x), RBP(x), mHL(x), pHL(x)	0.64 ± 0.03	0.50 ± 0.03	0.58 ± 0.02	0.54 ± 0.05	0.57 ± 0.04	0.50 ± 0.11
mF(x), RBP(x), tAI(x)	0.76 ± 0.03	0.60 ± 0.04	0.67 ± 0.04	0.64 ± 0.03	0.69 ± 0.04	0.66 ± 0.09
RBP(x)	0.10 ± 0.04	0.15 ± 0.07	0.14 ± 0.08	0.13 ± 0.07	0.10 ± 0.07	0.09 ± 0.07
mHL(x), pHL(x)	0.13 ± 0.04	0.24 ± 0.08	0.11 ± 0.09	0.06 ± 0.12	0.10 ± 0.09	0.00 ± 0.18

When exploring the contribution of data features by using each dataset separately, we consistently identified the same features (see Table I). The three features that yielded the greatest accuracy in predicting protein abundance were tAI(x), mRNA(x), and mF(x). Zur and Tuller previously observed that these features correlate individually with protein abundance (14). When tAI(x), mRNA(x), and mF(x) were used separately, the respective correlations were 0.71, 0.61, and 0.63 for S. cerevisiae and 0.66, 0.56, and 0.53 for S. pombe. Pairing tAI(x) with mRNA(x) and tAI(x) with mF(x) yielded ρ = 0.75 and 0.76 (S. cerevisiae) and ρ = 0.73 and 0.53 (S. pombe), respectively. Additionally, combining these three features improved ρ to 0.77 and 0.74 for S. cerevisiae and S. pombe, respectively, supporting the hypothesis that these three features are the major determinants of protein abundance.

We observed that adding RBP(x), mHL(x), and pHL(x) did not improve the raw accuracy further (ρ = 0.77 and 0.74, respectively, for the S. cerevisiae and S. pombe datasets). We cannot dismiss the contribution of these features all together only because the Spearman correlation does not increase, however. RBP(x), mHL(x), and pHL(x) could still help explain the transcriptional, post-transcriptional, and translational states for a protein of interest. Furthermore, in the absence of any other reliable data, these features can be still used to predict protein abundance, although with less accuracy (see Table I).

Prediction with Missing Values

Despite improvements in high-throughput technologies, generated data typically have missing values. The unavailability of complete datasets has impeded proteome-wide computational studies, including predictions of protein abundance.

In our combined dataset, there were 505 and 1721 proteins in S. cerevisiae and S. pombe that had one or more missing feature values. Similarly, when using four protein abundance datasets (of S. cerevisiae) separately, the numbers of proteins with missing values were 1825, 737, 736, and 696 (G2003, N2006-YEPD, N2006-SD, and L2011, respectively). To fairly appreciate the accuracy of the different methods, it must be emphasized that these proteins were not used in the results discussed in the previous and following sections.

For proteins with one or more features missing (in the combined dataset) but with observed protein abundance, we found that our model predicted abundance in S. cerevisiae and S. pombe with moderate accuracy (ρ = 0.50 and 0.58, respectively). Similarly, for the separate protein abundance datasets, we obtained values of ρ = 0.45, 0.60, 0.56, and 0.33, respectively. Because missing values vary from one protein to another, the predicted protein abundance was less accurate than when using the smaller, but complete, dataset. It might also be that entries with missing values are generally of lower quality, interfering with both training and testing. Yet again, we observed that mF(x) was an important feature in our model. The combined N2006-YEPD and N2006-SD sets did not contain any folding energy information. 70% and 93% of proteins in the datasets of L2011 and G2003 were missing mF(x), respectively.

Parameters Learned by the Model

To illustrate how the model operates and what direct probabilistic relationships best describe the datasets, we provide example conditional probability and density tables of our trained models in supplemental Tables S1–S9. (These tables vary slightly between cross-validation folds.) Supplemental Tables S1–S9 were generated for the combined protein abundance data. For Boolean nodes, the entries map to a simple binomial distribution (a probability of the node being true), given the values of the parents. For continuous nodes, each entry contains a Gaussian density represented by a mean (μ) and a variance σ² (shown as ±σ).

Supplemental Tables S1 and S2 show that half-life was modeled with two distinct Gaussian distributions, with the shorter half-life having a smaller variance. Supplemental Tables S3 and S4 show that when L₃ = False (short half-life), the mRNA regression coefficients were smaller. This means in both yeast species, a weak mRNA expression will result in a short protein half-life. Additionally, for S. cerevisiae, low folding energy and tAI values result in a long protein half-life (see supplemental Tables S3 and S4).

In supplemental Tables S5 and S6, we note that a greater number of interactions between mRNA and RBPs increased expression levels of transcripts, supporting the hypothesis that RBPs regulate post-transcriptional expression of bound transcripts (18).

We note from supplemental Tables S3 and S4 that regression weights were smaller (low abundant mRNAs) when latent node L₃ was false and greater when L₃ was true. This suggests that low mRNA expression (which is usually the case for short half-life proteins) leads to low protein abundance. Conversely, high mRNA expression (typical of long-half-life proteins) leads to greater protein abundance.

Further inspection of supplemental Table S3 reveals that highly expressed mRNAs tend to have low fold strength and codon usage, resulting in high protein abundance. We also note that the mRNA fold strength is associated with short protein half-life and high codon usage, resulting in low protein abundance. Previous studies have observed that strong fold energy negatively influences translation elongation and initiation rates (38–40). The model parameters support the observation that for short half-life proteins, folding energy is inversely related to protein abundance.

We introduced latent variables to represent indirect influence between features where such is known to exist. The latent variables are never observed, and therefore it is entirely up to the learning algorithm to decide their labels. The labels (and their interpretation) can thus change between tests, and between species. As shown in supplemental Table S9, the latent node L₁ was false with a probability of 93% for S. cerevisiae, compared with 19% for S. pombe. L₁ appears to represent mRNA half-life differently for the yeast species, exemplifying differences in the parameters of the latent variables due to variation between species-specific data. The box plot in supplemental Fig. S3 illustrates widely different mRNA half-life measurements in the two yeasts. By distinguishing between short and long half-life transcripts and proteins, the latent variables L₁ and L₃ appear to capture aspects of degradation.

Protein Abundance during the Cell Cycle

So far, our evaluation of the model has been restricted to a particular condition at a time. This section aims to investigate the ability of the model to predict protein abundance for the same transcripts across different conditions, that is, to model the change of abundance in light of changing circumstances. By exploring changes in abundance over the cell cycle, we seek to improve the evaluation beyond purely quantitative metrics so that we can discern qualitative differences between input features.

With DNA microarray technology now widely available, researchers have largely relied on mRNA expression levels to ascertain the role of each transcript and/or its product over the cell cycle (41, 42). We hypothesize that (predicted) measures of protein abundance over the cell cycle provide a more precise characterization of protein function, revealing regulatory pathways and involvement in processes, like (experimentally) observed for human (10). The parameters of our model indicate a nontrivial relationship between mRNA level and protein abundance, involving several factors modulating the relative abundance of proteins.

To predict the protein abundance across the cell cycle, we used the model trained on the combined dataset on high-quality cell cycle mRNA expression profiles (43, 44). We tried different input features (when available) to predict protein abundance (see Table II). We inferred PA(x) at each time point.

Table II. Prevalence of cell-cycle-related GO terms in S. cerevisiae with high fold-change (FC) in mRNA expression and protein abundance.

Features (where applicable)	Number of proteins with FC > 4	Cell-cycle-related proteins
		Cell cycle process (E-val)	Regulation of cell cycle (E-val)	Cell cycle (E-val)	Cell division (E-val)
mRNA(x), tAI(x), mHL(x), pHL(x), mF(x)	825	160 (8.39E-17)	63 (6.92E-08)	174 (1.43E-16)	69 (1.92E-03)
mRNA(x), mHL(x), pHL(x), mF(x)	1629	245 (1.20E-08)	69 (1.00E-00)	271 (1.64E-09)	142 (1.13E-04)
mRNA(x), tAI(x)	1316	208 (1.20E-08)	63 (1.45E-01)	232 (1.64E-09)	126 (3.51E-06)
mRNA(x), mHL(x), pHL(x)	1656	261 (2.58E-12)	73 (4.3E-01)	279 (4.97E-10)	154 (9.93E-08)
mRNA(x)	1688	281 (2.32E-10)	79 (1.00E-00)	301 (5.06E-08)	164 (4.32E-06)

Gene Ontology (GO) enrichment analysis (45) is routinely used to assign roles (including participation in biological processes and molecular functions) to groups of gene products. By identifying such groups on the basis of data collected during the cell cycle, statistical analyses should highlight GO terms that relate to the cell cycle. If our hypothesis (above) is true, then we expect that predicted protein abundance data will identify cell-cycle-related terms more reliably than mRNA expression profiles.

We expect that proteins with a high fold change in abundance over the cell cycle are enriched with cell-cycle-specific GO terms relative to the genome at large. In our analysis, we identified the following GO terms as encompassing cell-cycle-related annotations: cell cycle, cell cycle process, regulation of cell cycle, cell division, and all of their descendants (or specializations).

As detailed under “Experimental Procedures,” we identified 825 proteins (or transcripts) out of a total of ∼5600 as changing their abundance (or expression level) substantially. In what follows, we refer to these two qualitatively defined (and partially overlapping) groups as the PA and mRNA high fold-change sets.

We retrieved the GO terms for all gene products identified in the PA and mRNA high fold-change sets. The number of high fold-change proteins assigned with cell cycle process, regulation of cell cycle, cell cycle, and cell division were 160, 63, 174, and 69, respectively (see Fig. 2). In the mRNA set, the corresponding numbers were 76, 23, 83, and 41, respectively. By using predicted PA data (with >4-fold change in PA) and experimented mRNA expression data (with >2.84-fold change in mRNA expression), we identified 179 and 87 gene products, respectively, related to the cell cycle generally.

Fig. 2.

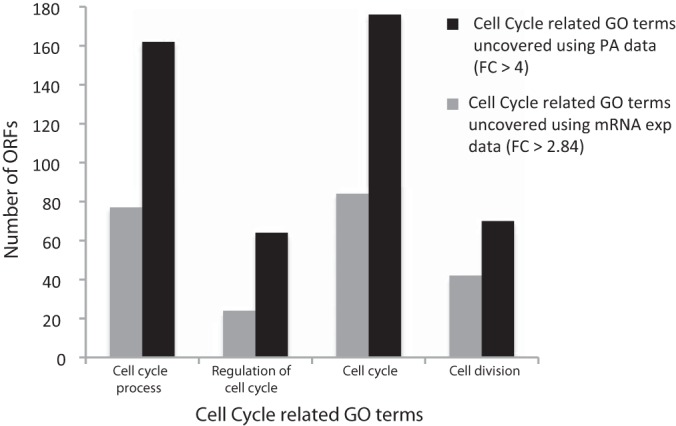
Prevalence of cell-cycle-related GO terms in S. cerevisiae with high fold-change (FC) in mRNA expression and protein abundance.

In preceding section, we showed that tAI(x) alone predicts protein abundance as accurately as assessments with all features provided as input. To understand to what extent tAI contributes to the dynamics of PA, and other combinations of invariant and variant features, we again used the model trained on all data (results shown in Table II), but we tested it on the data collected over the cell cycle, providing only these specific combinations of features as input. Each of the other combinations of input features displayed a greater absolute number of proteins assigned with cell cycle process, regulation of cell cycle, cell cycle, and cell division but had poorer enrichment of cell cycle terms. We note that using mRNA as an input feature led to the greatest absolute count of proteins with a predicted fold change. This count decreased dramatically when tAI was provided in addition. With more condition-invariant features, the model tended to predict fewer proteins that changed greatly, but those that did were more significantly associated with the cell cycle. In general, with more (complementary) features, the model identified a greater proportion of genes with biologically coherent terms. This was not clear from the simpler, correlation-based tests.

To explore the difference in functional characterization resulting from these two alternative levels of analysis more broadly, we created supplemental Table S10, which lists the statistical enrichment of GO terms for proteins and mRNA with high fold-change. We note that 19 cell-cycle-specific GO terms were identified as overrepresented. The corresponding statistical enrichment analysis for mRNA expression profiles is given in supplemental Table S11.

To further illustrate the difference in enrichment of cell-cycle-related annotations, we collected all gene products identified by predicted protein abundance and mRNA expression, noting which had one or more cell-cycle-related terms. Each GO term deemed significant by either approach was then assigned a pair of (log-transformed) p values (one for each approach). Fig. 3 shows these data as a scatter plot. A higher value on either axis represents high enrichment when the corresponding data source is used. A large portion of cell-cycle-related GO terms can be observed at the higher end of the axis for protein abundance but fall much lower down the scale on the alternate, mRNA expression axis. Cell-cycle-related proteins are thus more readily identified with predicted protein abundance data than with mRNA expression data.

Fig. 3.

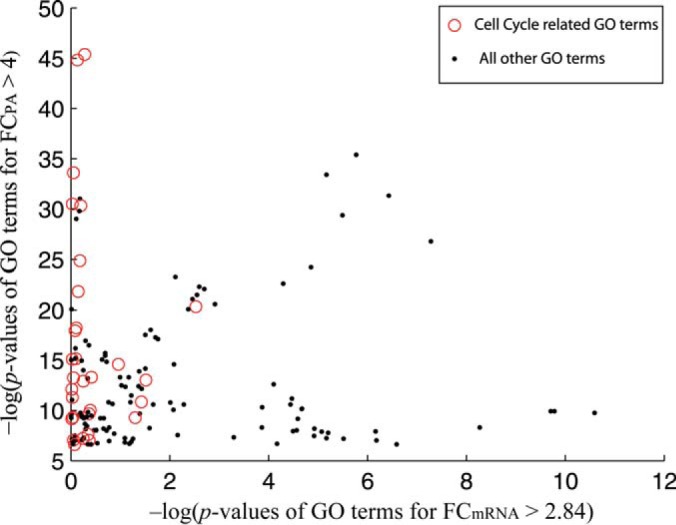
A scatter plot between log(p^mRNA) and log(p^PA). Here, log(p^mRNA) and log(p^PA) are the log-transformed p values of GO terms uncovered using mRNA expression and protein abundance data, respectively. The union of 825 high fold-change proteins and 825 high fold-change mRNA FC was used to uncover GO terms. We regarded the GO terms cell cycle, cell cycle process, regulation of cell cycle, cell division, and all of their descendants in the GO hierarchy as cell-cycle-related GO terms, marked with circles. (All other GO terms are marked with dots.)

Many of the statistically enriched GO terms for the PA high fold-change set are associated with mitosis (e.g. meiotic cell cycle, mitosis, mitotic sister chromatid segregation, mitotic sister chromatid cohesion, cell division, spindle pole body). There are also terms related to DNA damage and repair, which suggests that protein abundance levels better reflect the regulation of related processes. The same analysis on mRNA expression data identified cellular functions (i.e. cellular catabolic process). We provide visualizations of enriched GO terms (biological process), created using GOrilla (46), in supplemental Figs. S1 and S2. The cell-cycle-related GO terms identified using protein abundance predictions are highlighted.

A study in a human cell line measured protein abundance across six stages in the cell cycle (10). The authors made several observations that are further corroborated by the results presented in this paper. Olsen and colleagues reported that 21% of the proteins studied had an abundance fold-change of greater than 4, compared with 5% in the mRNA high fold-change set, implying that the proteome is more dynamic than the transcriptome. Interestingly, the 825 high fold-change proteins constituted 15% of our dataset. Only 187 mRNA transcripts, or 3.4%, had a fold-change greater than 4. The results from the yeast data are notably similar to the experimental results obtained from the human cell line used by Olsen and colleagues. Furthermore, the ratio of high fold-change transcripts to proteins is almost identical in the two organisms: 0.24 in the human cell line, compared with 0.23 in yeast. Our results agree with the hypothesis of Olsen and colleagues that the proteome is more dynamic than the transcriptome, and they give rise to the possibility that the dynamic proteome is a common feature of eukaryotic organisms. If true, this points to the need for accurate models of protein abundance that can reliably represent changing protein abundance throughout the cell cycle.

Predicting the mRNA Folding Energy

In the absence of specific information about the folding of mRNA nucleic acids, the prediction of folding energy provides useful hints about their stability and function. It has been shown that current predictors of folding energy are inaccurate (34). These methods determine energy solely from nucleic acid sequence data. It is thus tempting to see what can be achieved by considering the combination of data we have been using.

A Bayesian network does not designate nodes as inputs and outputs, which allows us to make inferences about any node in the network. We used 6-fold cross-validation on the full coverage data to infer the value of the variable that represents the feature mF(x) given all of the other features, including protein abundance. We thus used the model we previously trained for the purpose of predicting protein abundance to predict the mRNA folding energy for both S. cerevisiae and S. pombe datasets. We compared the predicted folding energy with the RNAfold program from the Vienna RNA folding package (47) and the MATLAB Bioinformatics toolbox. For each transcript, we first calculated the folding energy of each position using a sliding window of 40 nucleotides. To obtain the overall folding energy, we then averaged the folding energies of 40 nucleotide sequences at all of the positions of the mRNA transcript (14). Again, we used the Spearman rank correlation coefficient as a measure of prediction accuracy.

For the combined S. cerevisiae and S. pombe datasets, the model predicted the folding energy with ρ = 0.72 ± 0.03 and 0.53 ± 0.07, respectively. Similarly, by cross-validating the model on the four protein abundance datasets separately (all of the other features, including the folding energy, were the same), we obtained ρ = 0.69 ± 0.02, 0.71 ± 0.03, 0.71 ± 0.03, and 0.72 ± 0.04 for G2003, N2006-YEPD, N2006-SD, and L2011, respectively.

We found that predicting the mRNA folding energy from available predictors was worse than random. The negative correlation between predicted and experimental folding energy had been observed previously (14). The above cross-validation results show that our model yielded modest accuracy but a major improvement over available RNA folding predictors. To our knowledge, our model is currently the only predictor that explicitly incorporates experimental data to predict folding energy. When explaining this performance, we attribute a large amount of value to the node mF(x) that links mRNA(x), RBP(x), and tAI(x) with protein translation.

DISCUSSION

Models can help us to understand functional relationships between molecular components by combining different datasets, each of which provides a limited but complementary perspective. With proteomic technology lagging behind genomic and transcriptomic technologies in terms of throughput, it is of significant interest to understand the link between routinely measured transcripts and more elusive protein copy numbers. We provide a model of protein abundance as a tool to allow scientists to experiment with conditions of specific interest to them (using proprietary mRNA expression data).

Predicting protein abundance on a proteome-wide scale is an important goal in proteomics. The model presented in this paper aims to recognize and ultimately explain the involvement of a range of features in transcriptional and translational events that are in turn relevant to cellular functionality and stability. The model integrates features that are derived from a variety of sources, including nucleic acid sequence, mRNA expression, protein expression, mRNA–protein interaction, mRNA folding, and mRNA and protein half-life. Current protein abundance models are incapable of handling queries that have missing values. We show that Bayesian networks can answer queries in the absence of complete evidence.

We found that tAI(x), mRNA(x), and mF(x) were major determinants of protein abundance. The Spearman rank correlation was ρ = 0.77 and 0.74 for S. cerevisiae and S. pombe, respectively. We compared the models that use mRNA, tAI, and ER to Tuller and colleagues' linear regression model (6). Our S. cerevisiae model performed slightly better, and the S. pombe model performed equally well as that of Tuller and colleagues. tAI(x) and mF(x) are examples of condition-invariant features (i.e. features that depend only on sequence). tAI(x) alone gives an accuracy that is comparable to the accuracy achieved when variant features are provided. Zur and Tuller (14) made a similar observation in their analyses. We believe that the observed correlation between tAI(x) and actual abundance in a single condition is unsurprising. That mRNA expression level and folding energy correlate with actual abundance is even less surprising and has been illustrated by previous models of abundance. The differences in correlation among the three are smaller than expected, however.

In attempts to illustrate a model's ability to capture the dynamics of protein abundance, the single-condition assessment by itself is indirect and inconclusive. We therefore demonstrate that our model predicts protein abundance across the cell cycle with dynamics that (a) are in agreement with experimentally determined abundance collected in human cell lines and (b) cannot be recapitulated by mRNA expression profiles alone. Specifically, we show that predicted abundance over the cell cycle is more dynamic than the mRNA expression profiles, supporting previous experimental results obtained with a human cell line (10). We note that when mRNA(x) was used alone as an input feature, our analysis identified the greatest count of cell-cycle-related proteins. This count of highly variable proteins decreased substantially when tAI(x) was added, but this feature improved the quality of the predictions, with a significant proportion associated with the cell cycle.

We analyzed the functional enrichment (using Gene Ontology) of proteins whose abundance varies more than 4-fold, again compared with mRNA expression data. We found multiple GO terms related to cell-cycle-specific functions using the predicted protein abundance data, none of which were found in a GO term enrichment test on the mRNA data. The significant body of work that has used mRNA expression data to indicate protein dynamics needs to be revisited in light of these findings. We suggest that protein abundance (even if only predicted) is more informative.

Finally, we show that the model is capable of predicting the mRNA folding energy of yeast transcripts with moderate accuracy, and considerably better than other available methods. The model learns these additional parameters as a side effect of learning to predict protein abundance. Predicting folding energies can also improve our understanding of mRNA folding through study of the parameters mRNA(x) and PA(x) and observations of the influence of gene and protein expression.