Importance of Reversible Attachment in Predicting E. Coli Transport in Saturated Aquifers From Column Experiments

Abstract

Drinking water wells indiscriminatingly placed adjacent to fecal contaminated surface water represents a significant but difficult to quantify health risk. Here we seek to understand mechanisms that limit the contamination extent by scaling up bacterial transport results from the laboratory to the field in a well constrained setting. Three pulses of E. coli originating during the early monsoon from a freshly excavated pond receiving latrine effluent in Bangladesh were monitored in 6 wells and modeled with a two-dimensional (2-D) flow and transport model conditioned with measured hydraulic heads. The modeling was performed assuming three different modes of interaction of E. coli with aquifer sands: 1) irreversible attachment only (best-fit k_i=7.6 day^-1); 2) reversible attachment only (k_a=10.5 and k_d=0.2 day^-1); and 3) a combination of reversible and irreversible modes of attachment (k_a=60, k_d=7.6, k_i=5.2 day^-1). Only the third approach adequately reproduced the observed temporal and spatial distribution of E. coli, including a 4-log₁₀ lateral removal distance of ∼9 m. In saturated column experiments, carried out using aquifer sand from the field site, a combination of reversible and irreversible attachment was also required to reproduce the observed breakthrough curves and E. coli retention profiles within the laboratory columns. Applying the laboratory-measured kinetic parameters to the 2-D calibrated flow model of the field site underestimates the observed 4-log₁₀ lateral removal distance by less than a factor of two. This is promising for predicting field scale transport from laboratory experiments.

1. Introduction

In rural areas throughout the world, aquifer filtration of pathogens and fecal bacteria has long been relied on to supply drinking water^1,2. The practice has been called into question by growing evidence of widespread contamination of shallow sandy aquifers with fecal indicator bacteria (FIB)^3-7. In developing countries, however, centralized water treatment or point-of-use disinfection of water from wells affected by infiltration of microbially contaminated surface water remains technically and economically unrealistic for the foreseeable future^3,8,9. In rural Bangladesh in particular, microbial contamination of shallow groundwater is of concern for tens of millions of households relying on shallow tubewells because of the combination of an extremely high population density and generally poor sanitation^10,11. A recent analysis of household-level data collected over several years within the ICCDDR,B's (International Center for Diarrheal Disease Research, Bangladesh) study area of Matlab upazilla has shown that shallow aquifers that are vulnerable to microbial contamination are, indeed, associated with a significant increase in diarrheal disease in children under five¹². It is therefore particularly important in such settings to distinguish wells that are likely to be contaminated with microbial pathogens from those that are not.

Theoretical advances and a considerable number of laboratory and field experiments conducted in recent years have contributed to an improved understanding of pore-scale microbial removal processes^2,13-15 but some significant puzzles remain^16,17. For example, microbial removal efficiencies across distance (D^-1) observed in field experiments^16-25are usually lower than measured with columns in the laboratory^2,18,26,27. This has tentatively been attributed to preferential flow paths in the field that are not reproduced within sediment columns²⁸. Columns, moreover, are typically run under steady-state flow conditions whereas transient flow predominates in the field^1,28. Further, irreversible bacterial attachment is implicitly assumed to operate when up-scaling column results to field settings²⁹ and are frequently calculated directly from steady-state peak breakthrough concentrations (D^-1)²⁹ rather than modeling the entire breakthrough curve with reversible attachment and detachment rates^14,15,20,27. We hypothesize that kinetic attachment and detachment rates (T^-1) may be less sensitive to scale of measurement than irreversible attachment alone and may therefore allow more accurate predictions.

The impact of transient flow on microbial transport resulting, for example, from pulses of recharge due to heavy monsoonal rains has also rarely been studied systematically at the field scale³⁰. This is important because microbial removal efficiencies (D^-1 and T^-1) are sensitive to pore velocity¹⁵ and more bacteria may enter the saturated water table as the soil zone becomes more saturated³¹. In the present study, we seek to understand the reason for the apparently more restricted movement of bacteria in column experiments relative to the field²⁹. Kinetic interaction parameters modeled on laboratory column experiments packed with sand from the base of a freshly excavated pond in Bangladesh are compared with those obtained from modeling a previously documented breakthrough of E. coli through the bottom of the pond following an induced rise in pond water level²⁵.

Previous studies reported on widespread fecal contamination in private tubewells in sandy villages^6,7 and identified ponds dug recently into the unconfined aquifer as point sources of fecal contamination during the early monsoon²⁵. The field component of the present study was previously reported and carried out in the village of Char Para in Araihazar upazilla where the local sandy aquifer extends to the surface and is therefore vulnerable to microbial contamination^6,7,25,32. The vulnerability of the shallow aquifer was locally intensified by artificially raising the water level in a recently excavated pond whose base was not protected by the fine-grained sediments that tend to accumulate on pond bottoms over time. Under these conditions, simulating a recharge pulse to the aquifer during monsoonal rains, E. coli penetration into the aquifer over the course of several days was documented along a transect of 6 previously installed piezometers radiating from the pond. Here, we combine an expanded E. coli time series, including 5 post-pulse sampling events, and a more detailed reconstruction of the pond water recharging the aquifer to reproduce observed E. coli concentrations and hydraulic heads using the 2-D finite element model HYDRUS 2D^24,33,34. We present new column experiments with sand from the base of the pond. From these, kinetic attachment/detachment rates are derived and substituted into the calibrated 2-D flow model to predict E. coli transport under transient flow conditions.

2. Setting

2.1 Pond Infiltration Field Experiment

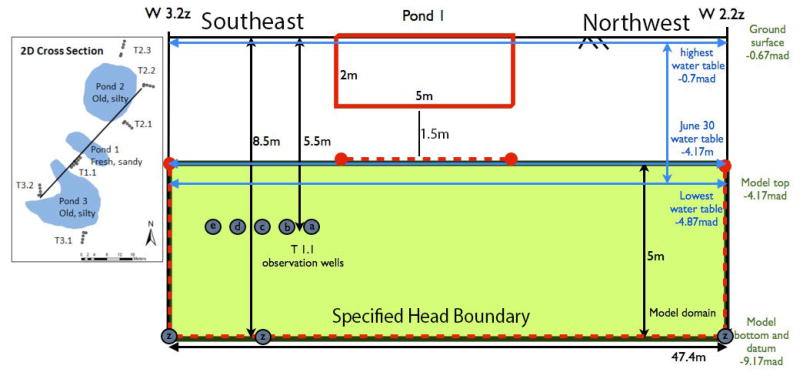
The Bangladeshi village of Char Para lies within Araihazar upazilla, 25 Km east of Dhaka (see Fig. 1 in reference 25). Pond 1 is a freshly excavated, sandy bottom pond located in the northeast corner of the village. A transect of five shallow monitoring wells 5.5 m deep, and one 8.5 m deep well were placed orthogonal to the edge of Pond 1 (Fig. 1). The first well was placed 2.5 m from the edge of Pond 1 and they were spaced 1 m apart. The wells had a screened interval length of 1.5 m. The construction details of these wells are described in Knappett et al. (2012)²⁵. Throughout this paper, the wells are named in the following way. Transects and the wells within them are labeled according to Δx.y.δ, where Δ is either T or W, referring to the transect or well, respectively, x and y numerically reference the pond (1-4) and the transect adjacent to pond x (1-3), respectively, and δ is a letter referring to a well in transect y (a-e for shallow wells, and z for the single deeper well) (Fig. 1).

Figure 1.

2-D model with specified head boundary conditions indicated by dashed red lines. All elevations are relative to an established datum²⁵. Blue lines indicate minimum and maximum observed limit of local water table during the years 2007-2009. . The shaded green area shows the modeled region within the saturated aquifer. The bottom of wells 3.2z (W3.2z) and 2.2z (W2.2z) are located at the southwestern (left) and northeastern (right) spefified head boundaries, respectively. Grey circles represent the location of well screens and are labeled to identify their position in the transect.

Of the four ponds studied in detail in Knappett et al. (2012)²⁵ only the bottom of Pond 1 was not lined with silt, and consequently was the only pond where an increase in E. coli concentrations in adjacent observation wells were measured in response to artificial filling and subsequent rainfall. Pond 1 penetrates a local 1.5 m thick silt layer and terminates in a medium sand aquifer used for drinking water. Neighboring Pond 3, used to artificially fill Pond 1, is a shallower pond that does not penetrate the local silt layer and receives effluent from surrounding latrines.

3. Methods

3.1 Pond Infiltration Field Experiment

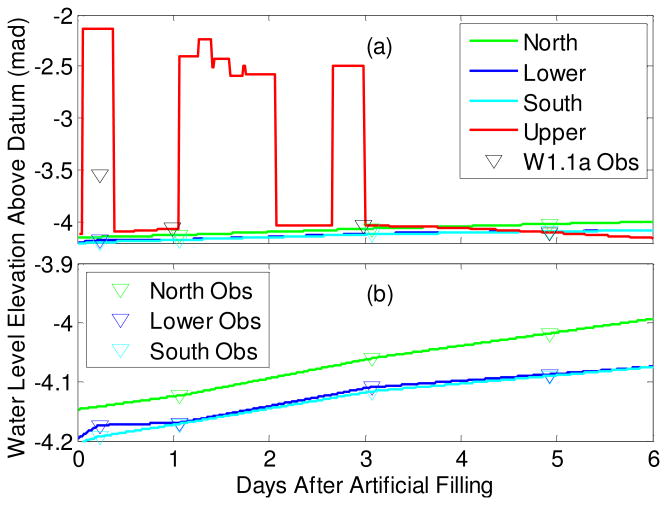
This study focuses on five days between July 1 and 6 in 2009 referred to herein as the experimental period²⁵. During this time, hydraulic head (Fig. 2) and E. coli concentrations (Fig. 3) were monitored at least once every two days in adjacent observation wells. The base of Pond 1 was perched approximately 1.5 m above the local saturated water table on June 30 before the artificial filling with contaminated latrine water began (Fig. 2). There were three major inputs of water through the base of Pond 1. The first, and largest, of these pulses was caused by the artificial filling of Pond 1 with contaminated latrine pond water from neighboring Pond 3. The second pulse resulted from several natural rainfall events spaced closely together over 24 hours, and the third resulted from a single rainfall event.

Figure 2.

Transient hydraulic head boundary conditions for the 2-D Hydrus model. (a) The upper boundary was simulated by combining a record of rainfall events at Char Para and a record of observations on Pond 1 levels. Black open grad symbols represent observed water table level in W1.1a. (b) Expanded view of the slowly varying specified head boundaries.

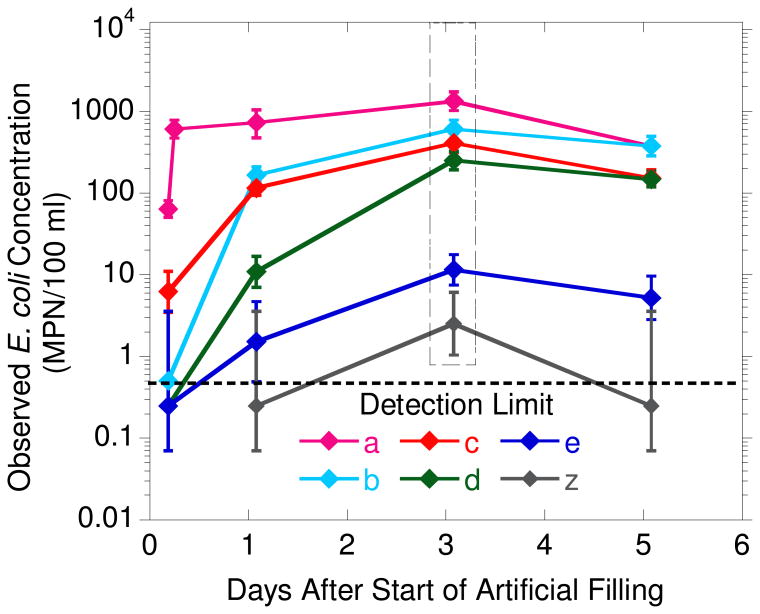
Figure 3.

Observed E coli concentrations in T1.1 wells following artificial pond filling on July 1, 2009. The error bars represent 95% confidence intervals and the horizontal dashed line represents the detection limit of 0.5 MPN/100 ml based on duplicate 100 ml water samples⁴⁰. The data in the box on day 3 has been published previously in Knappett et al. (2012)²⁵.

The chemistry of the water in Pond 1 and that in the adjacent shallow transect wells were very similar (Fig. S2 in reference 25). Specific conductance was typically low and similar in ponds and their adjacent shallow transect wells during the wet season (<400 μS/cm) (Tables A-III-10 and A-III-27 in reference 35). Specific conductance in shallow transect wells tends to increase during the end of the dry season (∼1,000 μS/cm), whereas ponds tend to remain low year round (Tables A-III-9, A-III-10, A-III-13 in reference 35).

The level of the water in Pond 1 wasn't measured immediately after all rainfall events, however the level of Pond 4, 200 m south of Pond 1 (Fig. 1 in reference 25), was measured every 20 minutes using a pressure transducer (Model 3001 Levelogger Edge, Solinst Canada Ltd., Georgetown, Ontario, Canada) during this period and was used to determine the timing and relative magnitude of rainfall events. In Bangladesh hourly precipitation amounts during the monsoon often vary over short distances³⁶. Therefore, daily rainfall measured in Dhaka (Bangladesh Meteorological Department, www.bmd.gov), 25 km to the west, was used to only to confirm the occurrence of rainfall on the days indicated by the transducer in Pond 4 within Char Para.

The porosity and bulk density of the aquifer were measured to be 0.4 (-) and 1500 (Kg/m³), respectively, using the water displacement method outlined in Brush et al. (1999)³⁷. Longitudinal and transverse dispersivities were estimated from to be 0.5 and 0.1 m, respectively based on broad scale-dependent dispersitivities presented in Gelhar et al. (1992)³⁸. Continuous 1.5 cm diameter direct push cores were taken in the middle of T1.1 at 0.3 m intervals from 3 to 5.5 m below ground surface to log the lithology in detail. With the exception of four <1 cm thick silt layers, the aquifer is homogeneous with respect to grain size distribution²⁵. Excluding the silt layers, the average values of d₁₀, d₅₀ and d₆₀, determined by log-linear interpolation³⁹ with standard deviations in parentheses are 0.13 (+/-0.03), 0.33 (+/-0.01) and 0.36 (+/-0.01) mm, respectively, corresponding to a uniformity coefficient (d₆₀/d₁₀) of 2.8. The terms d₁₀, d₅₀ and d₆₀ refer to the grain sizes for which 10, 50 and 60 percent of the sample was finer by mass, respectively. Grain size distributions were also measured on sand taken from the base of Pond 1 for the laboratory column experiments, and matched the cored sand to within the error tolerance. Based on visual inspection the sand was determined to be sub-angular to sub-rounded in texture. No silt was observed in the sand taken from the base of Pond 1. The horizontal hydraulic conductivity (K_h) was assumed to be the middle of the narrow range (26.8-38.9 m/day) of hydraulic conductivities determined by triplicate slug tests in the 6 wells in T1.1 (Supplementary Table 2 in reference 25).

3.2 2-D Modeling of Field Experiment

3.2.1 Governing Transport Equations

Hydrus 2D-lite version 2.01.1080³⁴ was used to model the transient flow and transport conditions in the saturated aquifer below Pond 1. The model solves Richard's equation for water flow and uses the Fickian-based advection-dispersion model for contaminant transport in saturated porous media using a finite element grid with 7,378 nodes. The model can fit both kinetic irreversible and reversible attachment parameters. The governing equations for bacterial transport in one dimension with both irreversible and reversible attachment are²⁴:

$$\frac{\partial c}{\partial t}+\frac{{\rho }_b}{\theta }\frac{\partial s_r}{\partial t}+\frac{{\rho }_b}{\theta }\frac{\partial s_i}{\partial t}=D\frac{{\partial }^{2}c}{\partial z^2}-\upsilon \frac{\partial c}{\partial z}-\mu c$$ Eq. (1)

$$\frac{{\rho }_b}{\theta }\frac{\partial s_r}{\partial t}=k_{a}c-\frac{{\rho }_b}{\theta }{k}_a{s}_r-\mu \frac{{\rho }_b}{\theta }{s}_r$$ Eq. (2)

$$\frac{{\rho }_b}{\theta }\frac{\partial s_i}{\partial t}=k_{i}c-\mu \frac{{\rho }_b}{\theta }{s}_i$$ Eq. (3)

where c is the concentration of bacteria in free suspension (cells/L³), θ is the effective porosity (-), v is the advective velocity of the water (L/T), D is the hydrodynamic dispersion coefficient (L²/T) which is equal to λv where λ is the dispersivity (L), z is the distance along the flow path (L), ρ_b is the dry bulk density of the porous media (M/L³), s_r is the concentration of bacteria at reversible sites (cells/M), and s_i is the concentration of bacteria at irreversible sites (cells/M). k_a is the forward attachment rate at reversible sites (T^-1), k_d is the reverse detachment rate at reversible sites (T^-1), and ki is the irreversible forward attachment rate (T^-1). μ is the first-order inactivation rate of bacteria (T^-1). This model assumes there are two different attachment modes (reversible and irreversible) taking place at constant rates simultaneously throughout the saturated sand. A more complex model than this is employed in this study, which assumes one population of bacteria interacting as the first model describes, and a second equal-sized population attaching at a unique irreversible attachment rate (Eq. S1-S4).

3.2.2 Hydraulic Head Modeling

The upper boundary of the 2-D model is located directly below Pond 1. Steep hydraulic gradients observed in the adjacent T1.1 wells (Fig. 2) located 2.5 m laterally from the edge of Pond 1 (Fig. 1) led to the assumption that the filling of the pond created a temporary groundwater mound resulting in a saturated flow path between the pond and the local water table. Hydraulic head for the upper model boundary was simulated using the available observations on the water level in Pond 1, rainfall events recorded in Pond 4, and hydraulic head measurements made in T1.1 (Fig. 2). Peak water levels in Pond 1 are calibrated to synoptic peak water levels in Pond 4 following two different rainfall events. Three “off-peak” (when Pond 1 had no water in it) dry pond observation time points are used to constrain the drainage time of Pond 1, found to be approximately 8 hours. Off-peak groundwater levels were measured on 3 occasions by manual hydraulic head measurements in T1.1 monitoring wells. The pond surface is assumed to represent the pressure head of the upper boundary subtracting head loss across the ^∼1.5 m of sediment between the bottom of the pond and the top of the model. This head loss is calculated using Darcy's Law assuming a Darcy flux of 1.86 m/day; consistent with the disappearance of 0.62 m of standing water in Pond 1 in approximately 8 hours.

Slowly varying, specified hydraulic head boundaries are imposed along the northeast, southwest and bottom of the model and heads at these boundaries are set to the observed heads in wells W2.2z, W3.2z and W1.1z, respectively (Fig. 1). The model domain is 47.4 m long and 5 m thick. It extends from a depth of 8.5 m below the local ground surface along T1.1, coinciding with the bottom of W1.1z, to 3.5 m below ground surface, coinciding with the saturated water table at the start of the experimental period (Fig. 1). The base of Pond 1 is approximately 2 m below the local ground surface.

3.2.3 Bacterial Transport Modeling

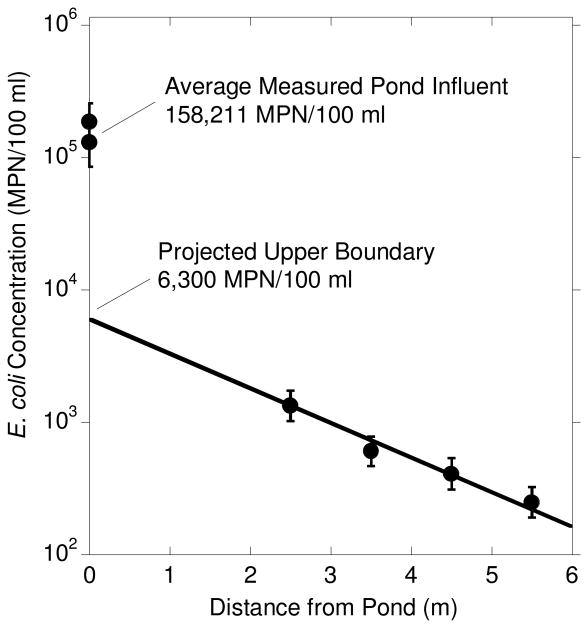
Pond water E. coli concentrations ranged from 100,000 to 200,000 MPN/100 ml. Pond water E. coli concentrations were substantially higher than observed in the aquifer and the spatial concentration trends in the saturated aquifer indicated E. coli concentrations were substantially reduced across the 1.5 m of vertical flow between the base of Pond 1 and the upper boundary of the model. The log-linear relationship between E. coli concentration and lateral distance from the edge of Pond 1 in the saturated aquifer on day 3 of the experimental period (Fig. 4a in reference 22) was used to determine the influent E. coli concentration at the model's upper boundary of 6,300 MPN/100 ml (Fig. 4). Day 3 after artificial filling was chosen since it represents the first observed time that the E. coli plume penetrated the entire T1.1 (Fig. 3).

Figure 4.

Estimation of E. coli input concentration at upper model boundary 1.5 m below the base of Pond 1. Concentrations at distances >0 m were measured in shallow T1.1 wells on day three after artificial filling of Pond 1, when the plume had reached the outer well. Error bars represent 95% confidence intervals⁴⁰.

3.3 Column Experiments

3.3.1 Experimental Measurements

Four replicate column experiments were conducted to compare laboratory modeled attachment/detachment rates to those modeled at the 2-D field-scale. The column experiment methodology exactly followed that in Feighery et al. (2013)²⁷ for unwashed sands with one modification. E. coli ATCC strain 700891, which is resistant to Streptomycin and Ampicillin, was used in the present study, whereas Feighery et al.²⁷ used ATCC strain 700609, a nalidixic acid resistant strain of E. coli.

Plastic columns 10-cm long with an inner diameter of 1.7 cm were dry packed with sand taken from the base of Pond 1 (see Section 3.1). All four columns were packed with sand from the same homogenized 2 kg bag of sand from the base of Pond 1. After slowly saturating the sand by upward flow, E. coli was injected in the top of the column at a concentration of approximately 300,000 MPN/100 ml, to ensure that effluent concentrations would be well above detection limit, and a volumetric flow rate of 0.5 ml/min using a multi-channel peristaltic pump (Gilson MiniPuls, Middleton, WI). A fraction collector (LKB-Bromma, Sweden) was used to collect samples in 15 ml polypropylene tubes (Fischer Scientific, Pittsburg, PA). This volumetric flow rate resulted in an advective velocity of approximately 8 m/day. An artificial groundwater solution (AGW) containing 3.5 mM KCl was used throughout the entire experiment. Each column was flushed for approximately 15 pore volumes with AGW while effluent pH and specific conductivity was monitored to ensure stabilization. Without stopping the pump, the influent water was switched over to contaminated groundwater solution containing E. coli and 20 mg/L KBr (0.17 mM) and appropriately adjusted KCl concentration to maintain the same ionic strength as the AGW. The contaminated water was run for 10 pore volumes before switching back to pristine AGW for 30 pore volumes. Within 8 hours of sampling, E. coli was analyzed by diluting samples in 100 ml sterile bottles and adding Colilert™ reagent (IDEXX, Westbrook, ME). The 100 ml bottles were poured into a Quanti-Tray 2000™ and incubated for 24 hours after which the compartments fluorescing under a UV light were enumerated and the number converted to a Most Probable Number (MPN) of cultured E coli⁴⁰.

To determine the attached E. coli profile, the two columns used for the last two experiments were sectioned into 8 equal lengths with a flame-sterilized knife immediately upon completion of the experiments. E. coli was extracted from the sand initially by vortexing for 5 seconds in 20 ml of sterile deionized water in 50 ml polypropylene tubes (Fischer Scientific, Pittsburg, PA). The tubes were then placed on an orbital shaker at 37 °C for 30 minutes. After this 5 μl were transferred via pipette from the 50 ml tubes to a 100 ml sterile Colilert bottle and processed exactly as the effluent samples. The sediment remaining in each 50 ml tube was dried at 80 °C overnight and weighed to obtain the bulk density of the packed sand at each interval (g/ml).

The inactivation rate of the laboratory-grown E coli at room temperature was determined in in Feighery et al. (2013)²⁷ to be 0.067 ln/day. This is comparable to a study that measured E coli inactivation of 0.15 ln/day at 20 °C¹⁸ and that reported in a review paper by Foppen and Schijven (2006)⁴¹ of 0.5 ln/day with a range of 0.1 to 1.0 ln/day. In slightly warmer groundwater in Bangladesh (26 °C), multi-day measurements made on E. coli concentrations in shallow wells adjacent to Ponds 1 and 2 during stagnant flow periods when no new E. coli was introduced to the well suggest a inactivation rate of 0.11 ln/day. Thus inactivation rates of 0.067 and 0.11 ln/day were assumed for the 1-D column and 2-D field model, respectively. These inactivation rates are so low that removing inactivation from the 2-D model has negligible impact on the modeled kinetic interaction parameters.

3.3.2 1-D Modeling of Column Experiments

Modeling of the Br breakthrough curve was performed with CXTFIT^42,43 a 1-D numerical advection-dispersion model, to determine the porosity and dispersivity of the packed sand. E. coli kinetic interaction parameters were determined by inversion using a 1-D Finite Element flow and transport model programmed in matlab™ operating on the same governing equations as the 2-D model (Eq. 1-3). The 1-D model was run at a constant 8 m/day advective flow velocity, which corresponds to peak advection in the saturated aquifer indicated by the 2-D flow model underlying Pond 1 during peak filling events.

The E. coli concentration retained in the sand was normalized according to the equation

$$\frac{s}{C_o}=\frac{\left(\frac{{\rho }_b}{\theta }\right)\left(\frac{\#Cs}{m_s}\right)}{C_o}$$ (Eq. 4)

where ρ_b is the bulk density of the dry sand (g/cm³), θ is porosity (-), #C_s is the cells extracted per gram of dry sand in each segment (cells/g), m_s is dry mass of the sand in the each segment (g), and C_o (cells/cm³) is the influent concentration during the pulse phase. This method of normalizing retained cell densities is useful since it represents multiples of the injected concentration found in the pore space volume of each segment^27,44.

4. Results

4.1 Observations

4.1.1 E. coli time series in the field

Concentrations of E. coli in all but two of the monitoring wells were at or below the detection limit of 0.5 MPN/100 ml on the day before the level of Pond 1 was artificially raised (Fig. 3). In the well closest to the pond (W1.1a), the concentration of E. coli measured in duplicate samples was 60 MPN/100 ml. Within a day of filling Pond 1, E. coli increased to greater than two orders of magnitude above detection limit in the 3 monitoring wells closest to the pond. In the single monitoring well at 8.5 m depth, E. coli was detected only once, on day three, and barely detectable on that single occasion (2 MPN/100 ml).

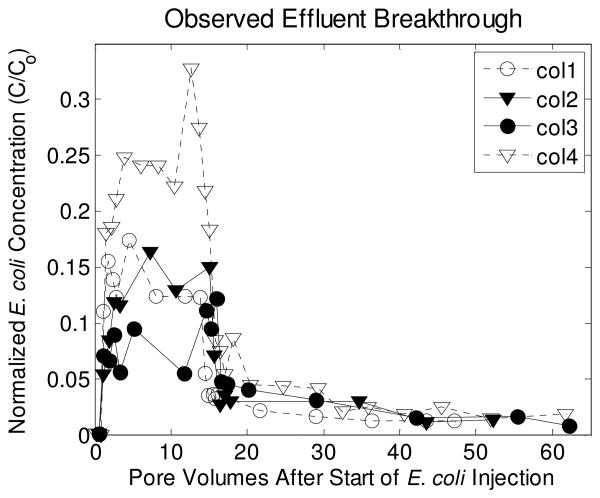
4.1.2 E. coli breakthrough in columns

The plateau in effluent E. coli concentrations reached during column experiments corresponds to only 10-25% of the influent concentrations which ranged from 1.7-3.7x10⁵ MPN/100 ml for the 4 replicate columns (Fig. 5). After switching the influent back to AGW, effluent concentrations of E. coli remained detectable for an additional 40 pore volumes of flushing. Retained concentrations of E. coli decreased within the first few cm but remained detectable through the length of the two columns. Summing total E. coli measured in the effluent with total retained E. coli on the sand corresponds to 60-70% of the total E. coli injected into the column.

Figure 5.

Observed effluent breakthrough curves from four replicate column experiments. Retention curves were only available for columns 3 and 4.

4.2 Modeling

4.2.1 Hydraulic forcing in the field

Observed hydraulic heads were used to constrain the hydraulic anisotropy K_h/K_v in the 2-D flow model, where K_v is vertical hydraulic conductivity. With the boundary conditions set (see above), hydraulic anisotropy is determined by manually minimizing the root mean squared error (RMSE) between the modeled and observed heads by entering anisotropies between 1 and 20⁴⁵ into the numerical model. Four sets of hydraulic head observations were available immediately after filling (day 0) and on days 1, 2, and 5 of the experimental period, but only one of these events represent peak filling conditions (Fig. 2a). Hydraulic heads from this event had the greatest influence on determining the best fit for aquifer anisotropy. The best fit between observed and modeled hydraulic heads was found with an anisotropy of 4. This was insensitive to varying K_h across the measured range in the six monitoring wells of T1.1 (Table 1).

Table 1.

Sensitivity analysis for K_h and anisotropy (K_h/K_v). Interaction parameters (k_a,k_d,k_i) were derived for Anisotropy=4, K_h=32.8 m/d. The lower and upper range of K_h was substituted into the model, while keeping k_a,k_d,k_i constant and the goodness of fit was calculated (RMSE). The same was done for horizontal dispersivity (λ).

	Kh=26.8m/d		Kh=32.8m/d	Kh=38.9m/d	λ=0.1m	λ=0.5m	λ=2.5m
Anisotropy	RMSE Hydraulic Heads (m)	RMSE E. coli (MPN/100 ml)
1	47.0
4	11.6	157	99	132	171	99	145
5	12.8
10	18.0
15	17.0

4.2.2 E. coli transport in the field

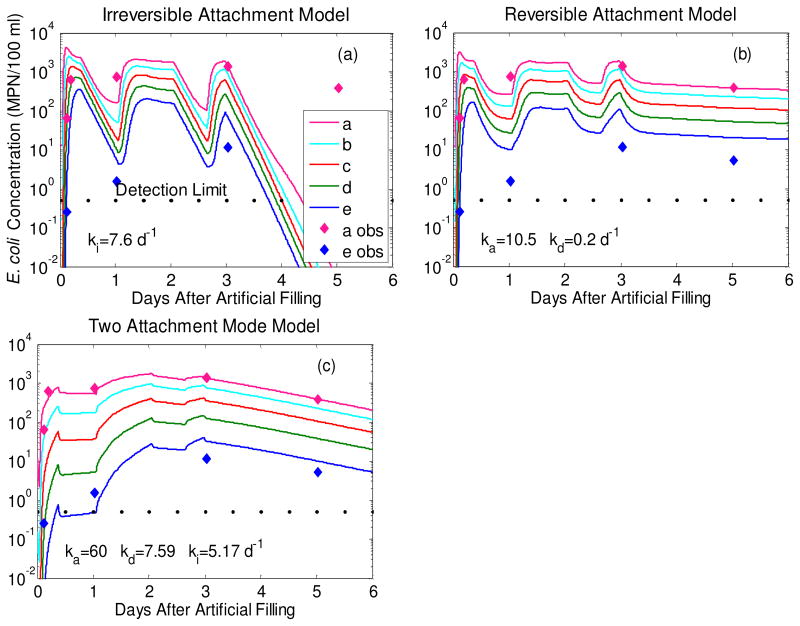
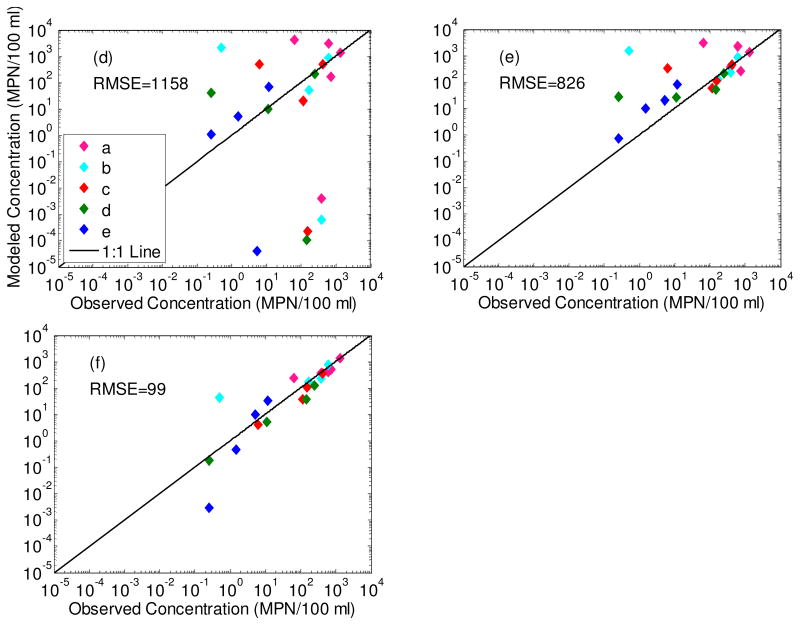
A total of 21 observations (4 sampling events in five wells plus an additional sampling event for well 1.1a) constrain the interactions of E. coli with aquifer sands. All three models (Irreversible, Reversible and Two Attachment Mode) can reproduce the rapid increase in E. coli soon after the filling of Pond 1. Irreversible attachment only, however, predicts a sharp drop-off in E. coli towards the end of the experimental period that was not observed (RMSE=1158 MPN/100 ml) (Fig. 6a). Reversible attachment only does not generate the full range of E. coli concentrations maintained throughout the experimental period along the length of the transect (RMSE=826 MPN/100 ml) (Fig. 6b). Applying both irreversible and irreversible attachment to an arbitrary equal division of sites reduces the RMSE in E. coli by almost an order of magnitude lower to 99 MPN/100 ml (Fig. 6c). The RMSE value is stable across a broad range of parameter values and the minimum is maintained as long as the k_a/k_d ratio remains close to 8 (Table 2).

Figure 6.

Modeled breakthrough of E. coli in T1.1 shallow wells during the experimental period (a-c). Input concentration at the upper boundary of the model was 6,300 MPN/100 ml. The lower three panels represent observed versus predicted E. coli concentrations for each of the three model types with the root mean squared error (RMSE) (d-f).

Table 2.

Manual optimization of the attachment/detachment kinetic parameters for the 2-D flow and transport model for K_h=32.8 m/d and Anisotropy=4. The parameters yielding the optimal fit are shown in dark grey. Estimated upper and lower bounds on k_a, k_d and k_i are shown in light grey.

ka	kd	ki	RMSE	ka/kd
110	13.9	5.3	113.6	7.9
100	12.6	5.3	110.7	7.9
90	11.4	5.3	108.0	7.9
80	10.1	5.3	104.9	7.9
70	8.9	5.2	102.1	7.9
60	7.6	5.2	99.4	7.9
50	6.3	5.2	100.3	7.9
40	5.1	5.1	109.7	7.9
30	3.8	5.1	142.9	7.9

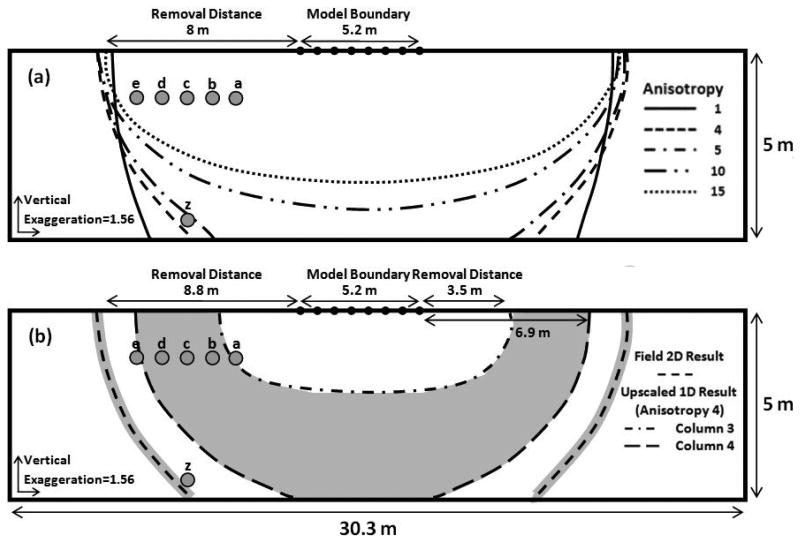
The anisotropy calibrated to hydraulic heads is consistent with the modeled E. coli concentrations in the transect wells (Table 1). For example, the 2-D model shows that E. coli would have been detected in abundance on day three of the field experiment with a hydraulic anisotropy of 1 and would have never been detected for an anisotropy of 10 (Fig. 8a).

Figure 8.

Modeled and predicted E coli 4-log₁₀ removal distance representing the maximum transport distance on day 3 after the start of artificial pond filling. (a) 4-log₁₀ removal distance as a function of hydraulic anisotropy. The long-dashed line represents the fitted 4-log₁₀ E. coli removal distance based on the optimal anisotropy of 4. (b) Comparison of 4-log₁₀ E. coli removal distances between 2-D model (2 attachment mode) fitted to E. coli concentrations from the field and predictions made from substituting kinetic parameters derived from 2 population (best fit) 1-D column experiments into the calibrated 2-D flow model. The shaded areas represent the estimated uncertainty in each method. The uncertainty band for the 2-D model was obtained by substituting the range of possible values of k_a, k_d and k_i into the model (Table 2).

The distribution of hydraulic heads that constrained anisotropy did not constrain K_h (Table 1). Triplicate slug tests, however, on each of the six transect wells measured a narrow range of K_h from 26.8 to 38.9 m/d representing approximately +/-20% difference of advective velocity using Darcy's Law. The midpoint of this range was assigned to the entire modeled aquifer.

4.2.3 E. coli transport in the columns

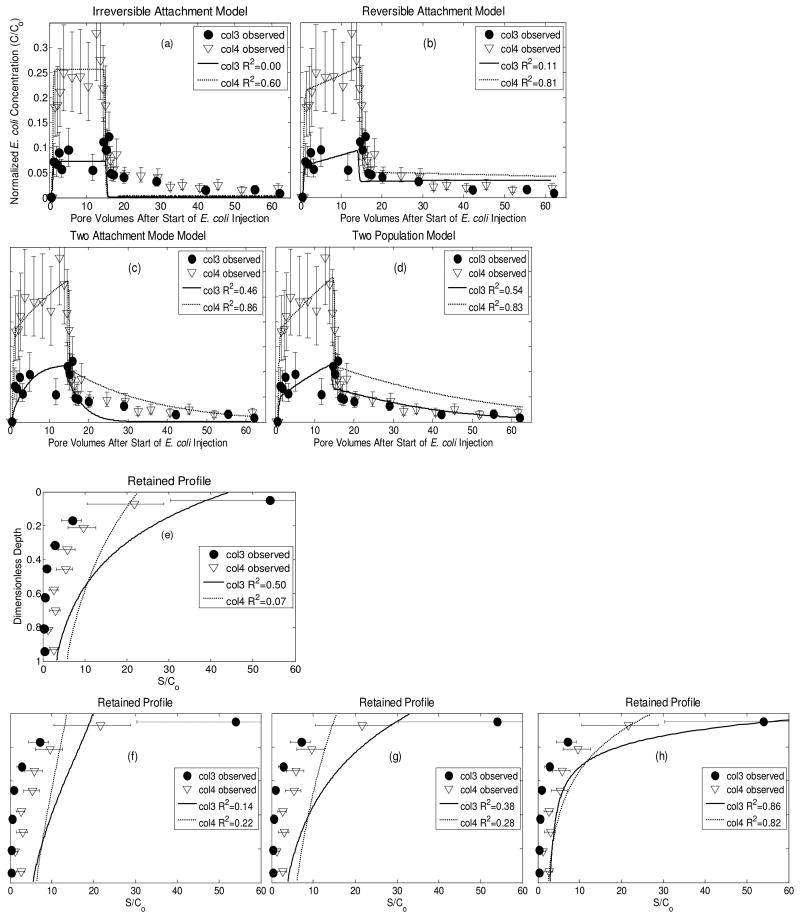
Column experiments 3 & 4 (Fig. 6) span the full range of steady-state breakthrough concentrations of E. coli measured in all four laboratory experiments. Two types of models were used to describe the movement of water and E. coli through re-packed sand columns. Bromide breakthrough was modeled with CXTFIT^42,43 to obtain a dispersivity and advective velocity of 0.003 m and 8 m/day, respectively. These conditions represent a Peclet number of 0.11. A 1-D 101 node finite difference transport model was developed using Crank-Nicholson and central difference weighting to obtain kinetic interaction terms between E. coli and the sand. Similar to the field modeling, the observations were fitted to four different models of interaction between E. coli and aquifer sands. Irreversible attachment only cannot reproduce the measured E. coli concentrations up to 40 pore volumes after the effluent has been switched back to AGW only (Fig. 7a). Reversible attachment only, on the other hand, does not reproduce the observed build-up of E. coli in the near the column inlet. As in the field, the combination of irreversible and reversible attachment provides a better fit to the observations than single attachment mode models (Fig. 7c,g), however even this model was unable to reproduce the very high deposition rates near the column inlet. The model that fit the data best assumed an equal proportion of two populations of E. coli, one that attached irreversibly and one that attached both irreversibly and reversibly (Fig. 7d,h). Model fits tend to overestimate E. coli concentrations since the experimental recovery in each column was lower than that expected based on the mass balance calculations which included the very low measured inactivation rates in the influent reservoir.

Figure 7.

Modeled effluent breakthrough curves (a-d) and retained profiles (e-h) of E. coli in saturated 10 cm duplicate columns of packed sand taken from the base of Pond 1. Solid and dashed lines represent results of 1-D inversion modeling which put equal weight on the effluent breakthrough and retained concentration profile. Error bars represent 95% confidence intervals⁴⁰.

The kinetic attachment/detachment rates for the two population models from columns 3 and 4 were applied to the calibrated 2-D flow model to obtain expected transport distances in the saturated aquifer underneath Pond 1. The predicted 4-log₁₀ removal distance for E. coli in the saturated water table directly below Pond 1, was 3.5 m for rates obtained from column 3 and 6.9 m for column 4 rates (Fig. 8b).

5. Discussion

5.1 Influence of Hydraulic Anisotropy on Spatial Extent of E coli Movement

Hydraulic anisotropy controls the relative proportion of horizontal to vertical groundwater flow. This aquifer property is not always measured during field transport studies, and thus may have gone unnoticed in its potential influence on field-scale bacterial transport. Modest changes in hydraulic anisotropy within the calibrated 2-D model strongly influence the depth of E. coli penetration into the aquifer. The sensitivity analysis indicated that if the aquifer was isotropic the deeper well (W1.1z) would have contained abundant E. coli (Fig. 8a). Anisotropy restricts this vertical movement into the aquifer.

In the present 2-D numerical model, hydraulic anisotropy influences the flow paths along which bacteria are advected but assumes the aquifer is homogeneous with respect to grain size distribution. Thus kinetic parameters are spatially uniform. In this floodplain aquifer, however, thin silt layers were present and bacterial attachment rates (T^-1) in fine material is much higher than in medium sand^27,44. The saturated aquifer underlying Pond 1 has few silt layers and the medium sand is homogeneous across the cored depth in the middle of the adjacent transect. Approximately 20 m northeast of T1.1, however, transect 2.1 contained numerous ∼1-2 cm thick, and one 20 cm thick, silt layer indicating a higher local hydraulic anisotropy (Fig. 2b in reference 25). This may explain why, in our previous study, the deeper well in transect 2.1 (W2.1z) was found to contain little FIB DNA, whereas the deeper well in T1.1 (W1.1z), less protected by silt layers, contained abundant FIB DNA²⁵.

5.2 Importance of Irreversible and Reversible Attachment

Microbial attachment modes operating at the column scale impact the observed transport distances at the field scale. In contrast to classic colloid filtration theory^46,47 irreversible attachment alone is not able to reproduce the spatial-temporal distribution of E. coli in the field characterized by its delayed arrival at the wells more distal to Pond 1 (Fig. 6a). Reversible attachment alone was also inadequate (Fig. 6b). The observed concentration convergence in the five shallow monitoring wells, indicative of a slowly arriving plume over 3 days (Fig. 2), can only be reproduced by the model that assumes both reversible and irreversible modes of attachment.

Attachment and detachment rates vary dynamically with pore velocity^14,15,48,49. In the present 2-D model, however, these rates are assumed to be static. This limits the ability of the simpler, single attachment mode models to predict E. coli transport under transient flow conditions. The sharp decrease in modeled E. coli concentration after the end of each hydraulic input pulse in single attachment mode reversible and irreversible attachment models (Fig. 6a,b) is the result of fixed rates. In the more complex two attachment mode model, the high detachment rate (11.4 d^-1) maintains elevated E. coli concentrations in the aquifer independent of flow velocity. Classic colloid filtration theory, valid for uniform-sized particles travelling through uniform-size spherical beads, predicts a positive linear relationship between k_i and pore velocity^46,47. This relationship is qualitatively the same in natural heterogeneously-sized sand since empirical researchers find a linear relationship between k_a, k_d, k_i and pore velocity^14,15,48,49. This means that when pore velocity stagnates, k_a, k_d and k_i, decrease and pore concentrations would remain more stable than in the single attachment mode models presented here. These simpler models would perform better if Hydrus 2-D allowed attachment and detachment rates to vary with pore velocity.

Detachment has been demonstrated at the laboratory column^27,47,50(Fig. 7) scale, and at the field scale^23,51 by extended tailing after a bacterial plume has passed¹³. Temporary attachment has been attributed to particles attracted to like-charged grain surfaces in the secondary energy minimum⁵². Empirical evidence and theory shows that under repulsive bacteria-grain conditions, typical in nature, temporary attachment may in fact be a slow rolling of the bacteria along the surface until they either detach back into the flow stream or come to rest in flow stagnation zones downstream of a sand grain⁵³. Although it is typically studied at the pore^52,53 and column scale^27,47,50, the present study shows that detachment cannot be ignored at the field scale^23,51.

Pore velocity didn't only vary transiently in the 2-D model, it also varied spatially during filling events, from 8 m/d near the upper model boundary to <0.1 m/d at the outer model boundaries (data not shown). Modeled pore velocities are linearly dependent on K_h, which ranges +/-20% from the midpoint, however this uncertainty in K_h has a minor impact on model fit (Table 1). Substituting the lower and upper extremes of measured K_h while keeping kinetic parameters derived for the midpoint K_h constant caused RSME to increase by 59 and 33%, respectively.

There was uncertainty in longitudinal dispersivity in the 2-D model (λ), since published values range from 0.1 to 2.5 m for studies at the 10 m scale^38,54. Varying λ across this range while keeping kinetic parameters derived for λ=0.5 m constant caused RMSE to increase by 73 and 46%, respectively. This indicates that the model is similarly sensitive to λ and K_h. If these were permitted to vary with the kinetic parameters in the 2-D model, it is likely the fits of the field measured E. coli concentrations would have improved, but not enough to negate the need for all three kinetic parameters, since the RSME for the three parameter (two attachment mode) model was an order of magnitude better than the reversible attachment model (Fig. 6).

5.3 Potential Confounding Factors Comparing Columns to Aquifers

The differences in attachment rates between columns and aquifers could be partly due to differences in bacterial metabolic state, background water chemistry, and geochemistry of the sand. The water recharging through the base of Pond 1 contained potentially older E. coli that may have lost some of its surface coatings that enhance adsorption²⁶. Hijnen et al. (2005)²⁶ reported greater transport of indigenous thermotolerant coliforms in river water flowing through saturated columns packed with gravel than E. coli grown in the laboratory. In the present study, freshly grown E. coli was injected into the column, possibly leading to higher attachment rates and under prediction of field transport. Dissolved organic matter has been shown to enhance bacterial transport⁵⁵, in some cases coating positively charged metal oxides which attract the negatively charged bacteria^13,56,57, but this depends on the type of organic matter²⁶. Ponds in Bangladesh contain substantial DOC⁵⁸ and water recharging through Pond 1 had a low reduction potential (Eh) (data not shown) and its dark brown color and high E. coli concentrations were the product of human and animal organic waste¹⁰. In contrast, no organic matter was co-injected into the columns with E. coli. Lastly, the sand taken from the base of Pond 1 for columns appeared oxidized being light brown in color and the transition to grey sand occurred at 2.5 m below the base of the pond, near the level of the lowest water table level during the time period September 2008-December 2009²⁵. The higher irreversible attachment rate modeled on the column data may have been due to the presence of more positively charged metal oxides in the sand from the base of Pond 1^26,56,59. Similar to natural reductive processes washing sand with HCl to remove metal oxides increased peak E. coli breakthrough concentrations more than two-fold in 10 cm columns²⁷.

5.4 Scaling Microbial Transport with Kinetic Interaction Parameters

At the column scale, E. coli effluent breakthrough and retention curves can be modeled with simple or more complex numerical models (Table 3). For the two attachment mode, single population model, reversible attachment rates are similar to that modeled on field data, but irreversible attachment rates are an order of magnitude higher in the columns (Table 3). When the kinetic parameters derived from the two population models are substituted into the calibrated 2-D model, the predicted spatial extent of the E. coli plume is shorter than observed in the field (Fig. 8b). The rates from columns 3 and 4 predict that 4-log₁₀ removal would occur after 3.5 and 6.9 m, respectively. Clearly, variability between small columns can result in large differences in predicted transport distances in the field (Fig. 8b). But in each column the best model, assessed by goodness of fit to the column breakthrough and retention curves (Two Population Model), most accurately predicted field scale transport (Table 3). Therefore, quantification of attachment and detachment mechanisms, in 10 cm column experiments, are required to predict the movement of E. coli into the aquifer.

Table 3.

Best-fit Model Parameters for E. coli in Column Experiments performed using Sand from Base of Pond 1. The analytical model type refers to that extracted simply based on the peak steady-state breakthrough concentration which was taken to be the average normalized concentration (C/C_o) along the flat plateau^43,44. Assuming the advective flow regime was steady-state flow of 8 m/day, used in the column experiment, ki was used to obtain the 4-log₁₀ removal distance. The 1-D numerical modeling results were up-scaled by substitution into the calibrated, transient flow 2-D model. The results from the 2-D modeling are shown for comparison.

			Population 1			Population 2			Field Scale
Experiment	Model Name	Model Type	ka (d-1)	kd (d-1)	ki (d-1)	ki (d-1)	BTC R2 (-)	R2 (-)	Advective Flow Regime	4-log10 E. coli Hoirzontal Removal Distance (m)
Column 3	Irreversible, Peak C/Co	Analytical	-	-	197.7	-		-	Steady-State	0.4
Column 3	Irreversible	Numerical	-	-	227.1	-	0.00	0.50	Transient	1.0
Column 3	Reversible	Numerical	240.1	1.2	-	-	0.11	0.14	Transient	3.4
Column 3	Two Mode	Numerical	159.1	43.9	184.1	-	0.46	0.38	Transient	2.4
Column 3	Two Population	Numerical	130.2	7.3	71.4	842.5	0.54	0.86	Transient	3.4
Column 4	Irreversible, Peak C/Co	Analytical	-	-	117.5	-	-	-	Steady-State	0.6
Column 4	Irreversible	Numerical	-	-	115.7	-	0.60	0.07	Transient	2.1
Column 4	Reversible	Numerical	132.6	0.9		-	0.81	0.22	Transient	4.3
Column 4	Two Mode	Numerical	69.3	5.7	78.3	-	0.86	0.28	Transient	3.8
Column 4	Two Population	Numerical	96.9	4.1	0.0	276.5	0.83	0.82	Transient	6.9
							RMSE
Field 2-D	Irreversible	Numerical		-	7.6	-	1158	-	Transient	-
Field 2-D	Reversible	Numerical	10.5	0.2	-	-	826	-	Transient	-
Field 2-D	Two Mode	Numerical	60.0	7.6	5.2	-	99	-	Transient	8.8

Researchers tend to apply overly simplistic models when up-scaling column experiments to the field scale. Often only irreversible attachment is accounted for²⁹ in keeping with classic colloid filtration theory^46,47. The assumption of irreversible attachment operating in the context of steady-state flow biases predicted field transport distances. As a result column experiments are perceived to vastly over predict removal rates in sand aquifers^17,18,26, although the degree to which they over predict removal has rarely been quantified even with simple models²⁶. Where this has been quantified assuming irreversible attachment only, columns over predict removal by one²⁶ or more¹⁸ orders of magnitude. Our findings contrast with this general perception exemplified by Table 1 in Pang, 2009²⁹. Removal efficiency can be described spatially (D^-1) or kinetically (T^-1)²⁹. But a simple translation between the two can only be performed when steady-state flow conditions are assumed. In the present study, if the column data is modeled based on the peak breakthrough concentration assuming irreversible attachment and steady-state flow, as in Pang et al. (2009)²⁹ the predicted 4-log₁₀ removal distances are less than 1 m (Table 3). When those same irreversible attachment rates were applied to the 2-D transient flow model 4-log₁₀ removal distances were higher, partly due to high modeled pore velocities close to the base of Pond 1 (Table 3).

The inclusion of reversible and irreversible attachment in the up-scaled 2-D model produced much more realistic transport distances. The model that was complex enough to accurately describe transport and retention in columns also made reasonable predictions at the field scale (Table 3). Even amongst 1-D models presented here that include reversible attachment, the goodness of fit and the predicted transport distances vary (Table 3). The only model that is able to adequately describe both column breakthrough concentrations and retention profile, however, is the two population model (Fig. 4h). This model assumes that there are two populations of E. coli present, differing in their attachment characteristics⁶⁰. These underlying mechanisms result in transport that cannot be accounted for by a simple first-order removal process, neither can their impact at the field scale be predicted by a spatial removal rate from snap-shots in time at the column scale²⁹.

5.5 Predicting Field-Scale Transport from Ex Situ measurements

Differences in filtration rates in the vertical and lateral directions, in the presence of fine layers, are expected to be substantial. Feighery et al.²⁷ demonstrated substantially higher kinetic removal rates for E. coli flowing through intact vertical cores, with the horizontal silt layers preserved, than in columns packed with homogenized sediment from the same site²⁷. The utility of column experiments in making predictions at the field scale could therefore be improved if fine layers were explicitly rendered in the field-scale model to account for the impact of both spatially varying flow field and filtration rates.

Transient flow conditions are typical in aquifers under the influence of surface water^1,28,30. In the present study, column experiments were run at constant high advective velocity (8 m/day). This velocity was derived from the simulated peak advective velocity in the 2-D calibrated flow model on the saturated aquifer immediately below the upper boundary when Pond 1 was full, and is not representative of the modeled aquifer. Much lower peak velocities predominated through most of the 2-D model domain, even when Pond 1 was full. This may be why higher kinetic attachment rates were modeled on columns than on the aquifer. In future experiments, therefore parallel column experiments should be conducted across the range of those velocities encountered at the field site and these empirical relationships should be incorporated into the predictive field scale model.

6. Conclusions

Reproducing the movement of E. coli in a well-studied shallow sandy aquifer required a 2-D model that assumed both reversible and irreversible modes of bacterial attachment. Anisotropy of hydraulic conductivity was also shown to greatly influence the depth that microbial contamination emanating from a latrine pond can negatively impact groundwater quality. Kinetic attachment rates for E. coli measured in 10 cm columns were somewhat higher than modeled at the field scale, yielding a shorter 4-log₁₀ removal distance even when hydraulic anisotropy and multiple rainfall events are accounted for. The underestimate in the maximum transport distance in the field predicted by the columns was only 39-78%, however, suggesting that predicting field-scale transport from laboratory studies could be within reach once the dependency of kinetic attachment and detachment rates upon temporally and spatially varying flow field and sediment size distribution are accounted for. This is important because non-steady state conditions with multiple pulses of water are more typical of the natural environment, especially in places with extreme rainfall events.