Eight channel transmit array volume coil using on-coil radiofrequency current sources

Abstract

Background

At imaging frequencies associated with high-field MRI, the combined effects of increased load-coil interaction and shortened wavelength results in degradation of circular polarization and B₁ field homogeneity in the imaging volume. Radio frequency (RF) shimming is known to mitigate the problem of B₁ field inhomogeneity. Transmit arrays with well decoupled transmitting elements enable accurate B₁ field pattern control using simple, non-iterative algorithms.

Methods

An eight channel transmit array was constructed. Each channel consisted of a transmitting element driven by a dedicated on-coil RF current source. The coil current distributions of characteristic transverse electromagnetic (TEM) coil resonant modes were non-iteratively set up on each transmitting element and 3T MRI images of a mineral oil phantom were obtained.

Results

B₁ field patterns of several linear and quadrature TEM coil resonant modes that typically occur at different resonant frequencies were replicated at 128 MHz without having to retune the transmit array. The generated B₁ field patterns agreed well with simulation in most cases.

Conclusions

Independent control of current amplitude and phase on each transmitting element was demonstrated. The transmit array with on-coil RF current sources enables B₁ field shimming in a simple and predictable manner.

Introduction

A major confounding factor for the development of MRI applications at ultra-high B₀ field strength is radio frequency (RF) field inhomogeneity (1-4). Typical RF volume coils consist of several sources of B₁ field and generate a uniform resultant B₁ field by constructive superposition of the individual B₁ fields in the volume of interest (5,6). RF energy is transferred through one or two ports to the RF coil, which is designed to ensure sinusoidal distribution of currents in the circumferential direction. At high Larmor frequency, the short wavelength of the B₁ field in high dielectric media, combined with multiple sources, causes significant inhomogeneity in the total B₁ field due to alternate regions of constructive and destructive interference. In addition, the enhanced coil-sample interaction leads to B₁ field inhomogeneity caused by perturbation of the sinusoidal current distribution due to either non-uniform loading or mode mixing or both (7,8).

Studies have shown that B₁ field shimming, implemented by adjusting the amplitude and phase of B₁ field from each individual transmitter may dramatically improve B₁ field homogeneity (9,10). Parallel transmission techniques that utilize two or more degrees of freedom are typically used for B₁ field shimming. Parallel transmission relies on the ability to drive separate coil elements with independent waveforms, amplitudes, and phases and requires the transmitting elements to be well decoupled from each other. Traditional RF volume coils, such as birdcage coils and transverse electromagnetic (TEM) coils, are multi-modal resonant structures. The transmitting elements of such structures are strongly coupled to each other, making independent control extremely difficult to achieve. The transmitting elements may be decoupled from one another using coil overlapping to achieve good decoupling between nearest neighbors (11), while distant neighbors may be decoupled using capacitive networks (12). This is a complicated arrangement that is difficult to design and is sensitive to changes in coil loading. Microstrip transmitting elements (13) have gained in popularity as parallel transmitting elements due to their favorable decoupling characteristics. However, microstrip transmitters require dedicated high power RF amplifiers because good decoupling is achieved at the cost of transmitting efficiency. This drives up the per-channel cost of the transmit chain, making the parallel transmission system expensive. The Cartesian feedback technique introduced by Hoult et al.(14), relies on subtraction of scaled coupled voltages from the input to the amplifier. The advantage of this technique is that it enables the use of transmitting elements of arbitrary geometry with little effect on the decoupling performance, thereby potentially increasing the transmit efficiency. This technique and isolation amplifier technique introduced by Chu et al. (15) are effective, but involve the use of sophisticated feedback circuits and output matching networks (16).

RF current source drives for series tuned transmitting elements seems to be a promising alternative technique to the above. The concept, originally introduced in (17) and followed by a number of variants (18,19) is an open loop technique that involves the use of the transmitting element as the output circuit of the RF power amplifier, where the active device is used as a controlled current source. The advantage of this design is that decoupling between neighboring transmitting elements is provided by the high internal impedance of the current source, enabling the optimization of the transmitting element for transmit efficiency.

In this paper, we present a novel transmit array design based on RF current source excitation (17) that enables B₁ field shimming. We describe the design and construction of an 8-channel transmit coil with coil-mounted RF current sources and demonstrate deterministic B₁ field pattern control through independent control of the amplitude and phase in each transmitting element.

Methods

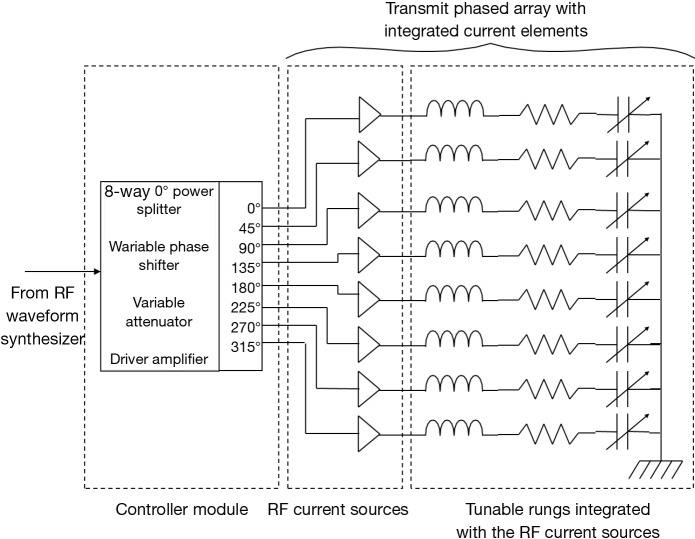
A block diagram of the transmit coil system is shown in Figure 1. The transmit coil system consists of an 8-channel controller module and eight current elements, arranged on a cylindrical former to form a transmit phased array volume coil. A current element consists of a series tuned transmitting element that forms the output circuit of a controlled RF current source.

Figure 1.

Block diagram of the 8-channel phased array transmit coil system. The B₁ field generator of each channel is a current element which consists of a rung integrated with a metal-oxide-semiconductor field effect transistor (MOSFET), voltage controlled current source. The control voltage is supplied by the controller module.

8-channel controller module

An 8-eight channel controller module (Figure 2) was constructed to provide drive voltage to the corresponding RF current source with independent amplitude and phase control. The module consisted of a single RF input that was split into eight channels using an 8-way, 0° power splitter (ZFSC-8-1, Mini-Circuits). Using coaxial delay lines, fixed phase shifts were implemented such that each channel was progressively lagging 45^o with respect to the previous channel. Each controller channel consisted of a DC voltage controlled attenuator (3-55 dB attenuation, 0-17V DC, RVA2500, Mini-Circuits), a DC voltage controlled phased shifter (180° linear phase shift, 0-12V DC, JSPHS-150, Mini-Circuits) and 2 stages of driver amplifiers [ERA-5SM (18 dBm output power) and HELA 10D (30 dBm output power), Mini-Circuits]. A bank of potentiometers provided the control voltages for the attenuators and phase shifters.

Figure 2.

The front panel of the controller module (A) shows 2 banks of 8 dials each. The upper bank of potentiometer dials is for amplitude control and the lower bank of potentiometer dials is for phase control. The controller module consists of 2 boards of 4 channels each. Each channel (B) consists of a voltage controlled phase shifter, a gain stage and a driver for the current source end stage.

8-channel transmit coil

A cylindrical acrylic former (OD: 305 mm, ID: 292 mm, length: 305 mm) was used as the base structural material for the transmit array coil design. Eight rectangular acrylic strips, 279 mm long and 19 mm wide were glued to the inner surface of the former at equal azimuthal angles, 45^o apart. Strips of copper tape 6 mm wide and 254 mm long were glued to the long edge of the rectangular strips, facing into the cylindrical cavity and formed the transmitting elements of the RF transmit coil.

An RF shield consisting of capacitively coupled strips of copper to minimize the formation of gradient induced eddy currents was tightly wrapped around the outer circumference of the cylindrical former. The PC boards containing the RF current source circuitry (17) were mounted on top of the RF shield. At one end, the transmitting elements were connected to the outputs of the RF current sources with strips of copper tape that were passed through the holes drilled into the former and RF shield. Each transmitting element was capacitively divided into five segments with 47 pF chip capacitors (ATC corp.). At the other end, each transmitting element was connected to a copper strip cut out on the RF shield. This copper strip was, in turn, connected to the RF shield via a trimmer capacitor, which was used to series tune the coil at 127.72 MHz. Figure 3 shows a picture of the completed coil.

Figure 3.

Top view of the completed transmit coil with the rung integrated current sources mounted on it. (a) is the output of the built-in magnetic field probe; (b) is the RF shield; (c) is gate voltage input connector; (d) is the trimmer capacitor connecting the rung to the RF shield; (e) is the drain voltage input connector and (f) is the MOSFET voltage controlled current source board. RF, radio frequency; MOSFET, metal-oxide-semiconductor field effect transistor.

The RF current source boards were divided into two groups of four boards each. The drain supply traces on boards of each group were connected in parallel using 14 AWG insulated copper wire. The two groups were in turn connected in parallel to an external high current, fixed voltage DC power supply (28 V, 12 A, Astron corp.) through heavy duty RF chokes. The gate supply traces on all eight boards were connected in parallel. In order to minimize heat dissipation from the MOSFET’s, the gate bias was provided to them only during the RF transmit pulse. The gate DC supply was derived from the ‘active low’ unblanking signal of the GE 3T transmitter, which is used to enable the system RF power amplifier during the transmit event. An op-amp inverter was implemented to invert the unblanking signal such that the MOSFET gate on each channel was provided with a DC bias of 3.6 V during RF transmit. The MOSFETs were thus biased to class AB linear operation during RF transmission and were turned OFF at all other times.

Integration with MRI scanner

The transmit coil was integrated with the GE Eclipse 3T scanner. The RF power input to the controller module was derived from the head coil port of the MRI scanner. The RF power was attenuated such that the maximum power input to the controller module did not exceed 15 dBm at the maximum transmit gain setting allowed by the system. The eight outputs of the controller module were connected to the inputs of the eight RF current sources mounted on the transmit coil.

Receive coil

An actively detuned quadrature saddle receive-only volume coil was constructed on an acrylic former (OD: 203 mm, ID: 191 mm, length: 254 mm) for imaging experiments (20). The coil was placed coaxially in the cavity of the transmit coil as shown in Figure 4. The quadrature coil outputs were connected to 2 channels of the 8-channel system receiver via a custom-built system interface. Active detuning of the receive coil during the transmit cycle was achieved using four PIN diode decoupling networks, two for each saddle pair. The PIN diode bias for the active decoupling networks was drawn from system PIN diode bias drivers.

Figure 4.

The picture shows the quadrature saddle receive-only coil placed coaxially with and within the volume of the 8-channel transmit array.

Imaging experiments

The goal of imaging experiments was to demonstrate B₁ field pattern control by recreating the characteristic modal patterns of linear and quadrature driven TEM resonators, using the 8-channel transmit array. A homogeneous cylindrical phantom filled with silicone oil was used for this purpose. A low flip angle Gradient Echo (GE) pulse sequence (TE/TR =20/800 ms, α=20°) was used to obtain images that approximated transmit field maps.

The current amplitudes and phases on the current elements were set using the controller module. For linear TEM resonator mode patterns, the relative phase between the current elements was set to zero and only the current amplitudes were dialed in as shown in Figure 5 (row C). For the quadrature TEM resonator mode patterns, the current amplitudes were set to a fixed value and relative phase between successive current elements was set to 45° (Figure 6, row C) for a cumulative phase of 360°. All the images obtained were compared to simulated field patterns of TEM resonator modes. Finally, the phase progression on the transmit array was reversed to obtain an anti-quadrature image in order to test the quality of circular polarization.

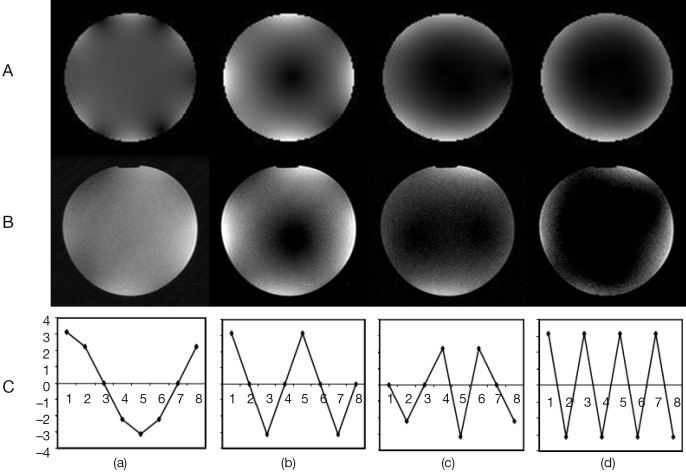
Figure 5.

Generation of modal patterns of a linearly excited resonant coil such as a TEM coil using the transmit array with a non-resonant structure. The figure is a [3×4] matrix with rows labeled (A-C) and columns labeled (a-d). The simulated modal patterns of an 8 rung TEM coil are [(A), (a-d)] are obtained by exciting the modes at their characteristic frequencies of 130.38 MHz (a), 131.94 MHz (b), 132.9 MHz (c) and 133.23 MHz (d). These modal patterns are generated at a single frequency (127.74 MHz) by the non-resonant transmit phased array [(B), (a-d)] by setting the current amplitude distributions on the current elements as shown in the charts of [(C), (a-d)]. The relative phases are set at zero. TEM, transverse electromagnetic.

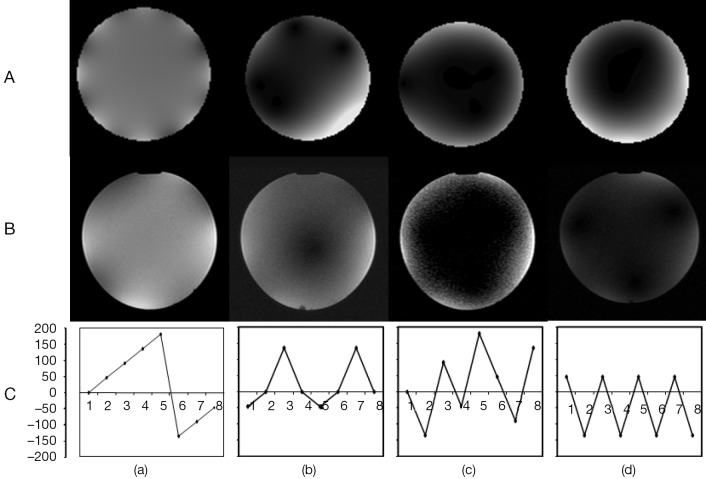
Figure 6.

Generation of modal patterns of a quadrature resonant coil such as a TEM coil using the transmit array with a non-resonant structure. The figure is a [3×4] matrix with rows labeled (A-C) and columns labeled (a-d). The simulated modal patterns of an 8-rung TEM coil are [(A), (a-d)] are obtained by exciting the modes at their characteristic frequencies of 130.38 MHz (a), 131.94 MHz (b), 132.9 MHz (c) and 133.23 MHz (d). These modal patterns are generated at a single frequency (127.74 MHz) by the non-resonant transmit phased array [(B), (a-d)] by setting the current phase distributions on the current elements as shown in the charts of [(C), (a-d)]. Current amplitudes are held constant for all four modes. TEM, transverse electromagnetic.

Simulations

The characteristic modal patterns of a TEM resonator were simulated for both 1-port linear excitation and 2-port quadrature excitation. For 1-port linear excitation, each modal pattern was obtained by exciting the resonator at the characteristic modal resonance frequency. For 2-port quadrature excitation, two geometrically orthogonal ports of the TEM resonator model were excited in phase quadrature. In both cases, the TEM resonator model was tuned to the appropriate mode of interest.

Results

The simulated field patterns of the degenerate modes of an 8-rung TEM resonator, excited at a single port, are shown in row (A) of Figure 5. These modal field patterns are generated at characteristic modal resonant frequencies due to current amplitude distributions as shown in the corresponding charts in row (C). For single port excitation, the relative phase between the rung currents is zero. Images obtained by setting up similar current amplitude distributions on the current elements that make up the transmit array show field patterns that are in close agreement with the simulated results. It should be noted however, that with the transmit array, the modal patterns are generated at a single frequency, the Larmor frequency, by independently controlling the current amplitudes on the current elements.

The simulated field patterns of the degenerate modes of a quadrature excited 8-rung TEM coil are shown in row (A) of Figure 6. In this case, the modal field patterns are generated at characteristic modal resonant frequencies due to the phase distribution of currents on the rungs as given by the charts shown in row (C). In theory, the vector sum of resonator currents due to the 2-port quadrature excitation should result in constant current amplitude for the uniform mode. The distribution of current amplitudes for higher order modes is more complex. Comparison of the real [row (B)] and simulated images shows that there is a good correspondence between modes 1 and 5 whereas modes 3 and 7 do not correspond. This could be explained by the fact that excitation ports are orthogonal to each other for modes 1 and 5 and hence the fields do not interfere with each other. However, for modes 3 and 7, the excitation ports are not orthogonal and hence there is cross-talk as shown by the simulations. In the case of the transmit coil, however, the current distributions were determined on the assumption of orthogonality of the excitation ports for all modes. Therefore, these images are closer to the linear excitation case.

Phantom images obtained by setting up quadrature and anti-quadrature phase progression of currents on the transmit array current elements are shown in Figure 7. Both images are set to the same window and level values. The anti-quadrature image exhibits very low signal compared to the quadrature in many regions with complete elimination of signal in some regions. With finer adjustments of the relative phase, it may be possible to achieve high quality circular polarization.

Figure 7.

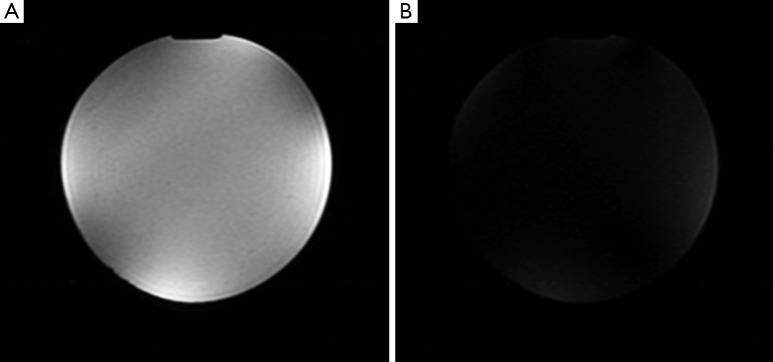
Circularly polarized B₁ field. (A) shows quadrature mode excitation which means that the B₁ field is co-rotating with the nuclear magnetic spins; (B) shows anti-quadrature mode excitation which means that the B₁ field is counter-rotating with respect to the nuclear magnetic spins. Anti-quadrature mode should not yield any image when the B₁ fields are perfectly circularly polarized.

The bright spots seen at the edges of the images are due to the fact that the phantom almost completely filled the cavity of the receive coil. Since the magnetic flux density is the highest near a current carrying conductor, the B₁ field patterns show bright spots in these regions. In the case of the anti-quadrature image, residual coupling between the receive and transmit coils may cause degradation in the circular polarization.

Discussion

The mode patterns of a birdcage or TEM coil occur at distinct frequencies as determined by the mutual inductances between their resonant loops. This is characteristic of a periodic, resonant structure. The resonant modes of a resonant structure are a potential liability at high field strengths. Load-coil interactions at high field strengths cause significant shift in the resonant frequency of the loops of a resonant coil. With asymmetric loading, the resonant frequencies of the heavily loaded loops may shift more than those of the lightly loaded loops, thereby exciting higher order modes in some loops. This causes field inhomogeneity due to mode mixing (7).

In contrast, the mode patterns of the non-resonant transmit array of current elements are generated at a single frequency, the Larmor frequency, by adjusting the amplitudes and phases of the currents on the current elements. This ability of the transmit array to generate controlled B₁ patterns could potentially be a useful tool to optimize homogeneity in the presence of lossy dielectric loads. For instance, it is known that images of samples with high dielectric constants have a bright central spot with alternating dark and bright bands around it (1,2,4,9,10,21). This is a typical interference pattern. In such cases, it may be advantageous to generate a mode 2 or mode 3 pattern or even a combination of modal patterns which would be possible with a current element array.

Resonant coils such as the birdcage and TEM coils are highly efficient as they exhibit high current gain. This is the nature of a resonant structure. The main disadvantage of the transmit array design is its low efficiency. The amplitude of the current driven through the rung is entirely dependent on the MOSFET drive voltage and the current handling capacity of the MOSFET. Therefore, the large current requirements of bigger volume coils would necessitate the use of MOSFET’s with very high current handling capacity and innovative heat dissipation designs. The primary advantage of the RF current source driven transmit array is its ability to generate controlled B₁ field patterns by independently controlling the current amplitude and phase on the component current elements. This feature may be used to perform B₁ field shimming in a simple and predictable manner.

Conclusions

The design and development of a novel 8-channel transmit phased array coil with dedicated RF current source drive per transmit channel has been described in detail. The volume coil has a non-resonant structure due to the weak coupling between the current elements, thereby enabling independent control of current amplitude and phase on each current element. B₁ field pattern control has been demonstrated by setting up desired currents on the current elements using the controller module. The coil design enables B₁ field shimming in a simple and predictable manner.