Genotype by Environment Interactions in Cognitive Ability: A Survey of 14 Studies from 4 Countries covering 4 Age Groups

Abstract

A large part of the variation in cognitive ability is known to be due to genetic factors. Researchers have tried to identify modifiers that influence the heritability of cognitive ability, indicating a genotype by environment interaction (GxE). To date, such modifiers include measured variables like income and socioeconomic status. The present paper focuses on GxE in cognitive ability where the environmental variable is an unmeasured environmental factor that is uncorrelated in family members. We examined this type of GxE in the GHCA-database (Haworth et al., 2009), which comprises data of 14 different cognition studies from 4 different countries including participants of different ages. Results indicate that for younger participants (4–13 years), the strength of E decreases across the additive genetic factor A, but that this effect reverts for older participants (17–34 years). However, a clear and general conclusion about the presence of a genuine GxE is hampered by differences between the individual studies with respect to environmental and genetic influences on cognitive ability.

Genetic and environmental influences on individual differences in cognitive ability have enjoyed extensive investigation (see Plomin & Spinath, 2004, for an overview). Using family-based designs, in which phenotypic variance is decomposed into additive genetic, unique environmental, and common environmental effects shared by family members (denoted A, E, and C, respectively), heritability estimates have been reported between roughly .5 and .7 for adolescents and adults (see McGue, 1997). For young children the heritability is somewhat lower than .5 (see Haworth et al., 2010), and for infants as young as 10 months, the heritability is appreciably lower (Tucker-Drob, Rhemtulla, Harden, Turkheimer, & Fask, 2011).

Having established that, at least beyond childhood, genetic factors explain a substantial part of the phenotypic variance in cognitive abilities, the question arises whether the heritability of cognitive ability is constant across the range of environmental effects. We consider variation in heritability as a function of an environmental variable to be a potential manifestation of Genotype by Environment interaction (GxE; Eaves, Last, Martin, & Jinks, 1977). Measures that have shown to influence or moderate the heritability of cognitive ability include parental income (Harden, 2007), socioeconomic status (Tucker-Drob et al., 2011; Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman, 2003), parental education (Grant et al., 2010; Rowe, Jacobson, & Van den Oord, 1999; Van der Sluis, Willemsen, de Geus, Boomsma, & Posthuma, 2008), and educational attainment (Johnson, Deary & Iacono, 2009). It is clear that the moderators in these studies are not strict environmental measures, although they may have a strong influence on the effective environment (Plomin & Daniels, 1987).

The present paper focuses on the detection of genotype by environment interaction in cognitive ability where the environment variable is unmeasured (Jinks & Fulker, 1970; van der Sluis, Dolan, Neale, Boomsma, & Posthuma, 2006; Molenaar, van der Sluis, Boomsma, & Dolan, 2012). Testing for genotype by unmeasured environment is important for a number of reasons, discussed below.

Screening

GxE can be studied in phenotypic variables while relevant environmental variables – i.e., variables that interact with genotype - are unknown or data on these variables are lacking. This opens the possibility to screen phenotypic variables for GxE, in the absence of any explicit theory identifying potential environmental moderators (see Molenaar et al., 2012). Once GxE is detected, one could investigate which environmental variables contribute to this interaction.

GWAS

Testing for gene by unmeasured environment is of interest in the context of Genome-Wide Association Studies (GWAS). In GWAS, GxE interaction is usually not modeled, although the presence of unmodeled GxE is hypothesized to affect the power to detect genetic variants. Several authors have suggested that the failure of GWAS to detect associations between phenotypes and common genetic variants (i.e., the ‘missing’ or ‘hidden’ heritability problem) might at least partly be due to unmodeled GxE (e.g. Eichler et al., 2010; Maher, 2008; Manolio et al., 2009). For those phenotypes that display GxE, the identification of the environmental factors causing the GxE would be of biological interest, and could facilitate the detection of associated genetic variants in GWAS.

Ability differentiation

Genotype by unmeasured environment interactions are relevant to substantive hypotheses. Most notably, Molenaar et al. (2012) discussed how the ability differentiation hypothesis (Spearman, 1927) can be investigated by testing for a GxE interaction on IQ test scores in the ACE-model. Ability differentiation concerns the hypothesis that correlations among IQ subtests scores decrease for increasing levels of the underlying general intelligence factor, g (Jensen, 1998; Spearman, 1927). Ability differentiation has been operationalized as a non-linear relation between g and the subtest scores (Tucker-Drob, 2009), a non-normal g-distribution (Molenaar, Dolan, & van der Maas, 2011), heteroscedastic residual variances (Hessen & Dolan, 2009), or smaller g variance at higher g levels (Reynolds, Keith, & Beretvas, 2010). GxE represents another important avenue to the conceptualization and analysis of ability differentiation. The observation that g is substantially heritable (e.g., McGue, 1997) may imply that the additive genetic factor, A, underlying g is a relatively weaker source of individual differences as the level of g increases. This implication may result if the unique environmental variance is greater at higher levels of A, i.e., an interaction between A and E.

Tucker-Drob, Harden, & Turkheimer (2009) related ability differentiation to gene by observed environment interaction. Specifically, they showed that when the environmental measure is correlated with g (as is the case with SES for instance), ability differentiation can result in spurious interactions between genotype and the observed environment measures. Other research related to ability differentiation and GxE concerns studies into the differential heritability of IQ (Detterman, 1990; Sundett, Eilertsen, Tambs, & Magnus, 1994; Thompson, Detterman, & Plomin, 1993; Brant et al., 2012), which addressed the question whether A is an equally strong source of individual differences across all levels of IQ (i.e., AxIQ interaction). Here, we follow Jinks and Fulker (1970) and address the question whether the environmental influences on IQ are an equally strong source of individual differences across all levels of A.

In the present article, we test for a genotype by unmeasured environment interaction on cognitive ability in a large dataset on cognitive ability from the GHCA consortium (Genetics of High Cognitive Abilities; Haworth et al., 2009). These data comprise IQ scores from 14 studies conducted in 4 different countries: US, UK, Australia, and the Netherlands. We analyzed the GHCA database, taking into account the variability of the IQ measures within the individual studies. Note that the same data has also been analyzed by Haworth et al. (2010). In this prior study, a linear increase of heritability was found across age. In the present study, we test for GxE in these data using the method proposed by Molenaar et al. (2012). This method is related to the test of Jinks and Fulker (1970, see above; see also van der Sluis et al., 2006), but has the advantage of including data of both MZ and DZ twins which increases power due to the separation of common and unique environmental factors. In the present paper we first present the GxE-model and describe the data in the GHCA database, and then present and discuss the results of fitting the GxE model to these data.

The Heteroscedastic ACE-model

Let Y_ij denote the phenotypic score of the j-th twin (j = 1, 2) of the i-th twin pair (i = 1, …, N). In the standard ACE-model, Y_ij is described by the following linear equation:

$${\mathrm{Y}}_{\text{ij}}=\mathrm{\nu }+{\mathrm{A}}_{\text{ij}}+{\mathrm{C}}_{\text{ij}}+{\mathrm{E}}_{\text{ij}},$$ (1)

where ν is an intercept. The additive genetic factor (A_ij), the common environmental factor (C_ij), and the unique environmental factor (E_ij) are assumed to follow a normal distribution with zero-means and variances σ_A², σ_C², and σ_E² respectively. In addition, it holds that cor(C_i1, C_i2) = 1, cor(E_i1, E_i2) = 0, cor(A_i1, A_i2) = 1, in MZ twins, and cor(A_i1, A_i2) = 0.5, in DZ twins. Under the assumption that A_ij, C_ij, and E_ij are uncorrelated, the phenotypic variance σ_Y² can be decomposed as follows:

$${{\mathrm{\sigma }}_{\mathrm{Y}}}^2={{\mathrm{\sigma }}_{\mathrm{A}}}^2+{{\mathrm{\sigma }}_{\mathrm{C}}}^2+{{\mathrm{\sigma }}_{\mathrm{E}}}^2.$$ (2)

Within the ACE-model, Molenaar et al. (2012) distinguished two possible GxE interactions, i.e., the interaction between A and C, and the interaction between A and E. To model these two interactions, we condition on A, i.e.,

$${{\mathrm{\sigma }}_{\mathrm{Y}\mid \mathrm{A}}}^2={{\mathrm{\sigma }}_{\mathrm{C}\mid \mathrm{A}}}^2+{{\mathrm{\sigma }}_{\mathrm{E}\mid \mathrm{A}}}^2.$$ (3)

In Equation (3), GxE can be modeled by allowing the variance of C and E to depend on the level of A. For instance, the variance of E can be decreasing across levels of A, which would mean that the heritability effectively increases. To this end, we specify a function to relate σ_E² and σ_C² to A. Van der Sluis et al. (2006) and Hessen & Dolan (2009) proposed to use the exponential function, as the range of this function is non-negative, which is desirable for a variance parameter. Thus, the ACE-model can be extended to include GxE in the following way:

$${{\mathrm{\sigma }}_{\mathrm{Y}\mid \mathrm{A}}}^2={{\mathrm{\sigma }}_{\mathrm{C}\mid \mathrm{A}}}^2+{{\mathrm{\sigma }}_{\mathrm{E}\mid \mathrm{A}}}^2=exp({\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1\mathrm{A})+exp({\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{A}),$$ (4)

where γ₀ and β₀ are baseline parameters which account for the part of the variance of C and E that does not depend on A, while γ₁ and β₁ are linear interaction parameters, which model the possible dependency of respectively the variance of C and E on A. We refer to this model as the heteroscedastic ACE model, as the C and E factor are heteroscedastic across A. From now, we use the term ‘GxE’ to refer to the general concept of ‘genotype-by-environment interaction’ and we use the term AxC or AxE to refer to a specific operationalization within the heteroscedastic ACE model. Thus, GxE can be established by testing β₁ to be significantly different from 0 (indicating an AxE interaction) and/or by testing γ₁ to be significantly different from 0 (indicating an AxC interaction).

In the heteroscedastic ACE-model, we cannot simply use σ_A² as an estimate for the heritability as this parameter is not appropriately standardized. In the presence of GxE effects in the ACE model, σ_A² needs to be standardized by using

$$h^2=\frac{{\mathrm{\sigma }}_A^2}{{\mathrm{\sigma }}_A^2+exp\left({\mathrm{\gamma }}_0+\frac{1}{2}{\mathrm{\gamma }}_1^2\right)+exp\left({\mathrm{\beta }}_0+\frac{1}{2}{\mathrm{\beta }}_1^2\right)}$$

The two terms involving exp(.) in the denominator concern the marginal variance of C and E respectively (see Hessen & Dolan, 2009). If γ₁ and β₁ are 0 (i.e., no AxC and AxE interactions), the formula for h² reduces to the traditional formula for heritability, σ_A²/(σ_A² + σ_C²+ σ_E²). It can therefore be seen that h² and the traditional heritability estimate diverge when the absolute value of γ₁ and/or β₁ increases.

The tests of β₁ and γ₁ discussed above (Equation 4) concern generalized linear GxE interactions.¹ It is possible to test for generalized curvilinear interactions by extending Equation (4) into

$${{\mathrm{\sigma }}_{\mathrm{Y}\mid \mathrm{A}}}^2={{\mathrm{\sigma }}_{\mathrm{C}\mid \mathrm{A}}}^2+{{\mathrm{\sigma }}_{\mathrm{E}\mid \mathrm{A}}}^2=exp({\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1\mathrm{A}+{\mathrm{\gamma }}_2{\mathrm{A}}^2)+exp({\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{A}+{\mathrm{\beta }}_2{\mathrm{A}}^2).$$ (5)

Here, β₂ and γ₂ are curvilinear interaction parameters that can be tested on significance similarly as discussed above.

The statistical properties of the model in Equation (4) are well documented (Jinks & Fulker, 1970; van der Sluis et al., 2006; Molenaar et al., 2012). It has been shown that parameter recovery is satisfactory, that both AxE and AxC interactions can be estimated together, and that power to detect AxE is generally good. The detection of AxC interactions, however, requires large samples (Molenaar et al., 2012).² It should be noted that the approach in Equation (4) does not take into account the possibility that C and E interact (i.e., CxE). Molenaar et al. showed that the presence of CxE does not appreciably affect tests of AxC. However, if C is the main source of variation, the detection of AxE is affected by the presence of CxE (i.e., unmodeled CxE may be incorrectly detected as AxE). Nevertheless, we found that, when A is the main source of variation, the presence of CxE hardly affects the detection of AxE. As A can be considered the predominant source of variation in IQ data (at least from childhood onwards), the presence of CxE in the data is not expected to affect tests on GxE using the present method (see Molenaar et al., 2012). We note, however, that there is empirical support for CxE in cognitive ability (Kremen et al., 2005; Hanscomb et al., 2011). Thus, although presence of CxE does not appreciably affect tests on GxE, heritability estimates might be affected. In a small simulation study based largely on the setting of the simulation in the Molenaar et al paper (results are available upon request), we found that the presence of CxE did not affect heritability estimates (percentage bias were close to 0). In addition, we found a minor effect on the estimate of σ_C², i.e., percentages bias of 3 to 8 percent for increasing effect size of the CxE effect. We believe that such biases are within the acceptable range given the purposes of the present undertaking. We therefore conclude that the presence of unmodeled CxE will not importantly affect the results as reported below.

The GxE model can be fitted to data of both MZ and DZ twins using marginal maximum likelihood (MML; Bock & Aitkin, 1981). In this procedure, the observed data, conditional on A, are assumed to follow a normal distribution. Note that unconditionally, the phenotypic data may be non-normal, as the presence of GxE will generally result in non-normality (Eaves et al., 1977). In principle, a marginal test on normality could be conducted on singleton data to test for GxE (e.g., the Shapiro-Wilks test on normality, Shapiro & Wilks, 1965). However, as the present tests on non-normality are more specific, power to detect non-normality is larger as compared to the marginal tests (see Molenaar, Dolan, & Verhelst, 2009). In addition, to be able to distinguish AxC from AxE, singleton data is not sufficient and twin data is required. The model from Equation (5) is fitted using the freely available software package Mx (Neale, Boker, Xie, & Maes, 2002). As both AxC and AxE can be combined in a single model, the free parameters to be estimated are: σ_A², β₀, β₁, β₂, γ₀, γ₁ and γ₂. Example script are available on the website of the first author.

Application to GHCA data

Description of the data

The database comprises univariate IQ scores of 14 studies conducted in four countries: US (Colorado, 3 studies; Minnesota, 2 studies; Ohio, 1 study), UK (1 study), Australia (1 study), and the Netherlands (6 studies). Aggregating all of these data yields a total of 10897 twin pairs (4911 MZ pairs and 5986 DZ pairs). The age of the participants varies from 4 to 71. For each twin in the database, an IQ measure is available. Across the different studies, different test batteries have been used to obtain IQ score. For instance, in one of the US studies, the short form of the Stanfort-Binet Intelligence Scale was used; in the UK study, 3 subtests of the WISC-III were administered together with Raven’s progressive matrices; and in another study from the US, the full WISC-III was used. We refer to Haworth, et al. (2009) and the references therein, for a detailed overview of the IQ test batteries used in the different studies.

Analysis

As the aggregated data are heterogeneous with respect to age, we follow Haworth et al. (2010), and perform the analysis within more age-homogenous subgroups. Haworth et al. considered 3 age categories: 4–10, 11–13, and 14–34. All participants above age 34 are omitted as there were too few participants in this age range to construct a reasonably homogenous subgroup with respect to age. In our analysis, we modified the age categories of Haworth et al., because we considered it possible that the nature of GxE differs between adolescents (who presumably are still in school and live at home) and young adults. Specifically, we created the categories: 4–10, 11–13, 14–16, and 17–34. We note that the general pattern of results, as presented below, does not depend on the exact age categories that are used: results are generally the same for the Haworth et al. age categories. However, our categorization does provide a clearer picture of how GxE changes across age. See Table 1 for the sample sizes within the age groups of both Haworth et al. and our age categorization.

Table 1.

Number of MZ and DZ twin pairs (N_MZ; N_DZ) within the age categories as used by Haworth et al. and as used in the present study.

	Haworth et al.			Present
Group no	Age	NMZ	NDZ	Age	NMZ	NDZ
1	4–10	1140	1613	4–10	1140	1613
2	11–13	2195	2722	11–13	2195	2722
3	14–34	1507	1582	14–16	807	966
4	-	-	-	17–34	700	616
total N	-	4842	5917	-	4842	5917

As can be seen in Table 1, in our alternative categorization, the third category of Haworth et al. (2010) is split into one relatively homogenous age group (14–16), and an additional group (age 17–34). We also considered a second alternative in which this additional group was made more homogenous (i.e., participants of ages 17–20), but this categorization did not alter the results.

The aggregated data are potentially heterogeneous as they originated from 14 different studies. To establish whether the results within the age groups hold across the different studies, we conduct the analyses on both the aggregated data and on the data of each of the 14 individual studies. Table 2 provides the distribution of participants over age categories and studies. Some studies include only participants in one age category (e.g., Netherlands #1), while other studies include participants in multiple age categories (e.g., Colorado #1). In some cases, a study contained too few participants in a given age category to enable model fitting on this subsample (e.g., Netherlands #4 only contains 13 MZ twins and 14 DZ twins between 14 and 16 years old). Therefore, for our analyses, we only select 17 subsamples that we considered large enough to provide stable parameter estimates. These samples are shown in boldface print in Table 2. Note that we omitted Netherlands #5 because we considered the total sample size to be too small, and we omitted Netherlands #6, as this study only contains participants of age 40–70. In the analysis on the aggregated data however, we do include Netherlands #5. The data are standardized within each study by the original authors (Haworth et al., 2009). We additionally standardized the data within each age group. The resulting data thus are standardized in each age × study cell of the design.

Table 2.

Number of MZ and DZ twin pairs (N_MZ; N_DZ) within each age category for each study in the GHCA database

Study	Total N	Age 4–10	Age 11–13	Age 14–16	Age 17–34
Netherlands #1	125; 112	125; 112	0; 0	0; 0	0; 0
Netherlands #2	49; 63	49; 63	0; 0	0; 0	0; 0
Netherlands #3	79; 111	0; 0	79; 111	0; 0	0; 0
Netherlands #4	79; 108	0; 0	0; 0	13; 14	66; 94
Netherlands #5	36; 58	0; 0	0; 0	0; 0	36; 58
Netherlands #6	69; 69	0; 0	0; 0	0; 0	0; 0
Colorado #1	752; 1025	391; 534	204; 280	126; 173	31; 38
Colorado #2	215; 175	17; 6	13; 14	153; 125	32; 30
Colorado #3	332; 364	0; 0	30; 44	99; 140	203; 180
Minnesota #1	777; 469	43; 16	734; 453	0; 0	0; 0
Minnesota #2	410; 214	0; 0	0; 0	92; 31	318; 183
Australia	338; 515	0; 0	0; 0	324; 483	14; 32
Ohio	121; 171	121; 171	0; 0	0; 0	0; 0
UK	1529; 2532	394; 714	1135; 1818	0; 0	0; 0

Note. Samples used for the analysis of the individual studies are in boldface.

Results

MZ and DZ twin correlations of the IQ measures in the 17 subsamples are presented in Table 3. In the Table the skewness, kurtosis, and the Shapiro-Wilks test of normality are also given as non-normality could be an indication of GxE. As can be seen, normality is rejected in the first two aggregated age categories. As indicated by the skewness, the IQ distributions have a heavier lower tail (negatively skewed), suggesting that the variance of E and or C might be decreasing across A. However, these are just indications; more elaborate tests are possible with the heteroscedastic ACE model. We present these results next.

Table 3.

MZ and DZ correlations, skewness, kurtosis and a test on normality of the IQ measures in the 17 subsamples within each age category.

Cat	Study	Cor		Skewness		Kurtosis		p-value S-W test
		MZ	DZ	Twin 1	Twin 2	Twin 1	Twin 2	Twin 1	Twin 2
4–10	Netherlands #1	0.70	0.49	−0.41	−0.56	2.99	3.56	0.01	0.00
	Netherlands #2	0.78	0.51	−0.16	0.21	3.73	2.99	0.23	0.27
	Colorado #1	0.81	0.52	0.09	−0.12	3.12	3.19	0.05	0.03
	Ohio	0.76	0.55	0.10	−0.06	2.85	3.03	0.69	0.69
	UK	0.66	0.50	−0.33	−0.35	2.94	2.88	0.00	0.00
	Aggregated	0.74	0.54	−0.12	−0.21	3.14	3.12	0.00	0.00
11–13	Netherlands #3	0.86	0.53	−0.02	−0.06	3.26	2.84	0.37	0.39
	Colorado #1	0.87	0.55	0.10	0.17	2.74	2.75	0.29	0.09
	Minnesota #1	0.76	0.51	0.17	0.05	3.10	3.35	0.01	0.06
	UK	0.68	0.44	−0.58	−0.67	3.39	3.52	0.00	0.00
	Aggregated	0.73	0.47	−0.31	−0.38	3.20	3.29	0.00	0.00
14–16	Colorado #1	0.84	0.52	0.29	0.20	3.27	3.25	0.05	0.38
	Colorado #2	0.88	0.46	−0.12	−0.11	3.33	2.91	0.05	0.19
	Colorado #3	0.77	0.49	0.21	−0.05	3.48	3.73	0.03	0.03
	Minnesota #2	0.81	0.42	0.27	0.16	2.39	2.50	0.05	0.48
	Australia	0.82	0.45	−0.13	−0.09	2.46	2.46	0.00	0.00
	Aggregated	0.83	0.46	−0.02	−0.04	2.94	2.93	0.22	0.17
17–34	Netherlands #4	0.86	0.34	−0.21	−0.21	2.48	2.27	0.08	0.05
	Colorado #3	0.86	0.57	−0.03	−0.03	2.74	2.89	0.44	0.82
	Minnesota #2	0.80	0.52	0.53	0.52	3.23	3.07	0.00	0.00
	Aggregated	0.82	0.49	0.13	0.13	3.00	3.08	0.16	0.05

Note. ‘cor’ denotes twin correlation. p-values of the S-W (Shapiro-Wilks) test smaller than one’s alpha level indicate non-normality. Normality is characterized by skewness and kurtosis of 0 and 3, respectively. Note that the aggregated analysis does include the Netherlands #5 and Netherlands #6 studies.

Table 4 gives the parameter estimates of the heteroscedastic ACE model with linear and curvilinear effects for the AxE and AxC interactions on the aggregated data. In the aggregated data, we investigated within each age group, whether the linear and quadratic effects improved model fit. These results are in Table 5. As can be seen, the model with a linear AxE effect only is favored by the likelihood ratio test (LRT), AIC and BIC in all age groups except age group 14–16. In this age group, results are mixed as the AIC favors the full model and the BIC indicates that none of the GxE effects (i.e., AxE and AxC) are significant. As the latter model is more parsimonious, we accept that in age group 14–16, no interactions are present. As none of the AxC interactions were significant and at most linear AxE interactions were found, we focused on the results of the ACE model with a linear AxE interaction in all age groups for the remaining analyses. See Table 6 for the heritability and standardized parameter estimates within each age group for each individual study and the aggregated data. As can be seen, in most cases h² is close to σ_A² indicating that heritability as operationalized in the ACE model (i.e., as the standardized estimate of σ_A²) is only mildly affected by the AxE.³

Table 4.

Parameter estimates of the heteroscedastic ACE model with linear and curvilinear effects for the AxE and AxC interactions.

age group	β0	β1	β2	γ0	γ1	γ2
4–10	−1.46	−0.37	0.04	−1.15	0.02	0.03
11–13	−1.53	−0.47	−0.13	−1.53	−0.13	0.08
14–16	−1.81	−0.09	−1.08	−2.44	0.54	−0.04
17–34	−1.90	0.39	−0.27	−1.70	−0.03	0.06

Table 5.

Model fit indices for the heteroscedastic ACE-model

Model	Description	age group	4–10	11–13	14–16	17–34
statistic
β1, β2, γ1, γ2	full model	LRT	-	-	-	-
		AIC	3121	5657	1795	1239
		BIC	−14706	−29099	−8789	−6172
β1, β2, γ1, -	drop curvilinear AxC	LL	0.28	1.83	6.76	2.97
		AIC	3120	5656	1799	1240
		BIC	−14710	−29102	−8790	−6174
β1, -, γ1, -	drop curvilinear AxE	LL	0.06	0.03	0.12	0.01
		AIC	3118	5654	1797	1238
		BIC	−14714	−29106	−8793	−6177
β1, -, -, -	drop linear AxC	LL	1.87	0.07	2.55	0.17
		AIC	3118	5652	1798	1237
		BIC	−14717	−29110	−8796	−6181
-, -, -, -	drop linear AxE	LL	42.06	258.91	0.01	18.93
		AIC	3158	5909	1796	1253
		BIC	−14699	−28985	−8800	−6175

Note. For the AIC and BIC, best values are in boldface. The unrounded AIC value for the third and fourth model equal respectively 3117.691 and 3117.565. The likeklihood ratio test (LRT) concerns one degree of freedom.

Table 6.

Age descriptives, heritability, standardized parameter estimates, and number of MZ and DZ twins within each age category for both the aggregated data and the data within each study.

Cat	Study	NMZ	NDZ	Age		Heritability	Variance of A	Variance of E Baseline and AxE parameter		Variance of C	χ2(1)
				mean	sd	h2	σA2	β0 (baseline)	β1 (AxE)	σC2
4–10	Netherlands #1	125	112	5.80	0.06	0.43	0.42 (0.18; 0.68)	−1.43 (−1.77; −1.13)	−0.70 (−1.09; −0.34)	0.26 (0.03; 0.50)	14.62
	Netherlands #2	49	63	9.10	0.10	0.53	0.52 (0.18; 0.98)	−1.54 (−1.92; −1.11)	−0.16 (−0.64; 0.29)	0.24 (0.00; 0.60)	0.53
	Colorado #1	391	534	8.92	0.80	0.64	0.65 (0.51; 0.84)	−1.82 (−2.04; −1.59)	0.42 (−0.17; 0.68)	0.19 (0.05; 0.32)	2.65
	Ohio	121	171	6.07	0.68	0.42	0.42 (0.21; 0.65)	−1.46 (−1.71; −1.20)	0.13 (−0.19; 0.46	0.34 (0.12; 0.55)	0.62
	UK	394	714	10.59	0.24	0.32	0.32 (0.18; 0.46)	−1.21 (−1.37; −1.06)	−0.53 (−0.72; −0.37)	0.34 (0.22; 0.45)	42.52
	Aggregated	1140	1616	9.06	1.79	0.42	0.41 (0.34; 0.49)	−1.42 (−1.52; −1.33)	−0.33 (−0.45; −0.22)	0.34 (0.26; 0.41)	33.98
11–13	Netherlands #3	79	111	12.02	0.08	0.64	0.64 (0.41; 0.87)	−1.95 (−2.25; −1.62)	−0.02 (−0.49; 0.51)	0.21 (0.00; 0.47)	0.01
	Colorado #1	204	280	11.85	0.81	0.65	0.64 (0.50; 0.80)	−2.06 (−2.26; −1.85)	0.14 (−0.13; 0.43)	0.22 (0.08; 0.38)	1.01
	Minnesota #1	734	453	11.82	0.40	0.49	0.49 (0.36; 0.62)	−1.44 (−1.55; −1.33)	0.23 (−0.001; 0.42)	0.27 (0.14; 0.40)	3.82
	UK	1135	1818	11.78	0.40	0.50	0.49 (0.41; 0.57)	−1.37 (−1.47; −1.28)	−0.73 (−0.83; −0.64)	0.16 (0.09; 0.23)	306.29
	Aggregated	2195	2720	11.83	0.47	0.56	0.52 (0.46; 0.59)	−1.45 (−1.52; −1.38)	−0.52 (−0.60; −0.45)	0.21 (0.15; 0.27)	203.10
14–16	Colorado #1	126	173	14.74	0.77	0.80	0.79 (0.63; 0.93)	−2.12 (−2.36; −1.86)	0.09 (−0.26; 0.46)	0.08 (0.02; 0.26)	0.27
	Colorado #2	153	125	16.00	0.00	0.75	0.76 (0.49; 0.96)	−2.03 (−2.31; −1.76)	0.57 (0.25; 0.93)	0.10 (0.02; 0.36)	11.58
	Colorado #3	99	140	14.75	0.84	0.54	0.54 (0.28; 0.81)	−1.54 (−1.97; −1.21)	−0.33 (−0.95; 0.12)	0.24 (0.00; 0.50)	1.89
	Minnesota #2	92	31	16.84	0.10	0.81	0.77 (0.62; 0.93)	−1.70 (−1.95; −1.42)	0.19 (−0.16; 0.52)	0.00 (0.00; 0.34)	1.13
	Australia	324	483	15.93	0.26	0.73	0.72 (0.59; 0.82)	−1.75 (−1.91; −1.59)	−0.24 (−0.45; −0.03)	0.09 (0.02; 0.22)	5.12
	Aggregated	807	966	15.66	0.81	0.71	0.71 (0.63; 0.78)	−1.77 (−1.86; −1.67)	−0.05 (−0.20; 0.10)	0.12 (0.06; 0.20)	0.41
17–34	Netherlands #4	66	94	17.62	0.38	0.80	0.85 (0.62; 1.00)	−1.93 (−2.28; −1.55)	−0.11 (−0.53; 0.35)	0.06 (0.00; 0.23)	0.24
	Colorado #3	203	180	19.46	2.00	0.53	0.53 (0.36; 0.73)	−1.85 (−2.11; −1.61)	−0.38 (−0.74; −0.05)	0.31 (0.11; 0.50)	4.94
	Minnesota #2	318	183	17.63	0.36	0.57	0.56 (0.38; 0.76)	−1.76 (−1.97; −1.57)	0.53 (0.27; 0.82)	0.23 (0.07; 0.43)	17.21
	Aggregated	700	615	18.78	2.71	0.69	0.69 (0.57; 0.80)	−1.77 (−1.88; −1.65)	0.19 (0.01; 0.37)	0.14 (0.05; 0.26)	4.39

Note. χ²(1) denotes a likelihood ratio test on parameter β₁. 95% confidence intervals are in brackets.

^*In a few cases we experienced numerical difficulties in estimating the lower bound of γ₀ because the number of DZ twins was too small. ‘Aggregated’ is based on the aggregated data within the corresponding age category including the Netherlands #5 and Netherlands #6 studies. As some samples are omitted in the analysis of the individual studies (see Table 2), N_MZ and N_DZ will not necessarily add up to the aggregated N_MZ and N_DZ.

In Figure 1, we plotted the heritability estimates within each of the 17 subsamples against the average age of the subsamples. The plot is consistent with the findings of Haworth et al. (2010) in this dataset, i.e., that heritability increases monotonically with age. As can be seen in the figure, there are substantial differences in the heritability estimates across studies. Some of these differences may be attributed to sample size (i.e., the small studies of approximately the same average age show differences due to sampling fluctuations). However, results of some of the larger studies also show substantial differences, even though the average age is approximately the same over the studies. We return to this point below.

Figure 1.

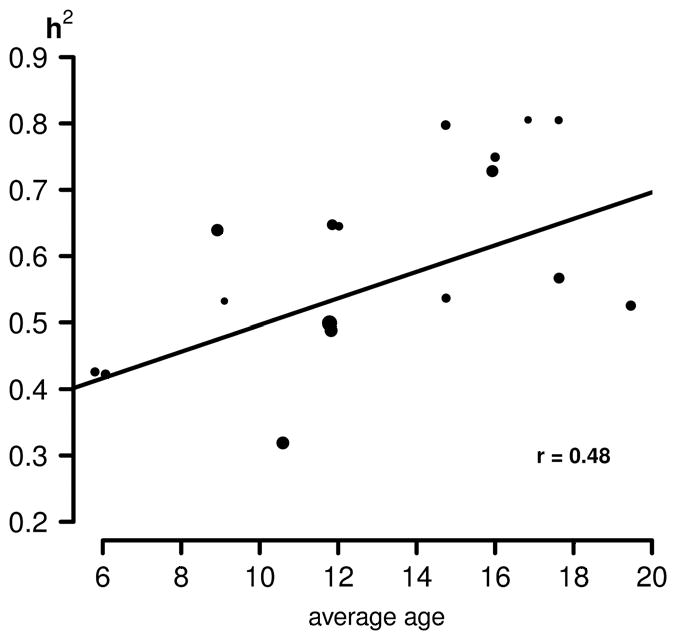
Heritability (h²), as estimated in the 17 samples from the 14 individual studies, plotted against the average age of the sample. Sizes of the dots are proportional to the sample size of the corresponding sample. Both the regression line and correlation coefficient take the differences in sample size into account.

The AxE interactions as obtained in each study and in the aggregated data are depicted in Figure 2 for each age group. From the results of the aggregated data in Figure 2a and Figure 2b, it appears that in age categories 4–10 and 11–13, the variance of E is decreasing across levels of A. The decrease is significant at α=.05, according to both the likelihood ratio test and the 95% confidence interval of β₁ (see Table 6).⁴ Within the individual studies some differences in the form of the GxE are apparent, but individual study results tend to follow the trend from the aggregated data. Main departures are Colorado #1 in age group 4–10, and Minnesota #1 in age group 11–13. Both studies show a significant effect in the opposite direction as compared to the effect in the aggregated data, i.e., the variance of E increases with A. Other studies show no effect or an effect consistent with the aggregated result.

Figure 2.

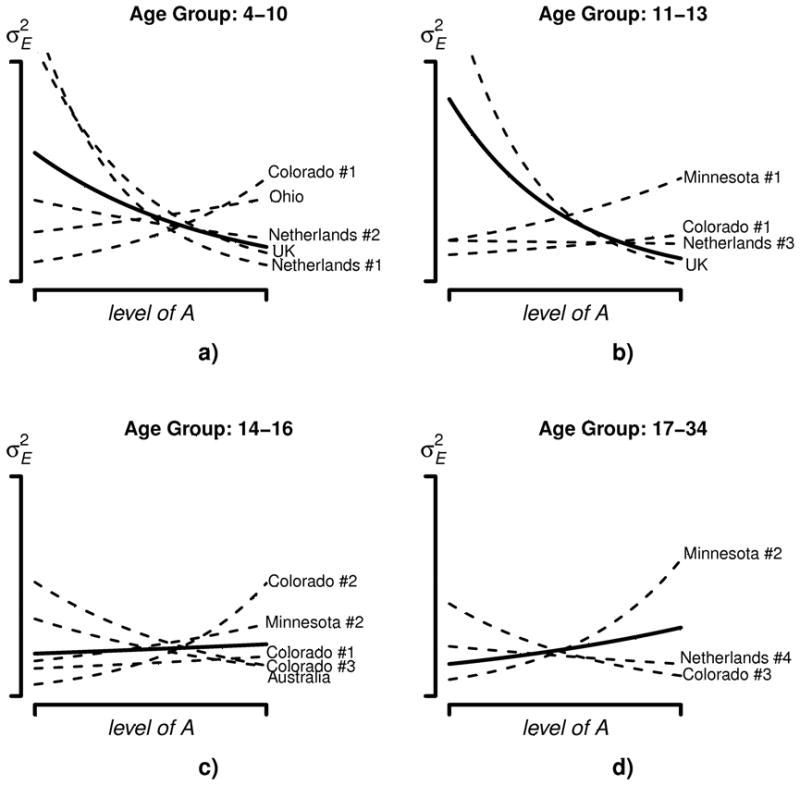
Variance of E (σ_E²) as a function of A within each age group. Dashed lines represent the results of the individual studies; the solid bold line represents the results of the aggregated data.

In age category 14–16, no effect is observed in the aggregated data according to the likelihood ratio test and the confidence interval of β₁ (see Table 6). Within the individual studies some differences in the form of the AxE are apparent, but results tend to follow the results from the aggregated data. Some studies show an effect in the opposite direction (i.e., Colorado #1, Ohio, Colorado #2, and Minnesota #1). However, none of these effects are significant at α = 0.05, see Figure 2c and Table 6. In age category 17–34, Figure 2d, the aggregated data show an increase of σ_E² across A. This effect is significant according to the likelihood ratio test and the confidence interval of β₁ (see Table 6). The effect in the aggregated data is reproduced in the Minnesota #3 study. However, the Colorado #3 study shows an effect in the opposite direction.

If we compare the results from Table 6 to those from Table 3, we can conclude that generally, GxE is present in the data (Table 6) if normality is rejected (Table 3). However, for some cases this does not hold. For instance, the Colorado #3 study in age group 14–16 is not associated with a GxE interaction, but normality is rejected. The opposite is also observed, e.g., in the Colorado #3 study GxE is present but normality is not rejected.

Conclusion on aggregated data

In the aggregated data, we observed that for participants between the age of 4–10 and 11–13, the influence of the unique environmental factor, E, decreases with increasing levels of the additive genetic factor, A. In participants between the age of 14 and 16, no effect was detected. In the participants between 17 and 34, the influence of factor E increased with increasing levels of A. Taken at face value, this pattern of results suggests that the direction of the AxE on IQ reverts during adolescence and young adulthood. However, as we discuss next, given the differences in the results between the samples, this conclusion should be drawn with care.

Different results across studies

The pattern of results as presented in Table 6 reveals substantial differences between the individual studies.⁵ First, estimates of the additive genetic effects, σ_A², within each age group vary considerably over the studies. For age 4–10, 11–13, 14–16, and 17–34, estimates range from .32 to .65, from .49 to .64; from .54 to .79; and from .53 to .85, respectively. Part of these differences can be explained by the small sample size of some of the studies, which renders the estimate of σ_A² subject to large sampling error. Still, some of the larger studies within the same age group show substantial differences in the estimates of σ_A². For instance, in the age category of 4–10, the estimate is .32 in UK study (N = 1108), but .65 in the Colorado #1 study (N = 925). In addition to the differences with respect to σ_A², we see some differences with respect to the effect of the common environment, σ_C². For age 4–10, 11–13, 14–16, and 17–34, estimates of σ_C² range from 0.19 to 0.34; from 0.16 to 0.27; from 0.00 to 0.24; and from 0.06 to 0.31, respectively. Again, some of these differences may be due to sampling error, yet, large studies do show variable results, for instance, the estimate of σ_C² is 0.34 in the UK study, and 0.19 in the Colorado #1 study in the age range 4–10.

Finally, we see similar variability with respect to the estimates of the AxE effect, β₁. Within age groups, estimates vary widely and can even be of opposite sign. Large studies also show substantial differences, e.g., within age group 17–34, the β₁ of the Colorado #3 study equals −0.38, while the Minnesota #2 study is associated with an opposite effect (β₁ = 0.53).

Differences in additive genetic and shared environmental influences

Given the variability we observed with respect to estimates of σ_A² and σ_C², even in the larger studies, the question arises how these differences come about. Here, we discuss possible causes.

First, studies differ substantial in the IQ measures that were used. Some studies used full test batteries (Colorado #1, Colorado #2, Netherlands #3, and Netherlands #4); others used only 2 subtests (Colorado #3), 4 subtests (Ohio, UK, Minnesota #1, Minnesota #2), 5 subtests (Australia), or 6 subtests (Netherlands #1 and Netherlands #2). These psychometric differences result in variation in the exact composition of the IQ measure. For instance, some studies rely only on the subtest from the Verbal Comprehension and Perceptual Organization domain (e.g., the Minnesota studies), while in other studies (e.g., Colorado #1 and #2 studies) measures are included from all major cognitive domains (Working Memory, Perceptual Speed, etc). This variation is important as genetic, unique and common environmental influences and GxE may differ across specific cognitive abilities (e.g., Finkel, Pedersen, McGue, & McClearn, 1995).

Another source of differences in results between the individual studies are the possible differences on background variables which are known to be related to heritability, e.g., parental income, educational attainment, or SES (Turkheimer et al., 2003). First, representativity of the samples may differ across countries. For instance, in the Australia study, twins are mainly from the entire Brisbane area while in the Minnesota studies, all twins lived close to the laboratory were testing took place. Thus the Minnesota sample is from a specific region (i.e., where the laboratory was located), while in the Brisbane sample, participants are from much more varied regions. In addition, there are differences between the individual studies in the way in which participants were recruited. Some studies relied on birth records (e.g.., Colorado #2), others relied on primary and secondary schools (e.g., Australia) or media advertisements (e.g., Ohio). Such variability in recruitment might have resulted in differences on background variables across countries.

Differences in genotype by environment interaction across studies

The differences in the estimates of the AxE effect, β₁, are such that they defy substantive explanation. From Table 6, it appears that the β₁ estimates vary, with opposite effects across studies within the same age group. For instance, in age group 14–16, the Colorado #2 study shows a significant effect with β₁ = 0.57, while the Australia study is associated with a significant effect in the opposite direction, β₁ = −0.24. Similarly, in age category 17–34, two opposite yet significant effects are observed: Colorado #3 with β₁ = −0.38 and Minnesota #2 with β₁ = 0.53. Such differences across studies render substantive conclusion in terms of genuine genotype-by-environment interaction difficult. Whether the AxE effects on the aggregated data can be interpreted substantively remains an open question. We discuss this further below.

Discussion

In this study we used a heteroscedastic ACE model to investigate the presence of GxE in cognitive ability in 14 different studies conducted in 4 countries covering 4 different age groups.

Similar to the standard ACE model, the heteroscedastic ACE model assumes that A, C, and E are uncorrelated and the question arises whether violations of this assumption affect results on GxE (i.e., tests on AxC and/or AxE). In the Molenaar et al. (2012) study, we showed that a linear correlation between A and E due to shared genetic effects between the phenotype and a measure of E did result in spurious GxE. However, it remains to be investigated whether a direct correlation between A and E influences tests on GxE. For instance, it is possible that AxE as operationalized in the heteroscedastic ACE model, could arise due to difference in the A–E or A–C correlation across environments or genotypes. This would imply a nonlinear relation between A and E or A and C which can possibly influence the results concerning AxE and AxC respectively. This is an interesting topic for further research.

In the present study, it appeared that results on the aggregated data are difficult to interpret in terms of a genuine GxE effect because results differed considerably with respect to presence, as well as direction of the GxE effect, across countries and ages. The possibility that differences in measurement instruments across countries caused artificial GxE in different directions cannot be ruled out (see Eaves et al., 1977). We would have been more confident about the genuineness and interpretation of the GxE results on the aggregated data if we had observed consistent effects across countries, studies, and age groups.⁶

Representativeness of the samples analyzed in a GxE analysis is another important issue. As mentioned by Turkheimer et al. (2003) and Hanscombe et al. (2012) unrepresentativeness can affect GxE results if the sample under consideration differs from the population on important background variables. For instance, it has been argued that the direction of GxE may be different at the extremes of SES (Scarr, 1992), suggesting that GxE results can diverge across samples that differ with respect to SES. Another problem with unrepresentative samples is that the unrepresentativeness itself may be an spurious source of non-normality (e.g., by oversampling either extreme of the IQ distribution), which in turn may result in the detection of spurious GxE.

Given its relative statistical and substantive importance, it is remarkable to see that the detection of GxE in general, and genotype by unmeasured environment interactions in particular, is a challenging task (see Eaves, et al., 1977; Eaves, 2006). A main problem is that measurement issues such as floor or ceiling effects, and poor scaling may give rise to spurious GxE. The question rises how we may overcome these problems. First, univariate applications, as in this paper, are particularly vulnerable to scale problems as the unique environment factor E in an ACE decomposition includes measurement error (Turkheimer & Waldron, 2000; Loehlin & Nichols, 1976). As a result, heteroscedastic measurement error due to floor, ceiling, and poor scaling effects can give rise to GxE (see also Tucker-Drob et al., 2009). A possible solution to this problem is to use multiple measures of the same phenotypic construct (e.g., multiple subtests scores of a given IQ domain). Given multiple measures, measurement error can be separated from the E component in the common-pathway model (McArdle and Goldstein, 1984; see also Martin and Eaves, 1977). To this end, a measurement model needs to be specified, linking the observed phenotypic measures to the latent phenotypic construct. In the measurement model, residuals may be heteroscedastic to accommodate poor scaling effects. GxE can then be tested at the level of the latent phenotype, in a similar way as above. Results pertaining to GxE at this level can then be more confidently interpreted in terms of a true GxE effect, as all measurement problems are captured in the residuals (Molenaar et al., 2012).

Another possible solution is to test for GxE on the phenotypic item level instead of on test or subtest level. Using the appropriate measurement models, e.g., a Rasch model (Rasch 1960) or a 2-parameter model (Birnbaum 1968), each answer category of the item is modeled explicitly. As a result, floor, ceiling, and poor scaling effects cannot give rise to spurious GxE. Tests for GxE on item level are readily available in the case of a measured environmental variable, see Medland, Neale, Eaves, & Neale (2009), and in case of an unobserved environment (the methodology proposed by Molenaar, Dolan, & De Boeck, 2012, could be used).

Taking all together, using the heteroscedastic ACE model we did not find a consistent pattern of results between age groups, datasets, and countries. We think that these results are a clear illustration of the profound scale issues that make investigations on GxE a challenging undertaking. However, we hope to have touched on some promising possibilities above, to address these scale issues in future research.