Abstract
Scoring functions are a critically important component of computer-aided screening methods for the identification of lead compounds during early stages of drug discovery. Here, we present a new multi-grid implementation of the footprint similarity (FPS) scoring function that was recently developed in our laboratory which has proven useful for identification of compounds which bind to a protein on a per-residue basis in a way that resembles a known reference. The grid-based FPS method is much faster than its Cartesian-space counterpart which makes it computationally tractable for on-the-fly docking, virtual screening, or de novo design. In this work, we establish that: (i) relatively few grids can be used to accurately approximate Cartesian space footprint similarity, (ii) the method yields improved success over the standard DOCK energy function for pose identification across a large test set of experimental co-crystal structures, for crossdocking, and for database enrichment, and (iii) grid-based FPS scoring can be used to tailor construction of new molecules to have specific properties, as demonstrated in a series of test cases targeting the viral protein HIVgp41. The method will be made available in the program DOCK6.
Keywords: Docking, virtual screening, de novo design, footprint similarity score, grid energy
Introduction
Virtual screening[1-3] and de novo design[4-9] are computational methods that can be used to identify lead compounds in the early stages of drug discovery. Despite the numerous successes of these two methods, they are both limited by a common factor: inaccuracies in the scoring function used to rank-order and prioritize compounds. Classical scoring functions typically employ molecular-mechanics principles with van der Waals (VDW) and electrostatic (ES) terms to predict non-bonded interaction energies between a ligand (e.g. small molecule drug) and receptor (e.g. protein drug target). However, such functions can bias towards ligands with large molecular weight and neglect prior knowledge of important conserved interactions.
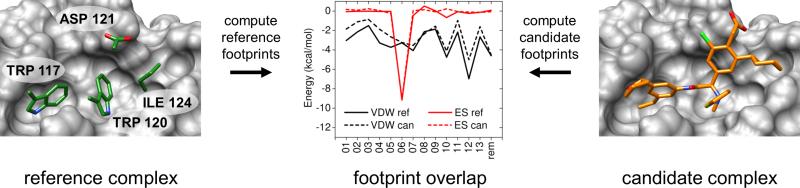
In an attempt to address these scoring limitations, we recently designed and reported a new scoring function to be used as a post-docking rescoring tool, termed molecular footprint similarity (FPS).[10] The FPS method was rigorously validated[10] using a large database consisting of 780 experimental co-crystal structures (SB2010 test set).[11] In this context, a footprint is the non-bonded interaction energy pattern (signature) between a ligand and individual receptor residues. The FPS scoring function computes footprints for both a candidate ligand and a reference ligand, then quantifies their similarity using straightforward metrics such as Euclidian distance or Pearson correlation. Candidate ligands are typically compounds under consideration for purchase or synthesis, and the reference is usually a substrate or inhibitor which is known to bind a receptor in a specific binding geometry (pose). To illustrate this concept, two footprints in the hydrophobic binding site on the important drug target HIVgp41 are shown in Figure 1. Here, the reference footprints (solid lines) are derived from four key C-helix sidechains which natively interact in the gp41 pocket (as observed in the crystal structure 1AIK),[12] and the candidate footprints (dashed lines) are made by a ligand identified using computational methods. Compounds which produce footprints with high similarity to the reference footprint (favorable FPS scores) are hypothesized to interact favorably in the binding site. The FPS scoring function has been implemented into the program DOCK6,[11,13-17] and used by us and our collaborators to identify lead compounds with experimentally verified activity to the hydrophobic pocket of HIVgp41.[18] Inhibitors targeting fatty acid binding protein (FABP) have also been identified using the footprint methodology.[19]
Figure 1.
(left / right) Image of the HIVgp41 binding site (gray surface) showing four crystallographic reference C-helix amino acid sidechains (green) and a candidate small molecule (orange). (center) Footprint comparisons showing per-residue van der Waals (VDW, black lines) and electrostatic (ES, red lines) interaction energies (kcal/mol) as a function of 13 primary residues (01 - 13) and the remainder (rem) set of residues (see Computational Details for discussion).
In the original implementation, the FPS scoring function was restricted to application as a post-docking rescoring tool because footprint calculations themselves were performed in Cartesian space, thus requiring O(M*N) time for a receptor of size M and a ligand of size N. Here, we report an extension of the method in DOCK6 that employs grids[20] to speed up the footprint calculations to O(G*N) time, where G is the number of grids, enabling its application in on-the-fly docking or design experiments.
We envision that the grid-based extension of the FPS scoring function can be applied to improve docking calculations in areas of (i) pose identification, (ii) virtual screening, and (iii) de novo design. In this work, we describe a generalization of the FPS scoring function that utilizes grids and we establish that this new functionality facilitates fast footprint calculations. Finally, we demonstrate the utility of the new implementation for pose identification with the SB2010 test set,[11] for crossdocking to a family of thermolysin proteins, for enrichment using three systems from the Directory of Useful Decoys (DUD) database,[21] and for an example de novo design application targeting the hydrophobic pocket of HIVgp41.[22,23]
Theoretical Methods
DOCK Cartesian energy function generalized to a single grid
The non-bonded interactions between a ligand and receptor using the standard DOCK Cartesian energy (DCE) scoring function can be written as follows (Eq. 1):
| (1) |
Here, DCE is the overall non-bonded sum and i and j are, respectively, atom indices for the ligand (L) and receptor (R); Ai and Bi are, respectively, attractive and repulsive VDW parameters for atom i; a and b are, respectively, attractive and repulsive VDW exponents (typically 6-9 or 6-12); qi is the partial charge on atom i; ri,j is the distance between atoms i and j; D is a dielectric screening function (typically D=4r); and the constant value 332 converts the ES term into units of kcal/mol.[20,24]
The above DCE calculation in Cartesian space can be approximated by pre-computing the interactions between probes and receptor atoms which are stored at individual points on a cubic grid.[20,25] Every point (p) on the grid () comprises three terms: attractive VDW (ga_vdw), repulsive VDW (gr_vdw), and ES (ges), as shown in Eq. 2:
| (2) |
The overall non-bonded interactions between a ligand with the receptor can then be calculated by interpolating grid point values onto ligand atoms (li) with known coordinates (Eq. 3) which, when using a single grid, is termed single grid energy (SGE).
| (3) |
Here, TLI is a function that performs a tri-linear interpolation of the set of values stored at the eight closest grid points in grid to the coordinates of atom li. While the accuracy in SGE increases with finer grid resolution (although at the expense of grid-generation time and grid size),[24] grids on the order of 0.3 - 0.4 Å resolution are typically used for most docking and virtual screening purposes.
Multi-grid implementation for footprint calculations
Importantly, the DCE and SGE scoring functions are pair-wise additive and non-bonded interactions can be decomposed on a per-residue basis. Thus, grid-based footprints can be obtained by simply generating a separate grid for each residue (Eq. 4), as is illustrated for the grid ES term (Eq. 2) at a single grid point (p):
| (4) |
Here, k is the residue index in the receptor (R), which contains M total residues, and Sk is the set of all atoms in a single residue. Here, ges,Sk (p) represents the contribution to the grid ES term at point p by the set of all atoms from a single residue (Sk), and the union of the residue atom sets is the set of all receptor atoms (Eq. 5):
| (5) |
Following this derivation, the grid energy for interaction between the ligand and a single residue () can be calculated by a modification of Eq. 3 to yield Eq. 6:
| (6) |
Moreover, by Eq. 4-5, the sum of these components (Eq. 7), termed here multi-grid energy (MGE), is equivalent to the single grid energy (SGE) provided that the grids are overlapped in Cartesian space (i.e. identical origin and x-, y-, z-dimensions).
| (7) |
In summary, the potential energy of a receptor can be stored on a single grid (SGE) or decomposed into multiple grids (MGE) which are numerically equivalent. And, through the use of multiple grids, footprints can be generated in grid-space enabling on-the-fly footprint similarity (FPS) score calculations.
Computational Details
Scoring method details and distinctions
The various scoring methods discussed in this manuscript (DCE, SGE, MGE, FPS, FPS+MGE) can be used in one of two primary ways: (i) they can be used to “guide” growth, meaning that the scoring function controls molecule pruning, clustering, and energy minimization during docking, or (ii) they can be used to “rescore” results, meaning that an ensemble of docked molecules is rank-ordered by the value of the score. In practice, one scoring function may serve both of these purposes in any one docking experiment. Alternatively, one scoring function may be used to guide sampling, and another may be used to rescore the resulting ensemble.
Further, the different scoring methods may be used alone, or in combination. Standard MGE docking, FPS docking, and FPS+MGE docking – the three scoring ensembles which are the focus of this manuscript – all follow Eq. 8:
| (8) |
As shown in Eq. 8, the scoring functions can be decomposed into VDW and ES components. In the case of MGE docking, coefficients C3 and C4 are equal to 0; in FPS docking, C1 and C2 are equal to 0; and in FPS+MGE docking, all coefficients are non-0 values as summarized in Table 1. Also listed are the pruning cutoff values employed, which were chosen based on the range of possible scores[10] for each experiment. The pruning cutoff is responsible for eliminating molecules from the ensemble which exceed a pre-defined energy cutoff score. It is additionally important to note that when footprints are employed, the overlap between the reference and candidate ligand can be quantified using standard Euclidean distance (d), normalized Euclidean distance (dnorm), or standard Pearson correlation (r) methods as previously described.[10]
Table 1.
Coefficient schema and pruning cutoffs for docking/scoring protocols.
| MGE | FPS | FPS+MGE | |
|---|---|---|---|
| Standarda Euclidean (d) | C1 = C2 = 1b | C1 = C2 = 0 | C1 = C2 = 1 |
| C3 = C4 = 0 | C3 = C4 = 1 | C3 = C4 = 1 | |
| Pruning cutoff = 200.0 | Pruning cutoff = 1000.0 | Pruning cutoff = 1000.0 | |
| Normalized Euclidean (dnorm) | C1 = C2 = 1 | C1 = C2 = 0 | C1 = C2 = 1 |
| C3 = C4 = 0 | C3 = C4 = 1 | C3 = C4 = 20 | |
| Pruning cutoff = 200.0 | Pruning cutoff = 200.0 | Pruning cutoff = 200.0 | |
| Pearson Correlation (r) | C1 = C2 = 1 | C1 = C2 = 0 | C1 = C2 = 1 |
| C3 = C4 = 0 | C3 = C4 = −1 | C3 = C4 = −20 | |
| Pruning cutoff = 200.0 | Pruning cutoff = 200.0 | Pruning cutoff = 200.0 | |
Methods used to compute footprint overlap.
Coefficients (C1, C2, C3, C4) used to compute a total score as a function of Eq. 8. Pruning cutoff refers to the DOCK parameter pruning_conformer_score_cutoff in kcal/mol (see text for discussion).
Threshold-based residue selection for grid generation
In practice, only a subset of the most important binding site residues are stored as individual grids which reduces the total number of grids required (including memory and storage requirements) and makes the footprints calculations tractable. Residue selection in this work was based on consideration of the standard DCE non-bonded interactions using optimized ligand crystallographic poses (see Balius et al.[10] for optimization protocol). Residues with absolute interactions exceeding 1.0 kcal/mol VDW energy or 0.5 kcal/mol ES energy were identified and constitute a “primary” set used for generation of individual docking grids. All remaining residues were grouped together and used to generate a “remainder” docking grid. Together, the “primary” and “remainder” grids comprise all protein residues and the sum is the multi-grid energy (MGE). The DOCK grid accessory program was used to generate the individual grids with a 0.4 Å resolution and 6-9 VDW exponents to crudely mimic receptor flexibility through a softening of the overall intermolecular landscape.[26]
Docking and rescoring
Docking experiments used the same flexible ligand (FLX) or fixed-anchor-docking (FAD) protocols described in Mukherjee et al.,[11] with the exception that the final clustering cutoff parameter was changed from 2.0 Å to 0.5 Å. DOCK uses a best-first clustering method, thus this modification will slightly affect sampling and rescoring of the ensembles. To facilitate comparisons between scores computed on the grid (SGE, MGE, and FPS) or in Cartesian space (DCE and FPS), all rescoring experiments employed 6-9 VDW exponents to match the exponents used in grid generation. In FAD, the initial anchor placement starts at the crystallographic coordinates and all torsions are sequentially grown out until the complete molecule is restored. Here, all rigid ligand segments with five or more heavy atoms were treated as anchors and harmonically restrained with a spring constant of k = 10 kcal/(mol Å2) during minimization. DOCK calculations were performed on a DELL PowerEdge C6100 cluster consisting of Intel x5660 2.8GHz hex-core Nehalem-based processors.
Pose reproduction
As in our previous footprint work,[10] the SB2010[11] dataset (N = 780 systems) was used for pose reproduction experiments which compares docking predictions with their crystallographic observed binding geometry (pose). Six runs were performed using different random seeds to better gauge noise and reproducibility with regards to docking success rates and failures. As previously discussed,[11] docking experiments may have one of three outcomes: (i) success occurs when the program selects a correct pose (within 2 Å rmsd of native pose), (ii) scoring failure occurs when the correct pose is sampled but is not selected as the best pose, and (iii) sampling failure occurs when the correct pose is not sampled. For any given experiment, the sum (successes + scoring failures + sampling failures) will equal 100%. All results employed symmetry-corrected rmsds using the Hungarian algorithm[27,28] recently implemented into DOCK as discussed in Brozell et al.[17]
Crossdocking
To evaluate how the different scoring functions would affect crossdocking performance, 26 ligand-bound structures of thermolysin were aligned into a common reference frame.[11] Each ligand was iteratively docked into each receptor which, for the 26x26 matrix, required 676 independent docking experiments. For each cell of the matrix the rmsd reference was either the cognate ligand from the crystal structure (on the diagonal) or the superimposed position of the ligand from another crystal structure (off diagonal). The footprint reference for each receptor was always derived from the cognate ligand. As before, docking outcomes were classified as a success, scoring failure, or sampling failure. Matrix rows were arranged using the MATLAB (R2010b, MathWorks) dendrogram hierarchical clustering algorithm which facilitates visual interpretation of results. The prepared and aligned protein-ligand complex structures for thermolysin as well as other protein families are freely available online at http://rizzolab.org under Downloads.
Database enrichment
The DUD database[21] was used to evaluate the different scoring functions for performing enrichment on three representative systems. Receiver operating characteristic (ROC) curves were used to measure the strength of the overall enrichment, and early enrichment was also evaluated, as described in Brozell et al.,[17] using area-under-the-curve (AUC) and examination of the number of actives and decoys recovered as a function of percent of database screened. Differences between the enrichment and pose reproduction docking protocols are summarized in Table 2.
Table 2.
Parameters for enrichment and pose reproduction experiments.
| DOCK Input File Parameter | Description | Enrichment | Pose Reproduction |
|---|---|---|---|
| pruning_max_orients | # anchor orients | 100 | 1000 |
| pruning_conformer_score_cutoff | pruning cutoff | 100.0 | 200.0 / 1000.0a |
| num_scored_conformersb | # molecules output | 1 | 5000 |
Cutoff of 200.0 kcal/mol used for SGE, MGE, and FPS or FPS+MGE with normalized Euclidean (dnorm) or Pearson correlation (r). Cutoff of 1000.0 kcal/mol used for FPS or FPS+MGE with standard Euclidean (d). See Table 1.
One conformer is saved during enrichment vs. 5000 conformers during pose reproduction for improved sampling statistics.
De novo design
Preliminary results employing a first-stage de novo design version of DOCK (currently being developed) are also presented in which construction of new HIVgp41 inhibitors from scratch is performed with and without grid-based footprints using a modified anchor-and-grow[14-16] algorithm. For clarity, we employ the phrase “de novo design” for all related experiments in which new compounds are assembled from fragments whether or not existing data (i.e. footprints derived from a reference molecule) was used to guide growth. The reference in the present case was four key amino acid sidechains (see Figure 1) from the known peptide inhibitor C34 which interact favorably within a highly conserved pocket region on HIVgp41.[12,29] In our de novo design protocol, molecules were constructed from scratch through the rational combination of fragments derived from a library of pre-existing “drug-like” molecules (13.3M total) that were obtained from the ZINC database[30] of purchasable compounds. In these experiments, several steps were taken to constrain growth. Particularly, following anchor selection, (i) fragments with only one or two attachment points were used during growth to prevent branching, (ii) two fragments were only combined if the bonded environment had previously been observed in an existing molecule, and (iii) growth was constrained to limit the maximum molecular weight (<1000 g/mol) and number of rotatable bonds (<15) of candidate molecules. Chemical space was also pruned using a new DOCK implementation of 2D fingerprints, inspired by the MOLPRINT 2D[31,32] procedure, to increase diversity in the resultant ensembles. The de novo implementation will be made available in a future release of DOCK (http://dock.compbio.ucsf.edu) pending additional development and testing.
Results and Discussion
Multi-Grid Energy Evaluation
All residues vs. a threshold-based subset
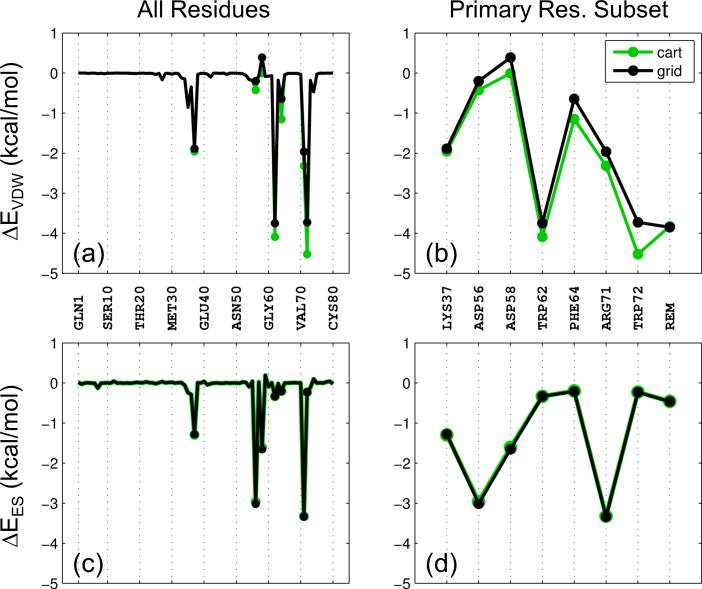
As described above, Cartesian energy can be closely approximated using a single grid, and through the use of multiple grids a per-residue energy footprint can be derived. To evaluate the multi-grid implementation in DOCK we examined several factors including footprints derived from individual proteins, for which Figure 2 shows a representative example. Here, the energy-minimized crystallographic position for the ligand epsilon-aminocaproic acid with plasminogen kringle-4 protein (PDB code 2PK4),[33] an important protein in blood clotting, is used to generate VDW and ES footprints. This system was chosen because the relatively small size (N = 80 residues) enabled individual grids to be computed separately for all protein residues.
Figure 2.
Comparisons between Cartesian-based (green) and grid-based (black) footprints for PDB code 2PK4 decomposed into VDW (a,b) and ES (c,d) contributions. Panels (a) and (c) show footprints across all 80 protein residues and panels (b) and (d) show footprints based on the subset of primary binding site residues (N = 7) plus the remainder residues (N = 73).
As expected, Cartesian vs. grid-based footprints from 2PK4 show close correspondence across all 80 residues (Figure 2a,c) and for a reduced set of 7 primary residues plus the remainder (Figure 2b,d). The small differences that are observed arise from the fact that the ligand was first energy-minimized in Cartesian space prior to both sets of footprint calculations. Although the receptors in both cases (Cartesian or grid space) are in fact identical and remain fixed, ligand minimization in one space can lead to minor energy differences in the other (Figure 2 black vs. green lines). Notably, the MGE sum across all 80 grids (VDW = −15.646042 kcal/mol, ES = −10.522523 kcal/mol) is identical to that for the 7 primary grids + remainder (VDW = −15.646046 kcal/mol, ES = −10.522522 kcal/mol) to within numerical precision, and in this case, seven significant figures. This agreement is important because for most protein systems it is not feasible to assign each residue separately to a grid as the run time and memory needed to perform docking calculations becomes prohibitive as more grids are used.
Grid vs. Cartesian energies
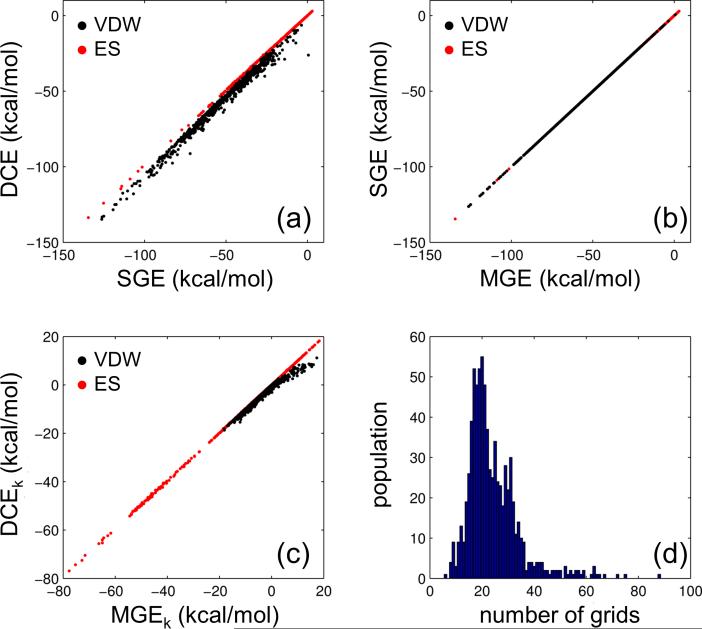
As a large-scale confirmation of grid accuracy we examined DCE vs. SGE scores for all 780 minimized crystallographic poses (decomposed into VDW and ES components) from the SB2010[11] test set (Figure 3a). Analogous to the 2PK4 example (Figure 2), DCE scores across the entire test set are effectively approximated by SGE scores using a 0.4 Å grid resolution (VDW r = 0.99, ES r = 1.00). As before, the slightly more favorable intermolecular VDW energies in Cartesian vs. grid space arise from the fact the ligands were initially minimized in Cartesian space prior to the footprint calculations. In expanding to multiple grids, Figure 3b demonstrates the exact correspondence (r = 1.00) between single (SGE) and multiple grid (MGE) energies (VDW and ES) across the test set. It is important to note that the inclusion of the remainder grid in the MGE results is required to maintain this exact correlation. The results in Figure 3c confirm that the energies across grids representing individual residues (MGEk) or the remainder grid also have high correlation with their Cartesian-space (DCEk) counterparts (VDW r = 0.99, ES r = 1.00, N = 18,876 data points each).
Figure 3.
Comparison of scores for crystallographic poses minimized in Cartesian space from the SB2010 test set (N = 780) for: (a) DCE (Cartesian) vs. SGE (single grid), (b) SGE (single grid) vs. MGE (multi grid), (c) individual residue DCEk (Cartesian) vs. individual residue MGEk (multi grid), and (d) number of residues above threshold (see Computational Details for energy cutoffs). Black = VDW energies, red = ES energies, blue = population histogram.
The results in Figure 3b,c in multi-grid space employed a primary set + remainder set of residues. To determine how many grids would be required to effectively define a footprint we earlier had enumerated the protein residues which interacted with each ligand in the test set (Figure 3d) above pre-defined threshold levels (VDW = 1.0 kcal/mol, ES = 0.5 kcal/mol). On average, 20 grids (representing 19 discrete residues and 1 remainder grid) meet these criteria and based on the results in Figure 3b,c should be sufficient to approximate all key ligand-protein interaction energies. Importantly, 20 is a much more tractable number of grids in terms of run time (and memory) required for docking than 322, which is the average number of protein residues across all 780 systems in the test set. Overall the experiments in this section indicate the following: (i) grid energies are an acceptable approximation of Cartesian energy at a 0.4 Å grid resolution, (ii) energy is conserved when decomposing a single grid into multiple grids, and (iii) a threshold-based method can be used to identify a “primary” plus a “remainder” set which, when approximated as grids, sufficiently encodes the key features of a Cartesian-space footprint (as further demonstrated in the Pose Reproduction section below).
Pose Reproduction
Outcome statistics of docking experiments
To evaluate how grid-based FPS scoring affects docking outcomes, multiple pose-reproduction experiments using the SB2010[11] test set were performed as shown in Table 3. Here, docking statistics (success, scoring failure, or sampling failure) and corresponding run times are shown when using the standard DOCK SGE scoring function alone (row a), SGE:FPS rescored results (rows b-d), the MGE scoring function alone (row e), the grid-based FPS scoring function alone (rows f-h), or the combination (FPS+MGE) of the grid-based FPS scoring function plus the MGE scoring function (rows i-k). For each experiment employing FPS, results are reported for the three different similarity metrics that can be applied (standard Euclidean d, normalized Euclidean dnorm, and Pearson correlation r). Moreover, each row of data represents the average outcome of six randomly-seeded docking experiments.
Table 3.
Pose reproduction statistics with flexible (FLX) ligand docking using SGE scoring, SGE:FPS rescoring, MGE scoring, FPS scoring, and FPS+MGE scoring with the SB2010 test set.
| A | B | C | D | ||||
|---|---|---|---|---|---|---|---|
| procedurea | divisionb | FPSc | success (%)d | score fail (%)d | samp fail (%)d | time (min)d | |
| a | SGE | all | 68.5 | 22.7 | 8.8 | 5.89 | |
| b | SGE:FPS | pri+rem | d | 83.6 | 7.6 | 8.8 | 0.29 |
| c | SGE:FPS | pri+rem | dnorm | 83.1 | 8.1 | 8.8 | 0.26 |
| d | SGE:FPS | pri+rem | r | 82.4 | 8.9 | 8.8 | 0.20 |
| e | MGE | pri+rem | 69.8 | 22.3 | 7.9 | 28.57 | |
| f | FPS | pri+rem | d | 82.3 | 7.0 | 10.7 | 27.85 |
| g | FPS | pri+rem | dnorm | 34.6 | 14.6 | 50.9 | 30.66 |
| h | FPS | pri+rem | r | 24.4 | 14.0 | 61.7 | 30.01 |
| i | FPS+MGE | pri+rem | d | 84.0 | 9.4 | 6.6 | 27.82 |
| j | FPS+MGE | pri+rem | dnorm | 84.4 | 8.6 | 7.0 | 28.39 |
| k | FPS+MGE | pri+rem | r | 77.8 | 14.3 | 8.0 | 28.93 |
SGE = single grid energy, MGE = multi grid energy, FPS = footprint similarity.
pri = primary set, rem = remainder set (see text for discussion).
d = standard Euclidean, dnorm = normalized Euclidean, r = Pearson correlation.
N = 780 systems, symmetry-corrected rmsds, average of six DOCK runs.
Consistent with our earlier work,[10,11,17] the flexible (FLX) ligand docking protocol with standard SGE scoring function alone is able to successfully predict the crystallographic ligand pose to within 2 Å for 68.5% of the systems in the test set (Table 3 row a, column A). And as before, most failures are a result of inaccuracies in scoring (22.7% row a, column B) rather than sampling (8.8% row a, column C). Similar to results reported by Balius et al.[10] in which a rescoring of SGE ensembles with Cartesian-based footprints improved overall success, use of the new grid-based FPS function to rescore SGE-derived poses (Table 3 rows b-d) yields greater accuracy (82.4 - 83.6%) depending on the comparison method used (d, dnorm, or r). As no new conformations are sampled during rescoring, the number of sampling failure remains constant at 8.8%, thus the theoretical maximum success rate for these experiments are 91.2% (100% - 8.8%). Under the present conditions, SGE docking requires on average 5.89 minutes per ligand followed by 0.20 to 0.29 minutes per ligand for footprint-based rescoring with one of the grid-based FPS methods.
Conceptually, the MGE scoring function should return the same docking outcome statistics as the standard SGE scoring function given the derivation presented in Theoretical Methods and the good correspondence seen in the large-scale energy validation tests (Figure 3). In practice, that conservation holds true (Table 3 rows e vs. a) with observed success rates for MGE = 69.8% vs. SGE = 68.5% being essentially equivalent. Importantly, both the scoring (22.3 vs. 22.7%) and the sampling (7.9 vs. 8.8%) failures are the same within the noise limits of the calculations, thus confirming that multi-grid and single-grid approaches are comparable. A stark difference, however, is that MGE calculations take ca. 5 - 6 times longer per ligand than does SGE (row a, column D) because each system comprises, on average, 20 grids instead of 1 grid. Nevertheless, such added expense could be warranted depending on the modeling application (see De novo Design section below).
Subsequent experiments using the grid-based FPS function alone (Table 3 rows f-h) require roughly the same amount of time as using MGE alone which is to be expected, however, there is a dramatic difference in docking outcomes. While FPS success using the standard Euclidean metric (82.3% row f) is equivalent to SGE:FPS rescoring (83.6% row b), the use of normalized Euclidean or Pearson correlation metrics perform significantly worse with success rates only in the range of 24.4 - 34.6%, dominated heavily by sampling failures (50.9 - 61.7% rows g,h; see Comparison of similarity metrics section below for further discussion). Interestingly, the observed scoring failures using FPS alone with standard Euclidean are actually the lowest of any of the experiments (7.0% row f) although sampling failures show a slight increase (10.7% row f) relative to standard SGE docking (8.8% row a).
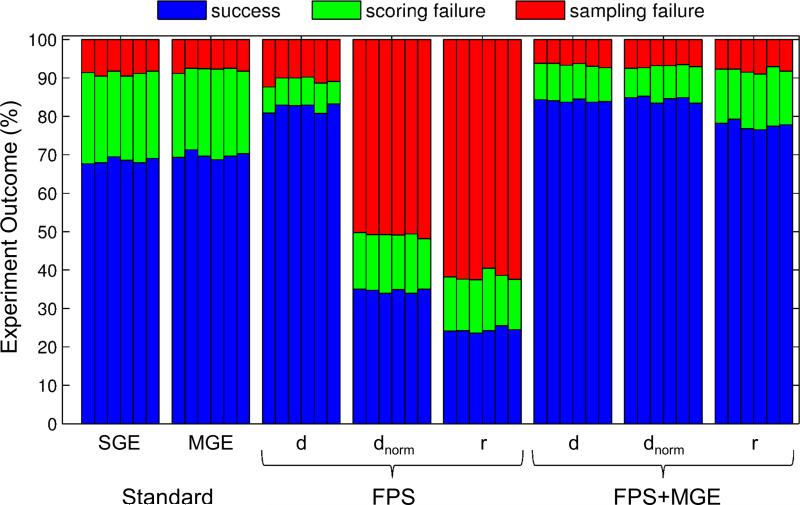
On the other hand, use of the combined scoring function (FPS+MGE) consisting of grid-based footprints plus multi-grid energy for all three similarity metrics yields good success rates (Table 3 rows i-k, 77.8 - 84.4%) effectively ameliorating the poor results observed when using FPS alone with normalized Euclidian or Pearson correlation metrics. Interestingly, the FPS+MGE experiments (rows i-k) yield fewer sampling failures (6.6 - 8.0% rows i-k) than standard SGE docking (8.8% row a) although scoring failures are slightly increased over the SGE:FPS rescores (rows b-d). Results for FPS+MGE with standard Euclidean (84.0% row i) or normalized Euclidean (84.4% row j) yield the overall highest success rates. Analogous to MGE, docking using FPS+MGE requires ca. 5 - 6 times increase in calculation time over a single grid. Figure 4 graphically demonstrates the accuracy of the eight different docking methods examined in this study and further illustrates the relative robustness (reproducibility) of the results over six random seeds.
Figure 4.
Pose reproduction experiments using alternative scoring functions and footprint similarity metrics: SGE = single grid energy, MGE = multi grid energy, FPS = footprint similarity, and FPS+MGE (d = standard Euclidean; dnorm = normalized Euclidean; r = Pearson correlation). Symmetry-corrected rmsds were employed for six randomly-seeded DOCK runs (N = 780 systems). Blue = success, green = scoring failure, red = sampling failure.
In summary, the results in Table 3 and Figure 4 suggest that the FPS method with Euclidian distance (d), or the FPS+MGE method with standard (d) or normalized Euclidean distance (dnorm) yields improved pose identification results when a known reference can be employed. Importantly, as described below, the incorporation of FPS scoring function to guide ligand growth during docking provides sampling advantages over the standard SGE scoring function which can be a key benefit, especially when applied to techniques such as de novo design.
Comparison of similarity metrics
The standard Euclidean similarity metric consistently yields good pose reproduction results with SGE:FPS rescoring (Table 3 row b), FPS (row f), and FPS+MGE docking (row i) all resulting in greater than 80% success. This consistency most likely involve the fact that the form of the standard Euclidean algorithm matches both magnitude and shape of the footprint signatures as previously noted.[10] On the other hand, when magnitude information is lacking, FPS results using normalized Euclidean (row g) or Pearson correlation (row h) show a poor success rate (24.4 - 34.6%). Under these conditions, as ligand growth proceeds without an explicit non-bonded interaction energy sum term, poses scored favorably by the FPS function may in fact be energetically less favorable in the binding site, which can be problematic. An interesting observation is that a lack of magnitude information appears to be tolerable (rows c,d) when rescoring, presumably because the ensemble already contains low-energy conformers (in this case derived by SGE docking). In any event, when sampling is used to help drive ligand ensembles toward a more favorable footprint similar to that of the reference, then either the combined function (FPS+MGE) with any similarity metric (d, dnorm, r), or the FPS function with the standard Euclidan metric (d), would be recommended.
Growth Tree Footprint Scores
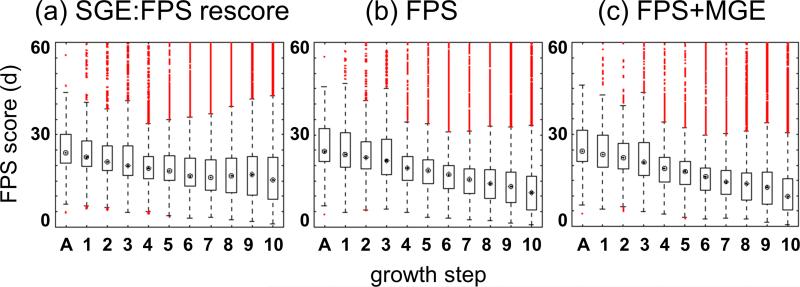
To more closely evaluate the performance of FPS scoring during molecule growth (Figure 5), we carried out fixed-anchor docking (FAD) experiments (see Computational Details) guided by: (i) SGE score and rescored with FPS (SGE:FPS), (ii) FPS score alone, or (iii) the combination of FPS+MGE. For these experiments, a subset of the SB2010 test set which only contained ligands with exactly 10 rotatable bonds was used (N = 59). At each stage of ligand growth, every conformer sampled by DOCK was rescored with the FPS score using the standard Euclidean similarity metric. It is important to note that the results in Figure 5 are based on single point calculations of partially grown conformers derived from the final set of successfully-grown conformers stored as DOCK growth trees. Thus, the number of vertical data points in each of the eleven growth tree steps will be identical in any individual experiment (SGE:FPS = 15,638, FPS = 12,824, or FPS+MGE = 12,378). The rough agreement in the total number of final conformers obtained in each case is primarily a function of the clustering cutoff which, for the present case, is 100 conformers. A quick calculation using the total number of systems (59), multiplied by the clustering cutoff parameter (100), multiplied by the average number of anchors per ligand (2.58), equals 15,222 which is approximately the number of conformers (ca. 12 - 16K) plotted in Figure 5 at each growth step.
Figure 5.
FPS scores using standard Euclidian distance for all ligand conformers generated at each growth step (left to right A → 10) for the 10 rotatable bond subset of SB2010 (N = 59) using three different sampling methods: (a) SGE guided growth (rescored with FPS), (b) FPS guided growth, and (c) FPS+MGE guided growth. Open circles indicate median FPS values, open box indicate middle 50th percentiles, dashed lines indicate upper and lower 25th percentiles, red circles are outliers.
As shown in Figure 5, docking begins with an anchor A (initiated from the crystallographic position) which is then incrementally grown out in layers (A → 10) until the complete starting molecule is restored. Interestingly, even without an FPS function, use of the SGE function to drive sampling (Figure 5a) shows a downward trend towards lower (more favorable) FPS scores as ligand segments are added. This can be explained by the use of crystallographic anchor positions as starting coordinates which helps steer a relatively large percentage of the ensembles towards native-like poses (thus reasonable FPS scores) as more and more contacts are created between ligand and the receptor during growth. However, the initial downward trend seen in the SGE:FPS results begins to level off, and around steps 8 - 9 there are slight increases relative to the previous growth step. The final ensemble of structures converges to a median FPS score of 15.30 (Figure 5a). In contrast, growth guided using FPS (Figure 5b) or FPS+MGE (Figure 5c) continually trends downward resulting in lower overall scores (FPS = 11.16, FPS+MGE = 9.76; Figure 5 b,c) and tighter final distributions at step 10. Of the three methods tested FPS+MGE yields the overall lowest final FPS scores.
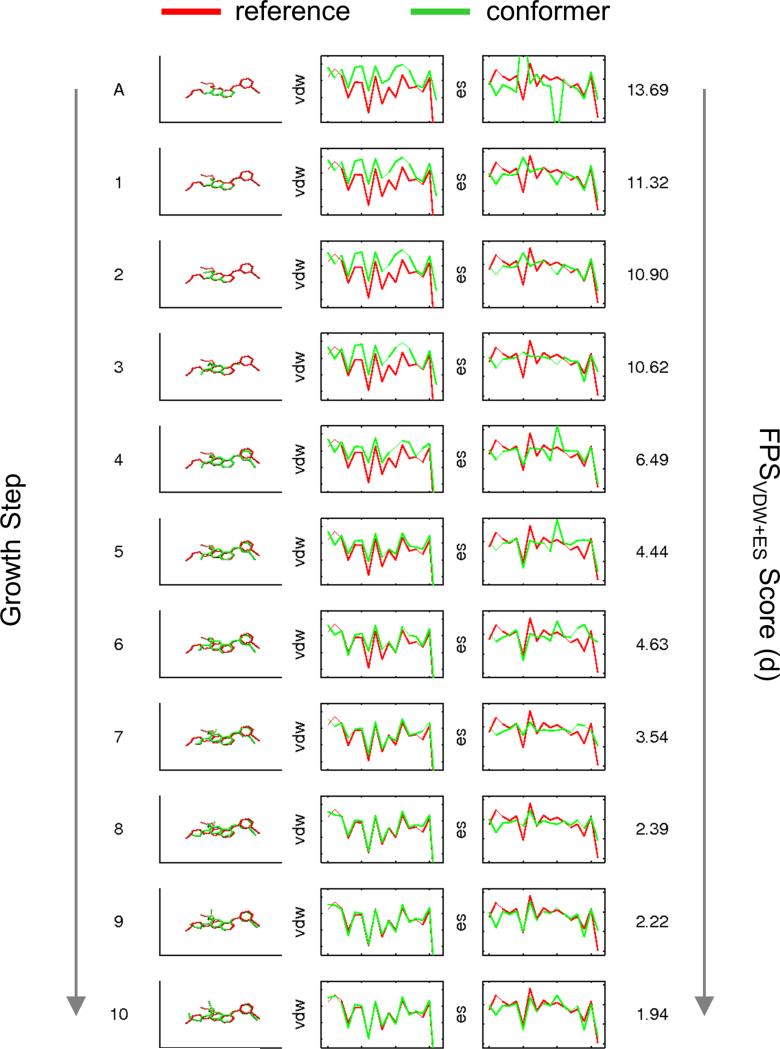
As a graphical view of convergence during growth, Figure 6 plots a representative growth tree which was guided by the FPS function in which structures, footprint overlap, and FPS scores (standard Euclidian distance) converge to a reasonable native-like answer. Here, the poor overlap seen for the inhibitor erlotinib complexed with epidermal growth factor receptor (PDB code 1M17)[34], in terms of the initial VDW and ES patterns (anchor FPS = 13.69), converges to lower and lower FPS values (final FPS = 1.94) as each layer of growth and minimization take place. Overall, the pose reproduction experiments in this section indicate that grid-based FPS and FPS+MGE growth yields more native-like structures.
Figure 6.
Graphical view of convergence for the inhibitor erlotinib complexed with epidermal growth factor receptor (PDB code 1M17) showing structures, VDW and ES footprints in kcal/mol (y-axis) derived from 16 individual grids plus 1 remainder grid (x-axis), and FPSVDW+ES scores as a function of growth step. Reference in red vs. partially grown conformers in green.
Crossdocking
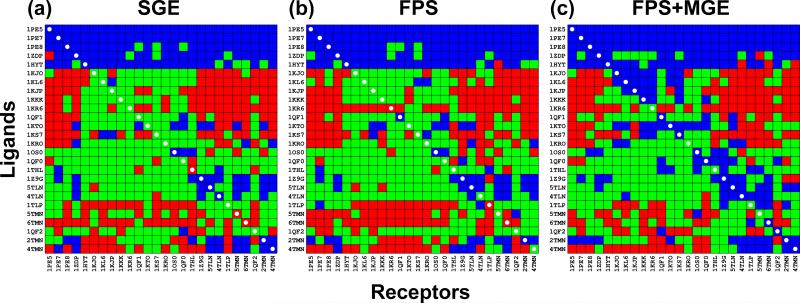
Crossdocking matrices are useful to evaluate the performance of a docking scoring function in the context of variable receptor conformations and ligands of different size and chemistry. We iteratively performed pose identification experiments on all combinations of thermolysin proteins and corresponding ligands (N = 26x26) from the SB2010 test set.[11] Thus, each column of the matrix can be viewed as a small-scale virtual screening experiment wherein multiple ligands are docked to the same receptor. Docking experiments were performed using either (i) SGE, (ii) FPS with standard Euclidean, or (iii) FPS+MGE with standard Euclidean. The reference footprint in each column of the matrix is the crystal ligand pose indicated by a white circle on the diagonal. Each docking outcome in the matrix was colored as a success (blue), scoring failure (green), or sampling failure (red). The results are presented in Figure 7 and Table 4.
Figure 7.
Pose reproduction successes (blue), scoring failures (green), and sampling failures (red) for crossdocking experiment of thermolysin proteins. Experiments were guided either by (a) SGE, (b) FPS with standard Euclidean, or (c) FPS+MGE with standard Euclidean. White circles on the diagonal indicate cognate protein-ligand pairs.
Table 4.
Summary of crossdocking success / failure rates for thermolysin family (N = 26 systems).
| SGE | FPSb | FPS+MGEb | ||||
|---|---|---|---|---|---|---|
| Na | (%) | Na | (%) | Na | (%) | |
| Matrix Success | 178 | 26.33 | 176 | 26.04 | 227 | 33.58 |
| Matrix Scoring Failure | 302 | 44.67 | 291 | 43.05 | 269 | 39.79 |
| Matrix Sampling Failure | 196 | 28.99 | 209 | 30.92 | 180 | 26.63 |
| Diagonal Success | 11 | 42.31 | 10 | 38.46 | 21 | 80.77 |
| Diagonal Scoring Failure | 12 | 46.15 | 13 | 50.00 | 5 | 19.23 |
| Diagonal Sampling Failure | 3 | 11.54 | 3 | 11.54 | 0 | 0.00 |
Total of success + scoring failure + sampling failure = 676 for entire matrix; 26 for matrix diagonal.
Standard Euclidean similarity metric.
Two important measures from the crossdocking experiments are the matrix (overall) success rate and the diagonal success rate. For standard SGE docking, the matrix success rate is 26.33% (Figure 7a, Table 4). Docking using the FPS scoring function alone yields a similar result at 26.04% (Figure 7b, Table 4), however docking using the FPS+MGE scoring function improves success to 33.58% (Figure 7c, Table 4), an ca. 7% increase over the standard SGE function. The observed improvements are the result of a 4.88% decrease in scoring failures and a 2.36% decrease in sampling failures, demonstrating that for this family, accounting for specific protein-ligand interactions and grid score simultaneously can be useful in targeting a receptor where binding site conformations may be variable. Previously, Balius et al.[10] performed an FPS-rescoring test for the carbonic anhydrase family (N = 29 systems) in which multiple ligand poses were reevaluated based on footprints derived from each cell's theoretical ligand-receptor complex pose. While this test was useful to evaluate FPS rescoring, and ultimately removed many scoring failures, it was not reflective of a true virtual screening experiment wherein only the top pose for each ligand would be saved and only a single footprint reference for each receptor would be available. Here, we achieved a 2.36% improvement in sampling success when keeping only one pose and using only the cognate ligand as a footprint reference for the FPS+MGE scoring function, something that is not possible by rescoring alone.
Finally, the diagonal of the crossdocking matrix (marked with white circles, Figure 7) was examined to assess family-based success for docking each ligand into its cognate receptor. The diagonal success rate for standard SGE docking is 42.31% (Figure 7a, Table 4), compared to FPS at 38.46% (Figure 7b, Table 4), and FPS+MGE at 80.77% (Figure 7c, Table 4), which represents a significant ca. 38% improvement over SGE. Remarkably, use of the FPS+MGE scoring function removed all sampling failures along the diagonal, and the diagonal success rate for an otherwise difficult family of systems is now on par with the above pose reproduction success rates reported over the entire test set (Table 3).
Enrichment Studies
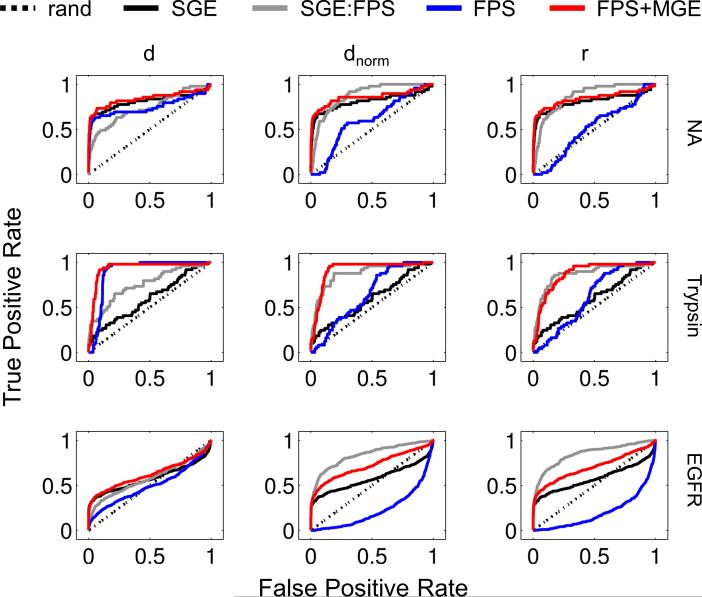
To evaluate how grid-based FPS functions affect database enrichment, we generated Receiver Operating Characteristic (ROC) curves for three protein systems of pharmaceutical interest – neuraminidase, trypsin, and EGFR – taken from the widely-used DUD[21] database. Standard SGE docking, SGE:FPS rescoring, FPS docking, and FPS+MGE docking were employed, and where applicable, experiments were repeated using standard Euclidean (d), normalized Euclidean (dnorm), or Pearson correlation (r) metrics to rank order the actives and decoys from each system. Figure 8 plots standard ROC curves for all scoring ensembles, while Table 5 shows area under the curve (AUC) values, number of actives (Nact), and number of decoys (Ndec) recovered at 1%, 10%, and 100% of the ranked database for only the standard Euclidian results. For comparison, the best possible and random AUC values at each percentage are also shown.
Figure 8.
ROC curves for neuraminidase (1A4G), trypsin (1BJU), and EGFR (1M17) using SGE (black), SGE:FPS (gray), FPS (blue), and FPS+MGE (red) scoring to rank order actives and decoys taken from the DUD database for comparison with random enrichment (dashed lines).
Table 5.
Enrichment statistics using DOCK scoring functions with standard Euclidian similarities to rank order actives and decoys for neuraminidase (NA), trypsin, and EGFR from the DUD database.
| 1% of database | 10% of database | 100% of database | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max AUC | 100.00 | 1,000.00 | 10,000.00 | ||||||||||
| Ran AUC | 0.50 | 50.00 | 5000.00 | ||||||||||
| Function | No.b | AUC | Nactc | Ndecd | No. | AUC | Nact | Ndec | No. | AUC | Nact | Ndec | |
| NAa | SGE | 19 | 6.53 | 13 | 6 | 191 | 489.84 | 33 | 158 | 1911 (1923) | 8112.30 | 49 | 1862 |
| SGE:FPS | 4.14 | 8 | 11 | 310.37 | 23 | 168 | 7381.24 | 49 | 1862 | ||||
| FPS | 4.79 | 12 | 7 | 482.76 | 31 | 160 | 7502.12 | 49 | 1862 | ||||
| FPS+MGE | 4.46 | 16 | 3 | 530.57 | 36 | 155 | 8423.00 | 49 | 1862 | ||||
| Trypsin | SGE | 17 | 5.40 | 5 | 12 | 166 | 155.88 | 12 | 154 | 1664 (1713) | 5957.98 | 49 | 1615 |
| SGE:FPS | 6.99 | 8 | 9 | 284.54 | 18 | 148 | 7562.30 | 49 | 1615 | ||||
| FPS | 0.00 | 0 | 17 | 86.71 | 17 | 149 | 8952.86 | 49 | 1615 | ||||
| FPS+MGE | 5.76 | 4 | 13 | 323.66 | 42 | 124 | 9342.87 | 49 | 1616 | ||||
| EGFR | SGE | 165 | 6.49 | 113 | 52 | 1647 | 307.71 | 180 | 1467 | 16465 (16471) | 5773.28 | 475 | 15990 |
| SGE:FPS | 3.93 | 43 | 122 | 202.81 | 147 | 1500 | 5800.56 | 475 | 15990 | ||||
| FPS | 3.72 | 32 | 133 | 137.90 | 99 | 1548 | 4947.67 | 475 | 15990 | ||||
| FPS+MGE | 6.55 | 101 | 64 | 308.52 | 190 | 1457 | 6222.10 | 475 | 15990 | ||||
NA = neuraminidase, EGFR = epidermal growth factor receptor.
No. = number of ranked ligands at 1%, 10%, or 100% of the databases which finished docking. Note that at 100% of the database not all ligands may finish docking (see Brozell et al.[16] for discussion). Values in parenthesis represent the initial total set of actives+decoys.
Nact = number of actives.
Ndec = number of decoys. Note that for trypsin one more decoy pose finished docking using FPS+MGE (N=1616) than with the other functions (N = 1615). NA (# decoys = 1874; # actives = 49), trypsin (# decoys = 1664; # actives = 49), EGFR (# decoys = 15996; # actives = 475).
Examination of the ROC curves in Figure 8 reveals that use of FPS with normalized Euclidian (blue lines, dnorm column) or Pearson correlation (blue lines, r column) yields poor enrichment which is consistent with the poor pose prediction results in Table 3 and Figure 4 that used the same protocols. Results for NA and trypsin are essentially random (blue lines near diagonal, dnorm and r) while for EGFR they are worse than random (blue lines below diagonal, dnorm and r). In sharp contrast however, use of FPS+MGE with any of the similarity metrics (red lines, columns d, dnorm, or r), or use of FPS with standard Euclidian (blue lines, column d) consistently yield good enrichment. Based on these observations, and for simplicity, discussion below is restricted to results employing FPS+MGE with standard Euclidian distance.
At 100% of the database, as demonstrated by the percent of maximum AUC, using the FPS+MGE scoring function provides more significant enrichment than the standard SGE function across all three systems examined (Table 5): neuraminidase (FPS+MGE = 84.23% vs. SGE = 81.12%), trypsin (FPS+MGE = 93.43% vs. SGE = 59.58%), and EGFR (FPS+MGE = 62.22% vs. SGE = 57.73%). While examination of total AUC is important, early enrichment is often considered to be a more useful metric given that the numbers of compounds that can be procured for experimental testing, for all practical purposes, are often limited by cost and time. Based on recent projects in our laboratory,[18,19] a reasonable number for purchase is on the order of 100-200 compounds per target. With these values in mind, partitioning of the results at 10% of the database for neuraminidase and trypsin and at 1% for EGFR yield a reasonable number of docked ligands for examination: (i) neuraminidase at 10% (N = 191 ligands) with FPS+MGE = 36 actives vs. SGE = 33; (ii) trypsin at 10% (N = 166 ligands) with FPS+MGE = 42 actives vs. SGE = 12; and (iii) EGFR at 1% (N = 165 ligands) with FPS+MGE = 101 actives vs. SGE = 113. Importantly, both methods yield a relatively large fraction of actives in these early rankings which provides confidence that virtual screening in a real-world application will yield useful numbers of lead-like compounds. And, in two of three cases (neuraminidase and trypsin), early enrichment appears to be enhanced using FPS+MGE over the standard SGE function. While more studies are desirable, the results provide support for using grid-based footprints “on-the-fly” instead of purely rescoring conformers that have been previously generated using standard DOCK procedures. This is expected to be especially important for de novo design as discussed in the next section.
De novo Design
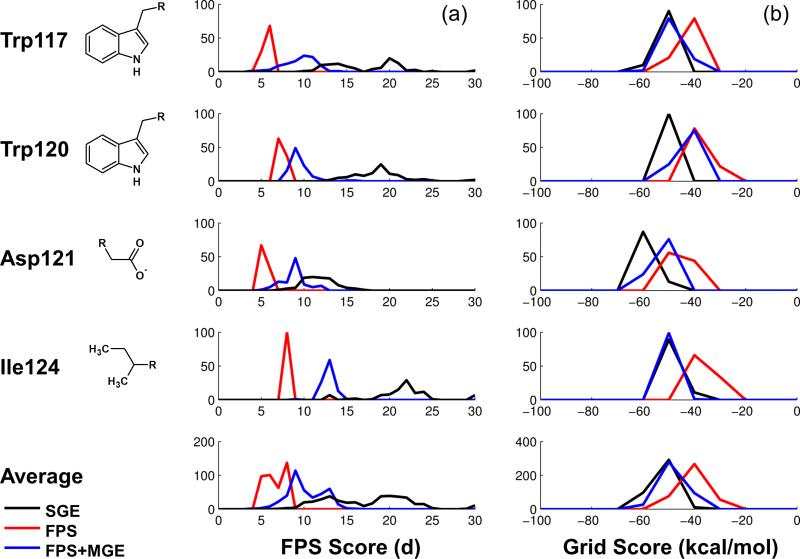
A key objective of de novo design is to construct new molecules which are chemically distinct from a known inhibitor or substrate, yet that interact in the protein binding pocket in a desired manner. To demonstrate the potential utility of using the FPS function to guide de novo design, we constructed ensembles of new ligands starting from four different anchors in the binding site of HIVgp41. Anchors were derived from the same four protein sidechains known to interact in the site and that constitute the reference (Trp117, Trp120, Asp121, Ile124). In separate experiments, de novo growth was guided by SGE alone, by FPS alone, or by FPS+MGE. Where appropriate, only the standard Euclidian distance metric was used to compute footprint similarity. Following de novo growth, the top 100 compounds grown under each condition (SGE, FPS, FPS+MGE) were then rescored to determine the FPS score (in the case of SGE) or the Grid Score (in the case of FPS). These experiments required 14 total grids: 13 representing the individual gp41 residues most important for binding (primary set) and 1 representing the remaining 95 residues (remainder set) of the protein receptor (PDB code 1AIK).[12] The results are summarized in Figure 9.
Figure 9.
Histograms of (a) FPS scores (Euclidian distance) and (b) Grid score (kcal/mol) for ensembles of molecules built using SGE (black line) vs. FPS (red line) vs. FPS+MGE (blue line) guided de novo design. The top four rows represent histogram results derived from four different starting anchors placed in the HIVgp41 binding site and the bottom row represents the population averages over all runs.
As expected, new molecules constructed from the starting scaffolds using the FPS method alone tend to have the lowest (most favorable) average FPS scores (d = 6.68), followed by FPS+MGE (d = 10.12), and finally SGE (d = 39.12; Figure 9a). Although perfect overlap is Euclidian distance of zero, which was not achieved in any of the present tests, use of FPS (Figure 9a red lines) or FPS+MGE (Figure 9a blue lines) to guide de novo growth yielded a significant number of compounds with low FPS scores indicating substantial footprint overlap with the reference. In contrast, use of SGE yielded much less overlap (Figure 9a black) and in many cases resulted in compounds with large unfavorable FPS scores. As anticipated, the combined function (FPS+MGE) yielded FPS score populations roughly in between that of pure FPS or pure SGE.
In terms of Grid energy (computed on a single grid for SGE, or as a sum over multiple grids for FPS and FPS+MGE) the lowest (most favorable) average energies are seen in ensembles generated using the SGE method (−51.45 kcal/mol), followed closely by the FPS+MGE method (−48.57 kcal/mol), then by FPS (−39.84 kcal/mol; Figure 9b). In sharp contrast to the average unfavorable FPS scores seen for SGE experiments (Figure 9a black), the average Grid energies, in all three runs, are generally considered favorable (Figure 9b all populations yield negative values). Encouragingly, this observation provides validation that molecules which are driven to have high FPS overlap with a reference will also generally have favorable Grid scores, presuming that the reference also has a favorable Grid score. Another interesting observation from Figure 9 is that the FPS+MGE-derived ensembles of molecules yield an average Grid score that is virtually the same as the SGE method. These observations in combination with the positive results from the pose reproduction, crossdocking, and enrichment experiments lead us to the conclusion that FPS+MGE is likely the most effective method for performing de novo design, despite the trade-off for longer computation time.
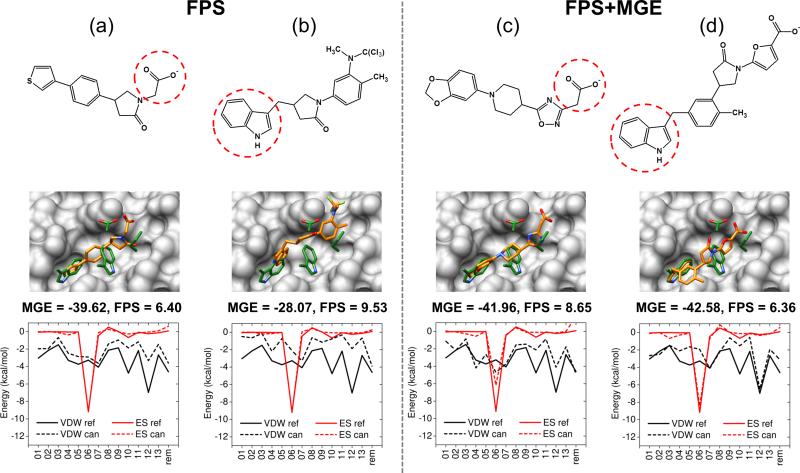
In terms of structure, visual examination of FPS-guided molecules showed numerous compounds with substituents that were chemically and physically similar to the reference employed during the construction. Figure 10 shows four examples: two were grown using the FPS method, and two were grown using the FPS+MGE method. For these experiments, growth was initiated either from a carboxylate anchor position which was derived from the C-helix residue Asp121 (Figure 10a,c), or from an indole anchor position which was derived from the C-helix residue Trp117 (Figure 10b,d). In the two examples starting from carboxylate anchors, growth proceeded into the HIVgp41 pocket and ultimately ended at either a thiophene ring (Figure 10a) or a 1,3-benzodioxole group (Figure 10c), both of which mimic the position and interaction of native C-helix residue Trp117. Conversely, in these two examples of growth beginning from the indole anchor derived from C-helix residue Trp117, we observed that growth proceeded into the pocket and ultimately ended at either a trichloromethyl (Figure 10b) or a carboxylate group (Figure 10d), both of which formed an electrostatic interaction with HIVgp41 residue Lys63, mimicking the conserved salt-bridge formed by the native C-helix residue Asp121.[35] Although considerable work yet remains, these initial de novo results from DOCK provide strong support that the grid-based implementation of FPS scoring is biasing growth as expected, and that additional testing and development is warranted.
Figure 10.
Example molecules constructed using de novo design in DOCK targeting HIVgp41 guided by footprints using either (a,b) the FPS scoring function or (c,d) the FPS+MGE scoring function. Red circles indicate starting anchor. Molecule 3D structures are footprint plots are colored as described in Figure 1. MGE energies in kcal/mol, FPS scores in Euclidean distance.
Conclusions
The implementation of a new grid-based footprint similarity (FPS) scoring method into the program DOCK has been described and extensively evaluated using pose reproduction, crossdocking, enrichment, and de novo design experiments. The generalization to multiple grids allows on-the-fly scoring and sampling to be performed in a computationally tractable manner and the method was shown to effectively reproduce footprints made in Cartesian space (Figures 2 - 3). In pose identification, the FPS+MGE rescoring method performs about 9-16% better than standard SGE docking, with all three comparison methods, but is on average ca. 5 - 6 times slower (Figure 4, Table 3). Nevertheless, this may be an acceptable tradeoff for specific docking scenarios. Efforts to increase the calculation speed are being explored.
Docking using FPS to guide ligand sampling on-the-fly also performs well but only when using the standard Euclidean similarity metric. Unacceptably high failures are observed when using FPS with normalized Euclidean or Pearson correlation, which is evidence that the magnitude of specific protein-ligand interactions should be included if used for pose reproduction (Figure 4, Table 3). Standard Euclidean matches both the magnitude and the shape of the footprint spectra while normalized Euclidean and Pearson correlation only match shape. Notably, all comparison methods perform well in FPS+MGE docking experiments (Figure 4, Table 3).
Relative to standard SGE sampling, the use of footprints during growth (FPS or FPS+MGE) yield molecular interactions which are more similar to the reference, as is made evident by FPS scores ultimately guided to lower values during the course of ligand growth (Figures 5 - 6). Although additional experiments are ongoing, the present pose reproduction studies indicate that the standard Euclidian similarity metric would be recommended if FPS alone is used to drive sampling. Otherwise, the combined function FPS+MGE, with either Euclidian method (standard or normalized), would be recommended. In fact, for virtual screening or de novo design application, it could be advantageous to use FPS+MGE scoring with normalized Euclidian to identify molecules that, in addition to matching a specific spectra, also make interactions with greater, more favorable magnitudes than the reference.
Crossdocking experiments for a challenging family of thermolysin proteins (N = 26 systems) demonstrated that the FPS+MGE scoring function yields moderately enhanced success (ca. 7%, Table 4) compared to SGE alone for reproducing binding poses in the context of slightly different receptor geometries and ligand sizes and chemistries (N = 676 protein-ligand pairs, Figure 7). These experiments also showed that the success rate on the diagonal was increased by ca. 38%, to a rate (80.77%, Table 4) which is more consistent with the success rate observed across the entire test set in pose reproduction experiments (84.0%, Table 3).
Analogous to the pose reproduction results (Figure 4, Table 3), enrichment results for the three test systems (Figure 8, Table 5) demonstrated that the FPS scoring function should be paired with the standard Euclidean similarity metric if it is used alone to drive sampling. Poor enrichment here is attributed to a lack of per-residue magnitude information for normalized Euclidean and Pearson correlation methods. In contrast, when using the FPS+MGE combination, any of the similarity metrics provided good enrichment over the standard SGE method as measured by total AUC. In terms of early enrichment at 10% (neuraminidase, trypsin) or 1% (EGFR) of the databases examined, use of the FPS+MGE function yielded a higher fraction of actives than the standard SGE function in two out of three cases.
Finally, we demonstrated that the grid-based FPS can be a useful scoring function to drive sampling for de novo design applications, as was made evident by the test applications to HIVgp41 (Figures 9 - 10). Ensembles of molecules built using the FPS or FPS+MGE scoring functions on average had higher footprint overlap with the reference structure, meaning that important binding site interactions were conserved, when compared to the SGE scoring function alone (Figure 9). In addition, in favorable cases, newly constructed molecules using FPS or FPS+MGE scoring functions contained functional groups that mimicked key reference positions and interactions in the binding site (Figure 10).
Overall, the present studies strongly suggest that the new grid-based footprint scoring method developed here for DOCK will be a practical alternative to the standard procedure for prioritizing docking, virtual screening, and de novo design results and a useful addition to the structure-based drug design toolkit. Our experiments indicate that the combined scoring function, FPS+MGE, is most robust. It is important to emphasize that the methods described herein are not limited to the systems studied in this manuscript but can be extended to almost any drug target for which there exists structural information and a suitable reference can be derived. Further, since the FPS function is a simple decomposition of the standard molecular mechanics-based energy score, parameterization beyond that already required to setup a standard DOCK calculation are not needed. The methods presented here, along with test case examples, will be made available in a forthcoming release of DOCK.
Acknowledgments
Gratitude is expressed to Lingling Jiang, Brian Fochtman, Yulin Huang, and Patrick Holden for helpful discussion. This research utilized resources at the New York Center for Computational Sciences at Stony Brook University/Brookhaven National Laboratory which is supported by the U.S. Department of Energy under Contract No. DE-AC02-98CH10886 and by the State of New York. This work was funded by NIH grants R01GM083669 (to R.C.R) and F31CA134201 (to T.E.B).
Contract/grant sponsor: National Institutes of Health; Contract/grant numbers: R01GM083669 (R.C.R.), F31CA134201 (T.E.B).
Footnotes
Author Contributions: T.E.B and W.J.A implemented the DOCK code described in this manuscript, designed and performed the experiments, and were responsible for the majority of the authorship. S.M. helped conceptualize the multi-grid protocol and provided assistance implementing the method into the DOCK code. R.C.R. provided mentorship in designing the experiments and significantly contributed to the editing of this manuscript.
References
- 1.Jorgensen WL. Science. 2004;303:1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 2.Kuntz ID. Science. 1992;257:1078–1082. doi: 10.1126/science.257.5073.1078. [DOI] [PubMed] [Google Scholar]
- 3.Shoichet BK. Nature. 2004;432:862–865. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bohm HJ, Comput J. Aided Mol. Des. 1992;6:61–78. doi: 10.1007/BF00124387. [DOI] [PubMed] [Google Scholar]
- 5.Gillet V, Johnson AP, Mata P, Sike S, Williams P, Comput J. Aided Mol. Des. 1993;7:127–153. doi: 10.1007/BF00126441. [DOI] [PubMed] [Google Scholar]
- 6.Schneider G, Fechner U. Nat. Rev. Drug Discov. 2005;4:649–663. doi: 10.1038/nrd1799. [DOI] [PubMed] [Google Scholar]
- 7.Jorgensen WL, Ruiz-Caro J, Tirado-Rives J, Basavapathruni A, Anderson KS, Hamilton AD. Bioorg. Med. Chem. Lett. 2006;16:663–667. doi: 10.1016/j.bmcl.2005.10.038. [DOI] [PubMed] [Google Scholar]
- 8.Barreiro G, Kim JT, Guimaraes CRW, Bailey CM, Domaoal RA, Wang L, Anderson KS, Jorgensen WL. J. Med. Chem. 2007;50:5324–5329. doi: 10.1021/jm070683u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schneider G, Comput J. Aided Mol. Des. 2012;26:115–120. doi: 10.1007/s10822-011-9485-2. [DOI] [PubMed] [Google Scholar]
- 10.Balius TE, Mukherjee S, Rizzo RC. J. Comput. Chem. 2011;32:2273–2289. doi: 10.1002/jcc.21814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mukherjee S, Balius TE, Rizzo RC. J. Chem. Inf. Model. 2010;50:1986–2000. doi: 10.1021/ci1001982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chan DC, Fass D, Berger JM, Kim PS. Cell. 1997;89:263–273. doi: 10.1016/s0092-8674(00)80205-6. [DOI] [PubMed] [Google Scholar]
- 13.Kuntz ID, Blaney JM, Oatley SJ, Langridge R, Ferrin TE. J. Mol. Biol. 1982;161:269–288. doi: 10.1016/0022-2836(82)90153-x. [DOI] [PubMed] [Google Scholar]
- 14.Ewing TJA, Makino S, Skillman AG, Kuntz ID, Comput J. Aided Mol. Des. 2001;15:411–428. doi: 10.1023/a:1011115820450. [DOI] [PubMed] [Google Scholar]
- 15.Moustakas DT, Lang PT, Pegg S, Pettersen E, Kuntz ID, Brooijmans N, Rizzo RC, Comput J. Aided Mol. Des. 2006;20:601–619. doi: 10.1007/s10822-006-9060-4. [DOI] [PubMed] [Google Scholar]
- 16.Lang PT, Brozell SR, Mukherjee S, Pettersen EF, Meng EC, Thomas V, Rizzo RC, Case DA, James TL, Kuntz ID. RNA. 2009;15:1219–1230. doi: 10.1261/rna.1563609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brozell SR, Mukherjee S, Balius TE, Roe DR, Case DA, Rizzo RC, Comput J. Aided Mol. Des. 2012;26:749–773. doi: 10.1007/s10822-012-9565-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Holden PM, Kaur H, Goyal R, Gochin M, Rizzo RC. Bioorg. Med. Chem. Lett. 2012;22:3011–3016. doi: 10.1016/j.bmcl.2012.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berger WT, Ralph BP, Kaczocha M, Sun J, Balius TE, Rizzo RC, Haj-Dahmane S, Ojima I, Deutsch DG. PLoS ONE. 2012;7:e50968. doi: 10.1371/journal.pone.0050968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Meng EC, Shoichet BK, Kuntz ID. J. Comput. Chem. 1992;13:505–524. [Google Scholar]
- 21.Huang N, Shoichet BK, Irwin JJ. J. Med. Chem. 2006;49:6789–6801. doi: 10.1021/jm0608356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Doms RW, Moore JP, Cell Biol J. 2000;151:F9–F13. doi: 10.1083/jcb.151.2.f9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eckert DM, Kim PS. Annu. Rev. Biochem. 2001;70:777–810. doi: 10.1146/annurev.biochem.70.1.777. [DOI] [PubMed] [Google Scholar]
- 24.Lang PT, Moustakas DT, Brozell SR, Carrascal N, Mukherjee S, Balius TE, Pegg S, Raha K, Shivakumar D, Rizzo RC, Case DA, Shoichet BK, Kuntz ID. University of California; San Fransico: 2006-2012. DOCK 6.5 User Manual. [Google Scholar]
- 25.Goodford PJ. J. Med. Chem. 1985;28:849–857. doi: 10.1021/jm00145a002. [DOI] [PubMed] [Google Scholar]
- 26.Ferrari AM, Wei BQ, Costantino L, Shoichet BK. J. Med. Chem. 2004;47:5076–5084. doi: 10.1021/jm049756p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kuhn HW. Nav. Res. Logist. Q. 1955;2:83–97. [Google Scholar]
- 28.Munkres J. J. Soc. Indust. Appl. Math. 1957;5:32–38. [Google Scholar]
- 29.Chan DC, Chutkowski CT, Kim PS. Proc. Natl. Acad. Sci. U. S. A. 1998;95:15613–15617. doi: 10.1073/pnas.95.26.15613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Irwin JJ, Shoichet BK. J. Chem. Inf. Model. 2005;45:177–182. doi: 10.1021/ci049714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bender A, Mussa HY, Glen RC, Reiling S. J. Chem. Inf. Comput. Sci. 2004;44:1708–1718. doi: 10.1021/ci0498719. [DOI] [PubMed] [Google Scholar]
- 32.Bender A, Mussa HY, Glen RC, Reiling S. J. Chem. Inf. Comput. Sci. 2004;44:170–178. doi: 10.1021/ci034207y. [DOI] [PubMed] [Google Scholar]
- 33.Wu TP, Padmanabhan K, Tulinsky A, Mulichak AM. Biochemistry. 1991;30:10589–10594. doi: 10.1021/bi00107a030. [DOI] [PubMed] [Google Scholar]
- 34.Stamos J, Sliwkowski MX, Eigenbrot C. J. Biol. Chem. 2002;277:46265–46272. doi: 10.1074/jbc.M207135200. [DOI] [PubMed] [Google Scholar]
- 35.He Y, Liu S, Li J, Lu H, Qi Z, Liu Z, Debnath AK, Jiang S, Virol J. 2008;82:11129–11139. doi: 10.1128/JVI.01060-08. [DOI] [PMC free article] [PubMed] [Google Scholar]