DeCon: A tool to detect emotional concordance in multivariate time series data of emotional responding

Abstract

The occurrence of concordance among different response components during an emotional episode is a key feature of several contemporary accounts and definitions of emotion. Yet, capturing such response concordance in empirical data has proven to be elusive, in large part because of a lack of appropriate statistical tools that are tailored to measure the intricacies of response concordance in the context of data on emotional responding. In this article, we present a tool we developed to detect two different forms of response concordance—response patterning and synchronization—in multivariate time series data of emotional responding, and apply this tool to data concerning physiological responding to emotional stimuli. While the findings provide partial evidence for both response patterning and synchronization, they also show that the presence and nature of such patterning and synchronization is strongly person-dependent.

The notion that our emotions are irrational passions that are detrimental or disruptive for normal functioning has long been abandoned in scientific thinking about emotion (Solomon, 2004). Instead, many, if not all, contemporary perspectives on emotions consider emotions to be dynamic, multicomponential adaptive responses to environmental threats and opportunities that motivate and enable an organism to quickly and efficiently deal with these challenges (e.g., Ekman & Davidson, 1994; Frijda, 1986; Gross, 2010; Izard, 1977; Sander, Grandjean, & Scherer, 2005).

A recurring proposal about how emotions achieve such adaptive function is framed in terms of response concordance (also termed synchronicity or response patterning, but see below). The idea is that during circumstances that have little personal or emotional relevance, the different components of emotions such as experience, appraisals, behavior, and physiology, are only loosely coupled and serve a multitude of different, largely unrelated, functions. During an emotional event, however, the different components become aligned in emotion-specific ways that provide the best and most efficient configuration to deal with the specific threat, challenge, or opportunity that elicits the emotional response (e.g., Davidson, 1992; Lazarus, 1991; Levenson, 1994; Sander et al., 2005).

There is, however, considerable theoretical debate about the usefulness of response concordance for understanding the nature of emotion. While some scholars give this construct a central place in their theory, or even their definition, of emotion (an emotion is “an episode of interrelated, synchronized changes in the states of all or most of the five organismic subsystems in response to the evaluation of an external or internal stimulus event as relevant to major concerns of the organism,” [Sander et al., 2005, p. 318]), others do not postulate response concordance as central or even of much relevance to understanding emotion (e.g., Russell, 2003). Also, response concordance has proven to be notoriously elusive; researchers have found it difficult to identify instances of response concordance in empirical data (Mauss & Robinson, 2009). As a result, the existence and role of emotional response concordance remains an enigma in understanding the nature of emotion.

Recently, technological advances have made it possible to collect the intensive time series data necessary to address the issue of response concordance in multiple types of contexts. This can range from data on recorded signals of multiple physiological indicators during standardized emotional stimulation in the lab (e.g., Mauss, Levenson, McCarter, Wilhelm, & Gross, 2005), recorded physiology and coded emotional behavior and experience during naturalistic interactions (e.g., Butler, Gross, & Barnard, in press), to ambulatory recordings of physiology, experience, and behavior in daily life (e.g., Ebner-Priemer & Kubiak, 2007). One of the main reasons that response concordance has remained difficult to capture empirically despite these advances is because it presents a difficult data-analytical challenge. Assessing response concordance requires detecting sudden or gradual changes in multivariate channels across time, with possibly large differences in how it manifests among individuals. Indeed, as Gross (2010) stated, “response coherence is quite a fragile flower, and very difficult to capture and quantify… Making sense of how experiential, behavioral, and physiological responses interrelate as emotions unfold over time represents a formidable challenge” (p. 213). To assess the existence and role of response concordance in understanding the nature of emotion, affective science needs appropriate data-analytical tools that are able to detect and examine the nature of response concordance. Or, again, to use Gross’s words, researchers in affective science are charged with “developing new tools for analyzing specific emotion-response components as well as cross-component coherence” (2010, p. 215).

Our aim in the present article is to respond to this need by describing a fast and robust method to scan multivariate time series data for the presence of response concordance. In this paper, we will first distinguish between two different phenomena that are referred to in the literature in the context of response concordance: response patterning and synchronization. Then, we review the major data-analytic challenges presented by the study of response concordance and propose a tool called DeCon to detect the occurrence of response concordance in empirical data. Finally, we illustrate the usefulness of the tool by analyzing data from a healthy sample on multimodal physiological responding during emotional stimulation.

Response concordance

Before continuing, it is important to disambiguate response concordance. Response concordance has traditionally been conceptualized in two different ways. In one sense, the term has been used to refer to the change in some or all emotional components according to a specific pattern of activation that is present during an emotional episode (which we refer to as response patterning). For instance, during an anger episode, psychophysiological parameters like heart rate and skin conductance become elevated (Herrald & Tomaka, 2002; Stemmler, 2004). In the other sense, the term response concordance has been used to refer to the increased covariation or synchronization across some or all response components over time during an emotional episode (which we refer to as response synchronization). For instance, heart rate and skin conductance become more strongly correlated with one another during an episode of anger (e.g., Mauss, Cook, Cheng, & Gross, 2007). Theorists have not always distinguished clearly between these two uses of response concordance, and have even used the two conceptualizations interchangeably. Yet, the distinction between these two conceptualizations of response concordance is crucial from a data-analytical point of view. Therefore, a first important step towards studying response coherence is to distinguish clearly between these two uses. We developed the DeCon tool that we present here to scan time series with respect to both of these phenomena, response patterning and synchronization, simultaneously.

Data-analytic challenges to detect patterning and synchronization

Assessing response patterning and synchronization is a data-analytic challenge for several reasons. First, although emotional concordance is sometimes measured by computing correlations across individuals (e.g., Matsumoto, Nezlek & Koopman, 2007), sudden or more gradual changes in response patterning and synchronization are, by definition, intra-individual phenomena and thus are best studied within individuals using intensive time series data (see Reisenzein, Studtmann, & Horstmann, 2013).

Second, in most concordance research, laboratory experiments are conducted in which different emotional states are induced using experimental manipulations (i.e., viewing emotional film clips; Mauss, Levenson, McCarter, Wilhelm, & Gross, 2005; Reisenzein et al., 2013). When analyzing the resulting data, the experimental manipulations are used as a manifest indication of the presence or absence of an emotional state. It is important to note, however, that such manipulations do not necessarily coincide with the onset and duration of emotional states because of anticipation effects, lags in emotional responding, and emotions that last shorter or longer than the corresponding manipulations (Lindquist, Waugh, & Wager, 2007; Waugh & Schirillo, 2012). The situation is even more difficult if one wants to examine concordance in more ecologically valid contexts (e.g., using recordings during spontaneous interactions or in real life), where no manifest indications of the presence and start and endpoints of emotional episodes are available. In sum, the onset and time course of induced or naturally occurring emotions is largely unknown, even in experimental contexts with clear onsets of emotional stimulation. Therefore, a method is needed that can detect latent (unknown) changes in response concordance, without having to rely on information regarding the occurrence and timing of emotional episodes.

Third, although synchronization is often studied by examining correlations (across time) between pairs of responses (Mauss, et al., 2005; Reisenzein, 2000), emotions clearly involve multiple experiential, physiological, and behavioral response channels. Therefore, methods are needed that allow the inclusion of many responses simultaneously (see Hsieh et al., 2011, for an exception that does not focus on changes across time).

Finally, the timing and nature of response patterning and/or synchronization is likely to differ significantly across individuals. Studying such inter-individual differences is crucial for understanding (mal)adaptive emotional responding. For instance, many hypotheses concerning problems in emotion regulation in mood disorders involve the timing, magnitude, and appropriateness of the emotional response across different channels (e.g., Waugh & Schirillo, 2012).

In sum, in order to detect patterning or synchronization in data of emotional responding, we need a method that is able to detect latent changes in intensive within-person data in the mean level (patterning) and covariation (synchronization) of multiple response channels to capture individual differences in the timing and nature of these changes.

DeCon: A method to detect response patterning and synchronization

To address these challenges, we propose DeCon as a tool that allows investigators to quickly and efficiently screen time series data of single individuals for (single or multiple) changes in mean level (response patterning) and covariation (response synchronization). Essentially, DeCon slides a fixed-length time window over the data, each time deleting the first time point and adding a new one. In each window, it examines whether the last time point deviates from the others in terms of means and/or (co)variance. If indications for such deviations accumulate across a number of consecutive windows, DeCon concludes that a change may have occurred in mean and/or covariance, and, therefore, in response concordance. Next, auxiliary analyses, such as regression analyses and jackknife procedures, are conducted to determine the precise nature of the changes in mean level and covariation. This allows us to pinpoint which (if any) of the variables show evidence of changes in level, in what direction, and with what size (to examine the nature of patterning); and changes in covariation by identifying which pairs of variables show increased, decreased, or largely unchanged synchronicity (to examine the nature of synchronization).

In the following paragraphs, we discuss the DeCon steps in more detail and illustrate them in Figure 1. The upper panel of this figure depicts a simulated time series data set that consists of three phases of 40 time points each. The X-axis represents the time dimension and the Y-axis the intensity level of the two variables involved. In the first and third phase the variables have zero means and are uncorrelated (see the first data panel of Figure 1). In the middle phase, the mean of one variable promptly changes to a high value (patterning) and the variables become strongly correlated (synchronization). Using this data set as an example, we will show how DeCon reveals both concordance changes.

Figure 1.

Overview of DeCon steps. The first panel shows a simulated bivariate time series. The second panel presents the ROBPCA outlier plots for the three time windows in the first panel. The third panel shows whether or not the respective time points are outliers in the time window in which they constitute the final observation. The fourth panel displays the moving outlier sum, with the vertical lines indicating the two detected change points.

Step 1: Apply robust PCA (ROBPCA) within each window

To detect change, DeCon uses robust statistical techniques that have been developed specifically to detect outliers (i.e., observations that deviate from others in terms of a particular statistic). Specifically, DeCon makes use of a robust variant of Principal Component Analysis (called ROBPCA) to detect changes in the mean or (co)variance of multiple variables across consecutive time windows (Hubert, Rousseeuw, & Vanden Branden, 2005). Before continuing, it is important to note that ROBPCA is performed on standardized variables to overcome the problem of scale dependency (i.e., if the variables differ strongly in variance, the ones with highest variance will dominate the PCA solution, Jolliffe, 2002). We now first discuss how to specify the size of the time window for DeCon, and how DeCon determines the number of components to be used in the ROBPCA analyses.

In a DeCon analysis, the number of consecutive time windows equals T − W + 1 (where T is the number of time points and W is the window size). The window size W should be determined by the user by balancing the time frame of the phenomenon under study (i.e., for how many time points is a person expected to stay in a specific emotional state) and the number of variables (i.e., W, the number of observations per window, should preferably be larger than five times the number of variables, as is often recommended in the literature on PCA and factor analysis, see e.g., Bryant & Yarnold, 1995). For instance, when examining emotional concordance (a phenomenon which takes place across seconds) in 5 variables measured every quarter of a second, a time window larger than 25 observations is minimally required, although the sensitivity of DeCon will increase with larger time windows (see Appendix). When determining the window size, it is advisable to conduct a sensitivity analysis in which the DeCon analysis is repeated using different sensible W-values to ascertain that the obtained results are stable.

To run ROBPCA, an optimal number of components for the first time windows has to be determined, in order to subsequently detect outliers with respect to this configuration. DeCon sets the number of components used to determine “outlyingness” by analyzing the data in each of the first ten windows and applying an automated scree test (Ceulemans & Kiers, 2006; Wilderjans, Ceulemans, & Meers, 2013) to each window. The performance of this automated scree test procedure was extensively studied for multiple models using simulations, yielding consistently good results (e.g., Bulteel, Wilderjans, Tuerlinckx, & Ceulemans, 2013; Ceulemans & Kiers, 2009; Ceulemans, Timmerman, & Kiers, 2011; Schepers, Ceulemans, & Van Mechelen, 2008). Still, some uncertainty in the selection of the number of components may remain due to sampling fluctuations. Therefore, the modus of the ten preferred number of components is used in the further analyses. Note that this implies that we assume that no changes occur in the first ten windows (i.e., in the first W+9 observations)¹. As DeCon is run on the data of each individual separately, the number of components is allowed to vary across individuals.

Step 2: Examine whether or not the final time point of each window is outlying

ROBPCA yields an outlier plot for each time window (see second panel in Figure 1), visualizing whether each time point is outlying in ways that may signal changes in patterning and/or synchronization. DeCon focuses on the last time point of each time window (indicated by a different marker in the figure) and determines whether it is outlying or not. Put simply: A time point is not deemed outlying when it is placed in the bottom left quadrant of the plot, and is deemed outlying otherwise.²

For instance, the second panel of Figure 1 (step 1) shows the outlier plots of three time windows. The first two windows are informative because they involve the first time point after a change has occurred in mean and correlation structure. Consequently, both plots show that the final time point is an outlier. In contrast, the last plot involves a window in which no changes were simulated. Consequently, in this plot the final time point is identified as a non-outlying, regular observation. This step of determining the “outlyingness” of the final time point of each window is automated in the DeCon software and yields a binary vector that indicates for each window whether (1) or not (0) the final time point is an outlier. The third panel of Figure 1 pertains to this step of the DeCon procedure. The X-axis represents the time dimension. A value of ‘1’ on the Y-axis means that the associated last observation in the window was identified as an outlier and a value of ‘0’ that the last observation is considered regular.

Step 3: Computation of moving sum and decision on concordance changes

In the third step, DeCon scans the binary outlier vector to decide whether and where changes occur. To this end, we build on the key idea of the Bernoulli scan statistic in change-point analysis (Ismail, Pettitt, & Webster, 2003) by computing a moving sum of the entries of the outlier vector. When this moving sum exceeds a threshold, evidence for change has been found. To incorporate this idea into DeCon, we conducted a small simulation study (see Appendix) to determine the optimal cutoff value (i.e., when are the resulting sums considered high enough to decide that a change in concordance has occurred). Results indicated that using a five-out-of-ten rule yields a good balance between Type 1 (false alarms) and Type 2 (misses) errors (although also for this tuning parameter running a sensitivity analysis is recommended). In other words, if subsequent final observations are outlying in at least five out of ten consecutive windows, DeCon signals a change point. The change point is set at the first outlying time point within the ten considered observations. For our example, the moving sum values that constitute the Y-axis in the bottom panel of Figure 1 indicate correctly that two concordance changes occur (around the 41^st and 81^st time points); these change points are indicated by vertical lines in the Figure.³

Step 4: Response patterning and/or synchronization?

In a final step, which is not illustrated in Figure 1, auxiliary analyses are conducted to investigate the nature of the change to gain more insight in which variables behave differently in terms of means and/or covariance. These analyses are conducted for each individual and each change point separately, discarding all time points before the preceding change point and after the subsequent change point. Moreover, if all individuals are subjected to the same emotion induction paradigm, analyses across all individuals can be conducted to investigate the existence of general response concordance changes.

Response patterning

To reveal intraindividual changes in response patterning, DeCon conducts a regression analysis for each response variable with a dummy variable indicating whether the time point occurred before or after the change point. If the regression weight of the dummy variable differs significantly from zero, evidence for response patterning has been found. To take into account the serial dependence, the predictor set of the regression includes the response scores at the previous time point (i.e., the auto-regressive effect). To study whether the obtained effects generalize across individuals, one can adopt the multilevel version (with random intercepts and fixed slopes) of the above described regression analysis.

DeCon also provides effect sizes of these changes, enabling to compare the magnitude of changes across different manipulations, contexts, or individuals. For instance, different emotions have been associated with different magnitudes of change in psychophysiological variables (e.g., heart rate and systolic blood pressure in fear and anger; Stemmler, 1988; 2003). Inspecting patterns of effect sizes can help to reveal such fine grained patterns of mean level changes.

Synchronicity

To detect synchronization changes, the eigenvalues of the time points before and after the change point will be examined. As mentioned above, the expectation is that the different emotion components become aligned during an emotional episode resulting in the first few eigenvalues becoming larger and the following ones being smaller when synchronization occurs. In contrast, more equally-sized eigenvalues are expected during a neutral state. Such synchronization changes can be revealed by conducting a paired t-test or a non-parametric alternative on the ‘before’ and ‘after’ eigenvalues of all individuals.

To decide whether subject-specific differences in ‘before’ and ‘after’ eigenvalues are significant, DeCon automatically performs a jackknife procedure (Efron & Tibshirani, 1994). In short, this procedure randomly selects and discards one time point before the change point and one after the change point, and recalculates the ‘before’ and ‘after’ eigenvalues. Next, the difference between both eigenvalues is computed. These steps are repeated 1,000 times. To decide on the occurrence of synchronicity, DeCon calculates a 95%-confidence interval for the difference in after and before eigenvalue. If the lower bound of this interval is positive, evidence for increased synchronicity is found.

The changes in eigenvalues reveal global changes in synchronicity without pinpointing the exact variables whose intercorrelations change. Therefore, to get more grip on which pairs of variables show increased, decreased or unchanged synchronicity before and after the change point, the before and after correlations of all pairs can be inspected, where stronger correlations, both positive and negative, after the change point are indicative of synchronization processes.

Software

We developed MATLAB code for running these analyses, using the Libra toolbox to fit ROBPCA (Verboven & Hubert, 2005). The code is available on request from the first or last author, and will soon be published in package form at http://ppw.kuleuven.be/okp/software/.

Illustrative application

To illustrate the tool, we will use data on multimodal physiological responses before, during, and after emotional stimulation. We analyzed a number of psychophysiological indicators (heart rate, skin conductance, facial muscle activity) collected during a task in which participants saw a cue indicating the valence of the emotional content of the pictures which were subsequently presented (in fact, we analyzed data before and during the first trial, see below). More information is presented below and a more detailed description of the task is also available in Waugh, Thompson, and Gotlib (2011). Data presented in the current paper are from a different sample of participants than what was presented in Waugh et al. (2011) and have not been presented elsewhere. By applying DeCon to these data, we determined whether and when changes in response patterning or synchronization took place, as well as the nature of these changes.

Method

Sample characteristics

The initial sample consisted of 30 women. Seven women were excluded due to technical problems (see below), leaving a final sample of 23 participants, ranging in ages from 18 to 55 years (M = 37.6 years, SD = 11.7). Participants’ race/ethnic composition was 57% White, 22% Asian American, 4% African American, and 17% indicated “other.” The sample was highly educated, with approximately 74% of the participants reporting having earned at least a bachelor’s degree. In terms of marital status, 52% were single; 35% were married or living with partner; and 13% were divorced.

Individuals were recruited from the community around Stanford, California, through advertisements posted online and at local agencies and businesses. All participants were native English speakers. Individuals completed a series of laboratory sessions, including diagnostic interviews to determine eligibility and the psychophysiological task described below. They also completed a number of self-report measures and tasks that were unrelated to those reported in the current study. The 23 participants whose data were analyzed for this paper had experienced no current or past history of any mental health disorders as assessed by the Structured Clinical Interview for DSM–IV Axis I Disorders (SCID-I; First, Spitzer, Gibbon, & Williams, 2001). Participants provided informed consent and were compensated for their participation. The protocol was approved by the university’s Institutional Review Boards.

Physiological acquisition

Multiple physiological signals were continuously measured during the experiment, representing multiple modalities of emotional responding. The physiological activity was monitored at a sampling frequency of 1 kHz with an integrated system and software package (Biopac PP150, AcqKnowledge; Biopac Systems, Goleta, CA). Heart rate was monitored with an electrocardiography module and a lead II configuration on the torso. After visual inspection and correction of the r-spikes, interbeat interval (IBI) was calculated. Skin conductance level (SCL) was monitored with two 6 mm Ag/AgCl electrodes placed on the distal phalanges of the first and second fingers on the nondominant hand. In addition to these autonomic measures of emotion, facial behavior was assessed with electromyography (EMG). Specifically, three muscle groups were targeted: i.e., the corrugator supercilii (Corr.), orbicularis oculi (Orb.), and zygomatic major (Zyg.). Pairs of 4 mm Ag/AgCl electrodes were placed over these muscles. Corrugator muscle activity corresponds to the furrowing of the eyebrows, and zygomatic activity to the elevation of the corners of the lips (Mauss & Robinson, 2009). The orbicularis muscle surrounds the eyes and is responsible for the crinkling around the eyes.

Procedure

The fragment of data used for the current purpose consists of the data collected during the baseline and the first trial, which spanned 75 s. After a 50-s baseline period in which the participants rested quietly, the first trial started with the participants viewing a positive cue (“+” cue) for 5 s, indicating that pleasant pictures will be shown next. Three successive positively valenced pictures from the International Affective Picture Set (IAPS; Lang, Bradley, & Cuthbert, 1997) followed the presentation of the cue. Each image was shown for 4 s. The trial ended with an 8 s recovery period in which the participants viewed a blank screen. From the original sample of 30 participants, 7 participants were excluded due to software triggering problems that led to a failure to collect data for this first trial.

Data reduction and scoring

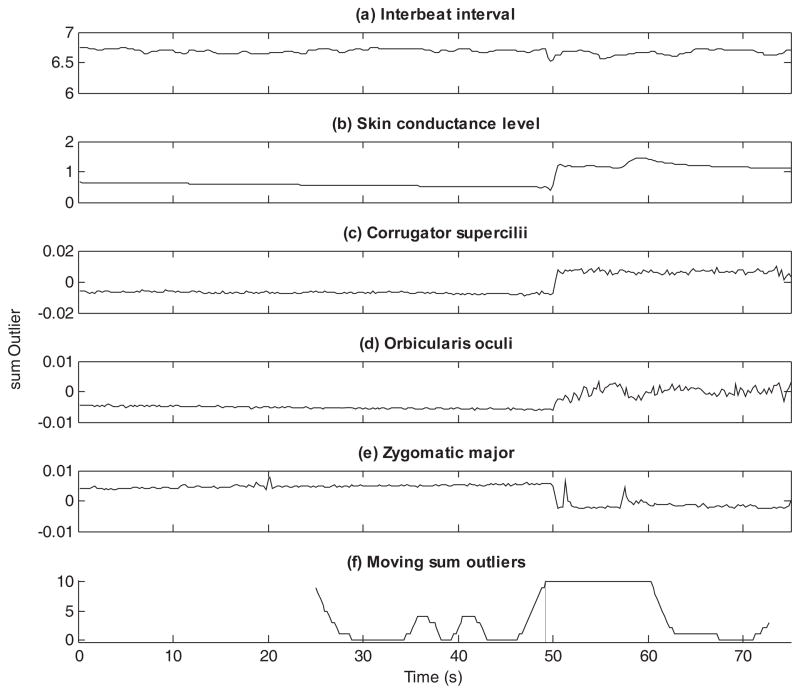
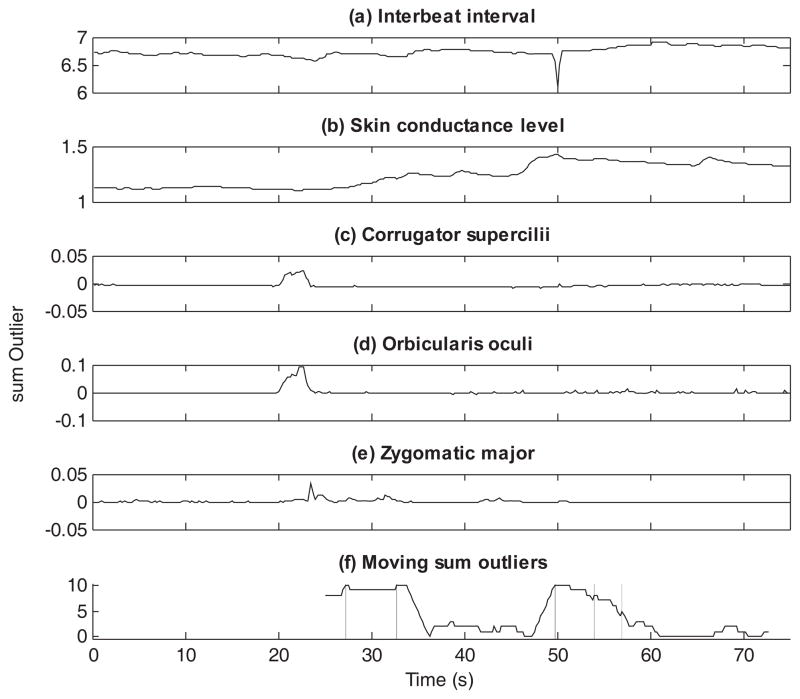
The scoring of the physiology data was conducted by means of the Autonomic Nervous System Laboratory (ANSLab v2.4, Wilhelm & Peyck, 2005) as well as with custom scripts implemented in MATLAB. The skin conductance activity was low-pass filtered at 1 Hz. The corrugator and zygomatic activity were high-pass filtered at 28 Hz, rectified, and smoothed with a moving average window of 50 ms. Next, the data on the activity of both muscles were linearly detrended across both the baseline period and the trials. The EMG signals of the orbicularis muscles were low-pass filtered at 100 Hz and rectified (Waugh et al., 2011). For the present analyses, additional processing was conducted. The sampling frequencies of the five measures, initially resampled at different rates during preprocessing, were re-aligned using linear interpolation to 4 measurements per second. Furthermore, IBI and SCL values were log-transformed (note that despite this transformation we will still use the labels IBI and SCL when reporting results). Figure 2 and 3 show the resulting time series data for two participants. Panels (a) to (e) of each figure show the data of, respectively, the interbeat interval, skin conductance level, and the activity of the corrugator supercilii, orbicularis oculi, and zygomatic major across baseline, first experimental trial, and recovery. While the data from the first participant (Figure 2) show clear indications of changes in the recordings around 50 seconds, the data from the second participant (Figure 3) are less clear to detect with the naked eye.

Figure 2.

For participant 6, the multivariate time series (panels [a]–[e]) and the evolution of the moving sum outlier statistic (panel [f]) is shown. Panels (a)–(e) display the time series data of the interbeat interval, skin conductance level, and the activity of the corrugator supercilii, orbicularis oculi, and zygomatic major, respectively. Panel (f) displays the moving sum outlier statistic as generated by DeCon. The vertical line indicates the detected change point.

Figure 3.

For participant 14, the multivariate time series (panels [a]–[e]) and the evolution of the moving sum outlier statistic (panel [f]) is shown. Panels (a)–(e) display the time series data of the interbeat interval, skin conductance level, and the activity of the corrugator supercilii, orbicularis oculi, and zygomatic major, respectively. Panel (f) displays the moving sum outlier statistic as generated by DeCon. The vertical lines indicate the detected change points.

Data analysis

To examine the occurrence of response patterning and/or synchronization, we analyzed the time series data of each single participant with DeCon. The window size was set to 25 s. The previously described five-out-of-ten rule was used to scan the binary outlier vector. Sensitivity analyses with smaller time windows (6.25 s and of 12.5 s) and four- to ten-out-of-ten rules yielded very similar results, though.

Results

We will first discuss the results of DeCon regarding the timing of the change points, and will then describe what changes occurred from one phase to the other based on the auxiliary analyses, both across and within individuals.

Change points

The proposed DeCon tool was used first to scan the multivariate time series data of each participant. This resulted for each participant in at least one change point. Examples of the results of DeCon are presented for the two participants in Figures 2 and 3. As can be seen from Figure 2, DeCon detected a unique change point for this participant around 50s (the presentation time of the cue). For the participant in Figure 3, five change points were detected (i.e., at 27.25 s, 32.75 s, 49.75 s, 54.00 s, and 57.00s). For the sample of participants, the number of identified change points varied between one and six (M = 3.29, SD = 1.31). However, a change point around 50 s was consistently found across all participants, except for two participants whose data were changing gradually across several seconds, which resulted in DeCon identifying a continuous string of outliers. Consequently, for these two participants it was impossible to define a distinct phase before and after the presentation of the cue. For reasons of clarity, these two participants were excluded in the subsequent analyses (including these participants in the analysis did not alter the obtained results).

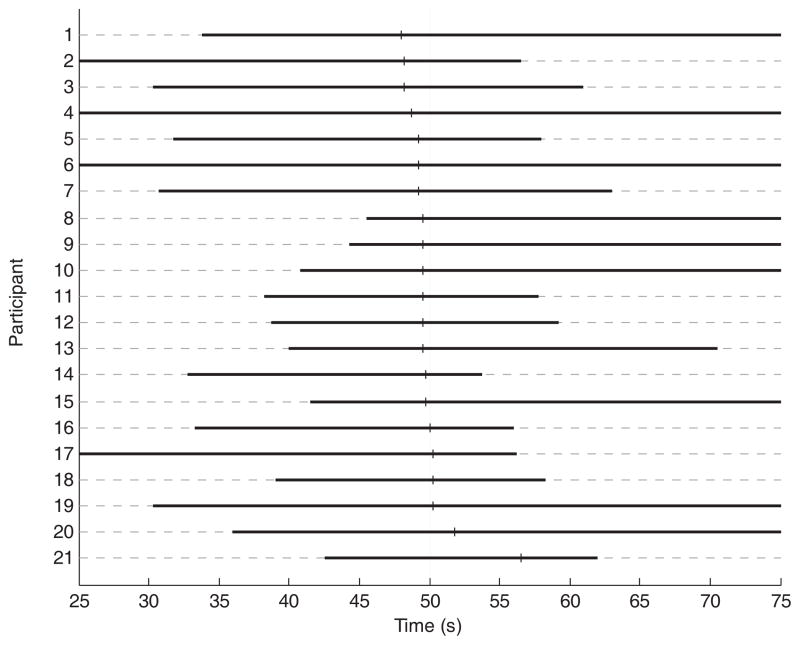
Despite the fact that (a) DeCon does not constrain the detection of change points (except that no change point can be detected during a first period equal to the window size minus 1), and (b) the number of detected changes points varied across participants, DeCon consistently detected a change point in the vicinity of 50s of elapsed time for all participants (see Figure 4 for a graphical illustration). The remaining detected change points were all idiosyncratic and were probably caused by individual spurious factors, such as bodily movement. Because the change point around 50s was consistent across all participants, we focused the remainder of our analyses on this common change point (which coincided with the presentation time of the cue). As a consequence, we clipped the time series at the change points directly preceding the cue presentation change point and the change point directly following it. This left us with a stable phase before and after the change point at cue presentation time to be used in the subsequent auxiliary analyses (see below).

Figure 4.

Overview of the detected change points with DeCon. Each line represents a single participant. The detected change points around the cue presentation time are represented by a small vertical black line (the vertical gray line at 50 s is the cue presentation time). For each participant, the horizontal thick black line refers to the phase directly preceding the change point at the cue presentation and the phase directly following the cue presentation change point (for two participants only one change point was detected and then the black line runs from the start to end). The time axis starts at 25 s because the window size was 25 s and a change point can only be detected starting from 25 s.

As can be seen in Figure 4, the detected transition points are often situated somewhat before the actual presentation time of the cue (the average difference between the change point time and the cue presentation time is 0.1667 s). This was due to an accumulated effect of two separate issues. First, this was partially due to the asymmetric influence in the outlier detection procedure of a false alarm and of a miss (see the third footnote). A second factor explaining the premature change point detections involves the interpolation and filtering algorithms used to preprocess the physiological signals. We will not discuss this issue in detail here but should note that filtering may distort the temporal dynamics and onset latencies (see e.g., VanRullen, 2011; Widmann & Schröger, 2012).

Response concordance

In this section, we will present results from auxiliary analyses comparing in detail the phase before and after the detected change point around cue presentation time in terms of response patterning and synchronization.

Response patterning

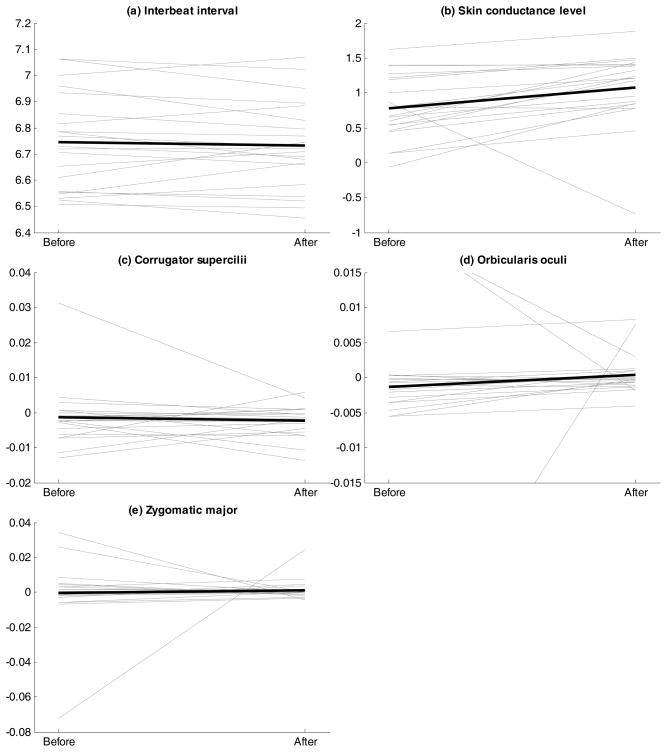
To examine changes in mean level, we used a regression approach with two predictors (see above): one predictor reflecting the previous measurement (to account for time dependency in the measurements), and one dummy coded predictor to indicate whether a time point occurred before/after the change point. The participant-specific findings can be found in spaghetti plots displayed in Figure 5, but are also summarized in Table 1; moreover, the distributions of the Cohen’s d effect sizes corresponding with the changes are displayed in Figure 6. A first conclusion from these results is that there are sizeable individual differences in response patterning, that is, the extent to which physiological indicators show significant decreases or increases varies strongly across participants.

Figure 5.

Spaghetti plots showing the participant-specific (thin lines) and sample average (thick lines) changes in mean level before and after the change point for all five measured variables (panels [a]–[e]).

Table 1.

Participant-specific response patterning. The significance of the regression coefficient of the before/after predictor was assessed (using as a threshold p = 0.05/(5*21) = 0.00048 making use of a Bonferroni correction for multiple testing). In the cells of the table, one may find the number of participants that show a decrease, no evidence for change, or an increase.

Variable	Decrease	No evidence for change	Increase
Interbeat interval	2	19	0
Skin conductance level	1	5	15
Corrugator supercilii	8	7	6
Orbicularis oculi	2	15	4
Zygomatic major	4	11	6

Figure 6.

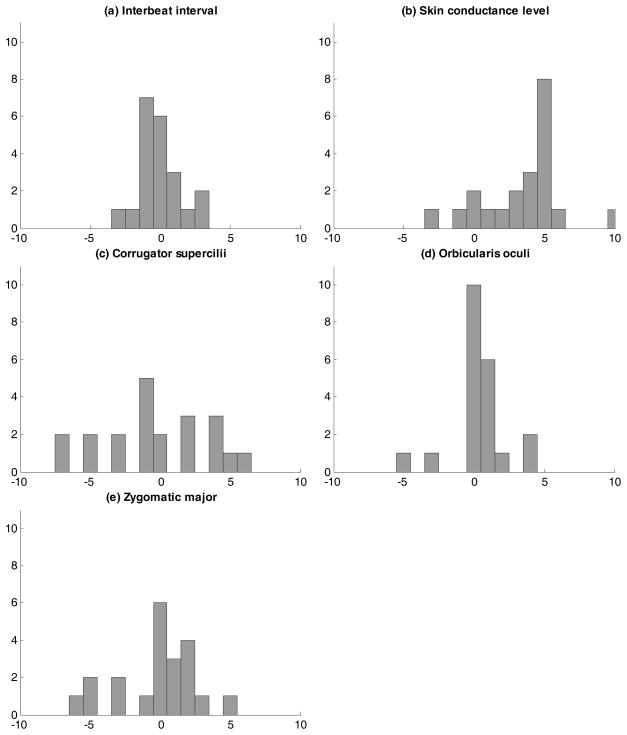
Effect sizes of changes in participant-specific mean levels in (a) interbeat interval, (b) skin conductance level, (c) corrugator supercilii, (d) orbicularis oculi, and (e) zygomatic major, from before to after the change point identified by DeCon.

Regarding general mean changes, conducting the multilevel variant of the above regressions (with random intercepts but fixed slopes), revealed that the fixed effect of the dummy variable was only significant in case of SCL (t(1342.645) = 4.503, p < .0001). For the other variables, there was no evidence for a change after the change point when considered across all participants (IBI: t(2620.703) = −1.620, p = 0.105; Corr.: t(2629.018) = −0.618, p = 0.537; Orb.: t(2219.247) = 1.489, p = 0.137; Zyg.: t(2629.003) = 0.767, p = 0.443). These results confirm the findings from the individual analyses, showing indeed that only for SCL large effect sizes were found (Figure 6).

Response synchronization

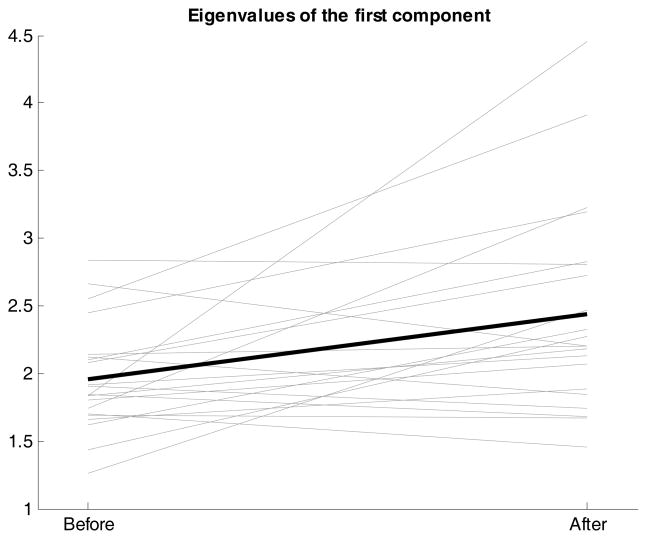
To detect global synchronicity changes per individual, we examined changes in the eigenvalues before and after the change point. To make sure that the eigenvalues reflect only changes in correlations and not in variance, the variables were standardized within each phase. In particular, we verified whether the first few eigenvalues increase and the later ones decrease, which provides evidence for synchronization. Our hypotheses are confirmed by pairwise t tests showing that, across all participants, the value of the first eigenvalues increased after the detected change points (eigenvalue of the first component: t(20) = −2.989, p = 0.007; Cohen’s d: 0.65; of the second component: t(20) = −0.251, p = 0.805; Cohen’s d: 0.05), whereas the last eigenvalues decreased after the change point (eigenvalue of the third component: t(20) = 2.938, p = 0.008; Cohen’s d: −0.64; of the fourth component: t(20) = 3.951, p = 0.001; Cohen’s d: −0.86; of the fifth component: t(20) = 2.612, p = 0.017; Cohen’s d: −0.57). Figure 7 illustrates this finding for the first component showing that, across all participants, there was indeed an increase in eigenvalue. This provides evidence for synchronization because it implies that there is a stronger degree of association among the five variables after the change point compared to before the change point. Thus, in general the dependence between the five variables increases after the cue, although it does not necessarily imply that all five indicators synchronize for each individual.

Figure 7.

Spaghetti plot showing participant-specific (thin lines) and sample average (thick line) changes in the first eigenvalue before and after the change point identified by DeCon.

As was the case with response patterning, there were substantial individual differences (see thin lines in Figure 7). To test whether the participant-specific changes in eigenvalues of the first component were statistically significant, DeCon performs the jackknife procedure described above. This procedure revealed that 13 participants showed some form of synchronization (i.e., significant individual increase in first eigenvalue); for 3 other participants, the first ‘after’ eigenvalue is smaller than the ‘before’ eigenvalue, indicating that the correlation among the different variables decreased. No evidence for a change was found for the 5 remaining participants.

Additionally, we investigated which physiological processes synchronize, by comparing the correlations between all pairs of variables before and after the change point. For ease of presenting the results, we operationalized synchronization as a correlation that has an absolute value lower than .50 before the change point and larger than .50 afterwards, with a minimum difference of 0.1. When the strength of the correlation changes in the opposite direction, the variables desynchronize. The results are summarized in Table 2. Synchronization occurs for each pair of variables at least once, but for at most six participants. Furthermore, large individual differences exist. For three participants no changes occur whereas for another participant each pair of variables synchronizes. The remaining participants show different patterns of which physiological processes synchronize.

Table 2.

Results depicting the number of participants for which correlations between each pair of variables showed evidence of synchronization, desynchronization, or no change from before to after the detected change-point.

	Increase in strength of correlation	Decrease in strength of correlation	No evidence for change
IBI-SCLa	6	2	12
IBI-Corr	3	0	18
IBI-Orb	1	1	19
IBI-Zyg	3	1	17
SCL-Corra	6	1	13
SCL-Orb	3	2	16
SCL-Zyg	6	1	14
Corr-Orb	6	2	13
Corr-Zyg	5	1	15
Orb-Zyg	4	1	16

^aThe change in strength of the correlation was not classified for one of the participants, because it concerns a strong correlation (i.e., > |.5|) both before and after the change point but with a reverse sign.

Discussion

Although response concordance, defined either in terms of response patterning or response synchronization, is a central element in several theories and definitions of emotions, it has proven to be difficult to capture empirically (Gross, 2011; Mauss & Robinson, 2009). One of the main reasons for this difficulty is that, despite technological progress to measure the unfolding of multi-componential emotional responses across time, data-analytical tools were not readily available to detect latent changes in patterning or synchronization of these components. In this paper we proposed a custom-made tool to enable the detection of response patterning and synchronization in the kind of data typically collected in the affective sciences. Our hope is that by making this tool available to researchers, we can contribute to the empirical study of the existence and boundary conditions of concordance in emotional responding. In the following, we will describe the methodological contributions and limitations of DeCon, and discuss the implications of the first empirical findings using this procedure.

DeCon: A method to detect response patterning and synchronization in emotional responding

From a theoretical point of view, DeCon targets two different instances of response concordance: response patterning and response synchronization. Both types of concordance feature in theoretical accounts of the changes occurring in the multi-componential architecture of emotion, yet may not always have been sufficiently distinguished from one another. A first important contribution of this paper therefore, is to distinguish between these two types of concordance, and propose a method that is sensitive to both.

Moreover, an important theoretical premise of DeCon is that it allows for individual differences in response concordance. Individual variation is pervasive in emotional responding (Davidson, 1998; Kuppens, Stouten, & Mesquita, 2009), and there is no reason to assume this would be different for the concordance of its components. Indeed, although many theories postulate response patterning and synchronization, it makes sense to expect that the occurrence of these phenomena and the forms they take are moderated by individual differences and situational factors (e.g., Stemmler & Wacker, 2010), as well as by their interaction. DeCon permits the examination of such differences and, therefore, the boundary conditions in which these phenomena take shape, while at the same time conclusions can be drawn on an inter-individual level. To be clear, DeCon in itself does not allow inferences about the cause of concordance. Yet, it enables the empirical study of its occurrence, antecedents, and consequences, for instance by linking results of DeCon to features of the experimental paradigm or manipulations, person or contextual covariates.

From a data point of view, DeCon was specifically designed to analyze the type of data needed to study response concordance in emotion: intensive multivariate time series of different variables across time, and has no limitations in terms of the number of variables involved, the time-scale on which data were collected, or whether they were harvested in standardized or in naturalistic settings. Indeed, one of the main advantages of DeCon in this respect is that it is able to detect latent changes in patterning or synchronization, which implies that explicit information on the start or ending of an emotional episode need not be known to find the exact change point. This allows studying concordance in data obtained in both more controlled laboratory settings as well as in more ecological contexts.

From a methodological/statistical point of view, the main assets of DeCon are that it is well founded in robust statistics, makes few distributional assumptions, and can easily handle a large amount of input channels and multiple change points within the time series. Moreover, results can be readily obtained in a few seconds (depending on the length of the time series) and can be easily visualized.

Of course, DeCon also has some limitations. First, DeCon only signals that the means and/or (co)variations have changed, without immediately pinpointing what has changed. Indeed, if the responses of people become more independent rather than more synchronized, DeCon would also yield a change point. To deal with this limitation, we proposed a number of auxiliary analyses (regression analyses and jackknife procedures) that can be conducted afterwards to reveal the nature of the obtained changes. Therefore, an interesting direction for future research is to explore whether the detection of changes and the auxiliary analyses can be further integrated.

Next, DeCon might not detect changes if it concerns very slow change. In case one can expect such changes, we recommend carefully determining the window size and the cutoff value. Continuous change can be found by inspecting the value of the moving sum since this value will remain high. It will also be reflected in the many detected change points close to each other (see higher regarding the two discarded participants).

A final limitation of DeCon is that it is geared towards linear forms of synchronization, as it looks for changes in correlation. However, some emotion researchers quite reasonably argue that synchronization may be more complex and non-linear (Lewis, 2005; Sander, et al., 2005; Scherer, 2000). Because such forms of synchronization cannot be detected by DeCon, it will be important to investigate whether and how such non-linear synchronization can be incorporated in the method. Given that non-linear relations can take many different forms, such adaptions will have to be based on (possibly competing) theories to make the endeavor feasible.

First lessons from applying DeCon to empirical data

In addition to proposing DeCon in this paper, we also provided a first empirical application of the method to data involving physiological recordings before and during the display of emotional pictures to participants. While this presents only a first and preliminary examination of the occurrence of response patterning and synchronization using DeCon, the method nevertheless yielded a number of interesting results concerning the nature of response concordance in emotion for a healthy sample.

One of the central topics of debate in the literature and in this special issue is whether response concordance indeed occurs during emotional responding or whether the different components of emotions are at best only loosely coupled (e.g., Mauss & Robinson, 2009; Russell, 2003; Sander et al., 2005). In the data analyzed and reported here, DeCon detected changes in patterning and synchronization for all participants during the first trial, which involved a preparatory cue and the display of positive pictures. This is noteworthy especially when considering that our data involved relatively weak emotional stimulation (in the forms of pictures), which is considered to evoke relatively weak coherence in comparison to more strong emotions (Davidson, 1992). On average, the most robust form of patterning was an increase in skin conductance in response to the cue, which is consistent with the role of skin conductance in anticipation of potentially emotional events (Epstein & Clarke, 1970). In terms of synchronization, on average our data supported the central idea of different (in this case peripheral physiological) emotion components becoming more synchronized during an emotional episode (or at least during the anticipation and viewing of emotional stimuli). These results are promising, and future research should apply DeCon to different types of empirical data to identify the conditions under which concordance findings can be reproduced.

Importantly, however, these findings were qualified by sizeable individual differences. Indeed, these healthy participants showed considerable variation in the physiological indicators for which response patterning was observed. Despite the average observed increase of skin conductance, Table 1 presents a strong testimony for the idiosyncratic nature of response patterning. Based on these data, we must conclude that response patterning may not come in universal form; instead, there is large idiographic variation in individuals’ physiological responses to emotional events, and hence, in the nature of response patterning that will be observed in different individuals. This conclusion is consistent with the notion of individual response specificity in emotion (Engel, 1960; Stemmler & Wacker, 2010), which considers individual differences the norm rather than the exception in physiological emotional responses.

While on average evidence for increased synchronization was found across participants, quite a few individuals deviated from this trend as well. In other words, synchronization is also subject to significant individual differences, to the point that some individuals displayed patterns of decreased rather than increased covariation between emotion physiological indicators during emotional stimulation.

Given such individual differences, an important avenue for future research will be to examine the factors that moderate the extent to which different components of emotions display concordance. For instance, with respect to well-being, an intriguing question is whether higher synchronization is indicative of more adaptive or rather more maladaptive (because perhaps less flexible) emotional functioning. Because DeCon maximally allows individual differences in response concordance to be detected, this opens up an exciting range of new research questions.

One particularly interesting finding was that, leaving aside minor idiographic variation, DeCon identified the most consistent changes in concordance not at the time when the emotional pictures were displayed, but at the time of the cue which indicated the valence of the subsequent pictures. This implies that physiological changes occur in anticipation of emotional stimuli rather than at the onset of emotional stimulation itself, although the positive cue could be conceived as an emotional stimulus in itself as well. An alternative explanation of this finding might be that the observed changes in response concordance reflect an orienting response rather than true emotional reactions. While this cannot be ruled out on the basis of the current data, it deserves further attention (and alternative study designs) to establish whether the observed patterns are indeed specific to emotional cues or generalize to non-emotional orienting as well. As mentioned above, however, while DeCon enables researchers to study the timing, size, and nature of response concordance, inferences about the cause of the observed processes are dependent on the study design.

In sum, this first empirical application leads us to advance the following preliminary conclusions regarding emotional response concordance. First, applying DeCon yields partial evidence for response concordance, both in the form of patterning and in the form of synchronization. Second, however, both response patterning and synchronization are subject to sizeable individual differences in terms of which components change and how. DeCon offers an ideal tool for future research to examine what are normative and aberrant patterning and synchronization as well as the sources and implications of these differences in both healthy and clinical samples.

Highlights.

• Emotional response concordance remains an enigma in affective science, partly due to a lack of appropriate statistical methods to study it

• We introduce a tool, named DeCon, to study two forms of emotional response concordance, patterning and synchronization

• Applying DeCon to data of physiological emotional responses found partial evidence for the occurrence of concordance

• The size and nature of observed patterning and synchronization was strongly person-dependent

Appendix: Simulation study to determine the optimal cutoff value to be used in Step 3 of the DeCon procedure and to examine the effect of the window size used

In this appendix, we will present the design and the results of a simulation study, conducted with three aims: (1) Showing that DeCon generally succeeds in detecting whether and when changes in response concordance occur, (2) selecting an optimal cutoff value for determining when a change point has occurred and (3) determining the optimal window size. The size of the generated data sets was based on the empirical data that we analyzed in the present paper, in that each data set consists of 300 measurement occasions and five variables. The following factors were varied in a completely randomized design:

1. Changes in mean level, at three levels: no change, an increase of one standard deviation for 3 of the 5 variables at time point 151, and an increase of two standard deviations for 3 of the 5 variables at time point 151;

2. Changes in correlation structure, at two levels: no change, with the underlying number of components being set to three, and a change at time point 151, in that the number of components changes from three to two;

3. The AR(1) coefficient, at three levels: no autocorrelation, .3, and .7.

The following data construction procedure was applied. First, error values were randomly sampled from a multivariate normal distribution, with a vector consisting of zeros as the mean and the identity matrix as the variance-covariance matrix. Subsequently, lag-one autocorrelation was induced on these error values by means of a recursive filter (Hamilton, 1994). After filtering the error values, the variance was rescaled to 1. Second, we generated scores that perfectly reflect principal component models. If there are no changes in correlation structure, a 300 × 5 matrix was constructed according to a model with three components. If there is a change in correlation structure, two 150 × 5 matrices were created; the first one based on three components, and the second one based on two components. To this end, we sampled the component scores of the measurement occasions from a standard normal distribution. The component loadings of the variables were randomly drawn from a uniform distribution on the interval (−1,1). Third, the loadings and error values were rescaled in order to obtain an error level of 25% in the final data matrices that are computed by multiplying the component scores and loadings and adding the error values. The scores in these matrices approximately follow a standard normal distribution. Finally, to induce the changes in mean level, a zero, a one or a two is added to the data of the first three variables for measurement occasion 151 to 300. For all 18 cells of the design, ten replications were generated.

Each of the 180 resulting data matrices was analyzed 18 times, by varying

1. The window size W, at three levels: 25, 50, and 100;

2. The cutoff value, at six levels: 4, 5, 6, 7, 8, and 9.

To determine the effect of the window size and the cutoff value on the detection of the change point, we examined whether or not DeCon signals the occurrence of a change point between time point 145 and 155. When multiple change points were detected (although only one true change point is included), we take the point that is closest to the true change point into account. The results are displayed in Table 3, as a function of window size and cutoff value. Generally, the performance of DeCon improves as the window size increases and as the cutoff value decreases.

Table 3.

The percentage of data sets for which DeCon correctly identified the change point, depending on the window size and the cutoff value.

Cutoff value	25	Window size
		50	100
4/10	53%	69%	77%
5/10	51%	73%	78%
6/10	46%	69%	72%
7/10	41%	59%	64%
8/10	28%	53%	58%
9/10	18%	44%	49%

We also computed the number of type I- and type II-errors, which are presented in Table 4. As could be expected, the number of type I-errors (false positives) decreases as the cutoff becomes more stringent, whereas the number of type II-errors (false negatives) increases. Moreover, the larger the window size the lower both kinds of errors. Based on these results, we recommend using a window size of 100 and a cutoff value of 5, as this combination yields the lowest sum of type I- and type II-errors.

Table 4.

The percentage of type I- and type II-errors, depending on the window size and the cutoff value.

Cutoff value	Window size
	25		50		100
	Type I	Type II	Type I	Type II	Type I	Type II
4/10	17%	2%	13%	4%	7%	2%
5/10	14%	16%	6%	15%	2%	9%
6/10	8%	35%	2%	25%	0%	18%
7/10	2%	54%	1%	37%	0%	29%
8/10	1%	71%	0%	46%	0%	38%
9/10	0%	82%	0%	55%	0%	49%

Regarding the effect of the manipulated factors (only considering the success rates for the window size of 100 and cutoff value of 5), as could be expected, success rates are highest when both the mean level and the correlation structure changes. The amount of autocorrelation does not influence the success rate.