Tumor Endothelial Marker Imaging in Melanomas Using Dual-Tracer Fluorescence Molecular Imaging

Abstract

Purpose

Cancer-specific endothelial markers available for intravascular binding are promising targets for new molecular therapies. In this study, a molecular imaging approach of quantifying endothelial marker concentrations (EMCI) is developed and tested in highly light-absorbing melanomas. The approach involves injection of targeted imaging tracer in conjunction with an untargeted tracer, which is used to account for nonspecific uptake and tissue optical property effects on measured targeted tracer concentrations.

Procedures

Theoretical simulations and a mouse melanoma model experiment were used to test out the EMCI approach. The tracers used in the melanoma experiments were fluorescently labeled anti-Plvap/PV1 antibody (plasmalemma vesicle associated protein Plvap/PV1 is a transmembrane protein marker exposed on the luminal surface of endothelial cells in tumor vasculature) and a fluorescent isotype control antibody, the uptakes of which were measured on a planar fluorescence imaging system.

Results

The EMCI model was found to be robust to experimental noise under reversible and irreversible binding conditions and was capable of predicting expected overexpression of PV1 in melanomas compared to healthy skin despite a 5-time higher measured fluorescence in healthy skin compared to melanoma: attributable to substantial light attenuation from melanin in the tumors.

Conclusions

This study demonstrates the potential of EMCI to quantify endothelial marker concentrations in vivo, an accomplishment that is currently unavailable through any other methods, either in vivo or ex vivo.

Introduction

Endothelial molecular markers expressed on tumor-infiltrating blood vessel cells are an area of much exploration in cancer research [1]. They have been examined as easily accessible targets of molecular therapeutics [2], to understand the biochemical effects of tumor growth and signaling on peripheral vasculature [3], and have been targeted to facilitate extravasation of large molecule (e.g., nanoparticle) therapies that generally suffer from restricted leakage into the tumor parenchyma [4]. While new tumor-specific endothelial markers are continuously being identified, there are no robust methods for quantifying levels of these markers non-invasively in vivo. Molecular imaging of targeted tracer retention can provide a relative sense of endothelial marker abundance; however, the signal measured can be affected by the rate of tracer delivery (blood flow), leakage of the tracer out of the vasculature (vascular permeability), nonspecific binding, and tissue attenuation of tracer signal [5], all of which can vary across tissues making endothelial marker quantification unrecoverable from a single time point and single tracer molecular imaging. In an attempt to correct for some of these factors in cancer imaging, a number of groups have employed tracer kinetic modeling approaches [6–10]. This study presents the development of a dual-tracer imaging approach, adapted from a cell membrane receptor concentration imaging approach [11] that is capable of quantifying tumor endothelial marker concentrations in vivo.

This endothelial marker concentration imaging (EMCI) technique involves the simultaneous injection of two tracers: (1) a tracer targeted to the endothelial marker of interest and (2) a similar tracer that has no specific targeting but can be imaged simultaneously with the targeted tracer [12, 13]. The uptake of the untargeted tracer, when measured in conjunction with the uptake of the targeted tracer, can be used to account for nonspecific uptake and retention of the targeted tracer [14], enabling the concentration of targeted endothelial marker to be measured through kinetic modeling principles first introduced in the positron emission tomography neurotransmitter community with respect to reference tissue input approaches [15, 16].

As an initial evaluation of the technique, EMCI was employed to image the intravascular marker of tumor angiogenesis, plasmalemma vesicle associated protein-1 (Plvap/PV1). PV1 is a type II integral membrane N-glycosylated protein [17] that is necessary for the formation of diaphragms in endothelial caveolae, fenestrae, and transendothelial channels on the surface of endothelial cells in normal and in tumor vessels [18–20]. PV1 and endothelial diaphragms are expressed in normal capillaries and venules in lung, endocrine and exocrine glands, intestinal villi, kidney, and tongue [20, 21], as well as in the endothelial cells of tumor vessels undergoing angiogenesis [22–24]. PV1 is also a novel target for cancer therapy [25].

In this study, PV1 concentration was studied with EMCI in the healthy skin and in melanoma induced in a triple mutant mouse model [26], using a two-wavelength planar fluorescent imaging system.

Materials and Methods

Dual-Tracer Kinetic Model for Endothelial Marker Concentration Imaging

In EMCI, the concentration of endothelial markers is measured by a tracer kinetics approach born out of a compartment model that relates marker concentration to the temporal uptake kinetics of a pair of imaging reporters/tracers: (1) a tracer targeted to the endothelial marker of interest, and (2) a similar untargeted tracer. Specifically, the compartment model describes the concentration of targeted tracer in a tissue bed as the sum of three concentrations: unbound tracer in the blood, C_p; unbound tracer in the extravascular space, C_e,1; and bound tracer, C_b (top of Fig. 1a); and the concentration of untargeted tracer as the sum of two concentrations: unbound tracer in the blood, C_p (being equivalent to the targeted tracer for an ideal untargeted tracer) and unbound tracer in the extravascular space, C_e,2 (top of Fig. 1b). From the blood, both tracers can extravasate at a rate governed by the constant k₁, and reenter the vasculature at a rate governed by the constant k₂. Additionally, the targeted tracer can bind to an endothelial marker at a rate governed by the constant k₃, and can dissociate back into the blood with a rate governed by the constant k₄, or into the extravascular space with a rate governed by the constant, k₅ (hence the different subscripts for C_e,1 and C_e,2). The equations in the lower part of Figs. 1a, b can then be used to express the compartment models in the tops of Figs. 1a, b, with the measurable signal from each tracer in a region of interest (ROI_T for the targeted tracer, and ROI_U for the untargeted tracer) being equivalent to the sum of the respective tracer concentration in each compartment. Red and green boxes in Fig. 1 highlight these expressions for the targeted and untargeted tracers, respectively. The key parameters of interest in this system of equations are k₃ or k₃/k₄, each of which is proportional to the concentration of targeted endothelial markers ([B]) in the ROI, with:

$$\begin{array}{l}{k}_3=k_{on}·[B]\text{and}\\ \frac{k_3}{k_4}=k_A·[\mathrm{B}],\end{array}$$ (1)

where k_on (the “on” rate of the targeted tracer) and k_A (the “affinity” of the targeted tracer) are measurable in ex vivo experiments or can be assumed to be a constant for a given tracer-target pair [27]. Equation 1 demonstrates that either k₃ or the ratio k₃/k₄ on their own is proportional to the targeted concentration by factors that are quantifiable in vitro. It should be noted that any nonspecific binding of either tracer to endothelial cells could be incorporated into the respective “extravascular” compartments as follows: assuming the “on” and “off” rates of nonspecific binding were k₆ and k₇, the new C_e,n (n = 1, 2) would be equal to C_e,n + C_ns (with C_ns equal to the concentration of nonspecifically bound tracer), k₁ would become k₁ + k₆, and k₂ would become k₂/(1+k₆/k₇) using mathematical strategies laid out in Lammertsma et al. [15].

Fig. 1.

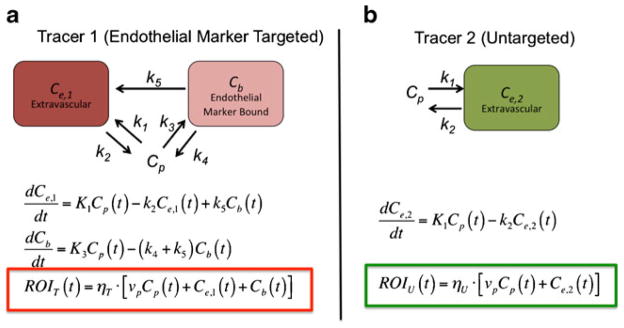
Compartment models for an endothelial marker targeted tracer (a), and an untargeted tracer (b). The rate constants k₁–k₅ represent (1) extravasation of the tracer from the blood (C_p) to the extravascular space (C_e,1 for the targeted tracer and C_e,2 for the untargeted tracer), (2) efflux of the tracer from the extravascular space to the blood, (3) binding to endothelial markers (C_b), (4) dissociation from endothelial marker into blood, and (5) dissociation from endothelial marker into extravascular space. Below each compartment model diagram are the differential equations that express the rate of change of tracer concentration in each compartment. The colored boxes highlight the relationship between tracer concentrations in each compartment and the signal measured in a given region of interest (ROI_T for the targeted in red and ROI_U for the untargeted tracer in green) as a function of time, t. The parameters η_T and η_U represent all factors associated with the relation of measured signal to tracer concentration for the targeted and untargeted tracers, respectively, such as detection efficiency, quantum efficiency of the tracers (for fluorescence imaging), tissue absorption of signal, and uneven excitation of tracer (for fluorescence).

To extract one or both of these parameters from the measurable uptake curves of a targeted and untargeted tracer pair (ROI_T and ROI_U, respectively) as a function of time, t, the equations in Fig. 1 can be solved in a number of ways. One approach is to start by taking finite integrals of the differential equations presented in Fig. 1 as follows:

$$\begin{array}{l}{C}_{e,1}(t)=k_1{\int }_0^t{C}_p(u)du-k_2{\int }_0^t{C}_{e,1}(u)du+k_5{\int }_0^t{C}_b(t)du,\\ C_b(t)=k_3{\int }_0^t{C}_p(u)du-k_4{\int }_0^t{C}_b(u)du-k_5{\int }_0^t{C}_b(t)du,\text{and}\\ C_{e,2}(t)=k_1{\int }_0^t{C}_p(u)du-k_2{\int }_0^t{C}_{e,2}(u)du.\end{array}$$ (2)

Then the expressions for ROI_T and ROI_U in Fig. 1 can be rewritten using the expression in Eq. (2) such that:

$$\begin{array}{l}\frac{1}{{\eta }_T}{\mathit{ROI}}_T(t)=C_p(t)+(k_1+k_3){\int }_0^t{C}_p(u)du-k_2{\int }_0^t{C}_{e,1}(u)du-k_4{\int }_0^t{C}_b(u)du\text{and}\\ \frac{1}{{\eta }_U}{\mathit{ROI}}_U(t)=C_p(t)+k_1{\int }_0^t{C}_p(u)du-k_2{\int }_0^t{C}_{e,2}(u)du.\end{array}$$ (3)

The expressions in Eq. (3) can then be simplified by taking the difference of the two expressions as follows:

$${\mathit{ROI}}_T(t)-\frac{{\eta }_T}{{\eta }_U}{\mathit{ROI}}_U(t)=k_3{\int }_0^t{C}_p(u)du-k_4{\int }_0^t{C}_b(u)du+k_2{\int }_0^t[C_{e,2}(u)-C_{e,1}(u)]du.$$ (4)

Equation (4) can be written as a function of only measurable quantities by subsequently substituting C_b = ROI_T−C_e,1−C_p, and then C_p = ROI_u−C_e,2:

$${\mathit{ROI}}_T(t)-\frac{{\eta }_T}{{\eta }_U}{\mathit{ROI}}_U(t)=(k_3+k_4)\frac{{\eta }_T}{{\eta }_U}{\int }_0^t{\mathit{ROI}}_U(u)du-k_4{\int }_0^t{\mathit{ROI}}_T(u)du+f(t),$$ (5)

where,

$$f(t)=(k_2+k_4){\int }_0^t[C_{e,2}(u)-C_{e,1}(u)]du-k_3{\int }_0^t{C}_{e,2}(u)du$$ (6)

Furthermore, if C_e,1 and C_e,2 are approximately equal (assuming the vascular permeabilities experienced by the two tracers are similar and C_p is a fairly constant reservoir: i.e., unaffected by specific binding, C_b) and C_e,2 is relatively small compared to the C_p at early time points (simulations of an antibody-sized tracer with K₁≅0.001 min⁻¹, suggest C_p would be at least an order of magnitude greater than C_e,2 for 24-h post-injection), then f(t) can be neglected and Eq. (5) can be expressed as follows:

$${\mathit{ROI}}_T(t)-\frac{{\eta }_T}{{\eta }_U}{\mathit{ROI}}_U(t)=(k_3+k_4)\frac{{\eta }_T}{{\eta }_U}{\int }_0^t{\mathit{ROI}}_U(u)du-k_4{\int }_0^t{\mathit{ROI}}_T(u)du,$$ (7)

which is a linear equation that can be used to solve for k₃ and k₄ using non-negative least squares fitting if η_T/η_U, ROI_T, and ROI_U are known or measurable.

In simulations with physiological levels of blood flow and targeted tracer binding (data not shown), the measured concentrations of the targeted tracer and the untargeted tracer were found to be roughly equivalent in the first few minutes after injection, if equal concentrations were injected. It is therefore possible to account for detection efficiency differences between measurement of targeted and untargeted tracer uptake (i.e., η_T/η_U) for linear systems by normalizing the untargeted tracer uptake curve to the targeted tracer uptake at early time points after tracer injection (~2 min).

Single Time Point Endothelial Marker Concentration Imaging

For reversible binding, it is possible to estimate the endothelial marker concentration at a single time point (EMCI_stp), avoiding the necessity of imaging temporal uptake kinetics of a targeted and untargeted tracer pair. This approach was introduced previously for cell surface receptor imaging [28], and essentially assumes that ${\mathit{ROI}}_T(t)-\frac{{\eta }_T}{{\eta }_U}{\mathit{ROI}}_U(t)\approx C_b(t)$, and that ROI_U(t)≈C_p(t). If these expressions are true, then:

$$\frac{\frac{{\eta }_U}{{\eta }_T}{\mathit{ROI}}_T(t)-{\mathit{ROI}}_U(t)}{{\mathit{ROI}}_U(t)}\approx \frac{C_b(t)}{C_p(t)},$$ (8)

at any instantaneous time point t. Under instantaneous equilibrium conditions, the ratio in Eq. (8) is also equivalent to the ratio of k₃/k₄, which from Eq. (1) is proportional to the endothelial marker concentration.

At the time of writing, there were no other published approaches for quantifying endothelial markers with molecular imaging; however, if a plasma input of the targeted tracer was to be measured, it would be relatively straightforward to develop a plasma input approach to estimate binding kinetics from the solution to the differential equations for the targeted tracer in Fig. 1 as follows:

$${\mathit{ROI}}_T(t)={\nu }_b{\eta }_T\left[C_a(t)+k_3{C}_a(t)\ast e^{-k_{4}t}\right]$$ (9)

This approach would also suffer from leakage of the tracer out of the vasculature (though it would result in an overestimation in leakage); however, the larger problem with the approach is that it is impossible to separate k₃ from the blood volume fraction, v_b, which could vary from tissue to tissue, unless it was independently measured.

Simulations

The EMCI and EMCI_stp algorithms were first tested in a set of simulation experiments by creating theoretical targeted and untargeted uptake curves using solutions to the differential equations in Fig. 1 under physiological conditions for antibody-sized tracers. In all simulations, the tracers were assumed to have the same plasma input curve C_a(t) (the concentration of tracer in the blood), taken from a fluorescent antibody plasma input function in a previous study [29]. This C_a(t) was then used as an input to an analytical solution for the one-tissue compartment model [30], which can be used to solve each of the differential equations in Fig. 1. The rate constants K₁ and k₂ were set to 0.007 and 0.19min⁻¹, respectively, taken from a study examining leakage of a 51 kDa dendrimer in tumors [31]. Note that K₁ = v_bK₁, where v_b is the blood volume fraction and was necessary to use here since C_a(t) was measured from blood samples, and therefore represents a blood concentration rather than a “tissue” concentration like C_p(t) represented in previous equations (note: C_a(t) = C_p(t)/v_b).

Since k₃ is a product of a tracer’s k_on (binding “on” rate) and the concentration of targeted endothelial markers, it can vary from tracer to tracer and tissue to tissue. In an irreversible binding simulation (k₄ = 0 min⁻¹ by definition), targeted and untargeted tracer uptake curves were simulated for a range of K₃ values from 0–0.05 at 0.001 min⁻¹ intervals (commensurate with the levels observed in animal experiments carried out in this study) for K₁ = 0.007 min⁻¹ (where K₃ = v_bK₃ as with K₁). Two percent Gaussian noise was then added to the curves randomly with 1,000 repetitions and all curves were fit with the full EMCI algorithm [Eq. (7)] to determine the accuracy and sensitivity of the algorithm for various levels of binding. This procedure was repeated for a slower K₁ = 0.001min⁻¹, to represent leakage rates of antibodies [7], with commonly used targeting agents (and employed in the animal experiment in this study), approximately three times larger (~150 kDa) than the 51-kDa dendrimer data that was used to approximate K₁ = 0.007 min⁻¹.

In a second simulation to explore the utility of the EMCI and EMCI_stp algorithms for reversible binding, K₃ was set to be 0.005, 0.03, and 0.05 min⁻¹ and k₄ was set to 0.1 min⁻¹ (commensurate with what may be expected for a typical natural ligand/receptor pair [32]). This resulted in three unique simulated targeted tracer uptake curves, each with the same untargeted tracer uptake curve (Fig. 2a). For the three pairs of curves, random Gaussian noise was added independently to the uptake of the targeted and untargeted tracers at 2 % of the peak simulated tracer intensity (commensurate with the single pixel noise level of the imaging system used in animal experiments in this study) prior to applying the EMCI and EMCI_stp algorithms to estimate k₃ and k₄, a process that was repeated 10,000 times with random noise added to explore the sensitivity of the algorithms to noise in each case.

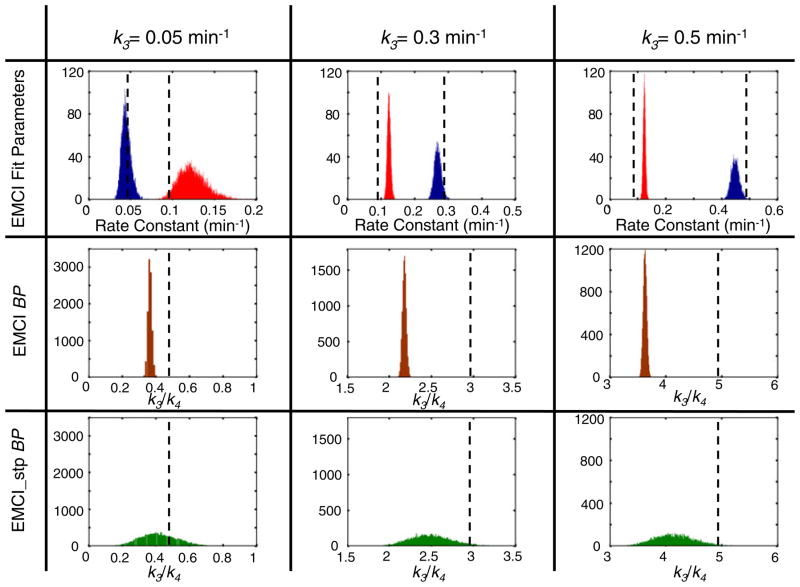
Fig. 2.

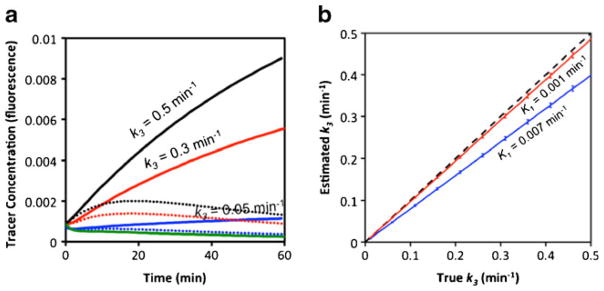
Simulated targeted tracer curves (blue, red, and black) and an untargeted tracer curve (green), prior to noise addition, are presented in a. The blue curves correspond to k₃ = 0.05 min⁻¹, the red to k₃ = 0.3 min⁻¹, and the black to k₃ = 0.5 min⁻¹. The solid targeted tracer curves correspond to k₄ = 0 min⁻¹ (irreversible binding) and the dotted lines to k₄ = 0.1 min⁻¹ (reversible binding). Results from fitting the endothelial marker concentration imaging (EMCI) algorithm to the simulated solid curves (irreversible binding) in a to estimate k₃ over a range of k₃ inputs are presented in b. The blue data represents the results for irreversible binding data simulated with a K₁ = 0.007 min⁻¹ while the red data corresponds to the same data simulated with a K₁ = 0.001 min⁻¹. The dashed line represents the line of identity between estimated and true k₃.

Animal Experiment

The EMCI approach was tested in an animal model on triple mutant Braf/Pten mice with melanomas induced on their right flank (n = 7) [26]. Specifically, triple mutant Tyrosinase-Cre-ERTtg/+;PtenL/L;BrafV600E/+ mice were generated by breeding Tyr-Cre-ERTtg/tg;PtenL/L to PtenL/L;BrafV600E/V600E mice. Deletion of Pten and activation of the mutated BrafV600E was achieved by intradermal injection into the dorsal flank of 4-hydroxytamoxifen (Sigma), which induced metastatic melanoma growth. PV1 is expressed on the cell surface of tumor endothelial cells in these inducible melanomas in direct contact with the blood. In response, the targeted tracer employed in this studied was the PV1-specific monoclonal antibody, clone MECA32 (Bio X Cell, Lebanon, NH), labeled with the fluorophore, IRDye-800CW (LI-COR Biosciences, Lincoln, NE), and the untargeted tracer was a negative control for anti-PV1 (Bio X Cell), labeled with the fluorophore, IRDye 700DX (LI-COR Biosciences). Fluorescent labeling of the antibodies was carried out as per manufacturer’s instructions. One day prior to imaging, the right flanks of the mice were treated with a depilatory cream to expose the skin.

Dual-Tracer Fluorescent Imaging

On the day of imaging, the mice were placed on their left flank in a commercially available two-channel planar fluorescence imaging system (Pearl Imager, LI-COR Biosciences), with fluorescent imaging channels at 700 and 800 nm, optimal for the fluorophores employed in this study. Five- 20-or 50-μg concentrations of targeted and untargeted tracers were injected into a tail-vein of two, three, and two mice, respectively (in all cases, the targeted and untargeted tracers were injected simultaneously). The uptakes of each tracer were imaged at 1-min intervals up to 100-min post-injection in the melanoma and skin along the entire right side of the mice. The EMCI algorithm was then applied to estimate the k₃ and k₄ rate constants on a pixel-by-pixel basis for all mice.

Statistics

All statistics were carried out with the statistical software package, SPSS (IBM®, Armonk, NY). Linear regression was employed to determine the presence of statistically significant correlations between imaging parameters and injected dose for the animal experiments and a within-subjects ANOVA was used to explore statistical differences between imaging parameter results in different tissue types. Statistical significance was based on p<0.05. All data are presented as mean ± SD.

Results

The results for the irreversible binding simulation study are presented in Fig. 2b. The EMCI algorithm was found to underestimate the value of the rate constant k₃ by a magnitude that was proportional to the extent of vascular leakage (i.e., extravasation or K₁). More specifically, true k₃ was found to be proportional to the estimated k₃(k̂₃) empirically by the following expression:

$$k_3=\frac{{\widehat{k}}_3}{1-30K_1}$$ (10)

From this, the approximate “percent underestimation” of the EMCI, algorithm can be expressed as equivalent to 3,000 K₁, which for the K₁ of a 51-kDa dendrimer in a tumor would lead to an underestimation of k₃ of about 20 %. For antibodies, which are approximately three times larger, K₁ is expected to be slower, on the order of 0.001 min⁻¹ [7], which would correspond to an underestimation in k₃ of only 3 %. For this irreversible binding simulation study, the standard deviation in estimated k₃ was found to be equivalent to the standard deviation in the noise, i.e., the 2 % noise added to the targeted and untargeted curves yielded a percent-standard deviation in estimated k₃ of about 2 %.

Figure 3 presents the results of applying the EMCI and EMCI_stp algorithms to the reversible binding simulated data. For reversible binding, the endothelial marker concentration can be estimated either through determination of k₃ using the EMCI algorithm as for the irreversible binding data, or through the ratio of k₃/k₄ (often called the “binding potential”), which can be determined directly using the EMCI algorithm by simply taking the ratio of k₃ and k₄ fitting outputs, or can be estimated at single time points using the EMCI_stp approach (presented for the 60-min time point post tracer injection in Fig. 3). Similar to the irreversible binding simulation results, k₃ was underestimated by a magnitude proportional to K₁, though to a lesser extent (~10 % underestimation in k₃ for a K₁ = 0.007 min⁻¹ for the reversible binding compared to ~20 % underestimation for irreversible binding). Further analysis demonstrated that the percent underestimation in k₃ for reversible binding could be empirically written as a function of both K₁ and k₄ as follows:

$$\%\text{Understimation}=3000K_1-100k_4$$ (11)

Fig. 3.

Fitting parameter results from applying the endothelial marker concentration imaging (EMCI) algorithm and the single time point EMCI (EMCI_stp) to simulated targeted and untargeted tracer curves for reversible binding (k₄ = 0.1 min⁻¹) are presented in the top two rows and the bottom row, respectively. Each column represents results for different input values of k3: first column k₃ = 0.05 min⁻¹; second column k₃ = 0.3 min⁻¹; third column k₃ = 0.5 min⁻¹. All results are presented in a histogram format where the results from repeated random noise additions to simulated curves were tallied to depict the accuracy and precision of the approaches for estimated endothelial marker concentration-related results. The EMCI fit parameters of k₃ (blue data) and k₄ (red data) are presented in the top row with the simulated input values (“true” values) denoted by the dashed vertical lines. The results of k₃/k₄ for EMCI are presented in the second row of histograms (dark red data), a ratio that is often referred to as the “binding potential” (BP) for its proportionality to available target concentration. Similarly, the results of k₃/k₄ for EMCI_stp are presented in the third row of histograms (green data).

Though k₃ tends to be underestimated, k₄ was overestimated by a percentage equivalent to the k₃ underestimation in irreversible binding, i.e., the percent overestimation in k₄ was equivalent to 3,000K₁, independent of the value of k₃. The standard deviation in the estimation of k₃ and k₄ with EMCI in the context of 2 % noise was approximately 7 % of the mean when k₃ was greater than 0.1 min⁻¹ but increased to 17 % for both at a k₃ and k₄ when k₃ was set to 0.05 min⁻¹.

By comparison, the absolute value of the standard deviation in k₃/k₄ was consistently 0.02 units for all simulations, suggesting that noise-related overestimations or underestimations in k₃ and k₄ tend to cancel each other out, making the ratio of k₃/k₄ a more noise-stable representation of endothelial marker concentration than k₃ alone for reversible binding studies. However, the combined mean underestimations in k₃ and mean overestimations in k₄, amplify the underestimation of k₃/k₄, so for a K₁ = 0.007 min⁻¹, k₃/k₄ underestimated the expected value by 25 %, whereas for K₁ = 0.001 min⁻¹, the underestimation fell to 5 %. The EMCI_stp approach demonstrated a slightly smaller bias in k₃/k₄ compared to EMCI; however, the approach was very sensitive to noise with standard deviations upwards of 20 % of the mean, compared to less than 2 % of the mean for the EMCI approach.

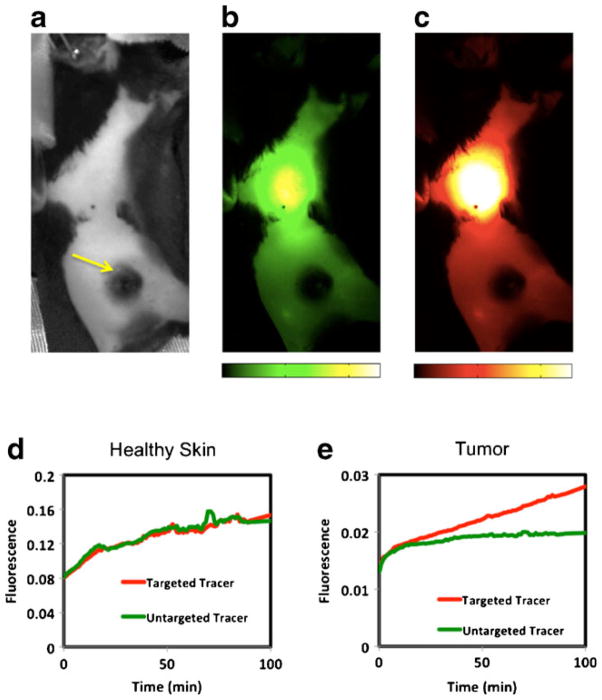
Figure 4 presents typical fluorescence imaging results from the mouse melanoma model experiments. Observation of the raw uptake images of the PV1 targeted tracer (Fig. 4c) and the untargeted tracer (Fig. 4b) on their own did not appear to match the expected distributions of PV1, with the most exposed PV1 expected to be in the vasculature of the lungs, the tumor, and the inflamed skin surrounding the tumor. In fact, most uptake of the targeted tracer at 100-min post injection appeared to originate from the liver, while very little tracer signal was measured in the tumors. In fact, the location of the tumor is only obvious in the fluorescent images in Fig. 4 from its absence of fluorescence owing two its high level of melanin, and therefore high level of fluorescence absorption. Analysis of the tracer uptakes in healthy skin versus tumor demonstrated that while the measurable fluorescence was an order of magnitude greater in the healthy skin, the targeted and untargeted tracers were taken up to a similar extent (Fig. 4d), suggesting little-to-no presence of PV1. It was only in the tumor that the targeted tracer demonstrated proportionately higher uptake than the untargeted tracer (Fig. 4e), suggesting binding to PV1.

Fig. 4.

A gray-scale white-light image of a shaved melanoma mouse positioned in the small animal fluorescence imaging system is presented in a. The yellow arrow highlights the location of the melanoma. Fluorescent images of the untargeted (green-scale) and targeted (red-scale) tracer uptakes at 100-min post-injection are presented in b and c, respectively. The images are equally scaled. Typical uptake curves of the targeted (red curve) and untargeted (green curve) tracer are presented in a region of healthy skin (d) and in the tumor (e). Note the scale of the tumor curves is approximately an order of magnitude lower than those in the healthy skin.

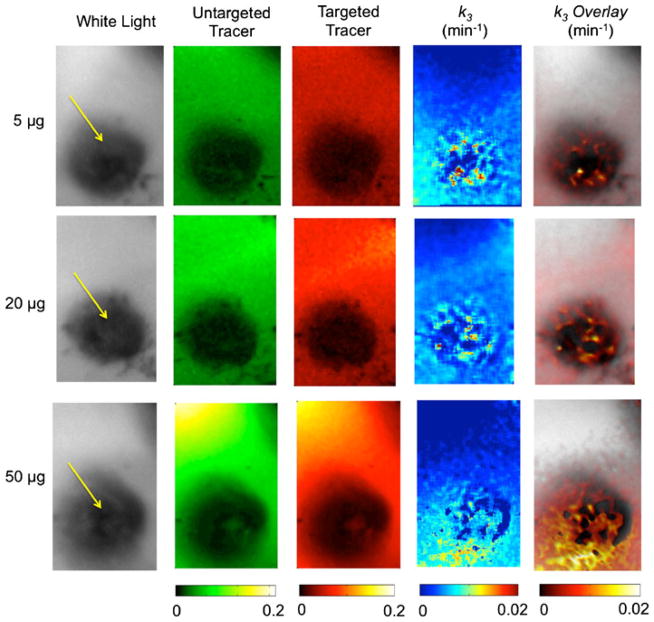
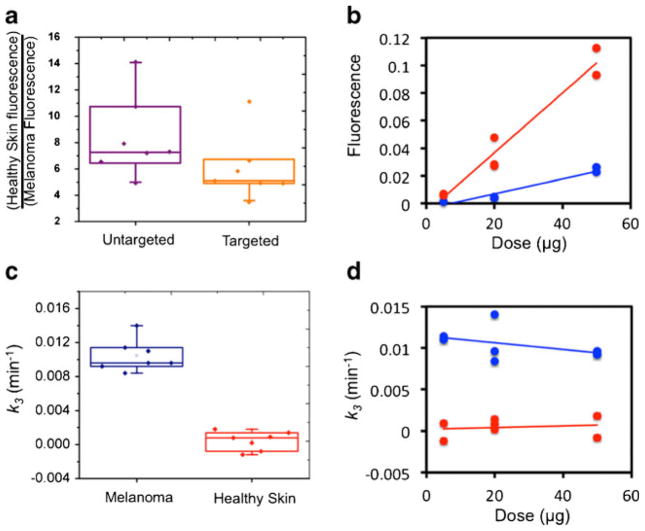
Figure 5 presents imaging results of the targeted and untargeted tracer fluorescence uptake and EMCI-derived k₃ maps for one melanoma mouse in each of the concentration groups (5-, 20-, and 50-μg injections). In all instances, the EMCI model produced null k₄ maps (k₄ = 0 min⁻¹ in all pixels), suggesting that the PV1-targeted tracer in this study exhibited irreversible binding kinetics. Therefore, the k₃/k₄ approach using either the EMCI or the EMCI_stp algorithms could not be employed. It was obvious from the fluorescent images that high concentrations of melanin in the melanomas caused severe absorption of the fluorescent light making it impossible to estimate PV1 binding from fluorescence alone. The k₃ maps, however, demonstrated positive contrast in the tumor (therefore suggesting PV1 binding as expected), despite the severe absorption effects. Figure 6a depicts a boxplot of the ratio of PV1-targeted and untargeted tracer fluorescence in healthy skin to that in the melanomas with the average fluorescence in the healthy skin being approximately 5 times higher at 100-min post-injection (0.009± 0.01 vs. 0.046±0.042) for the targeted tracer. As expected, the discrepancy was even higher for the untargeted tracer (0.007±0.008 vs. 0.047±0.043); however, the difference in the ratio of healthy tissue to melanoma fluorescence between the two tracers was not statistically significant (p>0.05) owing to high variation. The large variation in fluorescence among all mice was attributable to the variation in tracer dose administered. Figure 6b demonstrates the average pixel fluorescence from PV1-targeted tracer in healthy skin and melanoma tissue as a function of injected dose. A significant correlation was found between the PV1-targeted fluorescence uptake and the tracer dose injected in the healthy skin (slope = 0.0022 fluorescent units/microgram, r = 0.98, p< 0.001) and in the melanoma (slope = 0.0005 fluorescent units/microgram, r = 0.97, p<0.001). In contrast, the average pixel value of EMCI-derived k₃ was found to show no significant correlation with dose injected in either the healthy skin (slope = 1×10⁻⁵ min⁻¹/microgram, r = 0.17, NS) or the melanoma (slope = −4×10⁻⁵ min⁻¹/microgram, r = 0.41, NS) (Fig. 6d). Furthermore, the average k₃ in the melanoma was found to be significantly greater than that in the healthy skin across all mice (0.01±0.002 min⁻¹ vs. 0.000±0.001) (Fig. 6c).

Fig. 5.

Imaging results of melanoma mice administered 5-, 20-, and 50-μg of tracer are presented in rows 1, 2, and 3, respectively. The first column presents a gray-scale white-light image of each melanoma and surrounding healthy tissue (yellow arrow locates the melanoma). The second and third columns of images present the fluorescence uptake of the untargeted and targeted tracers, respectively, at 100-min post tracer injection (note that the 5-μg images are scaled to 0.02 rather than 0.2 in the 20- and 50-μg images). The fourth column of images presents the k₃ results from pixel-by-pixel analysis using the endothelial marker concentration imaging algorithm. The fifth column presents the same data overlaid on the white-light image.

Fig. 6.

A boxplot presenting the ratio of PV1-targeted fluorescence (orange data) and untargeted fluorescence (purple data) uptake at 100-min post tracer injection in the healthy skin vs. the melanoma tissue is presented in a. This fluorescence uptake is plotted in correlation with the injected concentration of tracer for the healthy skin tissue (red data) and the melanoma tissue (blue data) in b. Solid lines represent linear regressions of the data. Boxplots of the endothelial marker concentration imaging algorithm estimates of the binding parameter k₃ are presented in c for melanoma (blue data) and healthy skin (red data). Correlations between the k₃ estimates in each tissue and the injected tracer concentration are presented in d with the same color code as in c.

Discussion

Two methods of quantifying endothelial marker concentrations were presented and tested in this study of PV1 expression in melanomas: (1) a multiple time point approach (EMCI) that was shown to be adaptable to both reversible (k₄ non-negligible) and irreversible binding (k₄ negligible), and (2) a single time point approach (EMCI_stp) only adaptable to reversible binding conditions. Not surprisingly, simulations demonstrated that the multiple time point approach could provide considerably more precise estimates of endothelial marker concentration than the single time point approach (Fig. 3); however, it may not be practical to acquire multiple time point data in all scenarios such as during surgery, where a rougher estimate of marker concentration provided by EMCI_stp may be sufficient. A caveat to the EMCI_stp is that a minimum amount of time is required post-injection before the ratio of C_b/C_p reaches an equilibrium (~20 min for the kinetic rates simulated in this study), and in a surgical setting, the early time point wavelength normalization approach would be difficult to carry out. In response, the application of absorption-based imaging normalization would likely have to be developed [33].

One added complication to the results garnered from this study is that under reversible binding conditions, the endothelial marker concentrations can be estimated two ways using EMCI: (1) by k₃ alone or (2) by k₃/k₄ [27]. The k₃-alone estimate always resulted in the most accurate estimate in simulations; however, the k₃/k₄ was found to be considerably less sensitive to noise (Fig. 3). Both approaches were found to underestimate endothelial marker concentration (the k₃/k₄ more so than the k₃ approach) to an extent dependent on nonspecific uptake (i.e., leakage of the tracer out of the vasculature governed by K₁). However, simulations demonstrated that for a tracer the size of an antibody (~150 kDa), agents commonly used in targeted molecular imaging [34] and the underestimation in k₃ or k₃/k₄ will likely only be 1–2 %.

Countless molecular targeting agents are now on the market or have been developed in research laboratories that span a large range of binding kinetics. Typically, antibody-based agents have been designed to have very high affinities and would therefore be categorized as demonstrating irreversible binding kinetics in the time windows explored in this study. However, many other targeting agents are available such as affibodies [35] that have binding characteristics that would be associated with reversible binding. In general, it may be preferable to always estimate marker concentration using an EMCI estimate of k₃ alone, which is amenable to both irreversible and reversible binding, to avoid instabilities in k₃/k₄ when k₄ is slow or negligible (as in the current animal study); however, if a tracer is being used that is known to have reversible binding characteristics, it could be preferable to estimate based on k₃/k₄ to leverage its higher precision. In all cases, it is preferable to use tracers with as low K₁ as possible, as it was found that underestimations in estimated binding kinetics were proportional to K₁ [see Eq. (11)]. K₁ could presumably be determined from the untargeted tracer uptake alone; however, if the plasma input function was known using a Kety model [30] to correct for K₁-associated errors. A summary of this model comparison is presented in Table 1.

Table 1.

Comparison of endothelial marker concentration imaging (EMCI) approaches

Model	Reversible binding	Irreversible binding	Precision	Error from vascular leakage	Are multiple time points required?
EMCI k3	Yes	Yes	Good	Moderate	Yes
EMCI k3/k4	Yes	No	Best	High	Yes
EMCI_stp	Yes	No	Worst	Moderate	No

Another consideration when selecting optimal tracers for a dual-tracer EMCI study is that the targeted and untargeted tracers need to demonstrate similar “nonspecific” behaviors. Specifically, the plasma input curves need to be similar and the vascular leakage rates need to be similar. Many tracer characteristics such as molecular weight, charge, conformation, and lipophilicity, can influence a tracer’s pharmacokinetics, so it is best to choose two tracers that are as similar as possible in these regards. At the very least, the uptake of any set of new targeted and untargeted tracers should be observed in a tissue known to be devoid of the targeted molecular: if their uptakes are the same (as in Fig. 4d) in the time window of imaging, they are a suitable pair. On this note, any differences in detection efficiency between tracers need to be accounted for, for the accuracy of the EMCI model. In the case of fluorescence imaging, as was carried out in the animal experiment in this study, detection efficiency differences can be further complicated by chromatic variations in tissue optical properties from one region of interest to the next. A Monte Carlo Simulation (results not shown) demonstrated that under the kinetic parameters observed for the tracer pair used in this study, normalization of targeted and untargeted uptake images within 5 min of injection could reduce regional errors in k₃ estimates to less than 5 % even with substantial differences in blood volume, oxygen saturation, and melanin concentration.

The in vivo experimental testing of the EMCI approach presented encouraging results, with EMCI being able to identify significantly more PV1 in tumors than normal skin (as expected) despite over 5 times less fluorescence being measured in the tumors. The low fluorescence in the melanomas was presumably a result of high melanin concentrations: melanin has a significant absorption pattern in the 700- and 800-nm wavelength ranges. Micro-CT images of the melanomas (results not shown) demonstrate a vessel density comparable to normal tissue; however, high tumor pressure [36] could also have played a role in the low-measured fluorescence. Within the group of seven mice studied, three different fluorescent concentrations were injected, and while the fluorescence uptake in all tissues was highly dependent on the injected tracer concentration (Fig. 6b), there was no observable correlation amongst k₃ estimations at each concentration (Fig. 6d). This additional finding suggests that the EMCI approach is robust amongst subjects and over a considerable range of injected tracer concentrations. It further suggests that the highest concentration (50 μg), which provided the best noise characteristics, did not approach PV1 saturation levels, which would have resulted in an underestimation in k₃ at higher injected tracer concentrations.

Further studies are ongoing to measure the k_on rate of MECA32 to PV1 in order to calculate PV1 concentration from estimated k₃ values; however, even when this is completed, no alternative methods have been developed to quantify binding-available endothelial marker concentration either in vivo or ex vivo to validate the results. There are qualitative approaches to estimate relative PV1 concentrations amongst tissues; however, PV-1 is abundant in many endothelial cells without being exposed to the luminal surface of blood vessels [18–20], and therefore available for binding, compounding the problem of ex vivo validation. While these facts make it impossible to validate the EMCI approach at this time, it highlights the potential impact of this dual-tracer EMCI to offer researchers an unprecedented insight into endothelial marker concentrations in vivo for a wide range of applications.