CTER—Rapid estimation of CTF parameters with error assessment

Abstract

In structural electron microscopy, the accurate estimation of the Contrast Transfer Function (CTF) parameters, particularly defocus and astigmatism, is of utmost importance for both initial evaluation of micrograph quality and for subsequent structure determination. Due to increases in the rate of data collection on modern microscopes equipped with new generation cameras, it is also important that the CTF estimation can be done rapidly and with minimal user intervention. Finally, in order to minimize the necessity for manual screening of the micrographs by a user it is necessary to provide an assessment of the errors of fitted parameters values. In this work we introduce CTER, a CTF parameters estimation method distinguished by its computational efficiency. The efficiency of the method makes it suitable for high-throughput EM data collection, and enables the use of a statistical resampling technique, bootstrap, that yields standard deviations of estimated defocus and astigmatism amplitude and angle, thus facilitating the automation of the process of screening out inferior micrograph data. Furthermore, CTER also outputs the spatial frequency limit imposed by reciprocal space aliasing of the discrete form of the CTF and the finite window size. We demonstrate the efficiency and accuracy of CTER using a data set collected on a 300 kV Tecnai Polara (FEI) using the K2 Summit DED camera in super-resolution counting mode. Using CTER we obtained a structure of the 80S ribosome whose large subunit had a resolution of 4.03 Å without, and 3.85 Å with, inclusion of astigmatism parameters.

1. Introduction

In single particle cryo-electron microscopy (cryo-EM), images of biological specimen are collected in a bright field mode using a range of defocus settings of the microscope. The defocus settings have to be properly selected such that during the process of computational structure determination gaps in Fourier space coverage can be filled using mutually complementary information from variously under-focused data. More specifically, when the EM image data are combined using the Wiener filtration technique, the images are multiplied by their respective contrast transfer functions (CTFs) and summed to yield a two-dimensional (2D) average or a three-dimensional (3D) structure. It has been shown that the full range of Fourier space information, up to a preselected limit, can be properly recovered only if the zero crossings of CTFs do not coincide [1]. While the goal of achieving high resolution of the final three-dimensional (3D) structure favors the use of close defocus data, these images tend to be characterized by low contrast, which in combination with the noisy micrograph field makes it difficult to identify and reliably align the particles. The far defocus images are distinguished by higher contrast that facilitates both the particle picking and alignment process. However, the Fourier space oscillations of the CTF of the microscope that characterizes the EM image formation process set a limit on the highest defocus that can be used given other digital image processing settings, such as pixel size and window size. Hence, the higher the defocus the more rapid the oscillations of the CTF, particularly in high frequency regions, possibly exceeding what can be properly represented in discretized form given the pixel size and window size.

The problem of proper representation of far defocus CTF in discretized data has been noted in the past, and suggestions were made to either pre-multiply entire micrographs by their respective CTFs in reciprocal space, or increase the box size used, possibly exceeding what would be reasonably sufficient for a given biological object size. However, no simple rules were given so far that would allow the user to decide what the permissible defocus settings should be for selected pixel and window sizes such that there is no loss of information due to rapid oscillations of the CTF in the high frequency region.

The selection of proper defocus settings is best made at the very early stages of a single particle project, preferably either prior to or during data collection as otherwise much effort can be invested in the collection of ultimately unusable images. In addition, recent developments in electron microscopes, digital cameras, and sophisticated automated data collection packages have resulted in marked improvements in the speed of the data collection process, and hence, also a significant increase in the number of micrographs obtained per project [2]. The automation software varies from simple programs assisting the users in performing the basic tasks [3] to sophisticated systems, such as Leginon [4,5] and JADAS [6], that offer full automation and methods for assessment of grid quality. All vendors also offer some form of data collection automation installed on electron microscopes. The more recent trend, as proposed by designers of Appion, is to integrate data collection automation with single particle structure determination packages so that a full project could in theory be completed with minimal user intervention [7]. This progress is greatly aided and accelerated by the development of a new generation of digital cameras whose large field, excellent detective quantum efficiency (DQE), and speed of readout all but eliminates the need for film as a data collection medium, thus further facilitating automation [8,9]. Of particular importance is the emergence of affordable direct detection device (DED) camera systems [10–13] that makes it possible to correct for beam-induced specimen motion [14–16], particularly when used in electron counting mode, and to carry out atomic resolution cryo-EM on a routine basis [17,18].

Given the importance of CTF parameters estimation, it is not surprising that there is a large number of published methods and corresponding computer implementations. Currently, all single particle software packages have associated CTF analysis programs [19–24] in addition to independent applications [25–28]. One can divide CTF analysis methods into those that evaluate broader image formation characteristics, such as the envelope function (B-factor) [19,21], or even distribution of Spectral-Signal-to-Noise Ratio (SSNR) in the data, as implemented in EMAN2 [29], and those that only estimate fundamental parameters of the CTF, sometimes only defocus, but often also astigmatism and amplitude contrast [26]. Methods from the first group are closely associated with particular software packages since there is no generally accepted methodology of single particle determination that would include SSNR characteristics of the data, while the methods from the second group tend to be independently and generally usable, especially since a standardized CTF convention is finally emerging [30]. It has also been noted that as the volume of EM data obtained per project increases with the speed of data collection, there is a need for a new generation of more computationally efficient and reliable CTF estimation methods [24].

It is impossible to assert with any certainty which of the CTF estimation methods yields the “best” results as it is difficult to construct objective benchmarks. It is equally difficult to assert which application is most commonly used, but casual observation would single out CTFFIND3 [26] as a good candidate. The reasons for CTFFIND3 of becoming a de facto standard are straightforward. The program estimates only the basic parameters of the CTF (defocus and astigmatism) and is very robust. The results are output in a simple user-friendly format and can be easily transferred to other single particle packages. Furthermore, CTFFIND3 is independent of any external programs or libraries, so it can be easily installed and used without the need for challenging setups. However, CTFFIND3 is not entirely automated as the user has to provide a range of spatial frequencies within which the goal function is evaluated. Furthermore, unless the search ranges are restricted, it is relatively computationally intensive, which makes its use problematic for high-throughput EM [24]. And finally, it does not provide information about the reliability of the result. This shortcoming however is not specific to CTFFIND3 as there is currently no CTF estimation method that would provide assessment of reliability or errors of the estimated parameters.

Here we propose a computational method, CTER, for rapid estimation of basic CTF parameters, including defocus and astigmatism, whose computational efficiency makes it suitable for high-throughput EM. We introduce a simple formula that yields the maximum spatial frequency to which CTF is properly represented in the data given selected defocus, pixel and window size settings. This information is used either prior to data collection, or a posteriori to low-pass filter images whose defocus settings are too high with respect to the pixel and window sizes used. Moreover, we employ statistical resampling to provide a measure of reliability and errors for the estimated parameters. We begin with a brief presentation of the CTF convention used followed by a discussion of the rotational averaging of micrograph power spectra that includes the astigmatism information and a method for accuracy-limiting reciprocal space aliasing of the CTF caused by digitization of the data. Next, we introduce the CTF estimation algorithm and conclude with the presentation of test results obtained using data collected with a K2 Summit direct electron-detection (DED) camera.

2. Methods

2.1. Analytical form of the CTF

In the weak-phase approximation, the image formation process in electron microscope is assumed to be linear and is described by the contrast transfer function (CTF) [31]:

$$\mathit{CTF}(\mathit{s}:\mathrm{\Delta }z)=\sqrt{1-A^2}sin(\gamma (\mathit{s};\mathrm{\Delta }z))-Acos(\gamma (\mathit{s};\mathrm{\Delta }z))$$ (1)

where s = |s| is the magnitude of spatial frequency, Δz is the defocus, 0<A<1 is the amplitude contrast ratio that reflects presence of absorption, and γ is the phase perturbation function that, ignoring astigmatism, is given by [32]:

$$\gamma (\mathit{s};\mathrm{\Delta }z)=2\pi (-\frac{1}{2}\mathrm{\Delta }z\lambda s^2+\frac{1}{4}{C}_s{\lambda }^3{s}^4),$$ (2)

where C_s is the spherical aberration constant and, ignoring relativistic effects, $\lambda =\sqrt{h^2/2me-V}$ is the wavelength of electrons (h – Planck’s constant, m and e⁻ – electron mass and charge, respectively, V – voltage of the microscope). To analyze the reciprocal space oscillatory nature of the CTF it is more convenient to write Eq. (1) in the equivalent form [19]

$$\text{CTF}(\mathit{s};\mathrm{\Delta }z)=sin\left(\gamma (\mathit{s};\mathrm{\Delta }z)-\text{arctg}\left(\frac{A}{\sqrt{(1-A^2)}}\right)\right)=sin(\gamma (\mathit{s};\mathrm{\Delta }z)-Q).$$ (3)

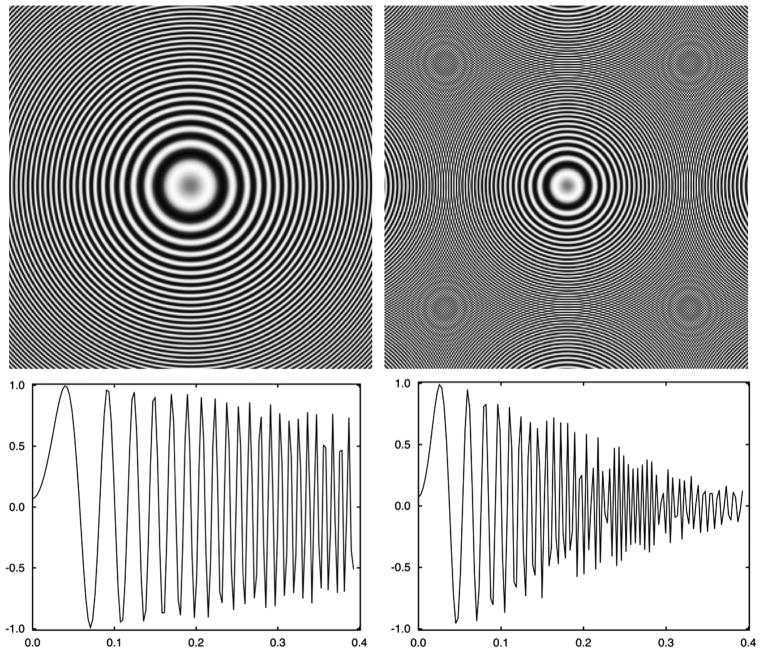
For simplicity, in the above exposition we omitted envelope functions that characterize suppression of high-frequency information due to various physical effects associated with the EM image formation process [20]. In the absence of astigmatism the CTF is rotationally symmetric, i.e., it is only a function of the modulus of the spatial frequency s and its modulus squared exhibits a characteristic pattern of concentric rings, i.e., Thon rings (Fig. 1a).

Fig. 1.

Discretized representations of astigmatism-free contrast transfer functions of an electron microscope using V = 300 kV, C_s = 2 mm, A=0.07, window size 280 pixels, pixel size 1.264 Å, and defoci (a) Δz = 1.5 μm and (b) Δz = 3.5 μ, respectively. The far defocus CTF (b) is incorrectly represented past spatial frequency ~0.26 Ǻ⁻¹ due to reciprocal space aliasing.

Presence of axial astigmatism results in a CTF that is no longer rotationally symmetric, as the respective phase perturbation function is, in polar coordinates [33]:

$$\gamma (s,\alpha ;\mathrm{\Delta }z)=2\pi \left(-\frac{1}{2}\left[\mathrm{\Delta }z-\frac{z_a}{2}sin(2(\alpha +{\alpha }_0))\right]\lambda s^2+\frac{1}{4}{C}_s{\lambda }^3{s}^4\right)$$ (4)

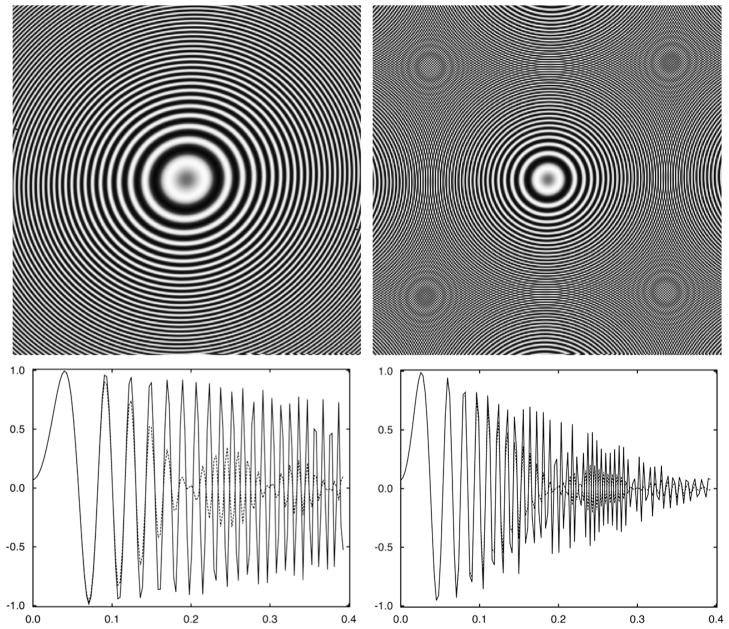
where z_a is astigmatism amplitude, α₀ amplitude angle, and α= atan(s_y/s_x) (Fig. 1b). We note that the accepted standard form of the phase perturbation function is [26,34]

$$\gamma (s,\alpha ;\mathrm{\Delta }z)=2\pi \left(-\frac{1}{2}\left[\frac{\mathrm{\Delta }{z}_1+\mathrm{\Delta }{z}_2}{2}+\frac{\mathrm{\Delta }{z}_1-\mathrm{\Delta }{z}_2}{2}cos(2(\alpha -{\beta }_0))\right]\lambda s^2+\frac{1}{4}{C}_s{\lambda }^3{s}^4\right)$$ (5)

where Δz₁ and Δz₂ are the defocus values in the two main perpendicular directions of astigmatic CTF, and β₀ is the angle between the direction of Δz₁ and x-axis (Fig. 2).

Fig. 2.

Discretized representations of astigmatic contrast transfer functions of electron microscope using V = 300 kV, C_s = 2 mm, A=0.07, window size 280 pixels, pixel size 1.264 Å, astigmatism amplitude 0.2 μm, astigmatism angle 25° (as in Eq. (4)) and defoci (a) Δz = 1.5 μm and (b) Δz = 3.5μ, respectively. The far defocus CTF (b) is incorrectly represented past spatial frequency ~0.26 Ǻ⁻¹ due to reciprocal space aliasing. The solid line represents rotational average of the 2D CTF with inclusion of astigmatism (Eq. (10)), the dotted line represents straightforward rotational average (Eq. (6)). The decreased amplitudes of the latter illustrate the loss of signal that would occur if astigmatism were not taken into account.

The parameters of the two respective forms are related as follows:

$$\begin{array}{l}\mathrm{\Delta }z=\frac{\mathrm{\Delta }{z}_1+\mathrm{\Delta }{z}_2}{2},\mathrm{\Delta }{z}_a=\frac{\mathrm{\Delta }{z}_1-\mathrm{\Delta }{z}_2}{2},{\alpha }_0=\pi /4-{\beta }_0;\\ \mathrm{\Delta }{z}_1=\mathrm{\Delta }z+\frac{\mathrm{\Delta }{z}_a}{2},\mathrm{\Delta }{z}_2=\mathrm{\Delta }z-\frac{\mathrm{\Delta }{z}_a}{2},{\beta }_0=\pi /4-{\alpha }_0.\end{array}$$

As will be shown below, the first form (Eq. (4)) facilitates the design and description of a particularly efficient algorithm for the estimation of CTF parameters.

2.2. Rotational averaging of the CTF

The CTF is a 2D real function in reciprocal space and the squared CTF forms a characteristic pattern of concentric rings or, in the presence of astigmatism, ellipsoidal shapes, known as Thon rings. The presence of Thon rings can be evaluated visually and serves as an initial indication of micrograph quality. However, due to presence of noise and contrast suppression by the envelope function it is difficult to discern the precise extent of the rings or minor deformations due to astigmatism. Hence, it is more convenient to calculate the rotational average of the power spectrum from experimental data and present the result as a one-dimensional (1D) plot. The resulting curve facilitates the visual examination of the oscillations of the CTF, their full extent irrespective of diminishing amplitudes, improvements, if any, when astigmatism is taken into account, and simultaneous plotting of the theoretical form of the CTF, which is instrumental in the evaluation of the accuracy of the CTF parameters estimation.

In the absence of astigmatism, the rotational average of the CTF (or its square) follows from Eq. (3):

$$a_{\mathit{CTF}}(s)={\int }_0^{\pi }\text{CTF}(s,\alpha ;\mathrm{\Delta }z)d\alpha .$$ (6)

Since the 2D CTF is rotationally symmetric, it follows that in the absence of noise, the rotational average is simply the 1D form of the CTF described above. For experimental data the advantage of the rotationally averaged form is that the improved SNR of the curve it yields greatly facilitates subsequent analysis of the CTF.

In the presence of astigmatism the angular averaging has to be done along closed isolines¹ of the CTF, which may no longer be circles. We proceed by finding for each given coordinate (s, α) of a point in 2D reciprocal space a corresponding spatial frequency u such that the following is satisfied:

$$\gamma (u,0;\mathrm{\Delta }z)=\gamma (s,\alpha ;\mathrm{\Delta }z)$$ (7)

Using Eq. (4), we obtain the following closed-form solution to the double quadratic equation above:

$$u=\frac{1}{C_s\lambda }\sqrt{C_s\left(\mathrm{\Delta }z-\sqrt{\mathrm{\Delta }{z}^2+C_s^2{\lambda }^4{s}^4-2C_s{\lambda }^2{s}^2\left(\mathrm{\Delta }z-\frac{z_a}{2}sin(2(\alpha +{\alpha }_0))\right)}\right)}$$ (8)

Given a set of parameters that characterize the CTF, coordinates of each point in a discrete 2D CTF (or CTF²) are converted to polar coordinates and values at these locations are added to bins in a 1D array whose coordinates u are computed using Eq. (8). This process yields a rotationally averaged CTF or power spectrum of EM data, i.e., CTF². In the absence of astigmatism, Eq. (8) reduces to u = s, thus yielding the standard algorithm for rotational averaging over circles (Eq. (6)).

2.3. Aliasing in reciprocal space restricts the family of CTFs that can be properly represented in the discretized form

The number of oscillation of the CTF within a selected range of spatial frequencies is proportional, albeit in a nonlinear manner, to the defocus Δz (Fig. 1). Once the CTF is discretized, its proper representation depends on the real-space pixel size and the window size (in pixels) used to window out particles. If pixel size or window size is not chosen correctly, the Fourier space aliasing will preclude faithful discrete representation of the CTF, thus making it impossible to correct the data for CTF effects during the computational structure determination process (Fig. 2). The aliasing artifacts are a consequence of Fourier space sampling theorem: if the frequency of Fourier oscillation is higher than the highest one that can be correctly represented in a discrete form, this frequency will be aliased, i.e., in discretized domain it will be incorrectly represented as a lower frequency, specifically, a frequency lower than the “Nyquist reciprocal space frequency” determined by the reciprocal space pixel size, which in turn depends on the real space pixel size and window size.² Simply stated, the aliasing will occur at frequencies at which the CTF will have a period T shorter than the length of two reciprocal space pixels. Equivalently, it also means that the CTF will change signs within a single reciprocal space pixel, which clearly precludes its proper representation in the discrete form. Hence, it is necessary to determine whether CTF can be properly represented for discretized EM data characterized by a combination of pixel size (with units in Ǻ), window size (as given by the number of pixels), and microscope settings (defocus, spherical aberration constant, and voltage). If the answer is negative, we would want to know the maximum frequency below which the transfer function is not corrupted by aliasing.

To provide the answer we have to be able to compute the Fourier space period of the grid T_grid(p, n_x) that depends on the real space pixel size p and window size n_x (in pixels) and the spatial frequency-dependent period T(s) of the CTF. Given the width of a reciprocal space pixel is 1/(pn_x), the corresponding period is simply T_grid(p, n_x) = 2/(pn_x). The period T of the CTF is frequency dependent and for each spatial frequency s₀ it is given by the solution of the following equation:

$$\mathit{sin}\left(2\pi \left(\frac{\gamma (s_0;\mathrm{\Delta }z)}{2\pi }+1\right)-Q\right)=sin\left(2\pi \left(\frac{\gamma (s_0+T;\mathrm{\Delta }z)}{2\pi }\right)-Q\right)$$ (9)

Eq. (4) reduces to a fourth order polynomial in T:

$$-\frac{1}{2}\mathrm{\Delta }z\lambda s_0^2+\frac{1}{4}{C}_s{\lambda }^3{s}_0^4+1=-\frac{1}{2}\mathrm{\Delta }z\lambda {(s_0+T)}^2+\frac{1}{4}{C}_s{\lambda }^3{(s_0+T)}^4$$ (10)

The roots of Eq. (10) can be found numerically (function roots of the NumPy package http://numpy.scipy.org) and the desired period T is given by the magnitude of a root of Eq. (10) with the smallest absolute value. Using this numerical procedure we find the periods of the CTF for all discrete spatial frequencies spanned by the given pixel size and window size, the number of which typically does not exceed a few hundred, and find the critical spatial frequency s_c for which T(s_c)≅T_grid(p, n_x) (Table 1). The computations are straightforward and the Python implementation is available as function ctflimit in module morphology.py of the SPARX system [35] that is freely available for download along with the source code.

Table 1.

Maximum reciprocal space extent of the CTF that can be represented in a discretized form within a finite window, as computed using Eqs. (9) and (10). The entries of the table designate, for a given combination of defocus, pixel size, and window size, a fraction of the reciprocal space within which CTF is properly discretized, i.e., free of aliasing artifacts. The remaining parameters are: voltage 300 kV and the spherical aberration constant 2.0 mm. Thus, given pixel size 0.8 Å, defocus 1.5 μm, and window size 128 pixels, the fraction of reciprocal space is 0.3, i.e., the artifact-free extent of the CTF is 0.3 × 128=38 Fourier pixels. It also means that even though in this case the maximum resolution (corresponding to Nyquist frequency) is 2 × 0.8 Å=1.6 Å, the actual maximum resolution that can be recovered from the data is only 1.6/0.3=5.3 Å.

	Window size	Defocus
		0.8 μm	1.0 μm	1.5 μm	2.5 μm
Pixel size 0.8 Å	64	0.3	0.2	0.2	0.1
	128	0.6	0.5	0.3	0.2
	256	1.0	1.0	0.6	0.3
	512	1.0	1.0	1.0	0.7
Pixel size 1.0 Å	64	0.5	0.3	0.2	0.2
	128	1.0	0.8	0.5	0.3
	256	1.0	1.0	1.0	0.5
	512	1.0	1.0	1.0	1.0
Pixel size 1.4 Å	64	1.0	0.8	0.5	0.3
	128	1.0	1.0	0.9	0.5
	256	1.0	1.0	1.0	1.0
	512	1.0	1.0	1.0	1.0

2.4. Computational estimation of CTF parameters and their errors

The design of the CTF protocol aims at high computational efficiency and minimal user intervention in order to increase throughput and facilitate statistical-resampling based estimation of parameter errors. This is accomplished by breaking the estimation procedure into several blocks, and within each block successive estimates are calculated by improving upon the estimate from the previous step. We also took advantage of some robust components of the previously published CTF estimation method [19] while simplifying the design of the method by eliminating the estimation of the envelope function and data SSNR. The proposed procedure includes 1D and 2D-based optimization procedures, and the scores in the respective goal functions are computed as the normalized inner product between a background-subtracted power spectrum estimated using periodograms calculated from the data and a simulated squared CTF multiplied by the envelope function. We note that with minor modifications, this is the same goal function used in the CTFFIND3 program [26].

The 1D goal function is a function of one argument, the defocus, and is used in the initial defocus estimation. The 2D goal function is used in searches for defocus, astigmatism amplitude and astigmatism angle. In order for the method to be computationally efficient and to avoid optimization in a multidimensional space of parameters that are mutually correlated (which hampers the search for a global extremum) [36], our 2D goal function is a function of only two parameters, the defocus and the astigmatism amplitude, and the search for astigmatism angle is effectively eliminated by determining its value implicitly. This is accomplished by taking advantage of the rotationally invariant discrepancy function defined as [37]:

$$L_r=\frac{1}{g}{\text{max}}_{\alpha }{\int }_{s_{\mathit{min}}}^{s_{\mathit{max}}}{\int }_0^{\pi }f(s,\gamma )\Vert g\Vert (s,\gamma +\alpha )d\gamma ds$$ (11)

where f is the experimental power spectrum, g is the simulated CTF², s_max and s_min define the region within which the similarity is evaluated, and alpha is the astigmatism angle. Note that the range of the angular integral extends only to π on account of Friedel symmetry in the power spectrum and the cross-resolution function that will be introduced in Section 2.5. A very efficient logarithmic-time implementation of Eq. (11) exists and a detailed description and analysis of its performance is given in [38,39]. Roughly speaking, we consider the experimental power spectrum to be a template image, so we resample it to polar coordinates and compute 1D FTs of polar rings. During the optimization process we generate simulated CTF using given defocus and amplitude values while setting the astigmatism angle arbitrarily to zero. This simulated image is resampled to polar coordinates, 1D FTs are computed, and an inverse FT of its Fourier product with the preprocessed template power spectrum yields a 1D cross-correlation function, which is a function of astigmatism angle. From Eq. (11) it follows that the position of the maximum yields the desired astigmatism angle for the assumed values of defocus and astigmatism amplitude. Hence, the overall optimization is done over the two latter variables, while the search for astigmatism angle is effectively eliminated as the needed value is established implicitly. The most important gain of this implementation is that the time of calculations is significantly reduced (logarithmically) as compared to direct implementations [26]. As we will see, this makes feasible the use of statistical resampling for estimating the errors of fit of the CTF parameters.

The proposed procedure for estimation of CTF parameters and their errors is comprised of the following steps:

1. The user sets the parameters that specify microscope settings: voltage, spherical aberration constant, amplitude contrast, and data pixel size. In addition, the target window size in pixels is required and it is recommended that the size be approximately that used for the windowing of particle images. The program takes as input data either the name of the micrograph to be processed, or a set of particle images windowed from a single micrograph.

2. If the input is a micrograph, we window out the maximum possible number of tiles of the user-specified size with optional user-set overlap between them (the overlap improves SNR of the power spectrum estimate [40,41]), and we compute periodograms for all the tiles. If the input is a set of windowed images, we simply compute periodograms of the images.

3. We initialize the bootstrap statistical resampling procedure [42] by setting a number of bootstrap samples n_B that will serve as a basis for estimation of CTF parameters.

4. We randomly select, with replacements, a set of B periodograms from those calculated in step 2 and obtain an estimation of the micrograph’s power spectrum (PWS) by computing the average of the B periodograms. We also compute the rotational average of the PWS, assuming no astigmatism, using Eq. (6).

5. Using the 1D rotational average of the PWS we find the low frequency cut-off point below which the PWS fails to follow an approximately linear fall-off in logarithmic scale [19]. This is done using a simple heuristic: for each frequency point the logarithmic curve of the 1D PWS is divided into two parts, and into each of these parts we independently fit a second-order polynomial, calculate average residual error, and add the values obtained for the two regions. The frequency at which this summed error is minimized is set as the low-frequency cut-off point. The maximum considered frequency is set to the Nyquist frequency.

6. We estimate the background curve within the frequency range determined in step 5 using the inequality and equality constrained linear optimization method, which is based on a modified simplex algorithm for linear programming, the so-called L1 solution [43], as described earlier [19]. Using the estimated background curve coefficients we extrapolate the background curve to the full frequency range and we subtract it from the PWS, thus obtaining the background-subtracted 1D power spectrum curve (PWSB).

7. We compute a first approximation of the defocus value using the PWSB calculated in step 6:

   1. We select ten equally spaced defocus values ranging from 0.5 to 10.0 μm and use them as initial values to find defocus values that optimize our goal function (i.e., the normalized inner product between experimental power spectrum and simulated CTF²) using a golden search method [44]. We retain the three defocus values with the highest score values.

   2. We use the highest score defocus value to compute the limiting maximum frequency for which it is possible to have aliasing-free analytical CTF considering the given pixel size and window size in pixels (Eqs. (9) and (10)). This value is set as the maximum frequency used in the goal function of subsequent estimation steps.

   3. We re-estimate defocus using the three best guesses from step 7.1 as initial values for the golden search method while limiting the frequency range considered in the goal function to that established by steps 5 and 7.2. The defocus value with the highest score is the output of this step.

8. We convert 1D background curves to a rotationally symmetric 2D image, which is then rotated about the origin to obtain the 2D background image. The background image is subtracted from the 2D PWS of step 4, and the 2D background subtracted PWS is resampled into polar coordinates (for details see [38,39]).

9. We find defocus value and astigmatism amplitude and angle using the following 2D strategy:

   1. We use the defocus value resulting from the 1D search of step 7 and a golden search strategy with a 2D polar-coordinates based goal function to find the astigmatism amplitude.

   2. We use the defocus value resulting from the 1D search of step 7 and the astigmatism amplitude found in step 9.1 in a downhill simplex optimization method to search simultaneously for defocus and astigmatism amplitude, with the astigmatism angle implicitly established due to the use of the 2D polar-coordinates based goal function.

10. Steps 4–9 are independently repeated n_B times, thus yielding B sets of estimated defocus and astigmatism amplitude and angle values. We calculate the average and standard deviation of each parameter and identify as outliers those not within three standard deviations of the average. A set of estimated defocus and astigmatism parameters is considered an outlier set if one or more of the parameters is an outlier. Outlier sets are removed from the B sets of estimated parameters, i.e., defocus, astigmatism amplitude and angle, and the average and standard deviation of each of the three parameters are computed using the remaining sets. The standard deviations are interpreted as the errors of average defocus and astigmatism amplitude and angle values.

In addition to the numerical output the program also returns two 1D rotationally averaged power spectra; the first using only the estimated defocus (Eq. (6)), and the second using the estimated defocus and the estimated astigmatism (Eq. (8)). They can be plotted and used to provide a straightforward verification of the result, particularly of the astigmatism. More specifically, if the astigmatism was correctly estimated and respective errors are small, the astigmatic rotational average should have higher values in the vicinity of the CTF extrema than the defocus-only rotational average.

2.5. Cross-resolution based CTF estimation

The methodology of CTF estimation using micrograph power spectra yields excellent results when thin layer of supporting carbon is used in preparation of EM grids. The carbon layer is a source of a relatively strong signal and results in easily discernible patterns of Thon rings in the power spectra. However, the concern is that in this case the defocus estimate refers to the value of defocus at a carbon layer level, and not at the level of particles suspended either on the surface of the carbon layer or even higher, i.e., at the water–air interface. It is thus reasonable to expect that the true defocus values will differ by at least half of the particle diameter. For larger molecules, e.g., ribosome and virus envelopes, this can be as much as a few hundred Angstroms, which difference would pose an obstacle to high-resolution structure determination. A second obstacle is that if there is no carbon layer and molecules are small the Thon rings are barely discernible and, for higher frequencies, very noisy. Hence, while the accuracy of the CTF estimates is sufficient for intermediate resolution structure determination, the inherent inaccuracy of the estimates limit the ability to obtain high-resolution structural information.

As a remedy it was proposed to repeat the CTF estimation step using Fourier cross-resolution (FCR) once an intermediate resolution CTF-corrected model becomes available during the structure determination process [45]. More specifically, a 3D reconstruction is computed without CTF correction for each subset of particle EM projection images that originate from the same micrograph. A cross-resolution correlation 1D function (FCR) is computed using the resulting volume and a CTF-corrected reconstruction computed using all remaining particle images in the data set. Similarly to the Fourier Shell Correlation function [46], the FCR is computed as

$$\text{FCR}(u,v;s)=\frac{{\sum }_{\mid \mid {\mathit{s}}_{\mathit{k}}\mid -s\mid \le \epsilon }^{k_s}U({\mathit{s}}_{\mathit{k}})V^{\ast }({\mathit{s}}_{\mathit{k}})}{{\{({\sum }_{\mid \mid {\mathit{s}}_{\mathit{k}}\mid -s\mid \le \epsilon }^{k_s}{\mid U({\mathit{s}}_{\mathit{k}})\mid }^2)({\sum }_{\mid \mid {\mathit{s}}_{\mathit{k}}\mid -s\mid \le \epsilon }^{k_s}\mid V({\mathit{s}}_{\mathit{k}}){\mid }^2)\}}^{1/2}},$$ (11)

where u is the structure computed using a set of particle images windowed from the same micrograph without CTF correction, v is the CTF-corrected structure computed using the remaining particle images from the data set, 2ε is a preselected reciprocal space shell thickness, s_k is an index of 3D spatial frequency, s = |s_k| is the magnitude of the spatial frequency, and k_s is the number of Fourier voxels in the shell corresponding to spatial frequencies with magnitude s.

The FCR yields a 1D (real-valued) curve whose values are indications of similarity between u and v as a function of spatial frequency. After normalization, the absolute values of the FCR that are close to one indicate high degree of similarity between the two structures. As one structure is CTF corrected and the other is not, FCR will change signs according to the signs of the CTF, the effects of which are present in the uncorrected structure u. Moreover, as the Spectral-Signal-to-Noise (SSNR) [46] of the uncorrected structure roughly follows the shape of CTF², with the exception of low frequencies, the shape of the FCR approximately corresponds to that of the CTF. It is therefore straightforward to use the FCR for estimation of the CTF parameters of the group of particles used to compute the structure u.

The FCR based approach described above has a number of advantages over power spectrum-based CTF estimation. Firstly, the outcome is now directly related to the signal from particle images and not from the supporting carbon or surrounding buffer. Secondly, there is no need to estimate and subtract the background from the FCR curves, which is a step that tends to be a source of considerable errors in power spectrum-based estimation. Lastly, the FCR has numerous zero crossing and changes signs, hence facilitating the design of a robust estimation process. The FCR based approach is not however without its shortcomings. The CTF parameters obtained tend to be biased toward the initial values used at the beginning of the refinement process during the alignment of images that depends on the signs of the CTF used. The FCR curves also tend to be noisy, particularly if the number of images in a group is small. Reliable estimates are impossible in extreme cases of very few particle images per group, and in cases of low resolution projects where the FCR curves may have very few zero crossings or none at all. The estimation process is also computationally intensive, as it is necessary to compute a large number of 3D reconstructions, and the original design of the method that was based on comparisons of volumes (Eq. (11)) did not include estimation of astigmatism parameters.

In the following we propose a modification of the FCR-based defocus estimation procedure described in Mouche et al. [45] that makes it possible to also estimate the astigmatism parameters. First, instead of a 3D FCR we compute a set of 2D-based FCR curves by projecting the CTF-corrected structure v into the directions of projection images that belong to a micrograph-based group and which were not included in the reconstruction of the structure v. We use the definition given by Eq. (11) with v replaced by a 2D projection of v, p_v, and u replaced by a 2D EM particle image d. All curves are averaged to yield a 1D FCR curve that to a good approximation is equivalent to a volume-based calculation of the original approach. In addition, we compute, in reciprocal space polar coordinates (r), a 2D cross-resolution function (CRF) as:

$$\text{CRF}(p_v,d;\mathit{r})=\frac{Re(P_v(\mathit{r})D^{\ast }(\mathit{r}))}{{\left\{\left({\sum }_{\mid \mid {\mathit{r}}_{\mathit{k}}\mid -r\mid \le \epsilon }^{k_r}{\mid U({\mathit{r}}_k)\mid }^2\right)\left({\sum }_{\mid \mid {\mathit{r}}_{\mathit{k}}\mid -r\mid \le \epsilon }^{k_r}{\mid V({\mathit{r}}_k)\mid }^2\right)\right\}}^{1/2}}.$$ (12)

The average 1D FCR curve and the 2D CRF image can be used in place of the power spectrum and its rotational average in the CTF estimation procedure described in Section 2.4 to obtain estimates for defocus and astigmatism amplitude and angle. The only modification required is that the CTF instead of the squared CTF should be used in the goal functions. Note that the estimation and subtraction of the background curve is omitted, and since approximations of defocus values are required to compute FCR and CRF estimates, the exhaustive searches for the initial defocus can also be eliminated, thus further improving the robustness of the method.

It is worth noting that FCR-based estimates are only possible for groups of particle images as the averaging of signal improves the SNR of FCR curves and thus the reliability of estimates. Ideally, one would want to have defocus and astigmatism estimates computed independently for individual particle images, but the reality of the low SNR of EM data precludes attainment of this goal. In addition, the number of cryo-EM structures determined at a better than 4 Å resolution is increasing, which suggests that within-micrographs defocus variations might not be the limiting factor.

2.6. Implementation

The program is implemented under the SPARX system as sxcter. py [35]. SPARX and its source code and essential dependency EMAN2 are available for free download at: http://sparx-em.org/sparxwiki. The outcome of CTER micrograph’s analysis program has also been integrated into the two data windowing programs of EMAN2, i.e., e2boxer.py for single particles and sxhelixboxer.py for helical filaments, so the CTF analysis can be done as a part of the automated windowing of data boxes. In the adopted protocol the data windowing programs input the CTF parameters and their errors, as computed by the CTER, and micrographs whose CTF errors, either defocus or astigmatism, exceeds user-defined thresholds, are omitted and no windows are extracted. As a consequence, the user has to only examine distribution of errors, set the threshold, and subsequent steps are performed automatically.

The code, including optimization procedures, is written in high-level Python with some CPU-intensive components, particularly polar coordinates based rotational alignment, written in low-level C+ +. The 1D Fourier transforms are done using native code while 2D Fourier transforms are computed using FFTW3 library [47]. The latter is used to compute initial 2D periodograms, but the time of this calculation is negligible in comparison with the fitting time. For user specified periodogram window size 360 × 360 pixels, a single fit takes ~2.5 s using a 3.33 GHz Intel Xeon processor. While exact comparisons are difficult to make, the recently reported computation times for CTF estimation programs are at least one order of magnitude larger: for a window size 350 × 350 pixels, Vargas and co-workers give 23 s for FASTDEF, 302 s for Xmipp, and 580 s for CTFFIND3 (see Table 7 in [24]). It is worth noting that in our experience much faster processing time with CTFFIND3 is possible when the parameters of the program are adjust to decrease the expected accuracy.

For n_B = 16 bootstrap fits, the total computation time with CTER is 45 s, which is within the time that is required to take an image on an electron microscope, thus indicating that the method is well suited for automated high-throughput microscopy. Since no effort was undertaken to optimize the program, it is likely that further improvements in speed are possible.

2.7. Analysis of the CTF parameters errors

CTER estimates the values and standard deviations of three CTF parameters: defocus, amplitude contrast, and amplitude angle (Eqs. (3) and (4)). The standard deviations are interpreted as errors and can be examined manually. However, it is straightforward to set a threshold on the maximum error one is prepared to tolerate and use the available information in an automated mode to eliminate from further processing micrographs with unusually high errors (Fig. 3).

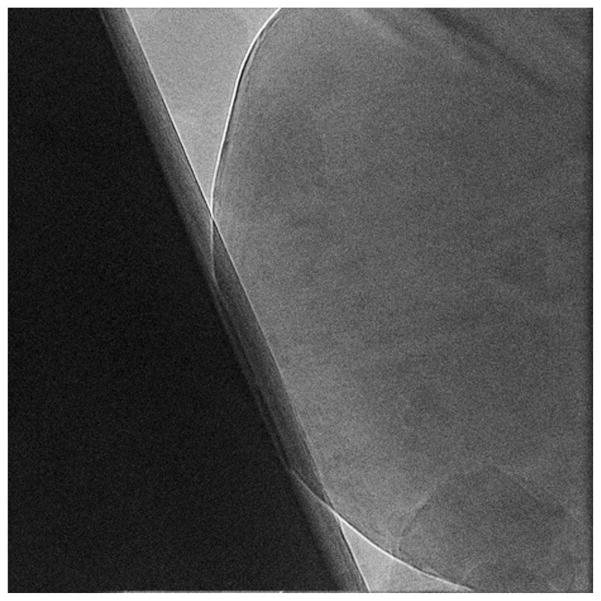
Fig. 3.

A micrograph with large errors associated with the estimated CTF parameters. It was collected with 300 kV Tecnai Polara (FEI) electron microscope using the K2 Summit DED camera. The size is 3710² pixels, and pixel size on specimen scale is 0.968 Å. The settings of the CTF were: C_s = 2 mm, A=0.07. The estimated CTF parameters and their standard deviations are: defocus Δz = 1.2±0.5 μm, astigmatism amplitude 0.2±0.5 μm, astigmatism angle 132.0±255.0°. The extremely large errors are indications of the non-uniformity of the imaged field.

While numerical values of defocus and astigmatism errors are informative, more instructive is their interpretation in terms of resolution limiting effects. In our structure determination protocol all particle images windowed out from a given micrograph have assigned the same average values of CTF parameters. However, large errors associated with these parameters mean that actual CTF parameters of individual images should have comparable dispersion, and the discrepancies between the actual and assigned values will result in a resolution-limiting fall-off of the effective CTF. The magnitude of this fall-off as a function of defocus spread was analyzed and found to be approximately Gaussian and thus could be expressed as an additional envelope function associated with the CTF [48]. However, to obtain a more general result that includes astigmatism, we estimate in CTER the fall-off using a Monte Carlo procedure. More specifically, we generate a large number of 2D CTF images, e.g., a few thousand, with the defocus, amplitude contrast, and amplitude angle randomly varied about their average values using a Gaussian random number generator and estimated standard deviations of the respective parameters. We compute the sum of all simulated CTFs and its 1D rotational average, again using the estimated average values of the CTF parameters (Eq. (8)). We square the resulting 1D profile and find the spatial frequency at which its value drops below 0.5, where 0.5 is an arbitrary cut-off value corresponding to the expected power loss of the signal of the particle images under consideration. Using this procedure, we calculate that half power loss occurs at a spatial frequency of 0.05 Ǻ⁻¹ (Nyquist frequency is 0.517 Ǻ⁻¹) for the ice-contaminated micrograph shown in Fig. 3 whose estimated CTF parameters and their standard deviations are: defocus Δz = 1.2 ± 0.5 μm, astigmatism amplitude 0.2 ± 0.5 μm, astigmatism angle 132.0 ± 255.0°. For the micrographs shown in Fig. 4, the estimated CTF parameters and their standard deviations are: defocus Δz = 1.540 ± 0.004 μm, astigmatism amplitude 0.04 ± 0.01 μm, astigmatism angle 128.0 ± 7.0°, and we obtain 0.255 Ǻ⁻¹ as the spatial frequency at which half power loss occurs.

Fig. 4.

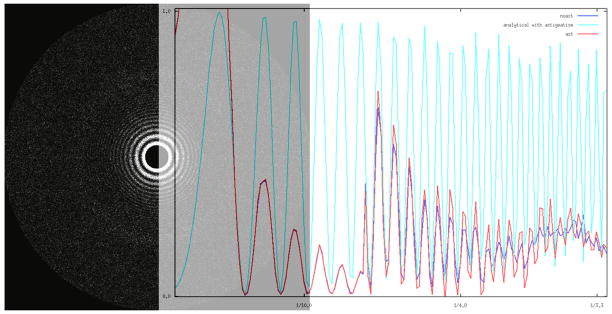
Signal power gain due to astigmatism estimation. (a) Power spectrum of a micrograph collected with settings as given in Fig. 3. The estimated CTF parameters and their standard deviations are: defocus Δz = 1.540 ± 0.004 μm, astigmatism amplitude 0.04 ± 0.01 μm, astigmatism angle 128.0 ± 7.0°. (b) Blue: rotational average of power spectrum without inclusion of astigmatism; red: rotational average of power spectrum with astigmatism taken into account; light blue: rotational average of simulated CTF² using estimated parameters and with astigmatism taken into account. For better visualization experimental rotational power spectra are plotted for frequencies higher than 1/7 Ǻ⁻¹ with increased amplitudes.

3. Results

The ability to compute the maximum frequency to which CTF is properly discretized within a limited-size window facilitates the decision making process as regards to the proper settings of the microscope prior to data collection. It also makes it possible to exclude some part of the data in high-resolution projects such that the aliased regions of reciprocal space do not adversely interfere with the properly sampled data. The examples provided in Table 1 illustrate the relationship between the three parameters over which user has considerable control, namely window size, pixel size and defocus. In single particle EM, the maximum diameter of the imaged macromolecular complex determines the window size used and for reasons of efficiency it is preferable to keep it as small as possible, with some additional margin to account for initial imprecise centering of 2D projection images windowed from micrographs [41]. The choice of pixel size is dictated mainly by the target resolution, i.e., the higher the resolution one hopes to achieve, the smaller the chosen pixel size should be, with some additional adjustment to account for unavoidable degradation of the data during image processing operations [49]. Similarly, while desire for high resolution favors the choice of close defocus settings of the microscope, work with small complexes will force the user to use far defocus settings in order to increase the contrast of the data so as to obtain a reliable alignment.

The main conclusion is that for a small object (i.e., those with diameter less than 64 Å) that fits into a window of 64 pixels, using far defocus would actually severely restrict the resolution due to Fourier space aliasing of the CTF. Assuming a voltage of 300 kV, spherical aberration constant 2.0 mm, pixel size 1 Å, it follows from Table 1 that a 2.5 μm defocus would restrict resolution to 2.0 Å/0.2=10 Å. Also from Table 1, we see that in this case one could properly represent the CTF and thus in theory achieve the full resolution of 2 Å by using a window size of 512 pixels. However, the amount of noise within the data window would increase 64 times with the ensuing decrease of the correlation function SNR, which most likely would preclude achievement of full resolution. Furthermore, increasing the window size by such a large factor would cause the windowed particle image to contain other objects or artifacts from the micrograph, which in turn would decrease the accuracy of alignment.

The second and somewhat counterintuitive conclusion is that for a given underfocus setting, in order to fully represent the CTF one can keep the window size constant but increase the pixel size. For defocus 1.5 μm, pixel size 0.8 Å, and window size 128 pixels, Table 1 informs us that only 30% of the reciprocal space range is usable; however, by interpolating the data to 0.9 Å while maintaining the window size at 128 pixels, the usable range increases to 90%. However, increasing the pixel size will cause the object size to decrease relative to the window size, thus resulting in an increase in the relative amount of noise. Furthermore, by keeping the window size in pixels constant while increasing the pixel size, the area of the window in Angstrom will increase, and thus also increase the chance of including additional particles or artifacts other than the particle being windowed.

The overall conclusion is that one can either pre-compute limiting CTF values appropriate for a given EM structure determination project and collect EM data using defocus settings only within the permissible range, or low-pass filter images to usable range after the data is collected and actual defocus values are estimated. It would appear that the second option is more practical since for many projects it may be necessary to collect far defocus data regardless of the maximum resolution desired, in which case appropriate low-pass filtration would eliminate the aliased part of the reciprocal space information and prevent valid data from being corrupted.

The target applications of the proposed CTF estimation methodology are high-throughput high-resolution projects. Towards this end, we chose to test the proposed methodology on a 80S ribosome data set collected on a 300 kV Tecnai Polara (FEI) using the K2 Summit DED camera in super-resolution counting mode, courtesy of Dr. Yifan Cheng at UCSF. The data was collected in “movie” mode at 39,000× magnification, and frames 3–20 were decimated twice, motion corrected with UCSHImage4, and averaged to yield a set of 893 micrographs, each of which is 3710 × 3710 pixels, with pixel size 0.968 Å on the specimen scale. We began with the estimation of CTF parameters using entire micrographs. We set the power spectrum window size to 600 pixels and the overlap between them to 50%, so the overall number of periodograms was B=121, and we set the number of bootstrap samples to n_B = 16. Hence, each set of parameters was estimated from an average of statistically resampled set of 121 tiles, in which some original tiles were omitted and some appeared more than once. For some micrographs the procedure yielded excessively large errors of parameters, particularly of the astigmatism angle. Upon visual inspection these micrographs contained various imperfections such as severe ice contamination (Fig. 3). After eliminating these micrographs, we were left with 872 out of the original 893 micrographs.

To verify that the astigmatism estimates indeed result in improved characterization of the CTF we compared rotational power spectra without and with inclusion of computed astigmatism values. Whenever the astigmatism amplitude is sufficiently high and its error small, the plots of rotational averages confirm the gain in power of the signal accounted for by the CTF model (Fig. 4). At the same time, the gain is only pronounced at relatively high frequencies (>1/6 Ǻ⁻¹), which is an indication of high quality microscopy (even though no special care was taken to align the microscope), and also suggests that improvement in the resolution of structure determination can be expected only for high-resolution projects. For frequencies lower than 1/8 Ǻ⁻¹, i.e., intermediate resolution work, the differences between the two curves are negligible.

Next we investigated whether the estimated CTF parameter values would differ if power spectra were estimated from windowed particle images instead of entire micrographs. As before, the window size was set to 600 pixels. The number of windowed particles per micrograph, and thus the number of computed periodograms, ranged from 11 to 81 with the majority containing 30–45 particles, which is much smaller than the 121 periodograms used for estimation from entire micrographs. However, we note that if there was zero overlap between the windows used to calculate power spectrum in the procedure using entire micrographs, then there would only be 36 periodograms, which is commensurate with the number of windowed particles per micrograph. We repeated the estimation of CTF parameters while keeping the remaining parameters the same as before. The agreement between both sets of results was excellent, and discrepancies were well within the error bounds. A typical result is: (1) micrograph-based estimate yielded Δz = 1.034 ± 0.014 μm, astigmatism amplitude 0.039 ± 0.028 μm, astigmatism angle 138.0 ± 7.0° and (b) windowed particles-based estimate yielded Δz = 1.038 ± 0.022 μm, astigmatism amplitude 0.042 ± 0.020 μm, astigmatism angle 140.0 ± 8.5°. The differences are well within the error bounds, and is most likely a reflection of the fact that the preparation was done using thin carbon film, which is the dominating contributor to the Thon rings pattern.

Ultimately, the success of any CTF estimation procedure should be based on the resolution of the CTF corrected 3D structure that emerged from the data. To this end we windowed 35,198 ribosome particle images from the set of 872 micrographs. We assigned to them the estimated particle-based CTF parameters and decimated them such that the window size was 280 pixels with a pixel size of 1.264 Å on the specimen scale. We determined a 3D structure that outside of testing purposes has little biological meaning as the sample contained 80S ribosome with ratcheting small subunit (40S), meaning that only the large subunit (60S) reveals proper features, and the computed resolution is only applicable to the large subunit. We carried out structure determination with the astigmatism values included and the ultimate resolution was found to be 3.85 Å using the FSC 0.5 cut-off criterion (Fig. 5, the structure is available in the 3D-EM data base with accession number EMD-5889). When the astigmatism amplitudes were set to zero, the resolution was found to be 4.03 Å using the FSC 0.5 cut-off criterion. Due to the high resolution of the structure and the small pixel size, the improvement obtained with the inclusion of the astigmatism estimation is more significant than it would first appear, as the gain is actually four Fourier pixels.

Fig. 5.

A fragment of a 60S subunit of a structure of 80S ribosome determined using 35,198 projection images collected with a 300 kV Tecnai Polara (FEI) equipped with the K2 Summit DED camera. (a) Cryo-EM structure at 3.85 Å (using FSC with 0.5 cut-off criterion). (b) A pseudo-atomic model of the 60S converted to electron density and filtered to the resolution of the EM map.

4. Discussion

We introduced CTER, a fast and effective computational method for estimation of the selected CTF parameters and their errors. CTER automatically determines the spatial frequency range that contains the usable part of the power spectrum of a micrograph or a set of windowed particle images. The position of the lowest frequency in this range corresponds to the location of a “kink” in the power spectrum, and the frequencies below it are those very low spatial frequencies that usually contain artifacts. The highest frequency in the range is computed as the spatial frequency beyond which the CTF cannot be properly represented in discrete space due to aliasing artifacts. The estimation of the CTF parameters (defocus and astigmatism) is done rapidly as the process is carried out in stages. First, a 1D rotational average of the power spectrum is used to obtain initial guesses of defocus, and then the 2D power spectrum is resampled into polar coordinates and both refinement of defocus value as well as estimation of astigmatism parameters is conducted using a logarithmic-time rotational cross-correlation function. A single search takes ~2.5 s, which makes repeated calculations and thus statistical resampling of periodogram data computationally feasible even for high-throughput projects. We applied a bootstrap technique that ultimately yields standard deviations, which are interpreted as errors, of the computed CTF parameters.

The overall time of calculations for one micrographs is below 1 min, thus making CTER suitable for use in high-throughput cryo-EM data collection. Most importantly, the error estimates enable automated screening out of inferior quality micrographs. The application of CTER to analysis of a human 80S ribosome data set of 35,198 particle images collected with a 300 kV Polara TEM equipped with K2 Summit DED camera operating in movie mode yielded a structure of the 80S ribosome whose large subunit had a resolution of 4.03 Å without, and 3.85 Å with, inclusion of astigmatism parameters. This attests to the high accuracy of the CTF estimates obtained using CTER and to the importance of astigmatism estimation for high-resolution cryo-EM.

In the design of CTER we applied statistical resampling to a set of tiled periodograms computed from overlapping regions of a micrograph. The estimated errors reflect mostly non-uniformity of defocus within the micrograph field and thus deviations of “true” particle defoci from the “average” value derived from the entire micrograph. While this is the most intuitive and straightforward approach to error analysis, there are also other possibilities based on statistical resampling. For example, one could resample the periodogram window size. It is easy to observe that for CTF estimation software that relies on SNR-improving averaging of periodograms, the results depend, often dramatically, on the window size used. The window-size bootstrapped error estimates would be primarily reflective of uncertainties due to discretization of the data and their adverse impact on the numerical stability of the fitting algorithm.

The current work was motivated by the need to develop a measure of CTF fit accuracy that could inform the user both about the quality of a micrograph and the reliability of the estimated CTF parameters. We were not striving to provide more accurate estimates as in the absence of an accepted metric it is not clear how such accuracy could be measured. For the fitting part of CTER we employed the goal function used in CTFFIND3, so on a fundamental level the results should be at least similar. On the other hand the result of the fit seems to depend equally strongly on the way the background is estimated and subtracted from the experimental power spectrum and on the spatial frequency range within which the goal function is evaluated. Since there is no objective way to determine how these two key steps should be executed, we expect a possibility of noticeable discrepancy between results reported by various programs.

It would be for practitioners of electron microscopy and for designers of automated data collection systems to decide which methods for estimation of CTF parameters errors are most informative for screening the micrograph data. Towards this end, we note that the statistical resampling-based paradigm of CTER’s design is very flexible and since the code is written in transparent high-level Python any modifications would be straightforward.

Appendix A. Supplementary material

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.ultramic.2014.01.009.