Integrated Continuum Dielectric Approaches to treat Molecular Polarizability and the Condensed Phase: Refractive Index and Implicit Solvation

1. INTRODUCTION

The newly introduced treatment of electronic polarization by an internal continuum (EPIC) was shown accurate in reproducing experimental and DFT molecular polarizability tensors with a remarkably small number of adjustable parameters{151}. Moreover, the accuracy found when computing intermolecular interaction energies, in which the appropriate treatment of electronic polarization is crucial, opens up the possibility of using EPIC to include polarizability in force fields{218}. This led us to propose the use of EPIC to embed polarizability in all-atom-explicit-solvent calculations. EPIC uses the continuum dielectric electrostatic theory to account for the way electronic density polarizes under the presence of an external electric field that can either come from other molecules, in explicit condensed phase calculations, or the reaction field in an implicit solvent calculation. In comparison with the point inducible dipoles{74, 88, 49} or the Drude’s oscillator models{12, 78} that use the atomic nuclear positions as polarizable centers, EPIC uses the notion of a polarizability density that induces a dipole density, normally referred as polarization, through the molecule volume as a response to the local electric field. In a recent study, Schropp and Tavan{194} proposed that the use of single centers in point inducible dipole polarizable calculations was responsible for the large difference between the best condensed phase atomic polarizability and the best vacuum phase atomic polarizabilities previously noticed{11, 8}. Other studies, based on QM assessment, suggest that the polarizability in condensed phase should only be slightly reduced{202}. The idea of using a continuum dielectric to account for electronic polarization was first formulated by Sharp et al.{27}, but was not further pursued until Tan and Luo{43} optimized the internal dielectric of solutes to produce the electrostatic potential in the context of Poisson-Boltzmann calculations with different implicit solvents. One of the difficulties with Tan and Luo approach is that the solute and the solvent polarization are treated as if it is a single phenomenon when they are actually distinct. They mainly focused on the dipole moments of the few molecules they studied, letting the atomic partial charges vary where the vacuum phase atomic partial charges should be used because the solute polarization should be sufficient to account for the change in solvent polarity. For this reason, we choose to separate the charge fitting from the polarizability fitting by optimizing separately an electronic volume on quantum mechanics (QM) polarizability tensors for a molecule in vacuum{151}, as was done originally with other polarizable models{75, 49, 74}. We found that in order to reproduce quite accurately the polarizability tensors of challenging molecules, the atomic radii needed to be much smaller than the van der Waals (vdW) contact radii usually used in implicit solvent calculations (like Bondi{108}). Furthermore, the internal dielectric needed to be surprisingly high and this was necessary to reproduce the anisotropy of the polarizabilities. On the one hand, that work allowed for a systematic way of adjusting a dielectric function to account for electronic polarization but, the abnormally high internal dielectric of 14 seems questionable and makes implicit solvent calculations impractical. Regarding the first issue, it is clear that the dielectric inside the molecule is closely related to the refractive index squared (ε_∞=n²) of the pure liquid and that its value should fall between 1.7 and 2.9, far below our large values. Regarding the second issue, with such small atomic radii defining the molecular cavity in solvent, the free energy of charging becomes unrealistically negative in Poisson-Boltzmann (PB) calculations. In this work, we specifically address both issues and show the physical soundness of the approach. An important change from our previous work is the use of a smooth dielectric boundary to represent both the solute and the solvent polarization. We present a newly design dielectric functional form that defines a 3-zone dielectric continuum that permits the use of EPIC for implicit solvent calculations. We think that this sort of description of the dielectric function is a better physical picture of reality than the usual 2-zone dielectric (inside and outside the cavity).

Another question that we examine is the ability to optimize the EPIC parameters in a general and robust way with few parameters on a larger variety of chemical functionality than in earlier work. For this purpose, we have formed a large database of QM molecular polarizability tensors containing 707 entries (or a total of 4242 polarizabilities) along with their optimized molecular geometries (c.f. Supporting Information). As will be outlined below, this dataset contains a large variety of chemical functional groups representing a significant component of bioorganic chemistry. The validity of not only the internal dielectric function but also of the 3-zone dielectric function is assessed with the independent fit of the solvent cavity atomic radii which define the third zone of the function on 485 experimental free energies of hydration.

In the remainder of this article, section 2 presents the theoretical basis and methods employed. More precisely, we present the 3-zone dielectric function for implicit solvent calculations and we review the polarizability tensor calculation. This is followed by the theoretical background for the calculation of the refractive indices. A theoretical layout for free energy of hydration calculations and computational details related to quantum calculations close this section. The section 3 describes the chemical datasets used in section 4 where the results and their analysis are presented. First the polarizable EPIC model parameterization is enlarged which allows for the calculation of refractive indices. Section 4 is terminated with a 3^rd zone dielectric optimization on experimental hydration free energies. Before the ending conclusion, section 5 gives a more general discussion that makes the link between the different sections.

2. THEORY AND METHODS

2.1 3-Zone dielectric in implicit solvents

The dielectric function in continuum approaches is fundamental as it is modulating all sources of polarization. In this work, we move away from our previous use of vdW envelop surface{159} surface toward a smooth functional form based on a sum of atomic Gaussian which has been previously proven successful{36, 117} in PB applications. Although useful, the hard dielectric boundary often leads to numerical problems: iterative convergence failure, slower convergence, strong dependency on orientation and translation, and unstable force evaluations{36, 125}. The use of smooth solute/solvent dielectric boundary was shown to improve over the hard boundary on all these aspects. More specifically, the molecular dielectric function used in the present work is given by

$$\epsilon (\stackrel{\rightharpoonup }{r})={\epsilon }_{in}-({\epsilon }_{in}-{\epsilon }_{\mathit{ext}})exp(-A·f_{in}(\stackrel{\rightharpoonup }{r}))$$ 1

where ε_in is the dielectric constant inside the molecular volume and ε_ext the dielectric value outside. It is to be mentioned that the dielectric here is expressed as a permittivity relative to the vacuum permittivity. The exponential behaves as a switching function that is turned on or off depending on the value of a molecular ‘density’ function f_in (r⃑). The A parameter modulates the steepness of the switching function. The details of the dielectric are then incorporated into the ‘density’ function

$$f_{in}(\stackrel{\rightharpoonup }{r})=\sum _{i=1}^{\mathit{Natoms}}p·exp\left(-k\frac{{\mid {\stackrel{\rightharpoonup }{r}}_i-\stackrel{\rightharpoonup }{r}\mid }^2}{{\sigma }_i^2}\right)$$ 2

The summation runs over all atoms and 3-dimensional Gaussian defines the radial extent of the atomic volume. More precisely, σ_i are atomic radii and r_i their positions. The σ_i will be the subject of an extensive parameterization in the next sections. The constant k is set to 2.3442 and p to 2.7 following Grant et al. recommendation{36}. These were fitted to obtain accurate molecular volumes under the constraint p(π/k)^3/2=4π/3 to ensure that the atomic radii (σ) have the meaning of a sphere radius. One can conceptually understands eq. 1 in terms of electronic density that would have a constant susceptibility (polarizability density) inside and drops rapidly as the density vanishes as shown in Figure 1a.

Figure 1.

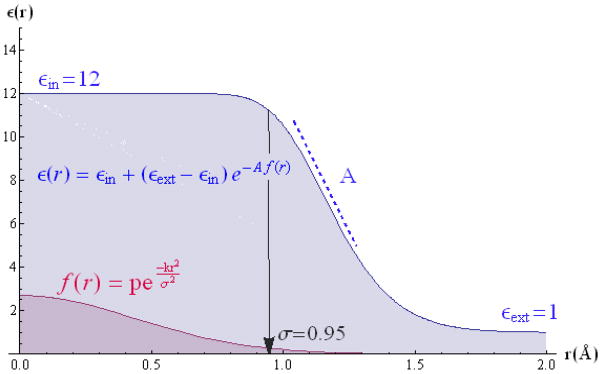
This figure shows the smooth dielectric function used in this work for a single atom with σ = 0.95Å, ε_in = 12, ε_ext = 1 and A = 10.0 (Cl of the G1-12 set). In a), starting from the center of the atom (r = 0), the dielectric stays constant until the ‘density’, expressed with a sum of Gaussian (pink curve), reaches a certain small value that cause the dielectric to smoothly reach the external dielectric value. The steepness and the position of the switching region depend on the value of the A parameter.

The main methodological novelty proposed in this work is the 3-zone dielectric for the coupling of EPIC with implicit solvation. When atomic radii are optimized on QM-based molecular polarizability tensors, their optimal small size prevents their use to define the cavity formed by the solute in implicit solvent calculations. Indeed, it is wrong to suppose that the solvent polarization would happen with a dielectric constant of 80 at distances such as 1.3Å {151} or 0.9Å (this work) from the center of an aromatic carbon atom given that the contact distance, according to Bondi{108}, is 1.7Å. This would result in clearly too negative free energies of charging (results not shown). Coming back to the electronic density picture, we believe that it is more reasonable to think that the radial extent of the electronic polarization can be different from the vdW radius, i.e. the distance at which implicit solvent starts to have a bulk dielectric constant of 80 (for water). The idea presented here is that both kinds of smooth surfaces could be simultaneously used: one formed with the smaller polarization atomic radii and one defined with the solvent cavity atomic radii. This leads to a 3-zone dielectric function to which we give the form

$$\epsilon (\stackrel{\rightharpoonup }{r})={\epsilon }_{in}+({\epsilon }_{\mathit{trans}}-{\epsilon }_{in})exp[-A·f_{in}(\stackrel{\rightharpoonup }{r})]+({\epsilon }_{\mathit{solv}}-{\epsilon }_{\mathit{trans}})exp[-B·f_{\mathit{solv}}(\stackrel{\rightharpoonup }{r})]$$ 3

where ε_in is the dielectric constant inside the molecular cavity, ε_solv the bulk solvent dielectric constant (80 for water), and ε_trans the dielectric constant in the zone of transition between the solute and the solvent. For the smooth inner dielectric boundary, A has the same meaning as in eq. 1 and f_in (r⃑) is given by eq. 2. The additional exponential term, for the outer dielectric boundary (with solvent), is a switching function that turns on when a second Gaussian sum (f_solv (r⃑)) becomes sufficiently small. The f_solv (r⃑) term is also given by eq. 2 with the difference that the atomic radii are larger as they define the solvent cavity. The B parameter is responsible for the steepness of the cavity boundary, but with a sufficiently large value has the effect of moving the position of the boundary as if the radii were scaled. The radial shape of the 3-zone dielectric is illustrated in Figure 2a for a single atom and for the 4-pyridone molecule, both with typical parameters.

Figure 2.

The 3-zone dielectric function allows an accurate description of both the solute polarization and the solvent polarization within the EPIC approach. The radial component for a single atom (G1-12 aromatic carbon) is shown (a) together with the polarization (σ_in) and the solvent cavity (σ_solv) atomic radii. Each plateau of the dielectric function defines a zone. The resulting dielectric function is also shown in the ring plane of 4-pyridone (b) when applying the G2-12 parameters.

2.2 Molecular polarizability tensor

In this section, we review the methodology previously developed to calculate molecular polarizability tensor with a finite difference Poisson solver{151} and we summarize how the involved parameters are optimized in this work.

2.2.1 Method

Our formulation of electronic polarization based on continuum electrostatics allows the calculation of induced multipolar moments by considering the bound charge density, which results from the polarizability density of the media (the electrons in our case). A formula to calculate the bound charge density is{143}

$$\begin{array}{l}\frac{{\rho }^b(\stackrel{\rightharpoonup }{r})}{{\epsilon }_0}=-\stackrel{\rightharpoonup }{\nabla }\left(\left[\epsilon (\stackrel{\rightharpoonup }{r})-1\right]\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})\right)\\ =-\stackrel{\rightharpoonup }{\nabla }·\stackrel{\rightharpoonup }{P}(\stackrel{\rightharpoonup }{r})\end{array}$$ 4

where ρ^b is the bound charge density and E⃑(r⃑) the total electric field. Physically, ρ^b is a consequence of the formation of dipoles at each point in space (the polarization P⃑(r⃑) or dipole density). Eq 4 is useful since it transforms the locally induced dipoles into a scalar value, the bound charge density, which can be used more easily as done below. Also, it is noteworthy to say that bound charges appear in region of spaces where ε(r⃑) varies such as the dielectric boundary of a molecule. In other words the polarization occurs everywhere the dielectric is larger than one, but the effects, through the bound charges, is much more localized. In eq. 4, ε(r⃑)−1 plays the role of a local polarizability density, also called the electric susceptibility, and P⃑(r⃑)= (ε(r⃑)− 1)E⃑(r⃑) corresponds to the induced dipole density (polarization). The analogy with the point inducible dipole model, a different polarizable model, is obvious since, in that case, the atomic induced dipole is given by μ⃑ (r⃑_i)= α_i E⃑ (r⃑_i) where μ⃑(r⃑_i), α_i and E⃑(r⃑_i) are the dipole induced at the atomic position r⃑_i, the atomic polarizability and the electric field at r⃑_i. Here, the polarization is more smoothly distributed over the molecular volume. Eq. 4 is intrinsic to the definition of Poisson’s equation.

A classical example, for which an analytical solution exists, is the dielectric sphere in vacuum experiencing an external electric field. In this case the mathematics show that bound charges appear on the surface of the sphere with opposite charge sign on both hemispheres, resulting in an induced potential equivalent to an ideal induced dipole moment aligned with the external field located at the center of the sphere. The induced dipole moment is proportional to the external electric field and the sphere polarizability α_sphere is given by the Clausius-Mossoti equation

$${\alpha }_{\mathit{sphere}}=\left(\frac{{\epsilon }_{\mathit{sphere}}-1}{{\epsilon }_{\mathit{sphere}}+2}\right)R_{\mathit{sphere}}^3$$ 5

where R_sphere is the sphere radius. For a molecular system, the analytical solution is unknown and we use a finite difference algorithm to solve Poisson’s equation numerically with a uniform electric field in the form of a voltage clamp applied by means of the boundary conditions. More precisely, a uniform electric field in the z direction can be produced with a null potential on one side of the grid boundary and the value −E_ext×L_z on the opposite side, where L_z is the box size in the z direction and E_ext the magnitude of the applied field. On the four other sides, parallel to the field, the grid boundary potential is simply calculated as a linear interpolation along the z direction: ϕ(z−z₀) = −(z−z₀)×E_ext. As with the dielectric sphere in vacuum, a molecular dielectric cavity responds linearly to the applied field and the proportionality constant is the molecular polarizability tensor. The field is applied in three orthogonal directions to build the polarizability tensor:

$$\overline{\alpha }=\left[\begin{array}{ccc}\frac{{\mu }_{x,x}}{E_{\mathit{ext}}}& \frac{{\mu }_{x,y}+{\mu }_{y,x}}{2E_{\mathit{ext}}}& \frac{{\mu }_{x,z}+{\mu }_{z,x}}{2E_{\mathit{ext}}}\\ & \frac{{\mu }_{y,y}}{E_{\mathit{ext}}}& \frac{{\mu }_{y,z}+{\mu }_{z,y}}{2E_{\mathit{ext}}}\\ & & \frac{{\mu }_{z,z}}{E_{\mathit{ext}}}\end{array}\right]$$ 6

where μ_x,y is the x component of the induced dipole moment when an external electric field of magnitude E_ext is applied in the y direction. Some experimental values are available for the eigenvalues of this tensor in vacuum (ε_ext = 1); also, the polarizability tensor, which depends on the orientation of the molecule, can be calculated using approaches based on quantum mechanics (QM) methods such as density functional theory.

The induced dipole moment is calculated analogously to the sphere dielectric system, integrating the bound charge density over space. From eq 4 (or simply from Gauss’s law), one can show that

$${\rho }^b(\stackrel{\rightharpoonup }{r})=-{\rho }^f(\stackrel{\rightharpoonup }{r})+{\epsilon }_0\stackrel{\rightharpoonup }{\nabla }·\stackrel{\rightharpoonup }{E}(\stackrel{\rightharpoonup }{r})$$ 7

In the present context, there is no free charge density ρ^f (r⃑) (from atomic partial charges, for instance) and as such the bound charge density, induced only by the external uniform electric field, is given by the divergence of the field. With a finite difference solver, the total charge (bound and free charges) can be calculated by integrating over each differential volume element (grid cube) which leads to bound charges on grid points. This can be done simply by calculating

$$\frac{q_{\mathit{ijk}}}{{\epsilon }_0}=\frac{q_{\mathit{ijk}}^b+q_{\mathit{ijk}}^f}{{\epsilon }_0}=-\left(\frac{h_y{h}_z}{h_x}\right)\left({\varphi }_{i+1jk}+{\varphi }_{i-1jk}-2{\varphi }_{\mathit{ijk}}\right)-\left(\frac{h_x{h}_z}{h_y}\right)\left({\varphi }_{ij+1l}+{\varphi }_{ij-1k}-2{\varphi }_{\mathit{ijk}}\right)-\left(\frac{h_x{h}_y}{h_z}\right)\left({\varphi }_{\mathit{ijk}+1}+{\varphi }_{\mathit{ijk}-1}-2{\varphi }_{\mathit{ijk}}\right)$$ 8

where q_ijk, q^b_ijk and q^f_ijk are the total charge, the bound charge and the free charge inside the volume element associated with the ijk grid point, ϕ_ijk and ϕ_ijk−1 the electrostatic potential at the (x,y,z) and (x,y,z−dz) grid points respectively. The grid spacing in x, y and z are given by h_x, h_x and h_z. The grid free charge q^f_ijk are zero for this calculation and, in general, it is given by the atomic partial charges as distributed on the grid. Finally, the total dipole moment is given by

$$\stackrel{\rightharpoonup }{\mu }=\sum _{i,j,k}^{\mathit{Grid}}{\stackrel{\rightharpoonup }{r}}_{\mathit{ijk}}{q}_{\mathit{ijk}}$$ 9

With the free charges equal to zero (no atomic partial charge), the dipole calculated is then the induced dipole and the only contributor is the bound charge density. More generally, any molecular electric moment can be calculated with analogs to eq. 9. The overall procedure to calculate the polarizability tensor requires three solutions from the numerical solver. The calculation does not involve atomic partial charges (free charges) which allow to fit them in a second independent step.

2.2.2 Computational details

The finite difference Poisson calculations were performed with a modified version of the OpenEye Inc. ZapTK{}. The distance between two grid points was set to 0.35 Å and the grid boundary was at least 5 Å away from the surface defined by the polarization radii. Atomic charges of ±0.001e were assigned randomly on the atoms as the grid energy was used to determine the convergence of the algorithm. Atom typing was assigned with the OpenEye Inc. OEchem toolkit{}.

2.2.3 Optimization of the polarizabilities

The atomic radii are optimized in order to minimize a chi-square function using a Levenberg-Marquardt algorithm as implemented in scipy{234}, a scientific Python library. The error is defined as the difference between the 6 components of the polarizability tensor obtained with B3LYP and EPIC

$${\chi }^2=\sum _i^{\mathit{molecules}}\sum _{\begin{array}{c}k=xx,xy,xz\\ yy,yz,zz\end{array}}{({\alpha }_{k,i}^{\mathit{EPIC}}-{\alpha }_{k,i}^{QM})}^2$$ 10

where α_xy,i is one of the six-independent polarizability tensor elements of molecule i either under optimization (EPIC) or from the QM target values. By using the six independent tensor elements, we include both the magnitude and the direction of the polarizability in a natural way{Darden}. We optimized the cube of the polarization radii as their contribution to the polarizability grows with the atomic volume (c.f. eq. 5). For analysis purposes, we also define the average polarizability (eq. 11) and the anisotropy of the polarizability tensor (eq. 12) below

$${\alpha }_{\mathit{avg}}=({\alpha }_1+{\alpha }_2+{\alpha }_3)/3$$ 11

$$\mathrm{\Delta }\alpha =\sqrt{\frac{{({\alpha }_1-{\alpha }_2)}^2+{({\alpha }_1-{\alpha }_3)}^2+{({\alpha }_2-{\alpha }_3)}^2}{2}}$$ 12

where α₁ ≤ α₂ ≤ α₃ are the eigenvalues of the polarizability tensor. The polarizability anisotropy is significantly harder to obtain than the average polarizability. We define the error in the average polarizability (eq. 13) and anisotropy (eq. 14) for a set of molecules as

$${\delta }_{\mathit{avg}}=\frac{1}{N}\sum _i^N\frac{\left|{\alpha }_{i,\mathit{avg}}^{QM}-{\alpha }_{i,\mathit{avg}}\right|}{{\alpha }_{i,\mathit{avg}}^{QM}}$$ 13

$${\delta }_{\mathit{aniso}}=\frac{1}{N}\sum _i^N\frac{\left|\mathrm{\Delta }{\alpha }_i^{QM}-\mathrm{\Delta }{\alpha }_i\right|}{{\alpha }_{i,\mathit{avg}}^{QM}}$$ 14

where N is the total number of molecules considered and QM corresponds to the target value. Finally, the relative root-mean-square deviation (RRMS) of the tensor is defined as

$$\mathit{RRMS}=\frac{{\displaystyle \sum _i^{\mathit{molecules}}}{\displaystyle \sum _{\begin{array}{c}k=xx,xy,xz,\\ yy,yz,zz\end{array}}}{({\alpha }_{k,i}^{\mathit{EPIC}}-{\alpha }_{k,i}^{QM})}^2}{{\displaystyle \sum _i^{\mathit{molecules}}}{\displaystyle \sum _{\begin{array}{c}k=xx,xy,xz,\\ yy,yz,zz\end{array}}}{\left({\alpha }_{k,i}^{QM}\right)}^2}$$ 15

and constitutes a single metric for the over-all fitness of the optimized polarizability tensors. If the RRMS is calculated for a single molecule, the summations on the molecules in the numerator and the denominator are simply omitted.

2.3 Refractive index calculations

2.3.1 Theory

The dielectric constant of a material at the high frequency limit (ε_∞) is related to the material refractive index{223} n by

$$n^2={\epsilon }_{\infty }$$ 16

where n is usually measured with the D line of the sodium spectrum at 589 nm (n_D). The ε_∞ corresponds to the material dielectric constant solely due to the electronic polarization since the frequency of the visible light is too high for nuclei relaxation to contribute. Typically, a pure liquid of an organic compound will have a refractive index comprised between 1.3 and 1.7 leading to a ε_∞ between 1.7 and 2.9. Since the work of Debye and Onsager{232,27}, it is a dogma that the interior dielectric (ε_in) of a solute cavity in implicit solvent models should be given by the experimental ε_∞ in order to capture the dipole moment change due to the cooperative solute-solvent polarization. It is when we seek for accuracy in solute polarization that we found the generally accepted relation ε_∞ = ε_in to badly fail{151}. A way to reconcile this puzzling finding is by computing a macroscopic refractive index instead of an internal refractive index (quoted from Onsager{232}). The Clausius-Mossoti equation relates the polarizability of a sphere to its interior dielectric. Since ε_∞ and n are macroscopic intensive quantities, their measurement should not depend on the size of the studied sample, given that it is large enough to exhibit a macroscopic behavior, the worst case being the use of a single molecule. It is not to say that Onsager uses of the Clausius-Mossoti equation with the radius of a single molecule was not justified. In fact, he was primarily interested in the molecular polarizability (α_mol)and used the formula

$${\alpha }_{\mathit{mol}}=\left(\frac{n_D^2-1}{n_D^2+2}\right)\frac{3v}{4\pi n}$$ 17

where v is the volume of the liquid sphere considered and n the number of molecules it contains. In eq. 17, the rightmost factor corresponds to the cube of an effective single molecule radius. It is however understood that the same molecular polarizability is obtained as long as the v/n factor is preserved and is therefore size independent with the assumption that ε_∞ is filling the space uniformly or that it is a spatially averaged value. In order to calculate the refractive indices for the general case where the internal dielectric is not uniformly distributed in the liquid, we generate pure liquid configurations from molecular dynamics (MD) simulations at room temperature and cut out spherical clusters (or droplets) from individual snapshots. We maintain the v/n ratio by fixing the density to experiment and calculate the droplet effective ε_in with the formula

$$n^2=\frac{R_{\mathit{droplet}}^3+2{\alpha }_{\mathit{droplet}}}{R_{\mathit{droplet}}^3-{\alpha }_{\mathit{droplet}}}$$ 18

where R_droplet and α_droplet are the droplet radius and polarizability. We assign the dielectric function on all molecules and apply the procedure outlined above to calculate the droplet polarizability and thereby access the droplet refractive index.

2.3.2 Computational details

To obtain the liquid phase droplets, molecular dynamic simulations, using the AMBER 8.0 package, were performed on 3375 molecules (15×15×15) in a cubic box. The NVT ensemble and periodic boundary conditions allowed density to be fixed to the experimental value and the temperature was set to 20°C to match the experimental conditions used to report refractive indices. The temperature was maintained constant with the weak coupling algorithm{} with the kinetic energy adjusted every 1 ps. The non-bonded interaction cutoff was set to 8.0 Å and long range interactions computed with particle mesh Ewald{} using the default Amber 8.0 setup. The molecules were charged with AM1-BCC{29, 30} and the Generalized Amber Force Field (GAFF){228} was used. The SHAKE procedure{} was used to fix all bond lengths to hydrogen.

The initial liquid box was generated by positioning the molecules on a cubic lattice, randomly oriented with the Marsaglia{235} quaternions method. The system was first minimized until the root-mean-square (RMS) of the gradient is less than 0.1 kcal/mol/Å. This was followed by a 8 ps annealing phase integrated by steps of 1 fs, during which the non-bonding interactions were gradually turned on and the temperature increased from 0K to 40K and decreased to 0K. The system was then heated over 20 ps up to 293.15K with a 2 fs integration time step. Following a 1 ns equilibration, 50 snapshots were written over a 2 ns production run. Each of the liquid boxes for a given molecule was then wrapped in the primary cell. A sphere with a diameter set to 85% of the box length formed a liquid droplet when picking all molecules with an atom lying inside the sphere. The droplet radius was then determined by considering the position of the outermost non-hydrogen atoms. The precise definition of the radius is not unique and we have verified, for example, that using the experimental density to calculate the radius of the corresponding ideal sphere gives refractive indices within ±0.01 of those obtained by the chosen algorithm. Also, this model assumes a perfectly spherical object, ignoring the dimples formed because of the finite size of the spheres. The relatively large size of the droplet and the averaging over 50 independent configurations reduced the effect of this approximation.

The solution to Poisson’s equation in the presence of the voltage clamp boundary conditions was obtained on a rectangular grid sized to encompass the full droplet plus half its radius on each side of the droplet. The target grid spacing was set to be 0.5Å. The smooth dielectric functions (eq. 1), fitted on the molecular polarizability tensors only, were assigned together with the matching internal dielectric ε_in and A parameter. The external dielectric was always set to the vacuum value ε_ext = 1. The convergence criteria for the ZapTk solver was based on the grid energy and set to 0.0001 kT. This convergence criteria required the assignement of atomic charges that we choose to be ±0.001e on half the atoms, keeping an overall neutral system. Given the strength of the external field applied, this was not perceptibly affecting the answer.

2.4 Free energy of hydration

2.4.1 Theory

Implicit solvent models are commonly used to incorporate the effects of solvation in molecular models as a mean field {Roux, Luo, Mobley}. These models considerably reduce the computational burden needed to sample the solvent configurational space when each atom of the solvent are explicitly simulated. An important validation for solvation models comes from experimental free energy of hydration (ΔG_hyd) that consists in the chemical potential difference for the transfer of a solute from vacuum to the solvent bulk. The computational evaluation of ΔG_hyd is separated into two processes. Firstly, the non-polar free energy of hydration (ΔG_np) comes from the formation of an empty cavity in the bulk solvent that causes a reorganization of the solvent molecules. Secondly, the electrostatic free energy of hydration (ΔG_elec) results from the work necessary to place of the solute atomic partial charges in the cavity that switched on the electrostatic interactions between the solvent and the solvated solute. This results in the equation

$$\mathrm{\Delta }{G}_{\mathit{hyd}}=\mathrm{\Delta }{G}_{\mathit{elec}}+\mathrm{\Delta }{G}_{np}$$ 19

The longstanding use of implicit solvent to evaluate ΔG_elec is based on a high continuum dielectric solvent region that gets polarized by the solute static electric field. Traditionally, the solute cavity is formed with a molecular surface with a discrete transition of the dielectric function at the solute-solvent boundary. As explained above, we choose a smooth boundary transition. The solute cavity volume and shape is determined by atomic radii. It is important that the solute cavity and atomic charges are appropriately balanced. For a given set of charges, too small atomic radii exaggerate the affinity of the solute for water and too large radii will have the opposite effect. The calculation of ΔG_elec is normally done with a non-polarizable solute or, if the cavity is assigned a ε_in > 1, the atomic partial charges are screened and require a special treatment that was not done until recently{208}. Because the solute is non-polarizable and water increases the dipole moment of solvated molecules, the atomic charges should not be fit on a gas phase QM ESP. For this reason, the charges are often generated from RESP{} or AM1-BCC{} that are known to be balanced for calculations in water.

In the 3-zone dielectric model that we propose in this article (c.f. eq. 3), the first zone should accurately account for the solute polarizability, which allows for the use of vacuum phase atomic charges obtained independently of the internal dielectric function. The second zone located between the internal dielectric and the solvent is set to vacuum and the transition to the third zone needs to be parameterized in order to have a full implicit solvent model. Following Grant et al. suggestion{} for their non-polarizable 2-zone dielectric function, we fix the B parameter in eq. 3 to 11.8, which leaves the solvent cavity atomic radii to be fitted on the experimental free energy of hydration. However, in order to compare the calculated ΔG_hyd to experiment, we need to evaluate ΔG_np that is done without innovation here. Fortunately, converged Alchemia{} calculations based on free energy perturbation (FEP) are available for each compound from our hydration free energy dataset{}. Since this is the best achievable theoretical estimation of ΔG_np, this is our preferred estimation in current study. However, since this is not very useful for prospective evaluations of ΔG_hyd, we also fitted a surface area based model that calculates ΔG_np as

$$\mathrm{\Delta }{G}_{np}=\gamma \times S$$ 20

where γ is a surface tension and S the surface area of the molecule as defined by a Richard molecular surface{} created with a 1.4Å rolling probe and the Bondi radii{}. This crude approximation has been proven useful and it can be improved by atom typing the γ{217} or by using some treatment of the dispersion energy{219, 220, 221, 222} instead.

2.4.2 Computational details

The atomic partial charges responsible for the permanent electrostatic potential (ESP) were minimized by a least-square-fit on the QM ESP calculated on a face-centered-cubic grid of points. Following Jakalian et al{}, the grid spacing was set to 0.5Å and the grid points were positioned around the molecule in a volume formed by two vdW surfaces, each built with Bondi radii scaled by a factor of 1.4 and 2.0. The dielectric has the effect of scaling down by a factor of 1/ε_in the charges, which effect is partly compensated by the bound charges appearing from the internal polarization. Hence, the least-square-fit requires a Poisson solver in order to capture the total effect, which depends on the shape of the dielectric boundary. It is noteworthy to mention that the charge fitting process is independent of the EPIC polarizability model and, as such, can be fit after the solute dielectric parameters are optimized. The details of the procedure, called DRESP, can be found elsewhere{218}. The AM1-BCC atomic partial charges were generated with the OpenEye Inc. Quacpak toolkit and the topologically equivalent atoms had their charges averaged.

A finite difference Poisson solver was written to allow the implementation of the 3-zone dielectric model. Here is a brief description of the algorithms implemented. We use successive over-relaxation (SOR) and a Gauss-Seidel iterative scheme{40,Varga}. The free charges of the system were assigned on the grid with a quadratic inverse interpolation scheme{36} that has the advantage of conserving the dipole moment, has a continuous first derivative and is more robust to the effects of rotation and translation. The same interpolation rule is used to calculate the potential in between grid points. In our calculations, we use a convergence criteria base on grid energy defined as the sum of the electrostatic potential times the distributed free charges on the grid. This convenient criterion is directly related to the energy in an absolute way and thus ensures that relative energies are also converged. The boundary conditions, in energy calculations, were determined with a Coulomb potential.

The ΔG_elec was computed by taking the grid charge energy difference between a solution obtained in vacuum (ε_ext = 1) and another solution in water (ε_ext = 80) from the resulting Poisson’s equation and calculated with

$$\mathrm{\Delta }{G}_{\mathit{elec}}=\frac{1}{2}\sum _i^{\mathit{Atoms}}{q}_i\left(\varphi {({\stackrel{\rightharpoonup }{r}}_i)}^{\mathit{water}}-\varphi {({\stackrel{\rightharpoonup }{r}}_i)}^{\mathit{vacuum}}\right)$$ 21

where q_i is the atomic partial charge of atom i, ϕ(r⃑_i)^vaccum is the interpolated electrostatic potential at atom i position r⃑_i. The grid spacing for the solver was set to 0.35 Å and the minimum distance between the solute internal radii and the grid boundary to 7 Å. In the cases where the solute was non-polarizable, ε_in was set to one. Finally, the parameters (solvent cavity atomic radii and tension surface) were adjusted with the same Levenberg-Marquardt algorithm used for the fit to the polarizability tensor. All parameters were simultaneously optimized.

2.5 Quantum calculations

The B3LYP exchange-correlation functional{} is used for all DFT quantum calculations of this work within the Gaussian 03 software{135}. All molecular structures of this work were initially relaxed with B3LYP and the 6-31G(d,p) basis set{137, 138, 139}. Property calculations required larger basis sets for accuracy. The electrostatic potential values were obtained with B3LYP and the 6-311++G(3df,3pd) extended triple zeta basis set{137, 138, 139}. Secondly, the molecular polarizability tensor computations used the aug-cc-pVTZ basis set{136}, as it was shown to lead to accurate results{105}. The implemented method in Gaussian 03 to calculate the molecular polarizability tensor is the Coupled Perturbed Hartree Fock (CPHF) method{}. The Hartree-Fock calculations performed to fit water adapted atomic partial charges were also performed with the Gaussian 03 software with the 6-31G(d,p) basis set.

3. DATASETS

In this work, we make extensive use of three kinds of data: B3LYP/aug-cc-pVTZ polarizability tensors, free energies of hydration and refractive indices. A total of five datasets are then created.

3.1 Polarizability training dataset (PTD)

A training dataset is used to optimize the internal radius in order to match B3LYP polarizability tensors. To this end, we make use of the previously published training datasets{151} in addition to new molecules for a total of 265 polarizability tensors. In this dataset, many neutral functional groups are represented: alkanes, alkenes, alkynes, halogens (bromo, fluoro, chloro), alcohols, thiols, amines, ethers, thioether, nitriles, aldehydes, ketones, esters, thioesthers, amides, acids, ureas, imines, amidines, sulfones, sulfoxides, sulfonamides, heteroaromatics, hydrazines, hydroxamic acids, N-oxides, pyridones and peptides. In addition, charged functional groups were also included with the sole purpose of covering charged side chains in amino acids. They are: carboxylates, guanidiniums, imidazoliums and ammoniums. The strength of the PTD is the wide coverage of functional groups, but its clear weakness is the lack of cross-functionalized molecules. To get to this level of coverage would require calculations on many thousands of larger molecules, and consequently an enormous amount of computational power. The intention in this paper is to provide a reasonably general first set of parameters to adequately treat many bioorganic molecules in addition to most biomolecules.

3.2 Polarizability validation dataset (PVD)

The polarization validation dataset is composed of the previously published validation sets{151} and 401 molecules from the hydration free energy dataset (below) not included in the polarizability training dataset. In addition, a few special molecules such as neutral and charged peptides, melamine, sugars, etc. were added, giving a total of 442 datapoints. T

3.3 Polarizability dataset. (PD)

The polarizability dataset is composed of all polarizability tensor available, in other words, the combination of the validation and training datasets. This work is thus making available a total 707 B3LYP polarizability tensors together with the molecule coordinates (see Supporting Information).

3.4 Hydration free Energy Dataset (HED)

This dataset is built from a compilation of 504 experimental free energies of hydration of neutral molecules recently published with the corresponding ΔG_np and ΔG_chg from Molecular Dynamics based absolute free energy calculations{226}. We took the published dataset, eliminated the iodine- and phosphorus-containing compounds and formed a dataset of 485 molecules on which we could fit the solvent part of the dielectric function (eq. 3) and surface tension (γ).

3.5 Refreactive Indices dataset (RID)

The refractive indices dataset contains 23 small organic molecules (c.f. Figure 5) that are liquids at 20°C, for which the density and the refractive indices are taken from the CRC Handbook of Chemistry and Physics{233}. They span a variety of functional groups and most of the entire spectrum of refractive indices measured for bioorganic molecules.

Figure 5.

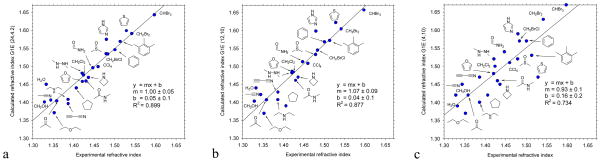
The calculated refractive indices (n) of 23 organic molecules are compared to experiment. Three dielectric parameter sets are used a) G1-24 b) G1-12 and c) G1-4 (Table 1). For each set, the pre-optimized radii can be found in Table 1. The reported refractive indices (n) were obtained by polarizing a liquid droplet formed by carving spheres from periodic MD liquid simulation snapshots. The Clausius-Mossoti equation leads to n²= ε_∞ close to experiment, in spite of the large ε_in. The predicted values are systematically higher than experiment, which can be explained by potential artifacts or a polarizability shift when passing from vacuum to condensed phase (see text). As with the polarizabilities, the predictions deteriorate with decreasing ε_in, in keeping with the results of the range-finding study on the small dataset.

4. RESULTS AND DISCUSSION

4.1 Polarizability tensor

This work follows the precedent of ref. {151} in fitting atomic polarizability radii and a single inner dielectric constant to QM molecular polarizability tensors to produce an accurate EPIC model of electronic polarization. In this section, we generalize the parameterization to account for most of the biomolecules and a significantly wider spectrum of bioorganic functional groups. In contrast to our previous work, we use a smooth dielectric function as described vide supra and a single internal dielectric (ε_in) value.

4.1.1 Choice of ε_in and A parameters

It was previously shown that a more accurate polarizable model was obtained when different ε_in were fitted for alkanes and aromatics. However, the single-ε_in model performed as well as the multi-ε_in model and DFT against experimental directional polarizabilities. Furthermore, in another study{218} that examined the local electronic polarization, the same single-ε_in model was only slightly worse than the multi-ε_in model. In this work we pursue the single-ε_in model because it greatly simplified the Poisson solver implementation and the robust parameterization for a wide spectrum of bioorganic chemistry.

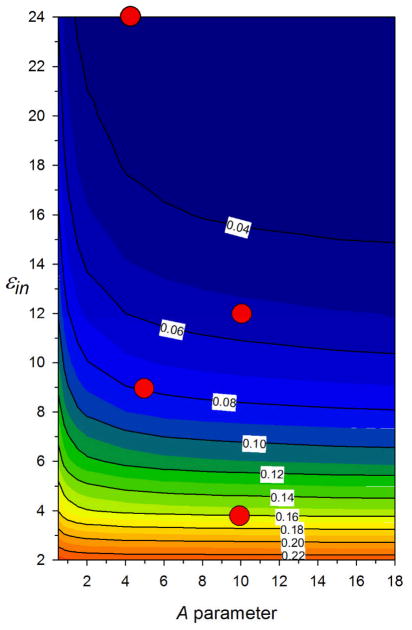
Before the global parameterization of polarizability atomic radii, a range-finding study was performed with a smaller training set examining which combination of ε_in and A (c.f. eq. 1) is best to use for extending the EPIC parameterization previously initiated{151}. We used a set of 13 alkanes (set g in ref. {151}) including methane, propane, cyclopropane, butane (cis, trans), hexane (cis, trans), neopentane, etc. together with a set of 10 heteroaromatic molecules (set a in ref. {151}). We formed the 2-dimensional grid of ε_in and A pairs and optimize four radii (hydrogen, alkane carbon, aromatic carbon and aromatic nitrogen) for each point of the grid. The polarizability tensor RRMS deviation from QM for this dataset at each (ε_in, A) pair is shown as an iso-contour plot in Figure 3. It is clear that in order to fit a general dielectric function, a sufficiently large ε_in is needed. Also, the flatness of the error surface allows for multiple equivalent choices, a potential advantage if other criteria become more stringent in the development of the polarizable model. As shown by red circles in Figure 3, four starting points were selected for further development: G1-24 (ε_in=24, A=4.188), G1-12 (ε_in=12, A=10), G1-9 (ε_in=9, A=10) and G1-4 (ε_in=4, A=10). In the case of G1-24 only, the A parameter was relaxed to a value of 4.18. The G1-12 seems slightly superior to the G1-9. Finally, the G1-4 parameter set showed the worst RRMS, still a good case for having a small value of ε_in, picked by Tan and Luo{} as being optimal. Each of the G1 ε_in and A choices was fixed in the global parameterization of polarization atomic radii described below. Finally, Figure 3 shows that making a poor selection of (ε_in, A), in particular having ε_in< 4, cannot be redeemed by adjusting the radii.

Figure 3.

The iso-contour plot of the RRMS error between B3LYP/aug-cc-pVTZ and EPIC polarizability tensors are shown as a function of the ε_in and A parameters of eq. 1. This RRMS surface was generated from a simultaneous fit of the H, alkyl C, aromatic C and aromatic N polarization atomic radii on 11 aromatic and 14 alkane molecules against the B3LYP polarizabilities. It shows that in order for a single dielectric model to fit well the polarizabilities of these 2 chemical classes, the ε_in needs to be sufficiently large (>4). Deviations in the anisotropy of the polarizability are the main source of error for lower values of ε_in.

4.1.2 The optimized polarization radii

The parameterization of the four G1 sets on the 265 molecules of the polarizability training dataset proceeded as described in the Method section. We kept the ε_in and A values fixed and optimized the polarization atomic radii σ_i on the B3LYP polarizability tensors. The atom typing of the radii was the primary concern and we aimed at minimizing the number of radii fitted to reduce the fitting complexity, ensure better generalization of the chemistry. Each non-symmetric molecule produced 6 data points from their polarizability tensor; symmetric tensors produced fewer data points due to structural symmetry. The number of fitted parameters was kept small compared to the number of associated data points. The determination of the atom typing was done iteratively in a non-automated manner. First, the polarizability training dataset was designed in terms of chemical functional-group classes. Often, the fit on an additional class lead to one or two additional parameters, easily fitted. For example, the alkane H and C radii were the first to be fitted. This was followed by aromatic C, H and N. It was determined early that a single atom type for C and H aromatic and alkyl could be utilized. Then the alcohol oxygen radius, halogen radii, alkene carbon and alkyne carbon radii were individually fitted. We also merged atom types when the radii values were similar and the fitness metrics (χ², δ_avg and δ_aniso) were not significantly affected. The final stage is a global simultaneous fit of all radii with all the molecules of the polarizability training dataset. Water was treated separately with its own special O and H radii.

The resulting polarization radii are given in Table 1 for the four G1 parameter sets. It is important to note that the ordering of atom types in Table 1 is important since the atom typing was done in the given order and a particular atom could fall in one or more categories (H for instance). The first observation is that all polarization radii are significantly smaller than vdW contact radii such as Bondi{108}, Pauling{237} or Parse{236} often used in Poisson-Boltzmann approaches. Instead of being a contradiction, this finding unveils the two different natures of the physical phenomena described. On the one hand, the polarization radii aim at calibrating how the electrons polarize in reaction to an external field created, for example, by an interacting molecule. On the other hand the vdW radii determine where the repulsive molecular wall raises. It is also noteworthy that the larger is the ε_in, the smaller the radii. To maintain the over-all polarization the dielectric has to go up as you decrease the radii. This is illustrating a general feature of the model that produces larger polarizabilities when either the ‘electronic volume’, decided by the radii, or the internal dielectric increases. The sort of relationship involved is given above for a hard sphere (eq. 5) and elsewhere for a diatomic{151}.

Table 1.

Reported optimal polarization radii (σ_in) and atom typing for the four G1 sets defining the internal dielectric (eq. 1).

SMARTS{}	Typical functional groups	Radius (Å)
	Model name:	G1-4	G1-9	G1-12	G1-24
Fixed parameters
εin		4	9	12	24
A		10	5	10	4.19
H
[H]	all H	0.83	0.65	0.55	0.52
C
[CX4]	alkanes	0.78	0.79	0.67	0.62
[c,CX2,CX3]	aromatic, sp, sp2	1.25	1.02	0.87	0.78
N
[n,NX1,NX3,$(Nc),$(NN)]	aromatic, nitriles, sp3, aniline, hydrazine,	1.09	0.89	0.76	0.69
					0.74a
[$(N[C,S]=*)]	amides, amidines, sulfonamides	0.89	0.77	0.64	0.58
[$(N=C)]	imine, amidine	1.07	0.93	0.81	0.76
[$([#7]~[OX1])]	N-oxides, nitro	0.00	0.79	0.68	0.59
O
[$([OX2]([H])[#6,#7]),o,$([OD2]([CX4,c])[CX4]), $(O=[c,C,S])]	alcohols, furan, hydroxamic acids, ethers, ketones, aldehydes, amides, sulfones	0.88	0.73	0.63	0.60
[$(OC=[O,N])]	Esters, carboxylic acids	0.68	0.55	0.46	0.46
[$([OX1]~[#7])]	N-oxide, nitro	1.08	0.89	0.77	0.74
Others
[S,s]	All sulfur atoms	1.44	1.22	1.06	1.01
[F]		0.77	0.62	0.53	0.51
[Cl]		1.30	1.09	0.95	0.91
[Br]		1.47	1.24	1.07	1.03
Water	Special fit
[$([OX2]([H])[H]]		0.93	0.86	076	0.75
[$([H][OX2][H])]		0.64	0.45	0.36	0.31
Charged atoms
[$([#1][#7+]),$([#1][#7][#6]=[#7+][#1]), $([#1][#7][#6]=[#7+]),$([#1][n+]~c~n), $([#1]n~c~[n+])]	proton in guanidiniums, amidiniums, ammoniums, pyridiniums	0.44	0.43	0.37	0.01
[$([O-]C=O),$(O=C[O-])]	O in carboxylates	1.20	1.02	0.88	0.85
[$([NX4+]),$([#7+]=C-N),$(N-C=[N+]))]	N in ammoniums, guanidiniums,	0.00	0.34	0.39	0.52
[$([n+]~c~n),$([n]~c~[n+])]	amidiniums, N in imidazoliums	0.00	0.00	0.00	0.42

It is however more interesting to compare polarization radii between elements and between the different chemical environments. First, it is remarkable that the carbon atom can be split into only two atom types: sp³ and others. It has a much smaller contribution to the overall polarizability when sp³ hybridized than when pi electrons are present, i.e. in the sp or sp² hybridization states. This can be justified by the presence of π^* molecular orbitals, the different number of connected H atoms, and the difference in the molecule shape and the related anisotropy.

The nitrogen atoms were subdivided into four atom types among which two encompass almost all intances in the datasets. The first of these is a general nitrogen type assigned to amines, nitriles, hydrazines or anilines for example. The second major nitrogen radius makes amide, amidine or sulfonamide nitrogen less polarizable. Surprisingly, the more specific nitro and N-oxide nitrogen radius, in the G1-4 set, has a radius of zero. The dielectric on this nitrogen atom is only slightly smaller than ε_in because of the large bound oxygen radii and the short N-O bond, typically 1.2 Å. It is also interesting to note that in the G1-24 set, there was a gain in accuracy when the nitrile nitrogen had its own radius.

The oxygen atom behavior can mainly be accounted for by two adjustable radii types, which was a significant advantage in the fitting process – the N-oxide and nitro functional groups still being an exception. Another interesting result is the large radius of the sulfur atom that is comparable to the bromine radius. However, it is not to say that the polarizability contribution of sulfur is equivalent. In fact, the bromine bonds are longer and hence offer a larger polarizable volume. This argument is also useful to explain why the fluorine radius is smaller than the hydrogen radius. For example, the model predicts a polarizability for tetrafluoromethane of 18 a.u. compared to 17 a.u. for methane, and a polarizability of 76 a.u. for hexafluorobenzene compared to 70 for benzene, all in close agreement with B3LYP. Because of water’s special importance, both the oxygen radius and the hydrogen radius were optimized to exactly match the B3LYP polarizability tensor. Finally, the charged species posed a special challenge that we decided to address specifically for charged side chains in proteins: Arg, Lys, Asp, Glu and His. Further generalization of the radii for charged species would require a more extensive parameterization. One reason for this is the expected effects on the neighbor atoms of polarizability reduction through the strong induction caused by the charged site. Generalizing it would require a more extensive parameterization.

4.1.3 Polarizability tensors

The G1 parameterizations clearly showed the capacity of EPIC to produce accurate polarizabilities with a minimum of atom types. The choice of ε_in and A combinations made based on the very small range-finding subset, showed the same behavior in the polarizability training dataset, the polarizability validation dataset and their combination (polarizability dataset), made of 265, 442 and 707 molecules respectively. Table 2, which summarizes the errors, shows the accuracy of the obtained models. The G1-24 dataset has an unsigned average error of 2% on the average polarizability (eq. 13) and a 5% error on the anisotropy of the tensor (eq. 14). With other polarizable models, such a low level of error was obtained only when anisotropic atomic polarizabilities were fitted{Applequist(N-aryls), Birge, Miller, Roux(NMA)}, making their generalization very challenging. The other G1 models are worse, and as predicted from the range-finding study results shown in Figure 3, the G1-4 set is inadequate to reproduce the directional difference in the polarizability (the large δ_aniso values in Table 2). The error obtained on both the PTD and the PVD being similar is an indication that our radii are not overfit. Finally, the three directional polarizabilities (eigenvalues of the tensor) obtained for the 707 molecules (2121 data points) are compared to the corresponding B3LYP values in Figure 4 for 3 representative G1 sets. The excellent correlation is obvious for the G1-24 and G1-12, and deteriorates in the G1-4 EPIC model. An apparent outlier is the α₃ (longitudinal polarizability) of (3E)-hexa-1,3,5-triene for which B3LYP gives a value of 176 a.u. compared to the EPIC value of 125 a.u. For this specific molecule, Sekino et al.{107} showed that B3LYP greatly overestimates the α₃ value of acetylene chains. Their better estimate, based on very accurate CCSD and MP2 QM results, predicts a value of ~135 a.u. Another remarkable discrepancy between EPIC and B3LYP is observed in Figure 4 for the α₃ of 1,4-dioxidopyrazine (doubly oxidized nitrogen on pyrazine) that is predicted to be 103 a.u. by the G1-12 model versus 129 a.u. by B3LYP. A similar observation can be made for 4-nitroaniline. Although we have not found better estimates for these molecules, they most certainly constitute a challenge both for classical and ab initio polarizability calculations.

Table 2.

Error obtained with the optimized polarization radii of the G1 sets when EPIC molecular polarizability tensors are compared to B3LYP for different molecule datasets.

Modela	δavg (%)	δaniso (%)	RRMS (%)
Polarizability training dataset: 265 molecules
G1-4	5.0	20.9	12.7
G1-9	3.2	9.1	6.7
G1-12	2.9	5.3	5.0
G1-24	2.3	5.2	4.4
Polarizability validation dataset: 442 molecules
G1-4	4.0	18.2	12.3
G1-9	2.7	7.6	6.7
G1-12	2.6	5.1	5.3
G1-24	2.1	5.4	4.6
Polarizability dataset: 707 molecules
G1-4	4.4	19.2	12.4
G1-9	2.9	8.2	6.7
G1-12	2.7	5.2	5.2
G1-24	2.2	5.4	4.6

^aModel using the parameters given in Table 1.

Figure 4.

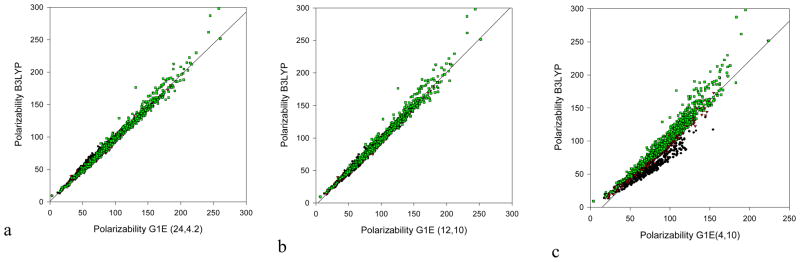
Correlation graph between the B3LYP/aug-cc-pVTZ directional polarizabilities (α₁ black circles, α₂ red triangles, α₃ green squares) for three G1 dielectric parameter sets (c.f. Table 1). Each figure shows the data for 707 molecules for a total of 2121 points. From these figures, it is clear that a small number of parameters (optimized on 265 molecules) can generalize well. A large ε_in= 24 (a) produces the best fit, a medium range ε_in= 12 produces slightly larger discrepancies and a small ε_in= 4 produces significantly larger deviations.

4.2 Refractive indices

In the previous subsection, we have developed dielectric functions that predict remarkably well, relative to QM, the polarizabilities of a single molecule in the gas phase. In this section we present the macroscopic refractive index calculations and the corresponding effective high frequency limit dielectric (ε_∞). In a previous publication{151}, we proposed that the vacuum of the intermolecular spacing may be sufficient to reduce the effective ε_∞ resulting from the high ε_in obtained in the optimization to polarizability tensors. Here we use a theoretical approach to verify this hypothesis. Another important point addressed by the refractive index calculation is the transferability of the dielectric function from the gas phase to the condensed phase.

As explained in further details in the Theory and Method sections, we form liquid droplets containing thousands of molecules from snapshots obtained by MD simulations and calculate the effective ε_∞ by the use of the Clausius-Mossoti equation. The small range spanned by experimental refractive indices makes this test somewhat stringent. Figure 5 shows the correlation between the results obtained with three representative EPIC parameterizations and experiment. The first observation is the close agreement between the magnitudes of the numbers that clearly demonstrate that the effective ε_∞ of the liquid droplets have the appropriate value in spite of the high ε_in, confirming our previous assertion. Also noticeable is that the correlation with experiment follows the previous assessment of the models based on molecular polarizabilities: the G1-24 parameterization (Figure 5a), has a R² of 0.899, slightly better than the G1-12 (Figure 5b) with R²=0.877, which is in turn significantly better than the G1-4 correlation with R²=0.734 (Figure 5c). However, Figure 5 shows a 0.05 systematic overestimation of the refractive indices which could correspond to a small overpolarization. The source for this deviation is not exactly clear to us, but we have few hypotheses. Firstly, the Clausius-Mossoti equation is valid for a perfect sphere whereas we are dealing with an imperfect surface created by nanoscopic droplets. Secondly, we have verified that an underestimation of the droplet radius by 3–4% (1Å in a range of 25–35Å) could systematically shift the calculated refractive indices by 0.05. Thirdly, it is also possible that the liquid phase polarizability may be truly smaller than the predicted gas phase polarizability since a drop of 11% of the polarizability could explain the 0.05 shift. This would be in agreement with other studies that found similar phenomena{202,194,17} and based their reasoning on the increased Pauli exchange repulsion from the closer contact of the molecules in condensed phase. The magnitude of this effect however differs considerably from study to study.

Figure 6 provides a visual explanation for the apparent mismatch between the small effective ε_∞ compared to the productives ε_in. This figure shows the molecular dielectric inside a CCl₄ droplet when it is sliced through its center. The G1-24, G1-12 and G1-4 models have a quite variable intermolecular space. The coloring scheme of the dielectric function (eq. 1) is such that red is assigned when ε(r) = ε_in and dark blue when ε(r) = 1. The intermolecular space increases with ε_in as the atomic radii decrease. It is striking that these three parameterizations produce the same refractive index, the same molecular polarizability and this in spite of the very different ε_in. Of course, if ε_in is further reduced, the whole droplet will be filled with a uniform dielectric (as the atomic radii increase and start to overlap) and the simultaneous prediction of the molecular polarizability and the refractive index gets compromised.

Figure 6.

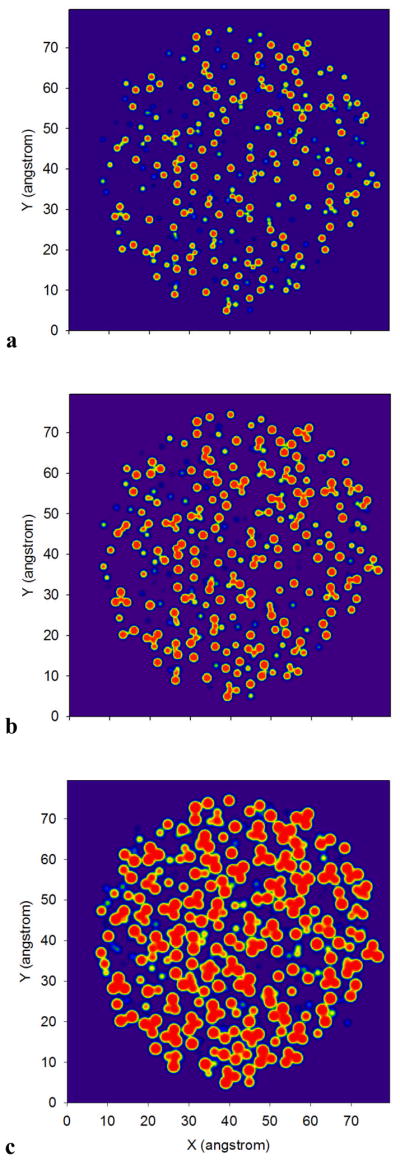
One of the 50 CCl₄ droplets is cut in its center and three dielectric functions (eq. 1) are plotted: a) G1-24 b) G1-12 and c) G1-4. The red color is attributed to ε(r)=ε_in and blue to ε(r)=1.

4.3 Hydration free energies

The hydration free energies are calculated with several solute models as can be found in Table 3. Each of the solute model is used to optimize the parameters in the second Gaussian summation in eq. 3 (noted G2), mainly the solvent cavity atomic radii (referred as cavity radii in what follows). We decided to set B = 11.8 in all calculations, following the Grant et al.{} suggestion as it was found to make the Bondi radii{} optimally reproducing the hard dielectric boundary results with the same smooth boundary as used in this work. The results reported in Table 3 are split into two main categories based on the method used to approximate ΔG_np. The surface area (SA) based method follows eq. 20 and required the optimization of the surface tension parameter (γ). The main effort here is however concentrated on the evaluation of ΔG_np by the Alchemical method{}, which is based on a more physical free energy perturbation (FEP) technique. This is the first category of results that we examine below.

Table 3.

Solvent cavity atomic radii (σ_cavity) and γ for the 3-zone dielectric model optimized on 485 experimental free energy of hydration with different G1-n solute models and ΔG_np sources

Modela:	G2-BCC	G2-HF	G2-1	G2-4	G2-12	G2-24	G2-12SA
	Solute
Chargesb	AM1-BCCe	HFc	B3LYPd	B3LYP	B3LYP	B3LYP	B3LYP	AM1-BCC
εinf	1	1	1	4	12	24	12	1
Af				10	10	4.19	10
Ref. Table 1			G1-1	G1-4	G1-12	G1-24	G1-12
ΔGnp	FEPg	FEP	FEP	FEP	FEP	FEP	SAh	SA
B	11.8	11.8	11.8	11.8	11.8	11.8	11.8	11.8
	Optimized implicit solvent parameters								Bondi
Hi	0.93	0.98	0.87	0.95	0.97	1.02	0.98	0.99	1.20
C	1.98	1.95	1.90	2.03	2.02	1.95	2.01	1.92	1.70
N	1.73	1.74	1.66	1.74	1.74	1.68	1.69	1.60	1.55
O	1.66	1.81	1.73	1.79	1.78	1.75	1.75	1.68	1.52
S	2.50	2.60	2.15	2.27	2.29	2.33	2.41	2.56	1.80
F	2.36	2.09	2.01	2.09	2.08	2.05	2.49	2.86	1.47
Cl	2.25	2.38	2.11	2.36	2.47	2.41	2.46	1.91	1.75
Br	1.42	2.18	2.06	2.23	2.46	2.45	2.63	1.69	1.85
γj							6.8	6.5
AUEk	0.95	1.06	1.05	0.99	1.04	1.08	1.13	0.91
Stdevl	0.81	1.00	0.97	0.96	0.99	1.00	0.90	0.74
RMSm	1.25	1.45	1.43	1.38	1.44	1.47	1.45	1.17
Rn	0.93	0.89	0.89	0.90	0.90	0.89	0.88	0.92
RRMSo	0.29	0.34	0.34	0.33	0.34	0.35	0.34	0.28
AEp	−0.26	−0.18	−0.15	−0.17	−0.17	−0.17	0.02	0.00

^aTag names for each of the optimized solvent cavity radii.

^bAtomic partial charges from an ESP-fit or a DRESP fit on the given quantum method.

^cPre-polarized charges from the AM1-BCC model{30,29}

^dPre-polarized charges from HF/6-31G(d,p)

^eVaccum charges from B3LYP/6-311++G(3df,3pd)

^fA and ε_in of eq. 3 for the solute internal dielectric. The atomic radii used in the internal dielectric are given in Table 1

^gΔG_np from free energy perturbation{226}

^hΔG_np calculated using the surface area (eq. 20) with the γ term optimized

ⁱAtomic radii are given in angstrom

^jNon-polar surface tension from eq. in cal/Ų

^kAverage unsigned error in kcal/mol

^lStandard deviation of the unsigned error

^mRoot-mean-square deviation in kcal/mol

ⁿPearson correlation coefficient

^oRelative root mean square deviation

^pAverage signed error in kcal/mol: experiment – calculated.

4.3.1 Results with FEP-based non-polar term

Two main classes of solute are studied as reported in Table 3. Firstly, we set ε_in = ε_trans = 1 in eq. 3, which effectively turns eq. 3 into a 2-zone dielectric function with a non-polarizable solute, as defined previously by Grant et al.{}. For the non-polarizable solute models, we use water polarized static atomic charges as given by AM1-BCC (G2-BCC optimized cavity radii) and the HF-6-31G(d,p) (G2-HF). These charge sets should produce the right level of static polarization of the solute in water. We also use charges obtained by fitting the B3LYP/6-311++G(3df,3pd) ESP that produces quite accurately the gas phase dipole moment of the molecules, being usually between 10% and 20% smaller than what is normally expected in water{}. This G2-1 set (the 1 indicates that the solute model is with ε_in=1) is a negative control as it should not be polar enough to induce the appropriate physical response from the solvent. The same B3LYP charge set is also used to fit the G2-n cavity radii that are now coupled with the corresponding Table 1 G1-n polarizable solute model where n = 4, 12 and 24. With these polarizable solutes, the gas phase derived atomic charges should produce naturally the right cooperative polarization of the solute and the solvent when the Poisson’s equation is solved.

It is quite interesting to observe in Table 3 that the same level of error over the 485 experimental free energies of hydration is obtained for the G2-HF, G2-1, G2-4, G2-12 and G2-24 solute models. The average unsigned error (AUE) compared to experiment is 1 kcal/mol with a standard deviation of 1 kcal/mol. The Pearson correlation coefficient (R) is around 0.89 in all these G2 models. The relative root-mean-square deviation (RRMS) obtained is 0.35 and the average signed error (AE) is found to be between −0.15 kcal/mol and −0.18 kcal/mol. The G2-BCC model gives the best fit to experiment with an AUE of 0.95 kcal/mol with a standard deviation of 0.81 kcal/mol, a R = 0.93, a RRMS = 0.29 and a RMS = 1.25 kcal/mol. It is possible that the special adjustment of oxygen and nitrogen BCCs (bound charge corrections) in the original parameterization of AM1-BCC to reproduce free energies of hydration be responsible for the better behavior of this charge set{Jakalian II}. These errors can be compared to the Rizzo et al.{} results, on almost the same dataset (460 neutral molecules included in the 485 that we use), that produce an AUE of 1.47 kcal/mol with RESP charges and R = 0.88. It is to be noted that these reported numbers were obtained with a SA evaluation of ΔG_np that allow them to subsequently optimize 14 atom typed surface tensions (γ), which improved the AUE to 1 kcal/mol while R = 0.89. For comparison, in the current study, we fit 8 atomic radii. In addition, the recent work of Mobley et al.{} on the same dataset as us (except for 19 additional molecules they use), obtained a root-mean-square deviation of 2.05 kcal/mol while they used the Bondi radii and the single γ fitted by Rizzo et al. Finally, in a different article, Mobley et al.{JCTC ASAP} obtained a RMS of 1.26 kcal/mol and R = 0.89 with explicit solvent converged Alchemical calculations. The FEP based ΔG_np used in this work are coming from this latter study. Our results are comparable or better to most other studies. We attribute the small errors to the optimization of the radii, not necessarily to the quality of the solute model. The fact that all the G2-n models are more or less giving the same quality of fit reflects the flexibility of implicit solvent models and the compensatory effect between solute atomic charges magnitude and cavity size. We can however examine the fitted cavity radii with the different solute models to understand the effects of the electrostatic model on the optimal solute cavity size.

The level of solute polarization brought by the polarizable solute models (G2-4 to G2-24) seems similar to what is obtained with the G2-HF solute model. This can be assessed by comparing the atomic radii and the cross-validation error showed in Table 4 where the G1-12 solute model is used with the different G2 radii sets. The level of error produced when n=4, 12 and 24 or with the G2-HF cavity radii is similar, the G2-4 being the worst. However, the level of error is significantly higher when the gas phase charges (the negative control) are used without polarizability in the G2-1 cavity radii set. In other words, the solute model obtained with pre-polarized atomic charges or with gas phase charges in a polarizable solute perform similarly. To understand this result, it suffices to note the systematically smaller cavity radii in the G2-1 column of Table 3. Indeed, the too small solute polarity is compensated by smaller cavity radii that enlarge the solvent response by a) exposing the solvent dielectric continuum to stronger solute field (as it is closer to the atomic charges) and b) by reducing the solute atomic charges to solvent bound charges distance. The cross-validation results of Table 4 also show the transferability of the third zone dielectric parameters given that the solute has the physically appropriate electrostatic behavior. A possible advantage of the polarizable solute model is when the solvation free energies are computed with a solvent other than water. In this case, one may think that the HF based charges may not be appropriate.

Table 4.

Effects of using different solvent cavity radii set (Table 3) with the G1-12 solute model (Table 1) on ΔG_hyd

	G2-12	G2-24	G2-4	G2-HF	G2-1
AUEa	1.04	1.08	1.17	1.10	1.83
Stdevb	0.99	1.03	1.19	1.01	1.47
Rc	0.90	0.90	0.86	0.89	0.89
RRMSd	0.34	0.35	0.39	0.35	0.55
AEe	−0.17	0.16	−0.23	0.15	1.50

^aAverage unsigned error in kcal/mol

^bStandard deviation on the AUE

^cPearson correlation coefficient

^dRelative root-mean-square deviation

^eAverage signed error in kcal/mol: experiment - calculated

The fitted radii of Table 3 are significantly different from the contact Bondi radii reported in the last column. Firstly, the H radius is a little smaller than the usual 1.1 Å contact radius in all cases (H Bondi radius was recognized to be a little too large and was revised to be 1.1 Å {Bondi, Roland & Taylor}). The carbon radius obtained here is much larger than the Bondi radius and make the C-H bonds behave like a united atom model. In this perspective the carbon radius size obtained here is similar to the Nina et al.{} carbon radius they calculated by looking at MD water charge density in explicit solvent simulations. For the other elements, we also find larger radii than Bondi. It is in agreement with a recent study by Nicholls et al.{}. This result can be rationalized by considering the difference between contact radii (Bondi) and the cavity radii needed in implicit solvent calculations. The former defines a zone where the hard sphere atomic radii of neighbor molecules do not interpenetrate and the latter defines where the mean solvent charge density appears. Indeed, the implicit solvent polarization conceptually results from the response of the explicit solvent molecules that adopt configurations with some charge excess when the thermal fluctuations do not average them to zero. Since the charge density around an atom in a solvent molecule is not uniformly distributed inside the contact volume, but more concentrated closer to the nuclei, it seems reasonable that the effective cavity radii be larger than the contact radii. This is illustrated in Figure 7, but a more quantitative assessment of this can be found elsewhere{Nina}. Although we claim here that having cavity radii larger than Bondi radii may be physically motivated, it is not possible at this stage to know if this effect should be as large as we find. In particular, the fluorine radii in Table 3 are surprisingly large. This was also found by Nicholls et al.{} where their optimal fluorine radius was 2.4 Å. Knowing that fluorine is particularly hydrophobic, this may be just another peculiar behavior of this atom. It seems also here that the AM1-BCC charging scheme gave significantly larger F radius as it may lead to more polar C-F bonds than the other charging methods. The Cl and Br radii difference in the G2-4, G2-12 and G2-24 sets uncover a drawback of using a small ε_in. Because the polarization radius of Cl and Br are larger in the G1-4 than in the other EPIC parameterizations, the transition zone shown in Figure 2 cannot reach ε(r) = 1 (in the case of Br, it goes down to ε(r) = 3) and the full polarizability coming from the halogen atom is not reached as the solvent cuts the first zone dielectric function. This prevents enough solute bound charge density to build up. Finally, the ordering of the halogen radii obtained in the G2-BCC optimization is also counter-intuitive. We noticed that the dipole moments of bromo-alkanes are systematically smaller with the AM1-BCC charges than with the other charge sets. The exact nature for this trend is not clear but must be due to the difference in the atomic partial charge generation.

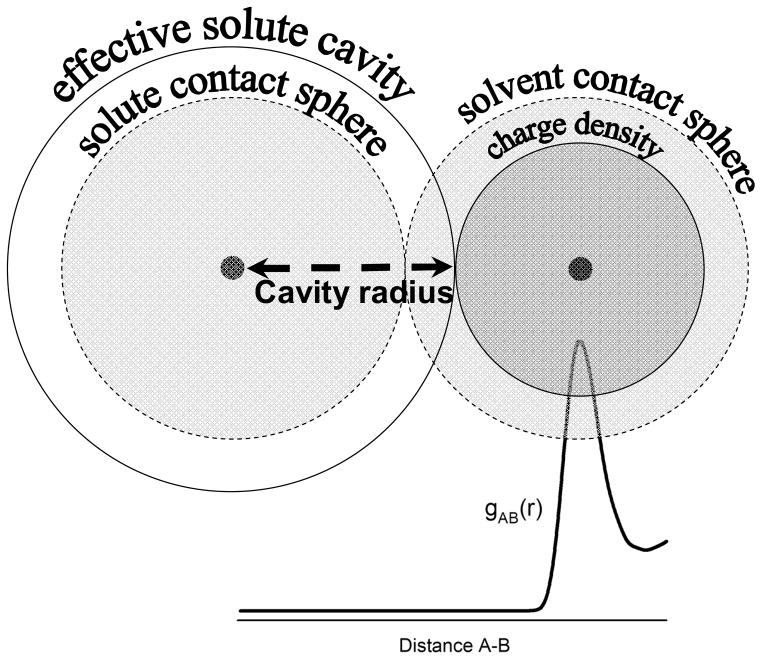
Figure 7.

The difference between the solute cavity radius and the contact radius is illustrated. The pair distribution function g_AB(r) shows the nuclei to nuclei distance distribution from the thermal averaging. Because the solvent charge density from electronic density and atomic nuclei is more concentrated closer to the nuclei, the solvent bound charge density in implicit solvent should appear not closer than where the solvent charges can get. As such, the cavity radii should have a tendency to be larger than the contact radii.

4.3.2 Results with surface area-based non-polar term

Although the use of FEP based ΔG_np may be more physically grounded, the obtained models cannot advantageously be used in a prospective manner. For this reason, we also optimized the cavity radii and the surface tension with the G1-12 and AM1-BCC based solute models. In these calculations the molecular surface area is calculated with the Bondi radii and kept constant. The results are reported in Table 3. The overall best results are obtained with the non-polarizable AM1-BCC/SA model that gives: AUE = 0.91 kcal/mol with standard deviation of 0.74 kcal/mol, R = 0.92, RRMS = 0.28, RMS = 1.17 kcal/mol and AE = 0.00 kcal/mol. These error levels are better than those obtained with a full FEP calculation{Mobley}. The G2-12/SA model gives error levels a little larger than the G2-12: AUE = 1.13 kcal/mol with a standard deviation of 0.90 kcal/mol, R = 0.88, RRMS = 0.34, RMS = 1.45 kcal/mol and AE = 0.02 kcal/mol. It is comforting that the optimal tension surfaces of the two optimizations are close to each other. The radii obtained for the G2-12/SA fit are similar to the G2-12 fit except for S, F, Cl and Br. It is possible that the hydrophobicity of these atoms be overestimated by the unique surface tension term used with the Bondi radii to determined Δ G_np.

5. Discussion

Integrate all the results that support the initial arguments (Introduction) and give a global picture.

• epsin=4 not a bad choice for free energy of hydration, but should not be used with Bondi radii. Tan and Luo have compensatory effects

• anisotropy does not seem to matter for free energy of hydration, but it may for intermolecular interaction, even when it happens in solvent

• fit of implicit solvent models only on exp. Free energy hydr. may be good for the wrong reasons

• 3-zone reduce the reentrant (artificial cavity) problem.

• Plug & play: optimization based on layers, each being physically grounded.