Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jun 27.
Published in final edited form as: J Biomech. 2013 Nov 11;47(9):2028–2034. doi: 10.1016/j.jbiomech.2013.10.054

Biomechanical and structural response of healing Achilles tendon to fatigue loading following acute injury

Benjamin R Freedman 1, Joseph J Sarver 1, Mark R Buckley 1,2, Pramod B Voleti 1, Louis J Soslowsky 1
PMCID: PMC4017004  NIHMSID: NIHMS541181  PMID: 24280564

Abstract

Achilles tendon injuries affect both athletes and the general population, and their incidence is rising. In particular, the Achilles tendon is subject to dynamic loading at or near failure loads during activity, and fatigue induced damage is likely a contributing factor to ultimate tendon failure. Unfortunately, little is known about how injured Achilles tendons respond mechanically and structurally to fatigue loading during healing. Knowledge of these properties remains critical to best evaluate tendon damage induction and the ability of the tendon to maintain mechanical properties with repeated loading. Thus, this study investigated the mechanical and structural changes in healing mouse Achilles tendons during fatigue loading. Twenty four mice received bilateral full thickness, partial width excisional injuries to their Achilles tendons (IACUC approved) and twelve tendons from six mice were used as controls. Tendons were fatigue loaded to assess mechanical and structural properties simultaneously after 0, 1, 3, and 6 weeks of healing using an integrated polarized light system. Results showed that the number of cycles to failure decreased dramatically (37-fold, p<0.005) due to injury, but increased throughout healing, ultimately recovering after 6 weeks. The tangent stiffness, hysteresis, and dynamic modulus did not improve with healing (p<0.005). Linear regression analysis was used to determine relationships between mechanical and structural properties. Of tendon structural properties, the apparent birefringence was able to best predict dynamic modulus (R2=0.88–0.92) throughout healing and fatigue life. This study reinforces the concept that fatigue loading is a sensitive metric to assess tendon healing and demonstrates potential structural metrics to predict mechanical properties.

INTRODUCTION

Achilles tendon ruptures result in significant pain and disability with long recovery times and affect between 5.5 and 9.9 per 100,000 individuals each year in North America (Suchak et al., 2005), and the incidence of these acute and chronic injuries is rising (Maffulli et al., 1999; Suchak et al., 2005). Although previous studies have aimed to elucidate the mechanisms of injury and healing, the basic science and efficacy behind many treatments and rehabilitation protocols for Achilles tendon ruptures remains “weak” or “inconclusive” as cited by a recent comprehensive review by the American Academy of Orthopaedic Surgeons (AAOS, 2009). Current clinical tests evaluating Achilles tendon injuries cannot rigorously evaluate tendon mechanical properties directly in vivo, and thus rely on surrogate measures such as the hop test to approximate tendon strength (Chiodo et al., 2010). Given that the Achilles tendon typically performs at high and repetitive loads at or near failure (Fukashiro et al., 1995; Komi et al., 1992), the clinical importance of utilizing methods to test this tendon at physiological levels via fatigue loading becomes increasingly evident (Dourte et al., 2012; Dunkman, 2012; Fessel and Snedeker, 2009; Fung et al., 2009; Ikoma et al., 2013; Schechtman and Bader, 1997, 2002; Wang et al., 1995; Wren et al., 2003).

Cadaveric and animal studies have shown that the response of tendon to fatigue loading is marked by changes in stiffness and deformation (among other properties) that consists of three phases (Figure 1A) (Fung et al., 2009; Wren et al., 2003). Specifically, tendon stiffness increases initially, reaches a maximum, and then gradually decreases. This gradual decrease in stiffness is attributed to accumulated sub-rupture damage, which ultimately leads to the dramatic increase in peak deformation and decrease in stiffness prior to failure (Fung et al., 2010; Fung et al., 2009; Wren et al., 2003). This induction of subfailure damage accumulation with repetitive loading is suggested as the primary benefit of fatigue testing over conventional quasi-static methods. Following injury, quasi-static test methods have shown decreased tissue stiffness, modulus, failure load, and increased tendon cross sectional area with healing (Gimbel et al., 2007). However, no study has examined whether these mechanical and structural property changes are also evident during fatigue loading and whether such assessment may be more indicative of in vivo tissue healing. Further, an often unstated assumption in histological studies of tendon healing is that alterations in tendon structure are closely associated with changes in tendon mechanical properties and function. Understanding how mechanical properties in injured tissue relate to changes in structure during healing in response to fatigue loading is therefore an important step to elucidating the mechanical and structural mechanisms leading to specimen failure and to better define benchmarks for mechanically robust tissue engineering constructs.

Figure 1.

Figure 1

Open in a new tab

(A) Typical mechanical response of a tendon undergoing fatigue loading. Briefly, changes in peak strain and stiffness undergo a three phase series of property changes leading to tendon rupture. 5%, 50%, 95% indicate the time points of fatigue life from which mechanical parameters were evaluated. (B) Typical displacement curve for an Achilles tendon during a ramp to failure. Dashed lines indicate the three loads that alignment maps were taken that approximate the toe, transition, and linear portions of the load displacement curve.

Therefore, the objectives of this study were to examine the mechanical and structural properties throughout the fatigue life of healing Achilles tendons, and to investigate whether structural properties assessed during fatigue loading could predict fatigue properties throughout healing. A mouse model was used to carefully control the injury and quantify tendon fatigue and structural properties using state-of-the-art mechanical testing techniques to evaluate fatigue mechanics and structure simultaneously. We hypothesized that fatigue loading would decrease mechanical properties (dynamic modulus, stiffness, hysteresis, peak strain, damage) in conjunction with altered structure (fiber realignment and birefringence) that partially recover with healing. We speculate that the new extracellular matrix synthesized through healing will increase tendon stiffness during fatigue loading. Our results should demonstrate the importance for fatigue and structural property assessment to evaluate tendon healing that may provide further benchmarks for image-based methods to assess tendon mechanical integrity.

METHODS

Study Design

A total of 60 tendons from 30 C57BL/6 mice were used in this University of Pennsylvania IACUC approved study. At approximately 120 days of age, 24 mice received bilateral excisional injuries to the midsubstance of their Achilles tendons under aseptic conditions (Beason et al., 2012). Briefly, a single skin incision parallel to the tibia and lateral to the Achilles tendon was made. A rubber-coated backing was placed deep to the Achilles tendon to provide support while a full thickness, partial width (~50%) region was excised using a 0.5 mm biopsy punch. Following the injury, the skin was closed with suture, and the animals returned to cage activity. To evaluate the effects of healing, 6 animals were euthanized at random after 0, 1, 3, and 6 weeks following injury and immediately frozen at −20°C.

Specimen Preparation and Tendon Mechanical Testing with Integrated Polarized Light Imaging

At the time of testing, animals were thawed and the Achilles tendon and calcaneus were carefully harvested, removing all musculature and surrounding soft tissue, and were hydrated in phosphate buffered saline (PBS). A laser device was used to measure tendon cross sectional area (Favata, 2006) and tendons were placed in custom fixtures to grip the calcaneus and tendon ends. Tendons were then tensile tested according to the following protocol in a PBS bath. Zero strain was set as the strain at preload. First, specimens were preconditioned between 0.1 and 0.2N at 0.5Hz for 30 cycles using a sinusoidal waveform on an Instron 5848 universal testing system (Instron Corp., Norwood, MA). To determine the necessary target loads for the load controlled fatigue test to simulate in vivo conditions, a preliminary study was conducted that determined the mean failure load of mouse Achilles tendons to be approximately 5N. Thus, during fatigue loading, specimens were cycled under load control between approximately 20 and 75% of their ultimate tensile strength (1–3.8N) at 1Hz until failure or 15,000 cycles. This upper cycle limit was determined from pilot tests to be an assumed theoretical endurance limit. During loading, force and displacement data were acquired at 100 Hz using the WaveMaker (Instron, Norwood, MA) data acquisition software and analyzed using custom MATLAB code (Mathworks, Natick, MA). Several post processing parameters were computed: 1) maximum/minimum cyclic displacement and strain, 2) tangent stiffness (calculated as the slope between the maximum and minimum force and displacements for each cycle), 3) stress (calculated as the force divided by the cross sectional area), 4) dynamic modulus (calculated as the slope between the maximum and minimum stress and strain for each cycle, 5) hysteresis (defined as the area enclosed by the stress-strain curve for a cycle), 6) damage (defined as the ratio of displacement and gauge length at a set threshold to the tissue displacement and displacement at a set threshold after the first cycle of fatigue loading) (Duenwald-Kuehl et al., 2012; Provenzano et al., 2002), and 6) cycles to failure (defined as the number of cycles until specimen failure).

Simultaneous evaluation of tendon structure via polarized light imaging was also conducted. This polarized light system (Lake et al., 2009) integrated with the mechanical testing system consisted of a backlight, 90º offset rotating polarizer sheets (Edmund Optics, Barrington, NJ) on both sides of the test sample (polarizer and analyzer), and a GigE aca2040gm camera (resolution: 2048×2048 pixels) (Basler, Exton, PA). Sets of alignment maps (15–18 images) were taken prior to fatigue loading, after 10, 25, 50 cycles of fatigue loading, and at intervals of 100 cycles at three distinct loads (0.1N, 1.0N, 2.4N). These loads were chosen to be indicative of the toe, transition, and linear regions of the mouse Achilles load displacement curve (Figure 1B), and were investigated to evaluate the sensitivity of structural properties to load. This protocol was fully automated during the fatigue tests using analog outputs acquired by a data acquisition device (USB 6008, National Instruments, Austin, TX) at 100Hz that was monitored by a custom Labview program (Version 8.6, National Instruments, Austin, TX). Following each test, an alignment map was acquired using a quarter-wave retarder (Edmund Optics, Barrington, NJ) to normalize tissue intensities to account for slight variations in light source intensity.

Polarized Light Image Analysis

A custom MATLAB program (MATLAB, Natick, MA) was used to divide the image into a series of regions of length 10 pixels and spacing of 20 pixels that were individually averaged to filter noise. From these data, the signal phase and magnitude within each region from each alignment image series were used to determine the circular standard deviation (CSD), a measure of collagen fiber disorganization (Lake et al., 2009), and the signal’s peak-to-peak intensity. Briefly, circular standard deviation is calculated by fitting a sin2 function (Glazer, 1996) to the pixel intensity-polarizer angle data to determine the angle corresponding to the minimum pixel intensity. This angle represents the average direction of fiber alignment. From photoelastic theory, the specimen’s peak-to-peak intensity and thickness can be related to determine tissue birefringence (Buckley et al., 2013a; Glazer, 1996; Timoshenko, 1969). Birefringence is a term used to describe the structural anisotropy of a tissue (i.e., the difference in index of refraction between its fast and slow axes) (Silva et al., 2013). As shown previously (Timoshenko, 1969), the intensity of light detected through the analyzer is given by the equation

Ic=Ipsin2(2α)sin2(Δ2) (1)

where Ic is the intensity of light detected by the camera, Ip is the intensity of light passing through the polarizer, α is the angle between P and the tendon’s slow axis (i.e., the aligned axis of the tendon), and Δ is the phase difference of light passing through the tendon. Since α varies from 0 to 360° as the polarizing sheets rotate during the test, Eq1 can be written as

Ip2p_t=Iosin2(Δ2) (2)

where Ip2p_t is the tendon peak-to-peak intensity of light detected by the camera, Io is the intensity of light passing through the polarizer, and Δ is the phase difference of light passing through the tendon. This phase difference Δ is related to the tissue birefringence (B), thickness (t), and wavelength (λ) of transmitted light as

Δ=2πBtλ (3)

Thus, a standardized peak-to-peak intensity, Ip2p* (Ip2p* = Ip2p_t/Ip2p_w), was computed for each specimen using the previously collected quarter wave plate peak-to-peak intensity (Ip2p_w) alignment maps. These equations assume that the initial thickness of the specimen determined from the optical-based method remains constant throughout the mechanical test. In addition, although π/λ is a scalar multiple for each specimen equivalent across all tests, we assumed λ to be 550nm as the mean wavelength of visible light. Given these assumptions, the apparent birefringence can be computed as

Bapp=λπtsin−1(Ip2p*) (4)

Statistical Analysis

One-way ANOVAs were used to determine whether mean mechanical and structural properties changed during healing. Properties that were significant were further analyzed with post hoc Student’s T-tests. Significance was set at α=0.05, with Bonferroni corrections applied to account for multiple comparisons. Next, single and multiple linear regressions (Enter Method, IBM SPSS Inc. Version 20, Armonk, New York), were completed to determine if mechanical fatigue properties could be predicted from structural properties.

RESULTS

Fatigue Mechanics

All animals who underwent surgery recovered well. The whole tendon mechanical properties measured in this study were peak strain, hysteresis, damage, dynamic modulus, tangent stiffness, and cycles to failure. Injury resulted in a significant increase in tendon cross sectional area at weeks 0, 1, 3, and 6 compared to control tissue (p<0.005; CTRL: 0.256± 0.047mm2, Week 0: 0.362 ± 0.040mm2, Week 1: 0.595 ± 0.166mm2, Week 3: 1.454 ± 0.829 mm2, Week 6: 1.056 ± 0.219mm2). In all tests, peak cyclic strain followed the three phase pattern for fatigue testing (e.g., Figure 1B), with no statistical differences in peak strain between groups at 5%, 50%, and 95% of fatigue life (Table 1). As hypothesized, injury caused a decrease in mechanical properties that was evident throughout fatigue loading. Specifically, the number of cycles to failure decreased dramatically after week 0 (CTRL: 12075±1872 cycles, Week 0: 325±311 cycles) (37 fold), p<0.001), and was not significantly different after 6 weeks of healing (Week 6: 7666±977 cycles) (Figure 2). In addition, and contrary to our hypothesis, the tangent stiffness decreased from control tissue by approximately 20–30% in healing tendons (Figure 3) and did not improve with healing when compared throughout fatigue life. Furthermore, hysteresis increased following injury, but declined as the stages of healing progressed (Table 1). As expected, damage increased with fatigue life (Table 1), but only differed statistically between healing time points at 5% of fatigue life.

Table 1.

Mechanical parameter comparisons throughout healing and fatigue life.

%Fatigue Life
Parameter Group 5% 5% 95%
Peak Strain (mm/mm) CTRL 0.195 ± 0.059 0.211 ± 0.062 0.225 ± 0.074
Week 0 0.190 ± 0.024 0.215 ± 0.029 0.248 ± 0.040
Week 1 0.293 ± 0.104 0.325 ± 0.116 0.361 ± 0.129
Week 3 0.324 ± 0.182 0.362 ± 0.197 0.406 ± 0.206
Week 6 0.244 ± 0.048 0.289 ± 0.067 0.319 ± 0.079
Hysteresis (MPa*mm/mm) CTRL 0.016 ± 0.004D,E 0.014 ± 0.004D,E 0.018 ± 0.003C,D,E
Week 0 0.026 ± 0.012D,e 0.021 ± 0.007e 0.035 ± 0.022d,e
Week 1 0.019 ± 0.011D 0.017 ± 0.009 0.020 ± 0.010A
Week 3 0.006 ± 0.003A,B,C,E 0.005 ± 0.003A 0.007 ± 0.004A,b
Week 6 0.005 ± 0.001A,b,D 0.005 ± 0.001A,b 0.006 ± 0.002A,b
Damage (mm/mm) CTRL 1.68 ± 0.88B 3.15 ± 0.82 4.67 ± 0.74
Week 0 0.55 ± 0.34A,D,E 2.56 ± 1.90 5.26 ± 3.14
Week 1 1.54 ± 1.38 2.96 ± 0.65 6.88 ± 4.32
Week 3 2.41 ± 1.15B 5.26 ± 2.81 8.29 ± 3.58
Week 6 2.43 ± 0.64B 5.99 ± 3.64 8.47 ± 4.93
Dynamic Modulus (MPa) CTRL 359.7 ± 98.0B,C,D,E 368.9 ± 103.0B,C,D,E 371.4 ± 109.9B,C,D,E
Week 0 179.7 ± 29.8A,C,D,E 167.8 ± 28.8A,C,D,E 146.8 ± 34.6A,D,E
Week 1 106.8 ± 31.2A,B,E 106.1 ± 33.1A,B,E 93.8 ± 39.0A,e
Week 3 64.0 ± 43.2A,B 61.6 ± 41.9A,B 53.7 ± 37.3A,B
Week 6 68.8 ± 18.4A,B,C 62.4 ± 17.2A,B,C 58.0 ± 17.0A,B,c
Open in a new tab
*A,B,C,D,E

denotes significant differences (p<0.005) from control, week 0, week 1, week 3, and week 6 specimens, respectively.

a,b,c,d,e

denotes a trend (p<0.01) from control, week 0, week 1, week 3, and week 6 specimens, respectively.

Figure 2.

Figure 2

Open in a new tab

Following injury, the number of cycles to failure decreased dramatically (37-fold, p<0.001), and eventually recovered by 6 weeks of healing. Solid lines indicate significant relationships. Dashed lines indicate trends. Final specimen cohorts ranged from N=6–10 specimens, since some specimens in the earlier time points were not able to withstand the fatigue testing protocol. Similarly, some control specimens reached a theoretical endurance limit.

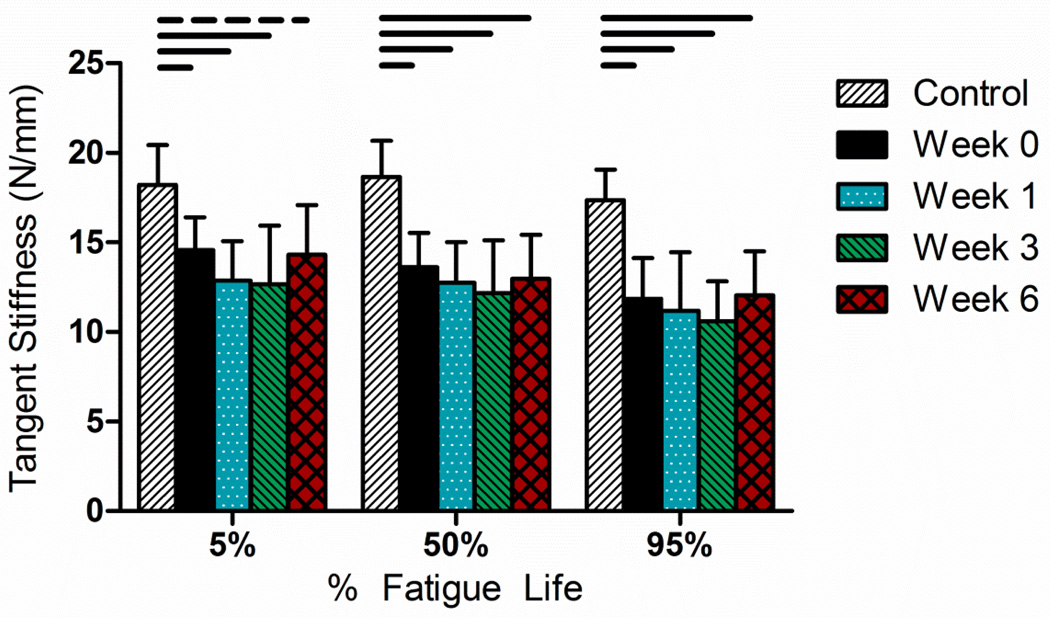
Figure 3.

Figure 3

Open in a new tab

Specimen tangent stiffness decreased following injury and this relationship remained consistent throughout fatigue life. On average, stiffness dropped by 25% and did not recover with healing. Final specimen cohorts ranged from N=6–10 specimens, since some specimens in the earlier time points were not able to withstand the fatigue testing protocol and some of the control specimens reached a theoretical endurance limit.

The dynamic modulus decreased following injury and did not recover with healing (Table 1). Specifically, the dynamic modulus was approximately 50% of control tendon following injury and 19% of control tendon by week 6 (Table 1). Taken together in the context of changes in tendon cross sectional area, this suggests that the initial decrease in tendon tangent stiffness was the primary contributor to a loss in modulus, and increases in tissue area due to scar tissue accumulation further degrade the dynamic modulus with healing.

Polarized light imaging

Injured tendon had increased CSD (i.e., increased disorganization) by weeks 1, 3, and 6 (p< 0.005, Figure 4A), and these changes in structure were observed throughout fatigue life at all loads tested (Figure S1). Following injury, Bapp decreased dramatically (Figure 4B) and did not demonstrate a return to control values with healing, during fatigue life, or at the different loads measured (Figure S2). Such changes could be due to the fact that tissue thickness alterations with healing were a dominant contributor to the birefringence calculations. The similar relationships in structural properties observed across loads and throughout tendon fatigue life primarily mirror alterations in mechanical properties with healing. However, because CSD and Bapp do not return to baseline levels, such properties are best suited to provide insight to early and moderate stage healing, rather than end stage healing. Interestingly, if Ip2p* was considered (that does not account for tendon thickness changes), induction of fatigue loading increased differences observed between control and healing tendons. For example, in the low load case, no deficit in structural properties was observed by week 6, but by 50% and 95% of the fatigue life, differences in structure between groups were evident (Figure S3). This increase in measured group differences may not be detected using standard histological tests or quasi-static mechanical testing, though the present study did not test this.

Figure 4.

Figure 4

Open in a new tab

Assessment of (A) circular standard deviation (CSD) and (B) the apparent birefringence (Bapp) throughout fatigue life and healing at 0.1 N. Together, these results demonstrate that the newly deposited matrix is highly disorganized throughout the specimen fatigue life. Final specimen cohorts ranged from N=4–10 specimens, since some specimens in the earlier time points were not able to withstand the fatigue testing protocol.

Linear and multiple regressions analysis

Structural properties were able to partially predict the full mechanical response of Achilles tendons to fatigue loading. In particular, Bapp strongly predicted dynamic modulus (R2 = 0.88–0.92) and moderately predicted hysteresis (R2 = 0.18–0.47) at all loads and throughout fatigue life (Table 2). Although damage, tangent stiffness, and peak strain had significant regressions with Bapp, these relationships were weak (Table 2, S1). CSD was also able to predict dynamic modulus at all loads and throughout fatigue life (R2 = 0.31–0.39, p<0.001, Table 2). At certain loads and stages of fatigue life, the tangent stiffness and hysteresis could be predicted by CSD (Table S1). Damage and peak strain showed similar relations to Bapp and CSD. Cycles to failure could not be predicted by any structural measure. For Bapp, all significant correlations between dependent and independent variables were positively correlated except damage and peak strain. For CSD, all significant correlations between dependent and independent variables were positively correlated except dynamic modulus, tangent stiffness, and hysteresis. As expected, these results indicate that a decrease in disorganization results in decreased damage and peak strain, and an increase in disorganization results in decreased dynamic modulus, tangent stiffness, and hysteresis. Interestingly, although Bapp and CSD were strong predictors for certain mechanical properties, coefficients of determination generally did not improve when the two were used together in a multiple regression model (Table S1). These results demonstrate that certain tissue level structural properties determined by image-based measure directly relate to ex vivo tendon fatigue mechanics.

Table 2.

Single linear regressions for structural and mechanical properties.

B CSD
Parameter r R2 p r R2 p
Dynamic Modulus (MPa) (0.94, 0.96) (0.88, 0.92) <0.001 (−0.56, −0.62) (0.31, 0.39) <0.001
Damage (mm/mm) (−0.35, −0.49) (0.12, 0.24) (NS, 0.009) (0.08, 0.29) (0.00, 0.08) NS
Tangent Stiffness (N/mm) (0.46, 0.65) (0.21, 0.42) (0.004, <0.001) (−0.24, −0.43) (0.05, 0.18) (NS, 0.007)
Peak Strain (mm/mm) (−0.40, −0.49) (0.16, 0.24) (0.013, 0.003) (0.05, 0.28) (0.00, 0.08) NS
Hysteresis MPa*mm/mm) (0.43, 0.69) (0.18, 0.47) (0.007, <0.001) (−0.27, −0.52) (0.07, 0.27) (NS, <0.001)
Cycles to Failure (0.21, 0.30) (0.05, 0.09) NS (−0.08, 0.17) (0.00, 0.03) NS
Open in a new tab
*

For each load, data are shown as ranges (min, max) between 5 and 95% of tendon fatigue life and all loads. Parameters with non-significant coefficients of determination are indicated as “NS.”

DISCUSSION

The purpose of this study was to characterize tendon mechanical and structural properties during fatigue loading following acute injury to the Achilles tendon. In doing so, our laboratory developed a novel ex vivo model to study changes in tendon mechanics and structure during simulated in vivo fatigue loading. This study provides a significant advancement to the tendon literature since quasi-static mechanical testing to evaluate the effects of healing may not capture the same sub-rupture induction mechanism acquired during fatigue loading (Shepherd and Screen, 2013). For tendons undergoing rigorous cyclic loading, such as the Achilles, it is of particular importance to accurately elucidate the fundamental mechanisms governing fatigue induced tendon failure. Knowledge of structural properties throughout fatigue loading and healing and their relationship to tendon mechanical properties further suggests potential metrics for image-based measures to assess tissue mechanical integrity and serve as benchmarks for tissue engineering strategies.

Despite a modest improvement in the number of cycles to failure with healing, the initial decrease in tangent stiffness, dynamic modulus, hysteresis, and damage with injury did not recover through 6 weeks of healing. These changes were in agreement with previous work that found that the modulus decreased throughout healing in conjunction with increased tendon cross sectional area (Beason et al., 2012; Gimbel et al., 2007). Thus, it is likely that a later healing time point may be necessary (e.g., 12 weeks) (Carpenter et al., 1998) to show full improved mechanical properties throughout fatigue life due to healing.

Changes in structural properties throughout fatigue life were less pronounced than previous reports of increased disorganization with fatigue loading (Parent et al., 2011; Sereysky et al., 2010; Shepherd and Screen, 2013). It is likely that majority of fatigue induced damage was not diffuse, as was likely done in these previous studies, rather that such changes were localized to the site of the excisional injury. Thus, the whole tissue response did not become as disorganized as was reported in previous studies (Parent et al., 2011; Sereysky et al., 2010; Shepherd and Screen, 2013). Tissue birefringence decreased in conjunction with an increase in the CSD following injury suggesting a decrease in the structural anisotropy of the tendon of collagen fibers deposited. The strong relationship between birefringence and dynamic modulus throughout healing was the first to be reported in tendon, but a similar moderate relationship was observed previously in mechanical evaluation of sclera (Nagase et al., 2013; Yamanari et al., 2012). Although Bapp and CSD were strong predictors of the dynamic modulus and moderate predictors of hysteresis, when they were used together in multiple regression analysis, their respective coefficients of determination did not advance, likely due to the fact that the two parameters are not independent. Additionally, since the regressions between structure and mechanics were similar across all loads and throughout fatigue life, this study demonstrates that such relationships are robust and should continue to be investigated. Although certain whole tissue structural properties correlated to mechanical parameters, the number of cycles to failure did not. This suggests that the structural mechanism governing this property originates from local damage accumulation rather than whole tissue level diffuse damage.

Several studies have used fatigue loading to induce damage in tissue (Fung et al., 2010; Fung et al., 2009; Sereysky et al., 2012; Wren et al., 2003), investigate theoretical endurance limits in tendon (Schechtman and Bader, 1997, 2002; Wang et al., 1995), quantify subsequent biological changes (Andarawis-Puri et al., 2012a; Andarawis-Puri et al., 2012b; Legerlotz et al., 2011), and identify potential causes of failure (Veres et al., 2013; Veres and Lee, 2012). Although the specific structural mechanisms leading to failure were not investigated in the current study, Veres and colleagues have suggested that repeated subrupture loading results in fibril denaturation events that form progressive fibril kinks and the accumulation of damage in bovine tail tendons (Veres et al., 2013; Veres and Lee, 2012). Such changes have been shown to primarily occur early during repeated loading (Veres et al., 2013), which was also observed in the current study. In addition, our laboratory has recently developed a novel method to investigate crimp during mechanical testing (Buckley et al., 2013a), which could be another imaged-based metric for subrupture damage accumulation. Still, other factors may contribute to the progression to failure in healing tissues, such as reductions in fibril continuity, and the role of glycosaminoglycans and other small matrix molecules (Ahmadzadeh H, 2013; Provenzano and Vanderby, 2006).

This study is not without limitations. The primary limitation is that no biological mechanisms were investigated that may further help elucidate the molecular events that govern changes in structural and mechanical properties during fatigue loading. For example, collagen type and other matrix components may be contributing factors to the overall tissue birefringence. Another potential limitation is that the injury made was acute and does not necessarily resemble the pattern seen in an acute Achilles rupture that may originate from preexisting damage. However, this injury method has previously been shown to be highly repeatable (Beason et al., 2012) and has been applied to study the dynamic properties of tendons (Dunkman, 2012). As mentioned previously, thickness measures during fatigue loading were assumed to remain constant to calculate Bapp. Interestingly, if assumptions regarding thickness are removed and Ip2p* is considered (Figure S3), it is observed that fatigue loading accentuates differences in structure observed during healing. For example, only evaluating the initial alignment maps prior to induction of fatigue loading may suggest partial tissue recovery of structural properties, however, following fatigue loading, decreased structural properties relative to control tissue become more evident. Despite the successful integration of polarized light imaging and mechanical testing systems in this study, we recognize that this imaging modality requires the transmission of light through tendon, which becomes increasingly difficult for thicker tendons in larger animals. Still, for the appropriate model systems, polarized light imaging remains a cost efficient and effective tool to study structural changes during loading (Buckley et al., 2013b; Lake et al., 2009; Miller et al., 2012; Quinn and Winkelstein, 2008). In addition, we recognize that in biological studies both limbs are typically not used based on an assumption that the two measurements are not statistically independent, and that this is a potential limitation of the current study. However, in the case that multiple limbs from the same animal were used in a given treatment group, we found that the variation within animals was not less than the variation for the group across animals for the mechanical and imaging properties of highest importance to the study (i.e., tangent stiffness, dynamic modulus, CSD, and Bapp) supporting the fact that data from two limbs of the same animal is no less independent than data from different animals. Therefore, we are confident that both limbs can be treated independently in this study. Future studies will investigate regional changes to the injury site that may further enhance the ability of measured structural properties to predict mechanical properties that may be reduced by averaging throughout the entire tissue. Work is being completed to develop a healing model (Buckley MR, 2013; Duenwald-Kuehl et al., 2012) that can predict mechanical properties throughout healing from structural properties.

In conclusion, this was the first study evaluate the effects of injury and healing on the fatigue properties in tendon. While decreases in tangent stiffness, dynamic modulus, and hysteresis are detected during healing, the most sensitive measure was cycles to failure. Knowledge that measured tendon stiffness drops by 25% whereas the number of cycles to failure decreases by nearly 37-fold was not expected and importantly, demonstrates that tissue properties only assessing stiffness metrics may provide an incomplete description of actual tissue healing. Thus, this information obtained at the early stages of healing is critical to fully characterize the healing response. The structural parameters Bapp and CSD show promise as potentially translatable metrics to predict tendon dynamic modulus and hysteresis, yet the majority of mechanical parameters could only be predicted weakly, suggesting the need for additional experiments investigating structure-function relationships in tendon studying the response to fatigue loading.

Supplementary Material

01
02
03
04

ACKNOWLEDGEMENTS

This study was supported by an NSF Graduate Research Fellowship and the NIH/NIAMS. We thank Andrew Dunkman for surgical assistance and Dr. Michael Hast for valuable discussion and machine shop assistance.

Grant Support: This study was funded by an NIH/NIAMS supported Penn Center for Musculoskeletal Disorders (NIH, P30 AR050950) and a National Science Foundation Graduate Fellowship.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Study approved by: University of Pennsylvania IACUC

CONFLICTS OF INTEREST

The authors have no conflicts of interest to report.

REFERENCES

  1. AAOS. Guideline on the Diagnosis and Treatment of Acute Achilles Tendon Rupture. 2009 [Google Scholar]
  2. Ahmadzadeh H, C B, Freedman BR, Soslowsky LJ, Shenoy VB. Determining the Contribution of Glycosaminoglycans to Tendon Mechanical Properties with a Modified Shear-Lag Model. Journal of Biomechanics. 2013 doi: 10.1016/j.jbiomech.2013.07.008. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Andarawis-Puri N, Sereysky JB, Jepsen KJ, Flatow EL. The relationships between cyclic fatigue loading, changes in initial mechanical properties, and the in vivo temporal mechanical response of the rat patellar tendon. J Biomech. 2012a;45:59–65. doi: 10.1016/j.jbiomech.2011.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andarawis-Puri N, Sereysky JB, Sun HB, Jepsen KJ, Flatow EL. Molecular response of the patellar tendon to fatigue loading explained in the context of the initial induced damage and number of fatigue loading cycles. J Orthop Res. 2012b;30:1327–1334. doi: 10.1002/jor.22059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Beason DP, Kuntz AF, Hsu JE, Miller KS, Soslowsky LJ. Development and evaluation of multiple tendon injury models in the mouse. J Biomech. 2012 doi: 10.1016/j.jbiomech.2012.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buckley MR, D A, Reuther KE, Kumar AK, Pathmanathan L, Beason DP, Birk DE, Soslowsky LJ. Validation of an Empirical Damage Model for Aging and In Vivo Injury of the Murine Patellar Tendon. Journal of Biomechanical Engineering. 2013;135 doi: 10.1115/1.4023700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buckley MR, Sarver JJ, Freedman BR, Soslowsky LJ. The dynamics of collagen uncrimping and lateral contraction in tendon and the effect of ionic concentration. J Biomech. 2013a doi: 10.1016/j.jbiomech.2013.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Buckley MR, Sarver JJ, Freedman BR, Soslowsky LJ. The dynamics of collagen uncrimping and lateral contraction in tendon and the effect of ionic concentration. J Biomech. 2013b;46:2242–2249. doi: 10.1016/j.jbiomech.2013.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Carpenter JE, Thomopoulos S, Flanagan CL, DeBano CM, Soslowsky LJ. Rotator cuff defect healing: a biomechanical and histologic analysis in an animal model. J Shoulder Elbow Surg. 1998;7:599–605. doi: 10.1016/s1058-2746(98)90007-6. [DOI] [PubMed] [Google Scholar]
  10. Chiodo CP, Glazebrook M, Bluman EM, Cohen BE, Femino JE, Giza E, Watters WC, 3rd, Goldberg MJ, Keith M, Haralson RH, 3rd, Turkelson CM, Wies JL, Raymond L, Anderson S, Boyer K, Sluka P American Academy of Orthopaedic, S. Diagnosis and treatment of acute Achilles tendon rupture. The Journal of the American Academy of Orthopaedic Surgeons. 2010;18:503–510. doi: 10.5435/00124635-201008000-00007. [DOI] [PubMed] [Google Scholar]
  11. Dourte LM, Pathmanathan L, Jawad AF, Iozzo RV, Mienaltowski MJ, Birk DE, Soslowsky LJ. Influence of decorin on the mechanical, compositional, and structural properties of the mouse patellar tendon. J Biomech Eng. 2012;134:031005. doi: 10.1115/1.4006200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Duenwald-Kuehl S, Kondratko J, Lakes RS, Vanderby R., Jr Damage mechanics of porcine flexor tendon: mechanical evaluation and modeling. Ann Biomed Eng. 2012;40:1692–1707. doi: 10.1007/s10439-012-0538-z. [DOI] [PubMed] [Google Scholar]
  13. Dunkman B, Adams Mienaltowski, Satchell Thomas, Pathmanathan Kumar, Iozzo Beason, Soslowsky Birk. Decorin Expression Is Required for Age-Related Changes in Tendon Structure and Mechanical Properties Matrix Biol. 2012 doi: 10.1016/j.matbio.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Favata M. Scarless Healing in the Fetus: Implications and Strategies for Postnatal Tendon Repair. University of Pennsylvania; 2006. [Google Scholar]
  15. Fessel G, Snedeker JG. Evidence against proteoglycan mediated collagen fibril load transmission and dynamic viscoelasticity in tendon. Matrix Biol. 2009;28:503–510. doi: 10.1016/j.matbio.2009.08.002. [DOI] [PubMed] [Google Scholar]
  16. Fukashiro S, Komi PV, Jarvinen M, Miyashita M. In vivo Achilles tendon loading during jumping in humans. Eur J Appl Physiol Occup Physiol. 1995;71:453–458. doi: 10.1007/BF00635880. [DOI] [PubMed] [Google Scholar]
  17. Fung DT, Wang VM, Andarawis-Puri N, Basta-Pljakic J, Li Y, Laudier DM, Sun HB, Jepsen KJ, Schaffler MB, Flatow EL. Early response to tendon fatigue damage accumulation in a novel in vivo model. J Biomech. 2010;43:274–279. doi: 10.1016/j.jbiomech.2009.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fung DT, Wang VM, Laudier DM, Shine JH, Basta-Pljakic J, Jepsen KJ, Schaffler MB, Flatow EL. Subrupture tendon fatigue damage. J Orthop Res. 2009;27:264–273. doi: 10.1002/jor.20722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gimbel JA, Van Kleunen JP, Williams GR, Thomopoulos S, Soslowsky LJ. Long durations of immobilization in the rat result in enhanced mechanical properties of the healing supraspinatus tendon insertion site. J Biomech Eng. 2007;129:400–404. doi: 10.1115/1.2721075. [DOI] [PubMed] [Google Scholar]
  20. Glazer A, Lewis JG, Kaminsky W. An Automatic Optical Imaging System for Birefringent Media. Proceedings: Mathematical, Physical and Engineering Sciences. 1996;452:2751–2765. [Google Scholar]
  21. Ikoma K, Kido M, Nagae M, Ikeda T, Shirai T, Ueshima K, Arai Y, Oda R, Fujiwara H, Kubo T. Effects of stress-shielding on the dynamic viscoelasticity and ordering of the collagen fibers in rabbit Achilles tendon. J Orthop Res. 2013 doi: 10.1002/jor.22424. [DOI] [PubMed] [Google Scholar]
  22. Komi PV, Fukashiro S, Jarvinen M. Biomechanical loading of Achilles tendon during normal locomotion. Clin Sports Med. 1992;11:521–531. [PubMed] [Google Scholar]
  23. Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Effect of fiber distribution and realignment on the nonlinear and inhomogeneous mechanical properties of human supraspinatus tendon under longitudinal tensile loading. J Orthop Res. 2009;27:1596–1602. doi: 10.1002/jor.20938. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Legerlotz K, Jones GC, Screen HR, Riley GP. Cyclic loading of tendon fascicles using a novel fatigue loading system increases interleukin-6 expression by tenocytes. Scand J Med Sci Sports. 2011 doi: 10.1111/j.1600-0838.2011.01410.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Maffulli N, Waterston SW, Squair J, Reaper J, Douglas AS. Changing incidence of Achilles tendon rupture in Scotland: a 15-year study. Clin J Sport Med. 1999;9:157–160. doi: 10.1097/00042752-199907000-00007. [DOI] [PubMed] [Google Scholar]
  26. Miller KS, Connizzo BK, Feeney E, Soslowsky LJ. Characterizing local collagen fiber realignment and crimp behavior throughout mechanical testing in a mature mouse supraspinatus tendon model. J Biomech. 2012;45:2061–2065. doi: 10.1016/j.jbiomech.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Nagase S, Yamanari M, Tanaka R, Yasui T, Miura M, Iwasaki T, Goto H, Yasuno Y. Anisotropic alteration of scleral birefringence to uniaxial mechanical strain. PLoS One. 2013;8:e58716. doi: 10.1371/journal.pone.0058716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Parent G, Huppe N, Langelier E. Low stress tendon fatigue is a relatively rapid process in the context of overuse injuries. Ann Biomed Eng. 2011;39:1535–1545. doi: 10.1007/s10439-011-0254-0. [DOI] [PubMed] [Google Scholar]
  29. Provenzano PP, Heisey D, Hayashi K, Lakes R, Vanderby R., Jr Subfailure damage in ligament: a structural and cellular evaluation. J Appl Physiol. 2002;92:362–371. doi: 10.1152/jappl.2002.92.1.362. [DOI] [PubMed] [Google Scholar]
  30. Provenzano PP, Vanderby R., Jr Collagen fibril morphology and organization: implications for force transmission in ligament and tendon. Matrix Biol. 2006;25:71–84. doi: 10.1016/j.matbio.2005.09.005. [DOI] [PubMed] [Google Scholar]
  31. Quinn KP, Winkelstein BA. Altered collagen fiber kinematics define the onset of localized ligament damage during loading. J Appl Physiol (1985) 2008;105:1881–1888. doi: 10.1152/japplphysiol.90792.2008. [DOI] [PubMed] [Google Scholar]
  32. Schechtman H, Bader DL. In vitro fatigue of human tendons. J Biomech. 1997;30:829–835. doi: 10.1016/s0021-9290(97)00033-x. [DOI] [PubMed] [Google Scholar]
  33. Schechtman H, Bader DL. Fatigue damage of human tendons. J Biomech. 2002;35:347–353. doi: 10.1016/s0021-9290(01)00177-4. [DOI] [PubMed] [Google Scholar]
  34. Sereysky JB, Andarawis-Puri N, Jepsen KJ, Flatow EL. Structural and mechanical effects of in vivo fatigue damage induction on murine tendon. J Orthop Res. 2012;30:965–972. doi: 10.1002/jor.22012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sereysky JB, Andarawis-Puri N, Ros SJ, Jepsen KJ, Flatow EL. Automated image analysis method for quantifying damage accumulation in tendon. J Biomech. 2010;43:2641–2644. doi: 10.1016/j.jbiomech.2010.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Shepherd JH, Screen HR. Fatigue loading of tendon. Int J Exp Pathol. 2013;94:260–270. doi: 10.1111/iep.12037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Silva DF, Gomes AS, de Campos Vidal B, Ribeiro MS. Birefringence and second harmonic generation on tendon collagen following red linearly polarized laser irradiation. Ann Biomed Eng. 2013;41:752–762. doi: 10.1007/s10439-012-0720-3. [DOI] [PubMed] [Google Scholar]
  38. Suchak AA, Bostick G, Reid D, Blitz S, Jomha N. The incidence of Achilles tendon ruptures in Edmonton, Canada. Foot Ankle Int. 2005;26:932–936. doi: 10.1177/107110070502601106. [DOI] [PubMed] [Google Scholar]
  39. Timoshenko S, Goodier JN. Theory of Elasticity. 3 ed. New York: McGraw-Hill; 1969. [Google Scholar]
  40. Veres SP, Harrison JM, Lee JM. Repeated subrupture overload causes progression of nanoscaled discrete plasticity damage in tendon collagen fibrils. J Orthop Res. 2013;31:731–737. doi: 10.1002/jor.22292. [DOI] [PubMed] [Google Scholar]
  41. Veres SP, Lee JM. Designed to fail: a novel mode of collagen fibril disruption and its relevance to tissue toughness. Biophys J. 2012;102:2876–2884. doi: 10.1016/j.bpj.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Wang XT, Ker RF, Alexander RM. Fatigue rupture of wallaby tail tendons. J Exp Biol. 1995;198:847–852. doi: 10.1242/jeb.198.3.847. [DOI] [PubMed] [Google Scholar]
  43. Wren TA, Lindsey DP, Beaupre GS, Carter DR. Effects of creep and cyclic loading on the mechanical properties and failure of human Achilles tendons. Ann Biomed Eng. 2003;31:710–717. doi: 10.1114/1.1569267. [DOI] [PubMed] [Google Scholar]
  44. Yamanari M, Ishii K, Fukuda S, Lim Y, Duan L, Makita S, Miura M, Oshika T, Yasuno Y. Optical rheology of porcine sclera by birefringence imaging. PLoS One. 2012;7:e44026. doi: 10.1371/journal.pone.0044026. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS541181-supplement-01.docx (15.9KB, docx)
02
NIHMS541181-supplement-02.tif (13.9MB, tif)
03
NIHMS541181-supplement-03.tif (14.2MB, tif)
04
NIHMS541181-supplement-04.tif (14MB, tif)

RESOURCES