A Computational Study of Stress Fiber-Focal Adhesion Dynamics Governing Cell Contractility

Abstract

We apply a recently developed model of cytoskeletal force generation to study a cell’s intrinsic contractility, as well as its response to external loading. The model is based on a nonequilibrium thermodynamic treatment of the mechanochemistry governing force in the stress fiber-focal adhesion system. Our computational study suggests that the mechanical coupling between the stress fibers and focal adhesions leads to a complex, dynamic, mechanochemical response. We collect the results in response maps whose regimes are distinguished by the initial geometry of the stress fiber-focal adhesion system, and by the external load on the cell. The results from our model connect qualitatively with recent studies on the force response of smooth muscle cells on arrays of polymeric microposts.

Introduction

In contractile cells, such as smooth muscle cells and fibroblasts, the generation of traction force is the result of two different actions: myosin-powered cytoskeletal contractility and external mechanical stimuli (applied stretch or force). The cooperation between these two aspects determines the level of the force within the cell and influences the development of cytoskeletal components via the (un)binding of proteins. Stress fibers and focal adhesions are important cytoskeletal components that mediate this interplay of mechanics and chemistry.

Stress fibers are bundles of 10–30 actin filaments held together by the binding protein α-actinin (1); fascin, epsin, filamin, and myosin, among other proteins, have also been detected in stress fibers. Cytoskeletal contractility originates from the action of myosin molecules: these attach themselves to the actin filaments and step along them, causing antiparallel filaments to slide past each other, thus generating a contraction of the stress fiber. The speed at which filaments slide past each other decreases with tensile force (2). The myosin stepping rate reaches a stall at some critical value of tensile force, at which contractility ceases.

The binding rates of actin and myosin (and presumably of other proteins, also) into the stress fiber is force-dependent (3). Within some regime of tensile force autogenerated by stress fiber contractility, the binding rates appear to be boosted, and the fibers grow in thickness (4,5). Eventually, a sufficiently high force, perhaps externally applied, must cause rapid unbinding of the proteins and cytoskeletal disassembly. The complexity of this mechanochemical response is enhanced because the stress fibers also demonstrate, in addition to the aforementioned active response due to myosin action, a passive viscoelastic force-stretch behavior (6).

Focal adhesions are integrin-containing transmembrane structures that anchor the cytoskeletal stress fibers to the extracellular matrix (ECM). In addition to integrin, they contain scores of other proteins including paxillin, tensin, focal adhesion kinase, talin, and vinculin. The latter two proteins connect the integrins to f-actin in the stress fibers, to complete the linkage of the cytoskeleton to the ECM. However, focal adhesions are not merely static anchors. They themselves demonstrate a complex dynamics of growth, disassembly, and even a translational mode in which they appear to slide over the interface between the cell membrane and ECM, strikingly shown by Nicolas et al. (7). These regimes of the dynamics are caused by (un)binding of focal adhesion proteins, and notably are force-sensitive; cytoskeletal contractility forces as well as externally applied loads may elicit this mechanosensitive response (8,9).

It is inevitable that the combination of two such mechanochemically dependent systems (stress fibers and focal adhesions) in the cytoskeleton leads to a rich dynamic response, where the forces as well as the systems’ structures themselves continuously evolve. Some of these aspects have been addressed in the literature, and a variety of models have been proposed that study stress fibers and focal adhesions separately (10–16) or, in some cases, in combination (17–20). They focus on different aspects of the problem, such as cell traction (21), effects of substrate stiffness (22,23), cell shape (24), cell contractility (25), cytoskeletal orientation under dynamic load (13,26–28), and stress fiber viscoelasticity (6,25). Some studies also address the role of the small GTPases, Rho and Rac, in regulating stress fiber formation (29–31).

In this article, we use a recently developed model for the coupled mechanochemical response of stress fiber-focal adhesion systems to study the development of contractile force and the behavior of such systems under load. The model is based on nonequilibrium thermodynamics and has been described in detail (32). Our focus here is on the modes of generation and decay of the force in the system, as well as on the growth and disassembly of the stress fibers and focal adhesions. These questions are addressed in the context of both cell contractility in absence of external load and system response to an external stretch. Our motivation comes from studies of force generated by smooth muscle cells plated on micropost arrays (33); nevertheless, our model is capable of much greater detail than is accessible experimentally. The experiments demonstrate variability in the response both between cells and between individual stress fibers in the same cell and, accordingly, our aim is to reproduce the broad trends seen in the experiments and provide a key to interpret the response variability observed in the experiments, while examining in greater detail the underlying mechanochemical dynamics that the model reveals.

The Underlying Model

Calculations were carried out using a modified version of a model proposed in another work (32). The model does not include chemical signaling; it explicitly highlights the role of mechanical force as a signal instead. The original layout has been adapted to include the presence of elastic microposts, to simulate the behavior of the stress fiber-focal adhesion ensemble under the conditions of the experimental tests performed by Mann et al. (33). Specifically, the model adopted here (Fig. 1) consists of a stress fiber connected to a focal adhesion at each end, with each focal adhesion being attached to the top of a polydimethylsiloxane micropost, and an elastic (i.e., polydimethylsiloxane) substrate underlying the microposts. The cytosolic reservoir supplying proteins to the stress fiber and focal adhesions is also included. The substrate can be stretched to introduce an external mechanical loading of the system. The stress fiber and the focal adhesions are mechanochemical subsystems formed by assembly of representative proteins supplied by the cytosol.

Figure 1.

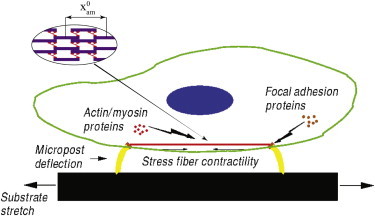
Schematic representation of the model. To see this figure in color, go online.

To substantiate the discussion of the results provided in this article, we briefly report the main concepts behind the model we adopted; further details can be found in the Supporting Material and elsewhere (Olberding et al. (34); Maraldi & Garikipati (32)). In the model, the stress fiber is considered to span between two focal adhesions and to be always under tension. Hence, its reference length, x⁰_sf, is fixed, because it would not be possible to add proteins at its ends without first abrogating the tension. Protein binding/unbinding therefore only affects the thickness of the stress fiber. However, protein binding/unbinding is allowed to occur anywhere along the focal adhesion; to compute the relevant kinematic quantities for this subsystem, only the binding rates at its ends need to be tracked. The force is assumed to be uniformly distributed along the focal adhesion and through the stress fiber’s thickness (32).

The number of stress fiber representative proteins (N_sf) and the focal-adhesion distal (x_d) and proximal ends’ (x_p) positions are the variables tracked with respect to time. The ordinary differential equations constituting the model are (Olberding et al. (34); Maraldi & Garikipati (32))

$${\dot{N}}_{sf}=\{\begin{array}{ll}{k}_{sf}^b\left(N_{sf}^{\text{max}}-N_{sf}\right)\left(1-e^{\left({\mu }_{sf}-{\mu }_{\text{cyt}}^{sf}\right)/k_{\text{B}}T}\right),\hfill & \left(b\right)\hfill \\ k_{sf}^u{e}^{{\chi }_{sf}}\left(e^{-\left({\mu }_{sf}-{\mu }_{\text{cyt}}^{sf}\right)/k_{\text{B}}T}-1\right),\hfill & \left(u\right)\hfill \end{array}$$ (1)

$${\dot{x}}_d=-{\lambda }^2\{\begin{array}{ll}{k}_{fa}^b\left(1-e^{\left({\mu }_{fa}^{\text{d}}-{\mu }_{\text{cyt}}^{fa}\right)/k_{\text{B}}T}\right),\hfill & \left(b\right)\hfill \\ k_{fa}^u{e}^{{\chi }_{fa}}\left(e^{-\left({\mu }_{fa}^d-{\mu }_{\text{cyt}}^{fa}\right)/k_{\text{B}}T}-1\right),\hfill & \left(u\right)\hfill \end{array}$$ (2)

$${\dot{x}}_p={\lambda }^2\{\begin{array}{ll}{k}_{fa}^b\left(1-e^{\left({\mu }_{fa}^p-{\mu }_{\text{cyt}}^{fa}\right)/k_{\text{B}}T}\right),\hfill & \left(b\right)\hfill \\ k_{fa}^u{e}^{{\chi }_{fa}}\left(e^{-\left({\mu }_{fa}^p-{\mu }_{\text{cyt}}^{fa}\right)/k_{\text{B}}T}-1\right),\hfill & \left(u\right)\hfill \end{array}$$ (3)

where the label (b) indicates the equations used for the case in which μ_α − μ^α_cyt ≤ 0 (proteins binding) for subsystem α = sf, fa, whereas (u) indicates the equations for the case in which μ_α − μ^α_cyt ≥ 0 (proteins unbinding). In Eq. 1, μ_sf is the chemical potential of representative proteins in the stress fiber, μ^sf_cyt is the chemical potential of stress fiber proteins in the cytosolic reservoir, and n_sf^max is the maximum number of stress fiber proteins available to the given stress fiber. In Eqs. 2 and 3, μ^d_fa and μ^p_fa are the chemical potentials of the proteins in the focal adhesion evaluated at its distal and proximal ends, respectively, μ^fa_cyt is their chemical potential in the cytosol, and λ is the size of a focal adhesion complex. For the detailed expressions of the chemical potentials, see the expressions in Eq. S1 in the Supporting Material. Moreover, k^b_α, k^u_α > 0 are, respectively, the binding and unbinding coefficients for subsystem α, k_B is the Boltzmann constant, and χ_α = χ_α (P) is a force-dependent exponent regulating the rapid dissociation of molecular bonds (G. Bell (35); Maraldi & Garikipati (32)). We note that the form of Eqs. 1–3 comes from classical nonequilibrium thermodynamics, and incorporates the assumption of local equilibrium (36).

Mechanical equilibrium is assumed to hold. Hence, the forces developed within the stress fiber, the focal adhesions and the microposts are equal to one another and identified as the force within the system: P = P_sf = P_fa = P_mp. The determination of P is essential for calculating the chemical potentials of the focal adhesion, the stress fiber, and the cytosol, which are the driving forces for the chemical processes (Maraldi & Garikipati (32)) and appear in the rate equations Eqs. 1–3.

In the Discussion, we will observe that the stress fiber’s constitutive nature plays a major role in the complex mechanical response of the system. Indeed, the contractile and viscoelastic features of the stress fiber strongly influence the development of the force within the whole system. In particular, the force developed within the stress fiber (and consequently within the whole system, due to mechanical equilibrium) can be expressed as the sum of three different contributions: P_sf = P^e_sf + P^ve_sf + P^ac_sf, where P_sf^e is the elastic component, P_sf^ve accounts for the viscous response, and P_sf^ac is the active contractile force. Fig. 1 also shows the actomyosin contractile units that make up the stress fiber. Each unit consists of one myosin motor and one half-length of each interleaved, antiparallel actin filament that the motor causes to intercalate. The units also are assumed to have the same length, and the total number of contractile units is therefore proportional to N_sf. We take each such unit to have the same strain rate in the stress fiber. See the expressions in Eq. 2 and the ensuing discussion in the Supporting Material for the complete active contractile force model.

A specific set of parameters was chosen (see Table S1 in the Supporting Material) and the model was tested for its ability to reproduce the main features of the force response of smooth muscle cells plated on an array of polymeric microposts (33). To access a variety of responses, the initial stress fiber length was varied over a range typically reported for a cell (10–65 μm), while the initial focal adhesion length was varied in the range of 0–2 μm. For the tests in which an external load was applied to the system, the extent of the substrate stretch was varied between 0.05 and 0.15, to make connections with Mann et al. (33).

Results

System response map and collapse mechanisms with no applied strain

We first seek to model the contractility of a cell on an array of microposts when the substrate is not subjected to an external strain. The corresponding system responses are collected in the map of Fig. 2.

Figure 2.

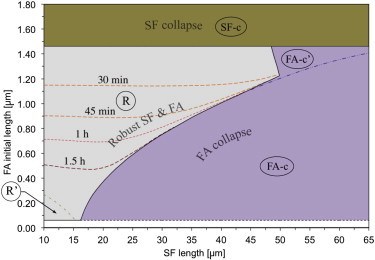
System response map with no applied stretch. R is the region in which the stress fiber and the focal adhesion reach full development (robust SF & FA (stress fiber and focal adhesion) region). (Dashed curves) Iso-time contours of micropost coverage by the growing focal adhesion. R′ is the region in which focal adhesion translation causes stress fiber force relaxation to zero. The system collapses in regions FA-c and FA-c′ due to focal adhesion resorption (FA collapse regions), and in SF-c due to stress fiber resorption (SF collapse region). To see this figure in color, go online.

In region R, a robust, fully developed system is obtained, with a stable stress fiber and a growing focal adhesion. Fig. 2 shows that this region may extend down to ${\hat{x}}_{fa}^0$= λ = 58 nm (black dashed line in Fig. 2), which is the size of a single complex of focal adhesion proteins, and represents the smallest focal adhesion in our model (the term “focal complex” may be more appropriate in this limit). Notably, even this smallest initial focal adhesion gives rise to a robust system if x⁰_sf is small. Region R spans a wider range of ${\hat{x}}_{fa}^0$ values than any other region. However, for larger values of x⁰_sf, this range of ${\hat{x}}_{fa}^0$ becomes increasingly narrow, as other failure mechanisms become dominant (regions FA-c and SF-c; focal adhesion and stress fiber regions, respectively).

Inside region R in Fig. 2, the system exhibits different behaviors, some of which are induced by the fact that the focal adhesion is constrained to develop on the surface of the micropost, which has finite area. The dashed curves indicate the times at which the focal adhesion has grown to the size of the micropost diameter. Smaller ${\hat{x}}_{fa}^0$ translates to greater growth times, as would be expected. Further details are provided in the following subsection. The dash-dot black line in Fig. 2 delimits the subregion R′, characterized by low values of x⁰_sf and ${\hat{x}}_{fa}^0$. For these configurations, the system does not collapse, but the stress fiber force vanishes at small times. Here, treadmilling of proteins through the cytosol allows the focal adhesion structure to translate in the direction of the force, causing the force in the system to relax to zero (solid curves in Fig. 3).

Figure 3.

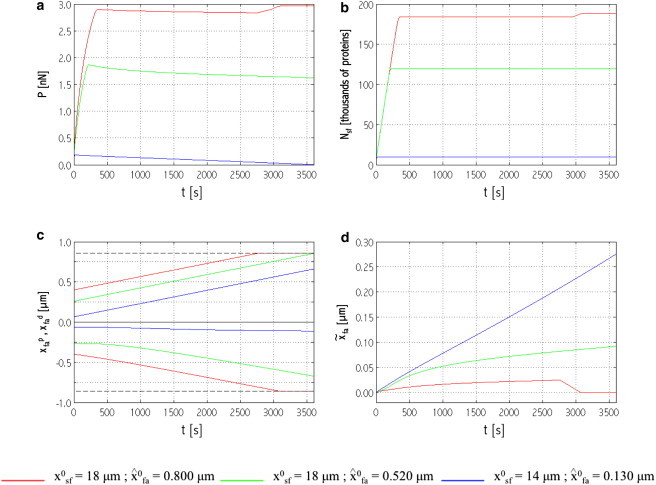
Time evolution of (a) force, P; (b) number of actin monomers in the stress fiber, N_sf; (c) positions of focal adhesion distal end, initially negative values, x^d_fa and proximal end, positive values, x^p_fa (dashed lines indicate the position of micropost edges); and (d) focal adhesion centroid position, ${\tilde{x}}_{fa}$, for three different system initial configurations belonging to region R in Fig. 2. To see this figure in color, go online.

Outside region R, the system collapses due to different failure mechanisms: in region FA-c, characterized by low values of ${\hat{x}}_{fa}^0/x_{sf}^0$, the collapse is due to the complete resorption of the focal adhesion. Under these conditions, in fact, the stress fiber is able to generate a high active force, P_sf^ac; as a consequence, the force within the system P is high and exceeds the focal adhesion’s ability to sustain mechanical load (see explanation of the focal adhesion critical load in the Discussion), causing its complete resorption by unbinding at its distal end. Similarly, for high values of x⁰_sf (subregion FA-c′), the system experiences focal adhesion collapse due to the finite surface area of the micropost, which constrains the growth of the focal adhesion (see Section S2 in the Supporting Material for details).

In region SF-c, the system collapses due to stress fiber failure. The large focal adhesion increases the system stiffness so that a high force P can be developed under strain control. This ultimately causes stress fiber resorption, and the system collapses even as the large focal adhesion survives.

Time-dependent response of the system with no applied strain

The detailed dynamics of the system in terms of the time evolution of force P, number of proteins in the stress fiber N_sf, position of the focal adhesion proximal and distal ends (x^p_fa and x^d_fa, respectively), and centroid position ${\tilde{x}}_{\text{fa}}$ are depicted in Fig. 3 for three typical system configurations belonging to region R of the response map in Fig. 2. For configurations in region FA-c of the response map, a similar discussion is provided in the Supporting Material. The force within the system, P, is often referred to as the “contractile force” in the literature. However, we prefer not to use this terminology, because, according to the stress fiber constitutive model used for this study (Maraldi & Garikipati (32)), this force depends not only on contractility, but also on the passive elastic or viscoelastic response of all the subsystems (see the expressions in Eq. S2 in the Supporting Material, and explanation of the stress fiber rheology in The Underlying Model) and on loads external to the system (see the later discussion related to Fig. 6).

Figure 6.

Time evolution of (a) force, P; (b) number of actin monomers in the stress fiber, N_sf; (c) positions of focal adhesion distal end, initially negative values, x^d_fa and proximal end, positive values, x^p_fa (dashed lines indicate the position of micropost edges); and (d) focal adhesion length, ${\hat{x}}_{fa}$, for the indicated applied strain. System initial configuration: x⁰_sf = 18 μm; ${\hat{x}}_{fa}^0$ = 0.520 μm. To see this figure in color, go online.

Fig. 3 a shows the evolution of P; in all cases, the force initially increases and, after a time interval that depends on the initial values ${\hat{x}}_{fa}^0$ and x⁰_sf, it attains a near-plateau characterized by a negative slope. Accordingly, N_sf increases until a critical concentration is reached at which protein recruitment stops (Fig. 3 b).

Although the cases in Fig. 3 all fall into region R, the detailed dynamics differ notably from one another. The solid curves, for instance, refer to a configuration in region R′; although P completely vanishes, neither the stress fiber nor the focal adhesion dissolves, as shown in Fig. 3, b and c. Indeed, the stress fiber grows continuously until the aforementioned critical actin concentration is attained and the focal adhesion also grows, by addition of complexes at both its ends. Interestingly, the relaxation of P corresponds with focal adhesion translation due to protein treadmilling, as seen in the evolving position of the focal adhesion centroid (Fig. 3 d). Region R′ may therefore be regarded as an enhanced translation region.

The shaded curves in Fig. 3 show the system dynamics when the finite cross-section of the micropost limits focal adhesion growth. A stiffening effect is imposed on the system (as seen from the shaded curve in Fig. 3 a, at t ≃ 3000 s). As shown in Fig. 3 c, the faster-growing proximal end of the focal adhesion is first to reach the corresponding micropost edge (this holds for all system configurations). Consequently, the focal adhesion continues to grow only at the distal end, and its centroid, which is the center of action of the stress fiber force, moves backward (Fig. 3 d). The focal adhesion translation away from the direction of the force induces a kinematic stiffening—in the same manner as a translation in the direction of the force induces a kinematic relaxation (see the preceding discussion, as well as the forthcoming one on the competition between stress fiber contractility and focal adhesion translation)—which makes the chemical potential term (μ_sf − μ^sf_cyt) of Eq. 1 negative and reestablishes a growth regime for the stress fiber. Consequently, more actin and myosin are recruited to the stress fiber and P starts rising again until the slower-growing distal end of the focal adhesion reaches the corresponding micropost edge. The focal adhesion has no more room for growth; N_sf reaches a second, higher, critical concentration and the contractile force plateaus out. The stress fiber-focal adhesion system is at equilibrium in this case.

When the system configuration falls outside region R′ of the response map in Fig. 2 and neither end of the focal adhesion reaches the micropost edge, the dynamics follow the dash-dot black curves of Fig. 3: the critical value of N_sf is reached in the stress fiber, which stops growing, whereas the focal adhesion continues to grow by recruiting complexes at both ends (Fig. 3 c). The observed force relaxation is related to translation, as explained above.

The maximum value attained by the force in the system, P, is of interest for robust systems; it depends on x⁰_sf and ${\hat{x}}_{fa}^0$, as reported in the contour plot of Fig. 4 for configurations in region R. It can be noted that a higher x⁰_sf results in a higher value of the maximum of P. However, ${\hat{x}}_{fa}^0$ also has some influence: especially for low x⁰_sf, a high ${\hat{x}}_{fa}^0$ leads to an increased maximum P. Turning to the stress fiber growth, the maximum, or critical, value of N_sf is proportional to the stress fiber radius r_sf and to the number of actin filaments N_fil. From our computations, we found that N_sf varies as the maximum value of P (data not shown). No equivalent quantities can be identified that are intrinsic to the focal adhesion, as it always remains far from equilibrium and, consequently, its length $\left({\hat{x}}_{fa}\right)$ and centroid position $\left({\tilde{x}}_{fa}\right)$ are always changing.

Figure 4.

Contour plots of the maximum contractile force P and of the focal adhesion resorption time t for configurations belonging, respectively, to regions R and FA-c of the map in Fig. 2. To see this figure in color, go online.

The time to failure is a relevant quantity for systems collapsing due to full resorption of the focal adhesion. A contour plot of this parameter is shown in Fig. 4 for configurations in region FA-c of the response map. The time to failure rapidly decreases for decreasing ${\hat{x}}_{fa}^0$, and slowly decreases for increasing x⁰_sf, i.e., for configurations far from the boundary between regions R and FA-c.

For large values of ${\hat{x}}_{fa}^0$ (region SF-c in the response map of Fig. 2), the system always collapses due to complete disassembly of the stress fiber over very short timescales (dynamic data not shown). A large focal adhesion acts as a very stiff support, allowing the force within the system, and hence the strain energy, to increase and drive the stress fiber to a rapid disassembly.

Collapse-mechanisms and system behavior with applied strain

Fig. 5 depicts the system response map under an applied step strain. The numbers in parentheses are the strains for which failure occurs by focal adhesion resorption for that configuration in region FA-c (Fig. 6, and see Fig. S2 in the Supporting Material). On comparing with the response map under no strain in Fig. 2, it is apparent that region FA-c has grown at the expense of R; this suggests that, upon stretching, the system is more prone to collapse due to focal adhesion resorption. The region in which the system does survive is restricted to initial configurations with progressively smaller x⁰_sf and larger ${\hat{x}}_{fa}^0$.

Figure 5.

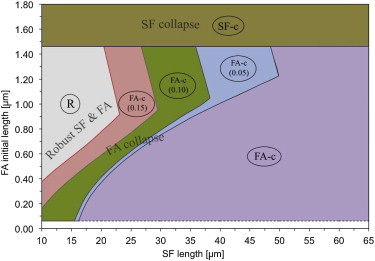
System response map for applied strain. Regions R and FA-c are modified from Fig. 2. The applied strain appears in parentheses in subregions of FA-c. To see this figure in color, go online.

Our model admits substrate strains that are arbitrary functions of time, but we chose to apply time-discontinuous strains to make connections with the results of Mann et al. (33). The strain was always applied at t = 1800 s, well after the system had attained a near-equilibrium state characterized by N_sf and ${\hat{x}}_{fa}$ being steady, and the contractile force in a near-plateau regime (Fig. 6). As in the unstretched test-cases, ${\hat{x}}_{fa}^0$ and x⁰_sf were varied; additionally, time-discontinuous strains of 0.05, 0.10, and 0.15 were applied to the system by varying the stretch of the underlying substrate.

Time-dependent response of the system under different levels of strain

The analysis of the detailed dynamics of the system for different strain amplitudes allows a greater appreciation of the effects of an external strain to the system and enables a more direct comparison with the experiments conducted by Mann et al. (33), in which two different levels of stretch were applied to the cells. The plots in Fig. 6 show the system dynamics for applied strains of 0.5, 0.10, and 0.12 (the initial geometric configuration being fixed to allow a meaningful comparison between the different cases). Upon stretching, P spikes instantaneously (Fig. 6 a) because of the elastic response of the system. The force then drops very rapidly due to the passive viscoelastic response of the stress fiber. The inset in Fig. 6 a shows these elastic and viscoelastic responses at a finer force-time resolution for the applied strain of 0.05. The externally applied strain also drives the dynamics of the stress fiber (Fig. 6 b): more actin monomers are recruited, and the stress fiber grows until a second critical value of N_sf is reached. As a consequence, P rises again, driven by P_sf^ac, until it reaches a second maximum (this will be referred to as the “global maximum force” for that strain) followed by a second near-plateau, with a slightly negative slope. Notably, the global maximum of P and the poststrain critical value of N_sf increase if the applied strain increases. An exception, however, occurs if the system experiences focal adhesion collapse: in Fig. 6 a, for instance, the global maximum of P for the strain of 0.12 is lower than that for the strain of 0.10.

The focal adhesion has a greater range of responses than the stress fiber (Fig. 6, c and d). The proximal end always grows upon stretching, whereas the distal end can either suffer an initial resorption followed by restoration of the growth regime (dash-dot black curve, green online, in Fig. 6 c, strain of 0.10) or grow monotonically (solid curve, blue online, in Fig. 6 c, strain of 0.05). Consequently, the focal adhesion can either have a transitory resorption stage or show monotonic growth (Fig. 6 d). In contrast to P, the focal adhesion length decreases for increasing strain (Fig. 6 d, strain of 0.10 vs. 0.05). At higher applied strains, the focal adhesion begins to shrink irreversibly, causing the system to collapse (shaded curves, red online, in Fig. 6).

Discussion

The key to deciphering the system’s complex mechanochemical coupling lies with the chemical potentials of the stress fiber, focal adhesion, and cytosol, and with the complex, nonlinear mechanochemical coupling in the model. On this basis, in the following subsections we highlight some aspects of the dynamics of the model that will be relevant to the discussion of the results presented in this article.

Critical loads for assembly and disassembly

The chemical potentials that drive stress fiber and focal adhesion dynamics are themselves functions of the force, P, developed within the system (Fig. 7). By comparing P with suitable critical values, it can be established whether the focal adhesion or stress fiber undergoes growth or disassembly. It is important to recognize, however, that these critical values vary, because they depend upon N_sf and c_fa, which evolve.

Figure 7.

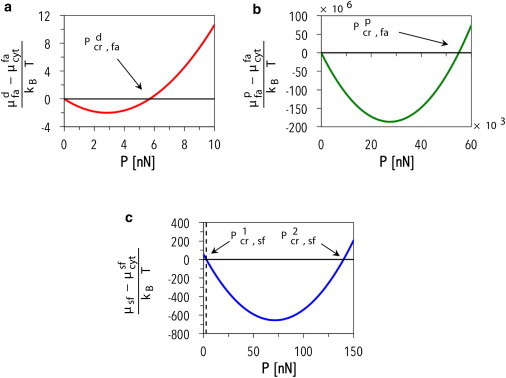
Chemical potentials as functions of the force P at (a) the focal adhesion distal end; (b) the focal adhesion proximal end; and (c) the stress fiber for the set of parameters listed in Table S1 in the Supporting Material. To see this figure in color, go online.

With regard to the focal adhesion subsystem, experiments show that no growth is observed in the absence of force (8,9); for this reason, all the parameters were chosen such that μ_fa − μ^fa_cyt = 0 if P = 0 (see Fig. 7, a and b). As a result, only one critical value of P can be identified for both the distal and the proximal ends of the focal adhesion (namely P^p_cr,fa and P^d_cr,fa in Fig. 7); below this force, the chemical potential drives focal adhesion complexes to bind, whereas above it unbinding is experienced at the given focal adhesion end. For P > P^d_cr,fa, it is the growth rate at the focal adhesion proximal end that determines whether the focal adhesion as a whole undergoes growth, translation, or resorption leading to eventual focal adhesion collapse; nevertheless, P > P^d_cr,fa is a necessary condition for focal adhesion resorption.

Given the parameter values chosen for this study and system configurations explored, the critical load P^p_cr,fa—above which (μ^p_fa − μ^fa_cyt) becomes positive, leading to protein unbinding at the proximal end—is much greater than the value of P observed in our simulations. Hence, it is not of interest.

On the other hand, for the set of parameters used here, two critical loads can be identified for the stress fiber subsystem: namely, P¹_cr,sf and P²_cr,sf in Fig. 7 c. The dynamics of the subsystem are therefore dictated by comparing P with such critical forces; in particular, for P < P¹_cr,sf or P > P²_cr,sf, the term (μ_sf − μ^sf_cyt) is positive and the stress fiber undergoes disassembly, whereas for P¹_cr,sf < P < P²_cr,sf, the term (μ_sf − μ^sf_cyt) is negative, and proteins are recruited to the stress fiber.

Our mechanochemical model highlights the interplay between the mechanics and chemistry in determining the dynamics of the system. Through the chemical potential, the force in the system affects the protein binding and unbinding rates, which determine the focal adhesion length and the stress fiber thickness. In turn, these system geometric parameters influence the chemical potentials by changing the critical loads. They also control the passive and active contributions to the stress fiber force, and, ultimately, the force in the system, by varying the system stiffness and the number of motor proteins in the stress fiber.

Nonlinearities, mechanochemistry, and response maps

The relevant critical loads P¹_cr,sf, P²_cr,sf, and P^d_cr,fa are nonlinear functions of the geometry of the system. The relations between the force P and these critical loads dictate assembly or disassembly of a subsystem. The overall system dynamics that yield the response maps in Fig. 2 and Fig. 5 depend on the rate of change of the critical loads with respect to that of P. In the next few sections, we will observe some aspects of the behavior of the system that arise from this mechanism. In summary, in our model the stress fiber can reach a critical concentration only because P¹_cr,sf increases faster than P and, after some time, the stress fiber reaches a configuration for which protein binding ceases (see Fig. 8 and its legend). Similarly, but with opposite results, Fig. 9 shows that the focal adhesion collapses because P^d_cr,fa increases faster than P and, after some time, the focal adhesion is in a configuration for which unbinding starts and proceeds at a increasingly faster rate (see the legend of Fig. 9 for further details). The rate at which P and the critical loads change is driven by the model’s coupled mechanochemistry, and by nonlinearities in the constitutive relations for chemical potentials, mechanical forces, and rate laws. These are critical to the form of the response maps (Figs. 2 and 5).

Figure 8.

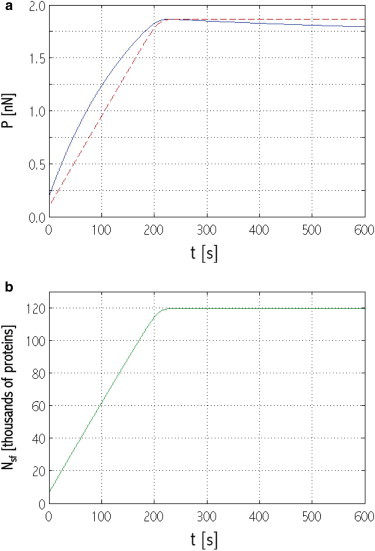
Time evolution of (a) stress fiber force P (solid line, blue online) and stress fiber critical force P¹_cr,sf (dashed shaded line, red online); (b) N_sf. System initial configuration: x⁰_sf = 18 μm; ${\hat{x}}_{fa}^0$ = 0.520 μm (see region R in Fig. 2). To see this figure in color, go online.

Figure 9.

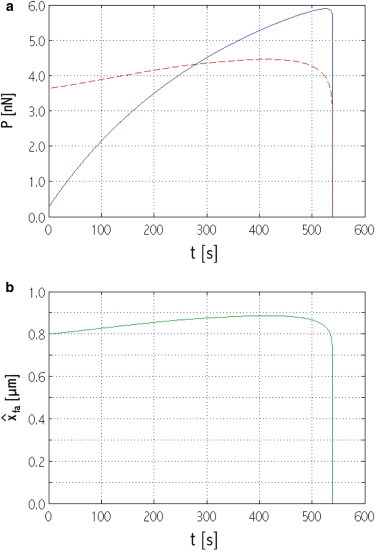
Time evolution of (a) P (solid line, blue online) and focal adhesion critical force, P^d_cr,fa (dashed shaded line, red online); (b) ${\hat{x}}_{fa}$. System initial configuration: x⁰_sf = 36 μm; ${\hat{x}}_{fa}^0$ = 0.800 μm (see region FA-c in Fig. 2). To see this figure in color, go online.

Stress fiber growth stops when the critical actin concentration is reached

The attainment of a critical value of N_sf at which the stress fiber stops recruiting proteins, is explained by the evolution of P relative to P¹_cr,sf, as shown in Fig. 8 a. Initially, P > P¹_cr,sf makes (μ_sf − μ^sf_cyt) < 0, which drives actin and myosin recruitment to the stress fiber (Fig. 8 b). Consequently, P increases due to both enhanced acto-myosin contractility and the increased system mechanical stiffness (the stress fiber becomes thicker and the focal adhesions longer). However, P¹_cr,sf, which is a function of N_act, also increases. When P¹_cr,sf exceeds the stress fiber force, (μ_sf − μ^sf_cyt) > 0 and actin unbinding should occur. However, χ_sf in Eq. 1 is negative; therefore, actual unbinding rates remain low, and the stress fiber appears stable at its critical concentration (Fig. 8 b). Correspondingly, P attains a near-plateau regime in which it slowly decreases under the effect of focal adhesion translation (see below for the competition between stress fiber contractility and focal adhesion translation).

From this state, if P increases due to external perturbations to the system, but P < P²_cr,sf is maintained, a growth regime can be reestablished because the condition (μ_sf − μ^sf_cyt) < 0 is regained. Actin and myosin are then recruited until attainment of a second critical value of N_sf for which the stress fiber stops growing. In this study, the perturbation was applied in the form of a substrate strain (see Fig. 6). A different perturbation induced by the finite cross-section of a micropost has also been shown in Fig. 3.

Stress fiber activity can trigger different focal adhesion responses

A longer stress fiber contains more myosin proteins and therefore is able to generate a higher active force, P_sf^ac. For this reason, as shown in Fig. 4, the maximum total force is higher for system configurations with longer stress fibers. Secondarily, the passive contribution to the stress fiber force also plays a role in determining its maximum value. As Fig. 4 shows, focal adhesions that are initially large lead to systems developing higher forces, because the mechanical stiffness is higher. In addition to having a major effect on the active force, stress fibers of different geometries also can trigger different focal adhesion responses: for instance, region R in Fig. 2 becomes increasingly narrow for longer stress fibers. The reason is that, to sustain the greater active force generated by a longer stress fiber, the initial focal adhesion needs to be longer. A longer focal adhesion has a higher critical load P^d_cr,fa and can be subjected to a greater force without collapsing. On the other hand, if the stress fiber is short, the active force generated is lower; hence, even focal adhesions developing from a single focal adhesion complex can sustain the load without failing (see the response map in Fig. 2 and its related discussion in the legend).

Fig. 9 a shows the evolution of both the total force, P, and the focal adhesion critical load, P^d_cr,fa, for a system with initial configuration in region FA-c of Fig. 2. Due to the incorporation of more actins and myosins in the stress fiber, P increases and exceeds P^d_cr,fa. Then, the focal adhesion’s growth slows down (Fig. 9 b) because unbinding occurs at the distal end (as a consequence, the focal adhesion critical load also increases more slowly). However, because N_sf is far from its critical value, P continues to increase above P^d_cr,fa, eventually leading to severe resorption at the distal end, and focal adhesion collapse (Fig. 9 b). Protein resorption is boosted by the force-dependent term χ_fa in Eq. 2, which makes the unbinding rate grow exponentially with the stress fiber force.

The focal adhesion size can determine the fate of the stress fiber

For initial configurations in region SF-c of Fig. 2, ${\hat{x}}_{fa}^0$ is large and the stress fiber disassembles within the first few milliseconds of the computation. The reason is that a large ${\hat{x}}_{fa}^0$ value makes the stress fiber-focal adhesion system mechanically very stiff. Therefore, contractility drives P to rapidly exceed P²_cr,sf, causing stress fiber disassembly. The disassembly is boosted by the force-dependent term χ_sf in Eq. 1, which enhances the actin unbinding rate. The focal adhesion thus can control the fate of the system, by acting as a very stiff support.

Competition between stress fiber contractility and focal adhesion translation determines the force behavior

For the system configurations in region R of Fig. 2 (or of Fig. 5 for the applied strain case), the force reaches a plateau after an initial growth stage. The slope of the plateau is regulated by the competition between stress fiber contractility and focal adhesion translation due to protein treadmilling. The action of motor proteins in the stress fiber causes the active component of the stress fiber force P_sf^ac (and, consequently, the total force P) to increase, whereas when the focal adhesion centroid moves toward the stress fiber, P relaxes. Our computations show that for the overall system dynamics this kinematic relaxation mechanism and its interplay with stress fiber contractility is more relevant than the relaxation induced by passive viscoelasticity, because the latter occurs over very short timescales (see the inset in Fig. 6 a). For instance, for system configurations in region R′ of Fig. 2, the relaxation induced by focal adhesion translation toward the stress fiber has a major influence and prevails over the stiffening effect provided by the addition of myosin to the stress fiber. Focal adhesion translation is enhanced for small values of x⁰_sf: the low values of the stress fiber force developed within the system lead to a large difference between the chemical potentials at the focal adhesion distal and proximal ends (Fig. 7); thus, the binding rates of the focal adhesion ends prove to be very different. This results in a high rate of focal adhesion translation, which in turn causes the stress fiber force to relax and vanish in a short time (solid curves, blue online in Fig. 3).

The influence of substrate loading on the overall system response

As shown in Fig. 6, larger external strains result in system collapse due to complete resorption of the focal adhesion. A high strain leads to a high value of the force in the system, P, which can exceed the focal adhesion critical load, P^d_cr,sf, and induce severe resorption at the focal adhesion distal end (as shown by the shaded curves, red online, in Fig. 6).

On the other hand, if the strain is sufficiently small, the stress fiber force reaches a second plateau; correspondingly, the stress fiber recruits more actins and myosins. The focal adhesion also grows, demonstrating that, to some extent, an external load can stimulate growth of the stress fiber-focal adhesion system. The strain is externally imposed as a substrate strain in our model, but in living cells may come from the ECM, neighboring cells, or other stress fiber-focal adhesion complexes within the same cell.

Connection to recent cell traction force experiments on micropost arrays

Our results can be related to the experiments of Mann et al. (33) on the force response of smooth muscle cells on arrays of polymeric microposts. Fig. 10 shows data from their study for the force on individual microposts versus time in response to a substrate strain of 0.06. Fig. 10 a corresponds to stress fiber-focal adhesion systems that remain robust over the period of the experiments (region R in Fig. 5). Notably, the computed response has a spike in force at the instant of strain application due to the intrinsic viscoelastic response of the stress fiber, which has a relaxation time τ = 10 s (see the inset in Fig. 6 a and the related discussion, and see Table S1). The 1-min time resolution of the experiments was too coarse to capture such a spike.

Figure 10.

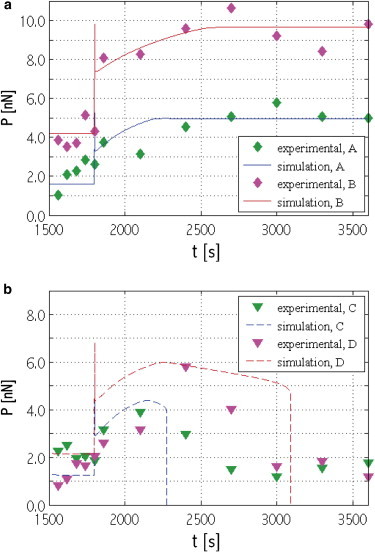
The computed stress fiber force versus time compared with force on individual microposts from the work of Mann et al. (33). (a) Robust stress fiber-focal adhesion systems (see region R in Fig. 5). (b) Systems that suffer focal adhesion collapse (see region FA-c in Fig. 5). The strain of 0.06 is applied at 1800 s in both cases. To see this figure in color, go online.

In Fig. 10 b, stress fiber-focal adhesion systems from the focal adhesion collapse (FA-c) region of Fig. 5 have been compared with experimental curves that show a significant decrease in force. Notably, whereas the computed curves demonstrate decreases down to zero force, the experiments show less sharp decreases followed by a plateau. Upon examining the experimental force data, we have found that the force trace on each of the two microposts represented in Fig. 10 b is not complemented by a force trace that is equal in magnitude and opposite in direction on another micropost. This suggests that while each end of a stress fiber is indeed connected to a focal adhesion on a micropost, different parts of the focal adhesion on these microposts have different stress fibers connected to them. Each stress fiber and the part of the focal adhesions connected to each of its ends would form a system of the type considered in the model, and this system would have well-defined dynamics. However, the force trace on a micropost is the magnitude of the vector resultant of all these different systems, some of which may collapse and all of which have different dynamics. This yields the experimental curves in Fig. 10 b characterized by sharply decreasing, but nonvanishing, forces. In all cases, matches to the experimental curves were obtained by varying the initial focal adhesion length and the stress fiber unstretched length.

Mann et al. (33) speculate that all the different observed behaviors may be due to the force acting on the focal adhesion before the application of the stretch. Our study shows that the force does affect the system behavior, but is itself determined by the system’s initial geometrical configuration (Figs. 2 and 5). This diversity of stress fiber and focal adhesion geometries has not been reported by Mann et al. (33).

Further capabilities of the model

The discussion of Fig. 3 identified an equilibrium state for the system when the focal adhesion grows to cover the micropost cross-section. A nonuniform force distribution over the focal adhesion (34) also allows the attainment of an equilibrium state, but has not been considered here.

The model discussed here can be embedded in a whole-cell model, where the effects of location within the cell and history, as well as of cell type, can be considered.

Notably:

• 1.Both stress fibers and focal adhesions vary in size and length throughout a cell, depending also on cell history, and from one cell type to another;
• 2.The external strain field to which cells are subjected is nonuniform; and
• 3.The kinetic rates of proteins binding/unbinding and the structural and chemical properties of both the stress fibers and the focal adhesions change with the cell type.

All these varying conditions, and the different responses they elicit, can be accounted for in the model presented here.