Critical Behaviour in DOPC/DPPC/Cholesterol Mixtures: Static ²H NMR Line Shapes Near the Critical Point

Abstract

Static ²H NMR spectroscopy is used to study the critical behavior of mixtures of 1,2-dioleoyl-phosphatidylcholine/1,2-dipalmitoyl-phosphatidylcholine (DPPC)/cholesterol in molar proportion 37.5:37.5:25 using either chain perdeuterated DPPC-d₆₂ or chain methyl deuterated DPPC-d₆. The temperature dependence of the first moment of the ²H spectrum of the sample made with DPPC-d₆₂ and of the quadrupolar splittings of the chain-methyl-labeled DPPC-d₆ sample are directly related to the temperature dependence of the critical order parameter η, which scales as ${\left[\left(T_c-T\right)/T_c\right]}^{{\beta }_c}$ near the critical temperature. Analysis of the data reveals that for the chain perdeuterated sample, the value of T_c is 301.51 ± 0.1 K, and that of the critical exponent, β_c = 0.391 ± 0.02. The line shape analysis of the methyl labeled (d₆) sample gives T_c = 303.74 ± 0.07 K and β_c = 0.338 ± 0.009. These values obtained for β_c are in good agreement with the predictions of a three-dimensional Ising model. The difference in critical temperature between the two samples having nominally the same molar composition arises because of the lowering of the phase transition temperature that occurs due to the perdeuteration of the DPPC.

Introduction

The phase behavior, particularly the coexistence of two fluid phases (liquid-disordered (l_d) and liquid-ordered (l_o)) (1), has been studied for a number of mixed lipid systems containing cholesterol (2–17) and in giant plasma membrane vesicles (18,19). Associated with this two-phase coexistence there is generally a line of critical compositions on the two-phase boundary separating the higher temperature single-phase region from the two-phase l_d/l_o coexistence region below. For temperatures and compositions close to this line of critical points, the local composition of the bilayer fluctuates. Such fluctuations not only have consequences for the physical properties of these model membrane systems, but, if they occur in natural biological membranes, may have important consequences for the biological function. The fluctuations and even the phase behavior can be influenced by external factors such as the interaction with actin (20), streptavidin (21), or anesthetics (22), or through surface adhesion (23).

Critical behavior can be observed in a tremendous variety of different physical systems (24,25), whether in superfluids, superconductors, binary liquids, or ternary lipid mixtures containing cholesterol. The phenomena observed, however, have remarkable similarities among systems which are members of the same universality class. For example, uniaxial ferromagnets, binary liquids, and multilamellar dispersions of DOPC/DPPC/cholesterol all would appear to belong to the same class. As the critical point is approached in any of these systems, quantities such as the specific heat, susceptibility, and the order parameter for the phase transition all vary with temperature according to the same power law. Thus, the specific heat varies as ${[\left(T-T_c\right)/T_c]}^{-{\alpha }_c}$, the susceptibility varies as ${[\left(T-T_c\right)/T_c]}^{-{\gamma }_c}$, and the order parameter varies as ${[\left(T-T_c\right)/T_c]}^{{\beta }_c}$. The three-dimensional (3D) Ising model describes this theoretically and predicts that α_3D = 0.11, β_3D = 0.325, and γ_3D = 1.24. If the physical system is only two-dimensional (2D), then the 2D Ising model would predict α_2D = 0 (actually, the specific heat diverges logarithmically), β_2D = 0.125, and γ_2D = 1.75 (26). In either case, theory predicts α_c + 2β_c + γ_c = 2.

An essential feature of critical behavior is the divergence of the length scale, ξ, describing fluctuations in the order parameter as the critical point is approached. Far above T_c the order parameter is zero and there is no correlation (for example in the orientation of the Ising spin) but as T approaches T_c, even though long-range order is still zero, locally there starts to be a correlation between neighboring spins. The correlation length varies as [(T − T_c) / T_c]^−ν_c. The exponent ν_c is related to those discussed above by the relation 2 − α_c = ν_c × d, where d is the dimensionality of the system (26). In the 2D Ising model, the exponent is ν_2D = 1, whereas in the 3D Ising model, ν_3D = 0.63. Above T_c, one can study the local fluctuations using a variety of physical techniques. Below T_c, one can measure the order parameter itself.

In giant unilamellar vesicles (GUVs), fluorescence microscopy has been used to study these fluctuations close to T_c, where the correlation length becomes longer than the wavelength of light. Since the thickness of a single lipid bilayer (or a biological membrane) is only 4–6 nm, it seems logical to expect these vesicles to behave approximately like a 2D system, since the wavelength of visible light is much larger than the thickness of the bilayer. On the other hand, NMR of multilamellar dispersions can be used to study the fluctuations farther from the critical point, where the fluctuations are not yet visible in optical microscopes. In addition, the close juxtaposition of very many lipid bilayers may result in these sytems behaving more as 3D systems in NMR studies.

Careful experimentation can reveal the physical character of these compositional fluctuations. Studies on GUVs using fluorescence microscopy techniques have led to the conclusion that these single-bilayer vesicles behave as 2D systems consistent with a 2D Ising model universality class (19,27,28). Our previous work on DOPC/DPPC/cholesterol multilamellar dispersions (10) led us to conclude that the critical behavior in multilamellar systems is better described within the 3D Ising universality class. This was a result of our observation that the sample spin rate dependence of the line width of the ²H NMR magic angle spinning (MAS) side bands scaled with temperature with an exponent ν_c = 0.628 ± 0.01 consistent with the 3D Ising prediction of ν_3D = 0.63, rather than the value ν_2D = 1 expected for the 2D Ising universality class (26).

In this article, we present static ²H NMR results on samples of DOPC/DPPC/cholesterol (with molar composition 37.5:37.5:25), where the DPPC is either chain perdeuterated or is deuterated only at the chain terminal methyl groups. Below the critical temperature, T_c, the first moment, M₁, of the spectra for the chain perdeuterated sample, and the ²H quadrupolar splittings of the methyl deuterated sample are both directly related to the critical order parameter. The temperature dependence of this order parameter, which goes to zero at the critical temperature, scales as ${[\left(T_c-T\right)/T_c]}^{{\beta }_c}$. Analysis of these data gives β_c = 0.391 ± 0.02 for the chain perdeuterated sample and β_c = 0.338 ± 0.009 for the methyl deuterated sample. Both agree quite well with the 3D Ising value of β_3D = 0.325, but not with the 2D Ising value, β_2D = 0.125.

In the next section, we describe the method of sample preparation, the experimental procedures used, and the method of analysis of the data. We then present the experimental results and a discussion of their interpretation. We conclude with a brief summary and comparison to other work.

Materials and Methods

Sample preparation

Cholesterol was obtained from Sigma-Aldrich (St. Louis, MO) and twice recrystallized from ethanol before use. 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-di-[d₃₁]-palmitoyl-sn-glycero-3-phosphocholine (DPPC-d₆₂) and chain methyl labeled 1,2-di-[d₃]-palmitoyl-sn-glycero-3-phosphocholine (DPPC-d₆) were obtained from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Sample preparation was as described by Davis et al. (10). We focus here on two samples having the same nominal composition, namely, a 37.5:37.5:25 molar composition of DOPC/DPPC/cholesterol. The first sample was prepared using chain perdeuterated DPPC-d_62, and the second using chain methyl deuterated DPPC-d₆. Each sample contained ∼20 mg of labeled DPPC. Each sample was hydrated using 50 mM potassium phosphate buffer, pH 7.0, at a buffer volume/total dry weight ratio of 3:4. Samples were accurately weighed before and after the NMR experiments were performed and no change in weight, i.e., no water loss, was observed. Spectra at 308.8 K, well above the two-phase coexistence region, taken at the beginning and end of the sequence of experiments were used to assess sample stability against hydrolysis of the lipids. No change in the spectrum was observed for either sample.

Static ²H NMR

All NMR experiments were performed on a 500 MHz wide-bore Bruker Avance II spectrometer (Bruker BioSpin, Milton, ON, Canada) at a ²H NMR frequency of 76.77 MHz. For these static ²H NMR experiments, a home-built probe was used with the quadrupolar echo pulse sequence (29). This probe uses a copper oven for regulating the sample temperature rather than the commercial air-flow system used by Bruker Biospin probes. This design significantly reduces the temperature gradient across the sample, permitting finer control. The probe temperature was sensed using a Pt-100 resistance thermometer embedded in the wall of the copper oven. The temperature was calibrated using the chemical shift of Pb(NO₃)₂ (30,31). The phase transition temperatures of DMPC-d₅₄ (32) and DPPC-d₆₂ (33) were used as reference points for this calibration. The temperature gradient across the sample, for temperatures near 300 K, is estimated to be <0.1 K (i.e., ±0.05 K).

In these experiments, we focused on the temperature range close to the critical region (from 306 K down to 298 K for the chain perdeuterated sample, and from ∼313 down to 287 K for the methyl deuterated sample). Near the critical point, sample temperature was decreased in small steps, either 0.1, 0.2, or 0.3 K. To permit a careful moment analysis of the spectra of the sample containing DPPC-d₆₂ (33,34), 4096 scans were collected and a simple shift algorithm (34,35) was used to position the start of the time domain signal precisely at the top of the quadrupolar echo. The receiver dead time, dominated by acoustic ringing, which occurs for frequencies in the range of 80 MHz or lower, required the use of echo delay times of at least 35 μs. Two 90° pulses of 2.9 μs duration were used to form the quadrupolar echo (except for the DOPC/DPPC-d₆/cholesterol sample where 90° pulses of 2.6 μs were used). The area and the first four moments of the spectra,

$$M_n=\frac{1}{A}\underset{{\omega }_0-{\omega }_M}{\overset{{\omega }_0+{\omega }_M}{\int }}{\left(\omega -{\omega }_0\right)}^n\times f\left(\omega \right)d\omega ,$$ (1)

were calculated and used for the analysis. Here, A is the area of the spectrum $f\left(\omega \right)$, centered at the Larmor frequency ${\omega }_0$, and M_n is its nth moment. The limits ($\pm {\omega }_M$) of the integral are chosen to be large enough to include all of the spectrum intensity. The systematic error in evaluation of the moments is minimized by the procedures discussed above (which provide a very flat baseline), whereas the random errors (determined by the signal/noise ratio) are reduced by using a large sample and a large number of scans in obtaining the spectra. We estimate the uncertainties for the series of experiments on the 37.5:37.5:25 perdeuterated DPPC sample to be ∼2% for the area, 0.5% for M₁, and 1% for M₂. (Note that the uncertainty in the first two moments turns out to be smaller than that of the area, since the intensity of the spectrum depends on small variations in probe tuning to which the shape of the spectrum is insensitive.)

For the DPPC-d₆ sample, where line shape fitting was to be used, only 2048 scans were taken at each temperature. The spectra were analyzed by fitting to a superposition of three Gaussian (or Lorentzian) broadened powder-pattern line shapes. Each powder pattern was characterized by an area, a quadrupolar splitting, and a line broadening. The l_o phase component consists of two powder patterns due to the inequivalence of the two DPPC methyl groups observed at high cholesterol concentrations, whereas the l_d phase component is fitted with a single powder pattern.

The fitting function was written in Origin C, and was run by OriginPro 9.0 (OriginLab, Northampton, MA). It consisted of the superposition of quadrupolar split doublets having either a Gaussian or Lorentzian shape. Initially, the superposition of splittings was weighted by sinθ, where θ is the angle between the bilayer normal and the magnetic field, as would be expected for spherical liposomes. It was found that both Lorentzian and Gaussian line shapes resulted in too much intensity for the 0° shoulders compared to what is observed in the spectra. One of the factors resulting in the reduced experimental intensity in the shoulders is the slight distortion of the spherical liposomes by the strong magnetic field. This distortion leads to slightly prolate ellipsoidal liposomes and results in an angular distribution of doublets weighted by (36)

$$P\left(\theta \right)=\text{sin}\theta d\theta \text{/}{\left({\text{sin}}^2\theta +{\rho }^2\times {\text{cos}}^2\theta \right)}^2.$$ (2)

Here, ρ is the ratio of the semimajor to semiminor axis of the prolate ellipsoid. The comparison of the experimental and theoretical line shapes is significantly improved when using this distribution.

The lowest temperature spectrum was fitted first, since the three overlapping powder patterns are easily distinguished at low temperatures. The two components corresponding to the two methyl groups in the l_o phase were constrained to have equal areas, to within 10% (to allow for slightly differing relaxation times). Having fit the lowest temperature spectrum, the parameter values obtained were used as the starting point for the fit of the next lowest temperature. This process was continued, gradually increasing the temperature, until the sample was within 1 K of the critical point using equal weights for the spectrum data. To continue the process, at <1 K from the critical temperature, we found that it was necessary to use direct weighting (proportional to signal intensity) to obtain reliable fits. The use of direct weighting had no effect on the parameters obtained by the fitting procedure for temperatures >1 K from the critical point. In this way, we were able to continue the fitting procedure until the sample temperatures was <0.25 K from the critical point.

Results and Discussion

The spectra in Fig. 1 illustrate the changes that occur as the sample temperature is lowered through the critical point into the two-phase coexistence region. As reported previously (2,3,37), well above T_c the ²H spectra of chain perdeuterated DPPC-d₆₂ in the 37.5:37.5:25 mixture (Fig. 1 a) are characteristic of the rapid molecular reorientation of the liquid disordered (l_d) phase. As the sample temperature approaches the critical point, there is noticeable line broadening (Fig. 1, b and c). Below T_c, the spectra show the coexistence of the two phases (Fig. 1, d–f). Although it is difficult to simulate the details contained in the spectra of perdeuterated samples, the moments of these spectra can provide a valuable perspective on the behavior occurring near the critical temperature.

Figure 1.

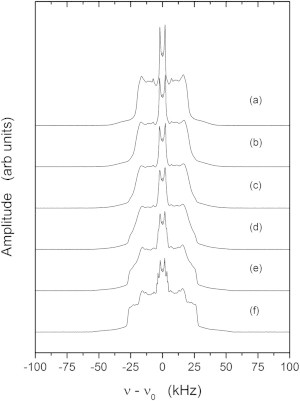
Static ²H NMR spectra of the 37.5:37.5:25 molar proportion DOPC/DPPC-d₆₂/cholesterol sample showing the changes in the powder-pattern spectra as the sample is cooled from the higher-temperature l_d phase into the fluid-fluid l_d/l_o two-phase coexistence region. Spectra are shown for 307.18 K (a), 303.13 K (b), 301.5 K (c), 301.09 K (d), 301.1 K (e), and 298.47 K (f).

Fig. 2 shows the temperature dependence of the first moment, M₁, for this sample. Above T_c the first moment increases approximately linearly as the temperature is decreased. In the region below T_c the sample has two phases, one rich in cholesterol and the saturated lipid (the l_o phase) and the other low in cholesterol and rich in the unsaturated lipid (the l_d phase). Because of the strong ordering effect of cholesterol on saturated lipids, there is a dramatic difference in the quadrupolar splittings of the ²H NMR spectra of these two phases (see Fig. 1, f). In such a two-phase coexistence region, the first moment of the ²H NMR spectrum can be written as the sum of two parts:

$$\begin{array}{c}{M}_1^{exp}=g_{lo}\times M_1^{lo}+\left(1-g_{lo}\right)\times M_1^{ld}\\ =g_{lo}\times \left(M_1^{lo}-M_1^{ld}\right)+M_1^{ld}\\ =g_{lo}\times \Delta M_1+M_1^{ld}.\end{array}$$ (3)

$M_1^{ld}$ and $M_1^{lo}$ are the first moments of the spectral components arising from the two different types of domain within the sample, and g_lo is the fraction of DPPC in the l_o phase. Since M₁ is proportional to the average quadrupolar splitting (33,34), and since the l_o phase is more ordered than the l_d phase, $M_1^{lo}>M_1^{ld}$ and ΔM₁ > 0. Thus, at the critical point, there is a dramatic change in the slope in the graph M₁ versus T. The shape of this curve depends on both ΔM₁ and g_lo.

Figure 2.

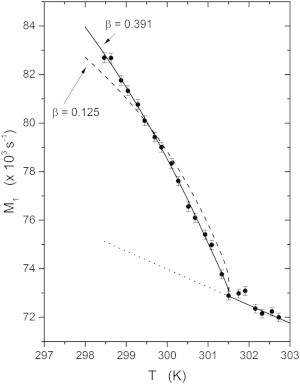
The temperature dependence of the first moment of the ²H NMR spectra of the 37.5:37.5:25 molar proportion DOPC/DPPC-d₆₂/cholesterol sample. The dotted line shows the baseline temperature dependence of M₁. The deviation of the experimental data from this baseline occurring at T_c is due to the separation of the sample into two phases. The solid curve below T_c shows the comparison with the best fit to a power law giving β = 0.391 ± 0.02, whereas the dashed line shows the prediction for a 2D Ising model with β = 0.125

The value of ΔM₁ = 4π / (3$\sqrt{3}$)Δ(< δν_Q >) depends on the difference in cholesterol concentrations in the two phases. For example, we have found that M₁ varies linearly with cholesterol concentration between 0 and 30 mol % for samples having equal molar proportions of DOPC and DPPC-d₆₂, with M₁ (z_chol) = 5.17 × 10⁴ + 8.75 × 10⁴ × z_chol (with an adjusted R² = 0.9986). Of course, for any given sample composition, on passing through the phase boundary from the l_d phase into the l_d/l_o coexistence region, the compositions of the two domains are determined by the lever rule, and the molar proportions of all three components change in accordance with the curvature of the phase boundaries. We note that the difference in quadrupolar splittings (and therefore in the values of M₁) of coexisting l_d and l_o domains (which may have, for example, 12 and 30 mol % cholesterol) is greater than that found for equimolar mixtures of DOPC and DPPC-d₆₂ having corresponding cholesterol concentrations. This is because there is also a large difference in the ratio of the unsaturated to saturated lipid in the different domains.

In pure fluids that exhibit critical behavior, the order parameter η used to describe the behavior is taken to be proportional to the fluid density. Below the critical temperature, there is a gas-liquid equilibrium, with the two phases having different densities. As the critical point is approached from below, the difference in the densities approaches zero as $\eta \sim {[\left(T_c-T\right)/T_c]}^{{\beta }_c}$, where β_c is the critical exponent for the order parameter. Above T_c, the distinction between the two phases vanishes. In ternary mixtures, it is expected that the composition can play the role of the order parameter, and in this case, the concentration of cholesterol seems to be the most important factor. Molecular density, or the inverse of molecular volume, may also be taken as the order parameter. In either case, the deuterium quadrupolar splittings provide an experimental measure of the order parameter: they are very sensitive to the relative concentrations of DPPC, DOPC, and cholesterol and they are directly related to the hydrocarbon chain length (16,38–41). In our analysis, we will assume that the difference between the first moments of the ²H NMR spectra of DPPC-d₆₂ in the l_o and l_d phases is proportional to the order parameter. We will also assume that the difference between the ²H quadrupolar splittings of the chain terminal methyl groups in the two phases provides an equally good measure of the order parameter.

Since the value of $M_1^{exp}$ depends on g_lo as well as on ΔM₁, we need to independently measure g_lo as a function of temperature to use the data in Fig. 2 to determine the value of the critical exponent β_c. Close examination of the spectra in Fig. 1 suggests that a careful analysis of the contribution of the chain terminal methyl groups to the spectrum may allow not only a determination of g_lo but also a direct measurement of Δ(δν), the difference in the quadrupolar splittings for the methyl groups in the l_o and l_d phases. Unfortunately, the sizable background from the methylene groups in the perdeuterated sample makes it too difficult to extract accurate results. For this reason, we prepared a second sample having the same nominal composition but using methyl deuterated DPPC-d₆.

Fig. 3 shows a series of ²H NMR spectra of 37.5:37.5:25 molar proportion DOPC/DPPC-d₆/cholesterol taken at different temperatures near the critical point. Well above T_c (Fig. 3 a), the spectrum is characteristic of a single homogeneous phase. The intensity of the 0° shoulders is weaker than expected for an ideal powder pattern where all orientations are equally probable. This can be partially accounted for by a slight elliptical distortion of the liposomes by the strong magnetic field. As the sample temperature approaches the critical point, there is substantial broadening of the powder pattern (Fig. 3 b). Below T_c, the inequivalence of the methyl groups becomes apparent, and three quadrupolar splittings can be seen; the smallest splitting corresponds to lipids within the l_d phase and the two larger splittings are for the lipids within the l_o phase. From the spectra in Fig. 3, it is clear that at lower temperatures, the relative amount of DPPC-d₆ in the l_d phase is reduced. The small sharp peak at the left of center of each spectrum is due to natural-abundance HDO in the buffer.

Figure 3.

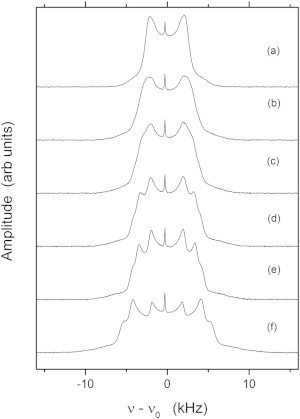
Static ²H NMR spectra of the 37.5:37.5:25 molar proportion DOPC/DPPC-d₆/cholesterol sample showing the changes in the powder-pattern spectra as the sample is cooled from the higher-temperature l_d phase to the fluid-fluid (l_d/l_o) two-phase coexistence region. Spectra are shown for 310.4 K (a), 305.56 K (b), 303.86 K (c), 303.38 K (d), 302.32 K (e), and 300.85 K (f). Notice that the critical temperature is slightly higher for the d₆-labeled sample than for the d₆₂-labeled sample (Fig. 1).

These spectra have been analyzed by fitting the line shapes to Gaussian or Lorentzian broadened powder patterns, allowing for an ellipsoidal distortion of the liposomes by the magnetic field. Fig. 4 shows the spectrum at a temperature of 310.39 K, well above the critical temperature. The best fit to a Lorentzian broadened powder pattern, shown by the dotted line in the figure, is obtained with a semimajor/semiminor axis ratio of ρ = 1.27. This line shape clearly has too much intensity in the wings of the spectrum. The best fit to a Gaussian broadened powder pattern, with ρ = 1.07, is shown by the dashed line. Although the fit in the wings of the spectrum is improved, the experimental line shape is not perfectly reproduced. Although further refinement, allowing a mixture of Gaussian and Lorentzian character in the line shape, would provide closer agreement with the experimental spectrum, it is felt that the Gaussian powder pattern with ellipsoidal distortion provides an adequate representation of the spectra. The spectra above T_c are fit with a single Gaussian broadened powder pattern. The parameter ρ was in the range 1.05–1.08 above T_c. The other parameters obtained are summarized below. Below T_c, a superposition of three Gaussian powder patterns, all having the same ellipsoidal ratio, ρ, was used. Each powder pattern was characterized by an area, a quadrupolar splitting, and a Gaussian broadening factor, σ. The areas of the two components from the l_o phase were constrained by the fitting procedure to remain within 10% of each other. The factor ρ varied from 1.0 to 1.08 as temperature was varied below T_c.

Figure 4.

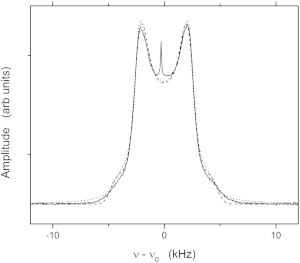
Comparison of the fit of the experimental ²H NMR spectrum (solid line) of 37.5:37.5:25 DOPC/DPPC-d₆/cholesterol at a temperature of 289 K to a Lorentzian broadened powder-pattern line shape (dotted line) and a Gaussian broadened powder-pattern line shape (dashed line). Notice that neither line shape fits the 0° shoulders very well, presumably due to an orientation-dependent T_2e.

Fig. 5 shows the quadrupolar splittings obtained both above and below T_c, the error bars are the standard errors returned by the fitting procedure. As expected, above T_c there is a gradual, almost linear, increase in quadrupolar splitting as the sample temperature is lowered. This can be compared to the roughly linear variation of M₁ with temperature shown in Fig. 2 for the chain perdeuterated sample. At the critical temperature, the powder pattern splits into three components, as previously mentioned. The uncertainties in the quadrupolar splittings are quite large near the critical point where all three splittings rapidly approach each other (as T_c is approached from below). The changes in the quadrupolar splittings shown here are the result of two factors: first, the splittings are gradually increasing as temperature is lowered; and second, the domain compositions are continuously changing as temperature is lowered. In particular, the cholesterol concentration of the l_d phase domains (those having the smallest splitting) decreases substantially from that of the nominal sample compositions (25 mol %) and the cholesterol concentration of the l_o phase domains increases somewhat.

Figure 5.

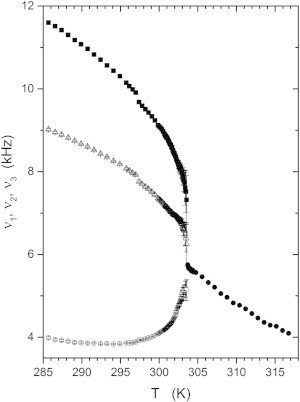
Temperature dependence of the quadrupolar splittings for l_d and l_o components of the ²H spectrum of the 37.5:37.5:25 molar proportion DOPC/DPPC-d₆/cholesterol sample. Solid circles represent the l_d component above the critical temperature, T_c, open circles the l_d component, ν₁, below T_c. Open triangles and squares represent the l_o phase components, ν₂ and ν₃.

At 297 K, there appears to be a small discontinuous step in the values of the splittings in Fig. 5. This is an experimental artifact caused by a change in the flow rate of the air used to extract heat from the oven. Regrettably, it was necessary to change this flow rate to further lower the sample temperature.

Each powder pattern is characterized by a Gaussian line width parameter σ, which changes dramatically with temperature both above and below T_c, as illustrated in Fig. 6. The solid circles give the powder-pattern line width, σ₁, in the l_d phase above T_c, and the open circles are for the l_d component below T_c. The open triangles and squares are the line widths, σ₂ and σ₃, of the two inequivalent powder patterns observed for the l_o phase component. These differ slightly from each other but do not appear to show the strong temperature dependence near T_c that the l_d component does.

Figure 6.

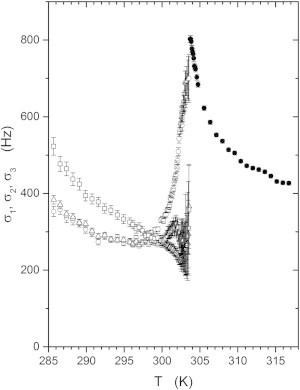
Temperature dependence of the Gaussian line widths of the DOPC/DPPC-d₆/cholesterol sample. Open and solid circles correspond to the l_d component below and above T_c, respectively; open triangles and squares, are for the l_o components below T_c.

The width of the static powder-pattern line shapes observed in ²H NMR spectra of lipid bilayers depends on several factors. Slow fluctuations of the quadrupolar interaction are an important contributor to the line width, but other factors include the temperature homogeneity across the sample and the homogeneity in the sample composition. There may also be a tendency for the two methyl groups to become slightly inequivalent (i.e., have different splittings) at high cholesterol concentrations at lower temperatures, even in the l_d phase (42).

Because of the strong dependence of the quadrupolar splittings on cholesterol concentration in these ternary mixtures, the homogeneity of the sample composition is a very important factor. Depending on temperature, the methyl group quadrupolar splitting may vary from something like 4 kHz for no cholesterol to 12 kHz for 30 mol % or more cholesterol. Thus, for a sample whose local cholesterol concentration varies by no more than 1 mol % across the entire sample, we might expect a contribution to the line width of as much as 200–300 Hz. Just below T_c, a temperature gradient of 0.1 K across the sample could also result in a contribution to σ₁ of as much as 200 Hz (though evidently this is not a significant factor above T_c, where the splitting of the l_d component varies relatively slowly with temperature). However, the line widths σ₂ and σ₃ remain relatively small and do not change as dramatically as σ₁, even though the splittings ν₂ and ν₃ change rapidly with temperature just below T_c. This suggests that the temperature gradient cannot be an important broadening factor. For this reason, we estimate that the temperature gradient across the sample, near T_c, must be <∼0.1 K.

Orientational fluctuations in the quadrupolar Hamiltonian provide an important contribution to the spectral line width (34,43). Quadrupolar echo relaxation measurements, to determine the echo decay time, T_2e, were performed at 308.8 K and 292.6 K using echo delay values varying from 50 to 800 μs. The relaxation across the powder pattern was exponential, with only a slight degree of orientation dependence (the 0° shoulders relax slightly faster than the 90° peaks). At 308.8 K, the relaxation time is T_2e = 711 ± 1 μs. Using the relation 2$\sqrt{2\text{log}2}$ × σ_2e = 1 / (π × T_2e), which relates the full width at half-maximum to the Gaussian width σ_2e leads to σ_2e = 190 Hz, which is much smaller than the static powder-pattern line width of σ = 502.4 ± 1.4 Hz measured at that temperature. In a similar way, in the l_o phase at 292.6 K, we obtained ${\text{T}}_{2e}^{\left(1\right)}=893\pm 7\mu \text{s}$, ${\text{T}}_{2e}^{\left(2\right)}=843\pm 6\mu \text{s}$, and ${\text{T}}_{2e}^{\left(3\right)}=656\pm 5\mu \text{s}$ which correspond to ${\sigma }_{2e}^{\left(1\right)}=151$ Hz, ${\sigma }_{2e}^{\left(2\right)}=160$ Hz, and ${\sigma }_{2e}^{\left(3\right)}=205.4$ Hz. These are smaller than the measured Gaussian line widths: ${\sigma }^{\left(1\right)}=303.5\pm 3$ Hz, ${\sigma }^{\left(2\right)}=336\pm 3$ Hz, and ${\sigma }^{\left(3\right)}=368.4\pm 4$ Hz. The uncertainties quoted above, both for the relaxation times and for the static line broadening parameters, are those returned by the fitting procedures used. Thus, relaxation accounts for only about half of the static powder-pattern line width observed. This prevents us from analyzing the static powder-pattern line widths in the same manner with which we previously analyzed the magic angle spinning side-band line widths (10).

The fraction of DPPC-d₆ that is in the l_o phase is given by the ratio of the areas of the spectra of the two inequivalent methyls in the l_o phase to the total area of the spectrum

$$g_{lo}=\left(A_2+A_3\right)/\left(A_1+A_2+A_3\right),$$ (4)

where A₁ is the area of the l_d component and A₂ and A₃ are the areas of the l_o components. Fig. 7 shows g_lo as a function of temperature below T_c. The solid curve in the figure is a fit to a simple function of T_c − T

$$g_{lo}=\left(a+b[T_c-T]\right)+c[1-exp\left(-[T_c-T]/d\right)],$$ (5)

which allows us to interpolate values of g_lo close to the critical point. No other interpretation is placed on the form of the function used. The parameters of the best fit give a = 0.1516 ± 0.014, b = 0.0102 ± 0.0008, c = 0.553 ± 0.013, and d = 1.59 ± 0.07.

Figure 7.

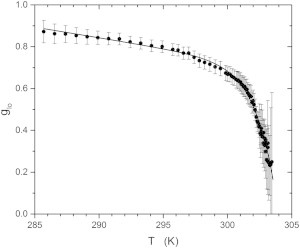
Temperature dependence of the l_o phase fraction g_lo of the DOPC/DPPC-d₆/cholesterol sample determined from the ratio of the combined areas of the l_o phase signals to the total spectrum area. The solid curve is a fit to an arbitrary function of T_c − T to facilitate comparison with the first-moment data in Fig. 2.

In the earlier discussion of the temperature variation of M₁ for the sample made with perdeuterated DPPC-d₆₂, it was pointed out that the behavior below T_c depended on ΔM₁ and on the l_o fraction g_lo (Eq. 3 and Fig. 2). We can use the parameters of the fit to the g_lo versus T data for the sample containing DPPC-d₆ to calculate the l_o fraction for the sample with DPPC-d₆₂ by replacing the value of the critical temperature for the d₆ sample, T_c = 303.74 K, by the value of the critical temperature of the d₆₂ sample, T_c = 301.51 K. Then, we can fit Eq. 3 to the data in Fig. 2 using $\Delta M_1=\Delta M_1^0\times {[\left(T_c-T\right)/T_c]}^{{\beta }_c}$, to obtain the solid line in Fig. 2. The parameters of this fit are $\Delta M_1^0=7.1\pm 0.7\times {10}^4$ s⁻¹ and β_c = 0.391 ± 0.02. This is close to the value of β_3D = 0.325 predicted by the 3D Ising model. Also shown for comparison (Fig. 2, dashed line) is the best fit to these data using the critical exponent β_2D = 0.125 that corresponds to the 2D Ising model.

Because we have the quadrupolar splittings of the l_d and l_o components from the analysis of the spectra of the sample containing DPPC-d₆, we can evaluate < Δ(δν) > directly (this corresponds to the ΔM₁ used for the perdeuterated lipid sample). This is given simply by the expression

$$<\Delta \left(\delta \nu \right)>=[\left({\nu }_2+{\nu }_3\right)/2]-{\nu }_1.$$ (6)

The results are plotted in Fig. 8. The error bars are based on the standard errors for the splittings returned by the fitting procedure. The solid line is the result of the fit to the function

$$\Delta \left(\delta \nu \right)=\Delta {\left(\delta \nu \right)}_0{[\left(T_c-T\right)/T_c]}^{{\beta }_c}.$$ (7)

The best fit parameters are Δ(δν)₀ = 17.37 ± 0.5 kHz and β_c = 0.338 ± 0.009. This is in close agreement with the value expected for the 3D Ising model, β_3D = 0.325. Also shown for comparison (Fig. 8, dashed line), is the best fit using the critical exponent β_2D = 0.125 that corresponds to the 2D Ising model.

Figure 8.

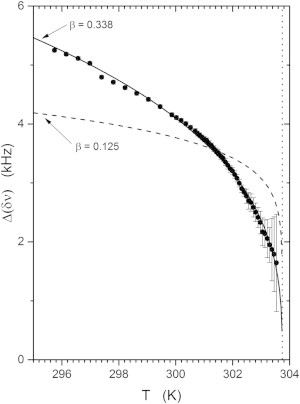
Temperature dependence of the difference between the average methyl group quadrupolar splitting of the l_o phase and the methyl splitting of the l_d phase below the critical point of the DOPC/DPPC-d₆/cholesterol sample. The best fit gives a critical exponent of β = 0.338 ± 0.009 and a critical temperature of T_c = 303.74 ± 0.07 K. The vertical dotted line indicates the critical temperature.

Conclusions

Multilamellar dispersions of the ternary mixture of DOPC/DPPC/cholesterol display a rich phase behavior that includes a broad range of fluid-fluid (l_d/l_o) phase coexistence when cholesterol concentration is high. Membrane rafts are thought to be manifestations of the same physical chemistry occurring in natural membranes. The existence of isolated domains of l_o and l_d membrane may be less important than the existence of a critical point for cholesterol concentrations comparable to that found in many cytoplasmic membranes. Proximity to a critical point results in local fluctuations in composition that may play an important role in membrane biochemistry.

In this article, we have presented measurements of ΔM₁ of the ²H NMR spectra of chain perdeuterated DPPC-d₆₂ and of Δ(δν) for chain methyl deuterated DPPC-d₆ in multilamellar dispersions of DOPC/DPPC/cholesterol with molar proportion 37.5:37.5:25. These two quantities are argued to be proportional to the order parameter, η, that describes the phase transition. These quantities approach zero at the critical point, with critical exponents β_c = 0.391 ± 0.02 for M₁ of the chain perdeuterated sample and β_c = 0.338 ± 0.009 for the methyl deuterated sample. These values, and our earlier results on the critical broadening of the ²H MAS side-band line widths (10), which gave a value for the critical exponent for the correlation length of ν_c = 0.628 ± 0.01, show that the multilamellar phospholipid dispersions belong to the 3D Ising universality class.

By comparing the powder-pattern line shapes obtained for these static (nonspinning) samples with simulations of Lorentzian or Gaussian broadened powder patterns, we conclude that neither shape can completely describe the experimental line shapes. Measurement of the quadrupolar echo decay time showed that dynamic fluctuations alone are not responsible for the line broadening and, therefore, that a line shape dominated by Lorentzian broadening is not expected. Inhomogeneities in sample composition and sample temperature, though both are estimated to be small, account for the non-Lorentzian contribution to the line width (amounting to ∼50% of the total broadening). For this reason, it was not possible to analyze the temperature dependence of the static powder pattern broadening as we had previously done for the MAS side-band line width.

Connell et al. (11) used atomic force microscopy to measure the difference in thickness between domains of the l_o and l_d phases in a DOPC/egg sphingomyelin/cholesterol mixture with a molar composition of 48:30:22. They found that the height difference approaches zero as (T_c − T)^0.334. Since bilayer thickness is related to the average ²H quadrupolar splitting in deuterated bilayers (38), which is also proportional to the first moment, M₁, the measurements of Connell et al. are comparable to those obtained here.

Fluorescence microscopy on GUVs, on the other hand, has yielded critical exponents for the correlation length, ν_c = 1.2 from line-tension measurements below T_c, and ν_c = 1 from measurements of the two-point correlation function above T_c (27,28). This work led to the conclusion that the GUVs belonged to the 2D Ising universality class.

Whichever theoretical model might eventually best describe critical phenomena in membrane bilayers, it is clear that the phenomena are a direct result of the large cholesterol concentration and of the differential interaction of cholesterol with long-chain saturated lipids compared to unsaturated lipids. What remains to be established is the extent to which membrane function depends on the critical fluctuations that must be present in natural membranes.