Nuclear Pore Complex Protein Sequences Determine Overall Copolymer Brush Structure and Function

Abstract

The transport of cargo across the nuclear membrane is highly selective and accomplished by a poorly understood mechanism involving hundreds of nucleoporins lining the inside of the nuclear pore complex (NPC). Currently, there is no clear picture of the overall structure formed by this collection of proteins within the pore, primarily due to their disordered nature. We perform coarse-grained simulations of both individual nucleoporins and grafted rings of nups mimicking the in vivo geometry of the NPC and supplement this with polymer brush modeling. Our results indicate that different regions or blocks of an individual NPC protein can have distinctly different forms of disorder and that this property appears to be a conserved functional feature. Furthermore, this block structure at the individual protein level is critical to the formation of a unique higher-order polymer brush architecture that can exist in distinct morphologies depending on the effective interaction energy between the phenylalanine glycine (FG) domains of different nups. Because the interactions between FG domains may be modulated by certain forms of transport factors, our results indicate that transitions between brush morphologies could play an important role in regulating transport across the NPC, suggesting novel forms of gated transport across membrane pores with wide biomimetic applicability.

Introduction

A particular membrane that sees a lot of cross-membrane traffic is the nuclear envelope in eukaryotes. The nuclear pore complex (NPC) is an important macromolecular structure that spans the nuclear envelope and regulates all nucleocytoplasmic traffic, including important processes such as the import of regulatory proteins from the cytoplasm and the export of RNA from the nucleus (1–5). It is a supramolecular structure composed of ∼30 different types of NPC proteins (nups) (2). A subset of the nups forms a structural ring or cylindrical-like structure that is embedded in the nuclear envelope. This structure forms an open aqueous channel, ∼50 nm in diameter, that connects the nucleoplasm and cytoplasm (Fig. 1). A second subset of nups, those which form the focus of this article, are grafted along the interior wall of the aqueous channel and are responsible for forming a selective diffusion barrier. Containing many phenylalanine-glycine (FG) repeats, these nups are called FG nups (2) and are structurally unique due to their large FG repeat domains, which are highly flexible and behave natively as polymerlike unfolded proteins. Hence, these FG nups are referred to as being intrinsically disordered or natively unfolded proteins (6). FG repeats further separate into different types, with commonly studied GLFG and FxFG repeat motifs known to have different binding affinities (7). In common Baker’s Yeast Saccharomyces cerevisiae, there are ∼150 copies of FG nups in each NPC and it has been hypothesized that the NPC pore is occupied by dozens of FG nups that interact with each other weakly via hydrophobic attractions to form a network that functions as a semipermeable diffusion barrier (see Fig. 1 A). This barrier maintains a tight seal against cytoplasmic particles larger than ∼4 nm while allowing smaller particles to passively diffuse through. However, amazingly, it also allows the facilitated transport of specially tagged particles up to 40-nm diameter (8), at rapid speeds of 5–20 ms per transported cargo for even large mRNP complexes (9). Additionally, the NPC does not exert any forces or expend any energy, with the only known free-energy consumption being limited to maintaining a gradient associated with the transport factors that generate the directionality of transport.

Figure 1.

Illustration of NPC models. Each NPC depicted spans the double lipid bilayer nuclear envelope, oriented such that the tops of the pores face the cytoplasm, while the bottoms of the pores face the nucleus. (A) FG nups form a hydrogel, which transport-factors and their cargo complexes transit by binding with FG motifs and temporarily disrupting cross-links in the FG nup meshwork (14). (B) FG Nups are collapsed and lie along the wall of the NPC, creating a surface to which transport-factors bind and diffuse along in a dimensionally reduced manner (36). (C) FG nups form a polymer brush that binds transport factors (possibly collapsing in their presence) but excludes unwanted molecules that do not interact with the FG nups (15). (D) Individual FG nups can have collapsed coil gel-like regions and extended coil brushlike domains, resulting in a microphase separation of these domains within the NPC. A central pluglike structure and another dense shrub region, which lies along the wall of the NPC, are separated by a polymer brush of extended disordered regions (stalks) of FG nups (26). To see this figure in color, go online.

Despite the NPC’s key role in biology and numerous studies on the structure and properties of individual nucleoporins (1–3,6,10–13), the actual structure of the polymer complex within the nuclear pore and its mechanism of operation are still under debate. For example, prominent models of nuclear pore transport, such as the selective phase/hydrogel (14) and virtual gate/polymer brush (15) models, assume very different morphologies for the polymer complex filling the nuclear pore (Fig. 1). The hydrogel model predicts that FG domains interact via hydrophobic amino acids to form a filamentous meshwork that physically blocks protein diffusion whereas the polymer brush model predicts that FG domains have limited hydrophobic interactions and instead behave as bristles that form an entropic gate at the NPC that blocks protein diffusion.

Most theoretical and polymer physics approaches (16–19) to this problem typically tend to assume a homogenous structure for individual FG nups, resulting in a relatively homogenous NPC architecture. There have also been recent attempts to perform coarse-grained simulations of NPC proteins and the entire transport process through the NPC (20–23), but these too suffer from either the intrinsic drawback of assuming that the NPC proteins are homogeneous, or of overreliance on simple amino-acid characterizations and assumptions, which could have left the ultimate underlying molecular architecture of the NPC unresolved. In this article, we attempt to overcome these issues by using a more reductionist approach starting from FG nups sequences combined with a detailed coarse-grain (CG) model that can reproduce secondary and tertiary structure of proteins. We show that different regions or blocks of an individual NPC protein can have distinct, quantifiably different forms of disorder and that this property appears to be a conserved functional feature. The unique diblock polymer structure of the longer FG nups, critical for transport, under certain conditions result in a mesoscale polymer brush structure with a dense FG domain core surrounded by brush of disordered proteins with a high concentration of charged amino acids. To understand the physics behind the emergent structure we developed a simple polymer brush model based on the properties of individual nups revealed by our CG model. Given that the interactions holding the dense FG domain core together are likely be modulated by certain transport factors, our polymer brush modeling suggests that the approach of certain forms of cargo could alter the local brush structure, to allow insertion and regulated transport.

Methods

The CG model of Hills et al. (24) was run using the large-scale atomic/molecular massively parallel simulator (LAMMPS) (25) software suite. Using the three separate calibrated CG models with α, β, and γ equal to 3.35, 4.30, and 5.26, respectively, at 300 K, simulated polypeptide chains representing the disordered regions of various FG nups from S. cerevisiae and humans were equilibrated for 1 μs, using starting conditions that consisted of fully extended protein configurations for the simulations without the cylindrical boundary conditions. Disordered regions of FG nups that were simulated used the nup-specific definitions defined in Yamada et al. (26) and the Supporting Material. For the porelike simulations with cylindrical boundary conditions, initial nup configurations (identical sequences as in the individual nup simulations) were as depicted in the Supporting Material. During the 1-μs equilibration, all individual FG nups collapsed from their initially fully extended configuration in <300 ns. After equilibration, data were then taken from a 4-μm production run. Postsimulation analysis was done to determine the average radius of gyration of different domains as defined in Yamada et al. (26). Contact proximity between two given side-chain beads was calculated by counting the number of times side chains were within 16 Ångstroms of each other in the trajectory snapshots (saved every 100 ps during the 4 μs of production simulation), then normalizing by the number of snapshots. Initial starting conditions for the ring simulations can be seen in the Supporting Material. Heat maps of the density of FG motifs and charged amino acids in the FG nup with the most FG repeats across 10 different species were only applied to sequence regions that were predicted to be disordered via a PONDR-FIT score >0.5 (27) and to have >40 amino acids. The resulting binary densities of FG motif/amino acids (aa) and charged aa/aa were smoothed by a running average over a 20-aa window.

Results

Coarse-grained simulations

Although all atom molecular-dynamics models can accurately reproduce the local secondary structure and nature of tertiary contacts for proteins, it is not computationally feasible to study even a single FG nup’s properties due to their large size (∼1000 aa) and the long timescales involved (in μs). Characterizing the overall structure formed by a hundred-odd FG nups becomes next to impossible. To overcome these issues we use a CG model (24) that is detailed enough so that it is able to reasonably reproduce secondary and tertiary structure and even fold small proteins ab initio starting from extended states, but simple enough such that multiprotein systems over microsecond timescales are computationally feasible. This CG model attempts to reproduce the energy landscape of real proteins by representing each amino acid by multiple CG interaction sites and by using specially developed interactions between these sites. The physical potentials between these CG interaction centers is derived from measuring the forces present in highly accurate all-atom simulations of diverse protein sequences, using the multiscale coarse-graining method (28). This method makes no assumptions about the type of interactions between CG sites, and additionally implicitly includes multibody correlations (29) in the resulting implicit solvent model with an effective CG potential. In this CG model, secondary and tertiary structure emerges naturally through the comprehensiveness of the physical model, and it is general enough to simulate proteins of arbitrary amino-acid sequence.

Typically, CG potentials for a specific protein simulation are scaled such that model results match well with experiment (24,30). This was achieved by multiplying the entire CG potential by a constant scaling factor. Experimentally measured properties of disordered FG nups have yet to converge, therefore we developed a number of CG models with different scaling factors (α, β, and γ), with each scaling factor corresponding to a different class of experimental results. FRET measurements of human nup153 by Milles and Lemke (31) have shown the disordered regions of this protein to consist of nearly entirely compact collapsed-coil configurations. The CG model α was therefore developed to mimic these results, scaled such that it produces a collapsed coil (molten globule) (32) for the disordered region of nup153. (Table S1 compares model and experimental radii in the Supporting Material). Other experiments have shown nup153 to take on more extended configurations, forming relatively extended brush configurations that undergo reversible collapse in the presence of transport factors (33). CG model γ was therefore developed to mimic these results, scaled such that it produces a relaxed coil (32) for the disordered region of nup153 (see Table S1). Bead-halo experiments by Yamada et al. (26) indicate nups are biphasic, with stalk domains noninteracting in general whereas, on the other hand, FG domains are sticky to other FG domains. FG nups were also found to be biphasic in terms of polymer structure, with stalk domains having expanded polymer conformations, whereas FG domains had more-compact polymer conformations. A scaling factor β precisely in the middle of the α- and γ-scalings (Methods) was found to produce such biphasicness, with this scaled CG model labeled β.

The FG nups we simulated were taken from evolutionary distant S. cerevisiae (Nsp1, Nup1, Nup100, and Nup116) and H. sapiens (Nup98 and Nup153), focusing on long FG nups with large disordered regions which have a biphasic sequence structure that can be separated into an FG domain and stalk domain. An FG domain corresponds to a sequence region with a low concentration of charged amino acids and a high concentration of FG motifs, whereas the stalk domain corresponds to a disordered sequence region with a high concentration of charged amino acids (nup specific amino-acid domain definitions and disordered domains used are defined in the Supporting Material and Yamada et al. (26)).

Structure and dynamics of single nups

Polypeptide chains representing the disordered regions of various FG nups from S. cerevisiae and humans were started from an initially fully extended configuration and equilibrated before the start of simulation. Fig. 2 shows a typical snapshot of one such nup, Nsp1, after collapse and equilibration. The snapshot seems to indicate that these proteins can exhibit distinctly different kinds of polymeric structure along a single chain with regions that look like swollen chains to other parts that resemble collapsed coils. In general, the proteins seemed to adopt a block polymer structure to varying degrees, dependent on the form of CG model employed. Amino-acid regions of the FG nups simulated and domain definitions used are in Table S2.

Figure 2.

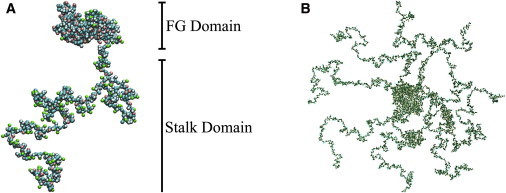
(A) Simulation snapshot of full length Nsp1 showing the biphasic FG domain and stalk domain structures in the α-model. Snapshots for the other models β and γ are shown in Fig. S7 in the Supporting Material. (B) Snapshot of a ring of eight Nsp1s in the α-model. To see this figure in color, go online.

To quantitatively characterize FG nup structure, we define the contact probability between a pair of amino acids as the percentage of time the corresponding CG backbone beads are within 1.6 nm of each other. The diblock polymer structure of these FG nups is particularly clear from the contact probability maps showing the contact probability over all possible amino-acid contact pairs (Fig. 3 and see Fig. S12 in the Supporting Material). In many cases these show a universal block diagonal structure with a part that is almost diagonal—representing an extended stalk and a square block that is uniformly lit up, indicating a collapsed disordered structure—the tip. The lack of contacts between the blocks indicates the blocks maintain their distinct identities over time. The diblock structure was most strongly seen in model β. Model α often produced significant contacts between FG and stalk domains that destroy diblock structure because the two domains often interact, whereas model γ produced nups with little difference between FG and stalk domains with the entire FG nups representing unstructured extended homogenous polymers.

Figure 3.

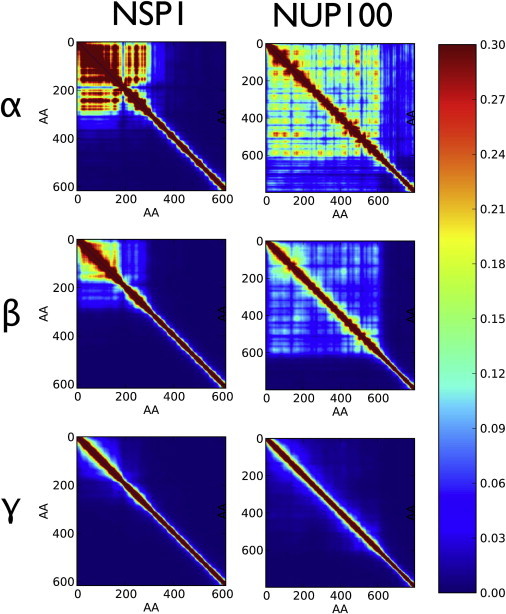
Contact maps for the different CG models α, β, and γ for Nsp1 and Nup100. Maps for Nup1, Nup98, Nup116, and Nup153 can be seen in Fig. S12 in the Supporting Material. Contact probability maps show the time-averaged contacts between all pairs of amino acids. A block diagonal structure is noticeable in numerous contact maps, with one block for FG domains and diagonal contacts for stalk domains. A diblock structure can be most strongly seen in FG nups simulated under scenario β. Model α shows some block structure but often produces significant contacts between FG and stalk domains, because the two domains often interact. In striking contrast to models α and β, model γ produced nups with little difference in contact probability between FG and stalk domains with the FG nups representing unstructured extended homogenous polymers. Amino-acid residues shown are with respect to the disordered domains of the simulated FG nups, whereas full protein amino-acid indexes can be determined by domain definitions in Table S2. To see this figure in color, go online.

Under all model assumptions, individual FG nups were highly dynamic and disordered. FG domains across all simulated nups maintained a relatively smooth block contact structure, with contacts between amino acids rapidly exchanging and no folded constant contacts visible. The consistency in the diblock structure that is exhibited across the different nups indicates that there must be some underlying general features in the sequence structure that is maintained. In particular, this would suggest that disruption or randomization of the sequence would result in a loss of such structure. To test this, we repeated the simulations with a shuffled version of the amino-acid sequence of Nsp1, which resulted in the loss of diblock structure (see Fig. S1). This clearly suggests that assuming nup sequences have an effectively homogeneous character could be problematic and that the biphasic sequence structure is responsible for producing two distinct types of dynamic domains via weak but specific interactions among portions of FG nups. The sequence features of the FG and stalk domains delineating these domains are discussed in the Bioinformatics subsection later in this article and in Ando et al. (34).

An earlier hypothesis that FG nups can form a treelike structure was based on the experimentally measured properties of fragments of FG nups from S. cerevisiae (26). Here, our simulation results on full-length FG nups support this hypothesis by demonstrating that it is clearly possible that individual fragment properties combine to form true diblock copolymers. Additionally, the CG model used here is, to our knowledge, the first such model capable of reproducing the observed interactions (26) between different fragments from different regions of the FG nups.

To quantitatively characterize the levels of disorder within distinct regions of the contact probability maps, we derived looping probabilities from the maps for different domains of the FG nups. We define the looping probability P_l(s) to be the probability that two monomers of size b, separated by a contour length of sb along the amino-acid chain, are within a spatial distance r < R_cut. In our analysis, R_cut = 1.6 nm. For two monomers of an ideal chain, the looping probability for a given monomer separation distance, sb, is given by the integral of the probability distribution of end-to-end distances up to R_cut,

$$P_l\left(s\right)=\underset{r<R_{cut}}{\int }\text{d}V{\left(\frac{3}{2\pi s{b}^2}\right)}^p\text{exp}\left(\frac{-3r^2}{2s{b}^2}\right),$$ (1)

with exponent p = 3/2 (35). An extended chain would have a power of p = 9/5 and a collapsed coil would have a p = 1, with appropriately scaled constant prefactors. Additionally, we quantitatively determined the statistical significance of the block structure of contact maps in the γ-model as they seem to disappear in this model. At a 40-amino-acid separation distance, we measured the average contact probability and standard deviation (SD) between all possible amino-acid combinations for the shuffled Nsp1 sequence that is shown in the Supporting Material. Measuring the same 40-amino-acid separation contact probabilities for the γ-model contact maps, we determined that the average of this contact probability over all contact maps in this model was only 1.02 SDs away from the corresponding value for the unstructured shuffled Nsp1 sequence. In contrast, the same contact probability averaged over the β-model contact maps was 3.58 SDs away from the shuffled Nsp1 sequence value.

Fig. 2 shows a log-log plot of the average measured looping probability as a function of s for the all FG and stalk domains simulated, with a numerically fitted theoretical looping probability (for the power p) over the amino-acid separations >5 and <65 monomers. Qualitatively, a high looping exponent power p for a particular domain would imply that that part of the polymer is relatively extended spatially, because the contact probability falls off more rapidly as s is increased within that domain.

As can be seen in Fig. 2, FG domains have looping exponents significantly lower than those of stalk domains, indicating the constantly large difference in ensemble structure between these two types of domains. For the α, β, and γ CG models, the average fitted scaling exponents for the FG domains were 1.16, 1.38, and 1.81, respectively. For the stalk domains, the average fitted scaling exponents were 2.08, 2.58, and 2.82 for the different models, respectively. We also note an important caveat that these simulations of individual FG nups by themselves were done ignoring the effects of the crowded pore environment (36) and other FG nups. Although we analyze aggregates of interacting FG nups in the next section, our simulations do not include the crowding effects from transport factors, cargo, and other molecules in the cellular milieu that can significantly modulate FG nup behavior (37).

Structure and dynamics of nup rings

To look at the structures formed by multiple interacting nups in vivo, we performed simulations of rings of Nsp1 and Nup100 (identical sequences as in the individual nup simulations) grafted in an eightfold symmetric manner to the inner surface of a neutral, nonreactive cylinder, with the grafted-end locations chosen in a manner consistent with the grafting orientation and FG nup anchor domain positions within the nuclear pore. For a single ring of FG nup trees, we chose the dimensions of the enclosing cylindrical boundary to be (5 nm axial length, 50 nm diameter), representative of the geometry of the NPC as shown in Fig. S4 (26).

Fig. 4 shows the total mass density of the simulated rings of Nsp1 FG nups. The mass density clearly reveals a dense central plug connected by peripheral cables to the pore walls in the α- and β-models, with a plug mass density which, in all scenarios, is much smaller than the mass density of folded proteins of ∼1400 mg/cm³ (38). The mass density can be tied directly to the microphase separation of the different blocks of the natively unfolded proteins. One block phase (the FG domains) separated along the center of the channel whereas the other block (the stalk regions) aggregated along the periphery (see Fig. S13). This microphase separation could explain the observation of a pluglike structure in cryo-electron microscopic examination of NPCs (39). This pluglike structure is currently not recognized as a structural element of the nuclear pore complex and is instead rationalized as an artifact of cargo in transit (40). Interestingly, in the γ-model, which represents an extended coil scenario, there is no microphase separation present—reminiscent of the virtual gate model.

Figure 4.

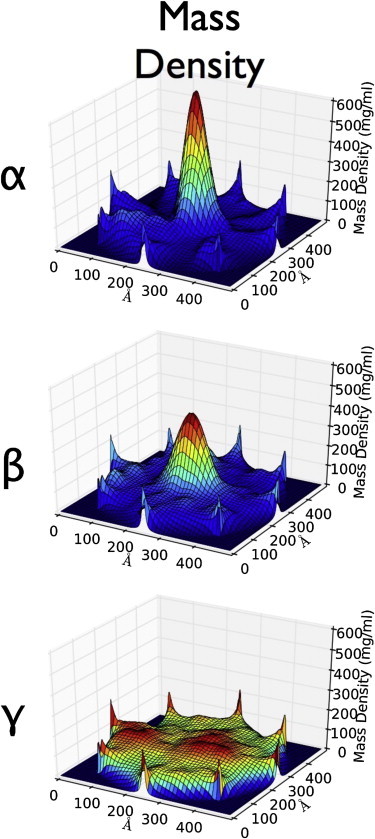
Density maps of a simulated pore containing eight Nsp1 FG nups. Plotted for all three models is the total mass density (mg/mL) along the pore. The total mass density clearly reveals a dense central plug connected by peripheral cables to the pore walls in the α- and β-models, whereas the γ-model produces a homogenous extended brush. Plots of the mass density of FG domains, the mass density of stalk domains, and the net charge density can be seen in Fig. S13 in the Supporting Material. To see this figure in color, go online.

Spatial net charge density of the ring of Nsp1 nups mirrors closely the mass density of the FG domain, because FG domains are in general positively charged (34). This produces a striking effect in the α- and β-models, with a strongly positively charged plug region forming that has a net charge density much higher than considered earlier by Colwell et al. (41) and Tagliazucchi et al. (23), with the same possible functionality but much greater attraction to negatively charged transport factors due to radial concentration toward the center of the NPC channel.

In contrast to nups like Nsp1 and Nup1 that have a long stalk region and comparatively small sticky tip, other FG nups, like Nup100 have large sticky tips and comparatively short stalk regions. We simulated rings of Nup100 in an identical manner to Nsp1, resulting in similar results except for a key difference that Nup100 rings in isolation are unable to close in the α- and β-models, unlike Nsp1 which can close the pore in these scenarios (see Fig. S5). In the next section, we use polymer brush modeling to understand the structure of Nup100 rings in the presence of closed Nsp1 rings, and find a cooperative effect where Nup100 rings will close in the presence of closed Nsp1 rings.

We did not observe any rigid contacts from the ring simulations that lasted for a time in excess of 1 μs, so we rule out the existence of amyloid or rigid hydrogel structures that have contacts on these timescales in the β-model used. This can also be seen by the high similarity of the contact map for an individual free Nsp1 (Fig. 3) and the contact map for a grafted Nsp1 (see Fig. S2) in the ring conformation. Even in the compact α-model, the dense FG domain central plug contains individual FG domains that maintain their disordered state and rapidly exchange contacts to form block diagonal contact maps for the full Nsp1 nup.

Polymer brush morphology and dynamics

To understand the underlying physics that governs the formation of different types of mesoscale structures and possible transitions between them, we turn to polymer physics modeling. Here we introduce a simple polymer brush model that treats an idealized polymer brush constructed of diblock polymers representing the FG nups. We assume that the nups can be described by neutral excluded volume polymers (representing the stalk domains) with an appropriate length and stiffness, and grafted to the inside of a cylinder of diameter equal to that of the nuclear pore. We then incorporate the biphasic structure of the nups in the α- and β-models by modeling the ends of the polymers as structureless cohesive blobs that correspond to the cohesive FG domains at the nup tips. The resulting configuration is a polymer brush as shown schematically in Fig. 5 A.

Figure 5.

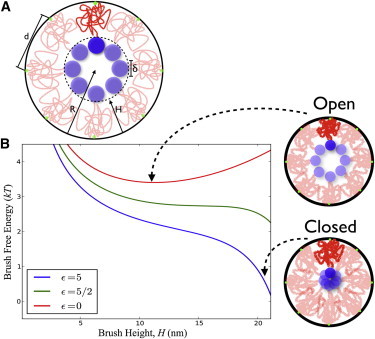
(A) Schematic of a polymer brush structure formed by diblock FG nups. Parameters H, height of the brush; R, radius of the pore; δ, diameter of the sticky tips; and d, the average distance between anchor points. (Green circles) Locations at which FG nups are grafted to the pore. (B) Free energy of the Nsp1 brush as a function of brush height for various values of the blob cohesive energy (ϵk_BT). Brush height can extend to a maximum of ∼22 nm, which is the radius R of the modeled pore minus the size of the sticky tips. (Right) Schematic diagram of the proposed diblock copolymer brush gate model at various minima of the brush free energy. When particular transport factors are present that are able to outcompete the inter-FG domain sticky-tips interactions, the brush is able to open up to a new free energy minimum that can accommodate the cargo. When interactions between sticky tips are able to recover into the several kT range, the pore is able to close with a free energy minimum at H∼R−δ. We estimated the self-interaction energy level of the Nsp1 sticky tip to be 4.7 kT (see the Supporting Material), which also sets the energy scale for blob-blob interactions of ϵkT. To see this figure in color, go online.

The question now becomes: What is the height H of this brush? Do the nups extend all the way into the center of the pore and fill the space, or are they collapsed along the sidewalls or do they form a brush with an intermediate height that still leaves an open transport conduit along the middle of the pore? The equilibrium height of this brush can be derived from a minimization of the free energy of the brush, which has contributions coming from the entropic stretching of the stalks, the excluded volume interactions (steric hindrance) between the stalks, and the cohesive energy interactions between the tip blobs. Even within this simple model, the curvature of the grafting surface and the cohesive tips result in the brush height being given by the solution to a nonlinear differential equation. We can, however, make another mean-field approximation to arrive at an algebraic form for the effective free energy per chain (see the Supporting Material)

$$\frac{F}{k_{B}T}\sim {\left(H/a\right)}^{5/2}{N}^{-3/2}+\frac{a^{5/2}{N}^{3/2}R{H}^{-1/2}}{d^2\left(2R-H\right)}-\frac{ϵ{\delta }^{2}R}{d^2\left(R-H\right)},$$ (2)

where ϵk_BT is the effective cohesive energy between a pair of blobs. The first two terms of the free energy follow directly from prior work on polymer brushes in cylinders (42,43).

To begin, we specifically choose one of the Nups to model: Nsp1. The extended stalk domains are modeled by excluded volume polymer chains with sizes as measured from the β-simulation, which determines the Kuhn length a and effective polymerization number N (see the Supporting Material). The cohesive domains at the tip are expected to be in a small, compact, collapsed state. We model these as featureless sticky blobs of size (diameter) δ = 3.6 nm, twice the radius of gyration as measured in the β-CG model simulations. We assume that the average spacing between grafting points of Nsp1 along the pore wall is d ∼ 10 nm, which we estimate by assuming that there are 32 copies (3) of Nsp1 anchored along the inner wall in a symmetric fashion along the geometry used in Yamada et al. (26) (see Fig. S4). The pore radius is taken to be R ∼ 25 nm.

Fig. 5 B shows a plot of the free energy as a function of the brush height for different values of the cohesive energy with all the other parameters being set by the values for Nsp1 that were detailed above. The minima in these curves correspond to equilibrium values of the brush height. For no cohesion (ϵ = 0) we see that the equilibrium actually corresponds to a brush height that is approximately one-half the pore radius, implying that if cohesion between the tips is lost, there will be a wide-open channel down the center of the pore. We call this the open state of the gate. As the cohesive energy is increased, we see a new minimum developing at H∼R−δ, which is the state where the stalks are extended so that the cohesive blobs are at the center, thus completely closing the conduit. This we will refer to as the closed state. This indicates that there will be a transition between the closed and open states as the cohesion energy is varied. Thus, the biphasic functional arrangement of domains with an extended stalk and cohesive tip leads to a brush structure that can be switched between two states of the brush: open and closed, as shown in Fig. 5.

With reference to gated transport, it is known that transport factors, such as karyopherin/importin, bind to cohesive FG motifs (44,45). This provides a mechanism to disrupt the intermolecular cohesiveness between nup tips by the competitive binding of karyopherin. We propose that the binding of certain particular transport factors in vivo results in such a switch from the closed to open state forming the basis for our model. In other words, specific types of transport-mediated cargo complexes could have the ability to dissolve into the central plug that keeps the gate closed, thus effectively opening it up to the desired diameter. These types of cargo can then undergo one-dimensional diffusion down the center of the channel. Enzymes on the nuclear side can cleave the transport factors, reducing the propensity of cargo to remain in the channel leading to escape to the nearest side—the nucleus. This picture works in the other direction with export signals as well and forms the basis of our diblock copolymer brush gate model. It is important to note that small cargo can also have alternate routes through the sides, and this aspect will be fully explored in future work.

We also used polymer brush modeling to understand the structure of Nup100 rings in the presence of closed Nsp1 rings. The free energy per chain is the same as in Eq. 2, but with an additional Nup100-Nsp1 cohesive cross-interaction term. Polymer sizes used were as measured in the Nup100 β-CG model simulations (see the Supporting Material). The per-chain cross-interaction free energy term between the two different types of FG nups can be simply modeled as the overlap fraction of an individual Nup100 sticky tip to the Nsp1 sticky tips at the center of the pore, multiplied by the blob interaction energy of the Nup100 sticky tips, ϵk_BT. The total Nup100 free energy is shown in Fig. S6 for different values of the blob-blob interaction energy, with ϵk_BT on the scale of the estimated self-interaction energy of Nup100 sticky tips (see the Supporting Material). Rings of Nup100 are unable to close the pore, except in the presence of an adjacent closed ring of Nsp1 nups.

Given how our brush modeling and CG simulation show that rings of Nup100 are unlikely to close the nuclear pore except in the presence of other closed rings of FG nups, cooperativity between FG nups could play an important role in nucleocytoplasmic gating. This idealized analysis where only Nup100 and Nsp1 are present ignores the excluded volume that shrub FG nups like Nup49 and Nup57 along the pore wall could have in crowding out stalk domains and similar effects induced by cargo and transport factors, although we tentatively conclude that Nsp1 or a FG nup with similar properties could be principal to the closing or sealing mechanism of the pore. Consistent with this hypothesis, combinatorial deletions of FG nups of the type performed by Strawn et al. (46), have shown perturbations in transport in mutants when Nsp1 or nups like Nsp1 are functionally impaired. Our idealized analysis also ignores possible compactification, extension, crowding, and cross-linking of FG nups via interactions with cargo and their transport factors, although the existence and/or nature of these effects in vivo remain unclear.

Bioinformatics

Our modeling connects the biphasic sequence structure across FG nups in S. cerevisiae to their diblock polymer properties, which, in turn, results in a bistable polymer brush morphology. If this unique brush structure is critical for NPC gating it would imply that the biphasic sequence structure should be conserved across eukarya. To examine this assertion, we analyzed FG motif density versus charged amino-acid density across the disordered regions of the FG nup with the most FG repeats across 10 diverse eukaryotic species; see Fig. S11. We found that these nups all showed a common feature where, within each individual FG nup, there are two domains—one high in FG motifs with another high in charged amino acids, with both domains disjoint from one another along the amino-acid sequence. One domain, labeled the FG domain (26), is low in charged amino acids and high in FG motif repeats, whereas the other domain, the stalk domain (26), has a high charged aa density and typically a low FG repeat density with an anchor domain that attaches the FG nup to the inner pore surface. A quantitative bioinformatic analysis of the distribution of motifs along nup sequences by Ando et al. (34) revealed a broad conservation across species of these bimodal sequence structures in FG nups. Our modeling work here suggests a possible explanation for the functional advantage gained by utilizing the bimodal sequence of FG nups in NPC transport regulation.

Discussion

Many experimental results regarding individual FG nup properties such as structure, location, and cohesive properties of different domains of nups are in conflict. What happens when these FG nups are put together within the confines of the nuclear pore channel is even more uncertain. Here we attempted to understand how the overall architecture of the assembly of disordered FG nups in the NPC channel is governed by the properties of individual FG-nups that make up the assembly using large scale physically accurate coarse-grained simulations. We calibrated our CG model against three main classes of experimental data on individual FG nup properties. We showed that, under certain conditions, a dynamic hydrogel-like structure does form, but only locally across spatial domains that have a high concentration of FG domains. We do not observe any scenario where FG nups form a dense layer located along the pore wall with a relatively open center as seen in some simulations (21–23), highlighting the importance of protein model structure on results. Using a calibrated model where the FG nups are relatively compact, our results indicate that a Forest type model structure (26) emerges, with the sticky tips of FG nups coalescing in the center to form a hydrophobic plug flanked by an extended coil brush zone.

Some recent experimental studies have measured that certain forms of facilitated transport take place near the walls of the NPC (47–51). Facilitated transport through peripheral routes does not appear to be a natural outcome from previous simulation efforts of the NPC (20–23). Such transport, however, appears to be supported by the α- and β-models where there exists a dense pluglike structure along the center of the channel that can block some forms of transport, forcing smaller actively transported cargoes to take the peripheral route along the channel walls. Other cargoes, larger in size and which have yet to be experimentally studied, may contain the proper transport factors that can open up the central plug as our polymer modeling suggests.

Our polymer brush modeling indicates that for the critical treelike nups to functionally open and close the pore in the Forest model, their sequence must follow a specific arrangement. The motifs and charges should form a diblock pattern and have a fixed polarity with the extended stalk region coming after the anchor region followed by the cohesive FG regions. Our analysis of 10 selected nups (with the largest number of FG motifs) across different species as well as earlier bioinformatic analysis of thousands of FG nups (34) clearly show that a biphasic sequence pattern is repeated across widely varying species, indicating that a diblock copolymer brush gating mode of transport may be a generic feature of certain types of nuclear import and export. Our modeling, therefore, sheds light on the underlying physics and biological function responsible for the presence of this biphasic pattern. Because the models α, β, and γ can also be viewed as roughly simulating FG nup properties under differing solvent conditions, other models of transport that do not rely upon individual FG nup biphasic sequence structure may also emerge as limiting cases of our model in different effective solvent conditions. We imagine that the γ-model loosely corresponds to poor solvent conditions because hydrophobic-hydrophobic interactions are weakened in poor solvent conditions, model γ represents a weakening of hydrophobic interactions, and that the FG nups are dominated by hydrophobic amino acids due to their compact size relative to neutral polymers of the same length. In the γ-model, the FG nups form a homogenous brush within the pore similar to the virtual gate polymer brush model, a gating mechanism the NPC may share with the diblock copolymer brush gate model under different types of solvent conditions.

Throughout this article, we have focused on the larger tree-type FG nups that have been shown to be critical for many forms of transport (46). Some details of NPC structure such as cytoplasmic filaments, nuclear basket structure, and short shrub FG nups that presumably lie along the pore wall have not been considered in our analysis. Because the cytoplasmic filaments and the basket are spatially well separated from the interior of the pore, we anticipate that they would not interfere with the copolymer brush structure. Given that the properties of the shrub FG nups are similar to the sticky-tip domains of tree FG nups in terms of bimodal adhesion (26), we anticipate that the shrub-sticky attractive tip interactions could help stabilize the wide open configurations of the copolymer brush in the presence of very large cargo in the middle of the pore. This sort of cooperativity could be relevant for the export of large ribonucleoprotein particles whose transport is facilitated by surface-bound transport factors. In the work of Strawn et al. (46), shrublike nups Nup49 and Nup57 were required for the viability of yeast cells, which indicates that the effects of shrubs are important and possibly necessary for the transport of large cargoes. It is interesting to note that we have shown that another form of cooperativity exists between different types of FG nups. Our modeling shows that the closure of the Nup100 ring requires the presence of a closed ring of Nsp1 or Nsp1-like nups. These and possibly other forms of cooperativity could play an important role in heightening the selectivity over a wider range of cargo sizes. Therefore, as is the case with numerous other biomolecular assemblies (52), cooperativity may be significant for NPC function.

Indirect evidence for the existence of a diblock copolymer brush gate mechanism in vivo include the fact that in mammals and yeast, weak alcohols such as hexanediol can loosen the permeability barrier of the NPC at low concentrations (5%) (53,54). Also, exposed electrical charges in cargos bound to karyopherins can slow down their passage across the NPC (55). Both these seem to indicate a hydrophobic plug but are also consistent with the hydrogel model. One way to truly differentiate between these models is to shorten/extend the stalk regions or to rearrange the cohesive regions within the same nups. We propose a plausible experiment where genetically engineered organisms have the anchor domains of their core FG nups moved away from their stalk domains and toward the end of their FG domains, a genetic rearrangement that we would predict to be lethal, whereas most other models, which assume homogenous FG nups, would predict identical function and viable organisms. Similarly, we also propose that genetically engineered organisms that have had their disordered FG nup sequence regions randomly shuffled should be lethal, whereas again most other models would predict identical function. Physically, we predict lethality in these genetic engineering experiments because they would destroy the specific microphase separation of the cylindrical brush that we predict would be key to the transport of certain types of important cargoes.

Our results not only increase the number of physical mechanisms by which we can understand nucleocytoplasmic transport, but also allow us to extend our model to designing and optimizing novel forms of biomimetic transport. Biomimetic membranes (56) have a wide variety of applications ranging from chemical and biological separation and purification (57), as a platform for analytical detection of antioxidants, antibiotics, antiviral, psychotropic and other substances, drug delivery (58), and self-contained reactors and mock cells (59,60). The regulated cross-membrane transport of material in such systems is of vital importance and our investigations of a well-defined biocompatible mechanism should be very useful. In general, any diblock polymers that follow the sequence-determined polymer properties of FG nups (excluded volume polymer stalk, with collapsed sticky tips) could be used to design biomimetic pores that regulate traffic using our diblock copolymer brush gate mechanism. In addition, amino-acid sequences of disordered proteins can be modified to change their overall polymer properties to be similar to FG nups in our diblock copolymer pore model, allowing similar regulatory pores to be created in many different contexts. Indeed, even though the NPC transport is poorly understood, there have already been efforts to make biomimetic gates inspired by the NPC (61,62).