Organelle Size Scaling of the Budding Yeast Vacuole Is Tuned by Membrane Trafficking Rates

Abstract

Organelles serve as biochemical reactors in the cell, and often display characteristic scaling trends with cell size, suggesting mechanisms that coordinate their sizes. In this study, we measure the vacuole-cell size scaling trends in budding yeast using optical microscopy and a novel, to our knowledge, image analysis algorithm. Vacuole volume and surface area both show characteristic scaling trends with respect to cell size that are consistent among different strains. Rapamycin treatment was found to increase vacuole-cell size scaling trends for both volume and surface area. Unexpectedly, these increases did not depend on macroautophagy, as similar increases in vacuole size were observed in the autophagy deficient mutants atg1Δ and atg5Δ. Rather, rapamycin appears to act on vacuole size by inhibiting retrograde membrane trafficking, as the atg18Δ mutant, which is defective in retrograde trafficking, shows similar vacuole size scaling to rapamycin-treated cells and is itself insensitive to rapamycin treatment. Disruption of anterograde membrane trafficking in the apl5Δ mutant leads to complementary changes in vacuole size scaling. These quantitative results lead to a simple model for vacuole size scaling based on proportionality between cell growth rates and vacuole growth rates.

Introduction

Organelles play critical roles in cell physiology by acting as reaction vessels for biochemical reactions. Eukaryotic cells are able to develop complex, overlapping metabolic pathways by using organelles to compartmentalize biochemical reactions and to optimize the environment needed for those reactions. For example, the internal redox state of the endoplasmic reticulum is tuned to promote proper protein folding, and degradative organelles like the vacuole/lysosome maintain an acidic pH necessary for catabolic processes to proceed efficiently. Because of the functional importance of organelles, it is perhaps not surprising that organelle size is responsive to various stresses or cell states (1).

Furthermore, it has been widely observed that as cells grow larger, their organelles also increase in size, i.e., organelle size scales with cell size (2–4) rather than maintain a constant absolute size. At a basic level, it is intuitive to think that as the cell grows, functional demand for its organelles increase, and therefore organelles grow to meet that increased demand. During cell division, organelles also need to increase in size such that enough can be provided to each daughter cell, as they generally proliferate via expansion and budding of existing organelles as opposed to de novo formation. There are thus strong a priori reasons to expect a positive scaling correlation between organelle size and cell size that would cause organelles to become larger as cells grow. Indeed, such scaling behavior has been observed for a wide variety of organelles, including the nucleus (3,5,6), mitochondria (7), and vacuole/lysosome (8,9). Although basic observations of organelle size scaling suggest active regulation of organelle size in response to cellular growth, very little is known about the nature of these scaling relationships or the mechanisms by which they are achieved.

The yeast vacuole presents an interesting model for organelle size scaling, as it carries out essential biochemical functions both in its lumen (degradation, storage) and at the limiting membrane (signaling). Therefore, the cell is likely to control both the organelle’s internal volume and surface area. Individual cells typically have 1–10 vacuoles that tend to be clustered (Fig. 1 A). Unlike other organelles such as the mitochondria that have a characteristic morphology that constrains the relationship between surface area and volume, yeast vacuoles can exhibit a range of morphologies. Consequently, the vacuole can adopt a wide range of volume to surface area ratios (10). Thus, the vacuole is an ideal model for determining how a single organelle’s volume and surface area are controlled in either an independent or coordinated fashion as well as how this relates to cell size.

Figure 1.

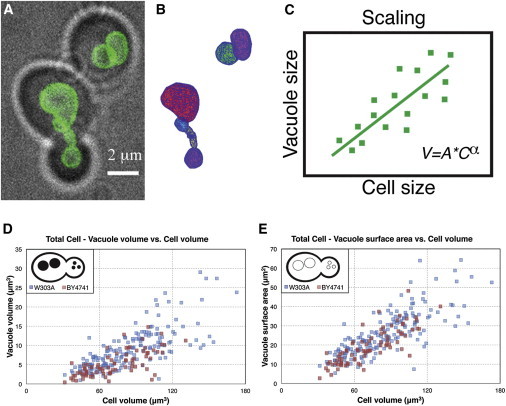
Vacuole size extraction and vacuole size scaling in WT strains. (A) Cells (brightfield) and vacuoles (VPH1-GFP) were imaged using a spinning disk confocal microscope. (B) Z-stacks were processed using a computational algorithm to reconstruct surfaces for each vacuole. (C) Cell and vacuole sizes measurements were fit with power-law scaling trends, which can be compared between different mutants and conditions. (D) Vacuole volume-cell volume scaling and (E) Vacuole surface area-cell volume scaling trends for W303A and BY4741 background strains.

Previous genetic screens have identified a great number of vacuole morphology mutants (11–14), but were unlikely to identify genes involved in vacuole-to-cell size scaling for two reasons. First, these screens typically relied on gross morphological criteria to categorize the mutants by visual inspection. Without a quantitative measure of vacuole size, it is not possible to detect more subtle variations. Second, because we suspect a priori that vacuole size may be correlated with cell size, any mutation affecting cell size would also exhibit an altered absolute vacuole size without necessarily affecting vacuole size control pathways per se. Only a change in vacuole-to-cell size scaling would strongly indicate some perturbation to vacuole size control. It is thus essential to measure vacuole size quantitatively in comparison with cell size if we are to begin a molecular dissection of the mechanisms of organelle scaling. To date, quantitative studies on organelle size have been limited due to the difficulty in extracting measurements of size on subcellular size scales. Thus, the precise scaling relationship between vacuole and cell size remains an open question.

We present here a novel, to our knowledge, method for measuring the size of objects on the size scale of the vacuole (Fig. 1, A–C). Using this method, we found that vacuole volume and surface area show distinct scaling trends with respect to cell size, and have found evidence for a molecular pathway, which contributes to establishing these scaling trends by adjusting the balance of membrane traffic to and from the vacuole.

Materials and Methods

Yeast strains and culture

BY4741 VPH1-GFP was taken from the yeast GFP insertion library. atg18Δ, apl5Δ, BYatg1Δ, and BYatg5Δ deletion mutant strains were obtained from the yeast deletion library. These strains and the W303A wild-type (WT) strains were transformed with VPH1-GFP at the chromosomal locus using the HIS3 selection marker. Autophagy deletion mutants atg1Δ and atg5Δ in the W303A background with integrated VPH1-GFP were kindly provided by the Walter lab (UCSF). A full strain list is shown in Table S1 in the Supporting Material.

Cells were grown overnight in liquid YPAD media at 30°C, and then inoculated into fresh YPAD and allowed to grow through at least two doublings to reach OD 0.3. For log-growth measurements, cells were allowed to continue growing until they reached OD 0.6. For rapamycin-treated cells, an aliquot of culture was taken at OD 0.3, and then rapamycin from a 1000× DMSO stock was added to a final concentration of 0.2 μg/mL. Cells were incubated at 30°C for an additional 4 h and typically doubled in OD during this time.

Imaging

Cells were mounted onto glass coverslips treated with Concanavelin A. Imaging was performed at room temperature using a Nikon-Ti Eclipse microscope equipped with a Hamamatsu Spinning Disk Head for optical sectioning. A 100× objective (NA = 1.49 PlanApo TIRF) and 1.5× optivar was used. 10 μm image stacks centered roughly at the cell equator were acquired using a 0.2 μm nominal z-spacing in brightfield (cell outline) and in fluorescence using a 491 nm diode laser for excitation (VPH1-GFP in the vacuole membrane).

Image analysis

Fluorescence images of vacuoles were visually scanned in ImageJ to determine and record center point coordinates for each individual vacuole. Data were then exported to MATLAB (The MathWorks, Natick, MA) for segmentation using the algorithm described in the Results section. Image stacks were resampled to equalize voxel dimensions. Intensity profiles along individual rays were calculated using linear interpolation of voxel intensities. A shallow weighting function of the form 1/(1+i/N)—where i is the distance along the ray and N is the total ray length—was applied to intensity profiles to bias the algorithm to select the nearest of multiple crossing points. Shape fitting was performed by least squares fitting using a linear combination of basis functions generated according to (15). These functions were defined as products of simple trigonometric functions in radial coordinates, and arbitrarily good surface fits can be obtained by generating large numbers of basis functions. In this study, the number of basis functions was limited to 18 to provide a balance between typical vacuole shape complexity and overfitting of noisy surfaces. Volume and surface area measurements were performed using the MATLAB program MyRobustCrust, which is available online. For cell volume measurements, brightfield stacks were scanned manually to find a consistent z-slice with respect to the cell equator. The cell outline in this plane was traced manually and fit to an ellipse (5,7). Cell volume was calculated assuming an oblate spheroid shape. Mother and buds were treated separately to allow for separation of total cell into the two compartments.

Scaling analysis

Scaling parameters were calculated using raw data (see Fig. 1 C) after transforming into log-log axes. Regression line analysis of log-log plots gave a slope (m) with a standard error (s_m), which was used as equivalent to the scaling exponent, α, and its standard error. Values for α in the text are therefore reported as m ± s_m. To validate this analysis, bootstrap resampling was performed on the log-log scatter plots to create 10,000 data sets with the same n as the original experiments. Resampling confirmed the mean values for m and gave 95% confidence interval errors ranging from 1 to 1.5× s_m.

Results

Vacuole size measurement algorithm

To understand vacuole size scaling, a key requirement is to be able to measure vacuole size precisely to ask how vacuole size may change as a function of cell size or genetic perturbations. We thus implemented a novel, to our knowledge, computational method to extract vacuole size measurements from optical images (8). The method entails five steps as follows (an example of segmented vacuole is given in Fig. 1 B):

• 1.Data acquisition: First, three-dimensional z-stacks are taken on a spinning disk confocal microscope through vacuoles that are fluorescently labeled at the limiting membrane with the fusion protein VPH1-GFP. Details of imaging conditions are given in the Materials and Methods.
• 2.Center point identification: Vacuoles typically exist as a clustered group of membrane-bound compartments. The images are scanned manually to identify a point(s) roughly at the center(s) of each individual vacuole compartment. This method is tolerant of minor errors in this step, as center point selection can vary by a few pixels without producing highly different volume or surface area measurements.
• 3.Ray drawing: For every vacuole center point, a number of rays (typically 500) are computationally constructed starting at the center point and radiating outward. The angular distribution of these rays is chosen to give a roughly constant density of rays over a spherical surface. The fluorescence intensity profile is interpolated at equally spaced points along each ray. Because the vacuoles are membrane labeled, the point of maximal intensity should be located where the ray crosses the membrane. The coordinates of the crossing points of every ray are collected to give a point cloud that defines the vacuole surface.
• 4.Surface fitting: Volume and surface area are then determined by fitting a mathematically defined surface to the point cloud, from which geometric parameters can be directly computed. A variety of surface representations can be used to fit the resulting point cloud. For instance, a triangle mesh can be constructed to connect nearest neighbor points, which would tend to overestimate the surface area of objects as there is some noise in the point cloud coordinates. A surface can also be fit using a priori knowledge of the shape of the object, such as using a prolate spheroid to fit yeast cells. However, though the vacuole compartments often seem to be spherical by eye, roughly 5% of vacuole compartments show sphericity <0.9. We therefore use a more general surface fitting method (15) rather than assuming a perfect sphere. In this method, a function generator defines a set of basis functions, and these are used to find a best-fit surface to the point cloud. The number of basis functions is constrained to prevent overfitting, which results in an overall smoothing of the point cloud. This method is able to address almost all of the vacuole morphologies observed to date. An example is given in Fig. 1.
• 5.Validation: The method was tested on two sets of spherical beads 0.96 μm (n = 101) and 2 μm (n = 38) in diameter. Averages of measured volumes and surface areas all came within 10% of expected values. The method was also tested on computationally generated ellipsoidal surfaces ranging from 0.8 to 2.0 μm in diameter, and again, measurements came within 10% of expected values. Larabell et al. (9) have used soft x-ray tomography to measure yeast cell and organelle size (strain DDY904). Our measurements of average cell and vacuole size in the W303A strain were generally larger, but values for BY4741 fell within reported size ranges (see Table S2), showing that the cell outline tracing and vacuole surface reconstruction methods give similar size distributions to reported values. The discrepancies in absolute size measurements may be reflective of differences in strains. On the other hand, the vacuole-to-cell volume ratios in W303A and BY4741 were 10 ± 0.2% and 7 ± 0.2%, respectively, both of which fall within the range of 3–14% reported for strain DDY904, which shows that these ratios are consistent between these two studies.

Vacuole volume and surface area scaling in WT cells

Vacuole volume and surface area were measured for yeast cells, which were grown to log phase (Fig. 1, D and E). Distinct scaling trends are found, such that on average, larger cells correlate with larger vacuoles both in volume (Pearson r = 0.8, p = 3 × 10⁻³²) and in surface area (Pearson r = 0.8, p = 9 × 10⁻³⁹). Qualitatively, the data from two different strains, W303A and BY4741, agree well with each other, indicating that as observed previously (9), size scaling of the vacuole seems to be a conserved property.

Taking logarithmic plots of the data allows the power-law exponent, α, to be calculated for the scaling trends. In this analysis, the two strains show slightly different behavior. In the W303A strain, the vacuole surface area-cell volume scaling exponent α = 1.0 ± 0.1, indicating a nearly linear trend and a roughly constant proportionality between vacuole membrane and cell size. However, the vacuole volume-cell volume scaling exponent α = 1.3 ± 0.2 suggests that the vacuole grows disproportionately larger in volume during cell growth. For the BY4741 strain, both vacuole surface area-cell volume (α = 1.2 ± 0.1) and vacuole volume-cell volume (α =1.3 ± 0.1) scaling exponents are slightly greater than linear.

Because yeast bud asymmetrically, scaling trends can also be measured for individual mothers and buds. Fig. 2, A and B, show that in W303A cells, vacuole size scaling is consistent between buds and mothers. Furthermore, vacuole size can be normalized to cell size to give the size scaling ratio for an individual cell. Consistent with the observed scaling trends, total vacuole volume-cell volume ratios increase with increasing cell size (Pearson r = 0.27, p = 4 × 10⁻³, Fig. 2 C). Total vacuole surface area-cell volume ratios, on the other hand, do not show a significant correlation with cell size (Pearson r = 0.04, p = 0.6, Fig. 2 D), indicating that they remain constant during cell growth, as predicted by the vacuole surface area scaling exponent of 1.0. Vacuole surface area-cell size ratios are also consistent when measured for buds, mothers, and buds+mothers (total cells).

Figure 2.

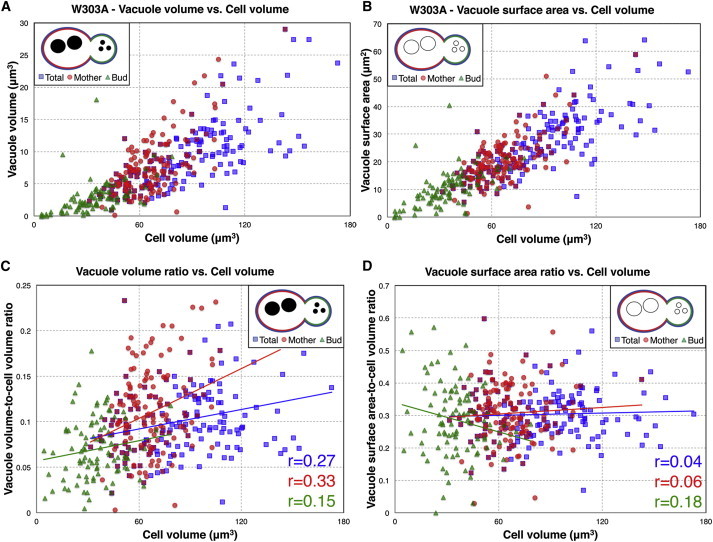
Vacuole size and size ratios in W303A WT. (A) Vacuole volume- and (B) Vacuole surface area-to-cell volume scaling plots. (C) Vacuole volume-to-cell size ratios and (D) Vacuole surface area-to-cell size ratios plotted against cell volume. Plots contain data for total (mother+bud) cells (blue), individual mothers (red), and individual buds (green). In (C) and (D), lines indicate least squares linear regressions to the data with listed Pearson correlation r values.

Because yeast cells can contain multiple vacuoles, total vacuole size will depend on the number and the individual sizes of the vacuoles. Measurements show that total vacuole number correlates with total cell size with Pearson r = 0.54 (p = 4 × 10⁻¹⁴, Fig. S1 A), but that average volume per vacuole size shows a weaker correlation with Pearson r = 0.23 (p = 0.005, Fig. S1 B). Vacuole shape can be evaluated using sphericity—based on the idea that a sphere maximizes volume for a given surface area—which ranges from 0 (zero volume) to 1 (perfect sphere). The average sphericity of all individual vacuoles measured is 0.97, indicating that vacuoles are generally very close to spherical with little variation in overall shape.

Normal scaling is broken in rapamycin treatment

Our ability to measure scaling relies on natural variation in cell volume during the division cycle, but for cells growing in log phase, the range of cell sizes is limited to a roughly twofold range because cell division prevents individual cells from growing very large. To see if the scaling trends hold at larger cell sizes, we arrested cells using the drug rapamycin that leads to an overall increase in average cell size. Rapamycin is an inhibitor of TORC1, which is a master regulator of cell growth and division. Upon incubation with the drug, yeast cells generally complete their current cell cycle, and then enter into an arrested state where individual cells are still able to grow in size. This leads to an average increase in cell size, even though the population no longer increases in number. As has been observed in many other studies (10,16), upon rapamycin treatment, vacuole morphology typically becomes fused and enlarged in W303A and BY4741 parent strains (Fig. 3 A).

Figure 3.

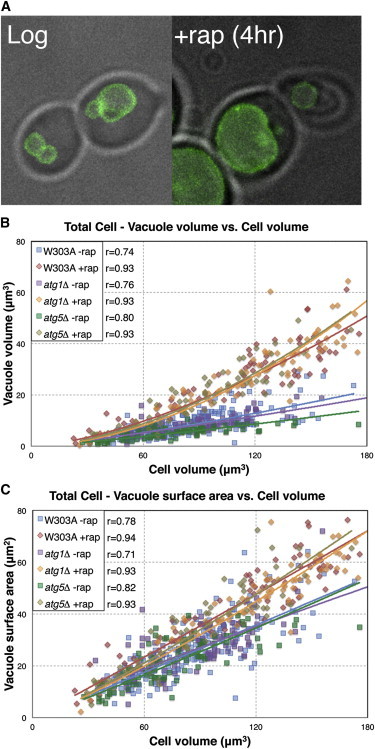
Rapamycin induces larger vacuole sizes independent of autophagy. (A) Yeast cells (grayscale) and vacuoles (green) growing in log phase (left) tend to become enlarged and more fused after incubation with 0.2 μg/mL rapamycin for 4 h (right). (B) Vacuole volume- and (C) vacuole surface area-to-cell size scaling trends are similar in W303A and in atg1Δ and atg5Δ autophagy mutants. Lines indicate power-law fits to the data, and Pearson’s r values are listed. Note that for all strains, both vacuole volume and surface area scaling trends are increased in rapamycin-treated cells compared to untreated cells.

This could mean that rapamycin affects vacuole size control, but it is also possible that this increase is just a reflection of the power-law relation governing vacuole-to-cell volume scaling. In the latter case, because rapamycin induces larger cell volumes, and because the observed vacuole-cell volume scaling trend is greater than linear, larger cells are then expected to have disproportionately larger vacuoles. Moreover, because larger spheres have a lower surface to volume ratio than smaller spheres, fusion of vacuoles could be a way for the cell to accommodate the reduced surface to volume ratio predicted by the observed scaling relations. Thus, both the reported enlargement of the vacuole and the fusion of vacuoles seen in rapamycin-treated cells may be a natural consequence of scaling.

To test this possibility, vacuole size was measured in cells that were treated with rapamycin for 4 h. Untreated cells have an average cell size of 86 ± 2 μm³, and rapamycin-treated cells arrest and grow to a larger average size of 130 ± 7 μm³ (p < 0.0001, Student’s t-test). The average number of vacuoles per cell decreases from 2.7 ± 0.1 to 1.8 ± 0.2 (p < 0.0001, Student’s t-test) reflecting the expected increase in fusion, and vacuoles expand in size to take up a greater proportion of total cell volume (ranging from 5% to 35%). Interestingly, rapamycin-treated cells had vacuoles that were larger both in volume (p = 5 × 10⁻³⁶, comparison of regression lines) and surface area (p = 3 × 10⁻¹³, comparison of regression lines) when compared to untreated cells of the same size (Fig. 3, B and C, Table S3 a). This result indicates that the increased vacuole size observed in rapamycin-treated cells is not simply a product of normal scaling, but instead reflects an alteration in the vacuole-cell size scaling relation upon rapamycin treatment.

We note that although rapamycin causes vacuole surface area to increase, it does not affect the exponent for the vacuole surface area-cell volume scaling relation, which is still linear in rapamycin-treated cells (α = 1.0 ± 0.04). Rapamycin only affects the prefactor slope of the scaling relation between vacuole surface and cell volume. The robustness of the scaling exponent to even a large perturbation in vacuole size by rapamycin suggests that this linear scaling may be a fundamental aspect of size control, a point we will revisit in the discussion below.

Rapamycin treatment alters scaling even in autophagy-deficient mutants

Vacuole volume increases during rapamycin treatment are due in part to the change in the vacuole’s fusion state—i.e., increased fusion/decreased fission. However, a change to the vacuole fusion state does not in and of itself explain why vacuole surface area increases. Previous studies have suggested that increased macroautophagy may be responsible for the increase in vacuole size in rapamycin-treated cells (16). Macroautophagy is the process by which double-membrane autophagosomes form around cytoplasm or organelles and fuse to the vacuole to deliver the contents for degradation. Inhibition of TORC1 by rapamycin induces higher levels of macroautophagy, and the increased levels of autophagosome fusion to the vacuole could provide the source of the increased surface area measured for rapamycin-treated cells.

To test this idea, we measured the size of the vacuole in atg1Δ and atg5Δ deletion mutants (in the W303A strain background), which are deficient in macroautophagy. In the absence of rapamycin, these mutants exhibit similar vacuole size scaling to WT cells, which indicates that vacuole size during log growth does not depend significantly on macroautophagy. Surprisingly, qualitative observation found that in the presence of rapamycin, vacuoles in atg1Δ and atg5Δ mutants appear enlarged, similar to WT. Quantitative measurements indeed show that vacuole volume increased in these autophagy mutants in the presence of rapamycin (atg1Δ: p = 2 × 10⁻⁴⁹, atg5Δ: p = 5 × 10⁻⁵⁷, comparison of regression lines, Fig. 3 B, Table S3 a), and that average vacuole number decreases in atg1Δ from 3.2 ± 0.1 to 1.0 ± 0.02 (p < 0.001, Student’s t-test) and in atg5Δ from 4.5 ± 0.2 to 1.3 ± 0.1 (p < 0.001, Student’s t-test). As with WT vacuoles, this volume increase during rapamycin treatment is due at least in part to the fusion of individual vacuoles together and their subsequent expansion. Interestingly, atg1Δ and atg5Δ also exhibit similar increases in vacuole surface area as with the WT in the presence of rapamycin (atg1Δ: p = 3 × 10⁻¹¹, atg5Δ: p = 2 × 10⁻¹⁷, comparison of regression lines, Fig. 3 C, Table S3 b), and the scaling trends are not statistically significantly different from one another (Table S3 b). Therefore, the rapamycin-induced growth in vacuolar membrane in these mutants is similar to that seen in WT cells, indicating that macroautophagy does not play a significant role in the growth of the vacuole under rapamycin treatment. The increased membrane amount in the vacuole must therefore be due to some other mechanism.

Using log-log plots (Fig. S2), scaling exponents were calculated for vacuole volume- and vacuole surface area-to-cell volume trends for WT, atg1Δ, and atg5Δ strains in the absence or presence of rapamycin (Table 1). All strains showed an increase in volume scaling exponents to roughly α = 1.5 in the presence of rapamycin. This result is consistent for vacuoles that have fused into one, roughly spherical compartment. In contrast, all surface area scaling trends gave scaling exponents in the range of α = 0.9–1.1, again showing that vacuole surface area maintains a linear relationship with cell size.

Table 1.

Scaling exponents for W303A, atg1Δ, and atg5Δ strains

	Volume		Surface area
	−rap	+rap	−rap	+rap
W303A	1.3 ± 0.2	1.5 ± 0.1	1.0 ± 0.1	1.0 ± 0.2
atg1Δ	1.2 ± 0.2	1.5 ± 0.1	0.9 ± 0.2	1.0 ± 0.1
atg5Δ	1.2 ± 0.2	1.6 ± 0.1	1.1 ± 0.1	1.1 ± 0.1

The role of membrane trafficking in establishing vacuole size

If autophagy is not the key regulated process by which TORC1 signaling affects vacuole surface area scaling, then what is? An obvious alternative candidate is membrane trafficking, which impacts vacuole growth through fusion of vesicles with the vacuole via anterograde pathways, and contributes to vacuole shrinkage by budding of vesicles from the vacuole, known as retrograde trafficking. ATG18 encodes a protein involved in binding to and regulating the levels of phosphatidylinositols (17) in the vacuole membrane, and it has been implicated in vacuole fission, which is expected to impact the vacuole’s fusion state and therefore volume. ATG18 is also involved in retrograde trafficking, which removes membrane material from the vacuole and is therefore likely to affect vacuole surface area (17,18). The deletion atg18Δ gives rise to vacuole morphology phenotypes that qualitatively match the enlarged and fused morphology of rapamycin-treated cells (Fig. 4 A). To ask whether ATG18 activity might contribute to the scaling effects seen in rapamycin treatment, we compared the vacuole volume-to-cell size and vacuole surface area-cell size scaling trends in WT and atg18Δ (BY4741 background) strains in the presence or absence of rapamycin. The response to rapamycin of the vacuole in atg1Δ and atg5Δ mutant strains was also verified in the BY4741 background (Fig. S3).

Figure 4.

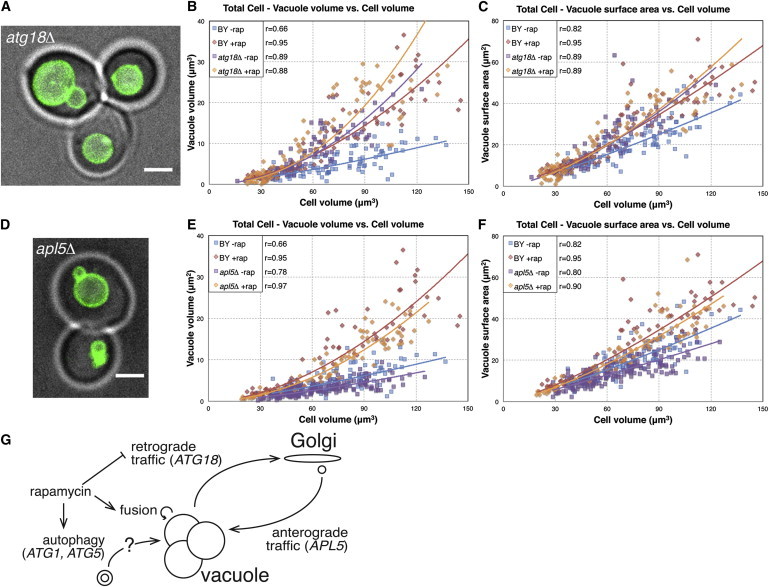
Retrograde and anterograde membrane trafficking affect vacuole size. Comparison of vacuole size-to-cell volume scaling trends between WT and atg18Δ ((A) image, (B) volume, and (C) surface area) or between WT and apl5Δ ((D) image, (E) volume, and (F) surface area). Lines indicate power-law fits to the data, and Pearson’s r values are listed. Without rapamycin, atg18Δ and apl5Δ show larger and smaller vacuole size scaling trends, respectively. In the presence of rapamycin, atg18Δ mutants show vacuole size scaling trends similar to WT yeast, whereas apl5Δ vacuoles still show smaller size scaling trends. (G) Based on these findings, we propose this interaction network in which rapamycin affects vacuole surface area primarily through effects on retrograde traffic and vacuole volume through effects on vacuole fusion.

Measurements show a significant increase in total vacuole size scaling both in volume and in surface area in untreated atg18Δ cells as compared to untreated WT cells (volume: p = 6 × 10⁻³³, surface area: p = 7 × 10⁻¹¹, Fig. 4, B and C, Table S3 c and d). If it was the case that inhibition of TORC1 function by rapamycin leads to vacuole surface area expansion by inhibiting ATG18-dependent retrograde trafficking, we would then expect atg18Δ mutant cells to mimic the vacuole surface area-to-cell size scaling changes seen in WT cells in the presence of rapamycin and atg18Δ mutant cells. Indeed, there is not a significant difference between atg18Δ and WT +rap vacuole surface area scalings (Fig. 4 C, p= 0.4, comparison of regression lines, Table S3 d). Furthermore, addition of rapamycin to atg18Δ does not significantly affect vacuole surface area-to-cell size scaling trends (p = 0.2, comparison of regression lines, Table S3 d), which is also consistent with rapamycin lying upstream of ATG18 in the pathway affecting vacuole membrane content. Based on these results, we propose a model in which rapamycin treatment leads to vacuole surface area growth as a consequence of reduced ATG18-mediated retrograde flux, rather than of increased anterograde flux from macroautophagy upregulation (Fig. 4 G). With respect to volume, WT –rap exhibits the smallest vacuole volume-to-cell size scalings. WT + rap, atg18Δ –rap, and atg18Δ +rap show increased vacuole volume-to-cell size scalings, with atg18Δ +rap slightly larger than the other two (Table S3 c). Again, these changes in vacuole volume result from increased vacuole fusion and expansion.

Given the notable effect of inhibiting retrograde traffic on increasing vacuole size scaling, we hypothesized that inhibition of anterograde trafficking, i.e., trafficking of vesicles from the Golgi to the vacuole, should have a complementary effect and lead to vacuole size decreases. We tested this using the apl5Δ deletion mutant in the BY4741 background, which blocks the alkaline phosphatase delivery pathway, which is thought to deliver vesicles directly from the Golgi to the vacuole (19). The apl5Δ deletion has not been reported to exhibit an obvious vacuole size or morphology phenotype, at least based on visual inspection (Fig. 4 D). However, when we performed quantitative measurements we found that apl5Δ vacuoles indeed have reduced vacuole volume- and vacuole surface area-to-cell volume scalings compared to WT (p = 7 × 10⁻¹⁵ and p = 9 × 10⁻¹⁰, respectively, comparison of regression lines, Fig. 4, E and F, Table S3 c and d). In the presence of rapamycin, vacuoles in apl5Δ cells do expand and grow into larger sizes (p = 2 × 10⁻³⁶, comparison of regression lines, Table S3 c and d), but their volume and surface area scaling trends are reduced compared to WT cells treated with rapamycin (p = 2 × 10⁻⁴ and p = 0.002, respectively, comparison of regression lines, Table S3 d). Therefore, blocking APL5-dependent anterograde trafficking leads to overall decreases in vacuole volume and surface area; both in the presence and absence of rapamycin.

Scaling exponents were also calculated for BY4741 parent, atg18Δ, and apl5Δ strains (Table 2 and Fig. S4). Measured vacuole surface area-to-cell volume scaling exponents ranged from α = 1.1–1.5, and were generally less sensitive to rapamycin treatment, which could indicate a conserved feature of vacuole morphology. Our analysis indicates that in the absence of rapamycin, BY4741 WT exhibits a nonlinear scaling with the power-law exponent α = 1.2, and that atg18Δ has α = 1.4. These values stand in contrast to the consistently linear scaling values observed for W303A background strains. Although these differences are not yet fully understood, we find empirically that if smaller cells are excluded from consideration for BY4741 or atg18Δ, values for α become closer to linear. Because smaller cells tend to be newborn mothers, the differences in scaling for these strains may in part reflect differences in inheritance during budding from their own mothers. For example, delayed inheritance might lead new cells to initially contain disproportionately smaller vacuoles, at which point other mechanisms (discussed in the next section) would begin to control the vacuole-to-cell size scaling. Such a scenario could account for the observed nonlinear scaling relationships observed in the BY4741 background.

Table 2.

Scaling exponents for BY4741, atg18Δ, and apl5Δ strains

	Volume		Surface area
	−rap	+rap	−rap	+rap
BY4741	1.3 ± 0.1	1.8 ± 0.1	1.2 ± 0.1	1.3 ± 0.1
atg18Δ	2.0 ± 0.1	2.1 ± 0.1	1.5 ± 0.1	1.4 ± 0.1
apl5Δ	1.3 ± 0.1	1.9 ± 0.1	1.1 ± 0.1	1.4 ± 0.04

Entries are the slope and the standard error of the slope of the linear regression to the log-log plots of measured cell and vacuole sizes. The vacuole-to-cell volume scaling exponents increased with rapamycin treatment in BY4741 and apl5Δ (but not in atg18Δ) due to vacuole fusion.

Models for establishing vacuole size scaling

The strong scaling trend between vacuole size and cell size raises the question of how this scaling is achieved, and particularly the question of whether or not the cell needs to actively measure the size of its vacuole and use a feedback loop to adjust the vacuoles to a size appropriate to the cell size. Is there any way to have scaling without such feedback? Vacuoles are dynamic organelles, and their volume and surface area are governed by competitive processes of growth and shrinkage, including both homotypic fusion/fission among vacuoles or anterograde/retrograde trafficking between vacuoles and other membrane compartments. Vacuoles do not show a constant absolute size, but rather a defined scaling with respect to cell size. Thus, a quantitative model of vacuole size control needs to explain how this scaling is achieved through the regulation of growth and shrinkage.

Here, we attempt to consider the simplest possible model for vacuole size scaling consistent with our data, and ask how much regulatory complexity is required to achieve scaling of the type that we have observed. We begin with the general power law expression of vacuole-to-cell size scaling:

$$V=A{C}^{\alpha },$$ (1)

where V and C represent vacuole and cell size, respectively, A is the scaling prefactor, and α the scaling exponent. The relationship between vacuole and cell growth rates, dV/dt and dC/dt, can be found by differentiation of Eq. 1 (using the chain rule):

$$dV/dt=\left(dV/dC\right)\left(dC/dt\right)=A\alpha C^{\left(\alpha -1\right)}\left(dC/dt\right).$$ (2)

In general, then, vacuole growth can be written as a function of both cell size and cell growth rate.

We consider the special case when α approaches 1—i.e., linear scaling—then C^(α-1) also approaches 1. Replacing dV/dt and dC/dt with rate_v and rate_c, each of which can potentially be a function of instantaneous cell size, Eq. 2 then reduces to

$$rat{e}_v=A\times rat{e}_c.$$ (3)

Given that vacuole surface area-to-cell volume scaling seems to show linear or near-linear scaling in the W303A background strains, we will focus specifically on vacuole surface growth. In the membrane trafficking model, net vacuole growth depends on a forward (anterograde, +) and a reverse (retrograde, −) rate:

$$rat{e}_v=rat{e}_{+}-rat{e}_{-}=A\times rat{e}_c.$$ (4)

Solving for rate₊ (or rate₋) gives a function of rate₋ (or rate₊) and rate_c. This general result indicates that a linear vacuole surface area-to-cell size scaling would constrain the possible relations between trafficking rates and cell growth rates.

Going further in this analysis, one straightforward case in which Eq. 4 holds true is when rate₊ and rate₋ are both proportional to rate_c with constants k₊ and k₋, so

$$rat{e}_v=A\times rat{e}_c=k_{+}^{\text{∗}}rat{e}_c-k_{-}^{\text{∗}}rat{e}_c.$$ (5)

With linear scaling, the slope of the scaling trend reflects the ratio between vacuole and cell growth. Thus, if there is proportionality among anterograde and retrograde trafficking rates and cell growth rates, then scaling will arise as an inherent consequence. Although this may occur coincidentally, such a scenario may also indicate coordination between cell growth rates and trafficking rates, which could be achieved if, for example, cell growth and vacuole growth both were rate-limited by the same cellular process such as biosynthesis or nutrient uptake.

In the limiting case of linear cell growth, which has been found for certain cell types (20,21), rate_c is constant, which would imply by Eq. 4 that rate_v is also constant. Linear scaling would then arise if vacuole growth and shrinkage rates are held relatively constant, and such a scenario would not require any direct regulatory linkages between cell growth and vacuole growth. It is thus possible to achieve linear scaling of vacuole surface area to cell volume in a quite simple way if both rates are constant and independent of cell size.

From Eq. 2, scaling exponents other than α = 1, as seen for vacuole volume-to-cell size measurements, indicate some other relationship of vacuole growth with cell size and growth rate. As noted in the discussion, the total volume of the vacuole in the cell will depend largely on its fusion state, i.e., the number of vacuoles in a cell. Because this number correlates with cell size (Fig. S1 A), that contributes to the overall vacuole volume-to-cell size scaling. It will therefore be interesting to study how vacuole fusion and fission rates relate to cell growth rates.

Another consideration is that in the asymmetrically budding yeast, vacuoles are distributed between mother and bud compartments such that both show similar scaling trends to the total cell. This trend stands in marked contrast to mitochondria, whose density in buds increases with bud cell size, plateauing after a certain bud cell size threshold, whereas mitochondrial density in the mother decreases with mother cell size (7). That vacuole size scaling is more consistent between compartments may indicate important differences in strategies for regulation of the size of the two organelle systems. Vacuole distribution between the larger mother and smaller bud depends on the localization of vacuole biogenesis and the employment of inheritance mechanisms (22). Future studies will use mutations in inheritance mechanisms to dissect their contributions to vacuole size control.

Furthermore, to better understand whether there is coupling between vacuole and cell growth, and how biogenesis and inheritance contribute to vacuole size control; it will also be useful to use time-resolved measurements and analysis to determine how rates of growth are correlated, and how they respond to perturbation. Such experiments would determine whether vacuole size is actively regulated to maintain the observed scaling ratio, and the precision of this regulation would give rise to the noise in the measured vacuole-to-cell size scaling plots.

Discussion

Scaling provides a powerful context for discovering and understanding the mechanisms of organelle size control (3,4,8). Using the computational algorithm described, quantitative measurements of vacuole lumenal volume and membrane surface area have revealed that both exhibit scaling with respect to cell size—i.e., larger cells tend to contain larger vacuoles. In W303A yeast, vacuole membrane content stays in proportion with overall cell volume, and the vacuole surface area-to-cell size ratio remains constant over all sizes measured and between mother and bud cells. Though our analysis measures total cell volume, it may also be that organelle size responds to cytoplasmic volume. Interestingly, increasing evidence suggests that total organelle volume scales with cell volume, in which case cytoplasmic volume would be a constant proportion of total cell volume.

Vacuole size can impact function in a number of ways. The lumenal volume is likely to affect the capacity of the organelle to carry out its degradative and storage functions. In addition, vacuole size determines its ability to respond to osmotic and toxin stress. Thus, the cell may maintain a vacuole at a size appropriate to perform these functions, but not too large as to waste energy or material.

Previous genetic screens have established that membrane trafficking pathways play important roles in establishing vacuole morphology (11), and it has been proposed that the flux of membrane to and from the vacuole via these pathways will determine how much limiting membrane and therefore surface area is available to the organelle (23). Measurements of vacuole size scaling for the apl5Δ and atg18Δ deletion mutants strongly support these models. The former illustrates that perturbations in anterograde trafficking lead to marked decreases in vacuole surface area-to-cell size scaling trends, presumably from the decreased delivery of membrane material to the vacuole. The latter provides evidence that blocking retrograde trafficking leads to increases in vacuole size scaling.

In rapamycin-treated cells, both vacuole volume and surface area increase to sizes greater than those predicted by WT scaling trends for the increased cell sizes. Rather, vacuole-to-cell size scaling has been altered by the drug treatment. The increase in autophagy represents a logical source for increased anterograde traffic and vacuole membrane, but the similar increases in size in autophagy-deficient mutants’ atg1Δ and atg5Δ show that increased delivery of autophagosomes to the vacuole is not necessary to give the observed increases in vacuole surface area. Rapamycin-treated cells and atg18Δ mutants show similar vacuole surface area-to-cell volume scalings, and rapamycin treatment fails to increase vacuole size in atg18Δ, suggesting that TORC1 and ATG18 may act in the same pathway affecting vacuole membrane content. It remains unclear how rapamycin influences anterograde trafficking, given that Atg18p has not been shown to be a substrate of TORC1. Another possibility involves vacuole lipid composition. Other proteins such as Fab1p and Vac14p interact physically and functionally with Atg18p in regulating PI(3,5)P₂ levels in the vacuole, and mutants in these genes also lead to vacuole enlargement similar to that observed for atg18Δ (24).

Interestingly, scaling plots for cells in log-phase show that the volume of the vacuole increases disproportionately with cell growth, even though in principle it is possible to achieve a linear vacuole-cell volume scaling using the volume control mechanisms described below. Because cell division prevents cells from growing too large, it may be that the cell does not generally enter the size regimes in which disproportionate vacuole volume growth becomes problematic. It will be interesting to explore whether these trends hold under other conditions, which perturb cell size to a greater extent, such as cell cycle blocks.

With a given surface area, the maximal lumenal volume is achieved if the vacuole is a single spherical compartment. The vacuole can achieve any volume less than this maximum in two main ways. One is to fragment the vacuole into multiple compartments, which is observed in the majority of log-phase cells. Fragmentation state will depend primarily on the equilibrium between fusion and fission, which has been the focus of much previous research (10,25). Indeed, the increase in vacuole volume in rapamycin-treated cells and atg18Δ mutants has been linked to increased fusion and decreased fission rates, respectively (10,17). To increase in volume after fusion, the vacuole must expand, which likely involves the transport of water, ions, and other species across the vacuole membrane. This inflation is driven in part by the high osmotic pressure inside the vacuole. Conversely, the fragmentation of a single spherical vacuole into multiple ones would necessitate a loss of volume, which would require some energy input to either constrict the membrane or for lumenal efflux.

Volume can also be adjusted by changes to vacuole shape. Although nonspherical vacuoles are observed, they seem largely restricted to transient segregation structures observed during cell division. Though individual vacuoles can themselves exhibit any shape, they typically are also roughly spherical. The shape of vacuoles has been shown to be due to the high osmotic pressure inside the vacuole, as shifting the cell to hypertonic conditions leads to invaginations, fragmentation, and other alterations in vacuole shape (26).

Total vacuole size can increase either by proliferating the number of vacuoles or by increasing the size of individual vacuoles. In budding yeast, the correlation of vacuole number to cell size suggests that the former mechanism contributes strongly to vacuole growth. Proliferation of similar sized vacuoles would tend to preserve the vacuole’s surface area-to-volume ratio, in contrast to the scenario where number is kept constant and individual vacuoles grow, which would decrease this ratio, and this may favor proliferation as the vacuole’s growth strategy. Fig. S1 C shows the vacuole surface area-to-volume ratio tends to plateau at higher cell sizes at a value higher than the expected value for a single spherical vacuole with the equivalent volume. In other plant and fungal cells, the expansion of vacuoles can drive cell expansion, and it will be interesting to study how scaling is established in such systems (27–29).

Conclusion

The results of our quantitative studies of the yeast vacuole illustrate the fundamental questions and concepts that can be addressed using quantitative measurements of organelle size scaling. The linear scaling trends measured in this study suggest a particularly simple way to explain scaling based on vacuole growth proportionality to cell growth, and indicate that the mechanisms of size regulation will need to be explored further using time-resolved analysis of organelle and cell growth to test whether and how vacuole and cell growth are coordinated, and whether there is active feedback to ensure proper organelle size.