Sequence analysis by iterated maps, a review

Abstract

Among alignment-free methods, Iterated Maps (IMs) are on a particular extreme: they are also scale free (order free). The use of IMs for sequence analysis is also distinct from other alignment-free methodologies in being rooted in statistical mechanics instead of computational linguistics. Both of these roots go back over two decades to the use of fractal geometry in the characterization of phase-space representations. The time series analysis origin of the field is betrayed by the title of the manuscript that started this alignment-free subdomain in 1990, ‘Chaos Game Representation’. The clash between the analysis of sequences as continuous series and the better established use of Markovian approaches to discrete series was almost immediate, with a defining critique published in same journal 2 years later. The rest of that decade would go by before the scale-free nature of the IM space was uncovered. The ensuing decade saw this scalability generalized for non-genomic alphabets as well as an interest in its use for graphic representation of biological sequences. Finally, in the past couple of years, in step with the emergence of BigData and MapReduce as a new computational paradigm, there is a surprising third act in the IM story. Multiple reports have described gains in computational efficiency of multiple orders of magnitude over more conventional sequence analysis methodologies. The stage appears to be now set for a recasting of IMs with a central role in processing nextgen sequencing results.

Jeffrey 1990

Over two decades ago, during a period of great excitement over the use of statistical mechanics approaches to the nascent field of Biocomplexity and Systems Biology, it was proposed in [1] ‘Chaos game representation of gene structure’ to apply iterated function systems (IFS) to the investigation of DNA sequences. There, HJ Jeffrey, a computer scientist with a formal background in Mathematics, borrows from work done in the preceding 15 years in non-linear dynamics studies of fractal geometries. The approach followed by that line of research was directed to the identification of IFS that produced fractal figures with desirable properties. That function is designated as a ‘mapping function’, or simply, as a ‘map’, therefore the modern ‘iterated maps’ (IMs) designation. Jeffrey’s Chaos Game Representation, CGR, proposes an IM for genomic sequences that places each nucleotide at the edges of a unit square, and then moves a pointer half the distance to the corresponding edge [Equation (1)]. The CGR article was part of a larger movement towards understanding ‘the fractal geometry of nature’ [2] that had been gaining momentum since the mid 60s [3]. This was the period when the concept of self-similar Markov processes driving the identification of iterated mapping functions took shape. One might therefore interpret the CGR approach to the analysis of nucleotide sequences as part of a broader movement towards the identification of organizing mathematical principles leading to ‘self-organized criticality’ [4], a concept generalized and popularized in [5] as a ‘order at the edge of chaos’. Coincidentally, that expression borrowed from the description, published the same year as CGR’s, of cellular automata results as ‘computation at the edge of chaos’ [6].

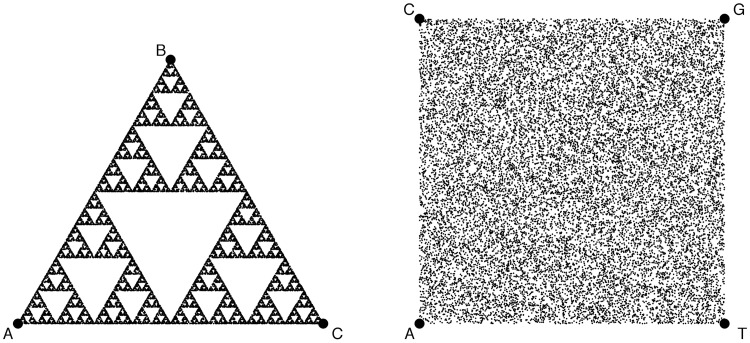
The Sierpinski’s triangle (Figure 1) is the paradigmatic example of a self-similar set with a fractal geometry. As described in the original article, the generation of this figure from a random set was the immediate inspiration for the CGR IM [1]. Specifically, if, in an equilateral triangle, one moves a pointer half the distance to each of the edges [the CGR game, Equation (1)] in a random order, a Sierpinski’s triangle is obtained. Using the same rule for a unit square will generate a uniformly covered distribution of points. As illustrated in Figure 1, the Sierpinski triangle and CGR share the same IM [Equation (1)], even if that may not be immediately apparent in the original IFS formalism. Although not approached in the CGR article, it is also worth noting that if the CGR game is played with only two points, using a uniformly binary sequence, a uniformly random distribution of points in a line will be generated. As discussed in the CGR report, the original motivation for these games was to assess the quality of a pseudorandom generator functions in a computer [8], a significant issue in those days. As found many years later [9], the equivalent solution for polygons with more than four edges (say, protein sequences would require a polygon with 20 edges) will in fact need to use increments bigger than half to preserve essential properties of the IM representation. Interestingly, to the best of our knowledge, Jeffrey’s milestone CGR article was his only peer-reviewed foray into the analysis of Biological Sequences, with the focus of the rest of his active research record directed to other fields. This cross-disciplinary advancement of IM applications to Biological Sequence analysis is a pattern that recurs, repeatedly, in the 23 years of work reviewed here.

Figure 1:

Sierpinski’s triangle (left) and CGR square (right), both generated by running the IM described in Equation 1 with a set of 20 000 random sets of, respectively, three symbols and four symbols - the edges (circles) of the corresponding figures. The square layout (on the right) is the one proposed in [1] to process genomic sequences, with four possible nucleotides, ACGT, one per edge of the CGR square. Any deviation from the uniform random distribution (any structure in the sequence) will produce a structure in the IM projection that is amenable to alignment-free and scale-free analysis. See Figure 1 of [7] for a graphic illustration of the process of generating CGR coordinates, applied to a gene sequence. The code used to generate this figure is available at http://bit.ly/imfig1.

THE IM FUNCTION

Originally, IMs (then designated as iterated function systems, IFS) were described as a set of linear equations, one per dimension. For example, CGR x,y coordinates would be generated by x = ax + by + e and y = cx + dy + f. However, as is immediately apparent by inspecting CGR’s IFS, each coordinate can be determined independently (b and c terms are zero). As a consequence, a more compact notation came into use over the years and will be adopted here. Equation (1) uses the modern description of the original CGR game as a procedure where an array of map positions, y, is generated from a set of Boolean values x.

(1)

In Equation (1), y contains the CGR positions, one per element of the sequence S:

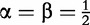• , the start coordinates and the position increment factor, respectively;

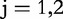• , i.e. the two dimensions, m, of the CGR square;

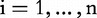• , n is the length of the genomic sequence S, so for each position, i,

• ,

• .

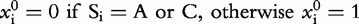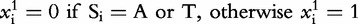which defines a unit square bound by the four nucleotides, ACGT, at positions, respectively, (0,0)(0,1)(1,1)(1,0).

THE FIRST DECADE, 1990–2000: FOUNDATION

The year the CGR article [1] was published, 1990, was also the year when BLAST, the Basic Local Alignment Search Tool [10] came out. The availability of a convenient tool to retrieve DNA sequences according to their similarity to a probe sequence was a game changer in molecular biology methodology, as reflected by close to 50 000 citations to date (Google Scholar). At a more fundamental level, the success of BLAST generated a significant drive in biological sequence analysis methods development towards exploring and advancing the probabilistic models associated with sequence alignment. This was also a key moment in the development of Bioinformatics as a discipline, to the extent that Durbin’s ‘Biological sequence analysis: probabilistic models of proteins and nucleic acids’ [11] was for many years the main textbook in graduate courses on the topic. In other words, in the 1990–2000 period, the study of biological sequence analysis was overwhelmingly the study of the Markov Chain Models (MCM), soon extended by Hidden Markov Models to model the succession of Biological units in genomic and proteomic sequences [12]. This context helps understand why the first probabilistic study of the application of IM to biological sequences followed a narrow Markov model perspective [13], and remains to this day its most severe critique. That study, published in the same journal as the original CGR article, concluded that the distribution of positions in the CGR space could be described in terms of oligomer frequencies (word statistics) and, therefore, ‘there is no justification for ascribing their patterns to anything other than’ that [13]. The author reached this conclusion by consecutively dividing the CGR plane in the middle, and each time, observing that the position frequency could be ascribed to a cell in a MCM transition probability table. Intriguingly, that study ignored the possibility of a different division rule, which would have uncovered what is probably the most exciting property of IMs: that it generates truly scale-free representations of transition (with an arbitrary Markov order). That observation would have to wait for the end of the decade to be reported [7], even if by 1999 there were already signs that order-free (scale free) MCM using IMs might be a distinct possibility [14]. However, the work described in the latter report was soon directed to applications to machine learning [15, 16], and the possibility of scale-free MCM remained ignored in the field of sequence analysis for another 2 years. In summary, a review of the literature in this period suggests that Goldman’s critique [13], as was its explicit intention, significantly cooled the interest in using IMs to study biological sequences any deeper than the word statistics that derive from its graphical representation.

While IMs as a sequence modeling approach were essentially on ice during the 1990’s, there was a profusion of studies making good use of the graphic representation it generates. The association between oligomeric nucleotide frequencies and evolutionary processes [17] were approached by several authors because CGR representations, as in [18], simply offered a convenient procedure to produce them. That practical advantage established a bridge between IMs and what was already the foundation [19] for what would latter be designated as alignment-based methods [20]. Retracing these developments, the trail of CGR-based studies of genomic sequences starts with fundamental studies like [21], just before [13] closes that door, and continues with several genomic signature results such as [22] and others, captured by the contemporary review of novel graphical representations of DNA sequences in [23]. This trail extends to the present day, with an increased emphasis on scalability and computational efficiency as in [24–27]. This was a period of growing interest in graphical bioinformatics and a wide variety of approaches have since been proposed, as illustrated by the extent of the recent review of graphical representation of proteins [28]. Although CGR is now recognized among the milestone developments in graphical bioinformatics [29], it is interesting to note the broader context where this early work took place. Resisting a novel numerical method with fundamental significance on the basis of lack of fundamental significance of the method itself, was then a recurring pattern in the development of the mathematics of fractal geometry [30]. This early period in IM development was a time when Experimental Mathematics had not yet gained full recognition [31].

This first decade of using IMs to study biological sequences saw another two important developments. One was an interest in using it to generate entropy profiles. This was initiated by [32] in 1993, quickly followed by [33] the following year. The understanding of scalability of IM representations more than a decade later, rekindled an interest in using it for entropic profiling, as in [34]. This important topic is separately reviewed in this special issue by the author of that study. The second development was a desire to generalize the 2D graphics of the CGR approach beyond the genomic sequences and the simpler domain of a four-nucleotide alphabet. A number of variations on the IM/CGR theme, such as [35], were pursued by different authors in this period. The description of this challenge as one of using IMs to efficiently inscribe non-overlapping polygons for alphabets longer than 4 (nucleotides) was clearly laid out by [36]. His solution, and the challenge it created (because it did not produce CGR as a solution for four unit alphabets), would remain unaddressed for another 15 years.

THE SECOND DECADE, 2001–2010: DISCOVERY

The previous decade had seen key questions, and objections, being raised. This second decade not only saw them answered but in the process discovered IM’s distinctive features as a mathematical tool, opening a window into a novel mathematical representation of transition. As is often the case, the process was largely driven by newcomers who, unintentionally, stumble into a new field. As many others, the author was attracted to this field by the intriguing visual representation of full genomes in reports such as [22], [37] or [38]. As Figure 1 in that report makes elegantly clear, the distribution of positions in the CGR plane provides, in a single representation, oligomeric frequencies (frequencies of nucleotides, dinucleotides, trinucleotides, … ) with multiple lengths. For someone not aware of the argument that that is indeed all that is there to see [13], it suggests something more comprehensive than the fixed order probability tables of MCM. It actually suggests the very opposite, that those transition matrices, of all degrees, are fully accounted for in a CGR map [14], and that, indeed, there may be a lot more to discover in the use of IMs to represent symbolic sequences. All it takes for that critical leap forward is then to divide the CGR plane into a number of quadrants, q, where log₂(q) is not an integer [7]. This procedure will resolve arbitrary Markov orders, including, unsettlingly, non-integer fractal orders. The critical advancement, as illustrated in the next paragraph, is that operations usually reserved to numerical results can be applied also to symbolic sequences.

After the leap into fractal degree is taken, as explored in [7] for multiple genes of the threonine operon of Escherichia coli, a succession of discoveries is unleashed by the bijective mapping between the sequence’s native symbolic form and its numerical representation by the IMs. For example, it suddenly becomes possible to assess how much a gene is like the genome that contains it (the similarity of thrA in E. coli is 7.7 nucleotides), or even what is its skewness (for the same gene, the average sequence differs from the median sequence by 0.13 nucleotides). Those numbers were obtained by noting the order statistics nature of the IM representation (Figure 9 in [7]), and taking the logarithm of its maximum coordinate distance, as described in Equation (2), where j indicates each dimension of the map, as per the notation defined for the previous equation.

(2)

These results, at a time when sequence alignment was the staple of bioinformatics methods, represented what can only be described as a radically alternative route for sequence analysis. Word counting and alignment methods had a shared trajectory that can, arguably, be stretched all the way to [19], the same year CGR was proposed. The shared foundation suggested that something important might have been amiss in alignment-based approaches to justify the subsequent divergence. The two approaches diverged quickly in the ensuing decade, as reviewed by other contributions to this issue. As a consequence, a newcomer to sequence analysis in this second decade of IM work would have a different perspective of the methodologies at hand. One such newcomer, starting her PhD thesis by reviewing the state of the art, saw ample justification to designate them collectively as being ‘alignment-free’ [20], a designation that is now widely used. Eventually, that would be interpreted, even by those at the root of alignment methods [39], as free not only from the constraints of conventional MCM but also free from the computational inefficiencies of using dynamic programming to align sequences.

A number of foundational questions were addressed in this second decade. Optimal 2D packing rules for IM that generates Sierpinski’s triangle and the GCR cube as solutions were found [9], resolving a challenge dating back to 1994 [36]. The scaling of entropy measures was approached in [34]. The use of alignment-free methods, typically associated with word statistics methods as in [40], quickly found application in a myriad of applications, sometimes even as a complement to conventional alignment methods, as in [41]. It is noteworthy that, by the beginning of this second decade, oligomer frequency-based methods (not reviewed here) had advanced substantially and had produced a wealth of alignment-free sequence distance metrics on their own [42]. Similarly, their statistical foundations, as in [43], were by then well established. As concerns the IM space itself, this was, on the contrary, still a decade of discovery.

The discoveries of novel properties of the IM procedure during this period have a relatively small, and recurring, list of authors. This is intriguing since some of those studies have nevertheless been abundantly cited. For example, the discovery of scale-independent measures in [7] was followed by its generalization for any symbolic sequence in [44], where both a new IM similarity metric (i.e. scale independent, not based on oligomeric frequencies) and a statistical framework are uncovered. However, these new properties appear to find application not in sequence comparison, but in sequence classification (see for example [45]). This pull of IM applications towards machine learning bears some similarities to the same pattern observed in the use of scale free MCM, as discussed previously. The fact is that a careful analysis of IM-based applications—including some of our own [46] or even the density kernel described in [47]—is really that of the oligomeric frequencies, ultimately falling prey of Goldman’s objection. The third act of IM applications to biological sequence analysis would have to wait, as is often the case, for a compelling and unmet need where existing solutions simply fall short.

THE THIRD DECADE, 2011: SCALING UP TO BIG DATA

The need for a new computational framework to handle the flood of sequence data produced by medical genomics [48, 49] was becoming clear by the end of the previous decade [50]: the need for solutions that rely on code distribution rather than data transfer. In a broader sense, not only the abundance of sequence data but the emergence of the Web as a global data space [51] set the stage for this third act of using IMs to analyze Biological sequences. Ironically, in a reversal of previous cross-pollination between disciplines, the generic abstraction that describes opportunities for distributed computing, first took root in the machine-learning community [52], before being commoditized as a cloud computing framework by Google [53]. Within 2 years, not only did it underlie the most important high-throughput sequence analysis frameworks [54, 55], but it was herald as the generic solution for computational biology in the Big Data era [56].

Ever since [46] and [24], there had been multiple reports highlighting the computational efficiency associated with the use of IMs in sequence analysis. These gains had become particularly impressive in applications where the use of alignment methods is notoriously problematic, such as in metagenomics [27]. The explanation for this computational advantage is now much better understood, as illustrated by the use of CGR as hash function within the Rabin-Karp algorithm [25]. Finally, the CGR iterated mapping procedure, as well of its generalization for any symbolic sequence, was found to be amenable to (distributable) Map Reduce decomposition [26]. The extent to which this result is ahead of the (in memory) dynamic programming of alignment methods, and the extent to which the field has advanced beyond the original CGR procedure, can be appreciated in the measure of sequence similarity in Equation (3). Its inspection will reveal that the length, L, of the shared sub-segment between two sequences can now be calculated directly, and solely, from the corresponding pair of IM coordinates. This is the antithesis of alignment as a computational application and is achieved entirely outside the MCM paradigm that entails it.

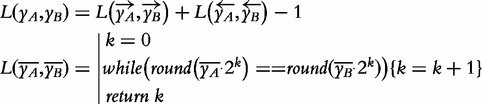(3)

In this equation, A and B indicate the two sequence positions being compared (in the same sequence or in distinct sequences) and the arrows indicate the direction of the iteration in the calculation of y in Equation (1). The value of L, the length of the longest shared segment, can then be determined solely from the coordinates of positions A and B, y_A and y_B, by incrementing an integer variable k until the rounding condition is no longer satisfied. The computational notation used in this equation is the same adopted in the original report [26]. It can be graphically described as a box counting procedure [13] in reverse: instead of halving the size of the box and counting the coordinates that fall within, the coordinates, y_A and y_B, are doubled until the resulting positions being compared fall outside a shared unit box. For a live resolution of this equation with arbitrary sequences see http://usm.github.io. The use of box counting procedures with IM coordinates is also a reminder of the deeper statistical mechanics roots of this procedure. The resulting sequence representation is amenable to methods that are more commonly associated with the extraction of fractal dimensions from phase-space representations [38, 57].

CONCLUSIONS

The use of IMs in sequence analysis has been object of intense study and application for the past 23 years. This field was initially driven, and objected, by the appeal of a single representation of multiple oligomeric frequencies. As the computational limitations of alignment-based methods mounted, IMs gained popularity as a convenient procedure to pre-compute those frequencies. However, during this process, the startling discovery was made that the IM representation is also a scale-free representation of transition. The Big Data era, and the commoditization of distributed computing via Map Reduce schemes, therefore opens a third act in the evolution of IM applications to sequence analysis. The procedure was found to be naturally decomposable into Map Reduce components, with IM-based measures of sequence similarity benefiting from the same implementation efficiencies as Big Data word counting workflows. Each of the three acts in the development of IM methods, and its applications to Biological Sequence analysis, has been defined by surprising advancements in bridging between symbolic and numeric data types. In conclusion, even if the fractal figures it produces are what attract most researchers to IM methods, there is clearly a lot more in this field than what meets the eye.

Key Points.

• Iterated Maps are procedures rooted in non-linear dynamics that represent strings as fractal phase-space diagrams.

• They are unique among alignment-free methods for also being scale free, i.e. the representation can be resolved for arbitrary Markov orders including, which is nothing short of unsettling, non-integer orders.

• They are currently the most efficient procedure to determine oligomeric frequencies.

• Its scale-free representation of transition is inherently distributable and appears to be a natural fit to Big Data sequence processing operations.

FUNDING

Center for Clinical and Translational Sciences of the University of Alabama at Birmingham under contract no. 5UL1 RR025777–03 from NIH National Center for Research Resources (in part).

Biography

Jonas S. Almeida. After a string of academic appointments in Engineering, Biostatistics and Bioinformatics Departments, in 2011 I became the inaugural director of a Division of Informatics charged with computational groundwork for Personalized Medicine. More at jonasalmeida.info.