Summary
We review mathematical modeling and related statistical issues of HIV dynamics primarily in response to antiretroviral drug therapy in this article. We start from a basic model of virus infection and then review a number of more advanced models with considering, e.g., pharmacokinetic factors, adherence and drug resistance. Specifically, we illustrate how mathematical models can be developed and parameterized to understand effects of long-term treatment and different treatment strategies on disease progression. In addition, we discuss a variety of parameter estimation methods for differential equation models that are applicable to either within- or between-host viral dynamics.
1. The basic HIV viral dynamic models
1.1 Introduction
Human immunodeficiency virus (HIV) primarily attacks the CD4+ T helper cells via, e.g., gp120 binding to the CD4 and CXCR4 receptors. HIV infection typically results in a vast replication of virus during the acute phase. The viral load then becomes much lower and approaches a quasi-steady state, called chronic phase. A balance between high rates of virus production and clearance [168] could explain why the viral load remains remarkably stable on the timescale of weeks [36, 124]. After that, the viral load will increase slowly until the onset of acquired immunodeficiency syndrome (AIDS) [112, 136], whereas the number of CD4+ T cells declines steadily. Eventually, the viral load will increase significantly after the development into AIDS, which is defined if the CD4+ T cell counts fall below 200 cells per μL plasma, or specific diseases in association with HIV infection occur. The typical stages of HIV infection can be found in references [21, 63, 106].
Highly active antiretroviral therapies (HAART), which consist of reverse transcriptase inhibitors and protease inhibitors, are currently the most effective treatment regime for HIV patients in terms of rapidly suppressing HIV viral load below the limit of detection. New and more effective antiretroviral therapies (ART) have turned out to be successful in slowing down the progression to AIDS and improving the life quality of HIV patients. However, ART may not work effectively for certain patients, and the suppression of viral replication by ART is not in itself sufficient for eradicating the virus. There are evidences showing that virus persists despite treatment, or the viral load rapidly rebounds shortly after antiretroviral therapy interruption [58, 99]. Latently infected memory CD4+ T cells (as well as macrophages and dendritic cells) actually become a reservoir of virus. These cells spread out almost everywhere (e.g., blood, lymphoid organs, biotissues, and neuro systems), which makes the eradication of HIV virus extremely challenging.
Mathematical models play a vital role in gaining a quantitative insight into HIV dynamics and pathogenesis [104, 115, 116, 117, 168]. The majority of HIV dynamic models, either deterministic or stochastic, describe the interaction between CD4+ T cells and virions [5, 28, 34, 62, 83, 90, 96, 97, 102, 104, 111, 117, 119, 121, 131, 153, 166, 174, 176]. In particular, many models developed before the mid-1990s, focused on understanding of CD4+ T cell decline [117], partially due to the lack of accurate methods that can measure the number of virus particles in blood. With the development of rapid and sensitive polymerase chain reaction (PCR)-based methods that can quantify genomic viral RNA copies (each virus particle contains two RNA strands), HIV-1 viral dynamics can be understood in a more precise manner and the host-pathogen interaction in HIV-1 patients can be studied quantitatively using modeling. Stochastic models [90, 153] are used to describe the early events after infection; when the numbers of infected cells and virions are small, occasional events such as viral blips [154] or the variability among individuals are of the primary interest. Stochastic models have been used to investigate the effects of increasing variability among viral strains, as a way of escaping immune response, in the progression to AIDS [105, 106, 109, 112]; however, such an approach could be problematic [171]. Stochastic models were also employed to capture the random fluctuations as well as the mean behavior of immune systems to gain insight into treatment-outcome variability [154], or to characterize the dynamics of early infection when virus is released from cells either continuously or in a burst. Deterministic models have been considered by a large number of studies ([117] and references therein) to examine the changes in mean cell numbers and viral loads, or to describe the late stages of infection progression. These models typically account for the effects of drug therapy besides CD4+ T cell and HIV virus kinetics, but there are some models that explicitly take more types of immune cells, such as macrophages and CD8+ cells, into consideration. More complex models considered time-dependent drug efficacy [77, 176, 133] or modeled the time between viral entry and the production and release of new virus particles [28, 83, 166, 179]. There exists numerous work on emergence of HIV drug resistance during antiretroviral treatment [98, 131, 133, 142, 170] and on treatment adherence [66, 133, 146, 175]. In particular, a class of hybrid differential equations has been proposed to model drug behavior [144, 146, 147, 148] or scheduled treatment interruptions [4, 40, 72].
1.2 Selected HIV infection models
Ordinary differential equations (ODEs) have been widely applied in describing the dynamics of immune system. By considering the dynamic changes and interactions among multiple biological components (e.g., virus, CD4+ T cells), ODE models can capture essential behavior of dynamic systems such as nonlinearity and delay. A substantial effort has been devoted to mathematical modeling of HIV dynamics [117], for which Nowak and May [104] provided an excellent and comprehensive review. We start with an overview of the general dynamical features of HIV infection [82]. The model, which is widely adopted to describe the plasma viral load changes in HIV infected individuals, has four state variables: T, the concentration of uninfected target T cells; L, the concentration of latently infected T cells; T*, the concentration of productive infected T cells; and V, the concentration of free virus particles in the blood. The model structure is
| (1.1) |
where k is the infection rate, η the fraction of latency, ν the transition rate at which latently infected cells become virus-production active, dL the death rate of latently infected cells, δ the death rate of infected cells, N (burst size) the total number of virus particles released by a productively infected cell over its lifespan, and c the clearance rate of viral particles. Note that the case i=1 in (1.1) accounts for the loss of a free virus particle once it enters the target cell, but this term can be neglected due to its small magnitude in comparison with the clearance term −cV [117, 166]. Furthermore, the function f (T) denotes the growth rate of uninfected target T cells and can take different forms:
| (1.2) |
where λ denotes the rate at which new CD4+ T cells are produced and d is the per capita death rate of uninfected cells. In the case f = f1 [117, 121], the healthy T cells are assumed to proliferate exponentially at a rate p until reaching the carrying capacity Tmax in the absence of virus particles or infected T cells. Perelson et al. [121] considered the case f = f2 where the proliferation of L and T* cells were considered although their proportions are very small. Dropping the growth term leads to the case f = f3 [104].
Perelson et al. [121] investigated Model (1.1) with i = 0 and f = f1 or f2, and their results suggest that if the number of infectious virions produced per actively infected T cell is less than a critical value, Ncrit, the free-of-infection state is the only steady state in the nonnegative orthant, and this state is stable. For N > Ncrit, the free-of-infection state becomes unstable, but the endemic state can be either stable or unstable within a stable limit cycle. Without considering dynamics of latently infected T cells (i.e., η = 0), De Leenheer and Smith [35] examined Model (1.1) with f = f1 or f3. Assuming f(T) is a smooth function and there exists a positive steady state T̄ for variable T such that
| (1.3) |
That is, homeostasis in a healthy individual is maintained at a steady state T̄. Note Model (1.1) with f = f1 or f3 is a competitive system with respect to the cone defined by G ={(T, T*, V) ∈ R3 : T, V ≥ 0, T* ≤ 0}, and thus solutions with initial states ordered according to the order of G (i.e., their differences are a vector in G) remain ordered for the backward time [143]. Using theories of the three-dimensional competitive dynamical systems, De Leenheer and Smith [35] conducted a global analysis of viral dynamics. If the basic reproduction number R0<1, virus will be cleared and the infection will be eradicated; if R0>1, virus persists in the host, solutions approaching either a chronic steady state (f = f2) or a periodic orbit (f = f1), and here R0 = kT̄(N − i)/c, with i = 0 or 1.
HIV dynamic models that consider intracellular delays are more accurate in terms of representing the real biological processes and pharmacokinetics. To account for the time between viral entry into a target T cell and the production of new virus particles, several delay differential models have been proposed [62, 83, 96, 97, 100, 102, 166, 179]. Herz et al. [62] initially assumed that CD4+ T cells became productively infected τ time units after initial infection and formulated a discrete delayed model. When fitting the proposed model to experiment data, they found that including a delay term will change the estimate of the viral clearance rate (c), but not the loss rate (δ) of productively infected T cells. Mittler et al. [96, 97] assumed that the intracellular delay follows a gamma distribution and proposed the model with a continuous but random delay. Fitting the model to experimental data, Mittler et al. obtained a different estimate for the viral clearance rate. When considering imperfect drug efficacy, Nelson et al. [101] formulated a model with a discrete infection delay and a constant target cell density, and found that the estimated values of the viral clearance rate and the loss rate of productively infected T cells were affected by introducing a delay. Nelson and Perelson [100] further investigated the effects of delays on the estimate of the loss rate of productively infected T cells, which became larger than the values estimated from a non-delay model. These facts suggest that intracellular delays may not be neglected.
A notable feature of delay differential equation models is that delays will generally destabilize an otherwise stable equilibrium and cause sustained oscillations through Hopf bifurcations. In recent studies of within-host viral models with intracellular delays and cell divisions [28, 166], it is shown that sustained oscillation can occur for realistic parameter values. However, Li and Shu [83] considered a viral dynamic model with intracellular delays but without cell divisions, and they showed that sustained oscillations are not possible for their model. Let τ1 be the time between viral entry into a target cell and the production of new virus particles, and τ2 be a virus production period for new virions to be produced within and released from the infected cells. Without considering the latent infected CD4+ T cells, Zhu and Zou [179] considered the following delay differential equations
| (1.4) |
where μ1 is a constant death rate for infected cells that are not producing viruses, and μ2 may differ from μ1. Model (1.4) is actually a simplified version of the model proposed by Nelson and Perelson [100]. For Model (1.4), Zhou and Zou [179] obtained a ‘global’ stability result for the infection-free equilibrium if R0 = λNke−μ1τ1−μ2τ2/(dc) < 1; otherwise, infection can establish and become locally asymptotically stable. Li and Shu [83] further studied the effects of delay by analyzing Model (1.4) in the presence of only one delay (i.e. assuming τ2 = 0), and showed that the basic reproductive number completely determines the global dynamics of Model (1.4). In particular, if R0 = λNke− μ1τ1/(dc) ≤1, the infection-free equilibrium is globally asymptotically stable, and hence viruses will be cleared completely; if R0>1, the unique chronic infection equilibrium is locally asymptotically stable and acts as an attractor. Finally, it should be mentioned that experimental data of CD4+ T cells in vivo may not well support the hypothesis of sustained oscillations [15, 164] although mathematical models with intracellular delays have predicted so [28, 166]. This could be due to data sparsity, and further experimental work could resolve this mystery.
Antigen-specific immunity against HIV infection includes cytotoxic T cells (CTLs) that can kill the infected cells. Let Z(t) denote the concentration of CTLs, then Model (1.1) without considering latently infected cells can be modified as
| (1.5) |
where p denotes the killing rate and b is the death rate of CTLs. The function g(T, T*, Z) describes the rate of antigen-specific CTL response [32, 33, 104, 116]. Some investigators [66, 163] assume that the production rate of CTLs depends only on the concentration of the infected cells and chose the linear form g(T, T*, Z) = ρT*. Based on this simple model, Arnaout et al. [6] explained the biphasic decay of blood viremia in HIV patients under treatment: viral load decreases quickly while CTLs are abundant, but slowly as CTLs are rare. Nowak and Bangham [110] assumed that the production of CTLs is also dependent on the concentration of CTL themselves, yielding g(T, T*, Z) = ρT*Z, and explored the effects of between-subject variation in immune responsiveness on virus load and viral strain diversity. The model in [110] has also been analyzed by Liu [86] and Kajiwara and Sasaki [71]. Culshaw et al. [29] further assumed that the production of CTLs is CD4+ T cell-dependent and accordingly chose the form g(T, T*, Z) = ρTT*Z. Assuming that the viral load is proportional to the level of infected cells since free virus is thought to be short lived in comparison with infected cells [6, 118], Culshaw et al. [29] considered the following model
| (1.6) |
where the ratio k′/k is the proportion of infected cells that survive the incubation period. It was shown that Model (1.6) had up to three equilibria and the local stability of these equilibria was analyzed by Culshaw et al. [29]. Also, Culshaw et al. investigated the optimal control problem in which they maximized the benefit in terms of levels of healthy CD4+ T cells and other immune cells and the systemic cost of chemotherapy. In particular, a self-regulating CTL response, g(T, T*, Z) = ρ, has also been discussed in [104].
HIV viral species that can successfully evade the host immune response are called “escape mutants”. It is challenging to investigate the dynamics of immune escape. However, there are some studies [5, 34, 104, 111] that made an attempt to tackle this problem by describing antigenic escape from CTLs using simple mathematical models. Specifically, Nowak and Bangham [110] proposed the following model to understand the interplay between selection forces in favor of and against viral mutation:
| (1.7) |
where and Vi denote the abundance of infected cells and free virus of type i, respectively, and Zi denotes the concentration of antigen-specific CTLs against mutant i(i =1, ···, n). Viral mutants differ in their antigenic specificity, the rate at which they infect cells (ki), and the rate of virus production (Ni). De Boer [34] extended Model (1.7) by including a density-dependent infection term which may better describe the dynamics of acute infection of the viral loads and the immune response. Althaus and De Boer [5] added stochastic events of viral mutation and considered the saturated interaction between infected cells and CTLs according to Michaelis-Menten kinetics. Their computational model of HIV/SIV infection has a broad cellular immune response targeting different viral epitopes. Their simulation shows that a higher degree of immunodominance will result in more frequent immune escape, a reduced control of viral replication, and a substantially impaired replicative capacity of the virus.
2. HIV viral dynamic models with antiretroviral intervention
From Zidovudine (AZT) to dual-drug therapy and then to highly active antiretroviral therapy (HAART), the treatment of HIV/AIDS has been exercised for more than 20 years. HAART uses at least three different antiretroviral drugs (ARVs), typically two nucleoside or nucleotide reverse transcriptase inhibitors (NRTI’s) and one non-nucleoside reverse transcriptase inhibitor (NNRTI) or a protease inhibitor (PI) or another NRTI called abacavir (Ziagen). Reverse transcriptase inhibitors (RTIs) can effectively block the infection of target cells by free virus, while PIs prevent HIV protease from cleaving the HIV polyprotein into functional units. Modeling of antiretroviral intervention can significantly advance our understanding of a variety of biological and clinical questions.
2.1 Modelling constant and variant drug efficacy
Let ηRT be the efficacy of RTIs and ηPI be the efficacy of PIs, the two parameters were assumed to be constant in [117, 100]. Based on Model (1.1), the HIV viral dynamic model with HAART treatment is given as
| (2.1) |
where VI and VNI denote the concentration of infectious and noninfectious virus, respectively, and V = VI +VNI is the total viral load. Model (2.1) is a simplified version of the model in [117], which considered a more complex form of T cell reproduction. Note that variable VNI does not show up in the first three equations of Model (2.1), and hence the qualitative dynamics of this model is the same as that of model (1.1) with f = f3 and i = 0. Based on this model, it is easy to show that the virus-free equilibrium (E0 = (λ/d, 0, 0)) is locally asymptotically stable if R0 ≤ 1, while the endemic state
is globally asymptotically stable when R0 > 1, where
| (2.2) |
Furthermore, the basic reproduction number is related to the threshold of drug efficacy to achieve virus eradication. For example, if we only consider RT inhibitors, then virus can be eradicated if drug efficacy ηRT is greater than a critical value .
Note that the drug concentration in HIV patients is not a constant, but can vary over time, especially during the medication intervals. In fact, once a dose is administered, drug concentration increases rapidly and reaches a peak value, then decreases gradually. When another dose is administered, drug concentration is likely to vary in a similar way [144]. We assume that drugs are taken at time tk (not necessarily equally spaced) and the effect of the drugs is instantaneous, leading to a system of impulsive differential equations which have a solution that is continuous for t ≠ tk and undergoes a sudden jump at t = tk (see [8, 9] for more details on the theory of impulsive differential equations). Let C(t) be the intracellular concentration of the drug and we have
| (2.3) |
where h(t) is the drug elimination rate and can be parameterized by either first order elimination kinetics or the Michaelis-Menten elimination kinetics. Considering a fixed dose and a constant time-interval T (that is, tk +1 − tk = T), then the solution C(t) to model (2.3) is a periodic and piecewise continuous function of time t, which can also be explicitly expressed [144, 154]. In most viral dynamic studies, either drug efficacy was assumed constant over treatment time, as in Model (2.1) [117, 174], or antiviral regimens are assumed to be perfect for blocking viral replication [63, 118]. However, in reality, the effect of antiviral treatment will change over time, primarily due to pharmacokinetic variation, fluctuating adherence, the emergence of drug resistant mutations and other factors.
Without considering drug adherence or drug resistance, a simple pharmacodynamic Emax model for dose–effect relationship can be given as [49]
| (2.4) |
where Emax is the maximal effect that can be achieved, C(t) is the drug concentration, and EC50 is the drug concentration that corresponds to the 50% of the maximal effect. Note that many different forms of Emax have been developed in previous studies; for example, the sigmoid Emax model, the ordinary Emax model, and the composite Emax model [49, 141]. It follows from Models (2.3) and (2.4) that the drug efficacy may be a periodic and piecewise continuous function of time and there are studies on HIV dynamic models with periodic drug efficacy [64, 176, 178]. Let drug efficacies ηRT(t) and ηPI(t) be periodic and continuous (or piecewise continuous) function of time. For system (2.1) with ϖ -periodic drug efficacies ηRT(t) and ηPI(t), Yang and Xiao [176] investigated the treatment dynamics by employing the persistent theory for the periodic system [7, 167]. They defined a threshold parameter, similar to the basic reproduction number, which determines the extinction or persistence of the disease. Their main results showed that the disease-free equilibrium of system (2.1) is globally asymptotically stable if r(ΦM (·) (ϖ)) < 1, while the disease is persistent if r(ΦM (·) (ϖ)) > 1, where r(ΦM (·) (ϖ)) is the spectral radius of ΦM (·) (ϖ), and ΦM (·) (ϖ) is the fundamental solution matrix of the linear and ϖ -periodic differential equation
| (2.5) |
Note that the threshold parameter cannot be expressed explicitly, but it can be calculated numerically [167, 176].
2.2 Emergence of drug resistance
Although HAART has proved to be extremely effective in suppressing the plasma viral load in most HIV-1 infected patients down to the detection limit (e.g., 50 RNA copies ml−1) of the standard assay to date [25], drug treatment often fails to achieve virus eradication primarily due to the emergence of drug-resistant mutants [37].
It is widely acknowledged that two reasons can account for the development of HIV drug resistance: the transmission of drug-resistant mutants to susceptible individuals, or the adaptive mutations generated during treatment [16, 128]. Ribeiro and Bonhoeffer [129] calculated the probabilities of both reasons and suggested that under a wide range of conditions, treatment failure is most likely due to the pre-existence of drug-resistant virus before therapy. Bonhoeffer and Nowak [21] showed that, given pre-existence of drug-resistant virus, a more efficient therapy could lead to a greater initial reduction of virus load, but would also cause a faster rise of drug-resistant mutants. A number of mathematical models have been developed to study the effect of ARV drugs on the evolution of drug-resistant HIV mutants. McLean and Nowak [98] examined the competition between drug-resistant and wild-type strains to determine which type of virus will eventually dominate the virus population during the course of AZT treatment. Nowak et al. [108] considered a two-strain model and compared the modeling results with experiment data on the development of drug resistance in patients treated with nevirapine. Kirschner and Webb [77] investigated drug resistance for the case of single drug treatment and compared the treatment outcomes for drug therapies initiated at different CD4+ T cell levels. The effect of an immune response on the emergence of drug resistance was investigated in [142, 170]. Rong et al. [133] proposed a mathematical model including both wild-type and drug resistant strains to understand the mechanism of the emergence of drug resistance during therapy. Let Ts(t) be the concentration of cells productively infected by drug sensitive virus, Tr(t) be the concentration of cells productively infected by drug-resistant virus, and Vs(t) and Vr(t) represent concentrations of drug sensitive and drug-resistant virus, then the model can be given as
| (2.6) |
where ks and kr denote the rate constants at which uninfected cells T(t) are infected by drug sensitive and drug-resistant virus, respectively; also, u(0 ≤ u < 1) is a rate at which cells infected by the drug sensitive virus become drug-resistant due to viral RNA mutation. Both types of infected cells are assumed to have the same death rate δ. Assume that the drug sensitive and resistant strains have different burst sizes, Ns and Nr, while they can have the same virion clearance rate c. Without antiretroviral intervention, the reproductive ratio for each strain
| (2.7) |
can be obtained. The infection-free steady state E0 = (λ/d, 0, 0, 0, 0) is locally asymptotically stable if Rs < 1/(1−u) and Rr < 1, and it is unstable if Rs > 1/(1−u) or Rr > 1. The steady state with only drug-resistant virus exists if and only if Rr > 1 and it is locally asymptotically stable if Rr > (1−u)Rs, and is unstable if Rr < (1−u)Rs. The co-existence steady state exists and is locally asymptotically stable if and only if Rs > 1/(1−u) and Rr < (1−u)Rs.
After drug intervention, the reproductive ratios for drug sensitive and resistant strains become
| (2.8) |
where are the efficacies of RTIs and are the efficacies of PIs for the drug sensitive strain and drug-resistant strains, respectively. An overall treatment effect for each strain can be defined as follows
| (2.9) |
Based on the stability results with ART, there are two threshold values ε1 and ε2 for εs such that: (i) both the wild type and the drug-resistant strains coexist if drug efficacy εs is less than ε1; (ii) only the drug-resistant virus will persist for ε1 < εs < ε2; and (iii) both strains will be eradicated if εs > ε2. This indicates that drug resistance is more likely to arise for an intermediate level of treatment effectiveness, at which the reproductive ratios of both strains are close. Furthermore, a pharmacokinetic model including both blood and cell compartments is employed to estimate the drug efficacies against the wild-type and the drug-resistant strains. Simulation results suggest that the perfect adherence to the regimen protocol will well suppress the viral load of the wild-type strain while drug-resistant variants develop slowly. However, an intermediate level of adherence may result in the dominance of the drug-resistant virus several months after the initiation of therapy. This result is similar to that of [145].
Experimental measure of adherence remains problematic and challenging. There are lots of evidence showing that suboptimal adherence is associated with a high risk of developing HIV drug resistance [10, 44, 140, 161] and is one of the major causes of treatment failure [63, 175, 113]. A number of mathematical models have considered the effects of imperfect adherence to drug regimens [45, 64, 122, 146, 161, 172] and see Heffernan and Wahl [60] for a comprehensive overview. A standard definition of adherence and reliable measures of adherence are still lacking. Fortunately, there have been substantial progresses in the two areas within the past few years. Wahl and Nowak [161] considered the outcome of a therapy as a function of the degree of adherence to drug regimen and determined the conditions under which a resistant strain would dominate. Phillips et al. [122] proposed a stochastic model to study the resistance development for different drug use patterns.
The effect of time-varying or constant drug concentrations on HIV dynamics has been modeled by a large number of studies [117, 174]. However, only a handful of studies have modeled the direct interaction between drug concentrations and the dynamics of a pathogen population, examining the necessary conditions for the emergence of drug resistance [95, 144, 145, 147]. In such models, the immune cells infected by virus (e.g., CD4+ T cells) are divided into multiple classes, depending on whether a cell has been infected or has absorbed any of the drugs. An impulsive differential equation can be used to model the change in drug concentration when a new dose is administered. Let R(t) denote the intracellular drug concentration that satisfies model (2.2), T(t) be the population of susceptible (uninfected) CD4+ T cells, Ts(Tr) denote the cells infected by the wild-type (mutant) infectious virus, TRs denote the uninfected cells which have absorbed sufficient amount of drugs such that the wild-type strain can be inhibited from replication, but not enough to prevent infection by the mutant strain. These cells may come into contact with the wild-type/mutant strain or the drug. TRr represents uninfected cells which have absorbed sufficient amount of drugs such that both wild-type and mutant strains are inhibited. Such cells will not become infected while they remain in this state. These cells will eventually revert back to TRs cells if the drug effect wears off, or if such cells undergo apoptosis. The model in [145] is thus given as
| (2.10) |
where ks(kr) is the rate at which wild-type (drug-resistant) virus infects T cells, Ns(Nr) is the number of virions produced per infected cell and ω is the fraction of infectious virions produced by an infected T cell. Furthermore, mRs and mRr are drug clearance rates for intracellular compartments with an intermediate or high drug concentration, respectively. d(d1) is the death rate of uninfected (infected) CD4+ T cells. Smith and Wahl [145] considered three treatment regimens corresponding to a low, intermediate or high drug level, respectively
| (2.11) |
where kP is the rate at which the drug inhibits the wild-type T cells when drug concentrations are intermediate (R1 < R < R2), kR and kQ are rates at which the drug inhibits the wild-type and drug-resistant T cells, respectively, when drug concentration is high (R > R2). By analyzing all possible equilibria (or periodic solution) and their stability for low, intermediate or high drug level, Smith and Wahl [145] predicted that drug resistance might arise at both intermediate and high drug concentrations, whereas at low drug levels resistance would not emerge. Smith [146] used a model similar to (2.10) to determine how many doses can be missed before HIV treatment is adversely affected by the emergence of drug resistance. In [146], the dynamics of drug, and hence adherence, is also modeled by the impulsive differential equations. Here the perfect adherence is that the dosage Rk is not zero at each medication time t = tk. Otherwise, for example, if Rk = 0, k = 2, 3, 4 indicates 3 doses missed after the first dose. Miron and Smith [95] extended the work from a single drug holiday during any given therapy [146] to the case of more than one drug holidays.
2.3 Short-term HIV dynamics and optimal controls
A large number of HIV dynamic models have been proposed by AIDS researchers [119, 174] to provide a theoretical guidance for development of new HIV treatment strategies. For simplicity, some modeling work focused on short-term dynamics while other models with constant or time-dependent drug efficacy are formulated to explore long-term viral dynamics [66, 69, 80, 170, 175]. Specifically, these short-term models either fit only the early segment of the viral load trajectory [72, 90, 128, 153], or design an optimal drug therapy regime in a short time interval [18, 29, 47, 70, 76, 133, 169].
The control-theory approach has been employed to design an optimal treatment strategy. Such investigations employed various types of mathematical models and different objective functions. For example, the studies in [18, 47, 76, 133] for optimal control of HIV chemotherapy used an objective function based on simultaneously maximizing the CD4+ T cell counts and minimizing the systemic cost of chemotherapy. Generally, drugs efficacies ηRT and ηPI in Model (2.1) are replaced by the control variables u1 and u2 (0 ≤ ui ≤ 1, i = 1, 2) which accounts for reverse transcriptase and protease inhibitors actions, respectively. The task then boils down to the determination of optimal control functions u1(t) and u2(t). For example, the objective function can be defined as
| (3.1) |
which is maximized subject to model (2.1). The nonnegative constants B1 and B2 represent the desired ‘weights’ of the benefit and the cost, respectively. By applying Pontryagin’s Maximum Principle to the constrained control problem, the optimal controls can be obtained. Joshi [70] considered controls representing immune boosting and viral suppressing drugs. Wein et al. [169] proposed a deterministic control problem which is based on a finite number of virus strains and allows virus mutations. Using numerical simulations, they demonstrated a dynamic strategy that can reduce the total free virions, increase the uninfected CD4+ counts, and postpone the emergence of drug-resistant strains. It should be mentioned that the optimal treatment strategies resulted from these studies are for a finite time window so the conclusions may not be applicable to a long-term treatment problem.
Recently, a handful of stochastic models were formulated to characterize the dynamics of early infection when virus is released from cells [55, 72, 129, 157]. For example, Tuckwell and Le Corefec [27, 156] applied the multi-dimensional diffusion process to model early HIV-1 population dynamics. Tan and Wu [152] developed a 4-dimensional stochastic infection model for HIV and studied the system using Monte Carlo simulations. They noted that there was a positive probability that the virus could be eliminated by the process. Monte Carlo approaches were also used by Kamina et al. [72] and Heffernan and Wahl [61] to study the probability that an infection would not be established after exposure to a pre-specified amount of pathogens. Tuckwell et al. [157] investigated the probability of a viral particle infecting one or more target cells before being cleared. A stochastic model of early infection was developed by Haeno and Iwasa [55] to study the generation of drug-resistant virus based on the assumption of exponential growth of virus. Ribeiro and Bonhoeffer [129] also developed a stochastic simulation model of early infection to determine the best timing to initiate antiretroviral therapy with considering the random generation of drug-resistant mutants. Pearson et al. [114] modeled early infection using a discrete random process, in which both the numbers of virions and infected cells are tracked for a gradual or a burst release of virus. They showed that different viral release patterns lead to different early dynamics (e.g., different probabilities of extinction, different distributions of time to establish infection).
3. HIV viral dynamic models with long-term treatment and different treatment strategies
Most HIV dynamic studies for short-term viral dynamics are under assumptions of ideal patient behavior, treatment potency, and drug susceptibility. Although these studies characterized HIV replication during a short period of antiretroviral (ARV) treatment, the effectiveness of ARV therapies and variations of HIV-1 dynamics during chronic treatment of HIV-1 infection in a more realistic setting have not been carefully studied quantitatively. In particular, there are evidences showing that the viral load trajectory may change its shape in the later stage due to variations in drug resistance, noncompliance or other clinical factors [66]. Hence, it is necessary to develop models to account for, e.g., drug susceptibility and drug adherence to quantify long-term dynamics under ARV therapies.
Note that for HIV subspecies within a host, the genetic diversity is usually notable, corresponding to a great diversity in response to various ARV agents. In clinical practice, genotypic or phenotypic tests can be used to measure the sensitivity of HIV-1 to ARV before a treatment regimen is selected. Molla et al. [98] suggested that the phenotype marker, median inhibitory concentration IC50, can be used to quantify agent-specific drug susceptibility. Wu et al. [64, 66] used the following drug resistance model to approximate the within-host changes over time of IC50
| (3.2) |
where I0 and Ir are respectively the values of IC50 (t) at the baseline and time point tr, at which resistant mutations dominate. Huang and Wu [64] investigated the relationship between actual failure time (the time at which the viral growth rate changes from negative to positive) and detectable failure time (the time at which viral load rebounds to above the limit of detection), and obtained an approximately linear relationship which could be used to estimate the actual rebound failure time from the detectable rebound failure time. They examined how different patterns of adherence affect antiviral response. Their results suggest that longer sequences of missed doses increase the chance of treatment failure and accelerate the failure.
Patients may occasionally miss doses or multiple consecutive doses for various reasons such as misunderstanding prescription instructions, serious side-effects and others. The deviation from prescribed dosing affects drug exposure in a predictable way. Wu et al. [64, 66, 175] used the following model to describe adherence
| (3.3) |
where 0 ≤ Rd <1 (d = 1, 2) with Rd denoting the adherence rate for drug d during the interval, and Tk denotes the adherence evaluation time at the k-th clinical visit. Wu et al. [172] developed a novel HIV-1 dynamic model with consideration of pharmacokinetics, drug adherence and drug susceptibility to link plasma drug concentration to the long-term changes in HIV-1 RNA observation after initiation of therapy. Their results show that any single factor of pharmacokinetic (PK) adherence measured by pill counts and drug susceptibility does not seem to contribute to long-term virologic response, but their combinations in viral dynamic modeling can predict virologic response.
The inherent risks and problems associated with HAART such as adverse effects, imperfect adherence and drug resistance have led to development of strategies of scheduled treatment interruptions (STIs); in particular, CD4+ T cell count-guided STIs might provide a good strategy to address these problems [4, 40, 72]. Several clinical studies have been done to compare STI strategies with continuous antiretroviral therapy, but unfavorable results have been reported [4, 40, 72]. Thus, more careful studies with appropriate quantitative approaches are needed to resolve the problem.
HIV dynamic models and control theory have been used together to study both non-adaptive and adaptive STI strategies [2, 54, 134]. Adams et al. [2] considered a complicated HIV dynamic model and used control theory to design non-adaptive STI strategies that involve several short-term interruptions after infection. They showed that such strategies could lead to a long-term control of virus in some patients. Hadjiandreou et al. [54] formulated a non-adaptive STI therapy as a dynamic programming problem and showed that STIs could control disease progression. Tang et al. [148] proposed models to use CD4+ T cell counts as a guide to start or halt the therapy. The proposed models extended the classical HIV dynamic models [104, 117] to the piecewise dynamic model and were sued to explore potential explanations why the controversial results were obtained from different clinical studies [148]. The recent clinical studies [40, 72] initiated the ARV therapy once the CD4+ T cell counts dropped below a lower threshold (denoted by CTH, say 200 or 350 cells/ml) and suspended the treatment once the CD4+ T cell counts increased above an upper threshold (denoted by CTH, say 600 cells/ml or more), where [CTH, CTH] is called the threshold window of treatment decision. In the absence of considering dynamics of noninfectious virus or latently infected individuals, we can extend Model (2.1) to include a threshold window as follows
Drug-off state
| (3.4) |
Drug-on state
| (3.5) |
For the drug-off and drug-on states, there are steady states and if the reproduction number for each subsystem is greater than one. And obviously we have . Note that according to Models (3.4) and (3.5), for a new patient, if T(t0) + T* (t0)>CTH, then this patient could be in the drug-off state; if T (t0) + T* (t0)<CTH, he/she could be in the drug-on state; and if CTH < T(t0) + T* (t0)<CTH, he/she may be either in the drug-off state or in the drug-on state, depending on whether the trend of CD4+ T cell counts is increasing or decreasing. Furthermore, if , the system reverts to the drug-off state before it can reach the equilibrium Eon; while if , the system must switch to the drug-on state before it can reach the steady state Eoff. The two observations together suggest that the system will persistently alternate between drug-off state and drug-on state if . Generally we assume that and . According to the relationships among , the lower threshold CTH and the upper threshold CTH, we have four possible cases:
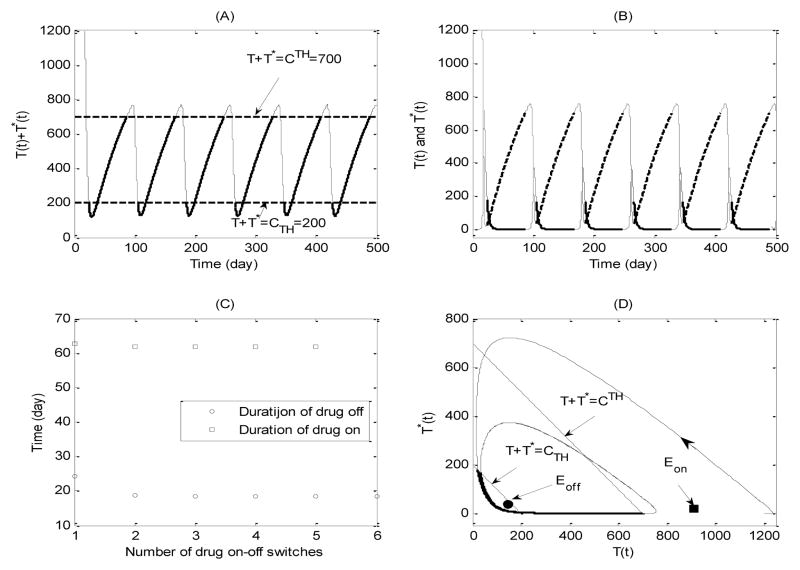
For Case 1 we can easily see that both equilibria Eon and Eoff are local stable in the given range and are also virtual (see definitions in [12, 46]). It is clear that these stable but virtual equilibria can never be actually reached, which indicates that the system may switch between the drug-off state (3.4) and the drug-on state (3.5) forever. It follows that for the given threshold window, the CD4+ T cell counts fluctuate periodically during the whole treatment period. The variations of healthy and infected CD4+ T cells are also given, respectively, in Fig. 1 (B). Fig. 1(C) shows that the durations of each drug-on/off are stabilized at fixed values and the duration of drug-on is much longer than that of drug-off. Numerical simulations show that the effects of the width of threshold window on the durations of drug-on and drug-off states are complex. The duration of the drug-on state is more sensitive to the variation of thresholds compared with that of the drug-off state [148].
Fig. 1.
Simulation of typical solutions of drug on-off state systems (3.4) and (3.5) with CTH = 700ul−1, CTH = 200ul−1. (A) Time trajectory of total CD4+ T cell population; (B) Time trajectory of health CD4+ T cell population (dashed line) and infected CD4+ T cell population (solid line); (C) Durations of drug on and drug off for each drug on-off switch; (D) Phase plane plot of health CD4+ T cell and infected CD4+ T cell populations.
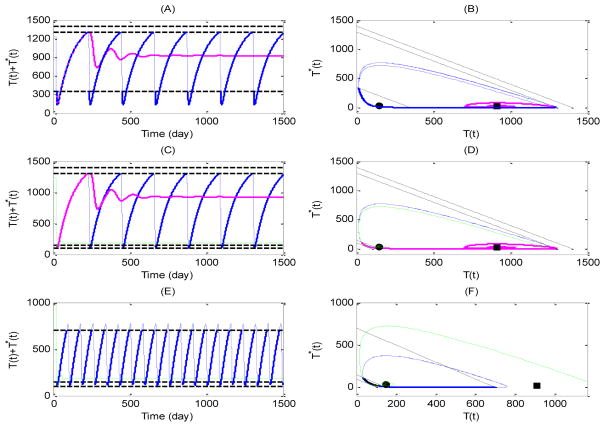
For Case 2, the drug-on equilibrium Eon becomes a regular steady state, which is globally stable for the drug-on system (3.5) only. Fig. 2(A, B) shows that one trajectory (pink curve) initiating from an initial point approaches the regular equilibrium Eon for CTH = 1400 ul−1, whereas another trajectory (blue curve) starting from the same point oscillates periodically if CTH = 1300 ul−1. Case 4 is similar to Case 2 except that the real drug-off equilibrium Eoff is globally stable for the drug-off system (3.4). The CD4+ T cell counts either approach a certain value (green curve), corresponding to free of therapy, or oscillate persistently (blue curve), corresponding to a drug-on/off treatment, as shown in Fig. 2 (E, F). For Case 3, we have that both equilibria Eon and Eoff are regular and globally stable for their own systems. Fig.2 (C, D) shows that the CD4+ T cell counts will approach certain levels represented by the equilibrium Eon or Eoff, corresponding to a continuous treatment strategy (pink curve) or free of therapy (green curve), under certain thresholds. It is interesting to note that, similar to Case 1, oscillation of the CD4+ T cell counts can also be observed, suggesting an STI strategy with a threshold window is required (blue curve). This indicates that the STI strategy with different thresholds may result in different treatment regimes such as drug-on/off, continuous therapy, and free of ARV treatment.
Fig. 2.
Numerical simulations of solutions of drug on-off state systems (3.4) and (3.5) with different low and upper threshold values. Case 2: (A–B) Blue cure for the solution with CTH = 1300ul−1, CTH = 350ul−1, pink curve for the solution with CTH = 1400ul−1, CTH = 350ul−1; Case 3: (C–D) Blue cure for the solution with CTH = 1300ul−1, CTH = 150ul−1, pink curve for the solution with CTH = 1400ul−1, CTH = 350ul−1, and green curve for the solution with CTH = 1300ul−1, CTH = 100ul−1; Case 4: (E–F) Blue cure for the solution with CTH = 700ul−1, CTH = 150ul−1, and green curve for the solution with CTH = 700ul−1, CTH = 100ul−1.
In summary, the results showed that the CD4+ T cell counts can either fluctuate around the two thresholds or stabilize at an equilibrium for drug-on or drug-off state. This implies that, for a fixed threshold window, whether a patient needs a continuous therapy or STI strategy depends on the initial CD4+ T cell counts of the patient at the treatment starting time. Further numerical studies show that the STI strategy is needed for a patient with a relatively high or low initial CD4 T cell counts, while the continuous therapy is required to maintain CD4+ T cell count above a safe level (Fig. 2 (C–D)) if the initial CD4+ T cell count of a patient is in the middle (data not shown here). This further confirms that it is important to personalize the treatment strategy for different patients at different stages of their disease progression with different initial CD4+ T cell counts.
4. Inverse problems for differential equation models
Solving inverse problems is more challenging and usually of great importance to mathematical modeling, especially when the majority of key model parameters are unknown. Although some parameter values found in literature can be plugged into models, biases are usually introduced into the estimates of the rest parameters, which will consequently affect the validity and generality of biological conclusions inferred. It is therefore desirable to rigorously determine all unknown parameter values from available data and given model structures in practice. In this section, we briefly review the main techniques for solving the inverse problems of differential equation models for HIV dynamics, including nonlinear least squares (NLS), time-varying parameter estimation, and the estimation methods for mixed-effect ODE models. More advanced nonparametric smoothing-based methods are also discussed.
4.1 Nonlinear least squares approach
Notice that the ODE identifiability, in particular nonlinear ODE identifiability problem should be carefully addressed before the ODE parameter estimation is carried out. The nonlinear ODE identifiability studies, in particular for HIV viral dynamics models, are recently reviewed by Miao et al. [94], and thus are omitted here. The solutions to even linear ODEs are usually nonlinear such that the nonlinear least squares (NLS) method has been widely used in practice by researchers in various fields. In this section, we review the basic principle of NLS and the associated practical issues.
For a nonlinear ODE system, the measurement model can be written as follows
where xi ∈ Rm a vector of state variables, θ* ∈ Rq the true parameter vector, yij the observed variable, n the number of observation points, and Ji the number of replicates at xi. For convenience, we introduce the notations y = (y11, y12,…, y1,J1,…, yn1, yn2,…, yn,Jn)T and ε = (ε11, ε12,…, ε1,J1,…, εn1, εn2,…, εn,Jn)T, and let Σ denote the covariance matrix; then the unbiased estimator θ̂ of the true parameter vector θ* is given by
where S(θ)is also called the weighted residual sum of squares (WRSS). When Σ is unknown and has to be estimated, the computing details can be found in Seber and Wild [139]. For simplicity, let Σ = σ2V and assume ε ~ MVN(0,σ2V), where MVN stands for multivariate normal distribution. The distribution of θ̂ is thus
where is also called the Fisher information matrix. The unbiased variance estimator of σ2 is given by
where is the total number of observations.
Although the NLS is conceptually simple, the associated computing issues need to be carefully addressed. Specifically, the NLS regression problem boils down to the determination of the global minima of S(θ), which becomes very challenging for a high-dimensional parameter space or for noisy data. Therefore, the choice of the appropriate optimization algorithms becomes critical to obtaining reliable estimates. Four categories of optimization algorithms have been widely used in practice, including direct search methods, gradient-based methods, global optimization methods, and hybrid (or memetic) algorithms. Briefly speaking, the direct search methods (e.g., the Simplex method [30]) search for local minima and are usually sensitive to the starting point and computationally expensive. The gradient-based methods, such as the Levenberg-Marquardt method and the Gauss-Newton method, can efficiently search for local minima based on the Jacobian and/or Hessian matrix of the objective function [103]. The sequential quadratic programming (SQP) algorithms are among the highly recommend algorithms in the gradient-based category. High-quality implementations of SQP can be found in the fmincon routine in MATLABTM (The MathWorks Inc.), SOLNP by Ye [177], or SNOPT by Gill etc. [50]. Although the gradient-based algorithms have been previously used for parameter estimation of ODE models [41], these methods can be easily trapped by local minima or just fail to converge for nonlinear ODE models. To overcome such problems, global optimization algorithms have been considered for ODE models (e.g., differential evolution [149], particle swarm [74], and scatter search [51]). Although the global optimization algorithms are capable of searching the global minima/maxima for spiny nonlinear objective functions, the associated computing costs are usually prohibitive for such methods to converge. It is thus natural to combine the global methods with gradient-based methods to achieve a better balance between estimation accuracy and computing efficiency, which results in the so-called hybrid or memetic algorithms. Rodriguez-Fernandez et al. [130] combined the scatter search algorithm with the SQP method and applied their algorithm to an example of HIV models for parameter estimation. However, the DESQP algorithm proposed in [84] may have a better performance in comparison with the approach in [130] primarily due to the superiority of the differential evolution algorithm over the scatter search method.
4.2 Parameter estimation for semi-mechanistic models
One common concern about mathematical modeling is that any given model structure can only take a limited number of biological factors into consideration such that the conclusions may become model structure specific. Furthermore, many biological mechanisms may remain unknown or undistinguishable such that the development of mechanistic models becomes infeasible. To address the problems above, semi-mechanistic modeling has been introduced and employed for a variety of biomedical problems [1, 18, 41, 44, 53, 73, 75, 148]. In particular, the work of Liang et al. [84] considered a more general framework for semi-mechanistic modeling and used the long-term HIV dynamics as an example. More specifically, the following model with both constant and time-varying unknown parameters was considered
| (4.1) |
where the biological meaning of state variables and model parameters are the same as those in Model (3.4) except that a time-varying parameter η(t) is introduced to describe the infection rate which may vary due to the change in antiviral drug efficacy (e.g., the development of drug resistance). To estimate both the constant and time-varying parameters in this model, the semi-parametric model was turned into a parametric model by approximating the unknown time-varying parameter η(t) using, e.g., splines. For example, Li et al. [82] used natural cubic splines to approximate the unknown time-varying parameters in a pharmacokinetic model. However, different types of splines can be used for approximation, such as the well-known piecewise polynomial splines and basis splines. Here we use the B-splines to illustrate the idea so Model (4.1) becomes
| (4.2) |
where is approximated by a linear combination of the kth-order basis spline function bi,k (t). Since bi,k (t) are uniquely determined once k is given and knots are specified, the unknown model parameters are now (λ, ρ, N,δ, c, a1, a2,…, as)T, which are all constant. In this way, the semi-parametric model becomes a parametric model so the NLS method introduced in the above subsection can be applied for parameter estimation.
Two practical issues need to be addressed for this approach. First, the spline order k is usually between 2 and 5. B-splines of order 2 are actually piecewise straight lines. Also, higher order B-splines (e.g., k> 5) can introduce unnecessary dramatic local oscillation called Runge’s phenomenon [135]. Second, the positions of knots can usually be selected by quantile such that the number of data points is nearly equal between any two consecutive knots. However, the knots’ position may have to be manually adjusted for some problems to achieve certain temporal patterns, and unfortunately there are no systematic and rigorous methods so far for automatic determination of optimal knots’ positions. That is the reason Liang et al. [84] did not select knots’ positions but spline orders using Akaike Information Criterion (AIC) [3], Bayesian Information Criterion (BIC) [138] and corrected Akaike Information Criterion (AICc) [19].
4.3 Parameter estimation for mixed-effects ODE models
Longitudinal dynamic systems were first introduced in Han, Chaloner and Perelson [54]; however, this work was formulated in the regular nonlinear mixed-effects model framework instead of general mixed-effects ODE models. Li et al. [82] and Huang, Liu and Wu [65] formally addressed this issue. Specifically, it was suggested in Huang et al. [65] that a general longitudinal dynamic system can be given as follows:
where the subscript i denotes the ith subject, xi(t) ∈ Rm is a vector of state variables, yi(tij) ∈ Rn the measured output variable vector, ui(t) ∈ Rp the known system input vector, θi ∈ Rq the parameter vector, and x0i the initial condition vector. In the two equations above, the structure of the dynamic system is the same for all subjects but the values of parameters and initial conditions could be different for different subjects. The between-subject variation of parameters and initial conditions can be generally specified as
where is the subject-specific parameter vector, μ the population parameter vector, and bi are random effects. For simplicity, it is usually assumed bi ~ MVN(0, D), βi = μ + bi, and εi (tij)|bi ~ MVN(0, Ri). In nature, the formulation above is still a nonlinear mixed-effects (NLME) model [31]. Guedj, Thiébaut and Commenges [52] proposed a maximum likelihood estimator (MLE) and investigated the associated statistical inference for ODE NLME models. As argued in [52], the advantages of the MLE approach over the Bayesian approach include a much lower computing cost, requiring no prior distributions, and a well-established framework of inference theories. Although the original work of Guedj et al. [52] accounted for the left-censored data, it is not the focus here and thus we only give the complete data log-likelihood function here
The key step to obtain the maximum likelihood estimates in Guedj et al. [52] is to compute the first order derivatives of the log-likelihood in two stages. At the first stage, the score of the full log-likelihood was calculated for given random effects; at the second stage, the score of the observed log-likelihood was calculated by integrating out the random effects as suggested in [87, 24]. In addition, a Newton-Raphson type of iterative method was proposed to reduce the computing burden associated with the calculation of the Hessian matrix. Their simulation studies suggested that the rate of successful convergence by the proposed method is greater than 90% for a specific ODE model. However, there also exist a number of alternative methods for fitting NLME models, among which the stochastic approximation EM algorithm (SAEM) [38] looks a promising solution to general NLME problems due to its accuracy and efficiency. The SAEM algorithm has also been extended and successfully applied in a number of studies [78, 79, 137, 91, 92, 93].
Finally, it should be mentioned that the estimation problem of mixed-effects ODE models has also been addressed using the Bayesian framework [54, 162] and the two-stage smoothing-based approach [43]. But limited by space, the technical details are not described here.
4.4 Nonparametric smoothing-based approach
Varah [158] proposed an alternative parameter estimation technique, based on the earlier work of Swartz and Bremermann [150] and Benson [11], that does not require repeated numerical solutions of ODEs. This method fits the discrete measurements of the measured dynamic variables, say y, empirically using a nonparametric smoothing method such as splines, which are then differentiated with respect to time to obtain the estimated time-derivative curves, dy/dt. This time-derivative information is then substituted into the ODEs, converting the parameter estimation problem from a dynamic optimization problem into a much simpler linear/nonlinear regression problem that can be solved using either the linear or nonlinear least-squares method. For this smoothing-based method, parameter values are selected to minimize squared residuals in the differential form of the model, (dy/dt–dŷ/dt)2 rather than the traditional integrated form of the model, (y − ŷ)2. Swartz and Bremermann [150] and Varah [158] claimed that the main benefits of such a smoothing-based technique include less computational time than other parameter estimation techniques for dynamic models, and no need for determining the initial conditions for the output variables. The drawback is that the estimate of the derivative curve is usually poor, which may result in poor estimates of interested parameters.
Ramsay [125] proposed another smoothing-based approach called the principal differential analysis (PDA) wherein coefficients (possibly time-varying) in linear ODEs are fitted empirically from the data. PDA has been used to fit linear differential equation models in a variety of applications [126]. However, for the smoothing-based methods, there is always a trade-off between the function being over-smoothed and being under-smoothed. In the spline-based ODE parameter estimation approach, Varah [158] attempted to tackle this trade-off problem by interactively adjusting the number and position of knots by hand until satisfactory smoothing was obtained. Alternatively, the extent of smoothing can be controlled by adding a penalty on higher-order derivatives of the splines [125]. Usually the second-order derivative (curvature) is used, which is similar to the idea of smoothing splines. Heckman and Ramsay [59] also considered the L-spline, i.e., replacing the second-order derivative penalty with the ODE model-based penalty. Recently, Poyton et al. [123] and Varziri et al. [159] proposed an iterative PDA (iPDA) approach for simultaneously minimizing the PDA objective function with the ODE model-based penalty. Ramsay et al. [126] proposed a new algorithm to minimize the penalized spline objective function to fit ODE models.
Liang and Wu [85] adopted a different perspective (the measurement error in regression model) to tackle the smoothing-based estimation problem, called two-stage pseudo least squares (PLS). For simplicity, assume that the X(t) is a univariate state variable which is directly observable, i.e.,
In this case, the first step is to estimate x(t) and its derivative ẋ(t), say x̂(t) and , using a smoothing method such as the local polynomial approach, and then at the second step a regression model can be fitted
where can be regarded as an error term due to replacement of ẋ(t) by its estimate. Now the least squares approach can be applied, that is, to minimize,
with respect to the unknown parameter vector θ. Liang and Wu [85] have also established the consistency and asymptotic normality of the PLS estimator under some regularity assumptions. In constructing consistency, we utilized the asymptotic properties of both the local linear estimator and the nonlinear least squares estimator. We have also shown that the proposed PLS estimator is still asymptotically normal. Chen and Wu [22, 23] also extended the above two-step PLS approach to estimate the time-varying parameters in the ODE models.
5. Summary and discussion
In this article, we reviewed differential equation modeling methods for HIV viral dynamics, especially those for understanding antiretroviral drug responses to HIV infection. Starting from the classic HIV infection models, we illustrated how such models were extended to account for drug efficacy. We then reviewed the studies on short-term and long-term treatment modeling. The combination of mathematical models with control theories has resulted in many interesting findings and predictions, which is also briefly reviewed. In particular, the STI treatment strategies were shown to be mathematically complex but effective; however, clinical evidences are still needed to support the development of treatment strategies along this line of ideas.
The usability of the models in this article is worth of further discussion. In general, model usability depends on the model assumptions, the goal of modeling and sometimes the data availability. More specifically, it is usually not possible to include every relevant biological detail in one model, so models are basically simplified mathematical representation of the real world. Besides the essential components, if some other biological processes are not explicitly included in a model, this model can be deemed as unusable for understanding such specific processes. For example, some HIV viral dynamic models (e.g., Models (1.4)~(1.7)) do not explicitly consider the latently infected T cells, so they cannot be used to investigate the effects of latent infection; however, these models can still be used to understand other aspects of HIV viral dynamics as in [118]. Also, a model can be constructed for different purposes such as simulation or parameter estimation. For simulation, more complex models can be used if the kinetics parameter values are known from literatures or experiments. However, if a model is used for estimation purpose, one has to consider whether sufficient data are available such that simpler models may be favorable. Furthermore, when multiple models are developed for the same biological problem, we can assess and compare them by considering the biological validity, the balance between complexity and parsimony, and the capability of data interpretation. In practice, one can use model evaluation scores such as AIC, BIC and AICc for model evaluation and comparison.
Parameter estimation techniques are of extreme importance in many settings to understand and control HIV infection (e.g., determination of key kinetic/epidemic parameters), we therefore also reviewed the classical and newly developed estimation approaches in this article. Although numerous approaches for parameter estimation of ODE models have been proposed within the last few decades, existing methods need to be further improved to achieve a better balance between accuracy and computing efficiency (e.g., least squares vs. smoothing-based methods). The introduction of semi-mechanistic modeling and the development of mixed-effects ODE models allow investigators to use more flexible structures to deal with more complex data.
In short, modeling of antiretroviral drug responses of HIV infected patients is far from being mature in the sense of designing novel and realistic regimes and generating accurate predictions of treatment outcomes. This review summarized a number of selected models to provide a basis for further discussions and communications.
Acknowledgments
This research was supported by the USA NIAID/NIH grants P30AI078498, AI087135 and its supplement, the NSFC-NIH (81161120403), the National Mega-project of Science Research No. 2012ZX10001-001 (China), and the National Natural Science Foundation of China (NSFC 11171268).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Aarons L. Physiologically based pharmacokinetic modelling: a sound mechanistic basis is needed. Br J Clin Pharmacol British. 2005;60:581–583. doi: 10.1111/j.1365-2125.2005.02560.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Adams BM, Banks HT, Kwon HD, Tran HT. Dynamic multidrug therapies for HIV: optimal and STI control approaches. Math Biosci Eng. 2004;1:223–241. doi: 10.3934/mbe.2004.1.223. [DOI] [PubMed] [Google Scholar]
- 3.Akaike H. In: Petrov B, Csáki F, editors. Information theory and an extension of the maximum likelihood principle; Second International Symposium on Information Theory; Budapest: Akadémiai Kiadó; 1973. pp. 267–281. [Google Scholar]
- 4.Ananworanich J, Gayet-Agernon A, Le Braz M, et al. CD4-guided scheduled treatment interruption compared to continuous therapy: results of the Staccato Trial. Lancet. 2006;368:459–465. doi: 10.1016/S0140-6736(06)69153-8. [DOI] [PubMed] [Google Scholar]
- 5.Althaus CL, de Boer RJ. Dynamics of Immune Escape during HIV/SIV Infection. PLoS Comput Biol. 2008;4(7):e1000103. doi: 10.1371/journal.pcbi.1000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Arnaout R, Nowak M, Wodarz D. HIV-1 dynamics revisited: Biphasic decay by cytotoxic T lymphocyte killing. Proc Roy Soc Lond B. 2000;265:1347–1354. doi: 10.1098/rspb.2000.1149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bacaer N. Approximation of the basic reproduction number R0 for vector borne diseases with a periodic vector population. Bull Math Biol. 2007;69:1067–1091. doi: 10.1007/s11538-006-9166-9. [DOI] [PubMed] [Google Scholar]
- 8.Bainov DD, Simeonov PS. Impulsive Differential Equations: Asymptotic Properties of the Solutions. World Scientific; Singapore: 1995. [Google Scholar]
- 9.Bainov DD, Simeonov PS. Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical; Burnt Mill: 1993. [Google Scholar]
- 10.Bangsberg DR, Perry S, Charlebois ED, Clark RA, Roberston M, Zolopa AR, Moss A. Non-adherence to highly active antiretroviral therapy predicts progression to AIDS. AIDS. 2001;15:1181–1183. doi: 10.1097/00002030-200106150-00015. [DOI] [PubMed] [Google Scholar]
- 11.Benson M. Parameter fitting in dynamic model. Ecol Mod. 1979;6:97–115. [Google Scholar]
- 12.Bernardo MD, Budd CJ, Champneys AR, et al. Bifurcations in nonsmooth dynamical systems. SIAM Rev. 2008;50:629–701. [Google Scholar]
- 13.Besch CL. Compliance in clinical trials. AIDS. 1995;9:1–10. doi: 10.1097/00002030-199501000-00001. [DOI] [PubMed] [Google Scholar]
- 14.Braake HAB, Van Can HJL, Verbruggen HB. Semi-mechanistic modeling of chemical processes with neural networks. Eng Appl Artif Intel. 1998;11:507–515. [Google Scholar]
- 15.Breban R, Blower S. Role of parametric resonance in virological failure during HIV treatment interruption therapy. Lancet. 2006;367:1285–1289. doi: 10.1016/S0140-6736(06)68543-7. [DOI] [PubMed] [Google Scholar]
- 16.Blower SM, Aschenbach AN, Gershengorn HB, Kahn JO. Predicting the unpredictable: transmission of drug-resistant HIV. Nat Med. 2001;7:1016–1020. doi: 10.1038/nm0901-1016. [DOI] [PubMed] [Google Scholar]
- 17.Bonhoeffer S, Nowak MA. Pre-existence and emergence of drug resistance in HIV-1 infection. Proc Roy Soc Lond B. 1997;264:631–637. doi: 10.1098/rspb.1997.0089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bueno L, de Alwis DP, Pitou C, Yingling J, Lahn M, Glatt S, Trocóniz IF. Semi-mechanistic modelling of the tumour growth inhibitory effects of LY2157299, a new type I receptor TGF-[beta] kinase antagonist, in mice. Eur J Cancer. 2008;44:142–150. doi: 10.1016/j.ejca.2007.10.008. [DOI] [PubMed] [Google Scholar]
- 19.Burnham KP, Anderson DR. Multimodel inference: Understanding AIC and BIC in model selection. Sociol Methods Res. 2004;33:261–304. [Google Scholar]
- 20.Butler S, Kirschner D, Lenhart S. Optimal control of the chemotherapy affecting the infectivity of HIV. In: Arino O, Axelrod D, Kimmel M, editors. Advances in Mathematical Population Dynamics-Molecules, Cells and Man. Word Scientific Press; Singapore: 1997. pp. 557–569. [Google Scholar]
- 21.Castro KG, Ward JW, Slutsker L, Buehler JW, Jaffe HW, Berkelman RL. Revised classification system for HIV infection and expanded surveillance case definition for AIDS among adolescents and adults. MMWR Recomm Rep. 1993;41:1–19. [PubMed] [Google Scholar]
- 22.Chen J, Wu H. Efficient Local Estimation for Time-Varying Coefficients in Deterministic Dynamic Models with Applications for HIV-1 Dynamics. J American Statistical Assoc. 2008;103:369–384. [Google Scholar]
- 23.Chen J, Wu H. Estimation of Time-Varying Parameters in Deterministic Dynamic Models. Statistica Sinica. 2008;18:987–1006. [Google Scholar]
- 24.Commenges D, Rondeau V. Relationship between derivatives of the observed and full loglikelihoods and application to Newton-Raphson algorithm. Int J Biostat. 2006;2:1–26. [Google Scholar]
- 25.Collier AC, Coombs RW, Schoenfeld DA, Bassett RL, Timpone J, Baruch A, Jones M, Facey K, Whitacre C, McAuliffe VJ, Friedman HM, Merigan TC, Reichman RC, Hooper C, Corey L. Treatment of human immunodeficiency virus infection with saquinavir, zidovudine, and zalcitabine. New Engl J Med. 1996;334:1011–1017. doi: 10.1056/NEJM199604183341602. [DOI] [PubMed] [Google Scholar]
- 26.Conway JM, Coombs D. A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLoS Comput Biol. 2011;7(4):e1002033. doi: 10.1371/journal.pcbi.1002033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Le Corfec E, Tuckwell HC. Variability in early HIV-1 population dynamics. AIDS. 1998;12:960–962. [PubMed] [Google Scholar]
- 28.Culshaw RV, Ruan S. A delay-differential equation model of HIV infection of CD4+T-cells. Math Biosci. 2000;165:27–39. doi: 10.1016/s0025-5564(00)00006-7. [DOI] [PubMed] [Google Scholar]
- 29.Culshaw RV, Ruan S, Spiteri RJ. Optimal HIV treatment by maximising immune response. J Math Biol. 2004;48:545–562. doi: 10.1007/s00285-003-0245-3. [DOI] [PubMed] [Google Scholar]
- 30.Dantzig GB, Thapa MN. Linear programming 1: Introduction. Springer-Verlag; 1997. [Google Scholar]
- 31.Davidian M, Giltinan DM. Nonlinear Models for Repeated Measurement Data. Chapman and Hall; London: 1995. [Google Scholar]
- 32.De Boer RJ, Perelson AS. Towards a general function describing T cell proliferation. J Theor Biol. 1995;175:567–576. doi: 10.1006/jtbi.1995.0165. [DOI] [PubMed] [Google Scholar]
- 33.De Boer RJ, Perelson AS. Target cell limited and immune control models of HIV infection: a comparison. J Theor Biol. 1998;190:201–214. doi: 10.1006/jtbi.1997.0548. [DOI] [PubMed] [Google Scholar]
- 34.De Boer R. Understanding the failure of CD8+ T-cell vaccination against simian/human immunodeficiency virus. J Virol. 2007;81:2838–2848. doi: 10.1128/JVI.01914-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.de Leenheer P, Smith HL. Virus dynamics: a global analysis. SIAM J Appl Math. 2003;63:1313–1327. [Google Scholar]
- 36.Deeks SG, et al. Variance of plasma human immunodeficiency virus type 1 RNA levels measured by branched DNA within and between days. J Infect Dis. 1997;176:514–517. doi: 10.1086/517278. [DOI] [PubMed] [Google Scholar]
- 37.Deeks SG. Treatment of antiretroviral-drug-resistant HIV-1 infection. Lancet. 2003;362:2002–2011. doi: 10.1016/S0140-6736(03)15022-2. [DOI] [PubMed] [Google Scholar]
- 38.Delyon B, Lavielle M, Moulines E. Convergence of a Stochastic Approximation Version of the EM Algorithm. Ann Stat. 1999;27:94–128. [Google Scholar]
- 39.Ding AA, Wu H. A comparison study of models and fitting procedures for biphasic viral decay rates in viral dynamic models. Biometrics. 2000;56:16–23. doi: 10.1111/j.0006-341x.2000.00293.x. [DOI] [PubMed] [Google Scholar]
- 40.El-Sadr WM, Lundgren JD, Neaton JD, et al. CD4-T count-guided interruption of antiretroviral treatment, the strategies for management of antiretroviral therapy (SMART) study group. New Engl J Med. 2006;355:2283–2296. doi: 10.1056/NEJMoa062360. [DOI] [PubMed] [Google Scholar]
- 41.Ellner SP, Bailey BA, Bobashev GV, Gallant AR, Grenfell BT, Nychka DW. Noise and nonlinearity in measles epidemics: combining mechanistic and statistical approaches to population modeling. Am Nat. 1998;151:425–440. doi: 10.1086/286130. [DOI] [PubMed] [Google Scholar]
- 42.Englezos P, Kalogerakis N. Applied Parameter Estimation for Chemical Engineers. Marcel Dekker; New York: 2001. [Google Scholar]
- 43.Fang Y, Wu H, Zhu L. A two-stage estimation method for random coefficient differential equation models with application to longitudinal HIV dynamic data. Stat Sin. 2011;21:1145–1170. doi: 10.5705/ss.2009.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Feil B, Abonyi J, Pach P, Nemeth S, Arva P, Nemeth M, Nagy G, Rutkowski L, Siekmann J, Tadeusiewicz R, Zadeh L. Artificial Intelligence and Soft Computing-ICAISC. Vol. 3070. Springer; Berlin/Heidelberg: 2004. Semi-mechanistic Models for State-Estimation – Soft Sensor for Polymer Melt Index Prediction; pp. 1111–1117. [Google Scholar]
- 45.Ferguson NM, Donnelly CA, Hooper J, Ghani AC, Fraser C, Bartley LM, Rode RA, Vernazza P, Lapins D, Mayer SL, Anderson RM. Adherence to antiretroviral therapy and its impact on clinical outcome in HIV-infected patients. J Roy Soc Interface. 2005;2:349–363. doi: 10.1098/rsif.2005.0037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Filippov AF. Differential Equations with Discontinuous Righthand Sides. Kluwer Academic; Dordrecht: 1988. [Google Scholar]
- 47.Fister KR, Lenhart S, McNally JS. Optimizing chemotherapy in an HIV model. Electr J Diff Eq. 1998;32:1–12. [Google Scholar]
- 48.Friedland GH, Williams A. Attaining higher goals in HIV treatment: the central importance of adherence. AIDS. 1999;13(Suppl 1):61–72. [PubMed] [Google Scholar]
- 49.Gabrielsson J, Weiner D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications. Stockholm: Apotekarsocieteten; 2000. [Google Scholar]
- 50.Gill PE, Murray W, Saunders MA. An SQP Algorithm for Large-Scale Constrained Optimization. SIAM Rev. 2005;47:99–131. [Google Scholar]
- 51.Glover F. Heuristics for integer programming using surrogate constraints. Decision Sciences. 1977;8:156–166. [Google Scholar]
- 52.Guedj J, Thiébaut R, Commenges D. Maximum likelihood estimation in dynamical models of HIV. Biometrics. 2007;63:1198–1206. doi: 10.1111/j.1541-0420.2007.00812.x. [DOI] [PubMed] [Google Scholar]
- 53.Gupta P, Friberg LE, Karlsson MO, Krishnaswami S, French J. A semi-mechanistic model of CP-690,550-induced reduction in neutrophil counts in patients with rheumatoid arthritis. J Clin Pharmacol. 2010;50:679–687. doi: 10.1177/0091270009346060. [DOI] [PubMed] [Google Scholar]
- 54.Hadjiandreou MM, Conejeros R, Wilson I. HIV treatment planning on acase-by-case basis. Inter J Biol Life Sci. 2011;7:148–157. [Google Scholar]
- 55.Haeno H, Iwasa Y. Probability of resistance evolution for exponentially growing virus in the host. J Theor Biol. 2007;246:323–331. doi: 10.1016/j.jtbi.2007.01.009. [DOI] [PubMed] [Google Scholar]
- 56.Han C, Chaloner K, Perelson AS, Gatsoiquiry C, Kass RE, Carriquiry A, Gelman A, Higdon D, Pauler DK, Verdinellinis I. In Case Studies in Bayesian Statistics. Springer-Verlag; New York: 2002. Bayesian analysis of a population HIV dynamic model; pp. 223–237. [Google Scholar]
- 57.Han Y, Wind-Rotolo M, Yang H, Siliciano JD. Experimental approaches to the study of HIV-1 latency. Nat Rev Microbiol. 2007;5:95–106. doi: 10.1038/nrmicro1580. [DOI] [PubMed] [Google Scholar]
- 58.Harrigan PR, Whaley M, Montaner JS. Rate of HIV-1 RNA rebound upon stopping antiretroviral therapy. AIDS. 1999;13:59–62. doi: 10.1097/00002030-199905280-00001. [DOI] [PubMed] [Google Scholar]
- 59.Heckman NE, Ramsay JO. Penalized regression with model-based penalties. Can J Stat. 2000;28:241–258. [Google Scholar]
- 60.Heffernan JM, Wahl LM. Treatment interruptions and resistance: a review. In: Tan WY, Wu H, editors. Deterministic and Stochastic Models of AIDS and HIV with Intervention. World Scientific; Singapore: 2005. pp. 423–456. [Google Scholar]
- 61.Heffernan JM, Wahl LM. Monte Carlo estimates of natural variation in HIV infection. J Theor Biol. 2005;236:137–153. doi: 10.1016/j.jtbi.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 62.Herz AV, Bonhoeffer S, Anderson RM, May RM, Nowak MA. Viral dynamics in vivo: limitations on estimations on intracellular delay and virus decay. Proc Nat Acad Sci USA. 1996;93:7247–7251. doi: 10.1073/pnas.93.14.7247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ho DD, Neumann AU, Perelson AS, Chen W, Leonard JM, Markowitz M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995;373:123–126. doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 64.Huang Y, Rosenkranz SL, Wu H. Modeling HIV dynamics and antiviral responses with consideration of time-varying drug exposures, sensitivities and adherence. Math Biosci. 2003;184:165–186. doi: 10.1016/s0025-5564(03)00058-0. [DOI] [PubMed] [Google Scholar]
- 65.Huang Y, Liu D, Wu H. Hierarchical Bayesian methods for estimation of parameters in a longitudinal HIV dynamic system. Biometrics. 2006;62:413–423. doi: 10.1111/j.1541-0420.2005.00447.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Huang Y, Lu T. Modeling long-term longitudinal HIV dynamics with application to an AIDS clinical study. Ann Appl Stat. 2008;2:1384–1408. [Google Scholar]
- 67.Hoggard PG, Back DJ. Intracellular pharmacology of nucleoside analogues and protease inhibitors: role of transport molecules. Curr Opin Infect Dis. 2002;15:3–8. doi: 10.1097/00001432-200202000-00002. [DOI] [PubMed] [Google Scholar]
- 68.Ickovics JR, Meisler AW. Adherence in AIDS clinical trial: a framework for clinical research and clinical care. J Clin Epidemiol. 1997;50:385–391. doi: 10.1016/s0895-4356(97)00041-3. [DOI] [PubMed] [Google Scholar]
- 69.Jackson RC. A pharmacokinetic–pharmacodynamic model of chemotherapy of human immunodeficiency virus infection that relates development of drug resistance to treatment intensity. J Pharmacokinet Phar. 1997;25:713–730. doi: 10.1023/a:1025781801322. [DOI] [PubMed] [Google Scholar]
- 70.Joshi HR. Optimal control of an HIV immunology model. Optim Contr Appl Math. 2002;23:199–213. [Google Scholar]
- 71.Kajiwara T, Sasaki T. A note on the stability analysis of pathogen-immune interaction dynamics. Discrete Cont Dynamical Systems - Series B. 2004;4:615–622. [Google Scholar]
- 72.Kamina A, Makuch RW, Zhao H. A stochastic modeling of early HIV-1 population dynamics. Math Biosci. 2001;170:187–198. doi: 10.1016/s0025-5564(00)00069-9. [DOI] [PubMed] [Google Scholar]
- 73.Kavli T, Lines GT. A unifying framework for mechanistic, fuzzy and data driven modeling, EUFIT’96. Aachen Germany. 1996:1241–1246. [Google Scholar]
- 74.Kennedy J, Eberhart R. Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks IV; 1995. pp. 1942–1948. [Google Scholar]
- 75.Kesteren CV, Zandvliet AS, Karlsson MO, Mathôt RAA, Punt CJA, Armand JP, Raymond E, Huitema ADR, Dittrich C, Dumez H, Roché HH, Droz JP, Ravic M, Yule SM, Wanders J, Beijnen JH, Fumoleau P, Schellens JHM. Semi-physiological model describing the hematological toxicity of the anti-cancer agent indisulam. Invest New Drugs. 2005;23:225–234. doi: 10.1007/s10637-005-6730-3. [DOI] [PubMed] [Google Scholar]
- 76.Kirschner D, Lenhart S, Serbin S. Optimal control of the chemotherapy of HIV. J Math Biol. 1997;35:775–792. doi: 10.1007/s002850050076. [DOI] [PubMed] [Google Scholar]
- 77.Kirschner DE, Webb GF. Understanding drug resistance for monotherapy treatment of HIV infection. Bull Math Biol. 1997;59:763–786. doi: 10.1007/BF02458429. [DOI] [PubMed] [Google Scholar]
- 78.Kuhn E, Lavielle M. Coupling a stochastic approximation version of EM with an MCMC procedure. ESAIM: Prob and Stat. 2004;8:115–131. [Google Scholar]
- 79.Kuhn E, Lavielle M. Maximum likelihood estimation in nonlinear mixed effects models. Comput Stat Data Anal. 2005;49:1020–1038. [Google Scholar]
- 80.Labbe L, Verotta D. A nonlinear mixed effect dynamic model incorporating prior exposure and adherence to treatment to describe long-term therapy outcome in HIV-patients. J Pharmacokinet Phar. 2006;33:519–542. doi: 10.1007/s10928-006-9022-4. [DOI] [PubMed] [Google Scholar]
- 81.Lassen K, Han Y, Zhou Y, Siliciano RF, Siliciano J. The multifactorial nature of HIV-1 latency. Trends Mol Med. 2004a;10:525–531. doi: 10.1016/j.molmed.2004.09.006. [DOI] [PubMed] [Google Scholar]
- 82.Li L, Brown MB, Lee KH, Gupta S. Estimation and inference for a spline-enhanced population pharmacokinetic model. Biometrics. 2002;58:601–611. doi: 10.1111/j.0006-341x.2002.00601.x. [DOI] [PubMed] [Google Scholar]
- 83.Li MY, Shu H. Global Dynamics of an In-host Viral Model with Intracellular Delay. Bull Math Biol. 2010;72:1492–1505. doi: 10.1007/s11538-010-9503-x. [DOI] [PubMed] [Google Scholar]
- 84.Liang H, Miao H, Wu H. Estimation of constant and time-varying dynamic parameters of HIV infection in a nonlinear differential equation model. Ann Appl Stat. 2010;4:460–483. doi: 10.1214/09-AOAS290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Liang H, Wu H. Parameter Estimation for Differential Equation Models Using a Framework of Measurement Error in Regression Model. J Am Stat Assoc. 2008;103:1570–1583. doi: 10.1198/016214508000000797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Liu W. Nonlinear oscillation in models of immune response to persistent viruses. Theor Popul Biol. 1997;52:224–230. doi: 10.1006/tpbi.1997.1334. [DOI] [PubMed] [Google Scholar]
- 87.Louis TA. Finding the Observed Information Matrix when Using the EM Algorithm. J Roy Stat Soc Series B (Methodological) 1982;44:226–233. [Google Scholar]
- 88.Maggioloa F, Airoldia M, Callegaro A, et al. CD4 cell-guided scheduled treatment interruptions in HIV-infected patients with sustained immunologic response to HAART. AIDS. 2009;23:799–807. doi: 10.1097/QAD.0b013e328321b75e. [DOI] [PubMed] [Google Scholar]
- 89.McLean AR, Nowak MA. Competition between zidovudine-sensitive and zidovudine-resistant strains of HIV. AIDS. 1992;6:71–79. doi: 10.1097/00002030-199201000-00009. [DOI] [PubMed] [Google Scholar]
- 90.Merrill S. Lecture Notes in Biomath. Springer-Verlag; New York: 1989. Modeling the interaction of HIV with the cells of the immune system, in Mathematical and Statistical Approaches to AIDS Epidemiology. [Google Scholar]
- 91.Meza C, Jaffrézic F, Foulley JL. REML estimation of variance parameters in nonlinear mixed effects models using the SAEM algorithm. Biometrical J. 2007;49:876–888. doi: 10.1002/bimj.200610348. [DOI] [PubMed] [Google Scholar]
- 92.Meza C, Jaffrézic F, Foulley JL. Estimation in the probit normal model for binary outcomes using the SAEM algorithm. Comput Stat Data Anal. 2009;53:1350–1360. [Google Scholar]
- 93.Miao H. MS Thesis. Department of Biostatistics & Computational Biology, University of Rochester; 2010. Understanding B cell kinetics in human via heavy water labeling using nonlinear mixed effects models and stochastic approximation EM algorithms. [Google Scholar]
- 94.Miao H, Xia X, Perelson AS, Wu H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev. 2011;53:3–39. doi: 10.1137/090757009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Miron RE, Smith RJ. Modelling imperfect adherence to HIV induction therapy. BMC Infect Dis. 2010;10:1–16. doi: 10.1186/1471-2334-10-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Mittler J, Sulzer B, Neumann A, Perelson AS. Influence of delayed virus production on viral dynamics in HIV-1 infected patients. Math Biosci. 1998;152:143–163. doi: 10.1016/s0025-5564(98)10027-5. [DOI] [PubMed] [Google Scholar]
- 97.Mittler J, Markowitz M, Ho D, Perelson AS. Refined estimates for HIV-1 clearance rate and intracellular delay. AIDS. 1999;13:1415–1417. doi: 10.1097/00002030-199907300-00023. [DOI] [PubMed] [Google Scholar]
- 98.Molla A, Korneyeva M, Gao Q, Vasavanonda S, Schipper PJ, Mo HM, Markowitz M, Chernyavskiy T, Niu P, Lyons N, Hsu A, Granneman GR, Ho DD, Boucher CAB, Leonard JM, Norbeck DW, Kempf DJ. Ordered accumulation of mutations in HIV protease confers resistance to ritonavir. Nat Med. 1996;2:760–766. doi: 10.1038/nm0796-760. [DOI] [PubMed] [Google Scholar]
- 99.Montaner JS, Harris M, Mo T, Harrigan PR. Rebound of plasma HIV viral load following prolonged suppression with combination therapy. AIDS. 1998;12:1398–1399. doi: 10.1097/00002030-199811000-00028. [DOI] [PubMed] [Google Scholar]
- 100.Nelson PW, Perelson AS. Mathematical analysis of delay differential equation models of HIV-1 infection. Math Biosci. 2002;179:73–94. doi: 10.1016/s0025-5564(02)00099-8. [DOI] [PubMed] [Google Scholar]
- 101.Nelson PW, Mittler J, Perelson AS. Effect of drug efficacy and the eclipse phase of the viral life cycle on estimates of HIV-1 viral dynamic parameters. J Acquir Immune Defic Syndr. 2001;26:405–412. doi: 10.1097/00126334-200104150-00002. [DOI] [PubMed] [Google Scholar]
- 102.Nelson PW, Murray JD, Perelson AS. A model of HIV-1 pathogenesis that includes an intracellular delay. Math Biosci. 2000;163:201–215. doi: 10.1016/s0025-5564(99)00055-3. [DOI] [PubMed] [Google Scholar]
- 103.Nocedal J, Wright SJ. Numerical Optimization. Springer Verlag; New York: 1999. [Google Scholar]
- 104.Nowak MA, May RM. Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press; Oxford: 2000. [Google Scholar]
- 105.Nowak MA. Variability of HIV infections. J Theor Biol. 1992;155:1–20. doi: 10.1016/s0022-5193(05)80545-4. [DOI] [PubMed] [Google Scholar]
- 106.Nowak MA, Anderson RM, Boerlijst MC, Bonhoeffer S, May RM, McMichael AJ. HIV-1 evolution and disease progression. Science. 1996;274:1008–1010. doi: 10.1126/science.274.5289.1008. [DOI] [PubMed] [Google Scholar]
- 107.Nowak MA, Anderson RM, McLean AR, Wolfs TFW, Goudsmit J, May RM. Antigenic diversity threshold and the development of AIDS. Science. 1991;254:963–969. doi: 10.1126/science.1683006. [DOI] [PubMed] [Google Scholar]
- 108.Nowak MA, Bonhoeffer S, Shaw GM, May RM. Anti-viral drug treatment: Dynamics of resistance in free virus and infected cell populations. J Theor Biol. 1997;184:205–219. doi: 10.1006/jtbi.1996.0307. [DOI] [PubMed] [Google Scholar]
- 109.Nowak MA, May RM. Mathematical biology of HIV infections: Antigenic variation and diversity threshold. Math Biosci. 1991;106:1–21. doi: 10.1016/0025-5564(91)90037-j. [DOI] [PubMed] [Google Scholar]
- 110.Nowak MA, Bangham CRM. Population Dynamics of Immune Responses to Persistent Viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]
- 111.Nowak MA, May RM, Phillips R, Rowland-Jones S, Lalloo D, et al. Antigenic oscillations and shifting immunodominance in HIV-1 infections. Nature. 1995;375:606–611. doi: 10.1038/375606a0. [DOI] [PubMed] [Google Scholar]
- 112.O’Brien TR, et al. Longitudinal HIV-1 RNA levels in acohort of homosexual men. J Acquir Immune Defic Syndr Hum Retrovirol. 1998;18:155–161. doi: 10.1097/00042560-199806010-00007. [DOI] [PubMed] [Google Scholar]
- 113.Paterson DL, Swindells S, Mohr J, Brester M, Vergis EN, Squler C, Wagener MM, Singh N. Adherence to protease inhibitor therapy and outcomes in patients with HIV infection. J Internal Med. 2000;133:21–30. doi: 10.7326/0003-4819-133-1-200007040-00004. [DOI] [PubMed] [Google Scholar]
- 114.Pearson JE, Krapivsky, Perelson AS. Stochastic theory of early viral infection: continuous versus burst production of virions. PLoS Comput Biol. 2011;7(2):e1001058. doi: 10.1371/journal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Perelson AS, Nelson PW. Modeling viral infections. Am Math Soc; Proceedings of Symposia in Applied Mathematics; 2002. pp. 139–172. [Google Scholar]
- 116.Perelson AS. Modelling viral and immune system dynamics. Nature Rev Immunol. 2002;2:28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
- 117.Perelson AS, Nelson PW. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 1999;41:3–44. [Google Scholar]
- 118.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 119.Perelson AS, Essunger P, Cao Y, Vesanen M, Hurley A, Saksela K, Markowitz M, Ho DD. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature. 1997;387:188–191. doi: 10.1038/387188a0. [DOI] [PubMed] [Google Scholar]
- 120.Perelson AS, Kirschner DE, de Boer R. Dynamics of HIV infection of CD4+ T cells. Math Biosci. 1993;114:81–125. doi: 10.1016/0025-5564(93)90043-a. [DOI] [PubMed] [Google Scholar]
- 121.Perelson AS, Kirschner DE, de Boer R. Dynamics of HIV infection of CD4+ T cells. Math Biosci. 1993;114:81–125. doi: 10.1016/0025-5564(93)90043-a. [DOI] [PubMed] [Google Scholar]
- 122.Phillips AN, Youle M, Johnson M, Loveday C. Use of a stochastic model to develop understanding of the impact of different patterns of antiretroviral drug use on resistance development. AIDS. 2001;15:2211–2220. doi: 10.1097/00002030-200111230-00001. [DOI] [PubMed] [Google Scholar]
- 123.Poyton AA, Varziri MS, McAuley KB, McLellen PJ, Ramsay JO. Parameter estimation in continuous-time dynamic models using principal differential analysis. Comput Chem Eng. 2006;30:698–708. [Google Scholar]
- 124.Raboud JM, et al. Variation in plasma RNA levels, CD4 cell counts, and p24 antigen levels in clinically stable men with human immunodeficiency virus infection. J Infect Dis. 1996;174:191–194. doi: 10.1093/infdis/174.1.191. [DOI] [PubMed] [Google Scholar]
- 125.Ramsay JO. Principal Differential Analysis: Data Reduction by Differential Operators. J Roy Stat Soc Series B (Methodological) 1996;58:495–508. [Google Scholar]
- 126.Ramsay JO, Hooker G, Campbell D, Cao J. Parameter estimation for differential equations: a generalized smoothing approach. J Roy Stat Soc Series B. 2007;69:741–796. [Google Scholar]
- 127.Ramsay JO, Silverman BW. Functional Data Analysis. Springer; New York: 2005. [Google Scholar]
- 128.Ribeiro RM, Bonhoeffer S, Nowak MA. The frequency of resistant mutant virus before antiviral therapy. AIDS. 1998;12:461–465. doi: 10.1097/00002030-199805000-00006. [DOI] [PubMed] [Google Scholar]
- 129.Ribeiro RM, Bonhoeffer S. Production of resistant HIV mutants during antiretroviral therapy. Proc Natl Acad Sci USA. 2000;97:7681–7686. doi: 10.1073/pnas.97.14.7681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Rodriguez-Fernandez M, Mendes P, Banga JR. A hybrid approach for efficient and robust parameter estimation in biochemical pathways. Biosystems. 2006;83:248–265. doi: 10.1016/j.biosystems.2005.06.016. [DOI] [PubMed] [Google Scholar]
- 131.Rong L, Perelson AS. Modeling HIV persistence, the latent reservoir, and viral blips. J Theor Biol. 2009;260:308–31. doi: 10.1016/j.jtbi.2009.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Rong L, Perelson AS. Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips. Math Biosci. 2009;217:77–87. doi: 10.1016/j.mbs.2008.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Rong L, Feng Z, Perelson AS. Emergence of HIV-1 drug resistance during antiretroviral treatment. Bull Math Biol. 2007;69:2027–2060. doi: 10.1007/s11538-007-9203-3. [DOI] [PubMed] [Google Scholar]
- 134.Rosenberg ES, Davidian M, Banksc HT. Using mathematical modeling and control to develop structured treatment interruption strategies for HIV infection. Drug Alocoho Depend. 2007;88:41–51. doi: 10.1016/j.drugalcdep.2006.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Runge C. Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten. Zeitschrift für Mathematik und Physik. 1901;46:224–243. [Google Scholar]
- 136.Sabin CA, et al. Course of viral load throughout HIV-1 infection. J Acquir Immune Defic Syndr. 2000;23:172–177. doi: 10.1097/00126334-200002010-00009. [DOI] [PubMed] [Google Scholar]
- 137.Samson A, Lavielle M, Mentré F. Extension of the SAEM algorithm to left-censored data in nonlinear mixed-effects model: Application to HIV dynamics model. Comput Stat Data Anal. 2006;51:1562–1574. [Google Scholar]
- 138.Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- 139.Seber GAF, Wild CJ. Nonlinear Regression. John Wiley & Sons, Inc; Hoboken, New Jersey: 2003. [Google Scholar]
- 140.Sethi AK, Celentano DD, Gange SJ, Moore RD, Gallant JE. Association between adherence to antiretroviral therapy and human immunodeficiency virus drug resistance. Clin Infect Dis. 2003;37:1112–1118. doi: 10.1086/378301. [DOI] [PubMed] [Google Scholar]
- 141.Sheiner LB. Modeling pharmacodynamics: parametric and nonparametric approaches. In: Rowland M, Sheiner LB, Steimer JL, editors. Variability in Drug Therapy: Description, Estimation, and Control. New York: Raven Press; 1985. pp. 139–152. [Google Scholar]
- 142.Shiri T, Garira W, Musekwa SD. A two-strain HIV-1 mathematical model to assess the effects of chemotherapy on disease parameters. Math Biosci Eng. 2005;2:811–832. doi: 10.3934/mbe.2005.2.811. [DOI] [PubMed] [Google Scholar]
- 143.Smith HL. Monotone Dynamical Systems. AMS; Providence, RI: 1995. [Google Scholar]
- 144.Smith RJ, Wahl LM. Distinct effects of protease and reverse transcriptase inhibitors in an immunological model of HIV-1 infection with impulsive drug effects. Bull Math Biol. 2004;66:1259–1283. doi: 10.1016/j.bulm.2003.12.004. [DOI] [PubMed] [Google Scholar]
- 145.Smith RJ, Wahl LM. Drug resistance in an immunological model of HIV-1 infection with impulsive drug effects. Bull Math Biol. 2005;67:783–813. doi: 10.1016/j.bulm.2004.10.004. [DOI] [PubMed] [Google Scholar]
- 146.Smith RJ. Adherence to antiretroviral HIV drugs: how many doses can you miss before resistance emerges? Proc Roy Soc B. 2006;273:617–624. doi: 10.1098/rspb.2005.3352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Smith RJ, Aggarwala BD. Can the viral reservoir of latently infected CD4+T cells be eradicated with antiretroviral drugs? J Math Biol. 2009;59:697–715. doi: 10.1007/s00285-008-0245-4. [DOI] [PubMed] [Google Scholar]
- 148.Tang S, Xiao Y, Wang N, Wu H. Piecewise HIV virus dynamic model with CD4+ T cell count-guided therapy: I. J Theor Biol. 2012;308:123–134. doi: 10.1016/j.jtbi.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Glo Optim. 1997;11:341–359. [Google Scholar]
- 150.Swartz J, Bremermann H. Discussion of parameter estimation in biological modeling: algorithms for estimation and evaluation of the estimates. J Math Biol. 1975;1:241–275. doi: 10.1007/BF01273746. [DOI] [PubMed] [Google Scholar]
- 151.Tam J. Delay effect in a model for virus replication. IMA J Math Appl Med Biol. 1999;16:29. [PubMed] [Google Scholar]
- 152.Tan WY, Wu H. Stochastic modeling of the dynamics of CD4+ T-cell infection by HIV and some Monte Carlo studies. Math Biosci. 1998;147:173–205. doi: 10.1016/s0025-5564(97)00094-1. [DOI] [PubMed] [Google Scholar]
- 153.Tan WY, Wu H. Stochastic modeling of the dynamics of CD4+ T-cell infection by HIV and some Monte Carlo studies. Math Biosci. 1998;147:173–205. doi: 10.1016/s0025-5564(97)00094-1. [DOI] [PubMed] [Google Scholar]
- 154.Tang SY, Xiao YN. One-compartment model with Michaelis-Menten elimination kinetics and therapeutic window: an analytical approach. J Pharmacokinet Phar. 2007;34:807–827. doi: 10.1007/s10928-007-9070-4. [DOI] [PubMed] [Google Scholar]
- 155.Tang SY, Xiao YN, Wang N, Wu H. Piecewise HIV virus dynamic model with CD4 T cell count-guided therapy. J Theor Biol. 2012;308:123–134. doi: 10.1016/j.jtbi.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Tuckwell HC, Corfec EL. A stochastic model for early HIV-1 population dynamics. J Theor Biol. 1998;195:451–463. doi: 10.1006/jtbi.1998.0806. [DOI] [PubMed] [Google Scholar]
- 157.Tuckwell HC, Shipman PD, Perelson AS. The probability of HIV infection in a new host and its reduction with microbicides. Math Biosci. 2008;214:81–86. doi: 10.1016/j.mbs.2008.03.005. [DOI] [PubMed] [Google Scholar]
- 158.Varah JM. A spline least squares method for numerical parameter estimation in differential equations. SIAM J Sci Comput. 1982;3:28–46. [Google Scholar]
- 159.Varziri MS, McAuley KB, McLellen PJ. Selecting optimal weighting factors in iPDA for parameter estimation in continuous-time dynamic models. Comput Chem Eng. 32:3011–3022. (200) [Google Scholar]
- 160.Verotta D. Models and estimation methods for clinical HIV-1 data. J Comput Appl Math. 2005;184:275–300. [Google Scholar]
- 161.Wahl LM, Nowak MA. Adherence and drug resistance: predictions for therapy outcome. Proc Roy Soc Lond B. 2000;267:835–843. doi: 10.1098/rspb.2000.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Wang Y. Semiparametric mixed-effects analysis on PK/PD models using differential equations In Statistics. University of Nebraska; Lincoln, Nebraska: 2007. [Google Scholar]
- 163.Wang K, Wang W, Liu X. Global Stability in a viral infection model with lytic and nonlytic immune response. Comput Math Appl. 2006;51:1593–1610. [Google Scholar]
- 164.Wang L, Li MY. Mathematical analysis of the global dynamics of a model for HIV infection of CD4+ T cells. Math Biosci. 2006;200:44–57. doi: 10.1016/j.mbs.2005.12.026. [DOI] [PubMed] [Google Scholar]
- 165.Wang L, Li MY, Kirschner D. Mathematical analysis of the global dynamics of a model for HTLV-I infection and ATL progression. Math Biosci. 2002;179:207–217. doi: 10.1016/s0025-5564(02)00103-7. [DOI] [PubMed] [Google Scholar]
- 166.Wang Y, Zhou Y, Wu J, Heffernan J. Oscillatory viral dynamics in a delayed HIV pathogenesis model. Math Biosci. 2009;219:104–112. doi: 10.1016/j.mbs.2009.03.003. [DOI] [PubMed] [Google Scholar]
- 167.Wang WD, Zhao XQ. Threshold dynamics for compartmental epidemic models in periodic environments. J Dyn Diff Equat. 2008;20:699–717. [Google Scholar]
- 168.Wei X, et al. Viral dynamics in human immune deficiency virus type 1 infection. Nature. 1995;373:117–122. doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- 169.Wein LM, Zenios SA, Nowak MA. Dynamic multidrug therapies for HIV: A control theoretic approach. J Theor Biol. 1997;185:15–29. doi: 10.1006/jtbi.1996.0253. [DOI] [PubMed] [Google Scholar]
- 170.Wodarz D, Lloyd AL. Immune responses and the emergence of drug-resistant virus strains in vivo. Proc Roy Soc Lond B. 2004;271:1101–1109. doi: 10.1098/rspb.2003.2664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Wolinsky S, Korber BT, Neumann AU, Daniels M, Kunstman KJ, Whetsell AJ, Furtado MR, Cao Y, Ho DD, Safrit JT. Adaptive evolution of human immunodeciency virus-type 1 during the natural course of infection. Science. 1996;272:537–542. doi: 10.1126/science.272.5261.537. [DOI] [PubMed] [Google Scholar]
- 172.Wu H, Huang Y, Acosta EP, Park JG, Song Y, Rosenkranz SL, Kuritzkes DR, Eron JJ, Perelson AS, Gerber JG. Pharmacodynamics of antiretroviral agents in HIV-1 infected patients: using viral dynamic models that incorporate drug susceptibility and adherence. J Pharmacokinet Phar. 2006;33:399–419. doi: 10.1007/s10928-006-9006-4. [DOI] [PubMed] [Google Scholar]
- 173.Wu H, Huang Y, Acosta EP, Rosenkranz SL, Kuritzkes DR, Eron JJ, Perelson AS, Gerber JG. Modeling long-term HIV dynamics and antiretroviral response: Effects of drug potency, pharmacokinetics, adherence and drug resistance. J Acquir Immune Defic Syndr. 2005;39:272–283. doi: 10.1097/01.qai.0000165907.04710.da. [DOI] [PubMed] [Google Scholar]
- 174.Wu H, Ding AA. Population HIV-1 dynamics in vivo: Applicable models and inferential tools for virological data from AIDS clinical trials. Biometrics. 1999;55:410–418. doi: 10.1111/j.0006-341x.1999.00410.x. [DOI] [PubMed] [Google Scholar]
- 175.Wu H, Huang Y, Acosta EP, Rosenkranz SL, Kuritzkes DR, Eron JJ, Perelson AS, Gerber JG. Modeling long-term HIV dynamics and antiretroviral response: effects of drug potency, pharmacokinetics, adherence and drug resistance. J Acquir Immune Defic Syndr. 2005;39:272–283. doi: 10.1097/01.qai.0000165907.04710.da. [DOI] [PubMed] [Google Scholar]
- 176.Yang YP, Xiao YN. Threshold dynamics for an HIV model in periodic environments. J Math Anal Appl. 2010;361:59–68. [Google Scholar]
- 177.Ye Y. Interior algorithms for linear, quadratic and linearly constrained non-linear programming, in department of ESS. Stanford University; 1987. [Google Scholar]
- 178.Yang YP, Xiao YN, Wang N, Wu JH. Optimal control of drug therapy: Melding pharmacokinetics with viral dynamics. Biosystems. 2012;107:174–185. doi: 10.1016/j.biosystems.2011.11.011. [DOI] [PubMed] [Google Scholar]
- 179.Zhu H, Zou X. Impact of delays in cell infection and virus production on HIV-1 dynamics. IMA J Math Med Biol. 2008;25:99–112. doi: 10.1093/imammb/dqm010. [DOI] [PubMed] [Google Scholar]