Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Mar 20;8(4):3546–3555. doi: 10.1021/nn406637c

Cellular Contact Guidance through Dynamic Sensing of Nanotopography

Meghan K Driscoll †, Xiaoyu Sun ‡, Can Guven †, John T Fourkas ‡,§, Wolfgang Losert †,§,*
PMCID: PMC4017610  PMID: 24649900

Abstract

graphic file with name nn-2013-06637c_0007.jpg

We investigate the effects of surface nanotopography on the migration and cell shape dynamics of the amoeba Dictyostelium discoideum. Multiple prior studies have implicated the patterning of focal adhesions in contact guidance. However, we observe significant contact guidance of Dictyostelium along surfaces with nanoscale ridges or grooves, even though this organism lacks integrin-based adhesions. Cells that move parallel to nanoridges are faster, more protrusive at their fronts, and more elongated than are cells that move perpendicular to nanoridges. Quantitative studies show that nanoridges spaced 1.5 μm apart exhibit the greatest contact guidance efficiency. Because Dictyostelium cells exhibit oscillatory shape dynamics, we model contact guidance as a process in which stochastic cellular harmonic oscillators couple to the periodicity of the nanoridges. In support of this connection, we find that nanoridges nucleate actin polymerization waves of nanoscale width that propagate parallel to the nanoridges.

Keywords: cellular migration, cellular shape, Dictyostelium discoideum

Cells can adjust their migration behavior based on the local shape of the surface on which they move.1 This process, which is termed contact guidance, is well established but poorly understood. One challenge in gaining insight into contact guidance is the broad range of natural surface nanotopographies that have been associated with the guidance of cell motion. Topographies implicated in contact guidance span a wide range of nanoscale length scales, from the hundreds of nanometer diameter of collagen fibers down to the 3 nm scales of typical surface proteins. In addition, cells couple to surfaces through both specific, integrin-mediated complexes and nonspecific adhesion.

There are many reported examples of nanoscale surface patterns that promote contact guidance and/or trigger changes in cell morphology.2−10 Silica spheres of 70 nm attached to a substrate lead to striking changes in the actin scaffolding of osteoblasts.9 Above a critical density, nanoparticle-coated surfaces lead to the formation of filopodia and a loss of stress fibers in osteoblasts.9 Grooves as shallow as 35 nm can lead to cell alignment in fibroblasts.10 Nanopatterned surfaces can also affect focal adhesion formation in fibroblasts.4,6 Compared to fibroblasts growing on flat surfaces, fibroblasts growing on nanocolumns have more filopodia and fewer actin stress fibers, which is consistent with the cells being in a more motile state.5,7

Two proposed mechanisms for contact guidance have received significant attention.11−13 The first mechanism is focal adhesion patterning.11 Recent studies have shown that focal adhesion complexes,14,15 which are structures that involve dozens (if not hundreds) of proteins,16 can organize with a preferred alignment in the presence of surface nanotopography. Actin stress fibers, which connect focal adhesions, have also been observed to align with surface topography.17 While this phenomenon is often observed, it is not clear whether this patterning causes or is a consequence of contact guidance. Furthermore, many fast-moving cells migrate without mature focal adhesions, relying instead on the simpler dynamics of actin polymerization (i.e., protrusions and retractions) coupled with nonspecific surface adhesion.18,19 Recently, T cells were observed to migrate parallel to nanogrooves even in the absence of integrin-mediated adhesion.20 Metastatic cancer cells can also revert back to this more primitive so-called amoeboid type of migration. Although it has been noted that the social amoeba Dictyostelium discoideum, the main model system for amoeboid migration, can sense and align with grooves on agar,21 contact guidance during amoeboid migration has yet to be quantified or even studied systematically.

The second proposed mechanism for contact guidance is preferential actin polymerization, particularly through filopodia, localized protrusions that are about 100 nm in diameter and up to micrometers in length. Filopodia have been reported to assist cells in sensing their environment.22 Fibroblasts on nanocolumns have more filopodia per unit length of perimeter than do cells on flat surfaces,5 and it has been suggested that filopodia are more likely to form parallel to ridges than perpendicular to them.23

Although both patterning of cell-surface adhesions and sensing by filopodia are plausible mechanisms for contact guidance, the evidence supporting either mechanism is limited. Fujita etal. found no correlation between filopodial alignment and ridge alignment in mesenchymal stem cells.17 On the basis of this observation, they suggested that sensing of topography may be achieved via protrusion dynamics. In support of this hypothesis, they found evidence that suggested that mesenchymal stem cell protrusions that are not directed along ridges are retracted more quickly than are other protrusions.

To gain deeper insights into contact guidance and its relationship to nanotopography, here we present quantitative studies of this phenomenon in D. discoideum. D. discoideum is commonly accepted as a model system for amoeboid motility. It is genetically tractable and bears a strong similarity to neutrophils in its fast motion and in its ability to detect and follow shallow chemical gradients (chemotaxis).24 Specifically, two key components of the gradient-sensing pathway are conserved between D. discoideum and neutrophils: (i) the actin polymerization machinery that generates leading-edge protrusions and (ii) the acto-myosin machinery that generates cell contractions.24 Additionally, D. discoideum does not have genes for integrins and so cannot form integrin-based adhesions. However, other types of local cell-surface adhesions may exist.

D. discoideum cells undergo chemotaxis in response to a cyclic adenosine monophosphate (cAMP) gradient. Wild-type D. discoideum cells self-aggregate by releasing cAMP as a directional cue. To avoid introduction of directional chemical cues between cells, we use mutant cell lines that lack ACA, the cyclase that produces cAMP. The statistics and dynamics of aca– cell migration, including protrusion and retraction dynamics, have been studied extensively on flat surfaces.25−27 Here we focus on the influence that well-controlled, nanotopographic cues have on aca− cell migration.

Multiphoton absorption polymerization (MAP)28,29 was used to create nanoridge patterns with adjustable pitch, width, and height. This technique allowed us to prototype surfaces with different nanotopographies rapidly. Master patterns created with MAP were molded to create acrylic surfaces upon which cells were run.30,31

By analyzing nearly 2 000 000 cell shapes on a range of custom-designed nanotopographic surfaces, we show that amoeboid cells can be directed effectively via surface contact guidance, even though these cells do not possess integrin-based adhesions. A detailed analysis of center-of-mass motion and shape dynamics allows us to estimate the characteristic length and time scales over which migrating cells respond to surface topography. Principal component analysis (PCA) of the shape dynamics shows that forward motion is enhanced in cells aligned parallel to the nanoridges, whereas turning motion is enhanced for cells aligned perpendicular to the nanoridges. We further find that actin polymerization occurs preferentially along nanoridges and that actin waves propagate in confined 500 nm wide regions along the nanotopography. On the basis of these observations, we propose a mechanism for contact guidance that is based on the generation of nanoscale actin polymerization waves triggered and guided by the surface nanotopography.

Results

Amoeboid Cells Exhibit Contact Guidance Even though They Lack Integrin-Based Focal Adhesions

To test whether contact guidance is possible in the absence of integrin-based adhesions, we studied the migration of Dictyostelium cells on surfaces with nanoridges. Aca– cells (in an AX3 background) were prepared, cytoplasmically dyed, and imaged as described in the Materials and Methods. Unlike wild-type Dictyostelium, aca– cells do not communicate with each other by releasing cAMP. Thus, in the absence of an imposed external signal, the direction of motion of aca– cells is random.

Gratings of 300 μm × 300 μm that are composed of parallel nanoridges with a width of ∼250 nm, a height of a few hundred nm, and a constant spacing that ranged from 0.4 to 10 μm were fabricated using MAP. Figure 1A shows a scanning electron micrograph (SEM) of one such grating with a spacing of 2 μm. To ensure the chemical uniformity of the surface, acrylic resin surfaces were replicated using microtransfer molding.30 While Dictyostelium is commonly studied migrating on glass, we have previously shown that it migrates with equal speed on acrylic surfaces.32

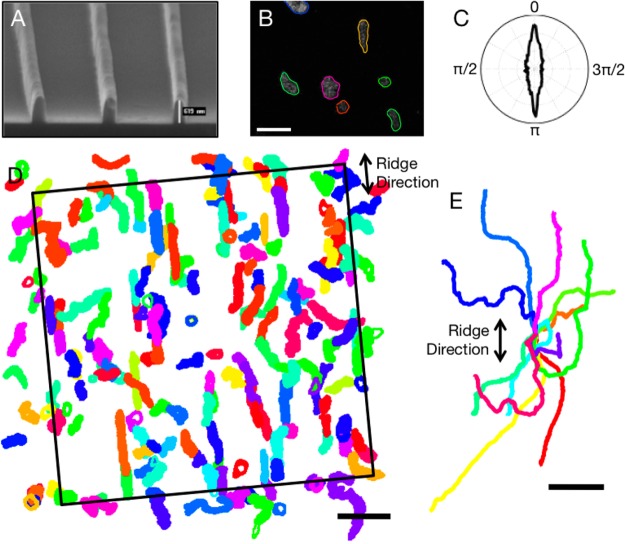
Figure 1.

Figure 1

Open in a new tab

Contact guidance of amoeboid cells on a grating of parallel nanoridges spaced 1.0 μm apart. (A) Gratings of parallel nanoridges. Shown is an SEM image of several nanoridges. Each nanoridge has a height of a few hundred nm and a width of ∼250 nm. (B) Cytoplasmically dyed Dictyostelium discoideum amoebae migrating on a nanoridge grating. The extracted shape of each cell is overlaid (see Movie S1). The scale bar is 20 μm. (C) Polar plot of velocity direction weighted by speed. From this plot it is apparent that cells migrate preferentially parallel to the nanoridges. 0 and π indicate motion parallel to nanoridges, while π/2 and 3π/2 indicate perpendicular motion. (D) Overlapped, extracted cell shapes over 22 min (355 frames). The scale bar is 50 μm. (Movies S2–S4 show the overlapped shapes of cells on ridges spaced 1.0, 1.5, and 3.0 μm apart.) (E) Centroid motion of 12 cells over 10 min. All tracks were constrained to begin at the graph’s origin. The scale bar is 20 μm.

Figure 1B shows a representative fluorescence image with overlaid shapes of cells migrating on 1.5-μm-spaced nanoridges. Cell centers and shapes were tracked using custom-written software. Figure 1D shows all extracted cell shapes from a representative 10 min, 150-frame image sequence. A “spider plot” of the tracks of 12 randomly chosen cells migrating over 10 min is shown in Figure 1E. It is clear from both the spider plot and the shape plot that cells prefer to align and migrate parallel to the nanoridges.

To quantify this observation and to measure how contact guidance depends on ridge spacing, we used several different metrics. First, we examined both the cell velocity and the alignment of the cell shape as a function of angle with respect to the nanoridges. (We define the alignment of the cell as the alignment of the ellipse that best fits the cell shape.) We found that cells prefer to align and to migrate parallel to nanoridges. However, as also occurs on a flat surface, not all cells are moving at any given time. Cell velocity is typically correlated with the degree of polarization. As a result, a nearly round, stationary cell contributes as much to histograms of the direction of alignment or the direction of migration as does a well-polarized (elongated), fast-moving cell. To compensate for this effect, when calculating preferred orientations and directions of motion, we weighted the direction of motion by its magnitude and the cell alignment by the cell’s eccentricity. Figure 1C is a polar histogram of weighted velocity for the experiment shown in Figure 1D. Here, 0 and π indicate motion parallel to the nanoridges, whereas π/2 and 3π/2 indicate motion perpendicular to the nanoridges. Figure 2A similarly shows alignment weighted by eccentricity for various nanoridge spacings.

Figure 2.

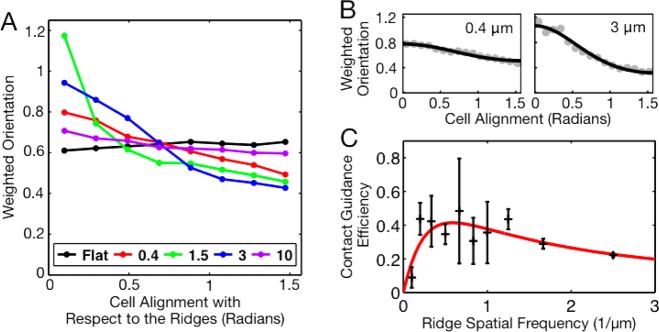
Figure 2

Open in a new tab

Cells migrating on gratings with a nanoridge spacing of 1.5 μm exhibit greater contact guidance than do cells migrating on surfaces with smaller or larger nanoridge spacings. (A) Alignment, weighted by eccentricity, of cells migrating on nanoridge gratings with ridge spacings of 0.4, 1.5, 3, and 10 μm. The weighted alignment for each nanoridge spacing includes data from two or three experiments. (B) To measure the surface contact guidance efficiency, weighted alignments from individual experiments were fit to a stochastic model of cell guidance. Two such fits are shown here. (C) Surface contact guidance efficiencies of various nanoridge gratings shown in black as a function of the inverse ridge spacing, with the fit to the stochastic harmonic oscillator model shown in red. Contact guidance is greatest on gratings with nanoridge spacings between 1.0 and 2.0 μm.

The strength of the directional cue provided by the ridges is comparable to that observed in chemotaxis. Figure S1 compares the migration of aca– cells on ridges spaced 1.0 μm apart to the migration of aca– cells near a chemoattractant-releasing needle. To measure guidance strength, we adapted the chemotaxis index (CI). The CI is 0 for undirected motion and 1 for entirely directed motion. (For cells in a chemotactic gradient, the CI is generally defined as the sum over cos(θ) for all cell velocities, where θ is the angle between the cell velocity and the needle direction. In contrast, for cells on ridges, we define the CI as the sum over cos(2θ) for all cell velocities, where θ is the angle between the cell velocity and the ridge orientation.) We found that for the cells shown in Figure S1 the CI of the chemotaxing cells is 0.32, whereas the CI of the cells experiencing contact guidance is 0.29. In general, the CI of cells undergoing contact guidance is comparable to that of chemotaxing cells.27

Contact Guidance Is Affected by the Nanoridge Spacing and Is Most Pronounced When Nanoridges Are between 1.0 and 2.0 μm Apart

To assess how sensitively contact guidance depends on the underlying surface topography, we measured the contact guidance of cells migrating on gratings with a variety of nanoridge spacings. We fabricated gratings with nanoridge spacings of 0.4, 0.6, 0.8, 1.0, 1.2, 1.5, 2, 3, 5, and 10 μm. Figure 2A shows the distributions of the alignment of the cell long axis with respect to the ridge direction (weighted by eccentricity) for several of these gratings. We found that the gratings with the larger nanoridge spacings induce little contact guidance. On average, cells are 10 to 20 μm long and 5 μm wide. A reduction in contact guidance is expected when the nanoridge spacing is greater than cell width. We also found that gratings with nanoridge spacings smaller than 1 μm exhibit reduced contact guidance.

The distributions of cell alignments (weighted by eccentricity) fit well to a Gaussian with periodic boundary conditions. Unlike a regular Gaussian distribution, a circular Gaussian has only one fitting parameter, which is proportional to the inverse variance of the distribution. This single fitting parameter, which we term the contact guidance efficiency, can be used to characterize the cell alignment distributions. Kemkemer etal. have previously found that a stochastic model of cell orientation dynamics leads to a modified circular Gaussian distribution of cell orientations.33 (For a description of how their model applies to our system, see the Supporting Information.) Analyzing D. discoideum migration, we find that the contact guidance efficiency is greatest for nanoridge spacings between 1.0 and 2.0 μm (see Figure 2C).

The measured contact guidance efficiency for a given nanoridge spacing can vary from experiment to experiment (see Figure 2C). We therefore used surface topographies with four different nanoridge spacings (0.4, 0.8, 1.5, and 5 μm) and a flat control in a single experiment. Comparing the four nanoridge spacings, we found that 1.5-μm-spaced nanoridges induce the greatest guidance, while 0.4-μm-spaced nanoridges induce the least guidance (see Supporting Information, Figure S2). This experiment confirms the existence of a peak in contact guidance efficiency at a nanoridge spacing of approximately 1.5 μm.

To explore the effect of nanoridge width on contact guidance, we fabricated nanogrooves (“negative” nanoridges) by making a second polydimethylsiloxane (PDMS) mold of the original PDMS mold and using this second PDMS mold to fabricate nanogrooves. We found that the surface contact guidance efficiencies of nanogrooves with 2 and 10 μm spacings (∼550 nm wide each) are similar to the efficiencies of nanoridges with the same spacings (see Figure S3). Due to this similarity, no other nanogroove spacings were studied.

We also explored the effect of overall ridge size on contact guidance using ridges with heights and widths of a few micrometers. We found that such large ridges induce behavior that differs from simple contact-mediated guidance. For instance, cells sometimes swing off of large ridges, a behavior similar to that observed for cells at the edges of tall cliffs.26 Nanoscale ridge widths therefore appear to be a prerequisite for simple contact guidance.

Cells That Are Aligned Parallel to Nanoridges Migrate Faster and Are More Elongated than Cells That Are Perpendicular to Nanoridges

We have shown that cells migrate and align parallel to nanoridges. However, there are several scenarios that could lead to the observed contact guidance. One possibility is that more cells move parallel to nanoridges than move perpendicular to them. Another possibility is that cells move faster parallel to nanoridges than perpendicular to nanoridges. To investigate these possibilities, we measured how cell speed and eccentricity are related to contact guidance. We began by plotting histograms of the direction of cell velocity relative to ridge alignment. First, we sort cells into six categories by speed. For each speed category, Figure 3A shows the probability of moving in a certain direction relative to the ridge alignment. Zero represents movement parallel to the ridges, and π/2 represents movement perpendicular to the ridges. (The probability distribution is weighted by cell speed.) The cells with the lowest speed (shown in red) show only slight contact guidance. However, with increasing cell speed, increasing contact guidance is observed. Figure S4 shows additional velocity histograms for cells on a variety of nanoridge spacings. Similar behavior holds for cell alignment. Figure 3B shows histograms of the eccentricity-weighted cell alignment as a function of cell alignment with respect to nanoridge direction for five different eccentricities. We found that the most circular cells show no preferred alignment, while the most elongated cells show the greatest alignment with the ridges. (We have previously shown that cell speed and eccentricity are correlated;25 for a discussion on this relationship see the Supporting Information.)

Figure 3.

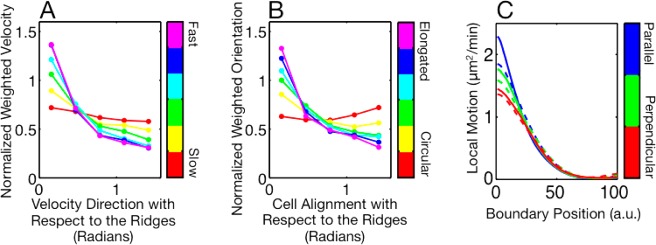
Figure 3

Open in a new tab

Contact guidance is related to cell speed, eccentricity, and the spatial patterning of protrusions and retractions along the cell boundary. (A) Distributions of velocity direction with respect to the nanoridge direction for cells moving on 1.2-μm-spaced nanoridges. Velocity direction is weighted by speed. The cells were ranked by speed and then binned. The red line represents the weighted velocity for the slowest sixth of cells, and the purple line the weighted velocity for the fastest sixth of cells. Faster cells are more likely to move parallel to the nanoridges than are slower cells. (B) Distributions of alignment, weighted by eccentricity, with respect to the nanoridge direction. The cells were ranked by eccentricity and then binned. The red line represents the alignment distribution for the most circular cells, and the purple line represents the distribution for the most elongated cells. More elongated cells are more likely to be aligned parallel to the nanoridges than are more circular cells. (C) Surface contact guidance efficiency as a function of cell eccentricity. One experiment is shown for each nanoridge spacing. (D) Protrusive and retractive motion as a function of arc length (x-axis) and alignment with respect to the nanoridges (color). For protrusions, shown as solid lines, the boundary position zero represents the front of the cell. For retractions, shown as dashed lines, the boundary position zero represents the back.

Cells That Are Parallel to Nanoridges Exhibit Increased Forward Motion and Decreased Turning Compared to Cells That Are Perpendicular to Nanoridges

Cells migrate and change shape by protruding and retracting. Because nanoridges influence the overall speed and eccentricity of cells, nanoridges are expected to couple to the underlying dynamics of protrusions and retractions. As shown in Figure 3C, the mean protrusive and retractive motion along the boundary is affected by cell alignment with respect to the nanoridges. For protrusive motion (represented as solid lines), 0 corresponds to the cell front and 100 (in arbitrary units) corresponds to the cell back. For retractive motion (dashed lines), 0 is the cell back and 100 is the cell front. We find that cells aligned parallel to nanoridges show greater protrusive motion at their front and greater retractive motion at their back than do cells aligned perpendicular to nanoridges. The cell alignment does not significantly affect retractive motion near the front of the cell.

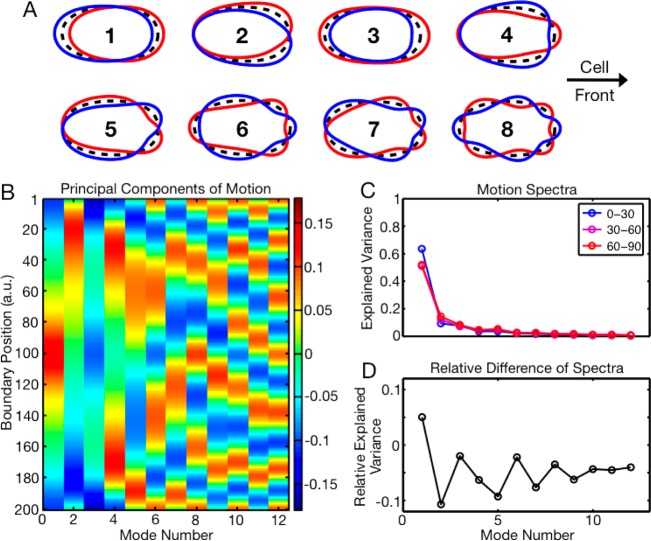
To analyze the differences in shape and motion between cells migrating parallel and perpendicular to the nanoridges in more detail, we measured the effect of the nanoridges on different types of motion and in particular on turning. First, we used PCA to measure the main modes of boundary motion. We analyzed approximately 225 000 shapes of cells migrating on a flat surface. PCA has previously been used to analyze collections of cell shapes;34−36 we here analyze the principal components of shape change, or boundary motion. To find the PCA modes, we first aligned the shapes by forcing them to have the same centroid position, alignment, and front–back directionality. We also labeled the cell front as boundary point 0. In PCA, the first principal component is the linear combination of features that represents the direction of greatest variance in the data. The second principal component, which is orthogonal to the first, is the linear combination of features that represents the direction of next greatest variance, and so on. Figure 4A is a schematic representation in real space of the eight most important principal components of boundary motion. Figure 4B is a kymograph representation of a larger number of principal components. In Figure 4A, the mean cell shape is shown in black and the characteristic dynamics associated with each mode are shown in red and blue. We assume that boundary motion is perpendicular to the cell boundary. The first few PCA modes are intuitive; the first principal component is uniform forward or backward motion, the second principal component is turning, the third principal component is elongation/contraction at the front and back of the cell, and the fourth principal component is compression/dilation of the cell front.

Figure 4.

Figure 4

Open in a new tab

Principal component analysis of boundary motion on nanoridges. (A) A real-space representation of the principal components of boundary motion. The principal components are ordered from most significant to least significant. For each principal component, the black shape is the mean cell shape, while the red and blue shapes are the mean shape ± 0.5% of the principal component. Boundary motion is assumed to be perpendicular to the mean shape. (B) Principal components of boundary motion. Here, boundary point 1 is the cell front. (C) Variance in the data explained by each principal component of motion for cells aligned between 0° and 30° relative to the ridges (shown blue), between 30° and 60° relative to the ridges (shown purple), and between 60° and 90° relative to the ridges (shown red). (D) Spectra of the cells parallel to nanoridges minus the spectra of cells perpendicular to nanoridges. (The blue line minus the red line.) (E) The difference spectra in D normalized by the mean spectra of the cells parallel and perpendicular to the nanoridges.

We also determined the principal components of several other measures, including boundary curvature and boundary position (see Figure S5A,B). The number of modes required to represent the data varies greatly depending on the measure. For example, the first mode accounts for more than 95% of the variance in boundary position, while 14 modes are needed to represent 95% of the variance in boundary motion (see Figure S5C.)

The principal components of the various representations share several common features (see Figures 4 and S5). In general, the principal components are ordered by significance from fewest number of peaks to largest number of peaks. The modes are further organized into mode pairs that have the same number of peaks. For example, in Figure 4B, the first and second principal components are mode pairs, as are the fourth and fifth principal components. For higher principal-component indices, the principal components in each mode pair are at a 90° offset from one another and describe roughly the same percentage of expected variance. The principal components thus form a Fourier-like basis.

With this analysis tool we can tackle the question of how nanoridges affect the modes of cell boundary motion. Figure 4C shows the mode amplitudes for cells aligned parallel to the nanoridges (blue) and cells aligned perpendicular to the nanoridges (red). Approximately 250 000 shapes of cells on 1.0- to 1.5-μm-spaced nanoridges were analyzed. We calculated the relative difference between the perpendicular and parallel spectra by subtracting the perpendicular spectrum from the parallel spectrum and then dividing by the mean of those two spectra (see Figure 4D). We find that the motion of cells aligned parallel to nanoridges is better described by the first principal component of motion (uniform forward or backward motion) than is the motion of cells aligned perpendicular to nanoridges. Cells aligned parallel to nanoridges also exhibit reduced turning compared to cells aligned perpendicular to nanoridges. The magnitudes of the second, fifth, and seventh principal components, which are all asymmetric turning modes, are reduced in cells migrating parallel to ridges. Thus, not only do cells that are aligned with nanoridges tend to retain their alignment, but cells that are perpendicular to nanoridges tend to turn to improve their alignment.

Cells Migrating on Nanoridges Have Wave-like Shape Dynamics

We have previously reported wave-like shape dynamics both in adhered cells migrating on a flat surface and in cells swimming without surface adhesion.26 We found that protrusions (i.e., bumps of high curvature) travel from the fronts to the backs of both migrating and swimming cells. Figure 5 shows that cells migrating on nanoridges have similar wave-like shape dynamics. Figure 5A is an overlay of shapes for a cell that is moving roughly parallel to the nanoridges, whereas Figure 5B shows a kymograph of the time-dependent cell shape. The shape is represented by the distance of each of the 400 boundary points to the center of the cell. Dark red regions indicate elongated cells, whereas uniformly green regions indicate round cells. The periodic appearance and disappearance of dark red regions as a function of time represents a global oscillation of the cell elongation, which is consistent with the known behavior of cells on flat surfaces.25 Furthermore, the cell shape oscillates not only globally, but also locally. Figure 5C shows the cell’s boundary curvature, while Figure 5D shows the protrusive (red) and retractive (blue) motion of the cell. In Figure 5C, red corresponds to regions of high boundary curvature. The slanted red lines going from the front to back with increasing time indicate that regions of high curvature travel from the cell front to the cell back, just as occurs on flat surfaces.25 The starting points for regions of high curvature correspond to protrusions.26 Even though this cell is migrating on nanoridges and its center moves mostly along a straight line, it still extends protrusions in a zigzagging manner, as seen in Figure 5D. Overall, the shape dynamics of cells on nanoridges strongly resemble the shape dynamics of cells migrating on a flat surface.

Figure 5.

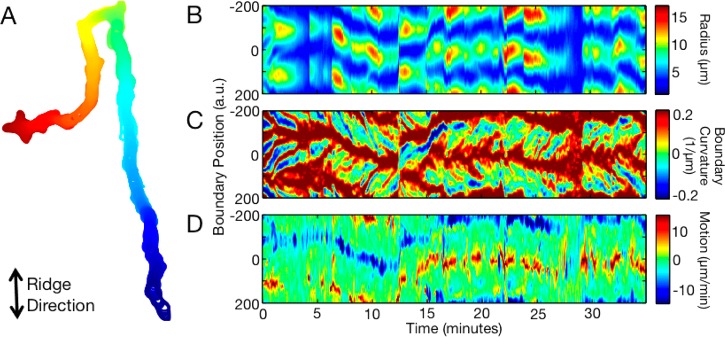
Figure 5

Open in a new tab

Cells have oscillatory shape dynamics. (A) Shape of a cell migrating on nanoridges spaced 0.4 μm apart. The shape’s color represents time, with the initial cell shape colored red and the final shape colored blue. The long stretches of straight motion and the two right-angle turns perpendicular to the ridges are not typically observed when D. discoideum migrates on flat surfaces. The shape dynamics of this cell are represented in panels B and C. (B) Cell elongation is oscillatory. Here, the color represents the distance from each boundary point to the centroid. Elongated shapes are shown as red and blue, whereas more circular shapes are green. (C) Local shape dynamics are also oscillatory. In this plot of boundary curvature, red represents regions of large positive boundary curvature and blue represents regions of large negative curvature. Regions of high curvature travel from the front to the back of the cell. (D) Local boundary motion of the cell. Red represents protrusive motion, and blue represents retractive motion.

Contact Guidance Can Be Modeled As a Resonance between Cell Oscillations and the Nanoridge Grating

As described above and as shown in earlier work of our group, the shape and surface-adhesion dynamics of migrating cells are oscillatory.26 Here we show that a coarse-grained model of a resonant interaction between internal force-generating oscillations and the nanoridge grating can account for our observations of contact guidance.

We model the forces generated by internal oscillations as being biased in the direction parallel to the nanoridges. The interaction of the internal oscillations with the surface nanotopography is described as an overdamped harmonic oscillator. We describe the dynamics using characteristic properties such as the natural frequency ω0 and the damping coefficient β. Since the interaction between the forces exerted by the internal oscillations and the surface is noisy, we model the normalized, biasing force from the nanoridge grating, F(t), as a stochastic cue that mimics a random square-wave signal. F(t) has amplitude a and a correlation time L/(v0|sin θ|), where L is the ridge spacing, v0 is a normalization constant with units of speed, and θ is the angle between the direction of the internal oscillation and the alignment of the ridges. The position of the stochastically driven oscillations, r, is described by the damped harmonic oscillator equation

graphic file with name nn-2013-06637c_m001.jpg 1

The inertial term is included for generality, but we expect the oscillations to be overdamped. In our model the interactions with the nanoridge grating provide a driving force for the internal oscillations.

When the nanoridge spacing approaches zero, the correlation time becomes zero. In this case, because forcing events are not correlated with one another, the net force is not biased. This situation results in no contact guidance. For large nanoridge spacings, correlations become large as well, suggesting the presence of a long-lasting forcing term. However, in this case the correlation time becomes independent of the angle. Therefore, the average force again does not result in bias in any direction. Details of how the modeled forcing events are correlated are given in the Supporting Information.

The average power of forces generated by the internal oscillations, ⟨P⟩, can be thought of as a measure of surface contact guidance efficiency. In the steady state, the normalized average power delivered by internal oscillations to the cell membrane is

graphic file with name nn-2013-06637c_m002.jpg 2

where β′ = β/v0, ω0′ = ω0/v0, a′ = a/v02, and ⟨P′⟩ = ⟨P⟩/(a/v0). Fitting the normalized averaged power, eq 2, to the contact guidance efficiencies measured for a broad range of nanoridge spacings, we find length and time scales that characterize the cell’s interaction with the nanoridges. The contact guidance efficiencies and the fit are shown in Figure 2C. The three scales correspond roughly to the spatial resonance length scale (the peak position in Figure 2C), a damping length scale (the width of the peak), and the signal strength (the height of the peak). We find a resonance in the interaction of the cellular oscillations with the nanoridge grating at 1/ω0′ = 1.7 μm, which is comparable to the size of protrusions and actin waves in D. discoideum cells.37 To interpret the remaining parameters extracted via the model, we set v0 = 10 μm/min, which is the average speed of the cells,27 the speed of protrusions relative to the cell, and the speed of actin waves.37 From the fit, we find a damping coefficient of 1/β′ = 1.6 μm, which leads to an oscillation decay time of 2v0/β′ = 18 s, which is roughly the duration of protrusions.38,39 The amplitude of the signal received by the cell is 1/a′ = 1.4 μm. Using v0, we can also interpret the spatial resonance scale, 1.7 μm, as a time scale. The mean sensing time is the frequency at which the intrinsic cellular oscillations sense the up–down symmetry of the ridges via the stochastic signal. This time is calculated as λ–1 = 2/ωs = 2/(ω0′v0) = 20 s, which is the frequency of protrusions.38,39

Actin Polymerization Is Guided by Nanoridges

In D. discoideum, cellular migration is the direct result of actin polymerization and depolymerization. Observations of actin polymerization dynamics and local morphological dynamics that have been made possible via novel nanoscale 3D imaging approaches demonstrate the existence of 3D actin waves.40 Actin waves have also been shown to interact with large obstacles by dissipating.41 We find that cells treated with latrunculin, which depolymerizes actin, are round on nanoridges, suggesting that actin may play a role in contact guidance (see Figure S6). To investigate the effect of nanoridges on actin polymerization directly, we imaged LimE(Δcoil)-GFP (aca– in an AX3 background) cells and Lifeact-RFP (wild-type in an AX3 background) cells on nanoridges.42 In D. discoideum, the actin-binding protein LimE is associated with polymerizing actin and in particular with dynamic protrusions.43 We find that actin preferentially polymerizes along nanoridges and that unlike on flat surfaces the actin polymerization wave remains localized to within 500 nm of the ridge. Figure 6A shows a representative cell migrating on 5-μm-spaced nanoridges, and Movie S5 shows cells migrating on 1.5-μm-spaced nanoridges. Actin polymerization preferentially occurs around each nanoridge; thus, in the focal plane of this figure and movie, each actin polymerization wave appears as two streaks on both sides of a ridge. Whereas an actin wave on a nanoridge extends into the grooves on both sides of the ridge, a wave on a microridge extends into only one of the two grooves. Figure S7 and Movie S6 show actin waves in cells migrating on nanogrooves (microridges). Actin waves in adjacent grooves are not coupled and propagate independently. Even in cells that migrate perpendicular to the nanoridges, such as the cell shown in Figure 6B, the actin polymerization regions are aligned parallel to the nanoridges. These regions enriched with polymerizing actin travel along the nanoridges in a wave-like fashion. Figure 6C shows one such representative wave traveling along a nanoridge at constant speed. This observation indicates that surface nanotopograhy can trigger dynamic nanoscale structures inside cells.

Figure 6.

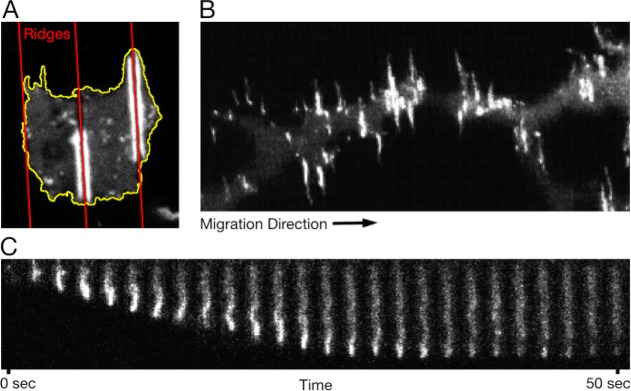
Figure 6

Open in a new tab

Actin polymerizarion is directed parallel to nanoridges. (A) Actin polymerization on nanoridges spaced 5 μm apart. The cell outline is shown in yellow, and the ridges are shown in red. (B) Maximum intensity projection of cells migrating perpendicular to 1.5-μm-spaced nanoridges. The nanoridges are aligned approximately vertically, while the cell is migrating horizontally. (C) Kymograph of an actin wave traveling between two 1.5-μm-spaced nanoridges. The wave’s initial velocity is 21 μm/min (vertical scale: 13 μm).

We also investigated whether myosin II contractility was required for contact guidance in D. discoideum. We found that myosin II– and aca– cells were similarly well directed by the nanoridges, which suggests that contact guidance in D. discoideum does not require myosin.

Discussion

We have shown that the amoeba D. discoideum exhibits contact guidance even though it does not have integrin-based focal adhesions. Gratings with nanoridge spacings between 1.0 and 2.0 μm show the greatest contact guidance, whereas gratings with nanoridges spaced farther apart or closer together show reduced guidance. In Dictyostelium, the full-width at half-maximum size of actin waves on flat surfaces is ∼1 μm and protrusions are ∼1.5 μm wide as measured from both the cell shape and the cell footprint.26,37 From our contact guidance model, we also extract an oscillation wavelength of 1.7 μm and a time scale of 20 s. A similar time scale can be seen in dynamic, actin-based protrusions, since cells generate new protrusions roughly every 20 s.26 The correspondence between our model and the spatial and temporal scales of actin dynamics provides support for the hypothesis that actin dynamics are involved in sensing and responding to surface topography. Indeed, our measurements of actin polymerization show that actin dynamics can be triggered and confined to the nanoscale via surface nanotopography. We call this mechanism dynamic sensing since it is linked to intracellular dynamic processes.

Conclusions

On the basis of our observations and model we propose that amoebae sense surface nanotopography at the length and time scales at which actin polymerization self-organizes into nanoscale waves. An interaction between actin dynamics and surface topography could allow cells to recognize and be guided by nanoscale topographical features. The preferred length scale for guidance is larger than both the typical size of integrin-based focal adhesions and the macromolecular ensembles typically associated with focal–adhesion-based contact guidance. Thus, dynamic contact guidance is potentially important even for cells that have integrin-based focal adhesions, since multiple mechanisms might play a role in contact guidance on multiple length scales. The ability to visualize directly the actin waves and the agreement of our observations with simple models should allow for the rational design and testing of nanotopography optimized for contact guidance.

Materials and Methods

Surface Fabrication

Sets of parallel nanoridges, each 300 μm long, were fabricated via MAP using a commercial Ti:sapphire laser (Coherent Mira 900 F). Gratings were composed of evenly spaced nanoridges that were 0.4, 0.6, 0.8, 1, 1.2, 1.5, 2, 3, 5, or 10 μm apart. The nanoridges were fabricated with an acrylic resin composed of 49 wt % tris(2-hydroxyethyl) isocyanurate triacrylate (SR368, Sartomer), 49 wt % ethoxylated(6) trimethylolpropane triacrylate (SR499, Sartomer), and 2 wt % Lucirin TPO-L (Ciba). The typical fabrication laser power was 13 mW as measured at the sample. The sample preparation and fabrication procedures have been described previously. To replicate ridges, a composite PDMS mold consisting of a thin layer of hard PDMS with relief features and a thick slab of soft PDMS was prepared. First, 1.7 g of vinyl PDMS prepolymer (VDT-731, Gelest), 9 μL of Pt catalyst (SIP6831.2, Gelest), 0.05 g of modulator (87927, Sigma-Aldrich), 0.5 g of hydrosilane (HMS-301, Gelest), and 1 g of hexane were mixed. The mixture was then spin-coated (1000 rpm, 40 s) on the master substrate, allowed to sit for 2 h, and baked at 60 °C for 1 h. The soft PDMS was prepared by mixing the prepolymer and curing agent (Sylgard 184, Dow Corning) in a 10:1 mass ratio. After degassing, the soft PDMS was poured onto the precured hard PDMS and baked at 60 °C for 1 h. When cured, the composite PDMS was peeled off the master substrate. Replicas of ridges were created by placing a drop of acrylate resin between the mold and an acrylate-functionalized coverslip and UV curing at 365 nm for 5 min. The PDMS mold for grooves was prepared using a double-molding process in which a ridge mold was treated as a master structure and a composite PDMS mold was made from it.

Cell Preparation and Imaging

To assess contact guidance, D. discoideum cells and adenylyl cyclase A null and myosin II null cells (both in an AX3 background) were prepared as described previously.25−27 Cells were cytoplasmically dyed with CellTracker Green CDMFA (Invitrogen).25,26 Fluorescence images were obtained on a Leica TCS SP2 confocal microscope with a 40× objective every 4 s. To assess actin polymerization, we used LimE(Δcoil)-GFP (aca– in an AX3 background) and Lifeact-RFP (wild-type in an AX3 background) cells. Fluorescence images were obtained on a Leica TCS SP5 confocal microscope with a 63× or 100× objective.

Measuring Contact Guidance

A variety of measures were used to assess the extent of contact guidance. Cellular motion was first tracked and velocity calculated as described previously.27 Cellular eccentricity and alignment were measured as the eccentricity and alignment of the ellipse that has the same second moments as the pixel positions of the binarized image of the tracked cells. Other measures of cell shape were calculated using boundaries extracted as described in the Supporting Information.

Acknowledgments

This work was funded by NIH grant R01GM085574. We would like to thank C. McCann for providing code that tracks and analyzes the centroid motion of cells, C. Wang for discussions on improving the shape analysis, J. Parker for discussions on refining the model, and C. Parent and P. Kriebel for guidance on culturing Dictyostelium cells and for supplying cell lines.

The authors declare no competing financial interest.

Supporting Information Available

Several videos and an expanded description of materials and methods. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States

Supplementary Material

nn406637c_si_001.avi (23.8MB, avi)
nn406637c_si_002.avi (34.4MB, avi)
nn406637c_si_003.avi (11.4MB, avi)
nn406637c_si_004.avi (10.7MB, avi)
nn406637c_si_005.avi (687KB, avi)
nn406637c_si_006.avi (9.1MB, avi)
nn406637c_si_007.pdf (74.2KB, pdf)
nn406637c_si_008.pdf (1.2MB, pdf)

References

  1. Weiss P.; Garber B. Shape and Movement of Mesenchyme Cells as Functions of the Physical Structure of the Medium. Proc. Natl. Acad. Sci. U.S.A. 1952, 38, 264–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Clark P.; Connolly P.; Curtis A. S.; Dow J. A.; Wilkinson C. D. Topographical Control of Cell Behaviour: II. Multiple Grooved Substrata. Development 1990, 108, 635–644. [DOI] [PubMed] [Google Scholar]
  3. Clark P.; Connolly P.; Curtis A. S.; Dow J. A.; Wilkinson C. D. Cell Guidance by Ultrafine Topography in Vitro. J. Cell Sci. 1991, 99, 73–77. [DOI] [PubMed] [Google Scholar]
  4. Wilkinson C. D. W.; Riehle M.; Wood M.; Gallagher J.; Curtis A. S. G. The Use of Materials Patterned on a Nano- and Micro-Metric Scale in Cellular Engineering. Mater. Sci. Eng. C 2002, 19, 263–269. [Google Scholar]
  5. Dalby M. J.; Riehle M. O.; Sutherland D. S.; Agheli H.; Curtis A. S. Changes in Fibroblast Morphology in Response to Nano-Columns Produced by Colloidal Lithography. Biomaterials 2004, 25, 5415–5422. [DOI] [PubMed] [Google Scholar]
  6. Cavalcanti-Adam E. A.; Volberg T.; Micoulet A.; Kessler H.; Geiger B.; Spatz J. P. Cell Spreading and Focal Adhesion Dynamics Are Regulated by Spacing of Integrin Ligands. Biophys. J. 2007, 92, 2964–2974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Choi C. H.; Hagvall S. H.; Wu B. M.; Dunn J. C.; Beygui R. E.; Kim C. J. Cell Interaction with Three-Dimensional Sharp-Tip Nanotopography. Biomaterials 2007, 28, 1672–1679. [DOI] [PubMed] [Google Scholar]
  8. Dalby M. J.; Gadegaard N.; Herzyk P.; Sutherland D.; Agheli H.; Wilkinson C. D.; Curtis A. S. Nanomechanotransduction and Interphase Nuclear Organization Influence on Genomic Control. J. Cell. Biochem. 2007, 102, 1234–1244. [DOI] [PubMed] [Google Scholar]
  9. Kunzler T. P.; Huwiler C.; Drobek T.; Voros J.; Spencer N. D. Systematic Study of Osteoblast Response to Nanotopography by Means of Nanoparticle-Density Gradients. Biomaterials 2007, 28, 5000–5006. [DOI] [PubMed] [Google Scholar]
  10. Loesberg W. A.; te Riet J.; van Delft F. C. M. J. M.; Schon P.; Figdor C. G.; Speller S.; van Loon J. J. W. A.; Walboomers X. F.; Jansen J. A. The Threshold at Which Substrate Nanogroove Dimensions May Influence Fibroblast Alignment and Adhesion. Biomaterials 2007, 28, 3944–3951. [DOI] [PubMed] [Google Scholar]
  11. Bettinger C. J.; Langer R.; Borenstein J. T. Engineering Substrate Topography at the Micro- and Nanoscale to Control Cell Function. Angew. Chem. 2009, 48, 5406–5415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Friedl P.; Wolf K. Plasticity of Cell Migration: A Multiscale Tuning Model. J. Cell Biol. 2009, 188, 11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Anselme K.; Davidson P.; Popa A. M.; Giazzon M.; Liley M.; Ploux L. The Interaction of Cells and Bacteria with Surfaces Structured at the Nanometre Scale. Acta Biomater. 2010, 6, 3824–3846. [DOI] [PubMed] [Google Scholar]
  14. Mitchison T. J.; Cramer L. P. Actin-Based Cell Motility and Cell Locomotion. Cell 1996, 84, 371–379. [DOI] [PubMed] [Google Scholar]
  15. Vicente-Manzanares M.; Webb D. J.; Horwitz A. R. Cell Migration at a Glance. J. Cell Sci. 2005, 118, 4917–4919. [DOI] [PubMed] [Google Scholar]
  16. Zaidel-Bar R.; Cohen M.; Addadi L.; Geiger B. Hierarchical Assembly of Cell-Matrix Adhesion Complexes. Biochem. Soc. Trans. 2004, 32, 416–420. [DOI] [PubMed] [Google Scholar]
  17. Fujita S.; Ohshima M.; Iwata H. Time-Lapse Observation of Cell Alignment on Nanogrooved Patterns. J. R. Soc., Interface 2009, 6, 269–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Seftor E. A.; Meltzer P. S.; Kirschmann D. A.; Pe’er J.; Maniotis A. J.; Trent J. M.; Folberg R.; Hendrix M. J. Molecular Determinants of Human Uveal Melanoma Invasion and Metastasis. Clin. Exp. Metastasis 2002, 19, 233–246. [DOI] [PubMed] [Google Scholar]
  19. Friedl P.; Wolf K. Tumour-Cell Invasion and Migration: Diversity and Escape Mechanisms. Nat. Rev. Cancer 2003, 3, 362–374. [DOI] [PubMed] [Google Scholar]
  20. Kwon K. W.; Park H.; Song K. H.; Choi J. C.; Ahn H.; Park M. J.; Suh K. Y.; Doh J. Nanotopography-Guided Migration of T Cells. J. Immunol. 2012, 189, 2266–2273. [DOI] [PubMed] [Google Scholar]
  21. Eckert B.; Warren R.; Rubin R. Structural and Biochemical Aspects of Cell Motility in Amoebas of Dictyostelium Discoideum. J. Cell Biol. 1977, 79, 339–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Faix J.; Rottner K. The Making of Filopodia. Curr. Opin. Cell Biol. 2006, 18, 18–25. [DOI] [PubMed] [Google Scholar]
  23. Teixeira A. I.; Abrams G. A.; Bertics P. J.; Murphy C. J.; Nealey P. F. Epithelial Contact Guidance on Well-Defined Micro- and Nanostructured Substrates. J. Cell Sci. 2003, 116, 1881–1892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Bagorda A.; Parent C. A. Eukaryotic Chemotaxis at a Glance. J. Cell Sci. 2008, 121, 2621–2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Driscoll M. K.; Fourkas J. T.; Losert W. Local and Global Measures of Shape Dynamics. Phys. Biol. 2011, 8, 55001–55009. [DOI] [PubMed] [Google Scholar]
  26. Driscoll M. K.; McCann C.; Kopace R.; Homan T.; Fourkas J. T.; Parent C.; Losert W. Cell Shape Dynamics: From Waves to Migration. PLoS Comput. Biol. 2012, 8, e1002392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. McCann C.; Kriebel P.; Parent C.; Losert W. Cell Speed, Persistence and Information Transmission during Signal Relay and Collective Migration. J. Cell Sci. 2010, 123, 1724–1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. LaFratta C. N.; Fourkas J. T.; Baldacchini T.; Farrer R. A. Multiphoton Fabrication. Angew. Chem. 2007, 46, 6238–6258. [DOI] [PubMed] [Google Scholar]
  29. Maruo S.; Fourkas J. T. Recent Progress in Multiphoton Microfabrication. Laser Photonics Rev. 2008, 2, 100–111. [Google Scholar]
  30. LaFratta C. N.; Baldacchini T.; Farrer R. A.; Fourkas J. T.; Teich M. C.; Saleh B. E. A.; Naughton M. J. Replication of Two-Photon-Polymerized Structures with Extremely High Aspect Ratios and Large Overhangs. J. Phys. Chem. B 2004, 108, 11256–11258. [Google Scholar]
  31. LaFratta C. N.; Li L.; Fourkas J. T. Soft-Lithographic Replication of 3D Microstructures with Closed Loops. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 8589–8594. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Li L.; Driscoll M.; Kumi G.; Hernandez R.; Gaskell K. J.; Losert W.; Fourkas J. T. Binary and Gray-Scale Patterning of Chemical Functionality on Polymer Films. J. Am. Chem. Soc. 2008, 130, 13512–13513. [DOI] [PubMed] [Google Scholar]
  33. Kemkemer R.; Jungbauer S.; Kaufmann D.; Gruler H. Cell Orientation by a Microgrooved Substrate Can Be Predicted by Automatic Control Theory. Biophys. J. 2006, 90, 4701–4711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pincus Z.; Theriot J. A. Comparison of Quantitative Methods for Cell-Shape Analysis. J. Microsc. 2007, 227, 140–156. [DOI] [PubMed] [Google Scholar]
  35. Keren K.; Pincus Z.; Allen G. M.; Barnhart E. L.; Marriott G.; Mogilner A.; Theriot J. A. Mechanism of Shape Determination in Motile Cells. Nature 2008, 453, 475–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Stephens G. J.; Johnson-Kerner B.; Bialek W.; Ryu W. S. Dimensionality and Dynamics in the Behavior of C. Elegans. PLoS Comput. Biol. 2008, 4, e1000028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Gerisch G.; Bretschneider T.; Muller-Taubenberger A.; Simmeth E.; Ecke M.; Diez S.; Anderson K. Mobile Actin Clusters and Traveling Waves in Cells Recovering from Actin Depolymerization. Biophys. J. 2004, 87, 3493–3503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Andrew N.; Insall R. H. Chemotaxis in Shallow Gradients Is Mediated Independently of PtdIns 3-Kinase by Biased Choices between Random Protrusions. Nat. Cell Biol. 2007, 9, 193–200. [DOI] [PubMed] [Google Scholar]
  39. Bosgraaf L.; Van Haastert P. J. The Ordered Extension of Pseudopodia by Amoeboid Cells in the Absence of External Cues. PLoS One 2009, 4, e5253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Gao L.; Shao L.; Higgins C. D.; Poulton J. S.; Peifer M.; Davidson M. W.; Wu X.; Goldstein B.; Betzig E. Noninvasive Imaging beyond the Diffraction Limit of 3D Dynamics in Thickly Fluorescent Specimens. Cell 2012, 151, 1370–1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Weiner O. D.; Marganski W. A.; Wu L. F.; Altschuler S. J.; Kirschner M. W. An Actin-Based Wave Generator Organizes Cell Motility. PLoS Biol. 2007, 5, 2053–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Riedl J.; Crevenna A. H.; Kessenbrock K.; Yu J. H.; Neukirchen D.; Bista M.; Bradke F.; Jenne D.; Holak T. A.; Werb Z.; etal. Lifeact: A Versatile Marker to Visualize F-Actin. Nat. Methods 2008, 5, 605–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schneider N.; Weber I.; Faix J.; Prassler J.; Muller-Taubenberger A.; Kohler J.; Burghardt E.; Gerisch G.; Marriott G. A Lim Protein Involved in the Progression of Cytokinesis and Regulation of the Mitotic Spindle. Cell Motil. Cytoskeleton 2003, 56, 130–139. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn406637c_si_001.avi (23.8MB, avi)
nn406637c_si_002.avi (34.4MB, avi)
nn406637c_si_003.avi (11.4MB, avi)
nn406637c_si_004.avi (10.7MB, avi)
nn406637c_si_005.avi (687KB, avi)
nn406637c_si_006.avi (9.1MB, avi)
nn406637c_si_007.pdf (74.2KB, pdf)
nn406637c_si_008.pdf (1.2MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES