The Effect of Small Tumor Volumes upon Intra-tumoral Tracer Uptake Heterogeneity Studies

Abstract

The number of studies in the literature involving quantification of the metabolic heterogeneity seen in ¹⁸F-fluorodeoxyglucose position emission tomography (FDG-PET) images has increased sharply over recent years. We hypothesize that inclusion of very small regions-of-interest as unique data points will have deleterious effects upon these studies.

Methods

Using a combination of probability theory and clinical FDG-PET data, we numerically calculate the curve describing the probability a given tumor volume is large enough to adequately sample the underlying tumor biology assayed via a Siemens Biograph 40 True Point Tomograph hybrid PET/CT scanner at a planar resolution of 4 mm and trans-axial resolution of 4 mm (64 mm³ voxel size). We then employ a computer simulation to isolate the effects of tumor volume upon the image local entropy.

Results

We computed the underlying global intensity distribution for 70 cervical cancer tumors ranging from 5 to 310 cm³) which were ensemble averaged over the same intensity scale. From this distribution, we determined that about 700 total voxels (45 cm³) are required to give 95% certainty that the global intensity distribution has been sampled adequately enough such that common statistical comparisons of individual tumor intensity distributions can be made canonically. We demonstrate that one previously suggested measure of heterogeneity is dependent on tumor volume. Furthermore, that heterogeneity measure is about 5 times more sensitive to volume changes for volumes below the proposed minimum than for those above it.

Conclusion

We find that inclusion of tumor volumes below 45 cm³ can profoundly bias comparisons of intra-tumoral uptake heterogeneity metrics derived from the current generation of whole-body FDG-PET scanner data.

INTRODUCTION

With advances in medical imaging techniques, there is increasing interest in the quantification of cancerous tumor micro-environments. Modern imaging enables the description of intra-tumor qualities in situ. One example of this is the use of the ¹⁸F-fluorodeoxyglucose (FDG) radioactive glucose analog with positron emission tomography (PET) (1). Consider, for example, the FDG-PET image of a cancer of the uterine cervix shown in Figure 1. There, greater grayscale pixel intensity (brighter) ostensibly implies greater metabolic activity. It is this type of heterogeneity that interests researchers of tumor biology (2).

Figure 1.

A trans-axial cross-section of a cancer of the uterine cervix is shown as assayed by FDG-PET where intensity variations are clear. For example, the upper-right corner of the tumor is brightest and several darker spots are visible throughout. These intensity variations represent variations in FDG uptake within the tumor. The vertical edge of the image corresponds to 10 cm within the patient.

In the specific case of FDG-PET images, spatial variations amongst differently shaded pixels are to be quantified. The goal is to objectively declare one tumor, or intra-tumoral region, to be more heterogenous than another tumor or intra-tumoral region with the hope that image heterogeneity quantifiers will provide prognostic clinical value. Toward this end, several quantifiers have been proposed (3–8). Regardless of the specific heterogeneity quantifier employed, the distribution of grayscale intensities constrains the values that quantifier can attain. In short, fewer unique intensities implies less possible heterogeneity.

The distribution of measured image intensities depends upon both tumor biology and imaging physics. In the case of FDG-PET, the well-known “partial volume effect” tends to lower uptake values while increasing apparent tumor volume (9). In other words, the partial volume effect is known to increase the number of unique intensities measured. This can render distributions of measured intensities to appear more heterogeneous than would be as dictated by tumor biology alone. Whatever their combined role, both physical and biological sources of image heterogeneity each could yield prognostic information about the tumor. Therefore inter-patient comparison of objectively quantified image heterogeneity could be important clinically.

Because the value of uptake heterogeneity quantifiers depends crucially on the distribution of the grayscale intensities for each patient, adequate sampling of those distinct distributions is paramount for comparative heterogeneity studies. Because the number of samples of each intensity distribution is the number of image pixels in the identified region-of-interest, the tumor volume itself indicates how well an individual intensity distribution has been sampled. We therefore hypothesize that there is some minimum tumor volume below which comparison of intra-tumoral uptake heterogeneity quantifiers is invalid due to under-sampling.

It is the purpose of this research to describe the computation of a lower bound upon tumor volume below which the effects of latent under-sampling are profound. We then demonstrate this small-volume effect upon one previously proposed metric of uptake heterogeneity, the image local entropy (5,6,10).

MATERIALS AND METHODS

Delineation of Tumor Regions

This is a retrospective study of 70 patients with cancers of the uterine cervix who underwent a pre-treatment hybrid PET/CT (Siemens Biograph 40 True Point Tomograph Scanner, Munich, Germany) scan using the ¹⁸F-fluorodeoxyglucose (FDG) radiotracer assay of glucose uptake by cells. The raw FDG-PET data are scatter and attenuation corrected via the proprietary software native to the PET machine. Images were reconstructed using ordered subset expectation maximization (8 subsets; 4 iterations). A Gaussian smoothing filter with 4-mm full width at half maximum was applied post-reconstruction. No additional processing was implemented. The relevant region of interest (ROI) first was identified visually by an experienced oncologist. In order to objectively delineate tumor from background, any ROI pixel brighter than 40% of the maximum ROI pixel brightness is to be considered part of the tumor (11). The oncologist then made slight manual adjustments to the ROI to remove any obvious non-tumor pixels such as those comprising bladder or bowel regions. This ROI is exported as a set of Cartesian coordinates in DICOM structure files. Use of these data for this retrospective research with waiver of informed consent was approved by the Washington University Institutional Review Board. Tumors ranged in size from 4 cm³ to 248 cm³ and approximately followed an exponential distribution with median volume 29 cm³. Because our FDG-PET data is given to a planar resolution of 4 mm and a trans-axial resolution of 4 mm, we employ the conversion factor of 0.064 cm³/voxel throughout this work.

Relative Intensity Scale

The ROIs and the original 15-bit-grayscale DICOM images are then imported into custom computer software written in Python v2.6.2 (http://www.python.org/) by using the pydicom library v0.9.3 (http://code.google.com/p/pydicom/). For each patient, our software automatically extracts the image pixels bounded by a given ROI, confirms those pixels to be above the clinical threshold and then stores the pixel intensities as observed radioactivity densities given in Bq/mL. Those values are then binned into probability histograms using the Freedman-Diaconis optimal bin width (12) for that group of radioactivity densities (i.e., the bin size is computed for each patient). The values are then rescaled such that the domain of each histogram is 0.4 (the clinical threshold) to 1.0. To facilitate inter-patient comparison of histograms, each histogram was resampled via cubic splines at intervals of 5% intensity using the scipy interpolation package v0.7.1 (http://www.numpy.org/). This interval was found to be the median Freedman-Diaconis bin size in the rescaled domain for all imaged tumors. The final result is that each tumor is associated with a common-scale histogram representing the probability that a given intensity interval appears within that tumor.

Creation of Test Images

To isolate the effects of tumor size on the example heterogeneity metric, we created shapeless “tumor” images with a known intensity histogram. A perfect square number of tumor voxels is used as the number of pixels in a square, two-dimensional, 8-bit grayscale image created via the Python Imaging Library v1.1.7 (http://www.pythonware.com/products/pil/). Each image pixel is chosen at random to have an intensity drawn from a known intensity histogram (which is presented in the Results section). The simulation in no way attempts to mimic the PET scan process; it only represents distinct, variable-size samplings of the distribution of measured FDG-PET intensities for our set of patients. This randomization may be repeated numerous times for a given number of voxels which we multiply by 0.064 cm³/voxel. The result is a set of many test images which, on average, obey the identical intensity distribution while having no consistent spatial intensity patterns. Thus, each set of test images represents tumors of identical: volume, average shape and average heterogeneity.

Example Heterogeneity Statistic

We compute the local information entropy of a two-dimensional image as described in Haralick et al. (13). In brief, the co-occurrence matrix describes the probability p that a pixel of a shade i occurs next to a pixel of shade j. This matrix can be computed for various directions, pixel separations and bit depths. We computed the horizontal and vertical co-occurrence matrices for the nearest pixel neighbors of 8-bit grayscale images. From each of these matrices, the local entropy

$$h=-\sum _{j=103}^{255}\sum _{i=103}^{255}p(i,j)lnp(i,j)$$ Eq. 1

local entropy value. The limits on the summations reflect the 40% clinical threshold within the 8-bit (0–255) color scale.

RESULTS

The Ensemble Intensity Histogram

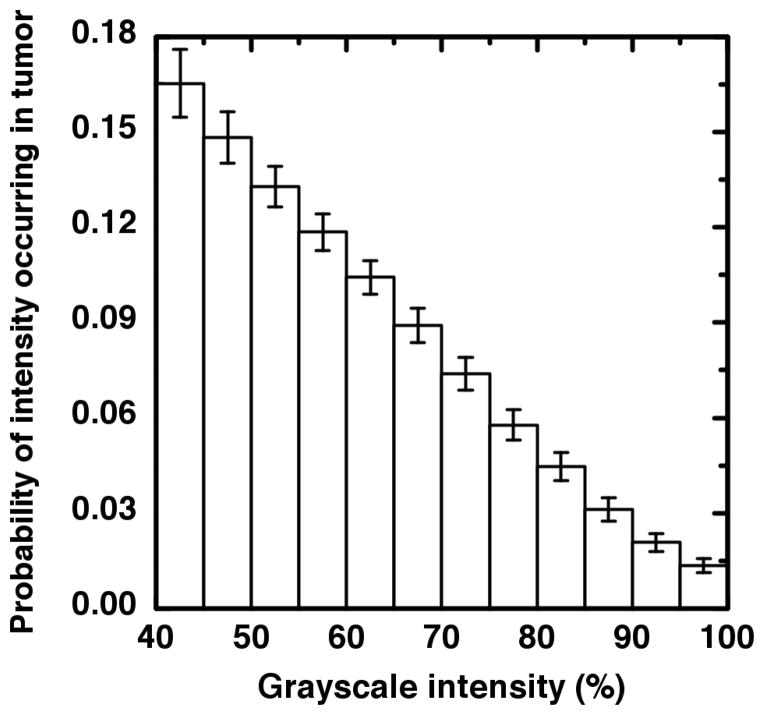
The relative intensity histograms for each patient were ensemble-averaged into a single relative intensity distribution. The resulting probability histogram is shown in Figure 2. This histogram enables the estimation of a minimum volume required for heterogeneity studies.

Figure 2.

The intensity histogram resulting from the ensemble average of 70 tumors each of which is measured on the same percent-of-maximum scale. The intensities are seen to be approximately linearly distributed until the flattening tail at the highest intensity values. The error bars represent the standard error within each intensity bin.

Derivation of the Minimum Volume

Given the probability ρ of an intensity being in the least-populated bin, the probability of having precisely L intensities in the least-populated bin after choosing v voxels is

$$p(v,L)=\left(\begin{array}{c}v\\ L\end{array}\right){\rho }^L{(1-\rho )}^{v-L}$$ Eq. 2

since there are “v choose L” ways of arranging a sequence containing L intensities amongst the v-L intensities from all other bins collectively (14). We, however, allow for at least L intensities, since higher bin-population scenarios could contribute probability to lower bin-population scenarios and since having many more samples than the bare minimum is preferable. We therefore sum the individual probabilities given in Equation 2 as

$$p(v,\lambda \ge L)=\sum _{\lambda =L}^{\infty }p(v,\lambda )$$ Eq. 3

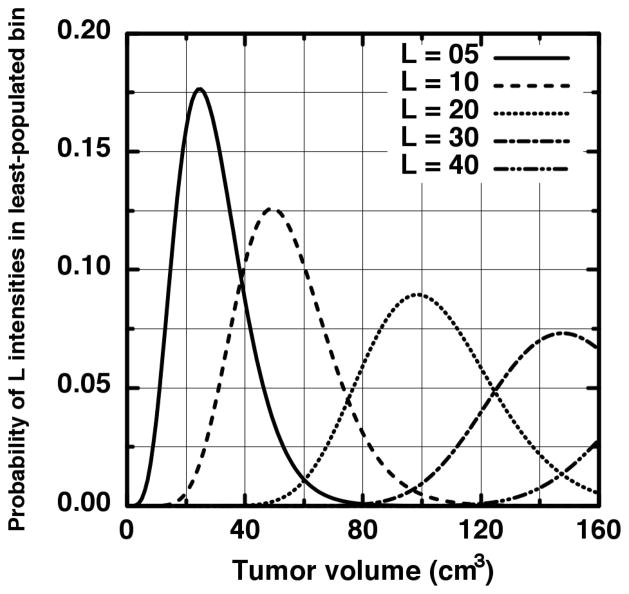
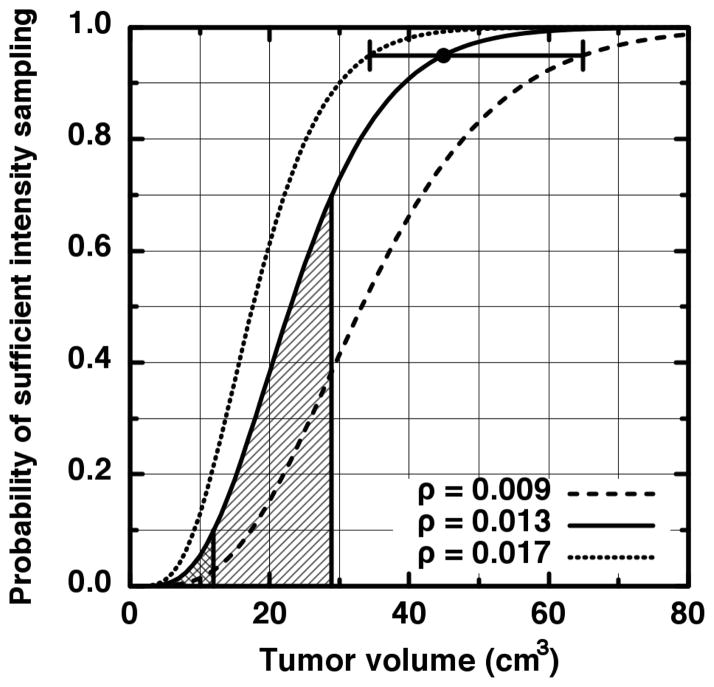
We need not derive a closed analytic form for p(v, λ ≥ L) in order to discover the requisite number of voxels to assure a minimum least-bin population is achieved. For the present derivation, we chose the traditional minimum of five frequencies per tested contingency as the required minimum population. Further reasoning behind this choice and its impact upon our results is discussed in the Discussion section. In Figure 3, the probability of having precisely L intensities in the least-populated bin is shown for several examples (L = 5,10,20,30,40) where we have rescaled v to more familiar units of cm³. The first curve (solid) shows that near a volume of 100 cm³, the probability of having precisely five intensities in the least-populated bin is approximately zero. This is because for this volume, so many samples have occurred that more than five intensities is virtually guaranteed to be in the least-populated intensity bin. We thus use 0–100 cm³ as a practical domain upon which to focus our search. As is seen in Figure 3, the precise-number probabilities are non-zero over this domain to L = 40 (dot-dot-dash). We may therefore sum Equation 3 from λ = 5 to 40 and be assured that we have included all scenarios where five or more intensities populate the least-populated bin for volumes within the 0–100 cm³ search domain. The resulting probability of having at least five intensities in the least-populated intensity bin for ρ = 0.013 (this value is read from the ensemble histogram) is plotted in Figure 4 as the solid curve.

Figure 3.

The probability that precisely L samples fall into the last intensity bin given in Figure 2 is plotted for several L values. It is seen that up to 100 cm³ the probability curves from higher numbers of samples (40 > L > 5) are not zero and therefore contribute to the probability that at least five samples fall into the final intensity bin.

Figure 4.

The probability (solid curve) that at least five samples fall into the last intensity bin given in Figure 2. The large dot indicates the level of 95% certainty that adequate sampling of the intensity distribution has occurred. The other curves represent the probabilities computed from 1.96 times one standard error above or below the ensemble average last bin probability. The horizontal error bar extends from 34 cm³ (531 voxels) to 65 cm³ (1016 voxels).

Impact upon Clinical Data Analysis

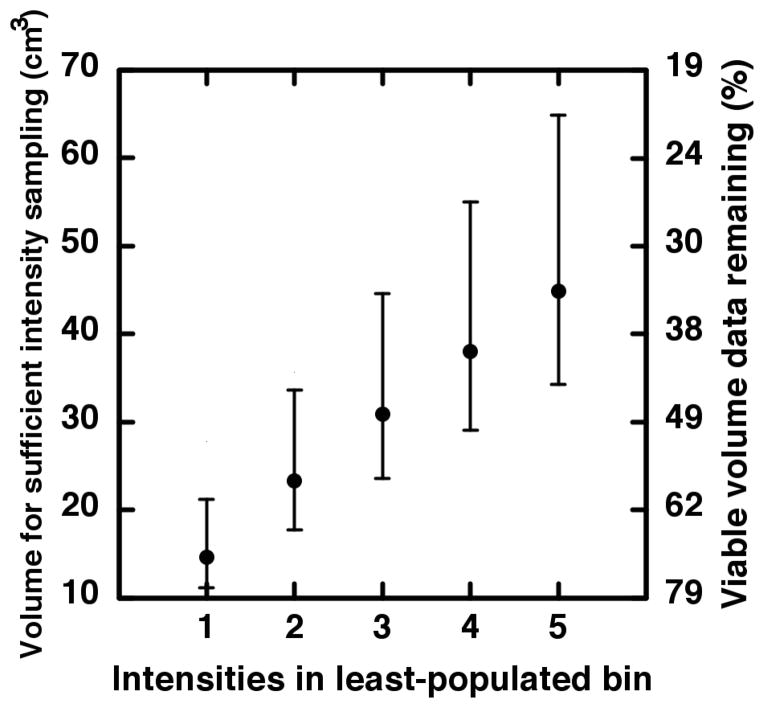
The severity of under-sampling upon clinical studies is shown by the vertical lines in Figure 4 which indicates the first and second quartiles of our tumor volume data. The adequate-sampling probability averaged over 1 cm³ to the first quartile (12 cm³; cross-hatched) is only 2%. Between 1 cm³ and the median (29 cm³; hatched), the average is 25%. The large dot at 45 cm³ indicates the intersection with p = 0.95, i.e., the volume where one may be 95% certain that enough samples reside in the least-populated intensity bin in order for meaningful statistical comparisons to be made. For our clinical data, this leaves less than half (34%) of the tumor volumes as viable data points for comparing FDG-PET heterogeneities. The other two curves in Figure 4 represent the probability of having at least five intensities in the least-populated bin but using ρ ± 1.96(0.002) as the probability of populating the least-populated bin (here, 0.002 is the standard error read from the ensemble histogram). The bar between the non-solid curves thus indicates the 95% confidence interval around 45 cm³. The results of the above calculation for less-stringent sampling criteria are shown in Figure 5. As we argue in the Discussion, requiring less than five samples in the least-populated intensity bin is unlikely to sufficiently abate the under-sampling effects we describe.

Figure 5.

On the left-hand scale, the volume associated with sufficient sampling is plotted versus increasingly strict criterion for adequate sampling of the intensity distribution. The non-linear right-hand scale indicates approximately how much of our volume data remains after imposition of each adequate-sampling criterion.

Demonstrated Effect upon Heterogeneity Studies

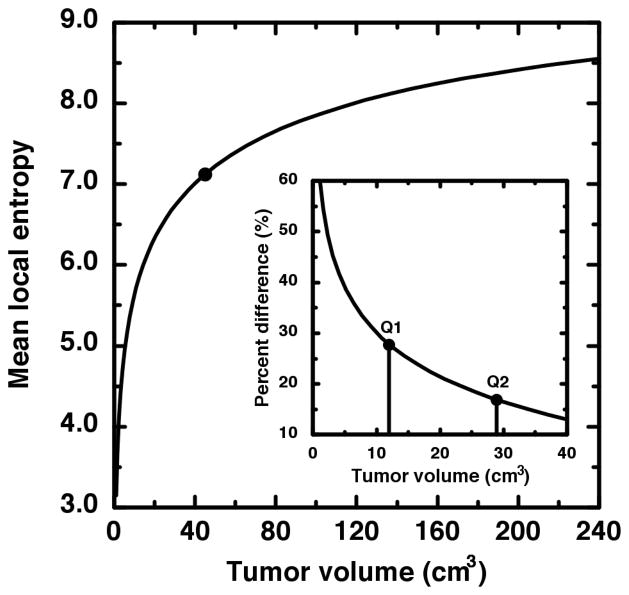
It has been proposed that the local entropy may be a useful clinical measure of uptake heterogeneity (5,6,10). Furthermore, the local entropy has been claimed to be the most reproducible metric amongst similar heterogeneity metrics (10). We therefore chose to demonstrate the small volume effect upon comparative heterogeneity studies via the local entropy metric described in the Materials and Methods section. We first sought to isolate the effect of tumor size from the effects of intensity distribution or intensity rearrangement. This was done by creating sets of two-dimensional, shapeless “tumor” images as described in the Materials and Methods section. For each tumor volume, 25 tumor images were created upon which the local entropy was computed then ensemble averaged to a single mean heterogeneity value. The result is the plot of local entropy (h) versus tumor volume (v) given in Figure 6. Foremost is the striking increase in h(v) over the first 45 cm³ of tumor volume compared to the flatness of h(v) for volumes greater than 45 cm³. For 240 > v > 45 cm³, the mean value is 〈h〉 = 8.1 and the individual h values differ (on average) by only 4% from that mean. We now compare this large volume mean to the small volume h values as is done in heterogeneity studies when tumors of widely varying volumes are analyzed together. The first quartile of tumor volumes—as indicated by the first vertical line in the inset of Figure 6—on average, differ by 38% from the large volume mean 〈h〉 = 8.1. For all v < 45 cm³, h(v) still differs on average by 23%. Therefore, the local entropy is about 5 times more sensitive to a volume change applied to a small volume than to the same change applied to a large volume. It is thus seen that before any assessment of tumor biology has been made, the statistic ostensibly doing that assessment has been saddled with a non-negligible value change that has nothing at all to do with tumor biology.

Figure 6.

The ensemble average of the root-mean-square local entropy is plotted as a function of image size (tumor volume). The local entropy is much less sensitive to volume for volumes greater than 45 cm³ (large dot). The inset shows the percent difference of the mean local entropy from the value averaged over only the large volumes. The vertical lines indicate the first and second quartile of our tumor volume data. It is thus seen that the first quartile exhibits large deviation from the large-volume average.

DISCUSSION

For any tumor assayed via FDG-PET, the tumor data are a distribution of grayscale intensities. It is this intensity data that represents the biology of the tumor. We have demonstrated a feasible clinical scenario were tumors following identical intensity distributions—i.e., identical measured tumor biology—have heterogeneity measures which depend strongly upon tumor volume. Therefore differences in uptake heterogeneity observed between disparate tumor volumes may not indicate actual biological differences between those tumors.

We chose to illustrate this point via the local entropy because that statistic has been proposed previously as a robust measure of uptake heterogeneity; however, we now argue that heterogeneity statistics generally are more sophisticated than the statistical moments familiar to most clinicians. Heterogeneity is a measure of the deviation from homogeneity. In image processing parlance, heterogeneity is the “texture” of the image; the differences from smoothness. In 1973, Haralick et al. described a comprehensive set of texture metrics for grayscale images (13). Those fundamental metrics, one of which is the local entropy, are each themselves computed from grayscale co-occurrence matrices. These matrices are simply the tallies of differences between pixel neighbors. That is, co-occurrence matrices track the probability that fixed-distance pixels are shaded differently. Over the entire image, these local variations accrue into the global texture statistics some propose to use as a measure of tumor heterogeneity. Precisely because they are accrued statistics, they measure only what information actually is contained in the image data and, as such, must to some degree depend upon sample size.

This dependence upon sample size is not a failing of existing texture metrics. In quantifying texture, one is interested in the spatial patterns and intensity variations observed in image data. In FDG-PET images, these variations ultimately are caused by some combination of the scanning process and tumor biology. If the total number of pixels is largely diminished, so too is the certainty that patterns and variations allowed by the underlying biology have had adequate opportunity to manifest. To put this another way, the set of intensities and intensity arrangements necessary to build a complete picture of the possible biology is itself incomplete for small volumes. Mathematically speaking, many texture metrics proposed to measure uptake heterogeneity are supposed to have completely different values for smaller volumes; values which may have no predictable relation to those computed for larger volumes. This is in stark contrast to the use of statistical moments such as the distribution variance as a first-order heterogeneity quantifier where, in the case of a common intensity distribution, moment values predictably regress to the mean values as sampling (of any size) is repeated across patients.

The minimum tumor volume we describe is a minimum with regard to the type of comparative heterogeneity analysis some researchers have proposed. That is, it is a minimum imposed by the desire for robust mathematical manipulation of intra-tumor statistics. Our point is that although very small tumor volumes may be sufficient for treatment planning or other clinical purposes, they do not necessarily contain enough intensity data to be further analyzed using the heterogeneity quantifiers earlier proposed.

We used a straightforward argument to estimate the minimum tumor volume required for adequate intensity sampling to be about 700 voxels (45 cm³ for our image data). This argument is based ultimately upon a tried-and-true criterion found in classic (14,15) and modern (16) textbooks alike regarding adequate sampling of unknown distributions which are to be compared via χ² goodness-of-fit test. We chose this test because, in essence, that’s what statistics derived from FDG-PET images are—a comparison of intensity distributions. Without sufficient frequencies in every possible contingency, the χ² statistic does not regress to the χ² distribution and table values regarding “significance” levels become moot. Although there are situations in which less strict sampling criteria are appropriate (14–16), for the present context, the reasoning against these lax criteria is clear from Figure 6. If, for example, a minimum intensity bin population of only one was required, the corresponding volume (≈15 cm³; see Figure 5) yields a local entropy value in the most steeply increasing portion of the h(v) curve. In other words, if the measured intensities have not sufficiently revealed the underlying intensity distribution, the heterogeneity metric is highly sensitive to tumor volume. Thus, inclusion of tumor volumes—or intra-tumor regions—so small as to essentially guarantee under-sampling has occurred must bias the results of any comparative uptake heterogeneity study. Therefore, in the context of such studies, the default presumption should be that no statistical inference whatsoever may be made from small FDG-PET volumes. The onus is on the researcher to demonstrate that a new heterogeneity result is not due to the effects of under-sampling.

As seen in Figure 6, h(v) is monotonic in v and therefore acts as a mere surrogate for tumor volume. This means that a decrease in volume must correspond to an decrease in heterogeneity. What is important here is the relative size of decrease. From Figure 6, it is seen that the derivative of h with respect to v is much less for the larger volumes than for the smaller ones. This indicates that h is much less sensitive to changes in v for large v. Thus, discovering a 20% change in heterogeneity between two large volumes actually could be significant since we suspect that h is not strongly affected by volume over the domain of only large volumes. Contrast this, for example, to the comparison of heterogeneities between a 80 cm³ tumor and a 20 cm³ tumor where a 20% change in h is seen to be caused by volume alone.

We feel that performing the analysis we presented in a higher dimension does not offer anything new while only serving to complicate subsequent discussion. The local entropy is extensible into three dimensions. However, because of the increased dimensionality, one must include much more detail as to which of the directional co-occurrence matrices are computed and how statistics derived from those matrices are implemented or combined. Furthermore, because these matrices already represent spatial averages over the entire image set (13), rearrangement of the image data is not likely to alter the qualitative dependence upon volume. In specific cases of quantitative dependence, added dimensionality increases the number of spatial intensity configurations possible while the sampling (tumor volume) remains the same. Intuitively, however, as the number of unique scenarios a quantifier can describe increases—whether through data dimensionality or quantifier sophistication—the minimum sample size for meaningfully comparing those scenarios increases as well. We therefore predict the deleterious small volume effect we describe to be even worse for three-dimensional data and for higher-order heterogeneity metrics but caution that the specific dependence of a given metric upon dimensionality quickly goes far beyond the intended scope of this work.

Another potential influence on the quantitative value of uptake heterogeneity metrics is the partial volume effect. In the case of FDG-PET, the partial volume effect renders voxels at the tumor/microenvironment interface to be less bright than voxels filled with tumor (9). In fact, any intensities measuring less than the brightest biologically possible intensity could result solely from partial filling with background or necrotic regions. It is therefore feasible that the partial volume effect creates at least some—if not all—of the heterogeneity which is visually evident in FDG-PET images. For this reason, one might expect that partial volume correction could influence our calculations. It is almost certain that such a correction will alter the overall distribution of measured FDG-PET intensities. However, this alteration is unlikely to profoundly affect the bright end of the intensity histogram. This is because the brightest pixels likely are already the closest to being completely filled with tumor and therefore are the least-affected by the partial volume effect (or partial volume correction). The non-solid curves shown in Figure 4 represent the effect of plus or minus one standard error around the probability of measuring the brightest intensities. The horizontal error bar in Figure 4 might therefore represent a reasonable bound on partial volume effects (or any systematic measurement effects) because, by ensemble averaging many same-scale histograms, we have allowed the biology of similarly-sized tumors numerous chances to manifest under the same scanning process.

The calculation of minimum volume we present is better thought of as a technique to be applied to distinct image data sets, rather than a justification for a rigid rule to be applied uniformly to all image data. What is crucial to our calculation is the number of samples of the underlying intensity distribution. While this means that calculation of the probability where at least L observations reside in the least-populated intensity bin is independent of voxel size (Equation 3), the input probability (ρ) is not. Because different PET scanners have voxels corresponding to different physical sizes, and because both partial volume effects and uptake can depend non-linearly upon tumor size and biology, the distribution of measured intensities itself likely is unique to the particular combination of tumor type, scanner resolution and scanner modality. In other words, the probability that any intensity resides in the least-populated bin—as well as the bin size definition itself—is sensitive to scanning process. In general, one can compute the ensemble intensity distribution for their image data set, find the probability (ρ) an intensity resides in the least-populated intensity bin, use Equation 2 construct a plot similar to Figure 3 from where the practical summation limit may be read and compute the minimum number of voxels by setting p = 0.95 (or whatever confidence level is desired) in Equation 3 and numerically solving for v.

CONCLUSION

Each PET-imaged tumor is one sampling of all radioactivities which are physically and biological permissible for that particular scanner/tumor combination. Because image heterogeneity statistics accrue manifestations of possibilities, it is the very nature of these statistics to reflect small sample sizes. Thus, inclusion of small tumor volumes necessarily biases tracer uptake heterogeneity studies toward statistically significant difference even when no difference in uptake exists. We have argued that this bias is lessened if all regions-of-interest included in comparative heterogeneity analyses are above a minimum number of voxels. We have described a technique for computing this number which, when applied to our specific FDG-PET image data, yields a minimum comparison volume of 45 cm³.