DEVELOPMENT OF THE “RICH CLUB” IN BRAIN CONNECTIVITY NETWORKS FROM 438 ADOLESCENTS & ADULTS AGED 12 TO 30

Abstract

The ‘rich club’ coefficient describes a phenomenon where a network's hubs (high-degree nodes) are on average more intensely interconnected than lower-degree nodes. Networks with rich clubs often have an efficient, higher-order organization, but we do not yet know how the rich club emerges in the living brain, or how it changes as our brain networks develop. Here we chart the developmental trajectory of the rich club in anatomical brain networks from 438 subjects aged 12-30. Cortical networks were constructed from 68×68 connectivity matrices of fiber density, using whole-brain tractography in 4-Tesla 105-gradient high angular resolution diffusion images (HARDI). The adult and younger cohorts had rich clubs that included different nodes; the rich club effect intensified with age. Rich-club organization is a sign of a network's efficiency and robustness. These concepts and findings may be advantageous for studying brain maturation and abnormal brain development.

INTRODUCTION

First reported for brain networks by Van den Heuval and Sporns in 2011 [1] and described in 2006 by Colizza et al. [2] for other complex networks, the ‘rich club’ coefficient is a metric that can inform us about the fundamental organization of the brain's networks, structural or functional. A rich club exists in a network, if there is a core of nodes with a high degree (k) – that is, rich in connections – that are more densely interconnected among themselves than lower-degree nodes in the network. In other words, the high-degree nodes form a club. The rich club coefficient Φ(k) is a ratio of the number of connections among nodes of degree k or higher versus the total possible number of connections if those nodes were fully connected. It is defined as:

$$\Phi \left(k\right)=\frac{2{\mathrm{E}}_{>k}}{{\mathrm{N}}_{>k}({\mathrm{N}}_{>k}-1)}$$ (Eq. 1)

As higher-degree nodes have a higher probability of being interconnected with each other simply by chance,Φ(k) is typically normalized relative to Φ calculated on a set of simulated random networks with the same degree distribution, and the same edge distribution, as a function of the nodal degree k. If Φ_norm>1 (i.e., Φ(k) >Φ_rand, for some k), then there is evidence of rich club organization (formal statistical testing of the rich club effect uses a null model based on randomized networks as a reference distribution).

Across development, the brain changes tremendously as we mature into adults. Ideally, networks adapt and become highly efficient. Short-range connections are pruned in favor of long-range ones [3], myelination continues [4], and the connectome continually changes. Through in vivo diffusion imaging and tractography, we can visualize and analyze fiber pathways. Graph theory has been applied to networks of anatomical fibers to model the brain as a set of nodes and edges and analyze the network topology and dynamics [5]. We previously showed how some graph theory metrics change over development [6]; here we set out to detect developmental changes in the rich club.

2. METHODS

2.1. Subjects and Image Acquisition

Participants were recruited as part of a 5-year research project scanning healthy young adult Australian twins with structural brain MRI and DTI [7]. We analyzed scans from 438 right-handed subjects (adult cohort: 210 female/126 male, average age=23.6 years, SD=2.2, 16-year-old cohort: 30 female/25 male, average age=16.2 years, SD=0.37, 12-year-old cohort: 23 female/24 male, average age=12.3 years, SD=0.18). This population included 145 monozygotic (MZ) twins, 260 dizygotic (DZ) twins, and 33 non-twin siblings, from 275 families. 336 were adults, 55 were adolescents, and 47 were children. Whole-brain anatomical and high angular resolution diffusion images (HARDI) were collected with a 4T Bruker Medspec MRI scanner. T1-weighted anatomical images were acquired with an inversion recovery rapid gradient echo sequence, with parameters: TI/TR/TE = 700/1500/3.35ms; flip angle = 8 degrees; slice thickness = 0.9mm, and a 256×256 acquisition matrix. HARDI was also acquired using single-shot echo planar imaging with a twice-refocused spin echo sequence to reduce eddy-current induced distortions. Imaging parameters were: 23cm FOV, TR/TE 6090/91.7ms, with a 128×128 acquisition matrix. Each 3D volume consisted of 55 2-mm thick axial slices with no gap and 1.79×1.79 mm² in-plane resolution. 105 images were acquired per subject: 11 with no diffusion sensitization (i.e., T2-weighted b₀ images) and 94 diffusion-weighted (DW) images (b = 1159 s/mm²) with gradient directions evenly distributed on a hemisphere in the q-space. Some subjects’ HARDI scans were acquired with a 77-gradient protocol (b = 1177 s/mm²), as the 105-gradient protocol was too long for some adolescents to sit through. For a fuller explanation of how the connectivity maps, and orientation density functions, are stable when such relatively high numbers of gradients are collected, please see [6]. Scan time was 14.2 min for the 105-gradient HARDI scan, and 10.8 min for the 77-gradient HARDI scan.

2.2. Cortical Extraction and HARDI Tractography

Connectivity analysis was performed as in [8]. Briefly, non-brain regions were automatically removed from each T1-weighted MRI scan, and from a T2-weighted image from the DWI set, using the FSL tool “BET” (FMRIB Software Library, http://fsl.fmrib.ox.ac.uk/fsl). A neuroanatomical expert manually edited the T1-weighted scans to refine the brain extraction. All T1-weighted images were linearly aligned using FSL (with 9 DOF) to a common space with 1mm isotropic voxels and a 220×220×220 voxel matrix. For each subject, the 11 eddy-corrected images (using FSL tool “eddy_correct”) with no diffusion sensitization were averaged, linearly aligned and resampled to a downsampled version of their corresponding T1 image (110×110×110, 2×2×2mm). Averaged b₀ maps were elastically registered to the structural scan using a mutual information cost function to compensate for EPI-induced susceptibility artifacts. 34 cortical labels per hemisphere, as listed in the Desikan-Killiany atlas [9], were automatically extracted from all aligned T1-weighted structural MRI scans using FreeSurfer (http://surfer.nmr.mgh.harvard.edu/). T1-weighted images and cortical models were aligned to the original T1 input image space and down-sampled to the space of the DWIs, using nearest neighbor interpolation (to avoid intermixing of labels). To ensure tracts would intersect cortical labeled boundaries, labels were dilated with an isotropic box kernel of size 5×5×5 voxels.

The matrix transforming the mean b₀ image to the T1-weighted volume was applied to each of the 94 gradient directions to properly re-orient the orientation distribution functions (ODFs). At each HARDI voxel, ODFs were computed using the normalized and dimensionless ODF estimator derived for q-ball imaging (QBI) [10]. We performed HARDI tractography on the linearly aligned sets of DWI volumes using these ODFs, using the Hough transform method [11]. Elastic deformations obtained from the EPI distortion correction, mapping the average b₀ image to the T1-weighted image, were then applied to the tracts’ 3D coordinates to accurately align the anatomy. Each subject's dataset contained 5000-10000 useable fibers (3D curves). For each subject, a full 68×68 connectivity matrix was created. Each element described the proportion of the total number of fibers connecting each of the labels; diagonal elements describe the total number of fibers passing through a certain cortical region of interest. Values were calculated as a proportion - normalized to the total number of fibers traced for each individual participant, to avoid skewing results by the raw fiber count.

2.3. Rich Club Analyses

On the 68×68 matrices generated above, we used the Brain Connectivity Toolbox (12, https://sites.google. com/site/bctnet/) to compute the rich club coefficient (Φ). The fiber count matrices were first binarized for each subject. We normalized our rich club coefficient based on coefficients calculated from 50 random networks to generate a normalized rich club coefficient (Φ_norm). Below we use the same symbols as the original paper on this topic [1].

2.4. Age Regression

Age effects on rich club coefficient were estimated using the general linear mixed effects model, as well as two simpler linear mixed effects models, as follows:

$$\text{Rich club coefficient}\sim \mathrm{A}+{\beta }_{\mathrm{age}}\mathrm{Age}+{\beta }_{\mathrm{sex}}\mathrm{Sex}+{\beta }_{\mathrm{TBV}}\mathrm{TBV}+{\beta }_{\text{age-squared}}{\mathrm{Age}}^2+\alpha$$ (Eq. 2)

$$\text{Rich club coefficient}\sim \mathrm{A}+{\beta }_{\mathrm{age}}\mathrm{Age}+{\beta }_{\mathrm{sex}}\mathrm{Sex}+{\beta }_{\mathrm{TBV}}\mathrm{TBV}+\alpha$$ (Eq. 3)

Here, “rich club coefficient” could be either the normalized or non-normalized version; both were assessed. A is a constant for each regression model, the βs are the covariate regression coefficients, and α is a coefficient that accounts for random effects. Random effects were used to account for family relatedness. We modeled the other variables (age, sex, TBV, age²) as fixed effects. TBV denotes total brain volume.

2.5. Null Model of Change

To test whether changes in node degree distribution that determined rich club membership could be attributed to sampling, we split the adults into 2 random groups and examined differences between them. We did this 20 times to generate a distribution of the change due to sampling. Degree was quite stable for each node, and the average change in which nodes were in the rich club was 1.05 nodes, SD 0.67.

3. RESULTS

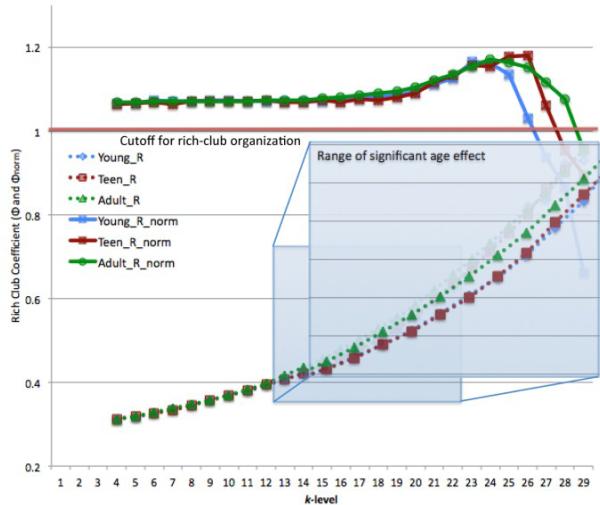
We found a significant linear age effect on Φ across the k-range 13-22; adults had a higher Φ across that whole range (Eq. 3). All groups had rich club organization (meaning Φ_norm was significantly >1) until k-level 26. Figure 1 shows the degree distribution for the adults and the young cohort. This histogram was made by generating a mean matrix for the 2 groups, thresholding them to only include connections found in at least 75% of the subjects, and then finding the degree of that average group network. The ranges of Φ and Φ_norm for all 3 cohorts are shown in Figure 2, along with a zoomed-in view of the significant differences across k-range 13-22. There were no significant non-linear age effects (Eq. 2). These plots were made by taking the mean of Φ and Φ_norm within each group.

Figure 1.

Histogram of degree distribution for adults (blue) and young cohort (red, 12 and 16 year olds combined).

Figure 2.

Range of Φ and Φ_norm for all three groups, 12 year olds (young) in blue, 16 year olds (teen) in red, 20-30 year olds (adult)in green. Zoomed in blue box highlights the range of Φ showing significant age effects.

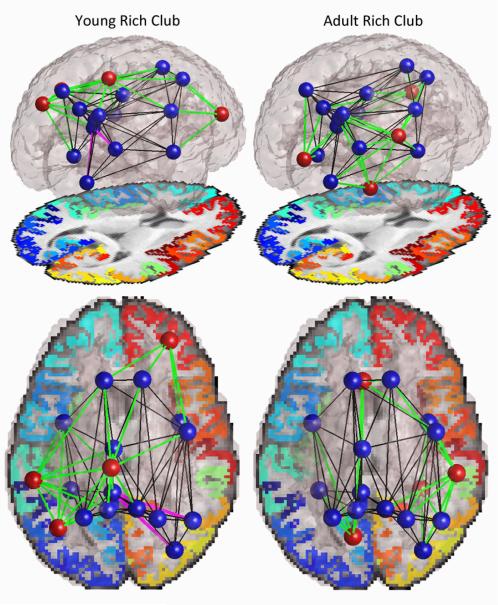
Perhaps more interesting than the quantitative analysis of the rich club coefficients is differences in which nodes constitute the rich club. When examining the nodes that were included in the rich club, we found a difference between the adult cohort and the younger cohort (12 and 16 year olds; to simplify testing we combined the two younger groups) (Figure 3). We examined these differences at k = 17, because at this degree threshold both groups had rich club organization and both groups had the same number of nodes included in the trimmed network, making comparison more appropriate. At this level there were 18 nodes in the rich club. Of these, 14 were in common between the adult and younger cohorts, and 4 were unique to each group. Both groups’ rich clubs included the bilateral insula, bilateral superior frontal gyrus, bilateral precuneus, bilateral superior parietal gyrus, left fusiform gyrus, left isthmus of the cingulate, left posterior cingulate gyrus, right inferior parietal gyrus, right lateral occipital gyrus, and right precentral gyrus. The adult-unique rich club nodes were the left caudal anterior cingulate gyrus, left lingual gyrus, right fusiform gyrus, and right supramarginal gyrus. The young-unique rich club nodes were the left inferior parietal gyrus, right rostral middle frontal gyrus, left paracentral gyrus, and left supramarginal gyrus.

Figure 3.

Rich club networks in young (12 and 16 year old) and adult (20-30 year old) cohorts. Blue nodes were present in the rich clubs of both groups; red nodes were unique to one of the groups. Black edges were present in both groups, green edges were unique to one of the groups as they involved unique nodes, magenta edges were unique to one of the groups among nodes common to both groups. Edges are thresholded to only show those present in >75% of subjects in either group.

As for the connections within the rich club, there were many differences, most stemming from differences in the nodes included in each group's rich clubs. Among the connections of the nodes common to both groups’ rich clubs, there were a few differences as well. The young cohort had connections between the left isthmus of the cingulate and the right inferior parietal gyrus, and the left isthmus and the right lateral occipital gyrus, which the adults did not have. This connection did not completely vanish, but it was not present in enough adults (>75%) to warrant inclusion in this analysis.

4. DISCUSSION

We found a linear increase in the non-normalized rich club coefficient between ages 12 and 30 in 438 subjects. The rich club coefficient represents the density of connections between rich club nodes. As our subjects aged, their rich club nodes became more closely integrated as the core of the connectome. This fits with prior reports of increased integration as brain networks develop [6]. We previously found shorter path length as subjects age; path length is the average distance, in edges, between all pairs of nodes in a network. A more densely connected rich club - the core of the connectome through which many network paths pass - would most likely lead to a shorter path length overall.

Among the nodes making up the rich club, we saw some differences between young and adult groups. With only 4 unique nodes to look at in each group, it is difficult to find a pattern, but it is interesting that they are changing, more than could be due to sampling (p<0.05). As rich club nodes, these nodes are central and highly important as hub nodes. For rich club membership to change in adolescence suggests that there are still significant maturational processes at work with non-trivial effects on the connectome as a whole.

The nodes that we found to make up the rich club overlap with the previous description [1], although here we considered only cortical nodes while Van den Heuval and Sporns also included subcortical nodes, and their sample was much smaller (N=21). The rich club nodes had members from both hemispheres across the frontal, parietal, temporal and occipital lobes, and many were included bilaterally. The rich club nodes overlapped largely with previously identified structural hub nodes [13]. Some nodes in our rich clubs had not been previously identified as hub nodes, such as the insula and the fusiform gyrus. This could be a result of our looking at binarized matrices, rather than matrices with the full weight. It may be that we were better able to recover fibers reaching those nodes with our 105-gradient HARDI scans and Hough-based tractography.

One recognized limitation of this study is the uneven sampling of different age groups; subjects aged 12 or 16 were available for scanning, but not in between. Nonparametric regression models may therefore be advantageous to derive empirical p-values for the fitted regression coefficients, but are unlikely to materially affect the conclusions as the age effects here are relatively strong.

5. CONCLUSION

This is the first study to our knowledge to investigate the developmental trajectory of the rich club across adolescence into early adulthood. The rich club coefficient increased with age, implying increasing integration of the rich club nodes as the brain develops. We also saw some changes in which nodes make up the rich club, evidence of significant re-modeling of the structural connectome through adolescence. Establishing the developmental trajectory of these brain connectivity metrics in healthy individuals is a first step towards determining how and when children with neurodevelopmental disorders may deviate from this trajectory.