Combat casualties undergoing lifesaving interventions have decreased heart-rate complexity at multiple time scales

Abstract

Purpose

We found that heart-rate (HR) complexity metrics, such as sample entropy (SampEn), identified trauma patients receiving lifesaving interventions (LSIs). We now aimed: 1) to test a new multiscale entropy (MSE) index; 2) to compare it to single-scale measures including SampEn; and 3) to assess different parameter values for calculation of SampEn and MSE.

Methods

This was a study of combat casualties in an Emergency Department (ED) in Iraq. ECGs of 70 acutely injured adults were recorded. Twelve underwent LSIs and 58 did not. LSIs included endotracheal intubation (9); tube thoracostomy (9); and emergency transfusion (4). From each ECG, a segment of 800 consecutive beats was selected. Off-line, R waves were detected and R-to-R (RR) interval time series were generated. SampEn, MSE, and time-domain measures of HR variability (mean HR, standard deviation, pNN20, pNN50, rMSSD) were computed.

Results

Differences in mean HR (LSI=111±33, NonLSI=90±17) were not significant. Systolic arterial pressure was statistically but not clinically different (LSI=123±19, NonLSI=135±19). SampEn (LSI=0.90±0.42, NonLSI=1.19±0.35, p<0.05) and MSE index (LSI = 2.58±2.55, NonLSI=5.67±2.48, p<0.001) differed significantly.

Conclusions

Complexity of HR dynamics over a range of time scales was lower in high-risk than in low-risk combat casualties and outperformed traditional vital signs.

1. Introduction

This study was motivated by the need for enhanced vital-sign monitoring in emergency combat casualty care. In 2009 Martin and colleagues analyzed 151 deaths at a Combat Support Hospital in Iraq; most occurred within one hour of admission, either from head injury or hemorrhage. Opportunities for improving risk assessment were noted in almost half of the cases, related to delays in hemorrhage control during transportation or in resuscitation efforts [1]. Earlier detection of hemorrhagic shock implies a need for improvements in the timely use and diagnostic accuracy of vital-sign monitors [2]. To improve current vital-sign monitors, without adding new sensors or boxes to the medic’s kit, we are examining the utility of computational tools that characterize and quantify the variability of beat-to-beat fluctuations in HR time series for risk stratification. Our underlying hypothesis is that information about the integrity of the body’s neuroautonomic control mechanisms is encoded in the way that the HR spontaneously changes over time, and that illness or injury impair these mechanisms in ways that can be measured.

Specifically, we have applied measures of irregularity such as approximate entropy (ApEn) [3] and sample entropy (SampEn) [4], to the analysis of time series comprising between 100 and 800 heart beats [5–7]. We have referred to these as measures of heart-rate (HR) complexity. HR complexity was lower in civilian trauma patients from the Trauma Vitals USA database who received prehospital lifesaving interventions (LSIs), than in those who did not [8]. HR complexity was also lower in trauma patients who went on to die, than in survivors [9]. Quantification of the degree of complexity, using SampEn and/or ApEn, consistently outperformed traditional vital signs--such as the mean HR, blood pressure (BP), or peripheral saturation of oxygen (SpO₂)--in identifying critically injured trauma patients [8–9].

In the present study, we applied a more recently described method for quantifying HR complexity tool, multiscale entropy (MSE). The rationale for MSE is as follows. Complex time series are typically highly irregular, but not all irregular time series are complex. For example, random signals, such as those obtained by shuffling any sequence of numbers, may be very variable but carry, by construction, no information. Thus, these shuffled sequences are not complex. Truly complex signals such as those produced by healthy physiologic systems are far from random; instead, they exhibit complex patterns on multiple time scales. The information encoded on these multiple time scales is not adequately captured by ApEn or SampEn. To help obviate this limitation, a more generalized method called multiscale entropy (MSE) was introduced [10–11]. As the name implies, MSE quantifies entropy over multiple time scales. In this study, we computed both SampEn and MSE along with traditional HR variability metrics (described below). We also computed quadratic sample entropy (QSampEn), a refinement of the original SampEn statistic, as described in the Appendix.

The goals of this study were two-fold. First, we sought to test the hypothesis that MSE would be lower in combat casualties who undergo a LSI upon arrival to the Combat Support Hospital Emergency Department, than in those who do not. Second, we sought to elucidate the implications of selecting different parameter values for the calculation of SampEn and MSE, using very short segments of data obtained under conditions of battlefield trauma where extreme variations in HR dynamics are observed.

2. Materials and Methods

Subjects

This study was conducted under a protocol reviewed and approved by the Brooke Army Medical Center Institutional Review Board, in accordance with the approved protocol, and in compliance with the Helsinki Declaration. The study was performed under provisions of waived consent. We acquired continuous electrocardiogram (ECG) recordings from a convenience sample of combat casualties arriving at the U.S. Army Combat Support Hospital (CSH) located at Ibn Sina Hospital, Baghdad, Iraq, during the recent conflict. The ECGs were obtained based on the availability of a Deployed Research Team (DRT) at this hospital. Data were collected on a total of 325 patients. Of these, 40 patients’ ECGs were too short; 25 were too noisy; 96 had an excessive amount of ectopy; and 94 had insufficient demographic data. These exclusions left 70 complete datasets. Of these 70 casualties, 12 patients underwent LSIs in the CSH ED (LSI group) and 58 (non-LSI group) did not. Only LSIs performed in the emergency department were considered in this study. The list of potential LSIs included cardiopulmonary resuscitation, cricothyroidotomy, endotracheal intubation, needle decompression of pneumothorax, pericardiocentesis, emergency transfusion, tube thoracostomy, and cardioversion.

Data acquisition and analysis

Upon admission to the Emergency Department (ED), casualties were placed on a PIC 50™ vital signs monitor (Welch Allyn, Skaneateles Falls, NY). These monitors had an analog-to-digital data acquisition rate of 375 Hz. Previous work by Voss et al. confirmed that a sampling rate of 128 Hz or greater was sufficient for nonlinear measures of HR variability [12]. ECG data were recorded on standard digital memory cards. Other patient data were retrospectively recorded on paper by the DRT. The memory cards, and the case report forms, were then mailed to the U.S. Army Institute of Surgical Research, Fort Sam Houston, TX for analysis. WinCPRS software (Absolute Aliens OY, Turku, Finland) was used to process the ECGs and to identify the R waves. A trained analyst then reviewed every R wave detected and made corrections as needed, selecting 800 beats of clean ECG from each dataset. WinCPRS software then outputted the RR interval time series. In these 800- beat datasets, each R waves represented a normal sinus (N) rhythm beat. (Therefore, the RR interval time series are identical to the NN interval series.) We wrote custom software in Java and C++ to perform all subsequent HR dynamics calculations.

Measures

We calculated standard time-domain metrics of HRV: mean HR, standard deviation of the normal to normal beats (SDNN), the square root of the mean squared differences of consecutive NN intervals (rMSSD), and the proportion of pairs of consecutive NN intervals that differ by more than 20 ms (pNN20), and 50 ms (pNN50) [13–15]. We calculated single-scale (SampEn, QSampEn) and multiscale (MSE) entropies as detailed in the Appendix.

Statistical Analysis

Statistical analysis was done using SAS v. 9.1 (SAS Institute, Cary, NC). T tests or Wilcoxon tests were performed to analyze continuous variables, and chi square tests were used to analyze categorical variables, as appropriate. Significance was accepted at p<0.05.

3. Results

LSIs performed included endotracheal intubation (9); tube thoracostomy (9); and emergency transfusion (“Code Red”) (4). There was one death in the LSI group and none in the non-LSI group. Basic clinical information for the LSI and non-LSI patients are presented in Table 1.

Table 1.

Basic Patient Data

Variable	LSI (n=12)	Non-LSI (n=58)
Age, y	23±15	27±10
Sex (male)	12 (100%)	52 (89%)
Blunt or explosive mechanism	1 (8.3%)	19 (32%)
HR	111±33	90±17
SAP	123±19*	135±19
GCStotal	12±5**	15±0
GCSmotor	5±2**	6±0

LSI, patients who did receive lifesaving interventions; Non-LSI, patients who did not receive lifesaving interventions; Blunt/explosive mechanism, number of patients in each group injured by a blunt or explosive mechanism; HR, heart rate; SAP, systolic arterial pressure; GCS_total, total Glasgow Coma Scale score; GCS_motor, motor component of the Glasgow Coma Scale score. Data are means ± SD.

^*p<0.05;

^**p<0.001.

HRV time-domain measures are presented in Table 2. The average time between consecutive NN intervals (AVNN) trended lower for the LSI group, i.e., the HR was faster, compared to the non-LSI group. However, this difference was not statistically significant (p=0.07). All standard time domain measures of HRV were significantly lower for the LSI than for the non-LSI group.

Table 2.

HRV time-domain measures

Variables	LSI	Non-LSI	p value
AVNN	0.589 ± 0.185	0.694 ± 0.135	0.067
SDNN	0.023 ± 0.013	0.038 ± 0.020	0.022
rMSSD	0.009 ± 0.008	0.019 ± 0.014	0.005
pNN20	7.13 ± 13.71	22.20 ± 22.77	0.006
pNN50	0.91 ± 2.84	5.42 ± 10.83	0.018

Values of heart rate variability (HRV) time-domain measures for the LSI and non LSI groups. AVNN: average of all normal-to-normal (NN) intervals, in seconds. SDNN: standard deviation of all NN intervals, in seconds. rMSSD: Square root of the mean of the squares of differences between adjacent NN intervals, in seconds. pNN20 and pNN50: percentage of differences between adjacent NN intervals that are greater than 20 and 50 seconds, respectively.

SampEn, QSampEn and MSE index values are presented in Table 3.

Table 3.

Single and Multiscale Entropy Measures

Measures	LSI	Non-LSI	p value
Single Scale
SampEn (r=20%)	0.90 ± 0.42	1.19 ± 0.35	0.035
SampEn (r=6 ms)	0.58 ± 0.56	1.17 ± 0.59	0.003
QSampEn	8.73 ± 3.40	12.58 ± 2.78	0.002
Multiscale
MSE index (scales 1 to 4)	2.80 ± 2.60	5.78 ± 2.45	0.001

Results for entropy-based measures. Values of sample entropy (SampEn) are presented for r = 20% of the time series' standard deviation and for r = 6 ms. Values of quadratic sample entropy (QSampEn; see appendix) are presented for a minimum number of matches (M) of 30. The multiscale entropy (MSE) index, defined as the summation of SampEn values for scales 1 to 4 is presented. In all cases, the parameter m was set to 2. See text for details.

SampEn, calculated using the most widely employed parameter values (m=2, and r=20% of the SD of the time series), showed reduced RR interval irregularity for the LSI group compared to the non-LSI group. Statistically, even more robust separation between the two groups was seen when SampEn was computed for a fixed r value of 6 ms and m=2. The MSE index, which incorporates the SampEn values for scales 1 to 4, was significantly lower for the LSI than the non-LSI group. The MSE index also provided more robust separation between groups than SampEn used as a single scale measure.

Of note, comparable results were obtained for SampEn calculated with fixed r values ranging from 3 to 10 ms, for m=1, and for m=3 In addition, comparable results were obtained with the QSampEn measurement.

4. Discussion

The principal finding in this study was that combat casualties who underwent LSIs in the Emergency Department of a Combat Support Hospital in Iraq had lower HR complexity than those who did not. This difference held across multiple time scales, as quantified by the MSE method. We have previously reported lower HR complexity in seriously injured patients and animals by use of two closely-related, single-scale measures: sample entropy (SampEn) and approximate entropy (ApEn). To our knowledge, this study is the first in which MSE has been applied to acutely injured patients, and the first specific application of these techniques to combat casualties in a theater of operations.

The rationale for using MSE is as follows. The entropy of a time series is a measure of its degree of randomness or unpredictability. Real-world time series that are very variable tend to have high entropy. However, there are variable time series with entropy close to (or equal) zero. Consider, for example, the time series of a sequence of sine wave oscillations varying between -100 and 100 in arbitrary units (signal A). Consider now that the data points from signal A are randomly shuffled to create signal B. Signals A and B have the same mean and standard deviation because the shuffling procedure does not change the values of the data points but only the order in which they appear. While signal A is regular and predictable, signal B has a random (uncorrelated) structure. Therefore, signal A has (theoretically) zero entropy, and signal B is maximally entropic. The temporal sequence in which the data points occur is what determines the entropy of the signal (http://physionet.org/tutorials/cv/).

Sample entropy (SampEn) is an algorithm designed for quantifying the entropy of relatively short and noisy signals. Multiscale entropy (MSE) generalizes SampEn to multiple time scales. One major advantage of using MSE over SampEn, especially for the study of physiology, is that SampEn only quantifies how random a signal is. It may fail to distinguish between complex and random signals. MSE probes a signal on multiple time scales, i.e., at various levels of resolution (http://www.physionet.org/physiotools/mse/tutorial/). By doing so, MSE can discriminate between truly complex signals, i.e., those containing information on multiple scales, from those that are just variable. MSE has been applied to a wide class of physiologic and biologic signals, including HR time series, intracranial pressure signals, magnetoelectroencephalographic recordings, red-blood-cell flickering motions, etc., to help quantify the output of systems controlled by regulatory mechanisms operating on multiple time scales [16–19].

When applied to the cardiovascular system, MSE integrates information about the processes underlying the control of the HR. High MSE values are consistent with the notion that the processes controlling the HR in healthy subjects operate over multiple time scales. For example, loss of HR complexity has been reported in a number of settings with altered (dysregulated) neuroautonomic control, including chronic heart failure, aging, and acute major depressive disorder [11, 20]

What is the rationale for developing complexity-based vital signs for injured patients? Vital-sign measurement is a core practice in prehospital, emergency, and critical care. The Centers for Disease Control’s (CDC) 2011 Guidelines for Field Triage of Injured Patients is a revision of the American College of Surgeons Committee on Trauma’s (ASCOT) Decision Scheme. It states that the first step in triage is to measure vital signs and level of consciousness. Injured patients with a Glasgow Coma Scale score (GCS) ≤ 13, a systolic blood pressure < 90 mmHg, or a respiratory rate < 10/min or > 29/min (or a requirement for ventilator support) are triaged to a trauma center, irrespective of anatomic findings or mechanism of injury [21].

Several large studies, however, have led to a reappraisal of these standard vital-sign-based triage criteria. Several studies have criticized established vital-sign-based triage criteria such as these [22–27]. These studies have found that: (i) vital-sign-based trauma triage, alone, is associated with a significant undertriage rate; (ii) undertriage is associated with increased mortality; (iii) vital-sign ranges previously considered “normal” may actually be associated with increased mortality; (iv) predictive equations based on multiple variables outperform single vital signs in the prediction of mortality, and (v) continuous vital-sign data outperform single vital signs.

Given these findings, some authors have introduced new devices into emergency care, e.g. to measure lactate levels [28–30]. In the present study we took a different approach to the diagnostic problem in trauma. We applied new mathematical methods of analysis to the beat-to-beat variability inherent in the HR. This approach takes advantage of the fact that the ECG is already acquired (but under-utilized) in severely injured patients. Therefore, we sought to obtain more information from an existing sensor, rather than to add new sensors to our patients.

Our previous work included studies in animal models, and in prehospital and ICU patients. In anesthetized sheep, severe hemorrhagic shock caused a decrease in the high frequency (HF) power of HR variability, as well as a decrease in the ApEn and the fractal dimension of the HR [6]. We saw similar changes in anesthetized swine with hemorrhage [5], and with chest trauma followed by hemorrhage [7]. In prehospital trauma patients, ApEn was an independent predictor of mortality, even when GCS and ISS were taken into account [9]. In the same database, there was no difference in HR or BP between patients undergoing an LSI and those not; but patients differed on SampEn and GCS (motor component) [8]. Low SampEn and ApEn were features of patients upon admission to the Burn ICU, and were restored to normal values with fluid resuscitation [31]. On further analysis, we found that SampEn retained its ability to discriminate survivors from non-survivors in prehospital trauma patients, even as we moved from large datasets (800 heart beats) down to much smaller datasets (100 heart beats) [32].

In the present study, we again note lower SampEn in patients undergoing LSIs. In addition, we extend these findings by detecting lower HR complexity at multiple time scales as documented by MSE. In trauma patients, there are at least two physiologically based explanations for this finding. One is that hypovolemia causes a loss of HR complexity through a vagally-mediated process, related to compensatory withdrawal of parasympathetic tone to the heart. This mechanism would explain, for example, the decrease in high-frequency and short-term time-domain HR variability measures, which often accompany the decrease in HR complexity. The other explanation is that brain injury or ischemia may cause a loss of HR complexity through central-nervous-system-mediated processes. The latter mechanism would explain the lower mean Glasgow Coma Scale score observed in the LSI vs. non-LSI patients in this study. Of note, HR complexity has been proposed as an indicator of the overall adaptiveness and plasticity of the HR control system, rather than as a diagnostic test for any specific type of injury.

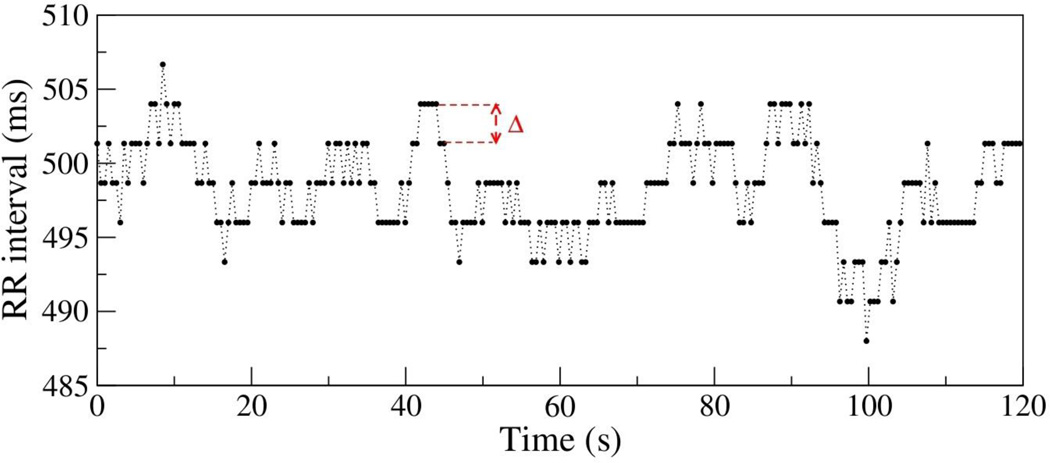
In this study, we also extended previous analyses by exploring different methodological approaches for choosing the parameter r for calculation of SampEn and the MSE index. Specifically, we compared the results using a fixed r value (based on the sampling frequency of the original ECG data) with those obtained using the “standard” implementation (based on an arbitrary percent (e.g., 15–20%) of each time series’ standard deviation. We found that for HR analysis the use of the fixed r value provided better discrimination for group comparisons using either single or multiscale measures. Furthermore, we found that in cases of very low time-series variance, sole reliance on the standard deviation-based method could lead to spuriously high values of SampEn or MSE due to “pseudo-fluctuations” generated by discretization errors (Fig. 1). This problem is particularly relevant in trauma conditions, in which low HR variance is most prevalent. Finally, we note that the computation of MSE, not just traditional SampEn (equivalent to Scale 1 of MSE), provides a more general assessment of HR complexity, and allows discrimination of irregularity due to random variations with low information content (e.g., R-R fluctuations with atrial fibrillation) vs. R-R fluctuations with intrinsically higher information content (e.g., sinus-rhythm dynamics in healthy subjects with intact neuroautonomic control) [10–11, 20].

Figure 1.

Time series of the RR intervals for a patient who underwent a life saving-intervention. The discretization interval Δ = 1/375 ~ 2.7 ms is the inverse of the sampling frequency of 375 Hz. Note that the RR intervals are multiples of Δ: 488, 490.7, 493.3, 496, 498.7, 501.3, 504, 506.7 ms. The time series standard deviation (SD) is 3.6 ms. Note that in this case 20% of the SD is 0.72 ms < Δ. Therefore, the number of matches obtained with r=20% of the SD is the same as with r = 0 ms.

Several other groups have contributed to the study of complex HR variability in critical illness. Norris et al. reported an increase “cardiac uncoupling” (defined by a higher percentage of 5-minute intervals within 24 hours for which the HR standard deviation fell within the range 0.3 to 0.6 bpm) in trauma patients who died in the ICU, regardless of etiology of death [33]. Seely and colleagues at the University of Ottawa have developed a multi-parameter HR variability system. In a pilot study in bone-marrow-transplant patients, both SampEn and MSE (as well as other HR variability metrics) decreased prior to the clinical diagnosis of sepsis [34].

Finally, Moorman and colleagues [35] studied the impact of information about heart rate dynamics in the neonatal ICU setting. They have developed a real-time index, termed “heart rate characteristics” (HRC), which takes into consideration multiple features of the neonatal RR interval time series [36–37]. Their randomized controlled clinical trial included 3003 very low birth weight infants, a group at increased risk for sepsis [35]. It showed that physician access to the real-time HRC index was associated with a significant reduction in infant mortality, from 10.2% to 8.1%. Their finding that measures of heart rate dynamics in an newborn ICU setting can lead to decreased mortality--presumably by increasing clinicians’ situational awareness--is an important contribution to the emerging field of anticipatory medicine.

5. Limitations

Our study’s limitations include the relatively small sample size and the potential inaccuracies inherent in collecting data in a busy ED in a war zone. Of the 325 patients on whom some effort was made to collect ECGs under this protocol, only 70 patients had ECG of sufficient length and quality, as well as accompanying demographic data. Also, the imbalance in the number of patients in the two groups (12 LSI vs. 58 Non-LSI) may introduce selection bias. We were unable to determine the relationship between the timing of LSIs, and the timing of ECG collection. We also did not record whether patients received sedative medications during their ED care which could influence HR complexity. The problem of the timing of interventions is a recurring theme in this type of research, which must be addressed in future prospective study designs. Decreased mental status is associated with the performance of LSIs in this study, manifested by differences between LSI and Non-LSI patients on both GCS_total and GCS_motor. In the present study, the Non-LSI group is essentially a group with normal GCS_total and GCS_motor scores of 15±0 and 6±0, respectively. This observation is consistent with our previous findings in prehospital trauma patients [9]. Prehospital and post-ED data were also lacking. Unfortunately, prehospital data from the battlefield have been notoriously difficult to obtain. It will be of great interest to study changes in MSE and other heart rate variability measures over time, in response to therapy.

Finally, future studies should also employ real-time (as opposed to off-line, post hoc) calculation of HR complexity. Once a sufficient number of heart beats have been recorded, the entropy algorithms take only about 1 sec to run. SampEn computation can be performed as soon as the first 100 beats have been collected. MSE computation can then be added as soon as the first 800 beats have been collected, serially updating the estimates as more data become available. Based on work by Moorman, Seely, and others, we are confident that such real-time computation is technologically quite feasible [34–35].

6. Conclusions

The amount of complex irregularity in beat-to-beat fluctuations in the HR can be quantified by Sample Entropy (SampEn). Multiscale Entropy (MSE) extends this measure to progressively longer time scales. In this study, we found that lower Sample Entropy and Multiscale Entropy index were associated with the performance of lifesaving interventions in combat casualties arriving at an Emergency Department in a combat zone. We also found that careful selection of the r parameter based on the ECG sampling rate significantly improves the ability of both SampEn and MSE index to discriminate such patients. Prospective studies of these “new vital signs” are needed to establish their potential role in clinical assessment and management of critically-injured patients.