Abstract
Recent multielectrode array recordings in ganglionated plexi of canine atria have opened the way to the study of population dynamics of intrinsic cardiac neurons. These data provide critical insights into the role of local processing that these ganglia play in the regulation of cardiac function. Low firing rates, marked non-stationarity, interplay with the cardiovascular and pulmonary systems and artifacts generated by myocardial activity create new constraints not present in brain recordings for which almost all neuronal analysis techniques have been developed. We adapted and extended the jitter-based synchrony index (SI) to (1) provide a robust and computationally-efficient tool for assessing the level and statistical significance of SI between cardiac neurons, (2) estimate the bias on SI resulting from neuronal activity possibly hidden in myocardial artifacts, (3) quantify the synchrony or anti-synchrony between neuronal activity and the phase in the cardiac and respiratory cycles. The method was validated on firing time series from a total of 98 individual neurons identified in 8 dog experiments. SI ranged from −0.14 to 0.66, with 23 pairs of neurons with SI>0.1. The estimated bias due to artifacts was typically < 1%. Strongly cardiovascular- and pulmonary-related neurons (SI>0.5) were found. Results support the use of jitter-based synchrony index in the context of intrinsic cardiac neurons.
1. Introduction
The heart receives sympathetic and parasympathetic efferent innervation via the intrinsic cardiac nervous system (ICNS). Central neurons located in the medulla and in the spinal cord exert tonic influences on the ICNS (Armour et al. 1994, Ardell 2004). Populations of afferent neurons distributed throughout atrial and ventricular intrinsic cardiac ganglionated plexi transduce the milieu of the heart and adjacent major vessels (Armour and Kember 2004). It has been hypothesized that the ICNS acts as a local processor of information to coordinate regional cardiac indices under the tonic influence of central adrenergic and cholinergic efferent preganglionic neurons (Ardell 2004, Gray et al. 2004, Armour 1986). Its largest neuron population is expected to consist of local circuit neurons that are involved in such processing (Armour 1991, Armour and Ardell 2004), leading to the concept of “little brain in the heart” (Armour 2007, Armour 2008). The structure and function of the network formed by the local circuit neurons (inter-neurons in cardiac intrathoracic ganglia) is however still largely unknown.
To study this neural network, electrophysiological recordings in ganglionated plexi can be performed by inserting an electrode in the nervous tissue, enabling the measurement of extracellular potentials (spikes) generated by neuronal action potentials (Robinson 1968). Assigning recorded spikes to specific neurons (spike sorting) is a task that can be very challenging when only a single electrode is used (Lewicki 1998). Electrodes with multiple closely spaced recording sites enable population recordings with single-unit resolution and improve the ability to identify artifacts (Buzsaki 2004). While multichannel electrodes are commonly used in the central nervous system, recordings in intrinsic cardiac ganglia have been so far essentially limited to one or a few electrodes.
Recently, Beaumont et al. (2013) have simultaneously recorded the activity of 5 to 28 neurons in canine right atrium ganglionated plexi (RAGP) for more than 5 hours using linear multielectrode array technology. These new data open the way to the investigation of the organization of RAGP neuronal population and its interactions with the cardiovascular system. As compared to the analysis of recordings in the cortex, some particularities of the ICNS create additional challenges: (1) the electrode is placed directly on a beating heart and moves with it; (2) the electrode also senses the activity of the atrial myocardium just beneath the RAGP which may mask neuronal activity; (3) the firing rate of intrinsic cardiac neurons is relatively low (0.1 to 5 Hz typically) which requires careful statistical analysis; (4) intrinsic cardiac neuron activity is highly non-stationary, notably due to the modulation by the cardiovascular and pulmonary systems, and sometimes alternates between periods of low (or even silent) and high activity; (5) owing to low firing rates, synchrony among intrinsic cardiac neurons could possibly be small, so its quantification needs to remain applicable and sensitive at low values.
The objective of this paper is to quantify the synchronization between pairs of intrinsic cardiac neurons, as well as between these neurons and the cardiovascular and pulmonary systems. Several types of synchrony measures have been defined and used to characterize neuronal time series recorded in the brain (Brown et al. 2004, Pereda et al. 2005). These measures were typically based on a cross-correlogram (Perkel et al. 1967), event synchronization (Quian Quiroga et al. 2002), phase synchronization (Lachaux et al. 1999), mutual information (Borst and Theunissen 1999, Quian Quiroga and Panzeri 2009), firing pattern detection (Abeles and Gerstein 1988), principal component analysis (Chapin and Nicolelis 1999), or parametric modeling (Schneidman et al. 2006), to name a few. The reliability of the results produced by these measures needed to be assessed by thorough comparison with carefully generated surrogate data representing a given null hypothesis (Grun 2009). The majority of the aforementioned techniques assumed either sufficiently high firing rates (i.e. like in the brain), stationary neuronal activity, Poisson-distributed spike trains, or exploited the possibility to average over a large number of experiments (neuronal activity triggered by a stimulus). These assumptions unfortunately do not apply to RAGP neurons.
With the aim of providing a robust measure to quantify synchrony, Agmon (2012) developed a well-normalized synchrony index that is independent of variations in firing rate. The so-called jitter-based synchrony index relies on analytical formulas so that its statistical significance can be assessed without explicit generation of numerous surrogate spike trains. Furthermore, the analysis does not require the creation of arbitrary time bins that could lead to missed synchronized firing events. This issue becomes important at lower firing rates.
In this paper, we apply and extend Agmon’s approach to RAGP neurons in order to: (1) determine the level of synchrony between recorded RAGP neurons; (2) estimate the possible effect of blanked intervals created by myocardial activity on the synchrony index; (3) quantify how much input RAGP neurons receive from the cardiovascular and pulmonary systems.
2. Material and methods
2.1. Neuronal recordings and spike sorting
Eight mongrel dogs underwent bilateral open chest surgery in a study approved by the Institutional Animal Care and Use Committee of East Tennessee State University and described in detail in Beaumont et al. (2013). In this protocol, different mechanical, vascular, and electrical stressors were applied to elicit a neuronal response in the RAGP. The activity generated by neurons located in the RAGP was recorded for about 5 hours by means of a multichannel microelectrode array (Linear Microelectrode Array, MicroProbes Inc., Guithersberg, MD) in situ under anesthesia (α-chloralose) and controlled respiration (using an artificial respirator). This microelectrode array, consisting of 16 platinum/iridium electrodes (25 µm diameter electrode with an exposed tip of 2 mm; impedance 0.3–0.5 MΩ at 1 kHz), was embedded in the right atrial fat that contained the RAGP such that its tip was placed adjacent to right atrial myocardium. In addition, a bipolar electrode was sewn to the atrial myocardium close to the RAGP to provide a reference atrial electrogram and assist the identification of atrial activity in neuronal recordings. Left ventricular chamber pressure was continuously recorded using a pressure transducer catheter. Respiration cycles were monitored using a gauge pressure sensor in the exit tube of the respirator. The signals were digitized at a sampling frequency of 5.26 kHz (neuronal signals) or 0.877 kHz (other signals) via a Cambridge Electronics Design data acquisition system (model 1401).
Spike sorting was performed and validated using Spike2 software (Beaumont et al. 2013). Between 5 and 28 different neuronal waveforms were identified in each of the 8 dogs. When supra-threshold activity was simultaneously present in >2 channels, the spike was classified as myocardial electrical activity or motion artifact and all channels were blanked in a 26-ms window around that spike. This identification was validated using the right atrium electrogram.
The data used in this paper are: (1) for each neuron, the time series of spike timings; (2) the list of time intervals (26 ms long) that have been blanked in all neuronal signals; (3) the left ventricular pressure signal; and (4) the respiration pressure signal.
2.2. Coincidence detection
In the framework of Agmon’s approach, neuron synchronization is analyzed by pair of neurons. Since the synchrony index is not symmetric, one neuron is considered the reference and the other one the target (figure 1). During the interval of analysis, the reference neuron fires at times and the target neuron at times .
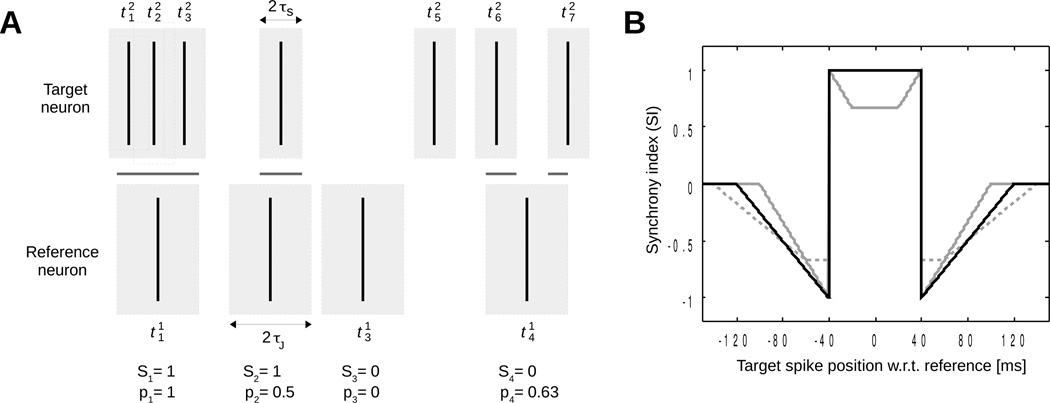
Figure 1.
Coincidence detection and synchrony index. (A) Two spike trains (target neuron and reference neuron . Gray rectangles around spikes of the target neuron represent windows for detecting coincidences (Si = 1) and those around spikes of the reference neuron represent jitter windows. The intersection between these two sets of windows (shown as horizontal gray lines) is associated with the pi values. Values of Si and pi are given below each spike of the reference neuron assuming πJ/τs = 2. (B) Synchrony index of two spikes as a function of the time interval between them (τs = 40 ms). Solid black line: πJ/τs = 2; solid gray line: πJ/τs = 1.5; dashed gray line: πJ/τs = 2.5.
Coincidence is defined as the reference and target neurons both firing within a time window of duration τs. For each spike i of the reference neuron, the occurrence of a coincidence is associated with the variable Si:
| (1) |
such that the number of coincidences is computed as:
| (2) |
Some of these coincidences may occur by pure chance. These random coincidences are identified by counting those remaining after random jitter of the spikes of the reference neuron within time windows of duration 2τJ, with the constraint τJ > τs. If the firing time of the i-th spike of the reference neuron is uniformly distributed in the interval [], the probability of coincidence is given by (see figure 1)
| (3) |
where μ(W) is the measure (total length) of the set W. Figure 1A depicts an example where the corresponding Si and pi values are given. The occurrence of coincidence after jitter is a Bernoulli random variable with mean pi. The number of random coincidences is:
| (4) |
Since the random variables are independent, the mean of is and its variance is . The exact probability distribution for can be computed iteratively by adding the Bernoulli variables one after the other: if the triangular matrix Pk,n, with 1 ≤ k ≤ n1 and 0 ≤ n ≤ k, is defined as (Agmon 2012)
| (5) |
then for 0 ≤ n ≤ n1, and obviously . This distribution will be used in the subsection 2.4 to test the statistical significance of coincidences.
2.3. Synchrony index
Agmon’s synchrony index SI is defined as
| (6) |
where β = τJ / (τJ − τs) if τJ ≥ 2τs and 2 otherwise. The factor β ensures that SI can reach its maximal value of 1 in case of perfect synchrony. Agmon (2012) demonstrated that the choice τJ = 2τs is the largest value for τJ that also guarantees maximal range of SI between −1 (anti-synchrony), 0 (no synchrony) and 1 (perfect synchrony). To illustrate that result, figure 1B shows the SI resulting from a single reference spike relative to one target spike plotted as a function of the target spike position for τJ/τs ratios of 1.5, 2 and 2.5. A ratio of 2 appears to be optimal, making it possible for SI to reach 1 in the case of perfect synchrony (delay = 0) and still attain a value of −1 for a delay of ±τs. Accordingly, we will use τJ = 2τs, and thus β = 2, for the rest of the paper, letting only one adjustable parameter (τs).
2.4. Synchrony detection
To test the hypothesis that the synchrony is not due to chance, the observed coincidence count is compared to the distribution of random coincidences. The p-value is defined as the probability that when SI > 0 and the probability that when SI < 0. The p-value can be computed using the exact distribution of (equation (5)). With low firing rates, pi values are often zero. Here, whenever the number of non-zero pi is smaller than 1000, we use the exact distribution for better accuracy. Otherwise, the distribution is approximately normal and to speed up computations the p-value is related to the Z-score:
| (7) |
For instance, p < 0.01 becomes Z > 2.326.
To roughly estimate how many spikes are necessary to perform the analysis, note that
| (8) |
Since is the sum of n1 terms, we may define . The variable sJ is bounded by:
| (9) |
The upper bound stems from the fact that 4pi (1 − pi) ≤ 1. For the lower bound, consider first the spike i of the reference neuron. If Si = 1, then from equation (3), 1/2 ≤ pi ≤ 1; indeed pi = 1/2 if there is a single single spike at a distance < τJ from spike i and pi > 1/2 when there are multiple spikes in this interval, see figure 1A. Therefore, β(Si − pi) ≤ 4pi(1 − pi), with β = 2 as usual. If Si = 0, β(Si − pi) ≤ 0 ≤ 4pi(1 − pi). After summation over i, we obtain the inequality (9).
In the case of anti-synchrony (SI < 0), we still have under reasonable assumptions. If Si = 1, β(pi − Si) ≤ 0 ≤ 4pi(1 − pi). If Si = 0 and pi ≤ 1/2, then β(pi − Si) ≤ 4pi(1 − pi) is verified, but not when Si = 0 and pi > 1/2. This case only occurs when two (or more) spikes of the target neuron are at a distance between τs and 2τs from spike i, one on each side. This might lead to −2 ≤ SI ≤ −1 in extreme cases. In our data, however, this situation (Si = 0, pi > 1/2) only occurred in less than 0.06% of the spikes in anti-synchronized pairs (because of the low firing rates), so was experimentally true.
In order to reach 1% significance (Z > Zth = 2.326), n1 needs to be larger than a threshold nth
| (10) |
Using the inequality (9), nth is bounded by:
| (11) |
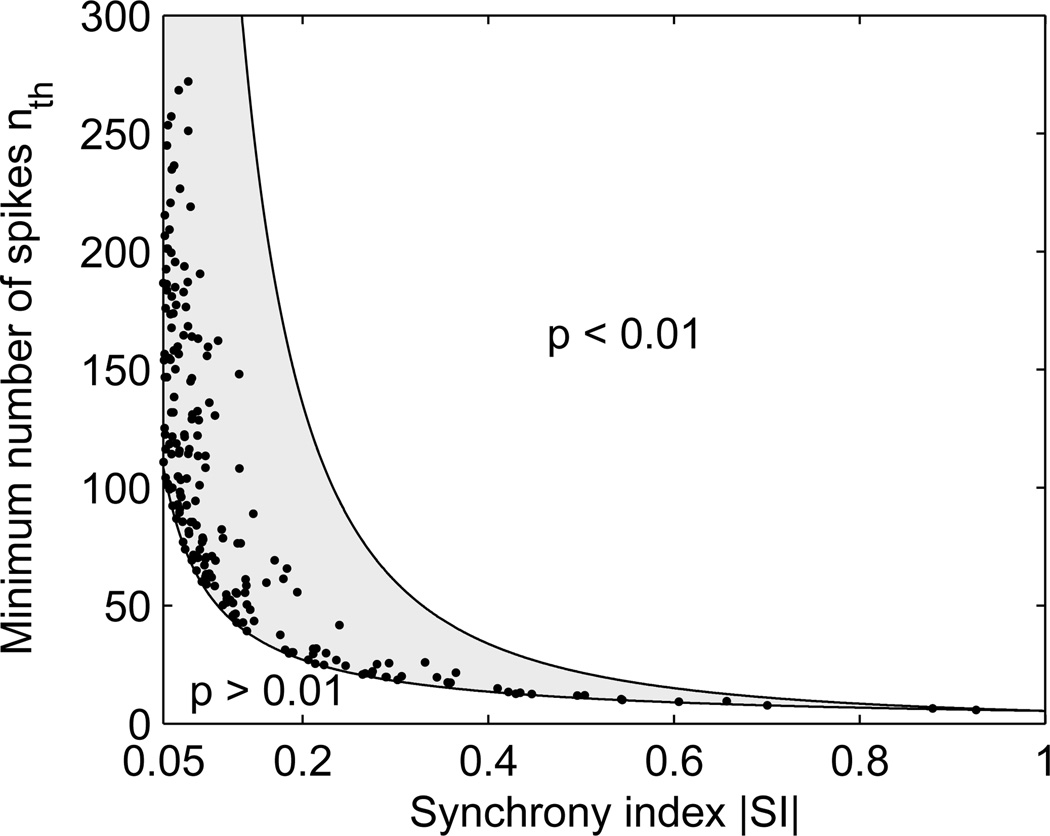
which gives the order of magnitude of the minimal signal length needed to identify a synchrony index of SI between a pair of neurons. Note that when nth is small, the approximation by a normal distribution may not be accurate. Figure 2 shows for all pairs of neurons in each dog the minimal number of spikes nth that would be needed to measure SI with 1% significance, computed using (10) with sJ and SI calculated from all available spikes in these signals. For all pairs of neurons investigated, nth lies between the theoretical bounds (11), typically closer to the lower bound.
Figure 2.
Number of spikes necessary to measure SI with 1% significance. Theoretical bounds are shown as solid lines. Dots are estimates based on experimental values for sJ and SI.
2.5. Effect of blanked intervals
When a set of short intervals are blanked due to the presence of large myocardial electrical activity or motion artifacts, the presence of spikes in these intervals may affect the measure of synchrony. We aim at quantifying this effect.
In the worst case scenario, these additional spikes would be purely randomly distributed. Suppose there are nb sorted disjoint blanked intervals [ak, bk] with ak < bk < ak+1 < bk+1. Spikes will be added only in the target neuron, not the reference neuron (each spike of the reference neuron is treated independently, so no interference between them is possible). This also avoids an artificial increase of synchrony that would occur if additional spikes were added to multiple neurons within the same blanked interval. In each interval [ak, bk], the probability πk of presence of a spike may be estimated from the local firing rate rk as πk = 1 −exp(−rk(bk − ak)), assuming a Poisson distribution on very short scale. Short interval lengths (typically 26 ms) and low firing rates make it very unlikely to have more than one spike in a blanked interval. Here, the local firing rate rk is estimated based on the average firing rate in a 4-sec window around the blanked interval.
The presence (= 1) or absence (= 0) of a spike in the interval [ak, bk] is denoted by ξk and its position by xk = ak + λk (bk − ak) where λk ∈ [0, 1]. We assume that ξk is a Bernoulli random variable with mean πk and that λk is uniformly distributed in the interval [0, 1]. The synchrony index taking into account these additional spikes is a random variable SIb = SIb ({ξl, λl}l=1,…,nb). Its mean is defined as:
| (12) |
Its variance can be defined the same way. This integral can be estimated using a Monte-Carlo approach. Due to large integration space dimension, many realizations of the random process are needed, resulting in long computational times. We will therefore seek an analytical formula.
If the blanked windows are sufficiently far from each other (ak+1 − bk > 2τs + 2τJ), the probability of coincidence of a spike in the reference neuron can only be affected by adding a spike in one single specific blanked window. What happens in the other blanked windows is irrelevant to this spike. Under these assumptions, and because we do not add spikes to the reference neuron (n1 remains the same), SIb can be decomposed into the sum of the synchrony index in the absence of blanked intervals (SI) and the separate, statistically independent effects of each window:
| (13) |
where depends only on the possible addition of a spike in the interval [al, bl]. The mean and the variance of SIb become:
| (14) |
| (15) |
since var(XY) = var(X)var(Y)+〈X〉2var(Y)+〈Y〉2var(X) for two independent variables X and Y. The mean and variance of are defined as:
| (16) |
To analytically compute these integrals, first note that the synchrony index SI is a piecewise linear function of the firing times {} and {}, as in the example of figure 1B. Suppose a spike is added to the target neuron at time t. Discontinuities in value or slope of SIb as a function of t can only occur: (1) when the additional spike creates a new coincidence, ; (2) when the coincidence window of the additional spike intersects with a jitter window, ; (3) when the coincidence window of the additional spike intersects with another coincidence window, . The set of possible discontinuities is therefore:
| (17) |
where ±ε indicates a possible discontinuity in value (we chose ε = 10−9). The set of discontinuities in the blanked interval [al, bl] is
| (18) |
where the bounds of the blanked interval have been added and all points have been sorted. The set Dl subdivides [al, bl] into ml sub-intervals [] in which is an affine function. After the transform , the function in each sub-interval is expressed as:
| (19) |
Then, the integrals can be computed analytically on each sub-interval and summed up:
| (20) |
| (21) |
These formulas are exact in the limit ε → 0, the error being bounded by ε (the jump is always ≤ 1). Note that ml is independent from ε.
2.6. Synchrony with respiratory inputs
Since respiration is mechanically controlled in our dog experiments, the duration of respiration cycles and the air pressure waveform associated with inspiration and expiration are very stable. To detect peak inspiratory pressure, the respiratory signal is first low-pass filtered and down-sampled at 50 Hz. Baseline correction is performed using a min-max filter (over a sliding time window of 8 s). Peaks are detected by thresholding. This provides for each dog a time series of peak inspiratory pressure .
Respiratory phase ϕr(t) is computed by setting , by linearly interpolating the phase in-between, and taking the value modulo 2π. This ensures that the phase is uniformly distributed over time. Then, synchrony between a neuronal time series and respiratory inputs can be assessed either by constructing the histogram of the values , or by computing the synchrony index between and . The respiration time series is treated as the “target neuron”. The corresponding SI represents the fraction of firings near peak inspiratory pressure (after correction for random coincidences).
2.7. Synchrony with cardiovascular inputs
In contrast with respiration, heart rate and blood pressure waveform are not always stable in our experiments. A more sophisticated approach is needed to define the cardiac phase. First, the left ventricular pressure (LVP) signal is low-pass filtered (cutoff at 10 Hz; used only to derive the phase), and corrected for baseline wandering using a min-max filter over a time window of 1 s (the mean between the min and max envelopes is averaged over 5 s sliding windows and subtracted), giving a signal PLV (t). Following an approach often used in cardiac electrophysiology (Iyer and Gray 2001), the cardiac phase ϕc(t) is defined as:
| (22) |
where atan2 denotes the four-quadrant inverse tangent. We used P0 = 0 since the mean of the filtered signal PLV (t) is close to zero, and Δt = 50 ms, a value close to the rising time of LVP. The resulting phase is shifted by a constant so that peak LVP approximately corresponds to ϕc = π. Finally, the phase signal is sorted in each cardiac cycle to ensure that ϕc(t) is strictly increasing even during diastole in the presence of noise.
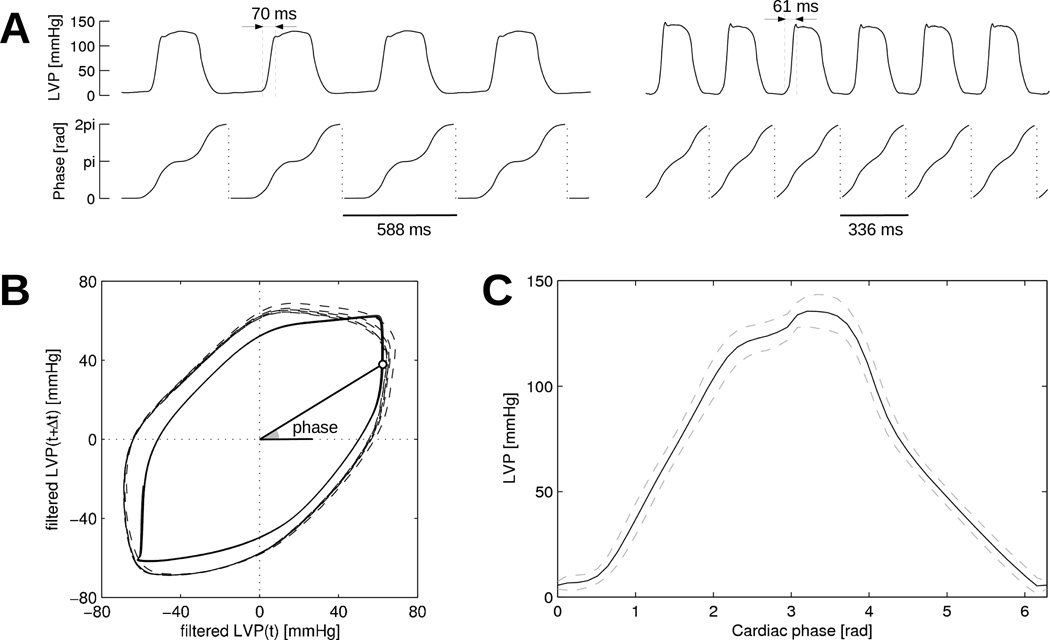
Figure 3 illustrates this process in two time segments with different heart rates in the same experiment. The mean LVP profile as a function of phase (panel C) constructed using the whole raw LVP signal shows little variability, thus demonstrating the robustness of the cardiac phase definition. Note that the LVP profile is distorted, that is, the cardiac phase is not uniformly distributed over time. For instance, LVP spends more time near phase 0 (diastole) that near phase π/2 (isovolumetric contraction).
Figure 3.
Determination of cardiac phase from left ventricular pressure (LVP). (A) LVP signal and corresponding cardiac phase in two time segments with slow (signals on the left) and fast (signals on the right) heart rates in the same dog. (B) Reconstruction of the cardiac phase. Solid line: slow heart rate signal from panel A; dashed line: fast heart rate. (C) Mean (solid line) and standard deviation (dashed lines) of LVP profile as a function of phase. Statistics are computed over the whole LVP signal.
From the cardiac phase signal, a time series can be generated for each value of the phase: {} is defined as {t | ϕc(t) = ϕ}, the time instants corresponding to the same stage in the cardiac cycle. The monotonicity of ϕc(t) ensures that {} contains exactly one spike per cardiac cycle. The synchrony index between these time series and each of the neuronal time series quantifies how much neuron firings tend to be synchronized with a particular cardiac phase (cardiovascular time series being treated as the “target neuron”). Another approach extending previous works (Beaumont et al. 2013) consists in computing the histogram of the values . Histogram equalization with respect to the histogram of ϕc(t) is however needed. For that purpose, the count in each bin is divided by the time ϕc(t) spends in that bin.
2.8. Implementation
The analysis software was implemented as a Matlab toolbox, with some critical parts of the code written in C and integrated as mex files. The synchrony index function was validated against Agmon’s program. After optimization, computing the synchrony index and p-value for 756 pairs of neurons (28 neurons from one dog; 4270 spikes/neuron on average) takes about 0.14 s on a standard computer. On the same data set, the estimation of the effect of blanked intervals (32,000 intervals of duration 26 ms) over the same 756 pairs takes 2.1 s using the analytical formula (equation (14)). With the Monte-Carlo approach (equation (12)), it takes about one day per million realizations.
3. Results
3.1. Synchrony between intrinsic cardiac neurons
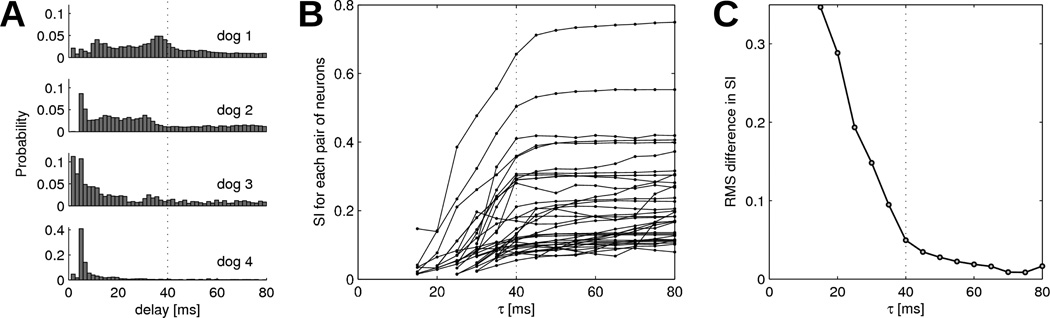
The only adjustable parameter in the synchrony index (SI) computation is τs, representing the half-duration of the coincidence window. To avoid overestimating the synchrony between neurons, we aim at identifying the smallest value of τs that provides sufficient robustness. Figure 4A shows in four dogs the histogram of time delay between each spike of each neuron and the nearest spike in any other neuron. The distributions for delays > 40 ms are relatively flat, suggesting that these are random coincidences and that τs ≤ 40 ms would be appropriate.
Figure 4.
Determination of appropriate values for τs. (A) Histogram of time delay between each spike and the nearest spike in any other neuron. In each dog, the distribution is constructed using all neurons. (B) SI as a function of τs for all pairs of neurons with statistically significant synchrony (p < 0.01). Pairs of neurons with SI < 0.05 when τs > 40 ms are not shown. (C) Convergence of SI values (pairs of neurons from panel B), computed as the root mean square (RMS) difference between SI at τs and its plateau value at τs = 80 ms.
This hypothesis is supported by figure 4B where the SI is calculated for each pair of neurons for τs values between 15 and 80 ms. For most pairs, SI converges to a stationary value when τs > 40 ms. This observation is quantified on figure 4C where the root mean square (RMS) difference in SI relative to the SI plateau value of each pair is plotted against τs. When τs is increased beyond 40 ms, there is not much gain in terms of RMS difference.
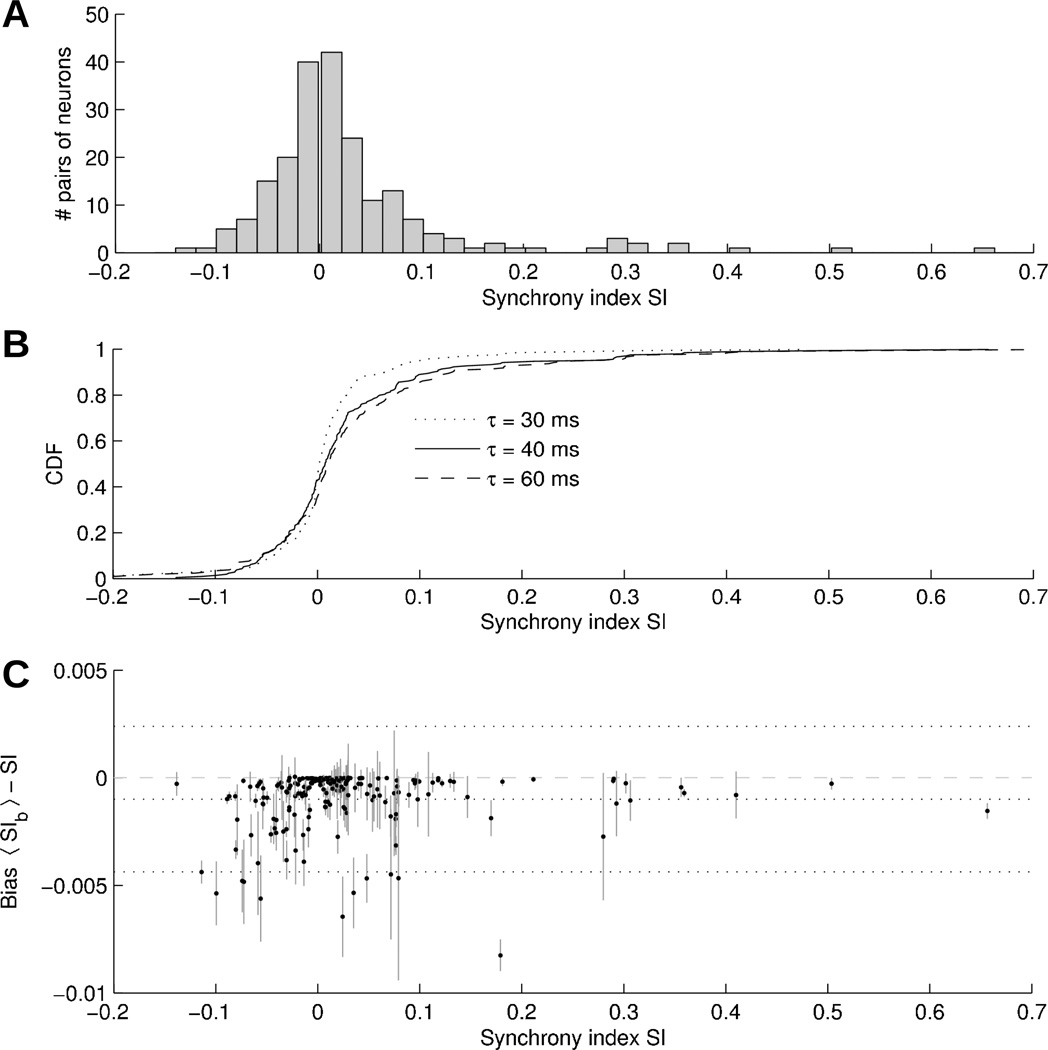
The distribution of SI values calculated for all pairs of neurons from all the experiments considered in this study is shown on figure 5A with τs set to 40 ms. Pairs of neurons with SI associated with a p-value > 0.01 are discarded. Most pairs of neurons are weakly synchronized (|SI| < 0.1), although no pair has |SI| < 0.002 (it would require more data to reach statistical significance). Note that (weakly) anti-synchronized (SI < 0) pairs are also observed. In the histogram, about 11% of statistically significant synchrony are such that SI > 0.1.
Figure 5.
(A) Histogram of SI values obtained in all pairs of neurons in all dogs using τs = 40 ms. Pairs are included only when synchrony is significant at p < 0.01 level. (B) Empirical cumulative distribution function (CDF) of SI values computed using τs = 30 ms (dotted line), τs = 40 ms (plain line), τs = 60 ms (dashed line). (C) Effect of blanked intervals on SI using the analytical formula: bias as a function of SI. Vertical gray lines represent the standard deviation of SIb. Horizontal dotted lines denote the mean bias as well as the 95% confidence interval.
From figure 4, it seems that τs = 60 ms would provide an even more robust estimate. Figure 5B compares the cumulative distribution functions (CDF) of SI values computed with τs = 30, 40 and 60 ms. By the Kolmogorov-Smirnov test, the difference between the CDFs with τs = 30 and 40 ms is statistically significant (p = 0.04), while the difference between τs = 40 and 60 ms is not (p = 0.41). The bias in |SI| obtained by increasing τs from 40 to 60 ms is 0.009 ± 0.029. As a result, more synchronized pairs have SI > 0.1 for τs = 60 ms (15% vs 11%).
3.2. Effect of blanked intervals on synchrony index
Figure 5C displays the effect of blanked intervals (due to myocardial activity) on synchrony index. The bias on SI, obtained by comparing SI with 〈SIb〉 resulting from the analytical formula (14), is plotted against SI. Spikes randomly added within the blanked intervals slightly reduce the SI. The mean bias is −0.001, with a standard deviation of 0.0017. For SI > 0.1, this corresponds to a relative error of <1%. Therefore, blanking atrial myocardial artifacts is not expected to significantly affect the identification of well-synchronized neurons.
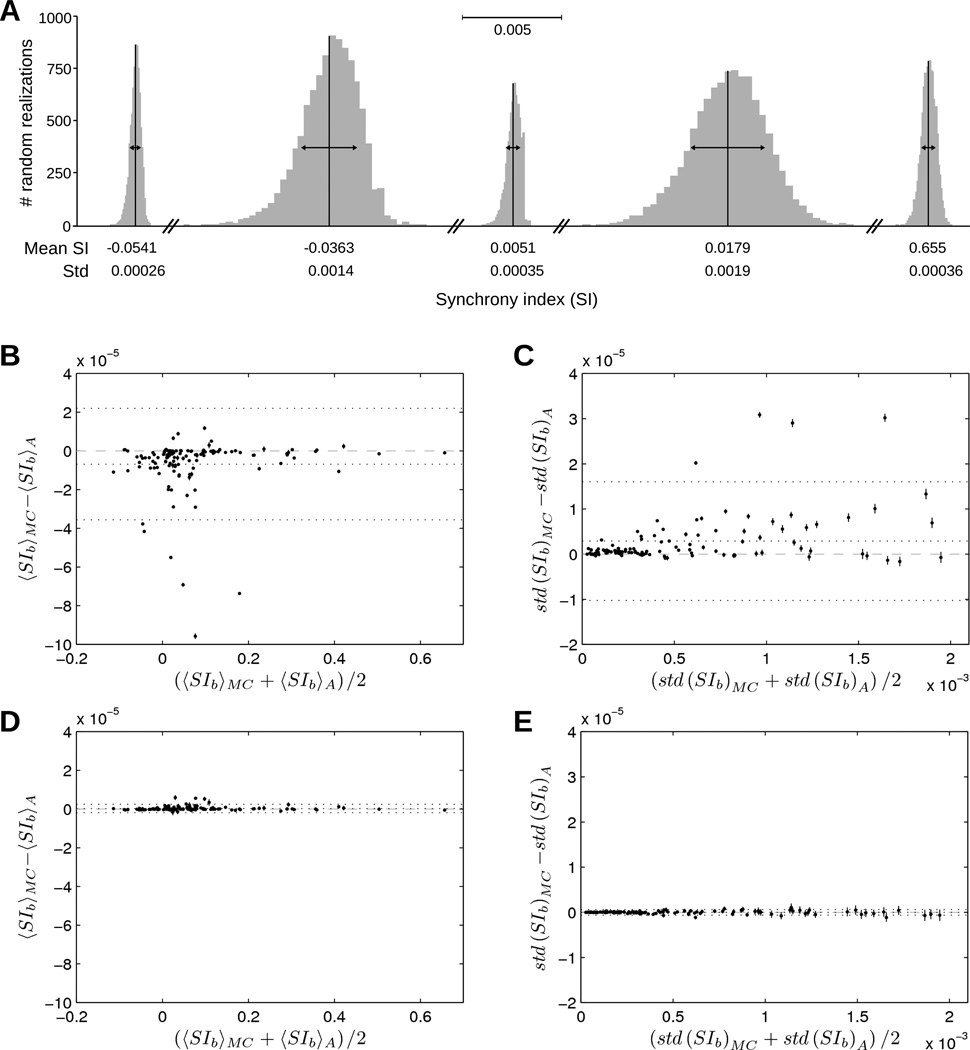
To validate our analytical formula for estimating the effect of blanked intervals, we evaluated the integral (12) using a Monte-Carlo approach. For every pair of neurons, each realization of the process consisted in randomly inserting a spike (with probability πk) in each interval [ak, bk] (position uniformly distributed) of the target neuron, followed by a recalculation of the SI on the whole signal. Examples of distributions resulting from 10,000 random realizations of the SI are shown on figure 6A for 5 pairs of neurons with different levels of synchrony. The shape of the distributions supports their characterization by their mean and standard deviation. The Monte-Carlo estimate of the integral with 1,500,000 realizations is compared to the analytical formula in figures 6B–C using a Bland-Altman plot. A large number of realizations is required since the dimension of the integration domain is of the order of 10,000. The small differences observed (<0.1% for the mean and <1% for the standard deviation) support the use of our analytical approach, thus considerably reducing computational expense. The interference between blanked intervals (i.e., when the condition ak+1 − bk > 2τs + 2τJ is not satisfied, which occurs in about 2% of the blanked intervals) typically slightly decreases the synchrony index and increases its variability (figures 6B–C). When these intervals are discarded (i.e., πk is set to 0 where ak+1 − bk < 2τs + 2τJ), the analytical formula and the Monte-Carlo estimate give essentially the same result (figures 6D–E).
Figure 6.
Estimating the effect of blanked intervals on SI. (A) Distribution of SIb values obtained after 10,000 realizations of random insertions of spikes within the blanked intervals. Mean and standard deviation (std) of SIb are indicated below each distribution. (B) Bland-Altman plot showing the difference in mean(SIb) between the Monte-Carlo (MC) formula (12) computed using 150 runs of 10,000 realizations and the analytical (A) formula (14). The mean over these 150 runs (dots) and their standard error of the mean (error bar) are shown. Horizontal dotted lines indicate the mean bias and 95% confidence interval. (C) Same Bland-Altman plot as panel B for the standard deviation of SIb. (D)–(E) Same plots as panels B–C after blanked intervals too close to each other (ak+1 − bk < 2τs + 2τJ) have been discarded.
3.3. Synchrony with respiratory inputs
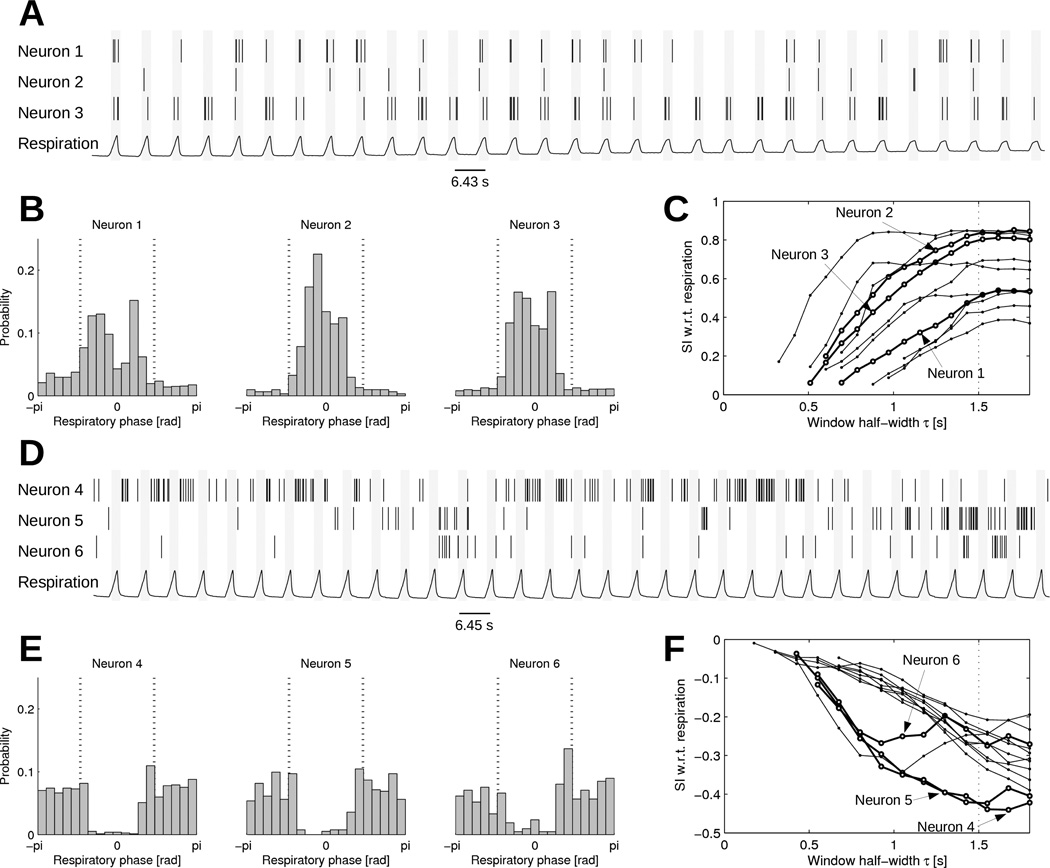
The synchronization of neurons with the respiratory signal was investigated in the first two hours of each recordings, before the experiment involves too many confounding factors (Beaumont et al. 2013). Figure 7 shows examples of neuronal activity synchronized and anti-synchronized with (inhibited by) respiration. Histograms of spike count as a function of respiratory phase (panels B and E) clearly demonstrate the effect of respiratory inputs. In panel B, neurons 1, 2 and 3 fire more frequently during high respiration pressure, with neuron 2 showing the sharpest phase locking. A subgroup of neurons have a clear propensity to fire when the respiration pressure is low (panel E). To facilitate automatic classification of respiratory-related neuronal activity, the synchrony index with respect to respiration can be computed (panels C and F). The relation between SI and τs suggests that the value τs = 1.5 s is appropriate to compute the SI since the value reaches a plateau. The resulting SI at τs = 1.5 s ranged from −0.4 to 0.8. Note that at longer τs, the SI would come back to zero because random coincidences become unavoidable when τs is longer than half the respiratory period.
Figure 7.
Synchrony with respiratory inputs. (A) Spike train time series of three selected neurons synchronized with respiration, aligned with the respiration signal. (B) Histograms of , i.e. the respiratory phase at the time of each spike. The vertical dotted lines indicate a 3-s time window around peak inspiratory pressure (phase = 0). (C) SI with respect to respiration as a function of τs. The thicker lines represent the three selected neurons. Non-statistically significant SI values (p > 0.01) are not shown. (D) Spike train time series of three selected neurons anti-synchronized with respiration, aligned with the respiration signal (in a different dog from panel A). (E) Histograms of , i.e. the respiratory phase at the time of each spike. (F) SI with respect to respiration as a function of τs in neurons anti-synchronized with respiration.
3.4. Synchrony with cardiovascular inputs
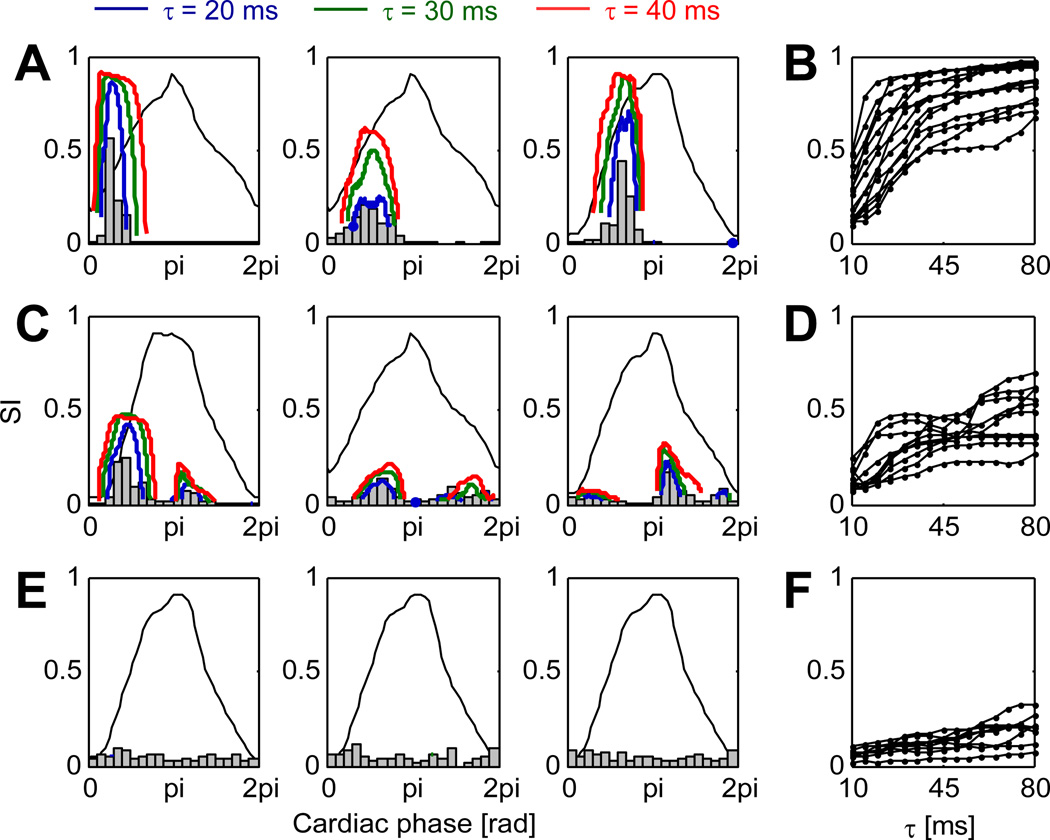
Intrinsic cardiac neurons are known to receive inputs from the cardiovascular system (Ardell 2004), notably through baroreceptors. To quantify this effect and classify neurons according to their synchrony with cardiovascular input, histograms of spike count as a function of cardiac phase is shown in figure 8 for three types of neurons (Beaumont et al. 2013): cardiovascular-related neurons firing during a specific phase of the cardiac cycle (panel A), cardiovascular-related neurons firing during more than one phase of the cardiac cycle (panel C), and non-cardiovascular-related neurons (panel E). The synchrony index curves as a function of cardiac phase (panels A,C,E) are in agreement with the histograms. In addition, these curves improve phase resolution and provide a p-value to assess statistical significance. Note that in panel A, the three neurons appear to fire at a different level of LVP. In the investigated population of 98 neurons, 56 were cardiovascular-related. Among those, 21 exhibited strong synchrony (SI > 0.5; panel A) at some phase value, while 35 were also synchronized with LVP, but to a lesser extent (panel B). The remaining 42 neurons had low synchrony values (SI < 0.2; panel C) or their firing rate was too low to reach statistical significance. From the sensitivity study for the parameter τs (panels B,D,F), the choice τs = 40 ms seems reasonable. The coincidence window (2τs = 80 ms) is of the order of magnitude of the rising time of LVP (figure 3).
Figure 8.
Synchrony with cardiovascular inputs. (A) Histogram of , i.e. the cardiac phase at the time of each spike, for three cardiovascular-related neurons firing during one specific phase of the cardiac cycle. Thick solid lines show the synchrony index (for three values of τs = 20, 30 and 40 ms) as a function of cardiac phase. Non-significant data points (p > 0.01) are discarded. The thin solid line represents the profile of left ventricular pressure as a function of cardiac phase. (B) Peak value of the synchrony index (SI) with respect to cardiac phase as a function of τs for a set of neurons of the type shown in panel A. (C) Same as panel A for cardiovascular-related neurons firing at more than one phase of the cardiac cycle. (D) Same as panel B for neurons of the type of panel C. (E) Same as panel A for non-cardiovascular-related neurons. (F) Same as panel B for neurons of the type of panel E.
4. Discussion and conclusion
We have adapted and extended Agmon’s jitter-based synchrony index for its application to intrinsic cardiac neurons. The main advantages of this measure of synchrony in our context are: (1) since the index is adequately normalized between −1 and 1, it enables the comparison between experiments, e.g. pooling data from different dogs; (2) synchrony detection is performed through a well-defined p-value computed using an analytical formula, without the need to run time-consuming tests on many realizations of surrogate data; (3) there is no stationarity assumption (jitter-based surrogates preserve local firing rate) and the index is almost independent from firing rate (Agmon 2012), which can vary a lot in intrinsic cardiac neurons, notably in response to cardiovascular events (Beaumont et al. 2013); (4) the method does not rely on inter-spike intervals, so the presence of short blanked intervals is not a problem, and the analysis of multiple time segments (e.g. successive episodes of arrhythmia) may be pooled together to increase statistical significance. In addition, we have developed a technique for taking into account the uncertainty resulting from the presence of blanked intervals, and have derived theoretical bounds to estimate the signal duration needed for statistical analysis.
The computation of SI depends on a single parameter, τs. Sensitivity analysis was systematically performed to find the smallest value of τs that gives sufficient robustness; τs = 40 ms was chosen. Larger values (e.g. τs = 60 ms) could be used to further improve robustness, with limited impact on SI values (figure 5B). Too large values for τs may however overestimate the SI and rely on synchrony windows beyond physiological relevance. More generally, it would be advisable to perform a sensitivity analysis for each specific application of the synchrony index, as the time scale of the underlying physiological processes may vary.
Note that SI only quantifies synchrony. It does not provide any information about causality. Constructing the histogram of time delay between the activations of two neurons may provide such evidence, as illustrated by one example in Beaumont et al. (2013), but synchrony may be due to a common input, for instance from the vagal nerve. A way to further investigate this issue would be to analyze the timing of the coincidences between these neurons in relation to cardiac or respiratory activity. This analysis may also rely on the synchrony index, as we did for left ventricular pressure.
Synchrony indices were computed over the entire signal. This measures long-term synchronization between the activity of neurons. At a shorter time scale, however, synchrony may be stronger or weaker, depending notably on changes in autonomic, central, cardiovascular and pulmonary inputs, or upon application of specific stressors. Figure 2 shows that with a firing rate of 1 Hz, a few minutes of neuronal activity are needed to identify synchrony index in the 0.1–0.2 range (at 1% significance), while shorter signals may be sufficient when synchrony is stronger. When firing rate is even slower (e.g. baseline activity in an anesthetized animal), longer time intervals would be required for the analysis.
In our data, the presence of blanked intervals due to myocardial activity masking neuronal activity introduced only a very minor negative bias to the synchrony index and small uncertainty (standard deviation). This stems from the fact that the total length of blanked intervals contributed to about 2–3% of signal duration. Note that it would be possible to estimate the relative contributions of artifacts and myocardial activity to the bias of synchrony index. Since the artifacts typically represented < 10% of the blanked intervals, they are expected to have very little influence on the SI. Estimating the effect of blanking becomes more critical during an atrial arrhythmia, where up to 15–20% of the signal may have to be blanked. Salavatian et al. (2013) explored the possibility of canceling artifacts or atrial activity instead of blanking them. This opens the way for extensions of our technique. Instead of relying on local rate, the probability πk of observing a spike in the blanked interval may be updated after artifact cancellation. In the best case scenario, cancellation would be perfectly reliable and no blanked interval would be necessary. Realistically, in many cases, πk may be set to zero if there is clearly no supra-threshold activity. When a neuronal activity is detected but its waveform extracted from within the artifact is too corrupted for reliable classification, the position λk would be fixed while the probability of occurrence ξk would be equiprobable among neurons of that channel. The uncertainty on the synchrony index would be further reduced after incorporating this information.
The synchrony index can also be used to identify and quantify synchronization with respiratory and cardiovascular inputs. Other possible applications include assessing direct response to nerve stimulation. The SI values obtained are qualitatively in agreement with histograms as used in Beaumont et al. (2013). A critical advantage over histogram-based methods is that the occurrence of random coincidences is taken into account and statistical significance can be determined. This is particularly important when a neuron receives inputs from multiple sources (e.g. inter-neuron), resulting in a lower SI value. In addition, avoiding the use of bins enables higher time resolution, while replacing bin size with another parameter, τs, that can be related to physiological parameters such as the rising time of left ventricular pressure.
The investigated population of intracardiac neurons has been hypothesized to be mostly composed of local circuit neurons (Beaumont et al. 2013). These neurons are believed to receive, process and coordinate multiple secondary inputs (e.g. cardiovascular, respiratory, regional control) dynamically. The synchrony index provides a tool to estimate how much input a (presumably) local circuit neuron indirectly receives from baroreceptors. This leads to a better classification and characterization of the neuron population. The synchrony index could also form the basis for the analysis and the quantification of neuron population dynamics in control conditions as well as in response to clinically-relevant interventions, such as (possibly long-term) vagal nerve stimulation, that may affect the coherence of intrinsic cardiac neuron activity. This would enable us to determine if these interventions have a direct effect on the intrinsic cardiac nervous system or if their mechanisms rely on different pathways.
In summary, our results support the use of jitter-based synchrony index in the context of intrinsic cardiac neurons. Analytical formulas were derived for computing the distribution of synchrony index of surrogates, the p-value, the minimum signal length needed to reach statistical significance and the effect of blanked intervals, which makes this approach robust and computationally efficient.
Acknowledgments
The authors thank Ariel Agmon (West Virginia University) for sending us a MathCAD version of his synchrony index code and Alain Vinet (Université de Montréal) for his valuable suggestions and comments. This work was supported by the Natural Sciences and Engineering Research Council of Canada (V.J.), by the Fonds de Recherche du Québec – Santé (V.J.) and by NIH grant HL71830 (J.L.A.).
References
- Abeles M, Gerstein GL. Detecting spatiotemporal firing patterns among simultaneously recorded single neurons. J Neurophysiol. 1988;60(3):909–924. doi: 10.1152/jn.1988.60.3.909. [DOI] [PubMed] [Google Scholar]
- Agmon A. A novel, jitter-based method for detecting and measuring spike synchrony and quantifying temporal firing precision. Neural Syst Circuits. 2012;2(1):5. doi: 10.1186/2042-1001-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardell JL. Intrathoracic neuronal regulation of cardiac function. In: Armour JA, Ardell JL, editors. Basic and Clinical Neurocardiology. New York: Oxford University Press; 2004. [Google Scholar]
- Armour JA. Activity of in situ stellate ganglion neurons of dogs recorded extracellularly. Can J Physiol Pharmacol. 1986;64(2):101–111. doi: 10.1139/y86-016. [DOI] [PubMed] [Google Scholar]
- Armour JA. Anatomy and function of the intrathoracic neurons regulating the mammalian heart. In: Zucker IH, Gilmore JP, editors. Reflex Control of the Circulation. Boca Raton, FL: CRC Press; 1991. pp. 1–37. [Google Scholar]
- Armour JA. The little brain on the heart. Cleve Clin J Med. 2007;74(Suppl 1):S48–S51. doi: 10.3949/ccjm.74.suppl_1.s48. [DOI] [PubMed] [Google Scholar]
- Armour JA. Potential clinical relevance of the ’little brain’ on the mammalian heart. Exp Physiol. 2008;93(2):165–176. doi: 10.1113/expphysiol.2007.041178. [DOI] [PubMed] [Google Scholar]
- Armour JA, Ardell JL. Basic and Clinical Neurocardiology. New York: Oxford University Press; 2004. [Google Scholar]
- Armour JA, Huang MH, Pelleg A, Sylven C. Responsiveness of in situ canine nodose ganglion afferent neurones to epicardial mechanical or chemical stimuli. Cardiovasc Res. 1994;28(8):1218–1225. doi: 10.1093/cvr/28.8.1218. [DOI] [PubMed] [Google Scholar]
- Armour JA, Kember GC. Cardiac sensory neurons. In: Armour JA, Ardell JL, editors. Basic and Clinical Neurocardiology. New York: Oxford University Press; 2004. [Google Scholar]
- Beaumont E, Salavatian S, Southerland EM, Vinet A, Jacquemet V, Armour JA, Ardell JL. Network interactions within the canine intrinsic cardiac nervous system: implications for reflex control of regional cardiac function. J Physiol. 2013;591(Pt 18):4515–4533. doi: 10.1113/jphysiol.2013.259382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borst A, Theunissen FE. Information theory and neural coding. Nat Neurosci. 1999;2(11):947–957. doi: 10.1038/14731. [DOI] [PubMed] [Google Scholar]
- Brown EN, Kass RE, Mitra PP. Multiple neural spike train data analysis: state-of-the-art and future challenges. Nat Neurosci. 2004;7(5):456–461. doi: 10.1038/nn1228. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Large-scale recording of neuronal ensembles. Nat Neurosci. 2004;7(5):446–451. doi: 10.1038/nn1233. [DOI] [PubMed] [Google Scholar]
- Chapin JK, Nicolelis MA. Principal component analysis of neuronal ensemble activity reveals multidimensional somatosensory representations. J Neurosci Methods. 1999;94(1):121–140. doi: 10.1016/s0165-0270(99)00130-2. [DOI] [PubMed] [Google Scholar]
- Gray AL, Johnson TA, Ardell JL, Massari VJ. Parasympathetic control of the heart. ii. a novel interganglionic intrinsic cardiac circuit mediates neural control of heart rate. J Appl Physiol. 2004;96(6):2273–2278. doi: 10.1152/japplphysiol.00616.2003. [DOI] [PubMed] [Google Scholar]
- Grun S. Data-driven significance estimation for precise spike correlation. J Neurophysiol. 2009;101(3):1126–1140. doi: 10.1152/jn.00093.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyer AN, Gray RA. An experimentalist’s approach to accurate localization of phase singularities during reentry. Ann Biomed Eng. 2001;29(1):47–59. doi: 10.1114/1.1335538. [DOI] [PubMed] [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J, Varela FJ. Measuring phase synchrony in brain signals. Hum Brain Mapp. 1999;8(4):194–208. doi: 10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewicki MS. A review of methods for spike sorting: the detection and classification of neural action potentials. Network. 1998;9(4):R53–R78. [PubMed] [Google Scholar]
- Pereda E, Quiroga RQ, Bhattacharya J. Nonlinear multivariate analysis of neurophysiological signals. Prog Neurobiol. 2005;77(1–2):1–37. doi: 10.1016/j.pneurobio.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Perkel DH, Gerstein GL, Moore GP. Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys J. 1967;7(4):419–440. doi: 10.1016/S0006-3495(67)86597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quian Quiroga R, Kreuz T, Grassberger P. Event synchronization: a simple and fast method to measure synchronicity and time delay patterns. Phys Rev E. 2002;66(4 Pt 1):041904. doi: 10.1103/PhysRevE.66.041904. [DOI] [PubMed] [Google Scholar]
- Quian Quiroga R, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat Rev Neurosci. 2009;10(3):173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Robinson DA. The electrical properties of metal microelectrodes. Proc IEEE. 1968;56(6):1065–1071. [Google Scholar]
- Salavatian S, Vinet A, Beaumont E, Armour JA, Ardell JL, Jacquemet V. Recording and identification of cardiac neuron activity in the right atrium ganglionated plexus. Computing in Cardiology. 2013;Vol. 40:1191–1194. [Google Scholar]
- Schneidman E, Berry MJ, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature. 2006;440(7087):1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]