Abstract
Many cognitive and clinical neuroscience research studies seek to determine how contextual factors modulate cognitive processes. In fMRI, hypotheses about how context modulates distributed patterns of information processing are often tested by comparing functional connectivity between neural regions A and B as a function of task condition X and Y, which is termed context-modulated functional connectivity (FC). There exist two exploratory statistical approaches to testing context-modulated FC: the beta-series method and psychophysiological interaction (PPI) analysis methods. While these approaches are commonly used, their relative power for detecting context-modulated FC is unknown, especially with respect to real-world experimental parameters (e.g., number of stimulus repetitions, inter-trial-interval, stimulus duration, etc). Here, we use simulations to compare power for detecting context-modulated FC between the standard PPI formulation (sPPI), generalized PPI formulation (gPPI), and beta series method. Simulation results demonstrate that gPPI and beta series method are generally more powerful than sPPI. Whether gPPI or beta series method performed more powerfully depended on experiment parameters: block designs favor the gPPI, whereas the beta series method was more powerful for designs with more trial repetitions and it also retained more power under conditions of hemodynamic response function variability. On a real data set of adolescent girls, the PPI methods appeared to have greater sensitivity in detecting task-modulated FC when using a block design and the beta series method appeared to have greater sensitivity when using an event-related design with many trial repetitions. Implications of these performance results are discussed.
Keywords: fMRI, functional connectivity, psychophysiological interaction analysis
Cognitive and clinical neuroscience theories generally hypothesize that the pattern of information processing between neural regions should vary depending on the context or cognitive process being performed. For example, the widely cited conflict monitoring and cognitive control theory (Botvinick, Braver, Barch, Carter, & Cohen, 2001) posits that the degree to which the dorsal anterior cingulate cortex elicits adjustments in top-down cognitive control in the dorsolateral prefrontal cortex (PFC) depends on the degree of cognitive conflict detected in the present context. In fMRI, these types of hypotheses are often tested experimentally through tests of context-modulated functional connectivity (FC). Indeed, careful experimentation has found that the degree of FC between the lateral PFC and the fusiform gyrus during a face processing task depends on whether or not cognitive control is experimentally manipulated to be high or low, thus providing evidence that top-down cognitive control resolves conflict by biasing processing of task-relevant information (Egner & Hirsch, 2005). This specific example highlights the larger concept that testing context-modulated FC in fMRI is an essential method for testing cognitive and clinical neuroscience theories. Given the obvious importance of testing hypotheses about context-modulated FC, it is essential that researchers have an understanding of the power of existing methods to detect true differences in context-modulated FC.
The purpose of the present series of experiments is to compare the power for detecting context-modulated FC between three common methods for testing context-modulated FC. Psychophysiological interaction (PPI) analysis was the first proposed exploratory method for testing hypotheses about context-modulated FC developed by Friston and colleagues 15 years ago (Friston, et al., 1997). The PPI framework follows the standard GLM framework for testing moderation (Baron & Kenny, 1986): in a three variable moderation model, the dependent variable y is regressed simultaneously onto the main effects of independent variable x and moderator m as well as on the interaction term computed as the product of x and m. In the context of fMRI, x and y are BOLD timecourses from voxels or region-of-interests and m is a contrast vector from the experimental task design matrix. Hypotheses about whether the relationship between x and y varies as a function of the task is tested through the significance of the β coefficient for the interaction term; that is, the β coefficient for the interaction term indicates the degree to which the relationship between the two neural regions differs depending on the context. One problem with the original formulation of PPI analyses is that the hypothesized interaction occurs at the neural level of analyses, while the statistical test occurs following a hemodynamic filter at the BOLD level of analysis (Gitelman, Penny, Ashburner, & Friston, 2003), which consequently makes the interaction term imprecise. Hemodynamic deconvolution was therefore introduced to estimate neuronal events from x, use these estimates to calculate the interaction term, then re-convolved the interaction term with a hemodynamic response function to create a predictor at the BOLD level of analysis. However, one prior simulation study of a block design suggested that deconvolution had little impact on sensitivity to detect context-modulated FC (Kim & Horwitz, 2008). Another problem, as pointed out more recently (McLaren, Ries, Xu, & Johnson, 2012), the standard PPI (sPPI) formulation does not span the entire space of the experimental design. That is, the PPI term is computed only as the product of the deconvolved neural estimates and the contrast vector of interest (e.g., contrast between condition 1 and 2). A subsequent simulation study found that computing a separate PPI term for each task condition, and then contrasting the resulting β coefficient for each separate PPI term (i.e., generalized PPI; gPPI), yielded more accurate estimates of context-modulated FC compared to the sPPI formulation (McLaren, et al., 2012). Comparisons of context-modulated FC on the same real fMRI dataset suggested increased sensitivity of the gPPI method compared to the sPPI (McLaren, et al., 2012).
An alternative exploratory method for testing hypotheses about context-modulated FC was later proposed by Rissman and colleagues (Rissman, Gazzaley, & D'Esposito, 2004) and termed the beta series correlation method. In this approach (referred to as the beta series method [BSM] henceforth), each individual trial, as opposed to each condition, is entered as a separate regressor in the standard GLM design matrix. This yields a β estimate of % BOLD signal change for each individual trial. Differences in connectivity between task conditions are assessed by comparing the magnitude of correlations in β estimates between conditions. For example, in a task presenting 30 faces and 30 houses, a β coefficient would be estimated for each trial (60 β estimates). FC between two regions during face viewing would be assessed by correlating the β estimates only for the face trials (30 β estimates) between the two regions. The magnitude of this correlation would then be compared to the magnitude of correlation in β estimates observed between the regions during house viewing. Note that this approach is strikingly different than PPI-based methods: PPI can be considered as a simple approximation to a dynamic system model1 that is at equilibrium during measurement (Friston, Harrison, & Penny, 2003; Stephan, 2004), where the task and fMRI signals are treated as simultaneous and bidirectional timeseries. By contrast, the BSM is not based on a system model of brain function and instead simply attempts to 1) isolate each brain regions’ response to the different aspects of the task, and then, separately, 2) characterize the covariance between these estimates of the brain regions’ responses during different aspects of the task (also see the vastly different graphical depictions of the different methods in Figures 1, 2, and 3). The BSM approach is less commonly used relative to the PPI method, though initial studies suggested its validity (Rissman, et al., 2004) and subsequent studies have used it successfully (Chadick & Gazzaley, 2011; Kalkstein, Checksfield, Bollinger, & Gazzaley, 2011; Rissman, Gazzaley, & D'Esposito, 2008). Further, no study has compared its power for detecting context-modulated FC with the sPPI or gPPI method.
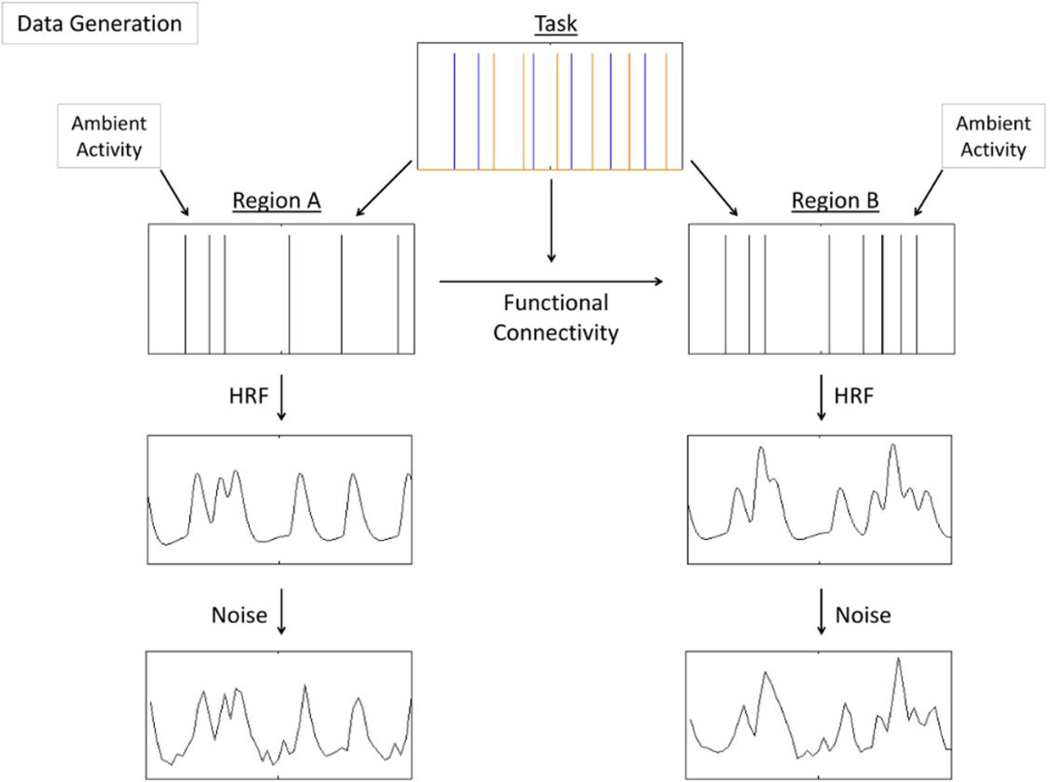
Figure 1.
For each simulation, a task with two stimulus conditions was randomly generated (shortened task sequence depicted). This task induced neural events probabilistically in two simulated neural regions, A and B. Region A then induced a lagged neural event in region B with some probability (i.e. functional connectivity strength), and this probability was dependent on the task condition that produced the original neural event in region A. Additionally, in some experiments, each region also displayed task-unrelated ambient activity between stimuli presentations. The neural events of each region were then convolved with the canonical hemodynamic response function (HRF) and random noise was added, resulting in the BOLD signal of two regions with context dependent functional connectivity.
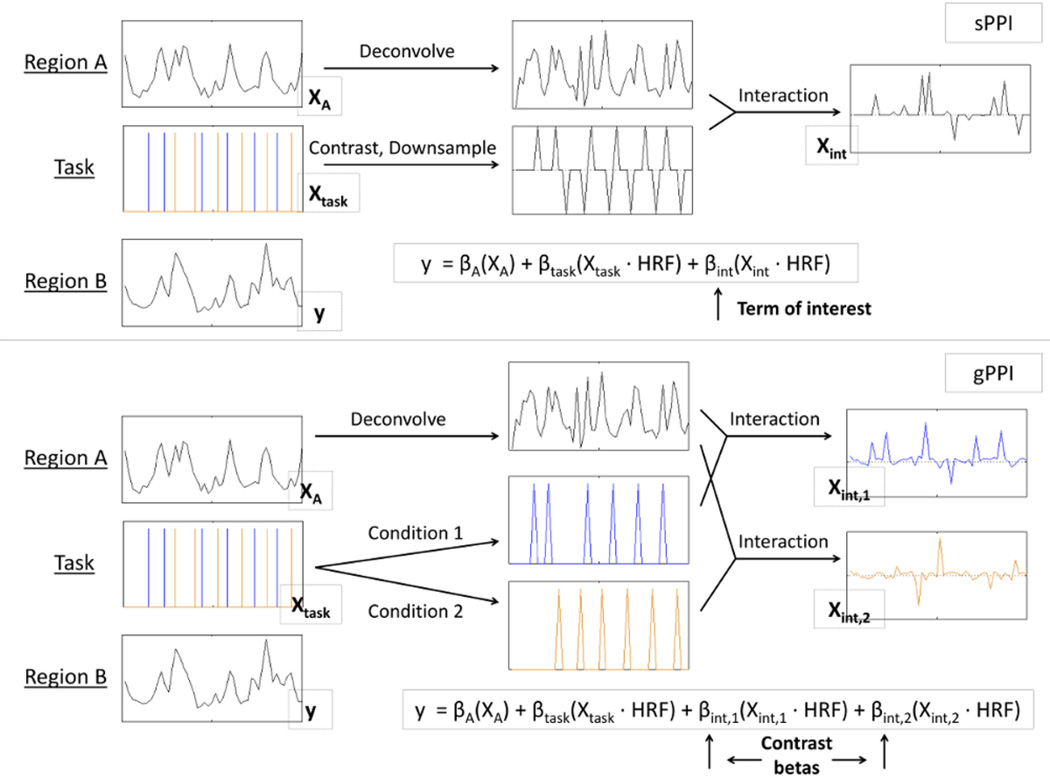
Figure 2.
Standard psychophysiological interaction (sPPI) provides a single interaction term describing the extent to which task conditions affect the functional connectivity between two regions. This term, βint, is obtained by first contrasting the task conditions and multiplying this contrast vector with the deconvolved neural event estimates of region A. This interaction term, Xint, is then convolved with the HRF and used as a predictor of region B’s BOLD activity in a multiple regression model that also includes the direct effect of the task, Xtask, and of region A, XA. Generalized PPI (gPPI) is similar to sPPI, except that instead of contrasting the stimulus conditions, the stimulus conditions are separated and each condition interacts with the neural event estimates of region A. Therefore the resulting model contains two interaction terms, βint,1, and βint,2, representing the functional connectivity for each stimulus condition. These betas are contrasted to obtain a measure of context-modulated functional connectivity.
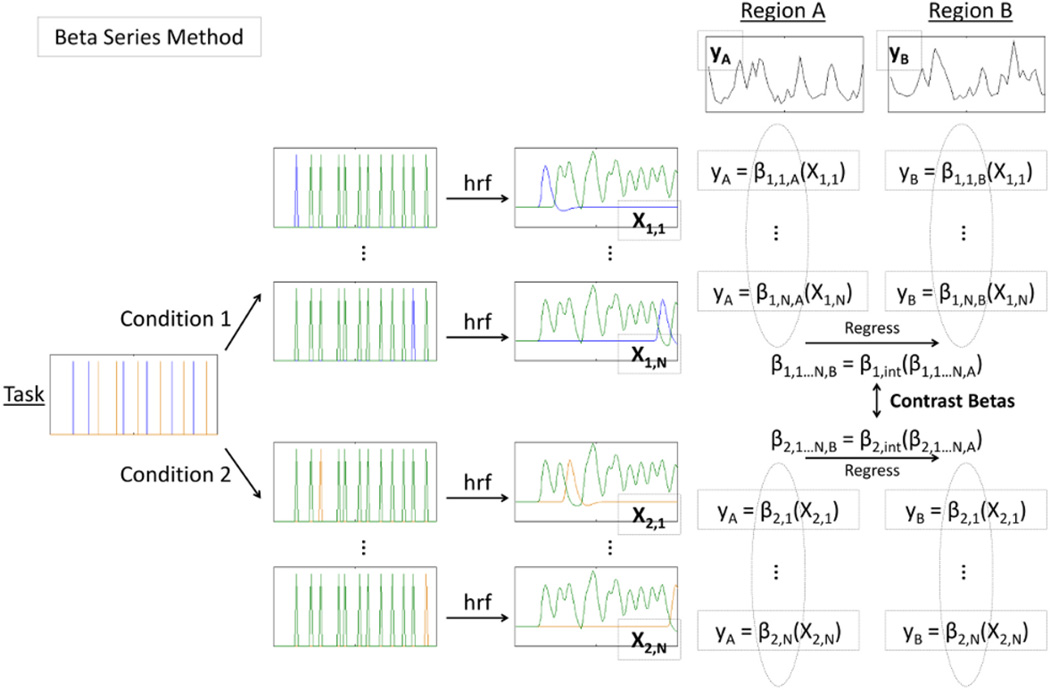
Figure 3.
The beta series method (BSM) uses an iterative approach to modeling context-modulated functional connectivity. For each region and each stimulus type, a series of regressions are performed in which BOLD signal is regressed onto two task predictors simultaneously: one predictor for a given stimulus of that stimulus condition and one including all other task events of all conditions. This results in a series of beta estimates describing each region’s response to each task event of a given condition. For example, region A’s response to each condition 2 stimulus from 1 to N is given by the series of betas, β2,1,A … β2,N,A, or β2,1…N,A. This series of betas for region B, β2,1…N,B, is then regressed onto the series of betas for region A, β2,1…N,A, resulting in a second-level beta term for each stimulus condition, β1,int, and β2,int, which represent the strength of functional connectivity for each condition. These betas are contrasted to obtain a measure of context-modulated functional connectivity.
Given the importance of testing hypotheses about context-modulated FC, we therefore conducted a series of experiments to test the sensitivity and specificity of these exploratory methods under a range of real-world parameters. While we focus on exploratory functional connectivity approaches, it is important to note that other exploratory methods exist for testing effective connectivity (i.e., where causal relationships between regions are explicitly tested), such as in structural equation modeling (James, et al., 2009) and Granger causality (Roebroeck, Formisano, & Goebel, 2005). We focus first on the exploratory functional connectivity approaches because they are relatively more commonly used; indeed, exploratory approaches are often used first and then tested later in a confirmatory manner using model-based approaches, such as dynamic causal modeling (Friston, et al., 2003; Penny, Stephan, Mechelli, & Friston, 2004).
Methods
Simulation Experiments
Simulation and Analytic Overview
The following description provides a general overview of the simulations and analytic approaches (also see Figure 1), with more details provided below. First, a task design with two conditions is pseudorandomly generated with given constraints (e.g., stimulus duration, number of events). Second, based on experimental parameters, the task design elicits neural activity at 100 Hz temporal resolution within two neural regions with a given probability, and activity within region A signals a lagged neural event in region B with a task-varying probability (i.e., context-modulated connectivity). Third, the vectors of neural events are convolved with an HRF (canonical or individually varying) to simulate BOLD data. Fourth, a layer of Gaussian noise is added to model physiological variability. Fifth, the BOLD data is downsampled to .5 Hz (i.e., a TR of 2) and another layer of Gaussian noise is added to model scanner noise. It is important to note that the PPI methods and BSM were always performed on the same raw data, thus strengthening validity of comparisons in their performances. There were 100 simulations for each experiment.
Task generation
Tasks were generated pseudorandomly to ensure sufficient design efficiency (Figure 1). The tasks were generated such that there were always two stimulus conditions that each occurred with 30 repetitions (except for experiment 3, where the number of stimulus repetitions varied). The task was generated with a default mean inter-trial-interval (ITI) of 6 s using a Poisson distribution, and the mean ITI was varied in experiment 2 to examine its impact on FC detection. The default stimulus duration was 1 s, except for experiment 4 where the stimulus duration was varied to examine its impact on FC detection.
Neural model simulations
All neural event simulations were generated at 100 Hz. Activity within two regions was generated such that each region had a given probability of responding to each task condition. For these simulation purposes that only focused on detecting differences in FC, the response of each region to each task condition was fixed to .5 (i.e., no context-modulated differences in activity between regions, conditions, nor an interaction). Regional neural event activity was simulated as a single punctuate event in response to each task condition, which occurred as a function of the specified probability (e.g., an activity probability of .5 indicates that for each stimulus condition in the task, the region has a 50% probability of responding). FC between two regions was modeled directionally and probabilistically, such that if region A responded to the task, then region A would signal activity in region B with a specified probability (e.g., a connectivity probability of .5 indicates that if region A fires, there is a 50% probability of that event generating a corresponding event in Region B). Connectivity between regions was additionally lagged by 100 ms. This created the realistic possibility that on any one trial of the task, region B could have two distinct inputs: the task (occurring at time 0) and region A (occurring 100 ms later). The probability that an event in region A signaled a lagged event in region B varied as a function of the task, thus simulating context-modulated connectivity. For example, based on model parameters, activity in region A may signal a lagged event in region B with 80% probability during condition 1 versus a probability of 20% in condition 2.
BOLD model simulations
Following simulation of the neural events at 100 Hz, the vectors of neural events were then convolved with an HRF (either canonical or individually varying) to create simulated BOLD data. To model physiological variability, a layer of Gaussian noise was added to the BOLD data with a fixed signal-to-noise ratio (SNR) of 6:1, based on estimations of real physiological confounds of BOLD data (Kruger & Glover, 2001). The simulated BOLD data was then downsampled to .5 Hz (i.e., a TR of 2 seconds), another layer of Gaussian noise was added to model scanner noise with an SNR of 9:1 based on prior estimations of scanner confounds in real data (Kruger & Glover, 2001), and the data were scaled to percent signal change.
Psychophysiological Interaction Analyses
The sPPI analyses (see Figure 2) were conducted as described by (Friston, et al., 1997) and (Gitelman, et al., 2003). First, a contrast vector was created from the experimental design (e.g., coded stimulus 1 = 1, stimulus 2 = −1). Second, the observed BOLD data for region A was deconvolved into estimates of neural events using a recently developed deconvolution algorithm shown to outperform contemporary algorithms (Bush & Cisler, in press). Third, the PPI term was defined as the product of the mean-centered estimate of neural events and contrast vector. Fourth, the PPI interaction term was convolved with a canonical HRF. Fifth, the observed BOLD data for region B was then regressed simultaneously onto 1) the convolved task predictor (i.e., main effect of task), 2) the BOLD data from region A (i.e., main effect of region A), and 3) the PPI term (i.e., interaction between task and region A). The β value of the PPI term for each experiment was recorded.
The gPPI analyses (see Figure 2) were conducted as described by (McLaren, et al., 2012). This approach is similar to the sPPI method, except that each column of the task design matrix (i.e., each stimulus condition of the experimental design) is separately multiplied by the deconvolved neural estimates and then convolved with an HRF. Each of these interaction regressors is then included in the GLM, such that the observed BOLD data for region B is regressed simultaneously onto 1) the convolved task predictors (i.e., main effect of task), 2) the BOLD data from region A (i.e., main effect of region A), and 3) each of the separate convolved PPI (task condition × neural estimate) regressors. The difference in magnitude of the β coefficients for the separate interaction regressors provides an estimate of task modulated FC. The β value for each of the PPI terms is recorded for each experiment.
Beta Series Method Analyses
The BSM analyses (Figure 3) were conducted as described in (Rissman, et al., 2004). First, a separate regressor was created for each individual event of each condition type (e.g., 30 regressors for condition 1, 30 regressors for condition 2) and convolved with a canonical HRF to create the design matrix. Second, separately for each region, a β coefficient estimate of activity was calculated for each individual trial using the method described in (Mumford, Turner, Ashby, & Poldrack, 2012). Briefly, this approach uses an iterative procedure to estimate task activity unique to each trial. For example, for a given task including 60 unique trials, one GLM is conducted with a design matrix including two columns: one column for the first trial and one column including every other trial. Another GLM is then conducted with a design matrix including two columns: one column for the second trial and one column including every other trial. This iterative procedure is repeated until a unique β estimate has been obtained for each individual trial (e.g., 60 separate GLMs). Second, separately for each task condition, the series of β values (corresponding to only one task condition) from region B was regressed on the series of β values from region A (corresponding to only one task condition) and repeated for each stimulus condition. The relative difference in β values (indicating functional connectivity between region A and B) between the stimulus conditions indicates the estimated magnitude of context-modulated FC.
Experiments
We used the above described simulation procedures to conduct six experiments and test the accuracy of the different context-modulated FC methods under varying conditions. Experiment 1 tested the accuracy of estimating context-modulated FC when only varying the true effect size of context-modulated FC. In this experiment, we used seven levels of true magnitude of context-modulated FC: 0 (i.e., no effect), 0.05, 0.1, 0.15, 0.2, 0.3, and 0.5. These values reflect the difference in probability of region A signaling a lagged event in region B between condition 1 and condition 2. The probability of connectivity in condition 2 was always .1; the probability of connectivity in condition 1 is the only aspect that changed across these experiments. The task was generated with 30 stimulus repetitions for each stimulus condition and a mean ITI of 6 s. A canonical HRF was used to generate the BOLD data. There was no individual variability in the shape of the HRF. There were 100 simulations across each level of the experiment.
Experiment 2 tested the effect of ITI on the accuracy of estimating context-modulated FC. This experiment tested four levels of ITI: 2, 4, 8, and 16 s. Each task was generated with a Poisson distribution of ITIs centered around a given mean. To examine the impact of ITI as a function of true effect size magnitude, we also manipulated the true FC difference to be either .2 or .5, and this manipulation varied factorially with the ITI manipulation. There were 100 simulations across each level of the experiment.
Experiment 3 tested the effect of trial repetition on the accuracy of estimating context-modulated FC. This experiment tested four levels of trial repetitions: 10, 20, 30, and 40. These manipulations again varied factorially with a manipulation of true underling FC difference (i.e., either .2 or .5). There were 100 simulations across each level of the experiment.
Experiment 4 tested the effect of stimulus duration on the accuracy of estimating context-modulated FC. This experiment tested four levels of stimulus durations: 1 s, 2 s, 4 s, and 8 s. These manipulations again varied factorially with a manipulation of true underling FC difference (i.e., either .2 or .5). There were 100 simulations across each level of the experiment.
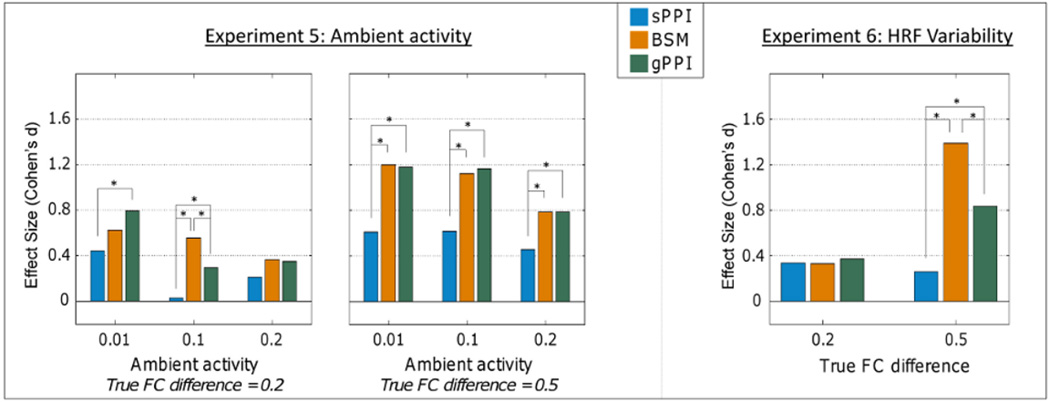
Experiment 5 tested the effect of ambient activity on the accuracy of estimated context-modulated FC. Here, ‘ambient activity’ refers to neuronal activity that can occur in the absence of either stimulus condition. The purpose of this manipulation is to test how mis-modeling neuronal activity (i.e., the ambient activity is not modeled in the analyses) affects the detection of task-modulated FC. As with task-related neural activity, ambient neural activity was simulated probabilistically. This experiment tested three probability levels of ambient activity: 0.01, 0.1, and 0.2 (e.g., 0.2 = neural firing during 20% of the rest periods on average).
Experiment 6 tested the effect of HRF misspecification of the GLM model. For this experiment, we allowed the time-to-peak of the true HRF used to generate the observed BOLD to vary with a mean of 6 and an SD of 1. Consequently, the task regressors from the GLMs, which used the canonical HRF shape, were misspecified by varying degrees. This manipulation again varied factorially with a manipulation of true underling FC difference (i.e., either .2 or .5). There were 100 simulations across each level of the experiment.
Simulation Analyses
The units of the estimates of context-modulated FC across the methods differ and do not allow for straightforward comparisons. That is, the β estimates from the sPPI and gPPI are partial coefficients indicating changes in the BOLD signal attributable to the interaction term relative to the baseline activity and changes due to all other sources of variance in the model. By contrast, BSM has a simpler second-level model (see Figure 3) and the β estimates more directly represent the degree to which task-based activity in region A changes in relation to task-based activity in region B. As such the β estimates from the PPI-based methods and BSM methods cannot directly be compared. To account for this difference in units of analysis and to foster comparisons between models, we generated effect sizes (Cohen’s d) (Cohen, 1992) for each method across the 100 simulations for each experiment, and used permutation testing (Moore & McCabe, 2013) to statistically compare the magnitude of the effect sizes across the methods. Cohen’s d effect size estimates can be interpreted as small, medium, and large for values of 0.2, 0.5, and 0.8, respectively, and are used in meta-analyses to compare the magnitude of effects across disparate outcome measures. As a point of reference, a typical neuroimaging experiment with ~30 participants would have power of ~.8 to detect a medium effect size (not accounting for multiple corrections due to whole-brain statistical testing), using the G*Power program to calculate power (Buchner, Erdfelder, Faul, & Lang, 2009). As an example of this approach for the current comparisons, the sPPI method generated 100 context-modulated FC estimates in Experiment 1 when the true FC difference was modeled as 0.5. The mean β estimate for task-modulated FC in this case was 0.19, the SD was 0.31; thus, the Cohen’s d effect size for this sample was 0.63 (0.19 / 0.31). The comparable gPPI effect size estimate for this level of the experiment was 1.55. To statistically compare these effect sizes, we used permutation testing, in which the labels (sPPI or gPPI) of the observed estimates are randomly shuffled and the effect sizes are recomputed, with 10000 iterations to generate a null hypothesis (i.e., that the labels are irrelevant for explaining effect size differences) distribution of effect size differences between the methods. In this example, zero of the differences in the effect sizes from the randomly shuffled samples matched or exceeded the observed difference in effect sizes; thus, the p value for the observed difference in effect size estimates is 0.0001 (number of observed shuffled cases exceeding the actual observed case +1 / number of iterations + 1). Note that this methodology of comparing effect sizes allows us to compare the power between the different methods, while inferences regarding the accuracy of the methods are less straightforward (i.e., more power to detect an effect does not necessarily indicate more accuracy in characterizing the effect). Nonetheless, the effect size metric and inferences regarding power allow researchers to examine which approach fosters the most statistical power to detect a hypothesized effect, depending on experimental parameters.
Real-Data Experiments
Real fMRI data were taken from a study comparing neural processing network function between adolescent girls with and without assaultive violence exposure histories. Analyses for the present study focused only on a subset of the control adolescent girls who had usable data for two separate fMRI tasks and who were all medically and psychiatrically healthy (N = 18). The mean age for this group of adolescent girls was 14.3 (SD = 1.3), 66% were Caucasian. We focus here on analyzing data from two tasks that each participant completed: a face processing task using a blocked design, and a pictorial Stroop task using a slower event-related design. All procedures were approved by the local Institutional Review Board.
Face processing task
In this task, participants made button presses indicating gender decisions while viewing faces taken from the NimStim facial stimuli set (Tottenham, et al., 2009). The faces contained either neutral or fearful expressions, presented either overtly or covertly, in alternating blocks. There were an equal number of female and male faces. Overt faces were presented for 500 ms, with a 1200 ms ISI displaying a blank screen with a fixation cross, in blocks of 8 presentations for a total block length of ~17 s. Covert face blocks used a similar design but were presented for 33 ms followed immediately by a neutral facial expression mask for 166 ms from the same actor depicted in the covert image, and the ISI was 1500 ms. Rest blocks were additionally included that displayed a blank screen with a fixation cross and lasted 10 s. The alternation between each block type (covert, overt, fear, neutral, rest) was additionally separated by 5000 ms of blank screen with a fixation cross. Thus, there were five total regressors: 1) overt neutral blocks, 2) overt fearful blocks, 3) covert neutral blocks, 4) covert fearful blocks, and 5) rest blocks. The task was presented in two runs, each lasting ~8 min, during which each block type was presented 5 times.
For this analysis, we focused on identifying context-modulated FC with the fusiform gyrus (FFG) (i.e., fusiform face area; (Kanwisher, McDermott, & Chun, 1997)) for the contrast of active task blocks versus rest. The site of the FFG was chosen from a group-level GLM for the contrast of active task blocks vs rest, which revealed a significant cluster in the FFG: center of mass XYZ = −40,−60,−15, peak t = 7.91, cluster size = 2545 voxels (extending across occipital lobe to the right FFG). We placed a spherical ROI with a 6 mm radius centered around the peak t and used this 48 voxel sphere as our FFG region-of-interest (ROI).
Pictorial Stroop task
In this task, participants were presented with a face image embedded within a scene image (Supplemental Figure 1). This task was created to manipulate several factors, thus its design is multifaceted. Participants were given the instruction to indicate whether the target image was danger-related or not. The valence of the images were manipulated in order to factorially manipulate emotional conflict: 2 (scene image: neutral vs fearful) × 2 (face image: neutral vs fearful). The participants were told to focus on either the scene or face image in alternating blocks of 32 trials, with the order of face and scene blocks counterbalanced across participants. Another experimental manipulation in this task design was whether the previous trial consisted of conflict or not, which manipulates whether the current trial is a ‘high cognitive control’ (previous trial had conflict) or ‘low cognitive control’ (previous trial did not have conflict) (Botvinick, et al., 2001; Egner & Hirsch, 2005). Finally, we also manipulated whether the fearful stimulus was a distracter (i.e., object to be ignored; e.g., scene stimulus was danger-related when told to pay attention to the face) or a target. Thus, there were eight stimulus conditions of interest: 1) no conflict on the previous trial, no conflict on the current trial, both stimuli (face and scene) neutral, 2) no conflict on the previous trial, no conflict on the current trial, both stimuli (face and scene) fearful, 3) no conflict on the previous trial, conflict on the current trial, fear stimulus is the target, 4) no conflict on the previous trial, conflict on the current trial, fear stimulus is the distracter, 5) conflict on the previous trial, conflict on the current trial, fear stimulus is the target, 6) conflict on the previous trial, conflict on the current trial, fear stimulus is the distracter, 7) conflict on the previous trial, no conflict on the current trial, both stimuli (face and scene) neutral, 8) conflict on the previous trial, no conflict on the current trial, both stimuli (face and scene) fearful. Errors were also included in the design matrix as a regressor of no interest. The task was presented in four runs of ~8 minutes, and there were a total of 256 trials balanced across the different manipulations. Each stimulus lasted 1000 ms in duration, with the ITI jittered in a range of 6 to 8 seconds.
For this analysis, we focused on identifying context-modulated FC with the dorsal anterior cingulate (dACC) for the contrast of incongruent vs congruent. The dACC ROI site was chosen from an automated meta-analysis from the neurosynth.org website (Yarkoni, Poldrack, Nichols, Van Essen, & Wager, 2011) using the term ‘conflict’. This automated meta-analysis revealed a significant cluster in the dACC, on which we centered a spherical ROI with 6 mm radius in the following coordinates, XYZ = 0, 20, 34, consisting of 48 voxels.
fMRI acquisition
A Philips 3T Achieva X-series MRI system using an 8-channel head coil (Philips Healthcare, USA) was used to acquire imaging data. Anatomic images were acquired with a MPRAGE sequence (matrix=192×192, 160 sagittal slices, TR/TE/FA=7.5/3.7/9°, FOV = 256,256,160, final resolution=1×1×1mm3 resolution). Echo planar imaging sequences were used to collect the functional images using the following sequence parameters: TR/TE/FA=2000ms/30ms/90°, FOV=240×240mm, matrix=80×80, 37 oblique slices (parallel to AC-PC plane to minimize OFC sinal artifact), slice thickness=3 mm, final resolution 3×3×3 mm3.
Image preprocessing
Image preprocessing followed standard steps and was completed using AFNI (Cox, 1996) software. In the following order, images underwent despiking, slice timing correction, deobliquing, motion correction using rigid body alignment, alignment to participant’s normalized anatomical images (using AFNI program @autotlrc to normalize the anatomical image and store the transformation matrix, then program align_epi_anat.py to align the native EPI image to the native space anatomical and then apply the transformation matrix to the EPI image), spatial smoothing using a 5 mm FWHM Gaussian filter, and rescaling into percent signal change (relative to mean baseline signal in each voxel). Images were normalized using the MNI 452 template brain. To correct for respiratory and cardiovascular artifacts, fluctuations in white matter voxels and CSF were regressed out of time courses from grey matter voxels following segmentation using FSL (Smith, et al., 2004) and using restricted maximum likelihood to account for autocorrelation (Behzadi, Restom, Liau, & Liu, 2007; Sala-Llonch, et al., 2012). This step was implemented directly after motion correction and normalization of the EPI images in the preprocessing stream. Additionally, to correct for residual motion artifacts in the signal that standard motion correction does not correct (Friston, Williams, Howard, Frackowiak, & Turner, 1996; Tohka, et al., 2008), Independent Component Analyses (ICA) were completed as a last preprocessing step separately on each participant and each run to identify and remove artifact components from the data (Kelly, et al., 2010; Tohka, et al., 2008; Zeng, Qiu, Chodkowski, & Pekar, 2009).
Real-Data Analyses
For the PPI methods, timecourses of the seed regions described above were extracted using singular value decomposition separately for each participant. These timecourses were then deconvolved using the Bush and Cisler deconvolution algorithm (Bush & Cisler, in press) to generate neural event estimates. For all analyses, the duration of the modeled events (or blocks) was set to the duration of the corresponding task trial. For the sPPI method, the PPI term was computed as the product of the neural estimates and the contrast vectors (task vs rest for the block design; incongruent vs congruent for the event-related design). For the gPPI method, separate PPI terms were computed as the product of the neural event estimates and the onsets of each stimulus conditions (5 PPI regressors for the block design; 8 PPI regressors for the event-related design). The canonical HRF provided in SPM software was convolved with the PPI regressors and task regressors. These regressors were then entered simultaneously with the seed region into whole-brain regression analyses using restricted maximum likelihood estimation to account for serial correlation implemented with AFNI software (3dREMLfit). For the BSM, each individual trial (256 total unique trials) was included as a separate regressor in a whole-brain regression analysis using restricted maximum likelihood estimation to account for serial correlation implemented with AFNI software (3dREMLfit). For each stimulus condition separately, the seed region timecourse of β estimates were extracted and regressed onto the timecourse of β estimates of every other voxel. This provided a whole-brain map for each stimulus condition indicating the degree to which activity fluctuations in the seed region were related to activity fluctuations in each other voxel. In estimating the β coefficients for each individual trial for the BSM, we did not use the iterative least squares approach (Mumford, et al., 2012) used in the above simulation experiments because of computational intractability. That is, using a Unix-based server with 16 processing nodes, a whole-brain GLM (3dREMLfit) for one participant requires ~4 minutes. Thus, the iterative least squares approach for this task would require ~ 17 hours (4 minutes × 256 iterations) per participant.
Group-level analyses to identify voxels with significant context-modulated FC with the seed region consisted of one-sample t-tests using cluster-level thresholding, with a corrected p < .05 cluster defined as 17 contiguous voxels surviving an uncorrected p < 0.005 based on Monte Carlo simulations (Forman, et al., 1995).
Results
Simulation Results
Experiment One
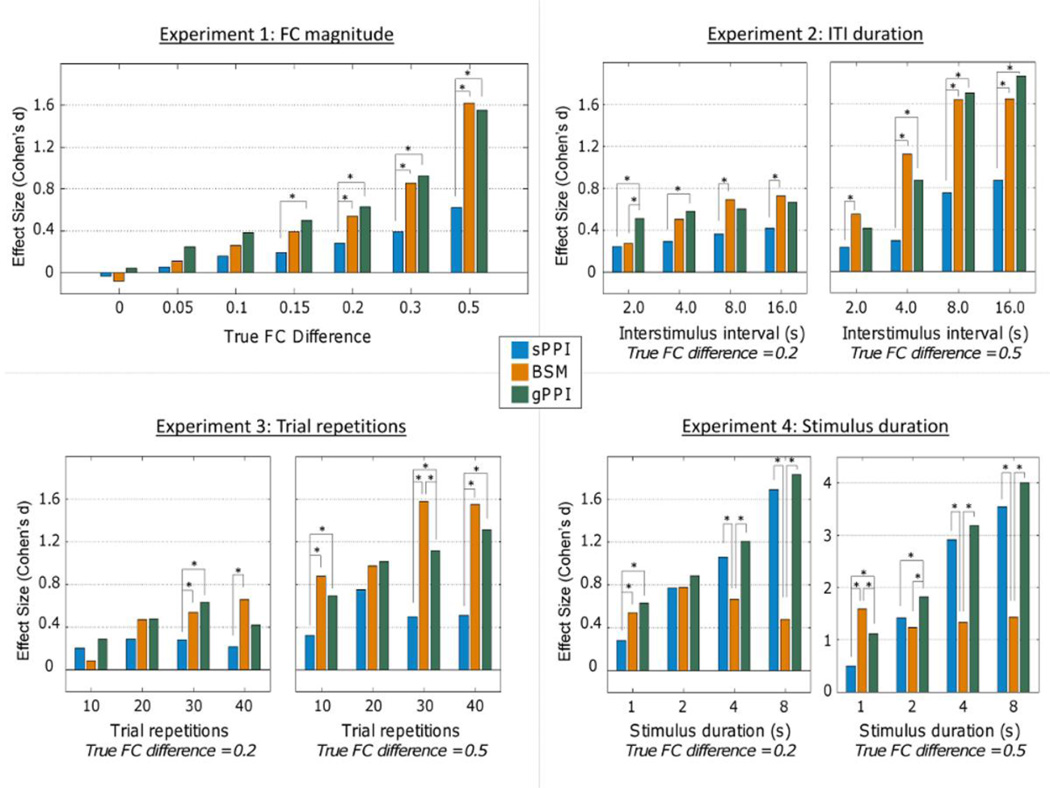
As indicated in Figure 4 (top left), the magnitude of the estimated effect sizes generally tracked the true underlying difference in FC for each of the three methods. The gPPI generally and BSM generally demonstrated greater effect sizes relative to the sPPI. There were not significant differences between the methods when the true FC difference was less than 0.15.
Figure 4.
Several experiments were conducted to compare the three methods under various functional connectivity (FC) strengths and task parameters. Significance bars indicate p<0.05.
Experiment Two
As indicated in Figure 4 (top right), longer ITI generally corresponded with more power to detect context-modulated FC, with the gPPI and BSM again generally demonstrating greater effect sizes relative to the sPPI.
Experiment Three
As indicated in Figure 4 (bottom left), increasing number of trial repetitions led to generally larger effect sizes for the gPPI and BSM but not for the sPPI. Effect sizes for the BSM were generally higher with trial repetitions of 30 or greater.
Experiment Four
As indicated in Figure 4 (bottom right), stimulus duration also had different effects on the accuracy of the different methods. The effect size of the BSM method was relatively stable across different levels of stimulus duration at both low and high magnitudes of true differences in FC. By contrast, both the gPPI and sPPI exhibited increasing effect size estimates of FC differences as a function of increasing stimulus duration.
Experiment Five
As indicated in Figure 5 (top left), increasing levels of ambient activity (i.e., mis-modeling the neuronal activity) led to decreasing effect size estimates of FC differences, though the overall pattern held of the gPPI and BSM effect size estimates generally being higher than the sPPI.
Figure 5.
Task-unrelated ambient activity impairs all three methods, such that the FC differences are underestimated with higher ambient activity, although BSM and gPPI tend to outperform PPI at high FC differences. When the HRF used to generate the BOLD signal of the two regions is allowed to vary between simulations (participants), PPI is most impaired at high FC differences, with gPPI and BSM less affected.
Experiment Six
As indicated in Figure 5 (top right), including individual variability in the HRF when simulating the BOLD data and using the canonical HRF when analyzing the BOLD data led to generally decreased effect size estimates across the three methods; however, the BSM method was significantly less negatively affected when the true FC difference was 0.5 (i.e., significantly higher effect sizes in this condition relative to the sPPI and gPPI).
Real Data Results
Block Design Task
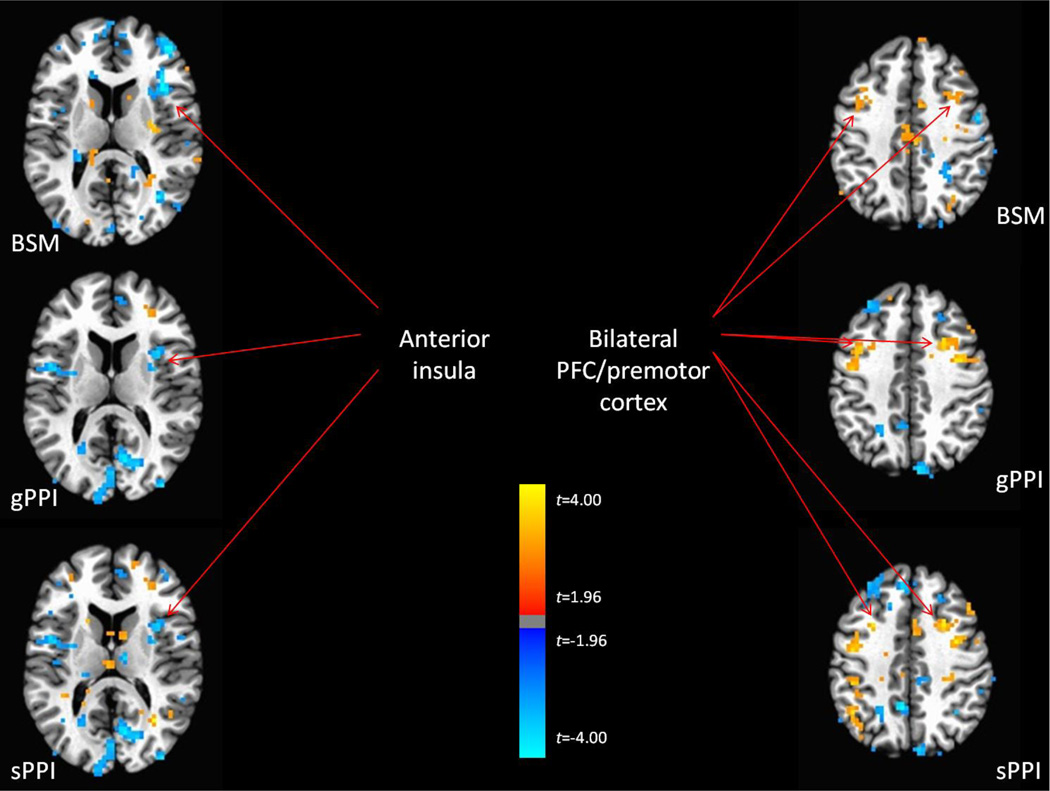
Supplemental Table 1 indicates all significant regions where connectivity with the FFG significantly differed between task and rest conditions. With the BSM method only two significant regions were detected. By contrast, four significant regions were detected with the gPPI method and seven regions were detected with the sPPI method. The regions detected by the BSM did not correspond to regions detected by either the gPPI or sPPI, whereas there was general correspondence between regions detected by the gPPI and sPPI methods. When dropping the threshold to p < .05 uncorrected in order to facilitate comparisons of overall similarity between the three methods, we did observe more evidence of correspondence across the three methods (Figure 6). In particular, each method detected greater FC between the FFG and dlPFC during task vs rest blocks, as well as weaker FC between the FFG and right anterior insular during task vs rest blocks.
Figure 6.
Regions of task-modulated functional connectivity detected (p < .05 uncorrected) across all three analytic methods for the block design task.
Event-Related Design Task
Supplemental Table 2 indicates the significant regions where connectivity with the dACC significantly differs between incongruent and congruent conditions. The BSM method detected five significant regions, whereas the gPPI method detected three regions and the sPPI method detected four regions. There was little correspondence in significant regions across the three tasks. However, when dropping the threshold to p < .05 uncorrected to facilitate comparisons of overall patterns between the methods, we again observed more evidence of correspondence across the methods (Figure 7). In particular, all three methods detected greater FC between the dACC and medial PFC/perigenual ACC during incongruent vs congruent conditions, as well as detected decreased FC between the dACC and superior dmPFC / pre-SMA during incongruent vs congruent conditions.
Figure 7.
Regions of task-modulated functional connectivity detected (p < .05 uncorrected) across all three analytic methods for the event-related design.
Discussion
Given the importance of testing hypotheses about context-modulated FC, the purpose of these experiments was to test and compare the statistical power for detecting context-modulated FC between three common methods. The overall pattern of results from the simulation studies generally indicates greater power for the gPPI method and BSM over the sPPI method in detecting context-modulated FC. The results demonstrating better overall power of gPPI method compared to the sPPI method is consistent with results of a recent study (McLaren, et al., 2012). However, the experiments also suggested specific conditions under which the BSM or PPI methods perform best. With an event related design, more trial repetitions tended to suggest greater power for the BSM. With block designs, there was strong evidence that the PPI-based methods were more powerful. The accuracy of the gPPI and sPPI methods appeared more negatively affected by modeling individual variability in the shape of the HRF, whereas the BSM demonstrated greater performance under conditions of variability in the HRF. The power of all methods dropped when simulating ambient neural activity that was not modeled in the analyses.
One interesting caveat when comparing these methods is to consider how to interpret the direction of any detected difference in FC between task conditions. The BSM and gPPI both provide an estimate of FC unique to each individual stimulus condition, and differences between the conditions are testing through contrasting these separate condition estimates. Accordingly, a detected FC differences of 0.5, for example, could mean that FC was positive in condition 1 (0.6) and less positive in condition 2 (0.1), or it could mean that FC was absent in condition 1 (0.0) and negative in condition 2 (−0.5). Thus, to completely interpret a detected context-modulated FC difference, one needs to interpret the FC estimates in the separate conditions. Supplemental Figure 2 displays the β estimates specific to each of the simulated task conditions for experiments 1–4 for the BSM and gPPI (sPPI does not provide estimates specific to each task condition). The estimates provided by the BSM are intuitively interpretable. Across all the experiments, the BSM provided accurate estimates of the connectivity during stimulus 1, which was fixed at .1, and the BSM estimates of connectivity during stimulus 2 appropriately scaled with the true underlying connectivity probability. By contrast, the β estimates from gPPI method are not as easily interpretable because these represent partial coefficients unique to the task × brain region interaction terms after controlling for baseline activity and each other source of variance included in the model (e.g., main effect of task, main effect of the brain region, covariates, etc). While the gPPI was powerful in detecting the difference in FC between the conditions, these partial coefficients are more difficult to interpret in regard to the absolute magnitude of the FC difference across conditions, and the actual value of the partial coefficients will be sensitive to how many and which other variables are included in the full gPPI model. Again, this does not detract from the power of the gPPI to detect context-modulated FC; however, there is just more difficulty in interpreting the actual direction of the context-modulated FC difference in gPPI2.
The results from the real data set of healthy adolescent girls provide some validity to the simulation results. To the extent that the detection of a significant cluster of context-modulated FC indicates a true positive, then the gPPI and sPPI methods were more powerful (i.e., detected more significant clusters) than the BSM on the block design task. This corresponds well with results from Experiment 4, where the PPI methods demonstrated increased power for block designs. Similarly, the BSM appeared more powerful (i.e., detected more significant clusters) on the event-related design with 32 trial repetitions than the PPI methods, which corresponds with Experiment 3 where the power of the BSM appeared greater than the PPI methods on event-related designs with an average ISI of 6 s and when there were 30 or more trial repetitions. However, without knowing the ground truth of context-modulated FC on this dataset, these inferences about the power of the methods are tenuous at best. Indeed, it is interesting to observe the correspondence in the detection of context-modulated FC across the methods. While we did observe common regions detected as context-modulated FC across the methods after dropping the threshold to p < 0.05 uncorrected, we also observed many areas of discrepancy. For the block design, the gPPI and sPPI generally detected similar regions (Supplemental Table 1 and Figure 5). By contrast, the gPPI and sPPI methods had considerably less correspondence in detecting context-modulated FC for the event-related design (Supplemental Table 2 and Figure 6). One explanation for this is to consider the number of regressors in each method across the different tasks: the sPPI method included 7 and 11 regressors for the block design and event-related design tasks, respectively, the gPPI method included 11 and 18 regressors for the block design and event-related design tasks, respectively. Accordingly, one explanation for why the correspondence decreased on the event-related design is that the difference in the number of regressors between the methods increased, and this increased number of regressors accounted for additional sources of variance and altered the ultimate estimate of context-modulated FC. The BSM similarly differs from the other methods by including many additional regressors in its model (e.g., 256 regressors in the event-related design). Finally, the prior study comparing sPPI to gPPI on a real fMRI dataset (McLaren, et al., 2012) also found discrepancies in clusters detected with sPPI and gPPI, indicating that the somewhat low correspondence between methods observed here is not due to properties of the sample (adolescents) or tasks (emotion processing and conflict) and instead reflects inherent differences of the methods themselves. As mentioned above, it is difficult to make inferences about these methods in the absence of ground truth on the real data, but the results from the real data nonetheless 1) strengthen some conclusions from the simulations (i.e., block designs versus event-related designs with 30 or more trial repetitions), 2) demonstrate some correspondence in detection of context-modulated FC between the three methods on a real dataset, and 3) highlight the need for future research to further delineate the parameters affecting performance of the methods.
It is also interesting to consider what differences in the statistical approaches are driving the differences in performance. There was consistent evidence that the PPI-based methods performed best during block designs. In fMRI methodology, block designs are optimal for detecting activation, whereas event-related designs are more preferable for estimating the shape of the HRF (Liu, 2004; Liu & Frank, 2004). It is likely the case that PPI-based methods are more powerful in block designs for the same reason that block designs lead to greater general power for detecting brain activation. Indeed, our simulation models FC directionally, such that if region A fires it signals a neural event in region B; thus, blocked designs that capitalize on detecting region A firing would naturally have more power to detect region A signaling an event in region B. The PPI-based methods are a simple extension of the general linear model (Friston, et al., 1995; Worsley & Friston, 1995) for detecting activation, so it follows that these methods should have greater power in blocked designs. This inference has important implications for researchers designing experiments to test hypotheses about context-modulated FC, such that blocked designs may generally have greater power for detecting the hypothesized effect. However, blocked designs are not always feasible, such as when habituation effects are possible or repeated presentation of a stimulus has psychological confounds for the task. The BSM did not similarly demonstrate an increase in power during block designs, and this can likely be attributed to the fact that the BSM uses a separate GLM to isolate the activity attributable to a single block (or event), thus statistically sacrificing power and potentially negating the benefit of a block design. Indeed, the BSM performed better when there were more trial repetitions, indicating that having a larger distribution of activations with which to correlate (e.g., 30 samples of activations for region A and region B to correlate) fosters more power for detecting whether the activations of region A and region B covary, which is rather intuitive given that the BSM is based on a second-level GLM to test the relationship between activations in region A and region B. Accordingly, researchers designing experiments to test hypotheses about context-modulated FC, and who cannot use a block design, would optimize power for detecting their hypothesized effect with the use of an event-related design with as many trial repetitions as possible and using the BSM. The BSM also appeared more robust to variation in the shape of the HRF, and this can likely be attributed to the fact that the PPI-based methods are influenced by the shape of the HRF in three ways: 1) convolving the task design, and 2) deconvolving the seed region into neural estimates, which uses an assumed HRF shape, to compute the interaction term, and 3) then re-convolving the interaction term with an HRF. Thus, there are multiple opportunities for the shape of the HRF to contaminate the FC estimates. Nonetheless, note that prior work has demonstrated the need for deconvolution for detecting context-modulated FC (Gitelman, et al., 2003), though this benefit may be less pronounced in block designs (Kim & Horwitz, 2008). Finally, as discussed in more detail elsewhere (McLaren, et al., 2012), the gPPI performance advantage over the sPPI is due to the fact that the greater number of parameters in the gPPI allows the model to span the entire space of the experimental design (as opposed to a truncated model in the sPPI) and thus more accurately partition variance and characterize the FC estimates of interest.
As noted above, the goal of the current series of experiments was to compare power for detecting context-modulated FC. The simulation results suggested that the gPPI and BSM generally had greater power, that block designs clearly favor the PPI methods and may generally optimize power for detecting context-modulated FC, and that event-related with many trial repetitions may favor the BSM. Results from an analysis of real data strengthened validity of the PPI methods’ performance on block designs and the BSM’s performance on event-related designs with greater than 30 trial repetitions. While there have been prior simulation studies of the PPI methods (Kim & Horwitz, 2008; McLaren, et al., 2012), to our knowledge, this is the first attempt to compare the power of the BSM and PPI methods and thus provides important data for future researchers seeking to test hypotheses about context-modulated connectivity; however, the current study is not without limitations. First, we used a basic simulation consisting only of two nodes; thus, the degree to which performance of the methods is influenced by more realistic large-scale network structure could not be determined. Second, we only used simulations with two stimulus conditions; thus, the performance of these methods under experimental designs with greater than two conditions is not readily clear from these experiments. Third, the real data included a small sample (N=18) of adolescent girls, and it is unclear how a comparison of methods among this unique sample would generalize to other samples (e.g., older adults, psychiatric populations, etc). Additional future research in this area that addresses these concerns and further tests the performance of analytical methods will continue to improve our knowledge of how to most accurately detect context-modulated connectivity, thus providing more powerful and accurate tests of cognitive and clinical neuroscience hypotheses.
Supplementary Material
Depiction of the pictorial Stroop task. Participants viewed faces embedded on scenes and were told to pay attention to either the face or scene image and indicate with a button press whether the target image depicted a danger-related object.
In addition to the difference in functional connectivity (FC) between the task conditions (Figure 4), the BSM and gPPI also provide estimates of the FC magnitude for each stimulus condition. In all experiments, the true FC during condition 2 was 0.1, and the true FC during condition 1 varied. As noted in text, due to the differences in the statistical model between these two approaches, only the BSM estimates for each condition are directly interpretable. The gPPI estimates are not as easy to interpret given that they represent partial coefficients controlling for all other sources of variance in the model. Thus, one cannot compare the estimates between the approaches in a straightforward manner.
Highlights.
-
-
We used simulations to compare statistical methods for detecting task-modulated functional connectivity (FC)
-
-
the more common psychophyiological interaction analyses were most sensitive on block designs
-
-
the beta series method was less negatively affected by variation in the hemodynamic response function
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
We thank an anonymous reviewer for this helpful observation.
We are similarly thankful to an anonymous reviewer for this helpful observation as well.
References
- Baron RM, Kenny DA. The Moderator Mediator Variable Distinction in Social Psychological-Research - Conceptual, Strategic, and Statistical Considerations. Journal of Personality and Social Psychology. 1986;51(6):1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage. 2007;37(1):90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Braver TS, Barch DM, Carter CS, Cohen JD. Conflict monitoring and cognitive control. Psychol Rev. 2001;108(3):624–652. doi: 10.1037/0033-295x.108.3.624. [DOI] [PubMed] [Google Scholar]
- Buchner A, Erdfelder E, Faul F, Lang A. G*Power (Version 3.1.2) 2009 [Google Scholar]
- Bush K, Cisler JM. Decoding neural events from fMRI BOLD signal: A comparison of existing approaches and development of a new algorithm. Magn Reson Imaging. doi: 10.1016/j.mri.2013.03.015. (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chadick JZ, Gazzaley A. Differential coupling of visual cortex with default or frontal-parietal network based on goals. Nat Neurosci. 2011;14(7):830–832. doi: 10.1038/nn.2823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. A power primer. Psychological Bulletin. 1992;112(1):155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29(3):162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Egner T, Hirsch J. Cognitive control mechanisms resolve conflict through cortical amplification of task-relevant information. Nat Neurosci. 2005;8(12):1784–1790. doi: 10.1038/nn1594. [DOI] [PubMed] [Google Scholar]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magn Reson Med. 1995;33(5):636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Buechel C, Fink GR, Morris J, Rolls E, Dolan RJ. Psychophysiological and modulatory interactions in neuroimaging. Neuroimage. 1997;6(3):218–229. doi: 10.1006/nimg.1997.0291. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. Neuroimage. 2003;19(4):1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Poline JB, Grasby PJ, Williams SC, Frackowiak RS, et al. Analysis of fMRI time-series revisited. Neuroimage. 1995;2(1):45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Williams S, Howard R, Frackowiak RS, Turner R. Movement-related effects in fMRI time-series. Magn Reson Med. 1996;35(3):346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- Gitelman DR, Penny WD, Ashburner J, Friston KJ. Modeling regional and psychophysiologic interactions in fMRI: the importance of hemodynamic deconvolution. Neuroimage. 2003;19(1):200–207. doi: 10.1016/s1053-8119(03)00058-2. [DOI] [PubMed] [Google Scholar]
- James GA, Kelley ME, Craddock RC, Holtzheimer PE, Dunlop BW, Nemeroff CB, et al. Exploratory structural equation modeling of resting-state fMRI: applicability of group models to individual subjects. Neuroimage. 2009;45:778–787. doi: 10.1016/j.neuroimage.2008.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalkstein J, Checksfield K, Bollinger J, Gazzaley A. Diminished top-down control underlies a visual imagery deficit in normal aging. J Neurosci. 2011;31(44):15768–15774. doi: 10.1523/JNEUROSCI.3209-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci. 1997;17(11):4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RE, Jr, Alexopoulos GS, Wang Z, Gunning FM, Murphy CF, Morimoto SS, et al. Visual inspection of independent components: defining a procedure for artifact removal from fMRI data. J Neurosci Methods. 2010;189(2):233–245. doi: 10.1016/j.jneumeth.2010.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Horwitz B. Investigating the neural basis for fMRI-based functional connectivity in a blocked design: application to interregional correlations and psycho-physiological interactions. Magn Reson Imaging. 2008;26(5):583–593. doi: 10.1016/j.mri.2007.10.011. [DOI] [PubMed] [Google Scholar]
- Kruger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med. 2001;46(4):631–637. doi: 10.1002/mrm.1240. [DOI] [PubMed] [Google Scholar]
- Liu TT. Efficiency, power, and entropy in event-related fMRI with multiple trial types. Part II: design of experiments. Neuroimage. 2004;21(1):401–413. doi: 10.1016/j.neuroimage.2003.09.031. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR. Efficiency, power, and entropy in event-related FMRI with multiple trial types. Part I: theory. Neuroimage. 2004;21(1):387–400. doi: 10.1016/j.neuroimage.2003.09.030. [DOI] [PubMed] [Google Scholar]
- McLaren DG, Ries ML, Xu G, Johnson SC. A generalized form of context-dependent psychophysiological interactions (gPPI): a comparison to standard approaches. Neuroimage. 2012;61(4):1277–1286. doi: 10.1016/j.neuroimage.2012.03.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore DS, McCabe GP, editors. Introduction to the Practice of Statistics - 5th edition. 5th ed. New York, NY: W.H. Freeman; 2013. [Google Scholar]
- Mumford JA, Turner BO, Ashby FG, Poldrack RA. Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses. Neuroimage. 2012;59(3):2636–2643. doi: 10.1016/j.neuroimage.2011.08.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny WD, Stephan KE, Mechelli A, Friston KJ. Comparing dynamic causal models. Neuroimage. 2004;22(3):1157–1172. doi: 10.1016/j.neuroimage.2004.03.026. [DOI] [PubMed] [Google Scholar]
- Rissman J, Gazzaley A, D'Esposito M. Measuring functional connectivity during distinct stages of a cognitive task. Neuroimage. 2004;23(2):752–763. doi: 10.1016/j.neuroimage.2004.06.035. [DOI] [PubMed] [Google Scholar]
- Rissman J, Gazzaley A, D'Esposito M. Dynamic adjustments in prefrontal, hippocampal, and inferior temporal interactions with increasing visual working memory load. Cereb Cortex. 2008;18(7):1618–1629. doi: 10.1093/cercor/bhm195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage. 2005;25(1):230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Sala-Llonch R, Pena-Gomez C, Arenaza-Urquijo EM, Vidal-Pineiro D, Bargallo N, Junque C, et al. Brain connectivity during resting state and subsequent working memory task predicts behavioural performance. Cortex. 2012;48(9):1187–1196. doi: 10.1016/j.cortex.2011.07.006. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Stephan KE. On the role of general system theory for functional neuroimaging. Journal of Anatomy. 2004;205(6):443–470. doi: 10.1111/j.0021-8782.2004.00359.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tohka J, Foerde K, Aron AR, Tom SM, Toga AW, Poldrack RA. Automatic independent component labeling for artifact removal in fMRI. Neuroimage. 2008;39(3):1227–1245. doi: 10.1016/j.neuroimage.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tottenham N, Tanaka JW, Leon AC, McCarry T, Nurse M, Hare TA, et al. The NimStim set of facial expressions: judgments from untrained research participants. Psychiatry Res. 2009;168(3):242–249. doi: 10.1016/j.psychres.2008.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley KJ, Friston KJ. Analysis of fMRI time-series revisited--again. Neuroimage. 1995;2(3):173–181. doi: 10.1006/nimg.1995.1023. [DOI] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. Large-scale automated synthesis of human functional neuroimaging data. Nature Methods. 2011;8(8):665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng W, Qiu A, Chodkowski B, Pekar JJ. Spatial and temporal reproducibility-based ranking of the independent components of BOLD fMRI data. Neuroimage. 2009;46(4):1041–1054. doi: 10.1016/j.neuroimage.2009.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Depiction of the pictorial Stroop task. Participants viewed faces embedded on scenes and were told to pay attention to either the face or scene image and indicate with a button press whether the target image depicted a danger-related object.
In addition to the difference in functional connectivity (FC) between the task conditions (Figure 4), the BSM and gPPI also provide estimates of the FC magnitude for each stimulus condition. In all experiments, the true FC during condition 2 was 0.1, and the true FC during condition 1 varied. As noted in text, due to the differences in the statistical model between these two approaches, only the BSM estimates for each condition are directly interpretable. The gPPI estimates are not as easy to interpret given that they represent partial coefficients controlling for all other sources of variance in the model. Thus, one cannot compare the estimates between the approaches in a straightforward manner.