Reflectivity enhancement in titanium by ultrafast XUV irradiation

Abstract

The study of highly photo-excited matter at solid state density is an emerging field of research, which is benefitting the development of free-electron-laser (FEL) technology. We report an extreme ultraviolet (XUV) reflectivity experiment from a titanium (Ti) sample irradiated with ultrafast seeded FEL pulses at variable incident photon fluence and frequency. Using a Drude formalism we relate the observed increase in reflectivity as a function of the excitation fluence to an increase in the plasma frequency, which allows us to estimate the free electron density in the excited sample. The extreme simplicity of the experimental setup makes the present approach potentially a valuable complementary tool to determine the average ionization state of the excited sample, information of primary relevance for understanding the physics of matter under extreme conditions.

The study of matter under extreme thermodynamic conditions is a longstanding and fruitful field of research that has generated a host of applications in fundamental physics and applied cutting-edge technology¹,². In the last few decades increasing efforts have been devoted to studying new states of matter such as strongly coupled plasma and warm dense matter (WDM)³. The latter is characterised by solid-like density and temperatures of a few eV, conditions actually found in astrophysical contexts⁴ or in devices for plasma creation and inertial confinement fusion⁵. The advent of ultra-fast/ultra-intense lasers has opened up the possibility to generate and probe such extreme states of matter in transient conditions²,⁶. However, the capability of optical lasers to probe the excited sample is hampered by the “screening effect” of the excited plasma, which drastically limits the penetration length for photons with frequency (ω) lower than the plasma frequency:

where N_e, e, m_e and 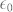are the free electron density, the elementary charge, the effective electron mass and the dielectric constant, respectively³,⁷.

In this context, the development of Free Electron Lasers (FELs) operating in the extreme ultraviolet (XUV) and x-ray spectral ranges represent a landmark result³, since the high energy photons emitted by these sources can penetrate matter at solid densities ensuring uniform excitation of the sample. FEL-based experiments have provided valuable new insights into this field, for example saturable absorption by core electrons at XUV/x-ray wavelengths⁸ or depression of the ionization potential in solid-density plasma⁹. Other FEL-based experiments aimed at the determination of the relevant parameters of these highly excited states of matter have been proposed, such as x-ray induced changes in optical reflectivity¹⁰,¹¹,¹², the parallel pyrometrical characterization of heat waves for the determination of the ion temperature (T_i)¹³ or Thompson scattering for the determination of both free electron density (N_e) and temperature (T_e)¹⁴. The latter approach is based on the measurement of the plasmon lineshape in the inelastic scattering spectra of the excited sample. These highly informative experiments rely on the development of sophisticated XUV/x-ray spectrometers and are limited by coherence issues¹⁵ and, in high-Z samples, by the low scattering cross-sections¹⁴.

Information on the plasma resonance (and thus on the related sample parameters) can be also gained by simpler reflectivity measurements¹⁶,¹⁷,¹⁸. For instance, a shift in ω_p upon photo-excitation, observable in Thompson scattering experiments, can be ascribed, through Eq. (1), to a change in N_e. However, the same shift in ω_p also leads to a change in the XUV reflectivity. This is illustrated in Fig. 1, which reports the XUV reflectivity (R) of a metal at given values of ω for a typical range in ω_p and γ, calculated using the Drude model (here γ is the inverse lifetime of the plasma resonance¹⁹,²⁰,²¹, see Methods for further details). If ω is tuned just above ω_p then the dependence of R on ω_p is more significant than that on γ. In this case any variation in R can be essentially attributed to a variation in ω_p and thus in N_e. Following this idea we performed an XUV reflectivity experiment on a Ti sample as a function of both photon fluence (F) and ω. The experiment was carried out at the TIMEX end-station of the Elastic and Inelastic Scattering (EIS) beamline²²,²³, exploiting the broad ω-tunability in the low frequency side of the XUV spectrum provided by the FERMI FEL source²⁴,²⁵,²⁶; experimental details are reported in the Methods section.

Figure 1. ω_p-dependence of R for ω = 18.9 and 20 eV (black/red lines) and γ = 1, 1.5 and 2 eV (higher to lower curves), calculated with Eqs. (3) and (4); the upper horizontal scale is the corresponding range in N_e calculated through Eq. (1).

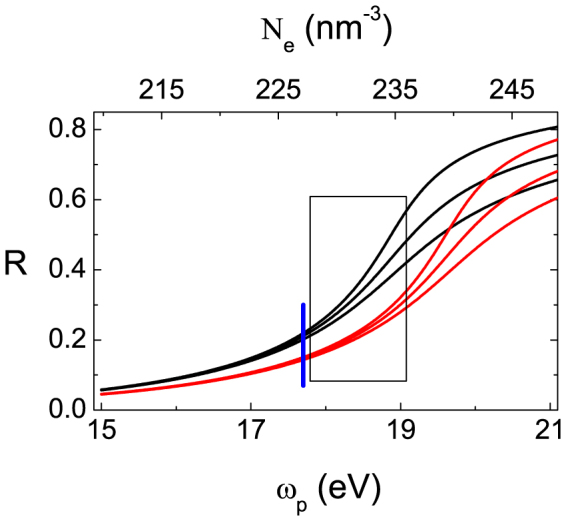
The vertical blue segment indicates the expected value of 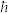ω_p = 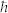ω_p(0) = 17.7 eV for the unexcited Ti sample²⁷,²⁸, while the hatched area sketches the 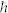ω_p-range reached in the excited sample in the exploited F-range.

Results

The dependence of R on F is shown in Fig. 2 for three representative values of 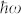ω and clearly show an increase of reflectivity up to about 40–50% for F-values as large as 20–25 J/cm². No appreciable changes in R has been observed for F < 0.02 J/cm² (see the Methods section). Assuming that the increase in N_e (and thus that in ω_p) is proportional to the energy density (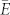) deposited into the sample close to the metal surface, it is possible to calculate the F-dependence of R at a given value of ω. For this purpose we used the Drude model to account for metal reflectivity, in which we consider the time and transverse spatial profiles of the FEL pulse and the fractional increase in N_e per unit 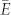, i.e.:

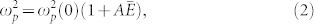where 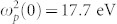²⁷,²⁸ is the plasma frequency of the unperturbed sample (more details of the model used for the calculations are reported in the Methods section) and A is an empirical constant. Curves reported in Fig. 2 were obtained using A = 7.5 · 10¹² m³/J; higher/lower dashed lines correspond to A-value 25% larger/smaller than 7.5 · 10¹² m³/J and can be regarded as an estimate of the confidence interval (see Supplemental Information), which roughly matches the deviation of the data from the calculated curves.

Figure 2. F-dependence of R(F)/R(0) for some selected ω-values, indicated in the individual panels.

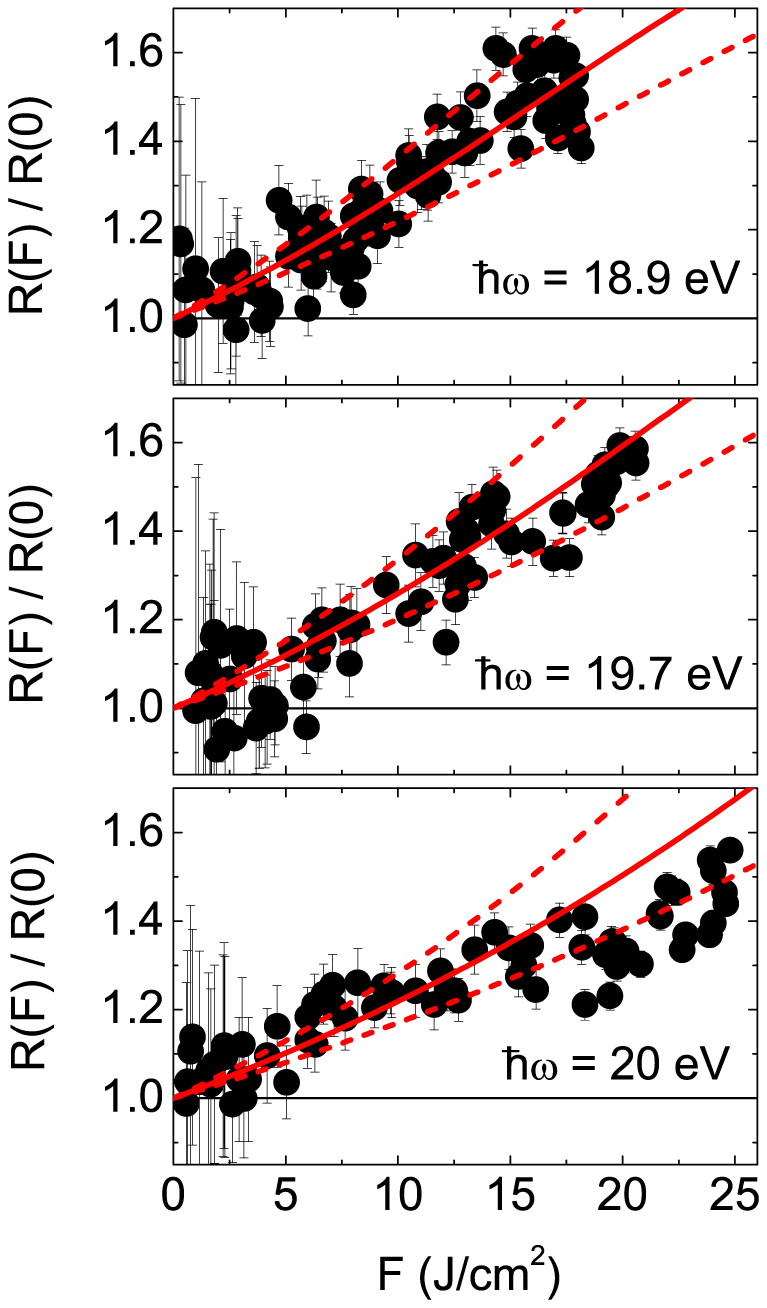
Each data corresponds to a single shot measurement taken in a fresh portion of the sample. Red full lines are the R(F)/R(0) trends calculated through Eq. (6); dashed lines are the estimate of the confidence interval.

Once the parameter A is determined, it is straightforward to compute the F-dependencies of ω_p and N_e, and these indicate an increase in ω_p and N_e (averaged over both the time and transverse spatial profiles of the FEL pulse) of up to ≈4% and 8%, respectively, at the highest F-values. Fig. 3 reports the variation with F of the mean ion charge: Z(F) = Z(0)N_e(F)/N_e(0), where Z(0) = 4²⁷,²⁸,²⁹. Such a variation is most likely due to the ionization of the shallower (3p) core electrons, that cannot efficiently recombine within the FEL pulse duration, thus leading to a net increase in the average density of free electrons. We note that the 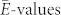reached in the present experiment compares well with the ionization energy (E⁺ = 99 eV/atom²⁹,³⁰) for the Ti⁴⁺ → Ti⁵⁺ process. If we assume that the latter is the leading ionization process, then the data shown in Fig. 3 indicates that at the highest probed F's and within the ≈45 fs FEL pulse duration ≈40% of Ti atoms are ionized. This is in qualitative agreement with the results reported in Ref. 8 for Al, where the onset of a FEL-induced saturable absorption is observed in a similar F-range. This corresponds to the situation where almost all atoms are ionized within the FEL pulse duration. Furthermore, by making the crude assumption that in a moderately excited sample 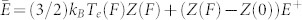³ one can derive T_e from Z. The T_e values estimated in this way are shown in the inset of Fig. 3 and compared with those reported in ref 8 for Al. The latter data were obtained by interpreting the soft x-ray emission spectra within a free electron gas model (like the one used in the present work), so that we can speculatively infer a common low-F behavior of highly photo-excited metals in the sub-0.1 ps timescale, which is mainly determined by the role played by free electrons.

Figure 3. Full lines are the F-dependencies of Z(F) at the employed ω-values; dashed lines are the confidence range.

Inset compares the low F estimate of T_e with data from Ref. 8 (circles).

Discussion

We have reported the experimental observation of a large XUV reflectivity enhancement in titanium upon irradiation with ultrafast high-fluence FEL-pulses, whose photon frequency was tuned above the plasma frequency of the sample. The FEL irradiation drives the titanium sample into a transient (short-lived) excited state that exhibits electronic temperatures typical of dense plasmas but still retains a cold atomic lattice. Reflectivity data were interpreted through a simple analytical model, based on the free electron gas approach, which employs a single empirical parameter to account for the increase in the plasma frequency within the FEL pulse duration. Such a simplified data analysis is able to capture the main physical process at the base of the observed phenomenology and allows us to determine the mean free electron density of the excited sample.

The information that can be gained from the present experiment is of the highest relevance for the study of highly excited states of matter. Analogous information can be deduced from the lineshape analysis of Thompson scattering spectra. However, the present approach has the advantage of the extreme simplification of the experimental setup and, additionally, reflectivity measurements do not suffer from cross-section or coherence issues. Substantial improvements in the experimental accuracy and data analysis can be achieved with moderate efforts and will likely open up the possibility to obtain additional information from this class of experiments, for example possible modifications of the electronic band structure. Also, the capability of FERMI to operate in the near future at photon energies down to ≈12 eV will allow one to probe the condition where the metal reflectivity is almost insensitive to plasma frequency variations but strongly depends on the plasmon lifetime. Since the latter is mostly determined by electron-electron and electron-phonon interactions, information on these dynamics could be gained as well. In summary, the possibility to map out FEL-induced reflectivity variations in a broad range across the low frequency side of the XUV spectrum can be profitably used as a complementary tool with respect to Thompson scattering methods by the growing community involved in the study of matter under extreme conditions.

Methods

XUV reflectivity measurements

A sketch of the experimental setup is shown in Fig. 4. A Ti mirror (substrate: Si, roughness ≈1 nm RMS, thickness 100 nm, passivated with 3 nm TiO₂) was loaded into the 5-axis manipulator (x,y,z,pitch,roll) of the EIS-TIMEX end-station. The FEL beam was focused onto the sample by a spherical platinum-coated silicon mirror (400 mm radius of curvature, 0.2 nm roughness RMS) placed close to normal incidence (angle of incidence 3°), which is able to provide a focal spot of area σ² ≈ 100 μm². The maximum energy/pulse delivered by the FEL source was in the ≈300 μJ level. The actual energy/pulse at the input of the photon transport system of the EIS-TIMEX beamline (I_FEL) was varied in the 1–300 μJ range by a gas attenuator and monitored on a shot-to-shot base by a gas monitor³¹. Each shot was tagged by a unique label (bunch number) to one-to-one correlate all the acquired data. F was determined from I_FEL taking into account σ² as well as the transmission of the TiO₂ layer, the beamline transmission and the mirror reflectivity that, in the used ω-range, are in the ≈73%, 52–56% and 15–20% ranges, respectively. Appreciable damage of the sample surface was observed after irradiation with a single FEL pulse with F > 0.1 J/cm². 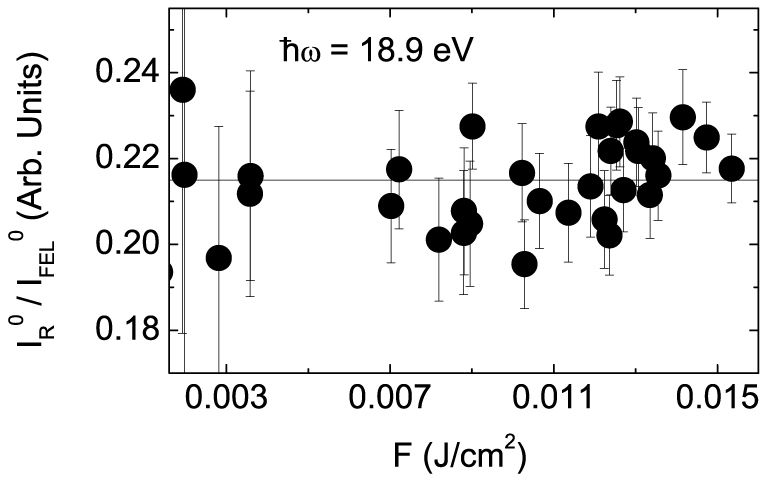The pulse energy reflected by the sample (I_R), at 6° angle of incidence, was collected at = 18.9, 19.1, 19.4, 19.7, 20.0 and 20.3 eV by a Silicon photodiode (UVG20S, IRD inc) coupled with a 0.5 mm thick YAG fluorescence screen having a 100 nm aluminum coating on the FEL side. In order to calibrate the high-F experiment we collected the ratio 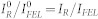in the 1–300 μJ I_FEL-range after having moved the sample 3 mm away from the focal plane (here F < 0.02 J/cm²). The results are shown in Fig. 5 and display a constant ratio, indicating no appreciable changes in the reflectivity in this low-F range. The 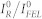value was used to determine the relative reflectivity variation in the high-F experiment, i.e.: .

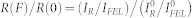Figure 4. Sketch of the experimental setup (side view - not to scale): GA, GM, SM and PD are the gas attenuator cell, the gas monitor, the spherical focusing mirror and the photodiode, respectively.

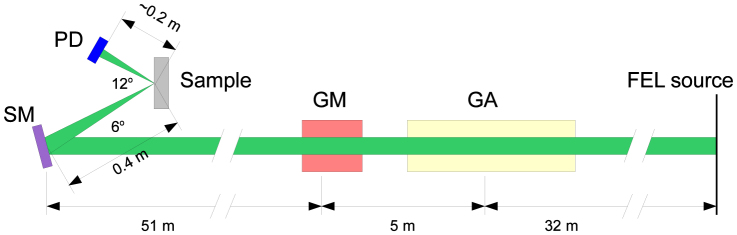
The FEL beam is shown in green. The relevant distances and angles are indicated.

Figure 5. 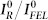-values as a function of F in the low-F range for 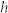ω = 18.9 eV.

Data analysis

The reflection coefficient at near normal incidence can be expressed in terms of the complex dielectric function () as⁷:

which is a sufficiently accurate approximation for sample thickness much larger than the penetration depth of the radiation (L < 23 nm in the present case). In metals a simple expression for is given by the Drude formula⁷:

In this model, a variation in R is ascribed to a change in ω_p or γ when the photon pulse impinges. However, as shown in Fig. 1, in the used ω range the dependence on ω_p is much more significant than on γ. So we arbitrarily set 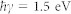, in analogy with what was found for Al (where γ ≈ 0.1 · ω_p(0)¹⁹) since a reference value for Ti is not available in the literature, and we drop a possible F-dependence of γ. We also stress that within the accuracy of the present experiment the results are only marginally affected by the choice of the 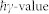within the 0.5–2.5 eV range, which essentially includes the observed in a large number of metals¹⁹,²⁰,²¹, as also shown in the Supplemental Information. For this reason the observed increase in R was related to an increase in ω_p and then in N_e through Eq. (1). As quoted in the main text, in order to provide a quantitative estimate we assumed that N_e is proportional to and we considered both the time (t) and transverse spatial (x, y) profiles of the FEL pulse. These result in a (t, x, y)-evolution of the reflectivity (R(F, t, x, y)), which can be calculated using Eqs. (3) and (4) assuming 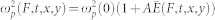, where

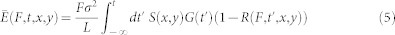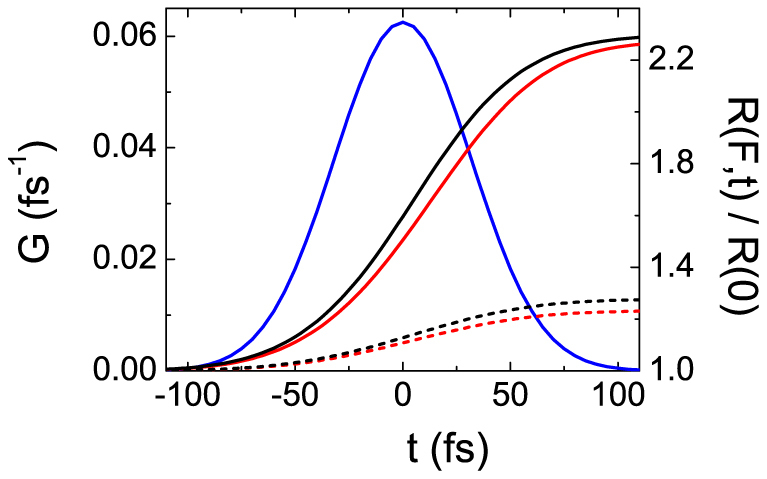
is the spatial profile of the energy density at time t deposited in a sample layer (involved in the reflectivity process) of thickness d < L below the surface, where G(t) and S(x, y) are the normalized time and space intensity distributions. These are approximated by Gaussian functions with σ_x = σ_y = 5 μm and σ_t = 45 fs. σ_t was evaluated as 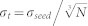³², where σ_seed = 70 fs is the time duration of the seed laser pulse (measured with an optical cross-correlator) and N = 4 is the harmonic number at which the FEL radiators were tuned. Representative t-traces of R(F, t)/R(0) = (1/R(0)) ∫ dx ∫ dyS(x, y)R(F, t, x, y) are shown in Fig. 6 along with G(t). It is worth stressing that the possibility to approximate G(t) with a well defined function (which ultimately permitted us to carry out the present data analysis) is one of the advantages related to the use of seeded FELs. Finally, the factor 1 − R(F, t, x, y) in Eq. (5) accounts for the reduction in the amount of energy available at later times for further excitation due to the t-increase in ω_p (and thus in R) within the FEL pulse duration. Finally, the observed R(F)/R(0) is simply given by the space-time average of R(F, t, x, y), i.e.:

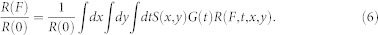The mean ion charge (or equivalently the average free electron density) can be calculated as well through the definition of ω_p (see Eq. (1)), i.e.:

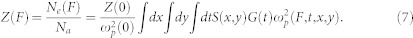Figure 6. t-dependence of G(t) (left scale; blue line) and of R(F, t)/R(0) (right scale; black/red and full/dashed lines are ω = 18.9/20 eV and F = 20/5 J/cm², respectively).

Author Contributions

F.B. conceived the experiment and data interpretation. E.P., E.G. and A.G. realized the experimental setup. F.B., E.P., E.G., R.C., A.B., F.D.A., A.D.C., S.D.F., M.M., L.P. and M.S. performed the measurements. F.B. carried out the data analysis. F.B., C.M., E.G., E.P., A.D.C., R.G. and A.F. discussed the data and wrote the paper.

Supplementary Material

Supplementary Information

Supplementary information