A bottom-up control on fresh-bedrock topography under landscapes

Significance

Hilly landscapes are typically mantled with soil and underlain by a weathered bedrock zone that may extend tens of meters beneath the surface before reaching fresh bedrock. The weathered bedrock zone influences water runoff to channels, the chemistry of that water, the rates and processes of erosion, and atmospheric processes due to plant uptake of moisture and return to the atmosphere. However, the spatial pattern of the underlying fresh-bedrock surface is essentially unknown. We present a testable model that predicts hillslope form and the depth to fresh bedrock. The depth increases upslope and depends strongly on the porosity and permeability of the bedrock and the rate of channel incision at the base of the hillslope.

Abstract

The depth to unweathered bedrock beneath landscapes influences subsurface runoff paths, erosional processes, moisture availability to biota, and water flux to the atmosphere. Here we propose a quantitative model to predict the vertical extent of weathered rock underlying soil-mantled hillslopes. We hypothesize that once fresh bedrock, saturated with nearly stagnant fluid, is advected into the near surface through uplift and erosion, channel incision produces a lateral head gradient within the fresh bedrock inducing drainage toward the channel. Drainage of the fresh bedrock causes weathering through drying and permits the introduction of atmospheric and biotically controlled acids and oxidants such that the boundary between weathered and unweathered bedrock is set by the uppermost elevation of undrained fresh bedrock, Z_b. The slow drainage of fresh bedrock exerts a “bottom up” control on the advance of the weathering front. The thickness of the weathered zone is calculated as the difference between the predicted topographic surface profile (driven by erosion) and the predicted groundwater profile (driven by drainage of fresh bedrock). For the steady-state, soil-mantled case, a coupled analytical solution arises in which both profiles are driven by channel incision. The model predicts a thickening of the weathered zone upslope and, consequently, a progressive upslope increase in the residence time of bedrock in the weathered zone. Two nondimensional numbers corresponding to the mean hillslope gradient and mean groundwater-table gradient emerge and their ratio defines the proportion of the hillslope relief that is unweathered. Field data from three field sites are consistent with model predictions.

Uplift and erosion of bedrock commonly leads to ridge and valley topography variably mantled with weathered bedrock and soil. Quasi-steady-state conditions may develop in which the topography is statistically constant as channels incise, hillslope surfaces erode, and fresh bedrock is uplifted to the surface. As this fresh bedrock rises up, it enters a near-surface zone where weathering irreversibly breaks and alters the rock before it is entrained into the mobile soil mantle and transported to adjacent streams. Variably weathered bedrock occupies the zone between the top of the fresh bedrock and the bottom of the soil. Here we identify Z_b as the elevation of the transition from fresh to weathered bedrock (Fig. 1).

Fig. 1.

Conceptual model showing the elevation of fresh bedrock, Z_b, under ridge and valley topography with a thin soil mantle overlying a weathered bedrock zone that extends to Z_b. Channel incision, at the rate C_o, drives hillslope erosion and drainage of fresh bedrock (flow paths illustrated with blue arrows). (Left) The model framework and assumptions. At the ridgetop (x = 0), the surface elevation is Z_s0 and the fresh-bedrock elevation is Z_b0. Groundwater flux, q_w, is horizontal and proportional to the water table gradient, Z_b. Soil transport, q_s, is proportional to the surface slope, 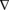Z_s. All soil and water leaves the hillslope at L where the hillslope meets the channel. At steady state, the rate of channel incision (C_o) is equal to the uplift rate such that the ground surface, Z_s and surface of the fresh bedrock, Z_b, are stationary.

The transport of sediment and water from hillslopes to stream channels is influenced by the rock property changes that result from weathering. Hence, the depth to and topography of Z_b is an important driver in runoff generation and landscape evolution. Weathering tends to increase bedrock hydraulic conductivity and porosity, allowing infiltrating waters to perch on underlying fresh bedrock and flow laterally to stream channels (Fig. 1). Field studies that have instrumented the weathered rock zone have shown that this perched groundwater path can deliver most of the stream runoff (1–4) and can be the source of sustained summer baseflow (5). The chemical evolution of hillslope runoff may be strongly dictated by the depth to Z_b and flow paths through the weathered zone (6–8). The weathering of bedrock may also increase moisture retention, which can be exploited by vegetation to sustain transpiration (9, 10). Furthermore, water exfiltration from this zone on steep slopes can cause localized elevated pore pressures and landslides (11), and the change in rock mass strength across this boundary due to weathering may localize deep-seated landslides (12, 13).

Collectively, these observations suggest that, aside from the ground surface, the topography of Z_b is the most important boundary controlling surface and near-surface processes, and as such, observation and theory are needed to understand what controls its structure across a landscape. Field studies that have directly documented the depth to fresh bedrock underlying ridge and valley topography (e.g., refs. 14, 15) are rare and none have depicted the detailed 3D pattern of Z_b relative to surface topography. Nonetheless, the few studies that have mapped Z_b under hillslopes have found a tendency for the weathered zone to be thickest at the ridge top and progressively thin downslope (14–18) (as illustrated in Fig. 1). Although Pavich (15) and Feininger (18) associate this trend with areas of low relief, studies in steep landscapes in the California and Oregon Coast Ranges (5, 6) have documented a systematic upslope thickening of the weathered zone as well (Fig. S1).

It is commonly assumed that the depth of weathered bedrock is controlled by downward propagating (top-down) processes driven by the advance of chemically reactive meteoric water into the underlying fresh bedrock (e.g., ref. 19). The top-down hypothesis leads to a weathered zone thickness that is set by the relative rates of erosion and the downward propagation of the weathering front. Approaches to addressing this hypothesis have included reactive transport modeling (e.g., ref. 20) and extension of the soil production function (21) to the weathered bedrock zone through a negative feedback between weathered zone thickness and erosion rate (e.g., ref. 22). For a convex 2D hillslope with a mobile weathered layer composed of soil and weathered bedrock, Lebedeva and Brantley (20) propose that the downslope steepening of the topographic surface may lead to progressively less water flux normal to the underlying reactive bedrock and, consequently, a weathered zone that thins downslope.

An alternative hypothesis for the downslope decrease in depth to Z_b under hillslopes is suggested by field observations of weathering profiles. Some of the earliest quantitative observations of weathering profiles identified the role of groundwater in impeding chemical weathering, and restricting the depth of the weathered zone (e.g., refs. 14, 16, 23, 24), such as occurs in supergene enrichment processes (25). In fresh bedrock of sufficiently low hydraulic conductivity, nearly stagnant or slowly moving water will reach chemical equilibrium and chemical weathering reactions will slow or stop (19, 26). In addition, the chronic saturation of fresh bedrock prevents mechanical breakdown due to swelling and contraction cycles associated with wetting and drying (27). Drainage of this fresh bedrock permits meteoric fluids to enter from above, thus allowing atmospherically and biotically controlled acids and oxidants to enter pore spaces and induce weathering reactions.

These observations suggest a “bottom up” control on the elevation of fresh bedrock under hillslopes in which drainage of saturated fresh bedrock is the key process. We propose that: (i) fresh bedrock that is advected into the near-surface environment through uplift and erosion arrives saturated with nearly stagnant pore fluid that is in chemical equilibrium with surrounding mineral surfaces; (ii) in this environment, channel incision creates a lateral head gradient in the fresh bedrock and induces drainage toward the adjacent channel; and (iii) drainage may cause drying and fracturing of the bedrock and permit meteoric water to enter the fresh bedrock, inducing weathering at the rate that the fresh bedrock is drained. For these conditions, we propose that the fresh-bedrock drainage profile defines Z_b. The depth of fresh bedrock along a hillslope will depend on both this groundwater-drainage control and on the erosion shaping the surface topography. Here we predict the thickness of the weathered bedrock zone by coupling a groundwater flow model with a surface erosion model.

Model for a Bottom-Up Limit To Bedrock Weathering

Consider the simplest case described above: a steady-state landscape in which hillslope erosion has adjusted to and matches the uplift rate and adjacent channel incision rate, C_o. The landscape is mantled with soil, and a steady-state groundwater flow system drains water from the uplifting fresh bedrock to the adjacent channel (Fig. 1). Assume that uplifted bedrock remains both unweathered and saturated until it reaches the top of the drainage profile to the adjacent channel. After the bedrock is advected above the elevation of the drainage profile (Fig. 1), it desaturates, weathers instantaneously, and develops a significant increase in porosity and permeability such that seasonal groundwater dynamics above Z_b do not influence drainage of the low conductivity, slowly draining bedrock. For a steady-state groundwater system, the shape of the drainage profile will be set, then, by the porosity and saturated hydraulic conductivity of the bedrock and the rate of channel incision. In effect, “recharge” to this groundwater system is only accomplished by the upward advection of saturated bedrock from below (Fig. 1).

The presence of a soil mantle allows us to assume that surface sediment flux is proportional to slope, the divergence of which is the erosion rate. For simplicity, we use the common expression 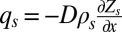, where q_s is the sediment transport rate per unit contour length (MT⁻¹ L⁻¹), Z_s is the local elevation, x is the distance from the hillslope divide, is the soil bulk density (M L⁻³), and D is a rate constant often referred to as the soil diffusivity (L² T⁻¹) (28). At steady state, uplift and erosion are equal to the channel incision rate, C_o, the soil thickness is constant, and erosion is matched by conversion of bedrock to soil at the rate of 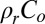in which 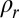is the weathered bedrock bulk density at the base of the soil column. For a constant C_o, the surface topography, Z_s, is a convex up profile given by

where L is the hillslope length (Supporting Information). Weathering of the bedrock in this case reduces the bulk density but does not lead to collapse or consolidation of the weathered bedrock column. The surface topography, Z_s, that results from a nonlinear relationship between soil flux and slope (Eq. S10), following Roering et al. (29), is also used in the analysis that follows however the linear form is shown here for simplicity (Supporting Information).

In the saturated fresh bedrock, the one-dimensional, steady-state form of the Boussinesq equation for groundwater flow (30) is

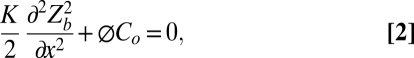where K is the saturated bedrock hydraulic conductivity (L/T) and recharge is defined as the channel incision rate, C_o, times the saturated drainable pore space, set equal to porosity, ϕ (Supporting Information). Assuming strictly horizontal flow, topographic symmetry about the ridge, and that the elevation of the channel is the bottom of the flow system, we arrive at

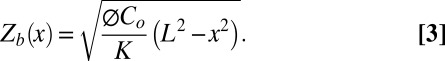The difference between Eq. 1 and Eq. 3 gives the thickness of the weathered zone (including soil), H, as a function of position along the slope

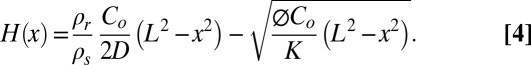H(x) always increases toward the divide, so to explore the controls on the weathered zone thickness (and thus the distance from the ground surface to fresh bedrock), we focus on the ridgetop (x = 0). At the ridgetop, the nondimensional ratio of bedrock relief, Z_b0, to surface relief, Z_s0, is given by

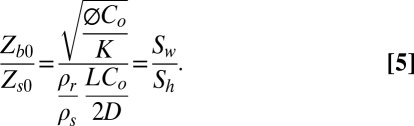Hence, the proportion of the hillslope underlain by fresh bedrock at the divide, Z_b0/Z_s0, is a function of the ratio of two dimensionless numbers: the numerator is the mean slope of the water table, S_w, and the denominator is the mean slope of the surface topography, S_h (Fig. S3). Seven terms must be evaluated to solve Eq. 5. The lowering rate, C_o, enters both dimensionless numbers, as C_o sets the pace for both landscape lowering and drainage of the bedrock.

The residence time of material that arrives at the soil bedrock boundary at the ridgetop, T_r0, is calculated as the ridgetop weathered thickness divided by the channel incision rate. Thus, from Eq. 4, the residence time at the divide is

The forms of Eqs. 4, 5, and 6 derived using the nonlinear relationship between slope and soil flux are given in the Supporting Information.

Fig. 2A shows qualitatively how the topographic profile, Z_s(x) and the bedrock profile, Z_b(x), vary with the two nondimensional variables corresponding to the mean slope of each profile. Higher mean hillslope gradients (S_h), due to high uplift or incision rates, longer hillslopes and lower soil diffusivity lead to a deeper weathered bedrock zone. A higher average groundwater-table slope (S_w), due to high C_o and low thins the weathered zone by increasing Z_b.

Fig. 2.

Controls on the fresh-bedrock profile and thickness of the weathered zone under hillslopes. (A) Conceptual illustration of the dependence of the weathered zone thickness on the mean hillslope gradient, S_h, and mean groundwater table slope, S_w, and thus soil transport and hydraulic properties (all terms defined in the text). (B) The dependence of the ratio of fresh-bedrock relief to hillslope relief at the ridgetop, Z_b0/Z_s0, on S_h and S_w illustrates the parameter space for which the weathered zone is expected to be limited in vertical extent by drainage of fresh bedrock. Observations from three sites (solid symbols) and data associated with the example profiles shown in Figs. 3 C–F (open symbols) are plotted. Open circles represent results of the linear soil flux model (Eq. 5) and open squares represent the nonlinear model (Eq. S12). The dark gray area indicates where S_w exceeds S_h and thus bedrock is expected at the surface. The light gray area indicates where S_w is so low relative to S_h that Z_b0 is essentially at the elevation of the channel. (C–F) Four example profiles for a fixed hillslope length (L = 100 m) and lowering rate (C_o = 0.1 mm/y) demonstrate the influence of soil diffusivity, D, and the ratio of hydraulic conductivity to porosity, 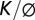, on the thickness and residence time of the weathered bedrock zone. Fresh bedrock is denoted by dark gray. The surface topography was calculated using the nonlinear model (29) assuming a critical slope, S_c, of 1.2 (Eq. S10). The corresponding linear profiles are shown in Fig. S2.

Fig. 2B plots the dependence of Z_b0/Z_s0 on S_w and S_h. If S_w is calculated to equal or exceed S_h, bedrock is expected at the surface and the model no longer applies. Steep slopes characterized by S_h above 1.0 are typically associated with exposed bedrock at the surface (31). For fresh bedrock to occupy a significant portion of the hillslope relief, S_w must be similar to S_h, which implies (according to Eq. 5) . If S_w is much less than S_h, then effectively Z_b is at the elevation of the adjacent channel bed.

Fig. 2 C–F show the predicted Z_s and Z_b profiles as well as the calculated residence time for material within the weathered bedrock zone for four cases. C_o is held constant and the effects of varying D (thus changing S_h) and varying 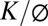(thus changing S_w) are shown. The resulting S_h and S_w for these four profiles are plotted in Fig. 2B for both the linear and nonlinear soil transport case. For sufficiently steep slopes such that nonlinear soil transport processes prevail, the nonlinear model (Eq. S10) is used to plot the surface profiles (Profiles resulting from the linear model are shown in Fig. S2). In general, the nonlinear model reduces the slope and relief of the hillslope, making it more likely that Z_b is some significant portion of the relief. Note that the modeled groundwater table is predicted to intersect the ground surface at the lowest, steepest portion of the hillslope. Although this does violate the model assumptions (e.g., soil mantled, no seepage face), this prediction is consistent with common field observations of relatively fresh, saturated bedrock exposed at the lower, steep portions of hillslopes (Fig. S1). The model also predicts a systematic thickening of the weathered bedrock zone toward the divide and, correspondingly, a systematic increase in residence time of material transiting through the weathered bedrock zone. Despite the relatively high incision rate (0.1 mm/y), the residence time through the weathered bedrock zone is calculated to be on the order of 10⁵ to 10⁶ years.

In Fig. 2B, we plot field data from three field sites where the Z_b surface was reported and estimates of erosion rates and bulk densities are available: Rivendell (14), Coos Bay (15), and Rondônia (32). The Rondônia site is located in the Rio Branco and Rio Massanagana watersheds near the town of Ariquiemes, Rondônia, Brazil (9°55′33 S; 63°2′ W) and is underlain by gneiss (32). Both the Rivendell and Coos Bay sites are located in the Pacific Northwest of the United States and are underlain by turbidite sequences of shale and sandstone, with the Rivendell nearly all shale (e.g., argillite; ref. 14) and Coos Bay mostly sandstone (e.g., greywacke; ref. 15). In Fig. 2B, the observed S_w and S_h are plotted for each site, leading to Z_b0/Z_s0 values of 0.5, 0.72, and 0.83 for Rondônia, Rivendell, and Coos Bay, respectively. C_o at the Rondônia site is estimated to be ∼0.004 mm/y (32) and the 500-m hillslope is roughly convex. C_o is estimated to be roughly 0.4 mm/y at Rivendell (33) and ∼0.1 mm/y at Coos Bay (6). The high S_h values for the Rivendell and Coos Bay sites and the apparent role played by periodic landsliding indicate that the nonlinear soil-transport relationship (Eq. S10) is the more appropriate soil flux relationship for these sites (29).

Although S_h can be observed from topographic data, and depends on relatively constrained values of transport parameters, C_o, and bulk densities, S_w defines the lower boundary and varies with both C_o and a material property, , which ranges over several orders of magnitude. The hydraulic conductivity, K, of consolidated rocks is known to range between 10⁻¹² to 10⁻² m/s, and effective porosity, ϕ, ranges from nearly 0 to 50% (30, 34). Observed values of S_w and C_o can be used to estimate 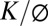(Fig. S4). For possible values of C_o, (0.001–10 mm/y; ref. 35), Z_b will be above the elevation of an adjacent channel for 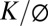between ∼10⁻¹³ and 10⁻⁸ m/s (Fig. S4). Based on lithologic permeability compilations reported by Freeze and Cherry (34) and recently supported by field data compiled by Gleeson et al. (36), this range of is associated with shales and unfractured metamorphic and igneous rocks (assuming ϕ = 0.1).

The observed persistence of the water table at the Z_b boundary at the end of summer in Rivendell over 7 y of monitoring (5), argues strongly for a very low bedrock value, consistent with the predicted value of 10⁻¹⁰ m/s. The value predicted for the Coos Bay site is 10⁻¹¹ m/s (Fig. S4). Ebel et al. (37) modeled the runoff and groundwater dynamics for a relatively short period at Coos Bay and assigned a 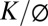value of 5 × 10⁻⁷ m/s for the fresh-bedrock zone. The groundwater table continually dropped, however, during the modeling period (38), hence the modeled did not lead to the observed condition of a persistent water table significantly higher than the channel elevation.

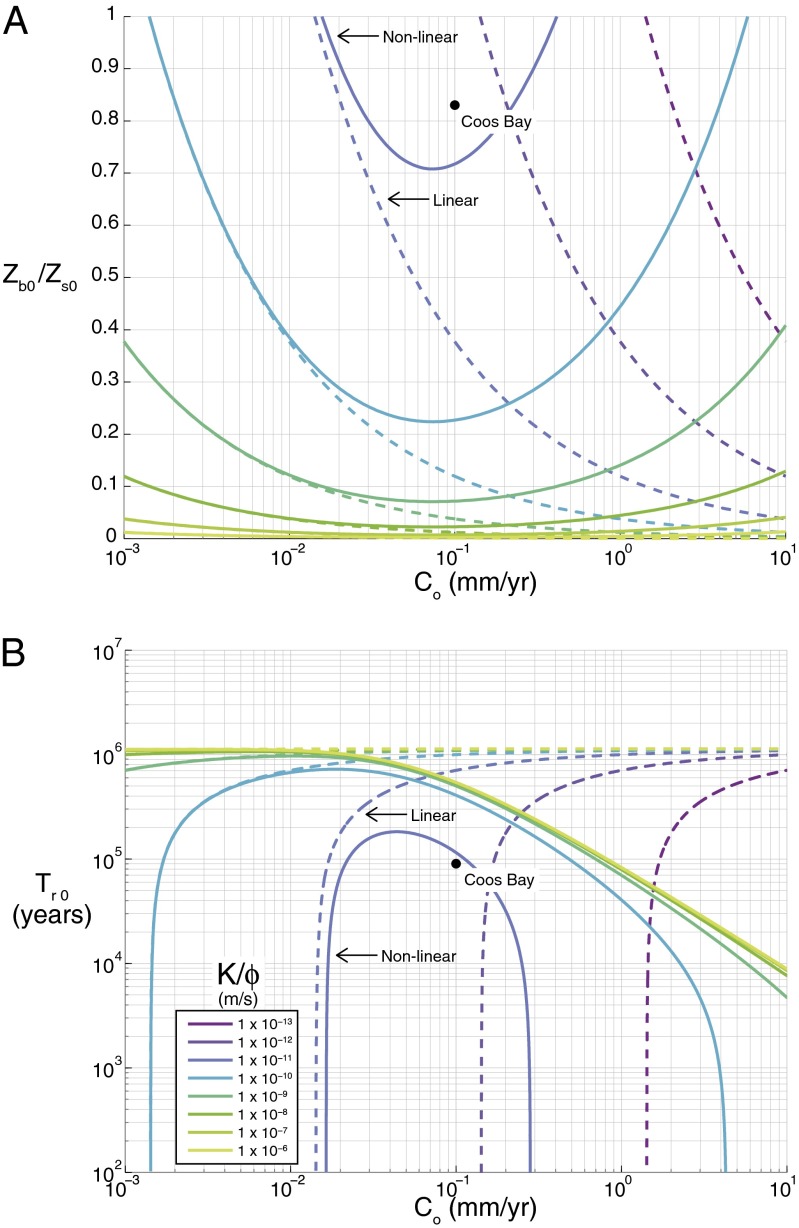
Using model parameters for the Coos Bay site (Table S1), Fig. 3 illustrates the influence of C_o on the relative weathered zone thickness (Z_b0/Z_s0) and the residence time of material arriving at the soil-weathered bedrock boundary at the ridgetop (T_r0). The linear model for Z_s(x) predicts that as channel incision rates and 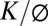increase, the weathered zone progressively thickens (Z_b0/Z_s0 decreases) and the material residence time correspondingly increases (Fig. 3). In contrast, the onset of nonlinear soil transport dominance, which generally applies as landscapes steepen (29, 39, 40), significantly slows the rate of increase of the hillslope gradient with increasing channel-incision rate. Consequently, because S_w continues to increase with incision, the predicted weathered bedrock zone reaches a maximum value (minimum Z_b0/Z_s0) and then thins as C_o increases (Fig. 3A). Increasing lowers the weathered bedrock zone to the channel elevation (Z_b0/Z_s0 approaches 0) but does not eliminate or shift the value of C_o at which the lowest Z_b0/Z_s0 occurs. The material residence time correspondingly has a maximum value, but it shifts to greater values with decreasing C_o and increasing . Although the general pattern illustrated in Fig. 3 holds, the specific values depend on L, , and transport parameterization (D, S_c).

Fig. 3.

Mapping the ratio of saturated hydraulic conductivity to porosity (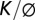), fresh-bedrock relief ratio (Z_b0/Z_s0) and mean residence time (T_r0). (A) The influence of channel incision rate, C_o, on the fraction of the total hillslope relief that is unweathered (Z_b0/Z_s0). (B) The influence of C_o on the residence time of the weathered material that arrives at the soil–bedrock boundary at the ridgetop (T_r0). In both A and B, solid lines represent predictions using a nonlinear relationship between soil flux and slope (Eqs. S12 and S13) and dashed lines represent the linear model. Model parameters for Coos Bay were used to generate predictions (Table S1). A range of is shown to illustrate how the deviation between the linear and nonlinear model predictions depend on 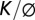such that higher will produce a thicker weathered zone. Deviations between the two model results are minimal at low C_o but increase with increasing C_o. Whereas the linear model predicts a thickening of the weathered zone (and thus an increase in residence time) with increasing erosion rate, the nonlinear model predicts a maximum weathered zone thickness that depends on the bulk density ratio, 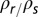, hillslope length, L, and critical slope, S_c.

Discussion

The coupled equations that predict the thickness of the weathered zone (Eq. 4), the ratio of fresh bedrock to surface relief (Eq. 5), and the residence time of material in the weathered zone at the divide (Eq. 6) depend on seven parameters for the linear soil flux case, and eight for the nonlinear case. Saturated conductivity and porosity of the fresh bedrock, which are treated here as the ratio 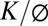, are the most difficult parameters to measure. For the likely range of C_o for which the model has applicability, significant S_w (i.e., Z_b above the elevation of the adjacent channel) only occurs for 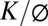between 10⁻¹³ and 10⁻⁸ m/s (Fig. S4). Hence, our model suggests that bedrock of low conductivity is required for a significant portion of the hillslope relief to remain unweathered. As argued by Hatijema and Mitchell-Bruker (41) and explored by Gleeson et al. (36, 42), the tendency for a water table to reflect the local topography increases with decreasing hydraulic conductivity, Gleeson and Manning (43) further suggest that low-hydraulic-conductivity crystalline rock within hillslope interiors limits the role of regional groundwater flow between watersheds.

Despite a few deep-conductive fractures in the bedrock, Z_b may remain elevated well above the channel floor. At the Coos Bay site (Fig. S1) for example, Anderson et al. (6) noted two fractures between 12 and 36 m below the surface at the divide that showed signs of oxidation in otherwise fresh bedrock. Similarly, Gburek and Folmar (44) noted the occurrence of local weathered and more conductive fractures within fresh sedimentary rocks in a drill hole used for characterizing groundwater dynamics on an unglaciated hill in Pennsylvania. This suggests that even though rare fractures may be seasonally dynamic in transmitting some deeper groundwater flow, Z_b might be maintained well above the channel elevation by the predominance of low-conductivity rock matrix and the absence of abundant conductive fractures (Supporting Information).

The boundary condition for Z_b(x) in Eq. 2 is that all lateral flow emerges at the channel surface at the base of the hillslope (Fig. 1). The flux of water per unit length of channel due to drainage of the fresh bedrock is simply 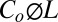, which, given very slow incision rates (less than 1 mm/y) and low porosity (less than 0.1), will be typically less than 10⁻³ m³/m-y. This is an undetectable amount of runoff addition to a channel. Even in a seemingly dry channel, slow flow to the channel may occur.

Although the model successfully predicts a thickening weathered zone toward the divide, it also predicts a surprising Z_b dependency on tectonics and climate. The depth of weathering and the degree of weathering is not a simple function of erosion rate. One might expect that faster erosion rates would thin a weathering profile, but instead the profile initially thickens with increasing uplift (Fig. 3) due to the more rapid steepening of the hillslope than the groundwater table. This thickness decreases once nonlinear soil transport prevails. Hence, for the nonlinear case, fresh bedrock could be at the surface if erosion rates are slow or fast, and, for the Coos Bay example this requires channel-incision rates less than 0.02 mm/y and greater than 0.4 mm/y. Residence time, and thus, degree of alteration of the weathered rock zone is correspondingly a parabolic function of incision rate, with shorter residence times and a narrower range of possible residence times with decreasing 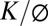. Observations in the slowly eroding landscapes of tropical Rondônia, Brazil (32) (Z_b0/Z_s0 = 0.5) and the humid temperature Appalachian piedmont (15) (Z_b0/Z_s0 = 0.64–0.8) suggest that the bottom-up limit on Z_b may have broad application beyond areas of rapid uplift.

Neither the elevation profile of Z_b (Eq. 3), nor the thickness of the weathered zone (Eq. 4) is an explicit function of rainfall or runoff rate but climate may play an important role (see full discussion in Supporting Information). Climate influences L (or valley wavelength; e.g., refs. 45, 46), C_o (e.g., ref. 47), D (48), and due to chemical weathering (e.g., ref. 6).

Three-dimensional topographic effects arising from ridge and valley topography and vertical or lateral heterogeneities, especially of , could significantly affect the Z_b profile. The timescale to develop the steady-state profile modeled here is possibly several relief replacement times (48, 49). For example, a 50-m-high hillslope eroding at 0.1 mm/y requires at least 500,000 y to reach steady state. C_o is unlikely to be constant over such timescales. Global climate cycles and internal dynamics of stream capture, episodic instabilities (e.g., landslides), variably resistant bedrock, propagating knickpoints, and lateral shifting of the channel will all contribute to nonuniform channel incision, even under relatively constant uplift. Such variations could also lead to perturbations in the Z_b profile, and in the case of lateral channel shifting, dissociation of the Z_b profile from the more rapidly adjusting surface topographic profile. Numerical modeling of unsteady C_o is needed to evaluate the degree to which the Z_b profile is damped in response to perturbations.

Conclusion

Until hillslope interiors are more accessible, either through geophysical imaging or extensive deep drilling, the relationship between surface topography (Z_s) and the topography of the transition to underlying fresh bedrock (Z_b) will remain essentially unknown. This knowledge gap is important to geomorphic, hydrologic, geochemical, ecological, and atmospheric processes. Our theory suggests that slow groundwater drainage of fresh bedrock creates a bottom-up control on the elevation of Z_b. Consistent with limited field data, the weathered zone is predicted to thicken toward the divide. Z_b can be a significant fraction of the hillslope relief under a specific set of circumstances for a given hillslope length: (i) the underlying fresh bedrock 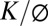is less than 10⁻⁹ m/s and fractures are rare and mostly nonconductive; (ii) channel incision rate is slow (order 0.1 mm/y or less) or sufficiently high that nonlinear soil transport dominates; (iii) dissolution significantly lowers the weathered bedrock bulk density (leaving less to be carried away by soil transport); and (iv) soil diffusivity is high. The model is testable because all variables can be determined with current technology of topographic surveying, cosmogenic nuclide measurements of erosion rates, field mapping of Z_b through drilling, and measurements of bulk density, porosity, and saturated hydraulic conductivity. The systematic drilling of ridgetops at well-chosen sites could demonstrate the circumstances where Z_b is below the surface and above the elevation of an adjacent channel and also evaluate if the model predicted corresponds with the observed rock type. Such work would illuminate the interior structure of hillslopes and allow for the systematic mapping of the fresh-bedrock topography under landscapes. Just as high-resolution digital elevation data of topography is revolutionizing earth-surface process research, we now need high-resolution maps of the topography of the weathering front, Z_b, under landscapes. This is a shallow frontier in earth-surface processes.