Abstract
In this paper we develop a novel approach for computing conformal maps between anatomical surfaces with the ability of aligning anatomical features and achieving greatly reduced metric distortion. In contrast to conventional approaches that focused on conformal maps to the sphere or plane, our method computes the conformal map between surfaces in the embedding space formed the intrinsically defined Laplace-Beltrami (LB) eigenfunctions. Utilizing the power of LB eigenfunctions as informative descriptors of global geometry, the conformal maps computed by our method can effectively align anatomical features on cortical surfaces. By computing such feature-aware conformal maps to a group-wisely optimal atlas surface, which is also computed with metric optimization in the LB embedding space, we develop a fully automated system for cortical labeling with the fusion of labels on a large number of atlas surfaces. In our experiments, we build our system with 40 labeled surfaces and demonstrate its excellent performance with leave-one-out cross validation. We also applied the automated labeling system to cortical surfaces reconstructed from MR scans of 50 patients with Alzheimer’s disease (AD) and 50 normal controls (NC) to illustrate its robustness and effectiveness in clinical data analysis.
1 Introduction
Automated analysis of neuro-anatomical surfaces such as the cortex plays an important role in brain mapping research where the ultimate goal is to accurately align corresponding anatomical regions and detect changes across population and time. In this work, we develop a novel approach for computing conformal maps between anatomical surfaces via metric optimization in the Laplace-Beltrami (LB) embedding space of surfaces [1, 2]. Guided by the LB eigenfunctions, the conformal maps from our method have the nice property of being able to align anatomical features and having significantly reduced metric distortion. As a demonstration of these properties, we apply the conformal maps to develop an automated labeling system of gyral regions on cortical surfaces by fusing labels from a large number of atlas surfaces. Cross-validation and application to clinical data analysis show that our method can achieve excellent performance.
Conformal maps were used successfully for medical shape analysis problems [3, 4], but the focus has typically been the mapping of surfaces to a canonical domain such as the sphere or plane. Because the canonical domains lack geometric similarity to anatomical surfaces, the conformal maps do not align anatomical features, but rather serve as a parameterization for downstream tasks such as registration [5]. While angles are preserved in conformal maps to canonical domains, large metric distortions are quite common. For example, we show in Fig. 1 the conformal map of a cortical surface to the unit sphere computed with the method in [4], where large variations of metric distortion can be seen clearly because of the geometric differences between the cortical surface and the sphere.
Fig. 1.
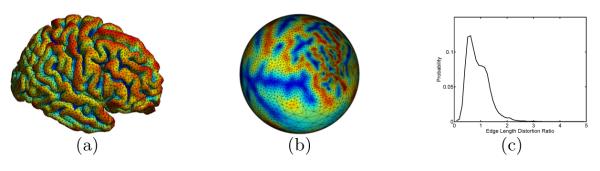
Spherical conformal parameterization. (a) Cortical surface. (b) Projection of the cortical surface mesh onto the sphere with the conformal map to the sphere. (c) After surface area normalization, the distribution of the ratio of the length of corresponding edges in the mesh of (b) and (a).
The eigen-system of the LB operator emerges recently as a novel way of studying anatomical shapes. It has been used for many surface classification and analysis works [6–8]. One important development is the embedding of a surface to a high dimensional space with eigenfunctions and the definition of rigorous distance measures[1, 2]. In particular, a surface mapping technique was proposed in the embedding domain with the optimization of conformal metrics[9]. In this work, we extend the method in [9] by establishing the connection between LB embedding and conformal maps, and thus developing a new way of computing conformal maps with metric optimization. As demonstrated in previous works [6–9], LB eigenfunctions are effective global descriptors of surface geometry. Minimizing distances in the embedding space is in effect the matching of these global descriptors, thus the conformal maps derived from metric optimization are feature-aware and can align geometric features on anatomical surfaces. Because of this property, there is no need of large metric distortion to match surfaces and the conformal maps generated by our method have greatly reduced metric distortions compared with maps to canonical domains.
Using the proposed metric optimization approach for computing conformal maps, we develop a new system to solve the challenging problem of automated cortical labeling [10–12]. Our cortical labeling system is based on the popular multi-atlas fusion approach in image segmentation [13–15]. Given a group of manually labeled surfaces, we first compute a group-wise atlas in the embedding space and align all individual atlas surfaces to it with metric optimization. To obtain the cortical labels of a new surface, we also perform metric optimization and align it with the group-wise atlas such that multi-atlas fusion can be performed using conformal maps between the subject surface and all individual atlas surfaces with labels. Note that we only need to compute one metric optimization to the group-wise atlas to obtain its conformal maps to all labeled surfaces. This allows the use of a large number of labeled surfaces in our system without significantly increasing the computational cost of the fusion process. In our experiment, we use cortical labels derived from the LPBA40 data set [16] to build the cortical labeling system. Leave-one-out cross-validation shows that our method can achieve accurate labeling of gyral regions. Application to 100 subjects from the Alzheimer’s Neuro Imaging Initiative (ADNI) [17] demonstrates its effectiveness in population studies.
The rest of the paper is organized as follows. We first develop the metric optimization approach for conformal mapping in section 2. After that, the multi-atlas fusion system for cortical labeling is developed in section 3. Experimental results will be presented in section 4 to demonstrate the effectiveness of our method. Finally, conclusions are made in section 5.
2 Conformal Mapping via Metric Optimization
Let (, g) be a genus-zero Riemannian surface where the metric g is the standard metric induced from . For a function f : , the LB operator on with the metric g is defined as:
| (1) |
where (gij) is the inverse matrix of g = (gij) and G = det(gij). Because the spectrum of is discrete, its eigen-system is defined as:
| (2) |
where λn and fn are the n-th eigenvalue and eigenfunction, respectively. The set of eigenfunctions Φ = {f0, f1, f2, ⋯ ,} form an orthonormal basis on the surface. Using the LB eigen-system, an embedding was proposed in [1]:
| (3) |
This embedding has the nice property of being isometry invariant. Given two surfaces and their LB embeddings, a rigorous distance measure called spectral l2 distance was proposed in [2].
Definition 1 (spectral l2-distance)
Let (, g1) and (, g2) be two surfaces. For any given LB orthonormal basis Φ1 of and Φ2 of , let
| (4) |
The spectral l2-distance d() between and independent of the choice of eigen-systems is defined as:
where and denote the set of all possible LB basis on and , and are normalized area elements, i.e., , and .
Because all genus zero surfaces are conformally equivalent, we propose here to minimize the spectral l2 distance as a new way to find conformal maps between surfaces. Given two surfaces (, g1) and (, g2), there exists a conformal metric wg1, where w : is a positive function defined on , such that the LB embedding of (, wg1) under this new metric will be the same as the LB embedding of because the LB embedding is completely determined by the metric, where and are the optimal basis that minimize the spectral l2 distance. Because (, g1) and (, wg1) are conformal, and the two manifolds (, wg1) and (, g2) are isometric when the metric w is chosen so that the spectral l2 distance is zero [2], we have a conformal map from (, g1) to (, g2) when we combine these maps. Let Id denote the identity map from to , the conformal map μ : from to is thus
| (5) |
where is the inverse map of the embedding
To find the conformal map, the critical question is the selection of the metric w such that we can minimize d(). As a first step, we develop the numerical scheme to compute the LB eigen-system given the weighted metric. After that, an energy minimization scheme will be developed to find the optimal weight. Let (, wg) denote a manifold with the weight metric = wg. The LB operator with the new metric is then and its eigen-system is :
| (6) |
For numerical computation, we represent as a triangular mesh with K vertices, where and are the set of vertices and triangles. At each vertex νi, we denote its barycentric coordinate function as ϕi, and represent the weight function as , and . By choosing η = ϕi as the test function, the weak form of (6) is:
| (7) |
To find the eigen-system under the weighted metric, we only need to solve a generalized matrix eigen problem:
| (8) |
where the matrix Q and U are defined as:
| (9) |
where ⟨·⟩ denotes the area of a triangle, (·) and (·,·) denote the neighborhood of vertices, and denotes the triangle formed by three vertices: νi, νvj, νk.
Because the definition of the spectral l2 distance includes the max and inf operations, it is non-differentiable with respect to the weight w. To find the optimal weight w that minimizes the spectral l2 distance of two surfaces (, wg1) and (, g2), we instead minimize a more tractable energy function. By solving the matrix eigenvalue problem in (8), we compute the eigenvalues and eigenfunctions of (m = 1, 2) and denote them as λm,n and fm,n. Assuming no multiplicity in the eigenvalues, the eigenfunctions are determined up to sign. For numerical approximation, we choose up to the N-th eigenfunctions to define the embedding space, thus the set can have 2N different basis. To match these two surfaces in the embedding space, we minimize the following energy function with respect to the conformal metric w:
| (10) |
When the energy equals zero, we can see that both distances have to be zero, thus the minimizer of the energy also minimizes the spectral l2 distance. For numerical solution, we represent the surfaces as triangular meshes (m = 1, 2). For the target surface, we fix its embedding by picking Φ2 randomly from . For the surface , we start with uniform weight w = 1 and iteratively update Φ1 and w to minimize E. At each iteration, we first compute the eigen-system and search Φ1 from to minimize E. With the current basis Φ1 and Φ2 for embedding, we denote Id1() = and Id2() = as the nearest point maps from to , and vice versa. Given these two maps, we write the energy in discrete form as:
| (11) |
where S() and S() are the surface area of and , the matrices U1 and U2 are defined in (9) with uniform weight, i.e., the standard metric induced from . Using the eigen-derivatives with respect to the weight functions, we can update the weight function w in the gradient descent direction as:
| (12) |
where and are the derivatives of the eigen-system with respect to the conformal metric. By repeating the above steps for searching Φ1 and updating w, we minimize the energy function until convergence. The final conformal map is then obtained by the composition of the embedding , the nearest point map Id1 and the inverse map as defined in (5).
3 Application for Multi-atlas Cortical Labeling
In this section, we develop an automated cortical labeling system using conformal maps computed from metric optimization. Given a set of P individual atlas surfaces with manually delineated labels, we first compute a group-wise atlas surface that minimizes its distance to all surfaces. After that, a multi-atlas fusion scheme is developed to automatically assign labels to unknown cortical surfaces.
3.1 Group-wise Atlas Construction
The group-wise atlas (, w*g) we want to compute has the smallest average distance to all individual atlas surfaces. Theoretically we can choose as any genus zero surface because they are conformally equivalent. In practice, we pick as the individual atlas surface that has the smallest distance to all other surfaces to speed up convergence. Our goal is to find the optimized metric w*g that minimizes the following energy function:
| (13) |
where Φ* and Φp are the LB basis for and (p = 1, ⋯, P).
To numerically compute the group-wise atlas, we follow a similar approach as in section 2 for metric optimization. For each surface , we compute its eigen-system and obtain the set for LB basis. At each iteration, we compute the eigen-system of (, w*g) and denote them as (λn, fn). The basis for each surface is then updated to minimize the energy and we denote them as (λp,n, fp,n) for . The gradient descent flow for the metric is then
| (14) |
where S(·) denote the area of surface, U and Up are defined as in (9) for , and , respectively. The interpolation matrix Ap, and Bp are used to represent the nearest point map between and in the embedding space. By repeating the above steps until convergence, we obtain the group-wise atlas (, w*g).
3.2 Fusion of Cortical Labels
Let Lp : denote the labels defined on the individual atlas surface, where is a set of discrete labels. Let denote the LB embedding of the group-wise atlas (, w*g). Using the metric optimization approach, we compute the optimized embedding for each surface that minimizes the distance to . For a new surface , we also compute its optimal metric wS such that the distance between its LB embedding and is minimized. As a result, the LB embeddings of the subject surface and individual atlas sufaces are all aligned and the conformal maps μp : can be defined easily:
| (15) |
where Idp denote the nearest point map from to .
Using these maps, we fuse the labels from (p = 1 , ⋯, P) with weighted voting to generate gyral labels on . Let be the i-th vertices, and be the Γ-ring neighborbood of νi. The correlation coefficient between the mean curvature of and the mean curvature of its map on is computed as:
| (16) |
For each label , its weight is calculated as Wq = Cp and the label is νi is
| (17) |
By applying the label fusion approach to all vertices on , we obtain the label map for the whole cortical surface.
4 Experimental Results
In this section, we present experimental results in cortical surface analysis to demonstrate our conformal mapping method with metric optimization. For all experiments, we choose the first N = 6 eigenfunctions, and use Γ = 4 as the size of vertex neighborhood for weight computation in label fusion.
4.1 Conformal maps between cortical surfaces
In the first experiment, we apply our metric optimization approach to compute the conformal map between two cortical surfaces. The source surface and the target surface are plotted in Fig. 2(a) and (b). With the iterative algorithm developed in section 2, the energy is minimized as plotted in Fig. 2(c). The final metric w for is plotted in Fig. 2(d). We can see that it intuitively captures the geometric differences between the two surfaces. For example, the metric w is less than one in the inferior temporal gyral region and shows that needs to shrink here to match corresponding region on . To illustrate the effect of the metric optimization process on matching geometric features, we plotted the 3rd and 6th eigenfunction of and in Fig. 3. As highlighted in regions enclosed by the dashed ellipses, the metric optimization process lead to much better match of eigen-functions in corresponding areas of the cortical surfaces.
Fig. 2.
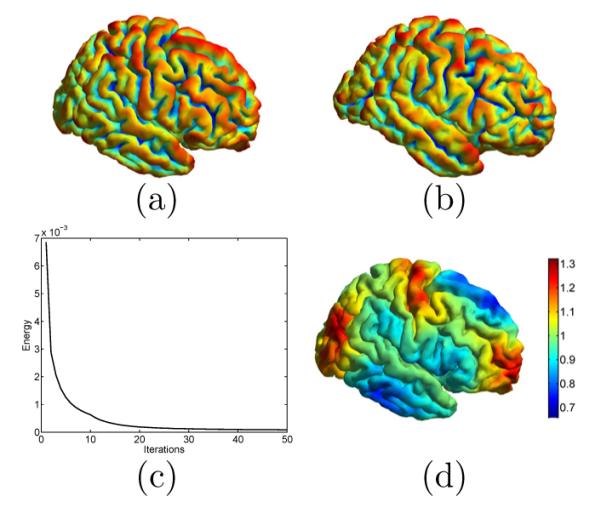
The computation of the feature-aware conformal map from the source surface (a) to the target surface (b). Both surfaces are color coded with their mean curvature. (c) The energy function decreases with the iterative metric optimization process. (d) The optimized metric w on the source surface .
Fig. 3.

Metric optimization results in better match of eigen-functions between and . (a)f1,3 on . (b) f2,3 on . (c) f1,3 after metric optimization. (d) f1,6 on . (e) f2,6 on . (c) f1,6 after metric optimization. Here fm,n denote the n-th eigenfunction on .
In Fig. 4(a), we plotted the projection of the mesh structure of onto using the conformal map, i.e., μ(), where the mean curvature of is also carried over to color code the surface μ(). By examining the mean curvature map with the sulcal and gyral pattern of , we can see the conformal map very well matches the folding patterns of the surface. Comparing the regular mesh structure in Fig. 4(a) with that of Fig. 1(b), we can see metric distortion is greatly reduced as compared with the spherical map. More quantitatively, we plotted the distribution of angle difference and edge length ratio between μ() and . Compared with the plot in Fig. 1(c), we can see the distribution of the edge length ratio here is centered around one. This clearly shows that the conformal map computed from our method only very well preserves the angle, but also greatly reduces metric distortion.
Fig. 4.
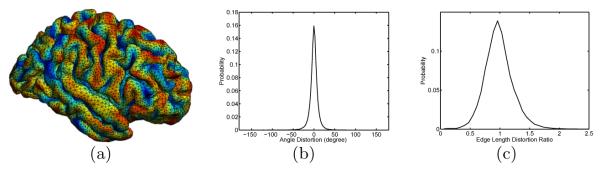
Angle and metric distortion in the conformal map. (a) Projection of the triangular mesh of onto with the conformal map. (b) Angle distortion distribution. (c) Edge length distortion ratio distribution.
4.2 Multi-atlas fusion with LPBA40 data
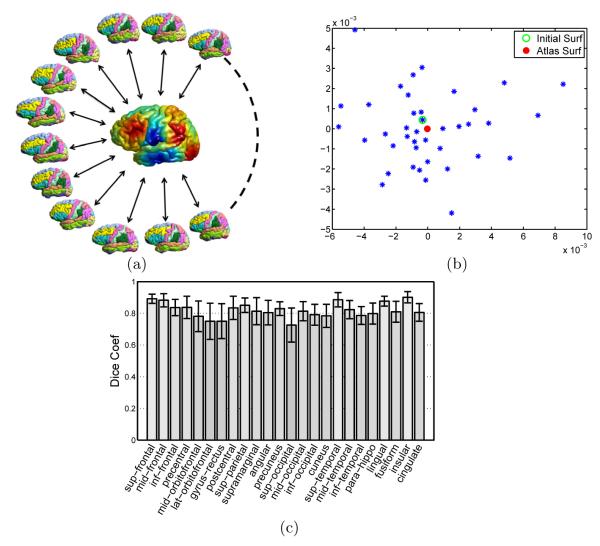
In the second experiment, we build the multi-atlas cortical labeling system using the publicly available LPBA40 data [16], which is a set of 40 MR images with manually labeled regions. We first applied a reconstruction method [18] to extract the triangular mesh representation of the cortical surfaces. In this work, we only use the left hemisphere of each image because the two hemispheres are intrinsically similar. A set of 24 gyral labels are projected onto the cortical surfaces to generate the 40 labeled individual atlas surfaces as plotted in Fig. 5 (a). A group-wise atlas is computed with the algorithm in section 3.1 using the 40 cortical surfaces and the result is plotted in the center of Fig. 5 (a), where the surface is color coded with the optimized metric. We also applied multi-dimensional scaling (MDS) analysis to the individual atlas surfaces and the group-wise atlas and projected them onto a 2D plane shown in Fig. 5(b), where the spectral l2 distance between surfaces are used in MDS analysis. From this plot we can see that the group-wise atlas moves the initial surface, which provides the geometric representation for the atlas, toward a more centralized location in this population.
Fig. 5.
Multi-atlas fusion for cortical labeling. (a) All labeled surfaces are mapped to the embedding space with metric optimization to match the group-wise atlas shown in the center. (b) A multi-dimensional scaling (MDS) illustration of the surfaces and their group-wise atlas surface. (c) Bar plots of Dice coefficients of the 24 gyral regions in leave-one-out cross-validation.
Using the 40 labeled surfaces, we validated our multi-atlas fusion algorithm in section 3.2 with leave-one-out cross-validation. Note that the group-wise atlas serves only as a geometric target for aligning LB embeddings and does not contain label information, thus it is fixed during the cross-validation. For each surface, we obtain its label by fusing the labels from the other 39 surfaces, and the Dice coefficient is computed for each gyral region by comparing with the manual labels. By repeating this process 40 times, we obtain the mean and standard deviation of Dice coefficients for each of the 24 gyral regions and show them collectively as bar plots in Fig. 5(c). The average Dice coefficient is 0.82 across all regions and surfaces. In an extensive validation study [19], for both state-of-the-art surface-based and volume-based registration methods, the mean Dice is below 0.8 on the same data. This shows that our method is able to achieve excellent performance in automated cortical labeling.
4.3 Results from ADNI Data
In the third experiment, we applied the cortical labeling system in the second experiment to MR scans from 50 AD patients and 50 NCs of the ADNI study[17]. Both the left and right hemispherical cortical surfaces are reconstructed with the method in [18]. The labeling system is fully automated and there is no need of any special handling for the left and right hemisphere because the metric optimization process is based on intrinsic geometry. For all 100 scans, our system successfully generated the gyral labels. As a demonstration, we plotted the results on three subjects in Fig. 6. We can see that excellent labeling performances were achieved on both hemispheres.
Fig. 6.
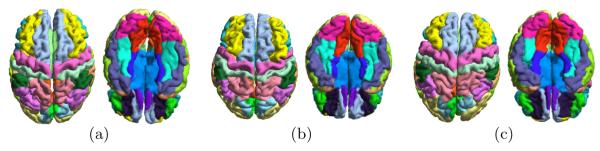
Three examples of labeling from the ADNI data are shown in (a), (b) and (c). The superior and inferior view of each case are plotted.
Using the average gray matter thickness in each gyral region as the statistical variable, we applied t-tests to all gyral regions to locate group differences between AD and NC. For both hemispheres, the map of p-values from the t-test on each gyrus are plotted in Fig. 7. We can see highly significant group differences were detected in regions that are consistent with previous findings in the literature such as gyri in the temporal lobe and precuneus. This demonstrates the effectiveness of our method in detecting population differences, and its potential in large scale studies.
Fig. 7.

Gyrus-based map of p-values from the testing of NC versus AD group differences on left hemisphere (LH) and right hemisphere (RH). The lateral and medial views are plotted in each hemisphere.
5 Conclusions
In this paper, we developed a novel approach for computing conformal maps between anatomical surfaces and successfully demonstrated its application in automated cortical labeling. Our method is based on the optimization of conformal metrics in the LB embedding space and is able to align global geometric features as guided by the LB eigen-functions. The proposed method is general and we will investigate its application in mapping high-genus surfaces in future work. We will also apply it to study other anatomical structures such as hippocampus and perform more extensive validations on the cortical labeling algorithm.
References
- 1.Rustamov RM. Laplace-beltrami eigenfunctions for deformation invariant shape representation. Proc. Eurograph. Symp. on Geo. Process..2007. pp. 225–233. [Google Scholar]
- 2.Lai R, Shi Y, Scheibel K, Fears S, Woods R, Toga A, Chan T. Metric-induced optimal embedding for intrinsic 3D shape analysis. Proc. CVPR. 2010:2871–2878. [Google Scholar]
- 3.Hurdal MK, Stephenson K. Cortical cartography using the discrete conformal approach of circle packings. NeuroImage. 2004;23:S119–S128. doi: 10.1016/j.neuroimage.2004.07.018. [DOI] [PubMed] [Google Scholar]
- 4.Gu X, Wang Y, Chan TF, Thompson PM, Yau ST. Genus zero surface conformal mapping and its application to brain surface mapping. IEEE Trans. Med. Imag. 2004;23(8):949–958. doi: 10.1109/TMI.2004.831226. [DOI] [PubMed] [Google Scholar]
- 5.Wang Y, Lui LM, Chan TF, Thompson PM. Optimization of brain conformal mapping with landmarks. Proc. MICCAI.; 2005. pp. 675–683. [DOI] [PubMed] [Google Scholar]
- 6.Reuter M, Wolter F, Peinecke N. Laplace-Beltrami spectra as Shape-DNA of surfaces and solids. Computer-Aided Design. 2006;38:342–366. [Google Scholar]
- 7.Qiu A, Bitouk D, Miller MI. Smooth functional and structural maps on the neocortex via orthonormal bases of the Laplace-Beltrami operator. IEEE Trans. Med. Imag. 2006;25(10):1296–1306. doi: 10.1109/tmi.2006.882143. [DOI] [PubMed] [Google Scholar]
- 8.Shi Y, Lai R, Morra J, Dinov I, Thompson P, Toga A. Robust surface reconstruction via Laplace-Beltrami eigen-projection and boundary deformation. IEEE Trans. Med. Imag. 2010;29(12):2009–2022. doi: 10.1109/TMI.2010.2057441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shi Y, Lai R, Gill R, Pelletier D, Mohr D, Sicotte N, Toga A. Conformal metric optimization on surface (CMOS) for deformation and mapping in Laplace-Beltrami embedding space. Proc. MICCAI.; 2011. pp. 327–334. [DOI] [PubMed] [Google Scholar]
- 10.Fischl B, van der Kouwe A, Destrieux C, Halgren E, Sagonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM. Automatically parcellating the human cerebral cortex. Cerebral Cortex. 2004;14(1):11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- 11.Wan J, Carass A, Resnick S, Prince J. Automated reliable labeling of the cortical surface. Proc. ISBI.; 2008. pp. 440–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yeo B, Sabuncu M, Vercauteren T, Ayache N, Fischl B, Golland P. Spherical demons: Fast diffeomorphic landmark-free surface registration. IEEE Trans. Med. Imag. 2010;29(3):650–668. doi: 10.1109/TMI.2009.2030797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rohlfing T, Brandt R, Menzel R, Jr., C.R.M. Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. [DOI] [PubMed]
- 14.Sabuncu M, Yeo B, Van Leemput K, Fischl B, Golland P. IEEE Trans. Med. Imag. 2010;29(10):1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang H, Suh J, Das S, Pluta J, Craige C, Yushkevich P. Multi-atlas segmentation with joint label fusion. IEEE Trans. Pattern Anal. Machine Intell. 2012 doi: 10.1109/TPAMI.2012.143. DOI:10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shattuck D, Mirza M, Adisetiyo V, et al. Construction of a 3D probabilistic atlas of human brain structures. NeuroImage. 2008;39(3):1064–1080. doi: 10.1016/j.neuroimage.2007.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mueller S, Weiner M, Thal L, Petersen RC, Jack C, Jagust W, Trojanowski JQ, Toga AW, Beckett L. The Alzheimer’s disease neuroimaging initiative. Clin. North Am. 2005;15:869–877. xi–xii. doi: 10.1016/j.nic.2005.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shi Y, Lai R, Toga A. Cortical surface reconstruction via unified Reeb analysis of geometric and topological outliers in magnetic resonance images. IEEE Trans. Med. Imag. 2012 doi: 10.1109/TMI.2012.2224879. DOI:10.1109/TMI.2012.2224879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Klein A, Ghosh SS, Avants B, Yeo B, Fischl B, Ardekani B, Gee JC, Mann J, Parsey RV. Evaluation of volume-based and surface-based brain image registration methods. NeuroImage. 2010;51:214–220. doi: 10.1016/j.neuroimage.2010.01.091. [DOI] [PMC free article] [PubMed] [Google Scholar]