A linear exponent AR(1) family of correlation structures

Abstract

In repeated measures settings, modeling the correlation pattern of the data can be immensely important for proper analyses. Accurate inference requires proper choice of the correlation model. Optimal efficiency of the estimation procedure demands a parsimonious parameterization of the correlation structure, with sufficient sensitivity to detect the range of correlation patterns that may occur. Many repeated measures settings have within-subject correlation decreasing exponentially in time or space. Among the variety of correlation patterns available for this context, the continuous-time first-order autoregressive correlation structure, denoted AR(1), sees the most utilization. Despite its wide use, the AR(1) structure often poorly gauges within-subject correlations that decay at a slower or faster rate than required by the AR(1) model. To address this deficiency we propose a two-parameter generalization of the continuous-time AR(1) model, termed the linear exponent autoregressive (LEAR) correlation structure, which accommodates much slower and much faster decay patterns. Special cases of the LEAR family include the AR(1), compound symmetry, and first-order moving average correlation structures. Excellent analytic, numerical, and statistical properties help make the LEAR structure a valuable addition to the suite of parsimonious correlation models for repeated measures data. Both medical imaging data concerning neonate neurological development and longitudinal data concerning diet and hypertension [DASH (Dietary Approaches to Stop Hypertension) study] exemplify the utility of the LEAR correlation structure.

1. Introduction

1.1. Available correlation structures

Repeated measures designs are often employed to examine longitudinal, spatial, or spatio-temporal data, as in the medical imaging studies now at the forefront of spatial and spatio-temporal research. Appropriate analysis of these types of data requires accurately modeling the correlation pattern induced by repeatedly taking measurements over time or in space. Proper specification of the correlation model is essential for the accurate estimation of, and inference about, the means and covariates of interest. Muller et al. [1] showed that severe test size inflation can occur in fixed effect inference if the correlation structure is badly misspecified.

Many repeated measures settings have within-subject correlation decreasing exponentially in time or space. The continuous-time first-order autoregressive correlation structure, denoted AR(1), sees the most utilization among the variety of correlation patterns available in this context. This model was briefly examined by Louis [2] and is a special case of the model described by Diggle [3]. Table I defines the AR(1) model along with other stationary correlation structures that are continuous functions of distance. The focus on stationary models reflects the desire to maintain parsimony across a variety of data types. A continuous-time analog of the ARMA(1,1), denoted CARMA(1,1), has been introduced in the time series literature (Tsai and Chan [4] has details). However, it appears not to have been presented as a correlation structure in the literature to date. Peiris [5] aimed to capture the degree of frequency in time series data with the development of the generalized autoregressive structure, denoted GAR(1). The exponential model, discussed almost exclusively in the spatial statistics literature, is in fact equivalent to the continuous-time AR(1) model with ϕ=−(1/lnρ). Schabenberger and Gotway [6] and Bowman [7] also noted this equivalence. The Matern, Linear, and Spherical structures have utility in many spatial applications. Cressie [8] and Schabenberger and Gotway [6] provide further details of the aforementioned spatial structures.

Table I.

Stationary correlation structures that are continuous functions of distance.

Structure	(j, k)th element*, j ≠ k	Params	Data types†
LEAR	ρ dmin+δ[(djk−dmin)/(dmax−dmin)]	2	L/T,S,O
AR(1)	ρ djk	1	L/T,S,O
DE	${\rho }^{d_{\mathit{jk}}^v}$	2	L/T,S,O
GAR(1)	${\rho }^{d_{\mathit{jk}}}\frac{\Gamma (d_{\mathit{jk}}+\delta )F(\delta ,d_{\mathit{jk}}+\delta ;d_{\mathit{jk}}+1;{\rho }^2)}{\Gamma \left(\delta \right)\Gamma (d_{\mathit{jk}}+1)F(\delta ,\delta ;1;{\rho }^2)}$	2	L/T
Exponential	exp(−djk/ϕ)	1	S
Gaussian	$\exp (-d_{\mathit{jk}}^2∕{\varphi }^2)$	1	S
Linear	(1 − ϕdjk)I(ϕdjk≤1)	1	S
Matern	[1/Γ(ν)](djk/2ϕ)ν2Kv(djk/ϕ)	2	S
Spherical	$[1-(3d_{\mathit{jk}}∕2\varphi )+(d_{\mathit{jk}}^3∕2{\varphi }^3\left)\right]∕(d_{\mathit{jk}}\le \varphi )$	1	S

^*d_jk, distance between jth and kth measurement of ith subject; Γ(·), gamma function; F(θ₁, θ₂; θ₃; θ), hypergeometric function; and K_v(·), modified Bessel function of the second kind of (real) order v > 0.

^†L/T, longitudinal/time series; S, spatial; and O, other.

We emphasize that all correlation structures have a role. A particular correlation pattern may work well for some study designs or certain research questions, but not for others. Its value is inextricably linked to the science and its context. Here we focus on situations in which the AR(1) model is generally deemed most useful as is the case in many longitudinal and medical imaging studies.

The DE (damped exponential) model serves as the most relevant competitor to the AR(1) structure given its simplicity and wide applicability. Munoz et al. [9] presented the DE structure, which allows for an attenuation or acceleration of the exponential decay rate imposed by the AR(1) structure. Murray [10] described the same model in an unpublished dissertation. D’Agostino et al. [11] compared the results of fitting the AR(1) and DE models to data concerning respiratory function. The DE family includes the AR(1), compound symmetry (CS), and first-order moving average correlation structures as special cases. As noted by Grady and Helms [12], the DE model has difficulties with convergence due to its parameterization.

1.2. An appealing and flexible correlation structure

We propose a two-parameter generalization of the continuous-time AR(1) structure, termed the linear exponent autoregressive (LEAR) correlation structure, which is more appropriate for many types of data than the competing AR(1) or DE models. It, like the DE model, includes the AR(1), CS, and first-order moving average correlation structures as special cases. However, the LEAR structure possesses superior statistical and convergence properties. It is also far more flexible and robust than the AR(1) model. Hence the LEAR model adds another tool to the set of parsimonious correlation structures for repeated measures data. Here we employ maximum likelihood (ML) estimation of the general linear model (GLM) with Gaussian errors to exemplify the benefits of the structure, although, notably, the LEAR structure can be imbedded within many other appropriate modeling and estimation methods. For our purposes, the assumption of Gaussian errors covers a wide class of practical problems and helps to provide tractable solutions for exploring the properties of the LEAR correlation structure.

For the following analysis of the LEAR structure, we describe motivating data examples concerning neonate neurological development and diet and hypertension in Section 2. A formal definition of the LEAR correlation structure is provided in Section 3. Graphical comparisons across parameter values illustrate its flexibility. We discuss model estimation in Section 4. Parameter estimators and their variances are derived under ML methods. Simulation studies in Section 5 help to compare the LEAR, AR(1), and DE models. We discuss the analyses of the example datasets in Section 6 and conclude with a summary discussion including planned future research in Section 7.

2. Motivating examples

2.1. Neonate neurological development

Several pediatric neurological disorders affect the myelin sheath of the nervous system. For example, infantile Krabbe disease, an inherited neurodegenerative disorder, causes demyelination of nerve cells leading to a rapid degeneration of mental and motor skills and death within the first two to four years of life. The understanding of myelination patterns in people with and without neurological conditions is critical in the radiologic assessment of disease progression and treatment response. Diffusion-tensor magnetic resonance imaging (DTI) allows gauging the degree of myelination via a proxy measure called fractional anisotropy (FA). McGraw et al. [13] give a more detailed description of DTI and Krabbe disease.

Our analysis includes DTI scans of fibers of the cortico-spinal tracts associated with motor functioning for 46 control neonates. FA values were obtained at 20 locations, spaced 3 mm apart, along fiber tracts. FA values can theoretically range between 0 and 1, with higher values representing a more myelinated and mature nerve cell, but are typically between 0 and 0.6 for neonates. The gender, race, birth weight, gestational age at birth, and the gestational age at the time of the scan were also recorded. It is hypothesized that the older neonates (those with a higher gestational age at the time of the scan) would have higher FA values. Gilmore et al. [14] provide a more detailed description of the data.

2.2. Diet and hypertension

The DASH (Dietary Approaches to Stop Hypertension) trial was a multicenter, randomized, parallel arm feeding study that tested the effects of dietary patterns on blood pressure. The three diets were a control diet (low in fruits, vegetables, and dairy products, with a fat content typical of the average diet in the United States), a diet rich in fruits and vegetables (a diet similar to the control except it provided more fruits and vegetables and fewer snacks and sweets), and a combination diet rich in fruits, vegetables, and low-fat dairy foods and reduced in saturated fat, total fat, and cholesterol (DASH diet). Participants were healthy adults 22 years of age or older who were not taking antihypertensive medication. Ambulatory blood pressure monitoring (ABPM) was used to take blood pressure measurements on the subjects over a 24-h period. The devices were programmed to take readings automatically every 30 minutes and to repeat a reading if it fell outside the acceptable range defined in the monitor’s internal algorithm. Appel et al. [15] and Moore et al. [16] provide more detail on the DASH study.

Our analysis includes blood pressure measurements for 194 subjects, a subset of those on the control and DASH diets. For each subject 24 measurements were constructed at hourly intervals. The data model consisting of the actual times of measurement would not converge with an AR(1) correlation model fit (though it did converge with a LEAR model fit), and thus only the hour-interval data are examined. The main objective of the study was to determine if there is an effect due to the diet. The race and age of participants are also included as covariates. The analysis of these data exemplifies the difference in fixed effect inference that can occur when modeling the correlation with the LEAR instead of the AR(1) model.

3. LEAR correlation structure

3.1. Definition

Suppose y_i is a p_i×1 vector of p_i observations on the ith subject i∈{1,… ,N}. Let $\mathcal{C}(y_{\mathit{ij}},y_{\mathit{ik}})={\rho }_{i;\mathit{jk}}$, where $\mathcal{C}(\cdot )$ is the correlation operator. Then for Γ_i = {ρ_i;jk}, the LEAR correlation structure is

$${\rho }_{i;jk}=\mathcal{C}(y_{\mathit{ij}},y_{\mathit{ik}})=\{\begin{array}{cc}{\rho }^{d_{\min }+\delta \left[\right(d_{\mathit{ijk}}-d_{\min })∕(d_{\max }-d_{\min }\left)\right]},\hfill & j\ne k,\hfill \\ 1,\hfill & j=k,\hfill \end{array}\phantom{\}}$$ (1)

where d_ijk = d(t_ij, t_ik)[or =d(s_ij, s_ik)] is the distance between measurement times or locations (t_ij and s_ij being the measurement time or spatial location of observation j for the ith subject), d_min = min_i;j<k d_ijk and d_max = max_i;j<k d_ijk are computational constants equal to the minimum and maximum number of distance units across all subjects, respectively, ρ is the correlation parameter, and δ is the decay speed. We assume 0≤ρ < 1 and 0≤δ. The d_min and d_max constants allow the model to adapt to the data and scale distance such that the multiplier of the decay speed δ, (d_ijk − d_min)/(d_max − d_min), is between 0 and 1 for computational purposes. One could also consider tuning these constants if necessary to address, for example, convergence issues. Here we set d_min = 1 for all analyses in this manuscript as that eliminated any convergence issues. See Section 3.3 for further details on setting the distance constants.

Implicit in this model formulation is the presence of a stationary correlation structure. When δ = 0, this model reduces to the well-known equal correlation model for which the correlation between measurements on a given subject is fixed at ρ no matter how far apart in time or space the measurements were taken. When 0 < δ < d_max − d_min, the correlation between measurements on a given subject decreases in time or space at a slower rate than that imposed by the AR(1) model. When δ = d_max − d_min, this model reduces to the AR(1) correlation model. When δ > d_max − d_min, the correlation between measurements on a given subject decreases in time or space at a faster rate than that imposed by the AR(1) model. As δ → ∞, this model approaches the moving average model of order 1, MA(1). Though values of δ < 0 yield valid autocorrelation functions for which the correlation between measurements on a given subject would increase with increasing time or distance between measurements, such patterns seem rare in biostatistical applications. Therefore the parameter space is restricted for reasons of practicality.

As alluded to in the previous two paragraphs, the LEAR correlation model is applicable to both temporally and spatially correlated data (as well as correlated data of any type for which it provides a good fit). The impetus for the LEAR structure was the need to be able to flexibly model correlations as a function of a distance metric (spatial, temporal, or others); thus the model is meant to be implemented at the covariance modeling stage of model formulation in the distance function space, and is not domain specific (e.g. time or space domain). Similarly, the AR(1) and CS models, initially derived in the time and space domains, respectively, can also be applied to any data type at the covariance modeling level. For example, as mentioned in Section 1.1, the exponential model used in spatial statistics is a reparameterization of the continuous-time AR(1) model.

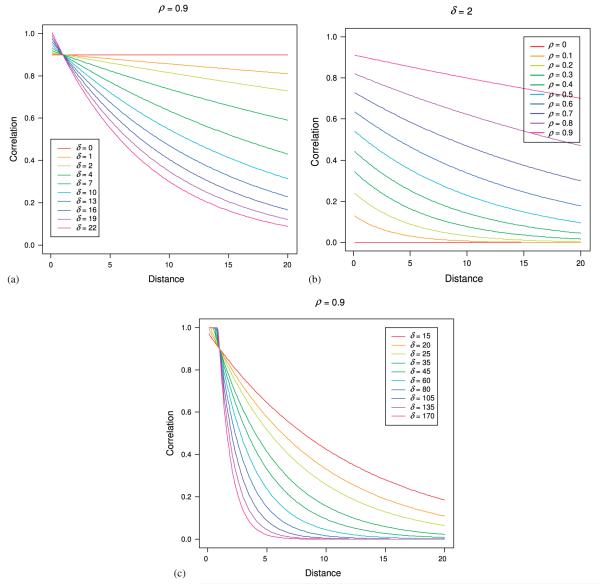
Graphical depictions of the LEAR structure help to provide insight into the types of correlation patterns that can be modeled. Figure 1 shows a subset of the correlation patterns that can be modeled with the LEAR correlation structure. Varying δ produces patterns that range from CS to a slightly faster than AR(1) decay rate in Figure 1(a). The decay rate is held constant in Figure 1(b) while ρ varies. Figure 1(c) exhibits decay patterns ranging from slightly slower than an AR(1) decay rate to much faster by again varying δ.

Figure 1.

(a) Plot of the various correlation patterns that can be obtained by varying the parameter δ while keeping ρ constant. δ = 19 corresponds to an AR(1) decay rate, whereas δ = 0 corresponds to compound symmetry; (b) Plot of the various correlation patterns that can be obtained by varying the parameter ρ while keeping δ constant; and (c) Plot of the various correlation patterns that can be obtained with larger values of δ while keeping ρ constant. Again δ = 19 corresponds to an AR(1) decay rate.

Here we adopt the technique of modeling the correlation and variance structures separately as in the approaches of Fan et al. [17] and others. We focus on modeling the correlation and henceforth assume an equal variance structure for simplicity. Thus,

$$\mathcal{V}(y_{\mathit{ij}},y_{\mathit{ik}})={\sigma }^2\{\begin{array}{cc}{\rho }^{d_{\min }\delta \left[\right(d_{\mathit{ijk}}-d_{\min })∕(d_{\max }-d_{\min }\left)\right]}\hfill & j\ne k,\hfill \\ 1,\hfill & j=k,\hfill \end{array}\phantom{\}}$$ (2)

where $\mathcal{V}(\cdot )$ is the covariance operator.

3.2. Statistical issues

Both the DE and LEAR correlation matrices can be negative definite (or indefinite), a complication which appears not to have been addressed in any detail for the DE model in the literature. This may occur when there is a faster decay rate than that imposed by the AR(1) model coupled with a ‘large’ ρ. The acceptable ρ for this situation depends on the number of observations per subject (p_i), the spacing of the observations, and the decay speed (δ). For 0 < δ < d_max − d_min (a slower than AR(1) decay rate), the LEAR model has the attractive statistical property that it can be reparameterized as the Hadamard product of an equal correlation and a continuous-time AR(1) model (Appendix A). Appendix A contains a proof of the positive definiteness of the LEAR for decay speeds slower than or equal to that of the AR(1) model (δ≤d_max − d_min) based on the Hadamard product theory. The DE model does not have this property, though enumeration studies show that it also appears to be positive definite for decay speeds slower than or equal to that of the AR(1) model (ν≤1).

There are currently no general approaches to deal with the issue of negative definiteness (and indefiniteness) in either the LEAR or DE models for decay speeds greater than that of the AR(1) model (δ > d_max − d_min; ν > 1) and thus further analytic work is needed. Restricting ρ≤0.5 provides one conservative ad hoc approach to dealing with negative definiteness and indefiniteness (though this awaits further analytic investigation). This follows from the restriction for the MA(1) model (the limiting structure for the LEAR and DE as δ, ν → ∞) discussed in Diggle [18]. To implement this restriction an analyst would need to code for it in the estimation algorithm prior to the final model fit. A more practical and less restrictive ad hoc solution for the LEAR structure is to rescale the distances since this complication seems to occur only when min_i[d(t_ij,t_ik)] = 1. In fact, enumeration studies show that with equally spaced intervals of two units or greater the LEAR correlation matrix is positive definite for every δ, ρ, and p_i (at least with p_i≤1000). This is not true for the DE model. In this case, for the LEAR model, it can be empirically shown that the det(Γ_i) = 1 − f(ρ; δ), where f(ρ; δ) ∈ (0, 1) and all eigenvalues of Γ_i are positive. The function f(ρ; δ) decreases in δ and interval size, and increases in ρ and p_i. Thus, in extreme cases (e.g. p_i = 500 and ρ = 0.99), f(ρ; δ) ≈ 1 leading to the possibility of a computationally singular correlation matrix despite being theoretically nonsingular. All discussion in this and the preceding paragraph assumes that we are using a Euclidean distance metric or a distance metric that can be isometrically embedded in Euclidean space [6, p. 205–210].

3.3. Setting distance constants

In general, the d_min and d_max constants should be left at their default values, namely the minimum and maximum number of distance units across all subjects, respectively. Potential reasons for tuning them include lack of model convergence, non-positive definiteness of the resulting covariance matrix (only an issue when δ > d_max − d_min), and a scientific interest in correlation patterns on a certain scale. For the first two issues, trial and error is often the only tuning approach. However, for certain cases of non-positive definiteness, the solutions presented in the previous section may give guidance. For example, with equally spaced measurements one could just rescale the inter-measurement distances to two units (i.e. 2, 4, 6, etc.) and set d_min = 2 (though this would also happen by default with the rescaling). Choosing another d_min (or d_max) in this case would change the interpretation and estimated value of ρ since, for example, with d_min = 1 ρ is the correlation for measurements separated by one unit (an interpolated value in this case), whereas with d_min = 2 ρ2 is the correlation for measurements separated by two units regardless of the decay speed δ. However, since the estimated value of δ (though not the interpretation) changes correspondingly, the overall predicted correlations as a function of distance will not change much. This change in the estimated value of ρ for different distance scalings also occurs for the pure AR(1) model (ρ^d_ijk) due to the nonlinearity inherent in the model and the necessary iterative estimation procedure.

For preciseness, it is important to note that the decay speed with respect to distance is δ/(d_max − d_min), though δ is the only parameter to be estimated. In other words δ, which is estimated relative to d_max and d_min, is the decay speed parameter in the decay speed function δ/(d_max − d_min) (which we will call δ*). The δ*(=δ/(d_max − d_min)) can also be thought of as a shape-like parameter since, in effect, it alters the shape of the correlation curve as exhibited in Figure 1. Given this, if one were to collect samples from the same population with different time (or distance) spans (ranges), different estimates of δ would be obtained. However, this should be the case given that the divisors in the decay speed function will also be different given the different ranges of distance. Table II further clarifies this point by illustrating that if one were to collect samples from the same population (in this case one with an AR(1) decay rate) with different spans and fit the LEAR model to each sample individually and then to the combined sample, the expected estimates of decay speed will still be the same despite having different δ estimates. In other words, the normalizing constant (d_max − d_min) ensures that the decay speeds are comparable regardless of the span of the data. If having comparable estimates of δ is desired (though there is no statistical reason for this), an analyst could set d_max and d_min to the same values for all model fits. The analyst would have to make sure to have 0≤d_min≤min_i;j<k d_ijk and d_max > d_min to avoid negative or undefined values in [(d_ijk − d_min)/(d_max − d_min)]. For example, an analyst could set d_min = 1 and d_max = 2 to make the estimate of δ invariant to the time span of the data. Setting the constants in this way gives ρ^{1+δ(d_jk − 1)} which allows the model to retain CS, AR(1), and MA(1) as special cases. However, including the span gives the model more computational flexibility.

Table II.

Values for the LEAR model assuming all samples come from an AR(1) population.

Sample	Measurement times	d min	d max	δ	δ* = δ/(dmax − dmin)
1	1,2,… ,10	1	9	8	1
2	1,2,… ,15	1	14	13	1
3	3,4,… ,7	1	4	3	1
4	16,17,… ,20	1	4	3	1
Combined	1,2,… ,20	1	14	13	1

^*Note: δ* = δ/(d_max − d_min) = 1: LEAR decay speed which yields an AR(1) decay rate.

It is also important to note that user-specified values of d_max and d_min outside of the span of the data pose no issues as long as they are restricted as noted in the previous paragraph (namely 0≤d_min≤min_i;j<k d_ijk and d_max > d_min). For example, if we set d_max = 14 for a model fit to sample 1 in Table II, the expected estimated δ is 13 resulting in the same decay rate (AR(1) in this case) since δ* = δ/(d_max − d_min) will equal 1. The flexibility of the LEAR model then not only allows for a range of correlation patterns that subsumes the patterns of the CS, continuous-time AR(1), and MA(1) models, but it also allows the user to determine whether or not to incorporate the span of the data. As detailed in the first paragraph of this section and Section 3.1, there are potential advantages of this incorporation in certain contexts.

4. Estimation

4.1. Overview

In this paper our primary focus is on the introduction and performance of the LEAR correlation structure itself, and not on the modeling and estimation approach used in its implementation. The LEAR structure can be imbedded within many other appropriate modeling and estimation methods. The best approach most likely varies by context. If ensuring positive-definiteness is a concern (discussed in Section 3.2), the method of Pourahmadi [19], which utilizes ML estimation of a Cholesky decomposition based modeling approach, has appeal. The LEAR structure adds greater flexibility to the non- and semiparametric approaches of Wang [20] and Fan et al. [17]. Future work will compare various estimation methods for the LEAR correlation structure as done in Shitan and Peiris [21] for the GAR(1).

For illustrative purposes, we consider here ML estimation of the GLM with Gaussian errors. Jennrich and Schluchter [22] detailed the Newton–Raphson and Fisher scoring algorithms for ML estimation of model parameters. Dempster et al. [23] first proposed the EM algorithm for parameter estimation. The Newton–Raphson method is more widely applicable than the Fisher scoring method due to the computational infeasibility of calculating the expected information matrix in certain contexts. As noted by Lindstrom and Bates [24], the method is also generally preferable to the EM procedure.

The benefits of profiling out σ² and optimizing the resulting profile log-likelihood to derive model parameter estimates via the Newton–Raphson algorithm was discussed by Lindstrom and Bates [24]. They noted that this optimization will generally require fewer iterations, will have simpler derivatives, and the convergence will be more consistent. There are also certain situations in which the Newton–Raphson algorithm may fail to converge when optimizing the original log-likelihood but converge with ease when utilizing the profile log-likelihood.

4.2. Maximum likelihood estimation

Consider the following GLM for repeated measures data with the LEAR correlation structure:

$${\mathit{y}}_i={\mathit{X}}_i\beta +{\mathit{e}}_i,$$ (3)

where y_i is a p_i × 1 vector of p_i observations on the ith subject i ∈ {1,… ,N}, β is a q × 1 vector of fixed and unknown population parameters, X_i is a p_i × q fixed and known design matrix corresponding to the fixed effects, and e_i is a p_i × 1 vector of random error terms. We assume ${\mathbf{e}}_i~{\mathcal{N}}_{p_i}(0,{\Sigma }_i)$ and is independent of e_i’ for i ≠ i’. It follows that ${\mathbf{y}}_i~{\mathcal{N}}_{p_i}({\mathbf{X}}_i\beta ,{\Sigma }_i)$ and is independent of y_i’ for i ≠ i’, where Σ_i is composed of the elements defined in equation (2).

In order to estimate the parameters of the model defined in equation (3), σ² is first profiled out of the likelihood. The first and second partial derivatives of the profile log-likelihood are then derived to compute ML estimates of parameters, via the Newton–Raphson algorithm, and the variance–covariance matrix of those estimates. The resulting estimates are then used to compute the value and variance of ${\widehat{\sigma }}^2$. A SAS IML [25] computer program has been written implementing this estimation procedure for the GLM with LEAR correlation structure and is available upon request.

Setting Σ_i = σ²Γ_i(τ), where τ = {δ,ρ}, the log-likelihood function of the parameters given the data under the model is:

$$\begin{array}{cc}\hfill l(\mathit{y};\beta ,{\sigma }^2,\tau )& =-\frac{n}{2}\ln \left(2\pi \right)-\frac{1}{2}\sum _{i=1}^N\ln \mid {\sigma }^2{\Gamma }_i\mid -\frac{1}{2{\sigma }^2}\sum _{i=1}^1{\mathit{r}}_i{\left(\beta \right)}^{\prime }{\Gamma }_i^{-1}{\mathit{r}}_i\left(\beta \right),\hfill \\ \hfill & =-\frac{n}{2}\ln \left(2\pi \right)-\frac{1}{2}\sum _{i=1}^N\left(p_i\ln \right({\sigma }^2)+\ln \mid {\Gamma }_i\mid )-\frac{1}{2{\sigma }^2}\sum _{i=1}^N{\mathit{r}}_i{\left(\beta \right)}^{\prime }{\Gamma }_i^{-1}{\mathit{r}}_i\left(\beta \right),\hfill \end{array}$$ (4)

where $n={\sum }_{i=1}^N{p}_i$ and r_i(β) = y_i − X_iβ. Taking the first partial derivative with respect to σ² gives

$$\frac{\partial l}{\partial {\sigma }^2}=-\frac{1}{2}\sum _{i=1}^N{p}_j{\sigma }^{-2}+\frac{1}{2{\sigma }^4}\sum _{i=1}^N{\mathit{r}}_i{\left(\beta \right)}^{\prime }{\Gamma }_i^{-1}{\mathit{r}}_i\left(\beta \right).$$

Setting the derivative to zero and solving for an estimate of the variance yields

$${\widehat{\sigma }}_{\mathrm{ML}}^2(\beta ,\tau )=\frac{1}{n}\sum _{i=1}^N{\mathit{r}}_i{\left(\beta \right)}^{\prime }{\Gamma }_i^{-1}{\mathit{r}}_i\left(\beta \right).$$

Substituting ${\widehat{\sigma }}_{\mathrm{ML}}^2(\beta ,\tau )$ into the log-likelihood function in equation (4) leads to the following profile log-likelihood:

$$l_p(\mathit{y};\beta ,\tau )=-\frac{1}{2}\sum _{i=1}^N\ln \mid {\Gamma }_i\mid -\frac{1}{2}n\ln \left[\sum _{i=1}^N{\mathit{r}}_i{\left(\beta \right)}^{\prime }{\Gamma }_i^{-1}{\mathit{r}}_i\left(\beta \right)\right]-\frac{1}{2}n\ln \left(\frac{1}{n}\right)-\frac{n}{2}.$$ (5)

The ML estimates of the model parameters are computed by utilizing the Newton–Raphson algorithm which requires the first and second partial derivatives. The derivation of these derivatives are available from the authors. The second partial derivatives of the parameters are also employed to determine the asymptotic variance–covariance matrix of the estimators.

After obtaining the estimates of β and τ utilizing the Newton–Raphson algorithm, an estimate of σ² is calculated by substituting the estimates into ${\widehat{\sigma }}_{\mathrm{ML}}^2(\beta ,\tau )$. An estimator of the variance for ${\widehat{\sigma }}_{\mathrm{ML}}^2(\beta ,\tau )$, assuming that β and τ are known, is then

$$\widehat{\mathcal{V}}\left[{\widehat{\sigma }}_{\mathrm{ML}}^2\right(\beta ,\tau \left)\right]=2{\widehat{\sigma }}^4∕n.$$ (6)

The derivation of this estimator is available from the authors.

5. Simulation studies

All model fits for the following simulation studies were done in SAS IML utilizing the Newton–Raphson algorithm.

5.1. Model fit assessments

To assess the relative robustness of the LEAR correlation model to misspecification with respect to model fit performance, data were generated under the GLM for repeated measures data with various exponentially decaying correlation structures and then fitted with the LEAR, DE, and AR(1) correlation models. Only the complete and balanced case was considered with N = 100 subjects and p_i = p ∈ {5, 20} observations each at two-unit distance intervals. The fixed effects included an intercept and three dummy variables indicating membership in one of four groups (25 subjects per group), with β = [1, 1, 1, 1]’. The simulated correlation model was constructed as a weighted sum of the LEAR and DE models with a scale parameter set to σ² = 1, namely Σ(ρ, δ, ν) = τΣ_LEAR(ρ, δ) + (1 − τ)Σ_DE(ρ, ν) with τ ∈ {0, 0.25, 0.5, 0.75, 1}. Four parameter sets were considered: (1) (δ, ν) = (0, 0) corresponding to CS for both Σ_LEAR and Σ_DE, (2) (δ, ν) = ((d_max − d_min)/4, 0.5) corresponding to a slower than AR(1) decay rate for both Σ_LEAR and Σ_DE, (3) (δ, ν) = (d_max − d_min, 1) corresponding to an AR(1) decay rate for both Σ_LEAR and Σ_DE, and (4) (δ, ν) = (1.5·(d_max − d_min), 1.2) corresponding to a faster than AR(1) decay rate for both Σ_LEAR and Σ_DE. All four cases had ρ = 0.8. For sets (1) and (3), all τs lead to the same model, namely CS and AR(1), respectively. Each simulation for p ∈ {5, 20} and the varying correlation parameters consisted of 5000 realizations. All model fits employed ML estimation with the profile likelihood as discussed in Section 4.2. Both the Akaike Information Criterion (AIC) [26] and the Bayesian Information Criterion (BIC) [27] were utilized to assess model fits. Fitzmaurice et al. [28] recommend the use of the AIC over the BIC in this context. Given their recommendation, and the fact that both criteria gave similar results, only the AIC results are reported. The AIC is AIC = −2l(y_i; β, Σ_i) + 2(q + w), where q is the number of fixed effect parameters and w is the number of unique covariance parameters.

Table III shows the results of the simulations for p ∈ {5, 20}. The table displays the percent of realizations for which the LEAR model better fits the data according to the AIC, and the median and maximum percent difference in AIC when this occurs. The percent differences allow gauging the relative disparity in AIC values between the LEAR and comparable models when the LEAR is selected as the best model. The difference in convergence times among the three models was negligible for all conditions.

Table III.

Summary of model fits: 5000 realizations, 100 subjects, 5 and 20 observations per subject.

	Simulated model		LEAR vs DE			LEAR vs AR(1)
ρ	τ	(ΣLEAR, ΣDE)	LEAR *	Median†	Max‡	LEAR*	Median†	Max‡
5	—	(CS,CS)	72	0.0	1340	100	401	1.2×107
	0	(0, Slow)	40	0.4	2.8	100	9.0	43
	0.25	(Slow, Slow)	45	0.5	2.6	100	9.7	55
	0.50	(Slow, Slow)	50	0.5	4.4	100	10	48
	0.75	(Slow, Slow)	57	0.6	7.5	100	11	74
	1	(Slow, 0)	64	0.7	5.3	100	12	63
	—	(AR(1), AR(1))	49	0.0	1.4	16	0.4	4.8
	0	(0 , Fast)	38	0.1	0.9	53	0.8	8.1
	0.25	(Fast, Fast)	42	0.1	0.7	48	0.7	5.5
	0.50	(Fast, Fast)	43	0.1	0.6	42	0.6	5.8
	0.75	(Fast, Fast)	45	0.1	0.7	39	0.5	6.0
	1	(Fast, 0)	46	0.1	0.6	36	0.5	5.0
20	—	(CS, CS)	72	0.0	0.5	100	107	160
	0	(0, Slow)	6	0.5	3.9	100	28	76
	0.25	(Slow, Slow)	23	0.7	7.3	100	31	99
	0.50	(Slow, Slow)	53	1.3	8.4	100	34	123
	0.75	(Slow, Slow)	80	2.3	22	100	39	250
	1	(Slow, 0)	95	3.9	48	100	45	740
	—	(AR(1), AR(1))	49	0.0	0.4	17	0.1	1.7
	0	(0, Fast)	30§	0.1§	102§	98	0.8	102
	0.25	(Fast, Fast)	36§	0.1§	102§	95	0.6	102
	0.50	(Fast, Fast)	42§	0.1§	102§	91	0.5	102
	0.75	(Fast, Fast)	48§	0.0§	104§	87	0.4	104
	1	(Fast, 0)	54§	0.0§	104§	82	0.3	104

Note: p—Number of observations per subject.

τ—Mixing fraction for simulated model, i.e. Model = τΣ_LEAR+(1 − τ)Σ_DE.

CS—Compound symmetric decay rate (i.e. no decay) for Σ_LEAR and Σ_DE.

Slow—Slower than AR(1) decay rate for Σ_LEAR and/or Σ_DE.

Fast—Faster than AR(1) decay rate for Σ_LEAR and/or Σ_DE.

^*Percent of realizations LEAR model selected by AIC as the better model fit (SE < 0.7).

^†Median percent difference in AIC when LEAR model is selected.

^‡Maximum percent difference in AIC when LEAR model is selected.

^§DE fitted with Quasi-Newton algorithm due to rare convergence with Newton–Raphson.

As evidenced by the simulation results in Table III, the LEAR correlation model is more appropriate than either the DE or continuous-time AR(1) models for a number of conditions. When the data exhibit a slower than AR(1) decay rate, the LEAR is always selected over the AR(1) as the better model even when they are both misspecifications. The magnitude of the disparity in fits increases with more observations per subject. The AIC’s penalization of models with more parameters explains the preference for the AR(1) model when the true within-subject correlation has an AR(1) decay rate. When the data exhibit a faster than AR(1) decay rate, the benefits of the LEAR over the AR(1) model become evident with an increase in the number of observations per subject.

Despite CS being a special case of both the LEAR and DE structures, the LEAR is still more often selected as the better model for data exhibiting this within-subject correlation pattern. When the data exhibit a slower than AR(1) decay rate, the LEAR model is slightly more robust to misspecification than the DE model. However, the opposite is true for faster decay rates. It is important to note that for this scenario in which the true decay rate is faster than that of the AR(1), a Quasi-Newton algorithm had to be used to ensure consistent convergence with the DE model for p = 20. Even when the data were generated from the DE structure, the model rarely converged when implemented with the Newton–Raphson method. The simulations make a strong case for the addition of the LEAR correlation model to the suite of parsimonious correlation structures for repeated measures data.

5.2. Fixed effect inference

To assess the relative robustness of the LEAR correlation model to misspecification with respect to fixed effect inference accuracy, data were again generated under the GLM for repeated measures data with various exponentially decaying correlation structures and then fitted with the LEAR, DE, and AR(1) correlation models. Simulated fixed effect test size was examined for the three correlation model fits. Only the complete and balanced case was considered with N = 100 subjects and p_i = p ∈ {5, 20} observations each at two-unit distance intervals. The fixed effects included an intercept and three dummy variables indicating membership in one of four groups (25 subjects per group), with β = [1, 1, 1, 0]’ to empirically evaluate test size for H₀ :β₄ = 0. The simulated correlation model was constructed as described in Section 5.1. Each simulation for p ∈ {5, 20} and the varying correlation parameters consisted of 5000 realizations. All model fits employed ML estimation with the profile likelihood as discussed in Section 4.2. Demidenko [29] provides further discussion of fixed effect inference in the GLM for repeated measures data.

Table IV shows the results of simulations for p ∈ {5, 20}. The table contains simulated test size (target α = 0.05) for the likelihood ratio test (LRT) of H₀ :β₄ = 0 for LEAR, DE, and AR(1) correlation model fits. The LRT was employed due to the utilization of ML estimation in a moderately large sample context.

Table IV.

Simulated fixed effect test size for H₀ : β₄ = 0 (Target α = 0.05) 5000 realizations, 100 subjects, 5 and 20 observations per subject.

	Simulated model		Fitted model
p	τ	(ΣLEAR, ΣDE)	LEAR	DE	AR(1)
5	—	(CS, CS)	0.058	0.058	0.097
	0	(0, Slow)	0.051	0.051	0.068
	0.25	(Slow, Slow)	0.062	0.061	0.081
	0.50	(Slow, Slow)	0.052	0.052	0.068
	0.75	(Slow, Slow)	0.052	0.051	0.070
	1	(Slow, 0)	0.060	0.060	0.076
	—	(AR(1), AR(1))	0.062	0.061	0.062
	0	(0, Fast)	0.058	0.059	0.052
	0.25	(Fast, Fast)	0.057	0.057	0.051
	0.50	Fast, Fast)	0.057	0.056	0.049
	0.75	(Fast, Fast)	0.056	0.056	0.050
	1	(Fast, 0)	0.054	0.054	0.047
20	—	(CS, CS)	0.060	0.060	0.235
	0	(0, Slow)	0.074	0.058	0.163
	0.25	(Slow, Slow)	0.066	0.051	0.159
	0.50	(Slow, Slow)	0.063	0.054	0.148
	0.75	(Slow, Slow)	0.060	0.051	0.144
	1	(Slow, 0)	0.057	0.045	0.127
	—	(AR(1), AR(1))	0.054	0.053	0.054
	0	(0, Fast)	0.048	0.053*	0.038
	0.25	(Fast, Fast)	0.049	0.053*	0.041
	0.50	(Fast, Fast)	0.048	0.049*	0.040
	0.75	(Fast, Fast)	0.048	0.051*	0.041
	1	(Fast, 0)	0.049	0.051*	0.040

Note: p—Number of observations per subject.

For p = 5, standard error<0.004; for p = 20, standard error<0.006.

τ—Mixing fraction for simulated model, i.e. Model = τΣ_LEAR + (1 − τ)Σ_DE.

CS—Compound symmetric decay rate (i.e. no decay) for Σ_LEAR and Σ_DE.

Slow—Slower than AR(1) decay rate for Σ_LEAR and/or Σ_DE.

Fast—Faster than AR(1) decay rate for Σ_LEAR and/or Σ_DE.

^*Fitted with Quasi-Newton algorithm due to rare convergence with Newton–Raphson.

For situations in which the true within subject correlation is constant (a misspecification for the AR(1) model, but not for the LEAR or DE models) both the LEAR and DE models control test size far better than the AR(1) model. This test size inflation with the AR(1) fit increases drastically as the number of observations per subject increases. When all the three models are misspecifications for correlation decay rates slower than that of AR(1), both the LEAR and DE models control test size better than the AR(1) model. Again, this disparity increases in p. With an AR(1) decay rate (not a misspecification for any of the models) the test size is essentially equivalent across the three model fits as expected. The average widths of the confidence intervals (CIs) for β₄ for the three model fits are also roughly equivalent in this case. For p = 5, the average CI widths are 0.807, 0.806, and 0.808 for the LEAR, DE, and AR(1) models, respectively. For p = 20, the average CI widths are 0.260, 0.261, and 0.266 for the LEAR, DE, and AR(1) models, respectively. Test size is fairly well controlled for all three models for misspecifications with a faster than AR(1) decay rate. The relatively smaller amount of overall variation in this context may mitigate the effects of misspecifying the correlation with an AR(1) model. Again, it is important to note that for this scenario in which the true decay rate is faster than that of the AR(1), a Quasi-Newton algorithm had to be used to ensure consistent convergence with the DE model for p = 20. Even when the data were generated from the DE structure, the model rarely converged when implemented with the Newton–Raphson method. The LEAR correlation model is as robust to misspecification in controlling fixed effect test size as the DE model, while possessing better convergence properties. The LEAR correlation model is far more robust to misspecification than the AR(1) model. These results further strengthen the case for the addition of the LEAR correlation model to the suite of parsimonious correlation structures for repeated measures data.

5.3. Correlation parameter inference

Hypothesis tests concerning the decay speed parameter of the LEAR correlation model were examined to assess the ability of the commonly used LRT to discern the model from its special cases. More specifically, simulated test size was examined for tests of H₀ : δ = 0 (corresponding to the CS) and H₀ : δ = d_max − d_min (corresponding to the AR(1) model). Only the complete and balanced case was considered with N = 100 subjects and p_i = p ∈ {5, 20} observations each at two-unit distance intervals. Three fixed effect scenarios were considered corresponding to signal strengths of none, moderate, and high, respectively: (1) β = 0 (one group with mean 0), (2) β = [0.3, 0.3, 0.3, 0.3] (one reference group with three additional groups; 25 subjects per group), and (3) β = [0.6, 0.6, 0.6, 0.6] (one reference group with three additional groups; 25 subjects per group). All three cases had ρ ∈ {0.5, 0.9} and σ² = 1. The R² statistic presented in Edwards et al. [30], denoted $R_{\beta }^2$, was used as a proxy for signal strength. Their statistic measures the multivariate association between the repeated outcomes and fixed effects in a repeated measures model. Scenario 1 has $R_{\beta }^2=0$ (no signal, only noise), and scenarios 2 and 3 have average $R_{\beta }^2$ values of 0.55 (moderate signal strength) and 0.80 (strong signal strength) across all parameter combinations, respectively. Each simulation for p ∈ {5, 20} and the varying mean and correlation parameters consisted of 5000 realizations. All model fits employed ML estimation with the profile likelihood as discussed in Section 4.2. Letting δ be slightly negative (e.g. −1 × 10⁻²≤δ) allows for avoiding the boundary issue discussed in Self and Liang [31].

Table V shows the results of simulations for p ∈ {5, 20}. The table contains simulated test size (target α = 0.05) for the LRT of H₀ : δ = 0 and H₀ : δ = d_max − d_min.

Table V.

Simulated correlation parameter test size for (target α = 0.05) 5000 realizations, 100 subjects, 5 and 20 observations per subject.

	Simulated model		Null hypothesis
p *	Signal strength	ρ	δ = 0	δ = (dmax − dmin)
5	None	0.5	0.048	0.033
		0.9	0.046	0.054
	Moderate	0.5	0.051	0.862
		0.9	0.050	0.076
	High	0.5	0.053	1.000
		0.9	0.053	0.195
20	None	0.5	0.047	0.049
		0.9	0.049	0.049
	Moderate	0.5	0.047	1.000
		0.9	0.044	0.260
	High	0.5	0.048	1.000
		0.9	0.046	0.776

^*For p = 5, standard error<0.006; for p = 20, standard error <0.007.

Test size is consistently controlled for H₀ : δ = 0 across all parameter combinations. Neither the signal strength nor the number of observations per subject has any bearing on this control. With no signal, test size for H₀ : δ = d_max − d_min is well controlled regardless of the initial correlation, ρ, or number of observations per subject. However, when a signal is present, test size becomes increasingly inflated with stronger signals, a lower initial correlation, and more observations per subject.

6. Data applications and results

All model fits for the following data applications were done in SAS IML utilizing the Newton–Raphson algorithm.

6.1. Neonate neurological development

We model the control neonate data discussed in Section 2.1 with the GLM for repeated measures data defined in Section 4.2. The initial full model is as follows:

$${\mathit{y}}_i={\beta }_0+{\beta }_1{\mathit{X}}_{i,\mathrm{loc}}+{\beta }_2{\mathit{X}}_{i,\mathrm{loc}}^2+{\beta }_3{\mathit{X}}_{i,\mathrm{gab}}+{\beta }_4{\mathit{X}}_{i,\mathrm{gas}}+{\beta }_5{\mathit{X}}_{i,\mathrm{gen}}+{\beta }_6{\mathit{X}}_{i,\mathrm{rac}}+{\beta }_7{\mathit{X}}_{i,\mathrm{bwt}}+{\mathit{e}}_i.$$ (7)

The FA values for each of the 20 locations for each subject are contained in y_i. The vectors X_i,gen and X_i,rac indicate the gender and race of the ith neonate, respectively. The gestational ages at birth and at the time of the scan are contained in X_i,gab and X_i,gas, whereas X_i,bwt contains the birthweights. Preliminary analyses showed that FA values are a quadratic function of the fiber location, thus X_i,loc and ${\mathbf{X}}_{i,\mathrm{loc}}^2$ were included to represent this trend. The location variable was shifted to start at 0, and all continuous covariates were centered about their respective means.

We model the correlation of the within-subject errors with the continuous-time AR(1), DE, and LEAR structures to assess the best model via the AIC. All three models are given initial parameter values such that they correspond at the beginning of the optimization process. The LEAR correlation model best fits the data with an AIC value of −4841, whereas the AR(1) model yields an AIC value of −4754 and the DE model fails to converge. An LRT of H₀ : δ = d_max − d_min corroborates this difference in fit between the LEAR and AR(1) models with p-value < 0.0001. The nonconvergence of the DE structure may be the result of the complexity in modeling a decay speed parameter that is nonlinear in the exponent of ρ (i.e. ρ^{d(t_ij, t_ik)ν}, where ν is the decay speed parameter). In contrast, the LEAR structure, as defined in equation (1), has a decay speed parameter that is linear in the exponent. The computational flexibility of the LEAR model due to the scaling constants d_max and d_min is another possible reason for the convergence disparity.

We continue the analysis employing the LEAR correlation model. In order to obtain a parsimonious model, the full mean model defined in equation (7) is reduced via backward selection with α = 0.10. The final mean model after reduction is

$${\mathit{y}}_i={\beta }_0+{\beta }_1{\mathit{X}}_{i,\mathrm{loc}}+{\beta }_2{\mathit{X}}_{i,\mathrm{loc}}^2+{\beta }_4{\mathit{X}}_{i,\mathrm{gas}}+{\mathit{e}}_i.$$ (8)

The resulting parameter estimates and p-values (based on the residual approximation of the F-test for a Wald statistic) associated with each of the covariates are presented in Table VI. As expected, neonates who are older at the time of the scan have significantly higher FA values, and thus are likely to have more developed cortico-spinal fiber tracts.

Table VI.

Neurological and DASH data: final mean model estimates, standard errors, p-values, and covariance parameter estimates.

		LEAR			AR(1)
Data	Parameter	Estimate	SE	p-value	Estimate	SE	p-value
Neuro	β 1	0.0303	0.0023	<0.0001	0.0299	0.0022	<0.0001
	β 2	−0.0015	0.0001	<0.0001	−0.0015	0.0001	<0.0001
	β 4	0.0137	0.0030	<0.0001	0.0140	0.0032	<0.0001
	α 2	0.0047	0.0002	—	0.0046	0.0002	—
	ρ	0.9875	0.0040	—	0.9109	0.0083	—
	δ/(dmax − dmin)	9.4107	3.0536	—	—	—
DASH	β 1	3.5053	0.8588	<0.0001	3.4971	0.7060	<0.0001
	β 2	2.4448	0.7368	0.0009	2.5004	0.6062	<0.0001
	β 3	0.1221	0.0412	0.0031	0.1107	0.0338	0.0011
	β 4	−1.8010	0.0947	<0.0001	−1.7992	0.0991	<0.0001
	β 5	−0.0096	0.0058	0.0976	−0.0144	0.0062	0.0198
	β 6	0.0129	0.0008	<0.0001	0.0130	0.0009	<0.0001
	α 2	128.15	2.6559	—	127.75	2.6477	—
	ρ	0.6853	0.0131	—	0.6853	0.0106	—
	δ/(dmax − dmin)	0.4786	0.0322	—	—	—	—

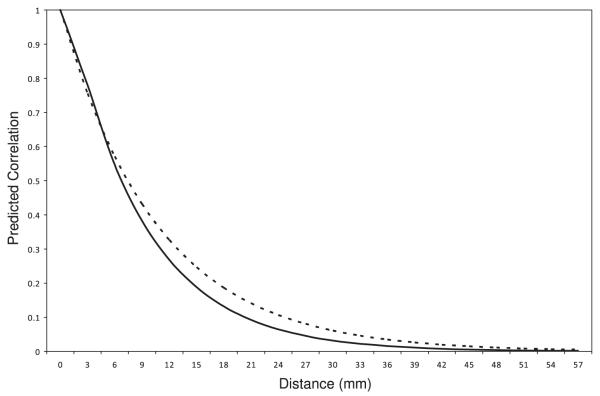
The within-subject error variance estimate and correlation parameter estimates of the LEAR (defined in equation (1)) and AR(1) correlation models for the final data model are also given in Table VI. The flexibility of the LEAR correlation structure allows it to model a correlation function in which the correlation is high for close measurements, but then decays at a faster rate than that imposed by the AR(1) structure as the measurements become farther apart. Figure 2 shows the predicted correlation as a function of the distance between measurement locations for both the best fitting LEAR model and the AR(1) model.

Figure 2.

Predicted correlation curve for the best fitting LEAR model (solid line) and AR(1) model (dashed line) as a function of the distance between measurements.

6.2. Diet and hypertension

We model the DASH data discussed in Section 2.2 with the GLM for repeated measures data defined in Section 4.2. The model of interest is as follows:

$${\mathit{y}}_i={\beta }_0+{\beta }_1{\mathit{X}}_{i,\mathrm{diet}}+{\beta }_2{\mathit{X}}_{i,\mathrm{race}}^2+{\beta }_3{\mathit{X}}_{i,\mathrm{age}}+{\beta }_4{\mathit{X}}_{i,\mathrm{hour}}+{\beta }_5{\mathit{X}}_{i,\mathrm{hour}}^2+{\beta }_6{\mathit{X}}_{i,\mathrm{hour}}^3+{\mathit{e}}_i.$$ (9)

The 24 blood pressure measurements for each subject are contained in y_i. The vectors X_i,diet and X_i,race indicate the diet and race of the ith participant, respectively. Their age is contained in X_i,age. The vectors X_i,hour, ${\mathbf{X}}_{i,\text{hour}},{\mathbf{X}}_{i,\text{hour}}^2$, and ${\mathbf{X}}_{i,\text{hour}}^3$ are included to represent the cubic trend in time present in the data.

We model the correlation of the model errors with the continuous-time AR(1) and LEAR structures to illustrate the difference in fixed effect inference that can occur with the disparate fits. The LEAR correlation model best fits the data with an AIC value of 24 265, whereas the AR(1) model yields an AIC value of 24 424. An LRT of H₀ : δ = d_max − d_min corroborates this difference in fit between the LEAR and AR(1) models with a p-value < 0.0001. The resulting parameter estimates and p-values (based on the residual approximation of the F-test for a Wald statistic) associated with each of the covariates are presented in Table VI for both the LEAR and AR(1) correlation model fits.

For both model fits, subjects who are on the DASH diet, white, and younger have significantly lower blood pressure than others. The difference in fixed effect inference occurs for the quadratic trend in time where the AR(1) fit leads to significance at the α = 0.05 level, whereas the LEAR fit does not. This disparity is corroborated by an LRT of the parameter. Given the better fit of the LEAR model and the simulation results of Section 5.2, the AR(1) fit most likely leads to a type I error in this context.

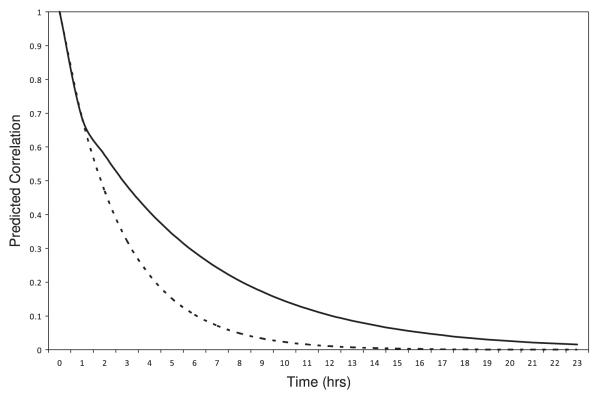
The within-subject error variance estimate and correlation parameter estimates of the LEAR (defined in equation (1)) and AR(1) correlation models for the data model are also given in Table VI. The flexibility of the LEAR correlation structure allows it to model a correlation function in which the correlation is high for close measurements, but then decays at a slower rate than that imposed by the AR(1) structure as the measurements become farther apart. Figure 3 shows the predicted correlation as a function of the distance between measurement locations for both the better fitting LEAR model and the AR(1) model.

Figure 3.

Predicted correlation curve for the better fitting LEAR model (solid line) and AR(1) model (dashed line) as a function of the time between measurements.

7. Discussion

As shown by the simulations in Section 5, the LEAR correlation structure performs better than either the AR(1) or DE models in a number of different conditions. The LEAR correlation model is far more robust to misspecification than the AR(1) model in terms of accurate fixed effect inference. Relative to the DE, the LEAR model is as robust to misspecification in controlling fixed effect test size, while having better convergence and statistical properties. The utility of the LEAR model becomes even more pronounced in data with more repeated measurements. The appeal of the LEAR correlation structure is also shown in the examples of Section 6. For the neonate neurological data, the AR(1) model fits the data more poorly and the DE model fails to converge. An AR(1) correlation fit to the DASH data likely leads to a type I error, whereas the LEAR fit does not. A better fit of the correlation model gives more confidence in the results of the analyses. Hence the LEAR model adds another tool to the set of parsimonious correlation structures for repeated measures data.

The appeal of the LEAR correlation structure also stems from its applicability to a variety of data types. Since the model allows for a wide range of exponentially decaying correlation patterns, it can handle the slow decays often seen in longitudinal data (as in our DASH data example) as well as the faster decays periodically encountered in spatial data (as in our neonate neurological data example). In addition, the LEAR model subsumes the classic temporal covariance structures, namely CS, continuous-time AR(1), and MA(1), while maintaining parsimony and appealing statistical and computational properties. There are many possible directions for future research with the proposed LEAR correlation structure. Including higher order polynomial functions in the exponent of the model would further increase its flexibility. Also, introducing a nonstationary LEAR correlation structure and/or variance model may prove extremely useful in neuroimaging studies of the developing brain since the variability of brain characteristics tends to change over time. Comparing the implementation of the LEAR structure with various modeling and estimation methods will prove valuable. For spatio-temporal data, or any data that have within-subject correlations induced by more than one factor, the development of a Kronecker product LEAR correlation model would be beneficial.

Examining mixtures of correlation functions is also of interest. Some data analysts may consider mixtures when a pure AR(1) model seems inappropriate. These combinations can take many forms including weighted sums of correlation structures (i.e. Γ_i = aΥ + (1 − a)Ω) and weighted Hadamard products (i.e. Γ_i = aΥ○(1 − a)Ω). Mixture functions allow a degree of flexibility not attainable by a single structure. However, careful attention must be paid to interpretability and to ensuring that the resulting combination is a valid correlation matrix. As mentioned in Section 3.2 and notated in Appendix A, the LEAR model can be written as an unweighted Hadamard product of an equal correlation and a continuous-time AR(1) model if 0 < δ < d_max − d_min. For all δ, the LEAR model can be written in the form of a weighted sum of an AR(1) model and white noise with a = ρ^{d_min{1−[δ/(d_max−d_min)]}}, and Υ_jk = {ρ^{[δ(d_max−d_min)]}}d_ijk, and Ω_jk = I(d_ijk = 0). However, it is not statistically equivalent to a mixture of a pure AR(1) model and white noise because of the additional, identifiable, decay speed parameter δ. The LEAR correlation structure is then a viable alternative to using mixtures since the structure may be easier to interpret and allows for a wide range of correlation patterns while retaining parsimony.

Appendix A. Condition for positive definiteness

The linear exponent autoregressive (LEAR) correlation structure (defined in equation (1)) may be reparameterized in terms of a Hadamard product. Let

$$\begin{array}{cc}\hfill {\langle {\rm Y}\rangle }_{\mathit{jk}}& =\{\begin{array}{cc}{\rho }^{d_{\min }\{1-[\delta ∕(d_{\max }-d_{\min })\left]\right\}},\hfill & j\ne k,\hfill \\ 1,\hfill & j=k,\hfill \end{array}\phantom{\}}\hfill \\ \hfill {\langle \Omega \rangle }_{\mathit{jk}}& =\{\begin{array}{cc}{\left\{{\rho }^{[\delta ∕(d_{\max }-d_{\min }\left)\right]}\right\}}^{d_{\mathit{ijk}}},\hfill & j\ne k,\hfill \\ 1\hfill & j=k.\hfill \end{array}\phantom{\}}\hfill \end{array}$$

Then,

$${\Gamma }_i={\rm Y}\circ \Omega \left(\text{Hadamard product}\right),$$

where

$$\begin{array}{cc}\hfill {\rm Y}& =\{\begin{array}{cc}\text{Equal correlation with}(\rho ={\rho }^{d_{\min }\{1-[\delta ∕(d_{\max }-d_{\min })\left]\right\}}),\hfill & 0\le \delta \ast \ast \ast d_{\max }-d_{\min },\hfill \\ {11}^{\prime },\hfill & \delta =d_{\max }-d_{\min },\hfill \end{array}\phantom{\}}\hfill \\ \hfill \Omega & =\{\begin{array}{cc}\text{Continuous}-\text{time}\mathrm{AR}\left(1\right)\mathrm{with}(\rho ={\rho }^{\delta ∕(d_{\max }-d_{\min })]}),\hfill & \delta >0,\hfill \\ {11}^{\prime },\hfill & \delta =0,\hfill \end{array}\phantom{\}}\hfill \end{array}$$

It is well known that the equal correlation and AR(1) models (assuming a Euclidean distance metric or a distance metric that can be isometrically embedded in Euclidean space) are both positive definite for 0≤ρ < 1 (see Muller and Stewart [32, p. 38] and Schabenberger and Gotway [6, pp. 141–144, 205–210] for details). Thus, by Theorem 7.22 in Schott [33, p. 270] , δ≤d_max − d_min is a sufficient (but not necessary) condition for the positive definiteness of the LEAR model.