Girls, girls, girls: Gender composition and female school choice

Highlights

► Causal impact of fraction of girls in schools on (vocational) school type choice for female students. ► Population variation: gender composition of adjacent cohorts within schools. ► The higher the share of girls, the less likely they choose a female-dominated school type at age 14. ► Results robust to falsification tests and sensitivity checks.

Abstract

Gender segregation in employment may be explained by women's reluctance to choose technical occupations. However, the foundations for career choices are laid much earlier. Educational experts claim that female students are doing better in math and science and are more likely to choose these subjects if they are in single-sex classes. One possible explanation is that coeducational settings reinforce gender stereotypes. In this paper, we identify the causal impact of the gender composition in coeducational classes on the choice of school type for female students. Using natural variation in the gender composition of adjacent cohorts within schools, we show that girls are less likely to choose a traditionally female dominated school type and more likely to choose a male dominated school type at the age of 14 if they were exposed to a higher share of girls in previous grades.

1. Introduction

While gender gaps in employment rates are narrowing in most OECD countries, the earnings differentials between men and women are still pronounced (see e.g. Weichselbaumer & Winter-Ebmer, 2005). One explanation for the persistency of the gender wage gap is the high degree of occupational segregation. Men and women are still concentrated in different occupations and men have ‘chosen’ the prestigious, powerful and well-paid jobs. The situation has not changed substantially since the 1970s, women predominantly work as clerks, in sales and services jobs, as teachers and in life-science and health professions, while men are found in physical, mathematical and engineering jobs, in managerial occupations and in manual and production jobs (Coré, 1999; OECD, 2002).

The high degree of gender segregation in the labor market may be explained by women's reluctance to choose technical and male dominated occupations, although the foundations for their career choices are certainly laid much earlier, i.e. during education. While educational attainment has converged across gender, considerable differences can be found in the fields of studies. Machin and Puhani (2003) showed that in the UK and Germany, in 1996, male and female students were strongly segregated among different degree subjects. This segregation translates into occupational segregation on the labor market and explains between 8 and 20% of the overall gender wage gap. Ten years later, the situation is not much different. In the OECD, the share of female graduates in science and engineering was about 30% between 2004 and 2006. On the other hand, more than 75% of graduates in education, health and social services were females (OECD, 2004–2006). Joy (2006) showed that gender differences in college majors explain a substantial part of gender segregation across occupational groups in the US.¹

What is the driving force behind the high degree of gender segregation in fields of studies and how can education policy make a difference? The debate on coeducation and single-sex schooling is closely related to this issue. Educational experts claim that girls are doing better in male dominated subjects, like math and science and are more likely to choose these subjects if they are in single-sex classes. Proponents of single-sex education argue that it gives more freedom in exploring interests and abilities, while coeducational settings reinforce gender-stereotypes. Possible explanations for the reinforcement of gender-stereotypes in coeducational schools are the lack of self-confidence of girls in subjects like math and science, the dominating behavior of boys in the classroom and an unequal treatment of boys and girls by teachers.

In this paper, we do not compare single-sex schools with coeducational schools but focus on the impact of the gender composition within coeducational schools. We believe that the gender-related mechanisms, described in more detail below, are less pronounced, the higher the share of females in class, thus allowing girls to make a less restrained career choice. Therefore, we expect that girls are less likely to choose a traditionally female dominated school type and are more likely to choose a male dominated school type at the age of 14 after spending the previous years in classes with a higher share of female students.

We test this generic hypothesis in the context of secondary school choice in the Austrian education system. Like many other countries, Austria has an education system that is characterized by a strong vocational orientation.² A multitude of intermediate and higher vocational school types are available, preparing for jobs in specific disciplines, such as engineering, arts and crafts, business administration and domestic science. A high degree of gender segregation among these vocational school types can be observed in the official school data. Girls are choosing traditionally female oriented vocational schools and boys are predominantly found in technical schools. For example, in Linz, the third largest city in Austria, the mean share of girls in technical schools between 1979 and 2002 was 5% on average and below 9% in each single year. In schools for domestic sciences, on the other hand, about 94% of students were girls (Statistik Austria, 1979–2002).

An unequal gender distribution is also observed across occupations in the labor market. Austria has one of the highest rates of occupational segregation among the EU countries and the US (Dolado, Felgueroso, & Jimeno, 2001).³

We identify the causal impact of having more female peers on the choice of school type for female students. Since the share of girls in schools is endogenous, we use population variation in the gender composition of adjacent cohorts within schools. School-specific time trends control for school trends in unobserved factors that may be correlated with the share of girls in a certain grade. The analysis is based on register data, covering 19 cohorts of compulsory school students from Linz.

The paper proceeds as follows. Section 2 gives an overview of the related literature from economic research as well as other disciplines and outlines our contribution. The literature review gives insight into the mechanisms and consequences of gender role formation and possible answers to the question, why gender composition in class might influence academic outcomes. Section 3 describes the research design, Section 4 presents the results and Section 5 contains powerful falsification and sensitivity checks. Finally, Section 6 concludes.

2. Previous studies and our contribution

It is a well known fact that men and women choose different majors and graduate in different fields of studies. Many factors influence the choice of major, such as prior achievement in various subjects, the individuals’ preferences for various subjects, the school or college environment and labor market expectations. Turner and Bowen (1999) focused on the explanatory power of prior test scores for men's and women's choices of studies in the US. The authors conclude that a small part of the gender gap in fields of studies can be explained with differences in verbal and math SAT scores. In engineering, about 31% of the gender gap can be explained with prior achievement, while in economics the fraction is even lower, about 17%.

Next to skills, organizational characteristics of schools and colleges seem to be influential. Previous research has shown that successful women in male dominated fields disproportionately graduated from single-sex colleges (Tidball, 1985, 1986). It seems that female colleges benefit women with respect to their occupational choices. However, students in coeducational and single-sex colleges might be different in terms of ability and aspirations and many unobserved factors may contribute to these results. In this context, Solnick (1995) used a more sophisticated empirical framework. She compared about 1400 females in single-sex colleges with about 700 female students in comparable coeducational colleges in the US. Data on intended majors at the beginning of college as well as final majors at the end are available. She found that women in the single-sex schools are more likely to switch to a different major during their studies. The presence of female students or other unobserved characteristics of single-sex colleges encourage students to shift from intended female dominated to neutral or male dominated majors. A comparable study was undertaken by Billger (2002), who investigated alumni from a female college that became coeducational. After the admission of men, female students were less likely found in male dominated subjects and occupations.

Coeducation versus single-sex schooling is an ongoing debate in primary and secondary education, too. The proponents of single-sex schooling argue that coeducational settings reinforce gender-stereotypes, while single-sex schooling gives more freedom in exploring interests and abilities, especially for female students. Two studies of Billger (2007, 2009) support this idea: female students from high-schools with more than 75% females earn higher wages later on, and the college majors of students from single-sex secondary private schools are less segregated by gender than those of coeducated students.

Studies in educational science show that female students are doing better in male dominated subjects, like math and science and are more likely to choose these subjects if they are in single-sex classes. For boys, this phenomenon seems to be less pronounced. While some authors conclude that boys in single-sex environments are doing better on reading and writing tests and are more likely to choose subjects like biology or languages, other studies find no significant differences (see e.g. Haag, 1998; Stables, 1990).

There are several reasonable explanations for these findings. First, the gender composition might have an influence on the self-concept and self-esteem in subjects that are perceived as inappropriate for the own sex. In this regard, developmental psychologists talk about ‘gender intensification’ and mean a period in adolescence in which children are extra-sensitive to gender-roles. With the beginning of puberty, boys and girls strongly adhere to gender-stereotypes and each departure from traditional gender roles is rated as inappropriate (Galambos, 2004; Lobel, Nov-Krispin, Schiller, Lobel, & Feldman, 2004).⁴ When boys and girls are educated together, their strong beliefs about the gender-appropriateness of attitudes and activities are amplified and they tend to conform to gender roles more strongly. Social cognition research shows that gender identity and the related self-concept of abilities (how people rate themselves in terms of abilities) is influenced by the social environment. Since gender is more salient in a coeducational setting, the self-concept is strongly determined by the knowledge about masculinity and femininity a person has. In single-sex schools, on the contrary, gender is not a useful category to think about and gender-related knowledge and beliefs are less important in constructing a self-concept of own abilities and interests.

In a randomized experiment, Kessels and Hannover (2008) showed that girls reported a significantly higher self-concept of physics-ability after being taught in single-sex classes. About 400 students in Berlin were randomly assigned to mixed and single-sex classes in physics throughout the 8th grade. After one year the students’ self-concept of physics ability and their gender-related self-knowledge (how they identify themselves with feminine and masculine traits) were measured. Girls who were taught in single-sex classes reported a higher self-concept in physics ability than girls in mixed classes. For the boys’ self-concept in physics the gender composition did not play a role. Furthermore, boys and girls in single-sex classes identified themselves with feminine and masculine adjectives more flexibly. In other studies, similar results were obtained (Brutsaert, 1999; Haag, 1998).

Besides gender identity formation, the atmosphere and learning climate as well as pupil-teacher relations may be different in single-sex classrooms. There is substantial social science research on gender differences in classroom interactions, showing that males are given and attracting a higher amount of teacher attention (Beaman, Wheldall, & Kemp, 2006; Einarsson & Granström, 2002; Sadker, Sadker, & Klein, 1991). Teacher beliefs about gender differences in various subjects might also play a role. In a review about gender-related teacher beliefs in mathematics, Li (1999) concludes that teachers tend to stereotype mathematics as a male domain, which is reflected in their propensity to underrate the abilities of girls and overrate that of boys.⁵

Recently, economists have become increasingly interested in the notion of (social) identity.⁶ Akerlof and Kranton (2000, 2002) were the first to integrate the concept of (gender) identity into an economic model of behavior. This model can explain why females are more likely to choose a female dominated occupation (or school type) although the pecuniary payoff is lower than the payoff from a male dominated occupation. Since the choice of an occupation is also associated with a non-pecuniary payoff in terms of identity, the total payoff from choosing a male dominated occupation may be lower if this behavior is considered as a non-conformance with prescribed social norms and therefore, involves a non-pecuniary penalty in terms of a conflict with one's self-image or identity.

The gender composition of the environment plays a role for other economic outcomes as well. Booth and Nolen (2009a, 2009b) conducted economic experiments on gender differences in risk taking and competitive behavior. The results support the idea that girls strongly respond to the gender composition. Female adolescents from single-sex schools (long-term effects) as well as those who were randomly assigned to all-girls experimental groups (short-term effects) behave like boys in terms of risk and competition behavior. Compared to their female peers in mixed-gender environments, they reveal less risk-averse preferences and shy away from competition less likely. These results are complemented by Lindquist and Säve-Söderbergh (2011), who show that females appearing in the game show ‘Jeopardy’ are more risk averse than males and this behavior is intensified when they play in a male dominated group.⁷

In this paper, we study the choice of secondary school type of 14-year-old compulsory school students in Austria. Our study contributes to the literature in multiple ways:

• •First, we do not compare students from single-sex schools to coeducated students, but focus on the share of females within schools. Single-sex schools might differ from coeducational schools in many other ways than gender composition, such as teaching principles or school philosophies. By looking at coeducational schools we analyze a general situation, most students in almost all education systems are exposed to. We believe that the gender-related mechanisms described above do not only apply to complete gender segregation but can also be detected with lower-level variation. Gender identity, classroom interactions and teacher beliefs are not only present in single-sex environments but should also depend on the gender domination in mixed groups.
• •Second, we are interested in the choice of (vocational) school type. In all education systems, either at some stage in upper secondary education or later on, students have to choose between different occupational orientations, be it a specific type of school or a college major. Thus, the topic is not only relevant for Austria or for schooling systems with a high degree of vocational orientation, but it is a general mechanism that we are interested in.
• •Third, we estimate the causal impact of having more female peers (in grades 5–8) on the female students’ choice of school type in grade 9 by using natural variation in the gender composition of 19 adjacent cohorts of compulsory school students in Austria. Our paper is the first one, studying this topic with a credible identification strategy.

The studies of Hoxby (2000), Lavy and Schlosser (2011) and Proud (2008) are related to our paper, since they also use population variation to identify the causal effect of gender composition on educational outcomes. However, these studies focus on student achievement in general and the identification of peer group effects in particular. Hoxby (2000) and Lavy and Schlosser (2011) found a positive impact of the fraction of females in the classroom on cognitive outcomes in math and reading. Proud (2008) obtained similar results for math and science, but found a negative effect of a more female classroom on boys’ English test scores and no effect for girls in English.

3. Research design

This Section presents our research design. First, we describe the data and outline institutional conditions of the Austrian education system (Section 3.1). Then, we discuss our econometric model and the identification strategy (Section 3.2). Subsequently, we develop our estimation samples and present some descriptive statistics (Section 3.3). In Section 3.4, we define male and female school types and describe some details of our estimation methods.

3.1. Data and institutional framework

We use register data covering the universe of compulsory school students in Linz, an Austrian city of about 189,000 inhabitants. We observe some basic individual characteristics of these students (age, sex, native language) and the nine compulsory years of their school career (school types, schools and classes), usually grades 1–9.⁸ The variable of interest is the school type in grade 9, which is observed for 19 cohorts between 1988 and 2006.

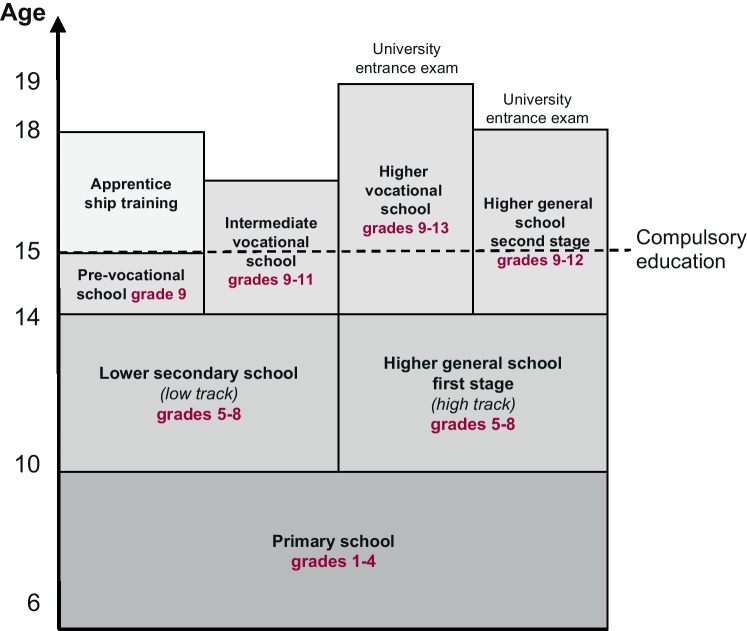
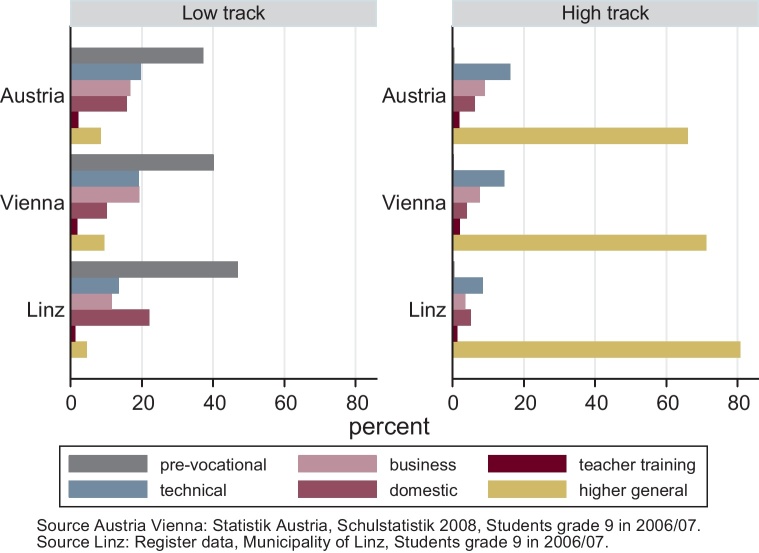
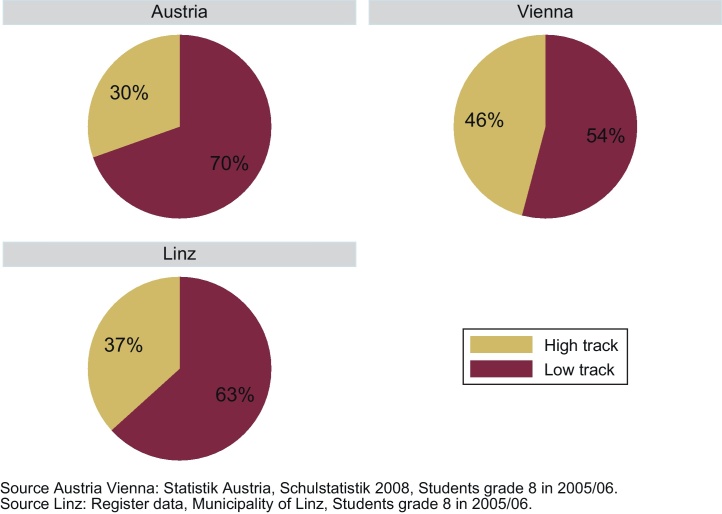
The structure of the Austrian education system is presented in Fig. 1. After four years of comprehensive primary schooling, students have to choose between two school tracks, the lower secondary school (low track) and the first stage of the higher general school (high track). The track choice is made by students and their parents, depending on previous academic records and recommendations of primary school teachers. Low track schools differ from high track schools in many aspects. High track schools offer an academically preferable curriculum, teachers have higher educational qualifications and earn higher salaries. Figs. 2 and 3 shows the distribution of students among high and low track schools in Linz, compared to the whole country and the capital Vienna. 70% of all Austrian students went to low track schools in the school year 2005/06. While this share was significantly smaller in Vienna, the figure for Linz can be found in-between.

Fig. 1.

Austrian education system.

Fig. 2.

School types in grade 9.

Fig. 3.

School types in grade 8.

After grade 8, students again have to choose a school type (see Fig. 1). There are four broad alternatives, a pre-vocational school, an intermediate vocational school, a higher vocational school and the higher general school. The pre-vocational school is a one-year school that prepares students for various types of apprenticeships. There is no occupational differentiation within this school type. Vocational schools comprise intermediate (grades 9–11) and higher (grades 9–13) school types, offering a range of vocational orientations (technical, business, domestic science, tourism and kindergarten teacher training⁹). In most cases the intermediate and higher vocational tracks of the respective orientations are located in the same building and students are taught by the same teachers. After the intermediate vocational school students enter the labor market directly, whereas after the higher vocational school students can choose between entering the labor market and starting tertiary education. The higher general school type lasts for four years and most students enter a post-secondary or tertiary education afterwards.¹⁰

Fig. 2 shows the distribution of students among school types in grade 9 for students coming from low and high track schools separately, again for Austria, Vienna and Linz. The higher and intermediate vocational schools are combined and plotted by orientations.

Although the admission requirements do not strongly restrict the school choice of low track students, the distribution of students coming from low and high track schools is very different in grade 9. While students from low track schools choose the pre-vocational school very often, this school type is hardly ever chosen by high track students. The vast majority of high track students choose the higher general school, which is the second stage of the high track school.¹¹

3.2. Identification strategy

Our hypothesis is that girls are less likely to choose a female dominated school type and more likely to choose a male dominated school type, such as a technical school in grade 9 after spending the previous years in grades with a higher fraction of female students.¹² The gender mix in schools may be endogenous and correlated with unobserved student or school characteristics, such as educational orientations in terms of subjects or teaching methods. Our identification strategy relies on random variation in gender composition of adjacent cohorts within schools, resulting from natural variation in the gender composition of birth cohorts.

Our econometric model can be written as:

$${\mathit{Female}}_{\mathit{ist}}^{*}={\beta }_0{X}_{\mathit{ist}}^{\prime }+{\beta }_1{G}_{\mathit{st}-x}+{\beta }_2{\mathit{Girls}}_{\mathit{st}-x}+{\gamma }_s+{\delta }_{1s}{t}_{\mathit{st}-x}+{\delta }_{2s}{t}_{\mathit{st}-x}^2+{\delta }_{3s}{t}_{\mathit{st}-x}^3+{ϵ}_{\mathit{ist}}$$

$${\mathit{Female}}_{\mathit{ist}}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\mathit{Female}}_{\mathit{ist}}^{*}>0\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right)$$

where ${\mathit{Female}}_{\mathit{ist}}^{*}$ is the latent probability of student i in year (cohort) t coming from school s to choose a female school type in grade 9. The vector $X_{\mathit{ist}}^{\prime }$ captures individual characteristics of the students. Girls_st−x is the variable of interest and gives the fraction of girls in school s at time t − x, where x = {4, 3, 2, 1} and determines whether we use the fraction of girls in grade 5, 6, 7 or 8. G_st−x is a control variable for the size of the grade. γ_s is a school fixed effect and δ_1st, δ_2st² and δ_3st³ are school-specific cubic time trends. The error term ϵ_ist consists of an individual-specific and a school-specific random part. We are interested in the coefficient β₂, which should have a negative sign.

Note that our identification strategy is based on school-fixed effects, thus we are exploiting the variation of the female share in a given grade among adjacent cohorts within schools. All unobservable school-specific characteristics that are constant over time are eliminated. Furthermore, we add time trends that are school-specific. Thus, we control for school trends in unobserved factors that may be correlated with the share of females in a certain grade. This is important because there may be some unobserved school characteristics that change over time. Imagine, for example, a school that introduces enrichment activities in foreign languages. The share of female students might increase as well as the probability of those females to choose female dominated school types after attending this school. Only relying on school fixed effects would bias β₂ downwards. Another example would be the following: A certain school starts a campaign to promote girls in technical subjects. The share of females might increase as well as the probability of those females to choose male dominated school types in grade 9. In this case β₂ would be biased upwards. Controlling for flexible time trends in each single school separately should eliminate this problem.

3.3. Estimation samples

We estimate our model for students in low track schools and focus on the share of female students at the grade level. In Austria, low track students are streamed in the main subjects German, Mathematics and English. In each of these subjects three ability groups are formed at the grade level and students are assigned to one group according to their subject-specific achievement. Thus, students spend most of their time in school with their classmates but are taught together with other students from the same grade in the main subjects. Finding the relevant peer group for these students is not straightforward since both, the class and the grade might be important. Since our identification strategy relies on population variation, i.e. the random variation in the gender mix of a grade (cohort), we focus on the grade level. For the class level we cannot be sure whether students are admitted to classes on the basis of some unobserved characteristics that are correlated with the gender composition.¹³

We restrict our analysis to students in low track schools because of three reasons. First, while low track students have to make a real choice after grade 8, the vast majority of high track students choose (stay in) the higher general school. Thus, there is only little variation in school types for high track students (compare Fig. 3). Second, we do not observe all students in high track schools because students from neighboring municipalities can choose a high track school in Linz and these students are not included in our data. In contrast, in low track schools we observe the universe of all students in grades 5–8. Hence, we are able to measure the fraction of girls in low track schools correctly, but not in high track schools. The third reason is track choice in grade 5. Students opting for high track schools can choose any school, while low track school students usually go to the low track school in their catchment area, which is based on residency.¹⁴

Since we look at low track school students only, our sample is not representative for the whole student population. On average 58% of all students from Linz have chosen a low track school (grade 5) after primary education between 1984 and 2002. The proportion of students in low track schools is higher and amounts to about 62% if grade 8 is considered. Some students change school types between grade 5 and grade 8. Most of them start in the high track school and change to the low track school. Upward mobility is also possible (see Appendix A) but rather uncommon.

While we observe the universe of all low track students between grades 5 and 8, school choice in grade 9 is not observed for all students. It is predominantly missing for students who already have nine years of schooling, i.e. students who repeated a grade or attended a pre-school. This peculiarity of the data is due to the purpose of data collection by the municipality, which is to document nine years of schooling for each student. However, whether we observe a student in grade 9 or not is orthogonal to the fraction of girls in grade 5.¹⁵

Overall, our sample of students is selected in two ways. On the one hand, it is negatively selected because we concentrate on low track students only. This group constitutes about 58–62% of the total student population in Linz. On the other hand, we do not observe, predominantly, pre-schoolers and grade-repeaters, implying a positive selection of students from low track schools. Thus, our study refers to students that are located in the lower tail and the center of the ability distribution.

We are interested in the effects of gender composition in the low track school on the choice of school type in grade 9. Since the share of females may vary from grade 5 to grade 8, we have chosen to use the share in grade 5 in our baseline estimations. Grade 5 is the best choice with respect to our identifying assumptions. Grade 5 is the first year in a new school. Therefore, students and their parents with certain unobserved preferences for female or male classes are not able to anticipate the actual gender composition when they decide to enroll in a school. Selection bias on the basis of the fraction of girls can therefore be ruled out for grade 5. Between grade 6 and grade 8 some students have changed schools and in some cases these decisions might be correlated with the gender composition they were exposed to.¹⁶

Table 1 shows summary statistics for two estimation samples, one for grade 5 and one that is called big sample. For the big sample we use grade 5 information primarily but for those students with no information in grade 5 (because they moved to Linz or they attended grade 5 in a high track school and switched to a low track school after grade 5), we use grade 6, grade 7 or grade 8. In both samples, about 45% are female, they are 14–15 years old and 11–12% have migration background. The average grade consists of about 58 students. Grade size is somewhat higher in the big sample because in the low track schools the grades 6–8 are usually larger than grade 5. This is because some students attend the high track school in grade 5 and change to the low track after some years. In the big sample, about 90% of the students are observed in grade 5, 4% in grade 6 and 3% each in grade 7 and 8. In both samples, about 13% attended preschool and about 5% repeated a grade.¹⁷

Table 1.

Summary statistics of student and grade-level variables.

Variables	Grade 5		Big Sample
	Mean	Stdev	Mean	Stdev
Student-level variables
Female	0.450		0.450
Age in grade 9	14.691	0.424	14.706	0.438
Foreign language	0.111		0.125
Grade-level variables
Grade size	57.784	17.172	57.996	17.093
Fraction of girls	0.436	0.114	0.436	0.112
Observed in..
Grade 5	100%		90%
Grade 6	–		4%
Grade 7	–		3%
Grade 8	–		3%
Preschool and grade repetition
Preschool	0.134		0.135
Grade repetition	0.049		0.044
Number of observations	6769		7472
Number of low track schools	18		18

Notes: For 0.27% of students in the grade 5 sample and 0.43% of students in the big sample the information on native language is missing, these observations are not dropped, but a missing dummy is included in the estimations.

In our sample period, there were 20 low track schools in Linz; three of them were private schools, among them two girls’ schools. These two single-sex female schools were dropped from the sample. Table 2 shows the variation in gender composition, decomposed into between and within school components for all 20 low track schools, the 18 coeducational schools as well as the 17 public coeducational schools.

Table 2.

Variance of the fraction of girls in grade 5 between and within schools.

Variation of Girls	Sum of squares	Share of total	N
All low track schools
Between	0.03542	83.60%	20
Within	0.00695	16.40%	18.50
Mean of Girls	0.500
Coeducational schools
Between	0.00693	47.24%	18
Within	0.00774	52.76%	18.44
Mean of Girls	0.443
Coeducational public schools
Between	0.00737	49.30%	17
Within	0.00758	50.70%	18.41
Mean of Girls	0.444

Notes: Three of all low track schools are private schools and two of them are female single-sex schools.

The variation in the fraction of girls within schools is about 16% in all low track schools (including single-sex schools) and 53% in coeducational schools.¹⁸ Our estimations are based on these 18 coeducational low track schools.¹⁹

3.4. Female and male dominated school types

In Austria, 14-year-old students can choose between a variety of school types, some of which are traditionally female oriented and others are traditionally male oriented. Our classification of schools into female and male dominated ones is based on the following criteria: (i) typical occupations the school types are preparing for, (ii) the fraction of female students in these schools and (iii) instructional time in math and science. Table 3 shows the different school types and the applied classifications.

Table 3.

Traditionally female and male dominated school types.

School type	Teacher training	Domestic sciences	Business schools	Higher-general	Pre-vocational	Technical schools
Typical occupations	Kindergarten teachers, social occupations	In hotels and restaurants, clerks	Clerks, book-keepers	Professionals (university)	Crafts and services	Engineers
Fraction females
1979–1987	0.995	0.979	0.673	0.541	0.439	0.039
1979–2002	0.983	0.943	0.655	0.544	0.418	0.051
Classes per week
Math	3	2.18	2.04	3.40	3.46	3.86
Science	2	2	2	2	1.61	4.54
% of all classes math &science	12.82	10.61	10.84	17.11	16.11	21.58
Binary models
Female weak	1	1	1	1	0	0
Female	1	1	1	0	0	0
Ordered models
Ordered	3 female	3 female	3 female	2 neutral	2 neutral	1 male
Ordered detail	5 female	5 female	4 female wk	3 neutral	2 male wk	1 male
#Schools
in the city	2	7	2	15	3	2
within 50 km	3	14	10	38	30	9
within 75 km	4	16	14	47	40	11

Notes: The figures of female shares are based on data from the central bureau of statistics (Schulstatistik Linz, Statistik Austria, 1979–2002). Classes per week in math and science are taken from the student questionnaires of PISA 2000 and 2003. The answers of all grade 9 PISA students are aggregated to the school level. The reported value refers to the median school from each school type. One class period consists of 50 min. Additionally, math and science classes are summed and given as percent of total classes per week for each school type.

The table also shows the number of schools of each type that are located in the city of Linz and in neighboring municipalities. The number of schools per school type is rather high, even within the city students can choose out of at least two schools per school type. For students opting for a school outside of Linz, we do not observe the specific school, but only the school type. About 11% of the students in our estimation sample choose a school outside the city. If they fulfill the admission requirements for a school type, students can choose relatively freely which school they want to attend in grade 9. If they decide for a higher vocational school (teacher-training, domestic sciences, business, technical) or a higher general school they may have to pass an admission exam, depending on their marks in grade 8. The entry restrictions for intermediate vocational schools (domestic sciences, business, technical) are weaker and no restrictions exist for the pre-vocational track.²⁰

We estimate binary as well as ordered models. Our classifications are primarily based on the typical occupations the various school types are preparing for. Attending, for example, a technical school often means a career in a technical occupation afterwards. We have these occupations in mind when classifying the school types into female and male dominated ones but use additional, more objective indicators for our classification, such as the fraction of females in the various school types or the math/science classes in the curricula.

In the binary case, we first apply a weak definition for female domination in schools, with teacher-training schools, schools for domestic sciences, business schools and higher-general schools being defined as weakly female dominated (Female weak). Note that in these schools more than 50% of the students were females between 1979 and 1987 (the time span prior to our sample period). For a narrower definition, we employ a minimum female share of about two thirds (Female). In these schools, the curricula are characterized by a relatively low degree of math and science education. Instructional time in math and science is below 13% in each school type.

To draw a more precise picture of gender aspects in the various school types, we also estimate ordered models. We estimate a three-category model with female, neutral and male school types (Ordered) and a five-category model with female, female weak, neutral, male weak and male school types (Ordered detail). Table 4 shows the distribution of students in our grade 5 sample among the different school types.

Table 4.

Distribution of students among school types.

	Grade 5 Sample
	All	Females	Males
Binary
Female weak	0.333	0.526	0.175
Female	0.256	0.436	0.109
Ordered
3 female	0.256	0.436	0.109
2 neutral	0.603	0.547	0.648
1 male	0.141	0.017	0.243
Ordered detail
5 female	0.153	0.299	0.033
4 female weak	0.103	0.138	0.076
3 neutral	0.077	0.089	0.066
2 male weak	0.526	0.457	0.582
1 male	0.141	0.017	0.243
Number of observations	6769	3046	3723

Notes: Summary statistics of the binary and ordered dependent variables for the grade 5 sample.

In a first step, we estimate linear probability models as well as logit models for choosing a weakly female dominated (Female weak) and a female dominated (Female) school type. In a second step, we estimate ordered logit models, using the three-category dependent variable (Ordered) as well as the five-category dependent variable (Ordered detail).²¹

In both sets of models we control for the students’ age at school choice, whether their first language is German and grade size. We cluster standard errors at the school × year level because the observations are not independent within school cohorts. As we only look at female students, the number of observations in our sample is higher for schools and grades with a higher share of female students. Thus, the treatment variable is positively correlated with the number of observations contributing to the estimation. To avoid any biases resulting from this fact, we additionally carry out weighted regressions with the weight being inversely related to the fraction of girls in the grade (Weight = 1/Girls).

4. Results

First, we present results for the binary models. Table 5 shows the estimated coefficients of the linear probability models as well as the marginal effects of the logit models for unweighted and weighted regressions and for the grade 5 sample and the big sample.

Table 5.

Effects of Girls – Binary models.

	Unweighted		Weighted		N
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Female weak
Grade 5	−0.357	−0.426	−0.429	−0.515	3046
	(0.162)**	(0.187)**	(0.166)**	(0.194)***
Big Sample	−0.375	−0.430	−0.432	−0.504	3366
	(0.149)**	(0.171)**	(0.151)***	(0.177)***
Female
Grade 5	−0.425	−0.391	−0.481	−0.457	3046
	(0.140)***	(0.132)***	(0.143)***	(0.140)***
Big Sample	−0.440	−0.378	−0.496	−0.430	3366
	(0.135)***	(0.117)***	(0.136)***	(0.121)***

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Big sample includes g6–g8 dummies. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

*Statistical significance at 10% level.

^**Statistical significance at 5% level.

^***Statistical significance at 1% level.

Each number represents a single regression including school-fixed effects, school-specific cubic time trends and some control variables.²² The estimated effects are similar across regressions and show the expected negative signs. The higher the share of girls in low track schools, the less likely a (weakly) female dominated school type is chosen by female students in grade 9. The coefficients are somewhat larger in the weighted regressions. The estimates range from −0.36 to −0.52, with a mean of −0.43 for Female weak and −0.44 for Female. Increasing the share of girls by one standard deviation (0.11), decreases the probability of choosing a female school type by 4.8 percentage points, which is a reduction of 11%.

The results of the ordered models are given in Table 6. The coefficients as well as the marginal effects for all possible outcomes are reported for the unweighted and weighted regressions and both samples. All coefficients of the three-category model are statistically significant and show a negative sign. The results give the same picture as those of the binary models. While the marginal effects for female school types are all around −0.48, the marginal effects for the technical school type are about +0.02. Thus, female students change from female school types to primarily neutral ones after spending the previous years of education with more girls in class. There is also a small effect for male school types.

Table 6.

Effects of Girls – Ordered models.

	Grade 5 Sample		Big Sample
	Unweighted	Weighted	Unweighted	Weighted
Ordered
Coefficient	−1.791	−2.092	−1.829	−2.118
	(0.614)***	(0.630)***	(0.588)***	(0.598)***
Marginal effects
3 female	−0.439	−0.514	−0.449	−0.521
	(0.150)***	(0.155)***	(0.144)***	(0.147)***
2 neutral	0.416	0.490	0.427	0.498
	(0.142)***	(0.148)***	(0.137)***	(0.141)***
1 male	0.023	0.025	0.022	0.023
	(0.009)***	(0.008)***	(0.008)***	(0.007)***
Ordered detail
Coefficient	−1.355	−1.603	−1.478	−1.695
	(0.595)**	(0.595)***	(0.569)***	(0.566)***
Marginal effects
5 female	−0.274	−0.325	−0.301	−0.347
	(0.120)**	(0.120)***	(0.115)***	(0.116)***
4 female weak	−0.059	−0.069	−0.062	−0.071
	(0.027)**	(0.027)**	(0.025)**	(0.025)***
3 neutral	−0.005	−0.004	−0.005	−0.004
	(0.004)	(0.004)	(0.004)	(0.004)
2 male weak	0.319	0.379	0.350	0.403
	(0.140)**	(0.141)***	(0.135)***	(0.135)***
1 male	0.018	0.020	0.018	0.019
	(0.008)**	(0.008)**	(0.007)**	(0.007)***
Number of observations	3046		3366

Notes: School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Big sample includes g6–g8 dummies. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

*Statistical significance at 10% level.

^**Statistical significance at 5% level.

^***Statistical significance at 1% level.

The results of the five-category model, with female school types comprising only the highly segregated teacher training schools and schools for domestic sciences (with female shares of above 90%), are very similar. The probability of girls to choose these school types is decreasing in the proportion of female students, with a mean marginal effect of −0.31. For the weakly female business schools, we get a small negative marginal effect. The neutral school types (from the 3-category model) are split into the neutral higher general schools and the weakly male dominated pre-vocational schools. Positive marginal effects are found for the weakly male dominated school type and the male dominated technical school type (with a female share of below 10%). Both school types are increasingly chosen the higher the share of female peers.

All estimations show that the share of girls in the grade has an influence on school choice for females students. It seems that in more female environments, girls are less restrained by gender stereotypes and are more likely to consider traditional male school types and careers. As discussed above, these estimates are not obtained for the whole student population but for a specific group. Since we consider only students in low track schools who predominantly did not attend pre-school or repeated a grade, our sample should capture only students in the lower tail and center of the ability distribution. These students might come from families with lower socio-economic status and they might differ from high track students with respect to free decision making, the importance of gender roles or with respect to peer influence. However, this is an important group, since the majority of Austrian students attends a low track school.

5. Sensitivity analysis

In this section, we discuss whether the results obtained are due to gender composition in grade or driven by other unobserved factors. First, we investigate the variation in the gender composition within schools in more detail. Second, using placebo treatments, we complement our arguments by showing that the share of female students is really exogenous in our empirical framework. Furthermore, we concentrate on the question, why female students exposed to a higher share of girls choose different school types than other students do and whether this result is driven by unobserved general achievement effects. Finally, we present further regressions for the grades 6–8 and IV estimates.

5.1. Trends in gender composition

Is the share of female students in low track schools really exogenous in our econometric model? Where does the variation come from? We argue that gender composition in grade 5 is exogenous because parents and students do not observe the female share when they enrol in a certain school and the variation is due to random variation in gender composition within catchment areas. However, the share of females varies not only due to natural sources but also due to gender selection into high and low track schools. This source of variation might be correlated with the average ability of the females attending the low track school.

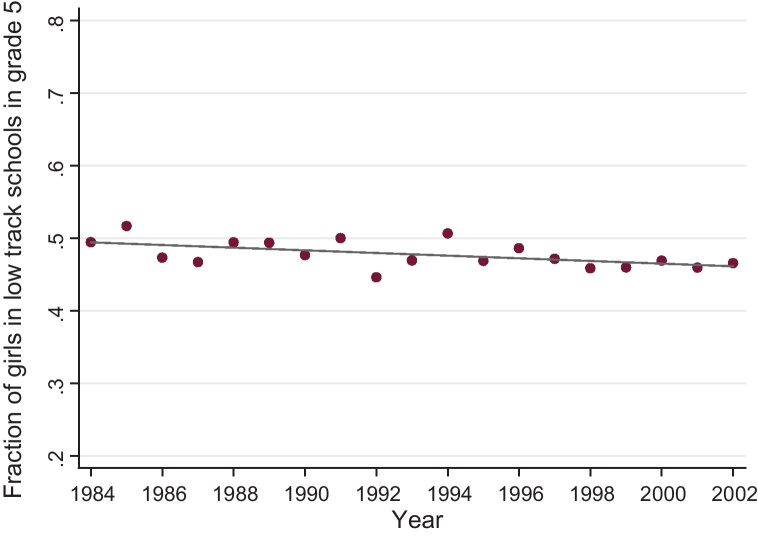
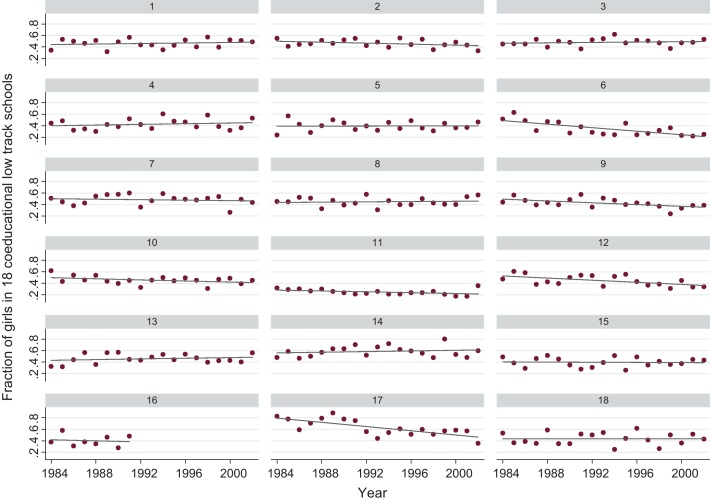
As can be seen in Fig. 4 there is a slight negative trend in the share of females in all low track schools. On average, 47.8% of low track students in grade 5 were females between 1984 and 2002. While in the first half or our observation period the fraction was about 48.5%, this figure declined to 47.2% in the second half.

Fig. 4.

Development of the fraction of girls in low track schools.

Fig. 5 investigates the trends in the share of females by school. The proportion of girls is relatively stable in most of the schools. Two schools show an outstanding decline in the share of female students (school 6 and 17) and two further schools show an above average negative trend (school 9 and 12).

Fig. 5.

Development of the fraction of girls by school.

Table 7 shows the results of the grade 5 sample if these 2 or 4 schools are excluded from the analysis. Due to space considerations, the coefficients of the ordered logit regressions are shown instead of the marginal effects. Overall, the results are very robust.

Table 7.

Grade 5 Sample – Certain schools excluded.

Binary models	Unweighted		Weighted		N
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Female weak
Drop 2 schools	−0.426	−0.519	−0.472	−0.580	2643
	(0.164)**	(0.192)***	(0.173)***	(0.205)***
Drop 4 schools	−0.492	−0.615	−0.556	−0.701	2309
	(0.179)***	(0.213)***	(0.188)***	(0.229)***
Female
Drop 2 schools	−0.458	−0.412	−0.507	−0.476	2643
	(0.147)***	(0.136)***	(0.148)***	(0.143)***
Drop 4 schools	−0.559	−0.489	−0.615	−0.566	2309
	(0.162)***	(0.145)***	(0.163)***	(0.155)***

Ordered models	Unweighted	Weighted	N
	Ordered Logit (Coef)	Ordered Logit (Coef)
Ordered
Drop 2 schools	−2.068	−2.331	2643
	(0.636)***	(0.647)***
Drop 4 schools	−2.519	−2.829	2309
	(0.711)***	(0.720)***
Ordered detail
Drop 2 schools	−1.81	−1.987	2643
	(0.601)***	(0.608)***
Drop 4 schools	−2.254	−2.464	2309
	(0.647)***	(0.653)***

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

*Statistical significance at 10% level.

^**Statistical significance at 5% level.

^***Statistical significance at 1% level.

We further estimate our model separately for two periods, 1984–1993 and 1994–2002. Most results are very robust and virtually the same coefficients are obtained for the first and the second period. An exemption is the binary model for weakly female dominated schools. In the first period the coefficients are negative but statistically not significant. In all other models, the results are robust.²³

Overall, we observe a slight negative trend in the number of females attending a low track school, indicating a decrease in ability of the marginal female student in our sample. However, as Section 5.3 shows, this is of less importance since our results are not driven by general achievement effects.

5.2. Placebo treatments

Following Lavy and Schlosser (2011), we apply placebo treatments in which the actual share of girls the students were exposed to (Girls_st−x) is replaced with the share of girls in the previous (Girls_st−x−1) and the following year (Girls_st−x+1), respectively. Since both years should not have an influence on the students, any significant effects would be due to selection. The school-fixed effects and the school-specific cubic time trends should control for unobserved school characteristics that are correlated with the share of female students as well as the choice of school type in grade 9. However, there is still some space for endogeneity if those unobserved characteristics change over time and are left untouched by the school-specific time trends.

The actual share of girls in grade 5 is not observable to parents and kids when they enroll in a certain school, thus, Girls_st−x should be exogenous. Though, students with preferences for female or male dominated classrooms may decide for a school with a certain share of girls in the previous period. On the other hand, a new school campaign starting in a given year might have lagged effects on the share of females in the next period.

The results of the placebo treatment estimations (based on the grade 5 sample) are given in Table 8. Each estimate has a positive sign and none of them is statistically significant. These results strongly support our identification strategy.

Table 8.

Effects of Girls – Placebo treatments.

Binary models	Unweighted		Weighted		N
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Female weak
Girlsst−x−1	0.231	0.273	0.205	0.241	2856
	(0.154)	(0.182)	(0.158)	(0.188)
Girlsst−x+1	0.046	0.050	0.015	0.020	2826
	(0.175)	(0.201)	(0.176)	(0.202)
Female
Girlsst−x−1	0.216	0.217	0.183	0.180	2856
	(0.149)	(0.163)	(0.144)	(0.160)
Girlsst−x+1	0.110	0.109	0.120	0.122	2826
	(0.146)	(0.154)	(0.151)	(0.160)

Ordered models	Unweighted	Weighted	N
	Ordered Logit (Coef)	Ordered Logit (Coef)
Ordered
Girlsst−x−1	0.977	0.801	2856
	(0.658)	(0.641)
Girlsst−x+1	0.189	0.253	2826
	(0.658)	(0.673)
Ordered detail
Girlsst−x−1	0.912	0.813	2856
	(0.596)	(0.603)
Girlsst−x+1	0.187	0.016	2826
	(0.633)	(0.662)

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

*Statistical significance at 10% level.

**Statistical significance at 5% level.

***Statistical significance at 1% level.

5.3. Are male school types better schools?

As the placebo treatments show, our estimates are not driven by selection effects and can be interpreted as causal. However, what is the mechanism behind these results? Is it true that female students choose the technical school type more often if they are in female classes because they establish a higher level of self-confidence in traditional male subjects, they are less troubled by male dominated classroom interactions or biased teacher beliefs? Are the results driven by confounding factors?

Hoxby (2000) as well as Lavy and Schlosser (2011) found that a higher share of female students has a positive impact on cognitive achievement of boys and girls. It might be the case that our classification of female domination is negatively correlated with achievement levels. Then the underlying mechanism would be a different one and the results would be driven by unobserved general achievement effects.

We apply two strategies to investigate this alternative explanation. First, we use data from PISA 2000 and 2003 to show how the applied classification into female and male school types is related to student achievement levels.²⁴ Second, we use boys as a ‘control group’. If the results were driven by unobserved achievement effects, we should also find some effects for male students.²⁵

The applied classification of school types used in this paper is probably not related to student achievement. First, the vocational schools are not classified by level but orientation, such as that each orientation includes students in the intermediate form (3 years) and the higher form (5 years, concluding with a university entrance exam). Thus, our classification of vocational schools should lead to a heterogenous student body.

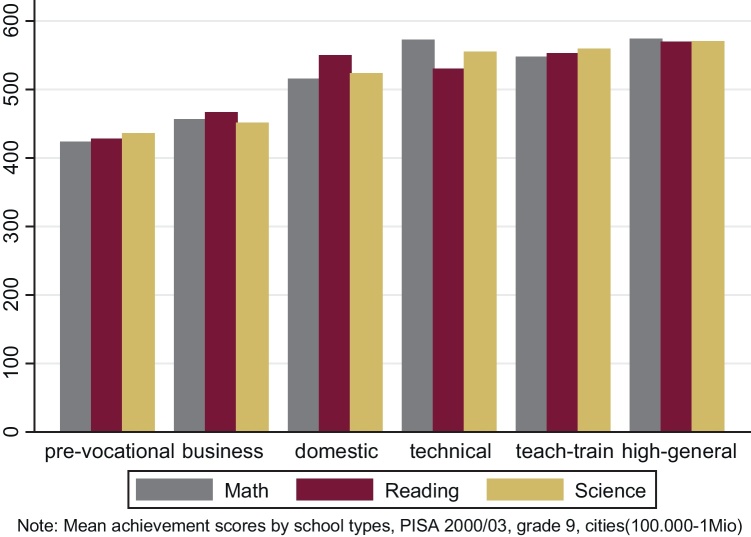
Fig. 6 shows the mean PISA test scores in mathematics, reading and science of Austrian students in the various school types. The school types are ranked by the mean test score over all subjects.

Fig. 6.

PISA achievement levels and school types.

This graph suggests that female and male domination does not correspond with achievement levels.²⁶ The highest PISA scores are achieved by students in higher general schools, which are classified as weakly female dominated or neutral school types. Students in pre-vocational and business schools achieve significantly lower test scores than those in the other school types. In both binary models, the pre-vocational school is classified as male school type and business schools are classified as female school types.²⁷ If the results were driven by achievement effects, females in classes with a higher proportion of girls would choose the pre-vocational track and the business schools less often. Table 9 shows that this is not the case.

Table 9.

Effects of Girls – Pre-vocational and business schools.

Effect of Girls	Unweighted		Weighted		N
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Pre-vocational and business
Grade 5	0.135	0.140	0.153	0.160	3046
	(0.157)	(0.178)	(0.163)	(0.187)
Big Sample	0.193	0.205	0.207	0.220	3366
	(0.144)	(0.164)	(0.147)	(0.168)

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Big sample includes g6–g8 dummies. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

*Statistical significance at 10% level.

**Statistical significance at 5% level.

***Statistical significance at 1% level.

For our second falsification test we use boys as ‘control group’. Hoxby (2000) and Lavy and Schlosser (2011) found that the fraction of girls has a positive impact on the cognitive achievement of boys and girls and Proud (2008) found a positive effect on boys’ and girls’ math and science achievement. If our results were driven by general achievement effects and not gender identity effects, the classification of school types would capture a hidden achievement classification, and this could apply for boys as well. The estimates for boys are given in Table 10.

Table 10.

Effects of Girls – Results for boys.

Binary models	Unweighted		Weighted		N
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Female weak
Grade 5	0.059	0.071	0.097	0.106	3723
	(0.111)	(0.097)	(0.121)	(0.100)
Big Sample	0.075	0.079	0.118	0.120	4106
	(0.105)	(0.093)	(0.116)	(0.099)
Female
Grade 5	0.086	0.081	0.127	0.113	3723
	(0.082)	(0.067)	(0.090)	(0.069)
Big Sample	0.099	0.082	0.146	0.120	4106
	(0.084)	(0.069)	(0.093)	(0.073)

Ordered models	Unweighted	Weighted	N
	Ordered Logit (Coef)	Ordered Logit (Coef)
Ordered
Grade 5	−0.142	0.074	3723
	(0.566)	(0.643)
Big Sample	−0.119	0.127	4106
	(0.547)	(0.622)
Ordered detail
Grade 5	−0.172	0.063	3723
	(0.563)	(0.662)
Big Sample	−0.137	0.122	4106
	(0.531)	(0.632)

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/(1-Girls). For the binary logit estimations 3717(4094) observations are used. The missing dummy for foreign predicts the outcome perfectly and those 6(12) observations with missing information on native tongue are dropped from the sample.

*Statistical significance at 10% level.

**Statistical significance at 5% level.

***Statistical significance at 1% level.

None of the coefficients and marginal effects is statistically significant. Male students are not influenced by the share of girls in their choice of school type, when schools are categorized as male and female dominated ones.

5.4. IV Estimations

The share of females in grade 5 is exogenous in our empirical model because the students and their parents do not observe the gender composition when they enroll in the school. From grades 6–8, gender composition may be endogenous if students change schools on the basis of unobserved characteristics that are correlated with the share of females (and not captured by the school-fixed effects and the school-specific cubic time trends). However, the share of girls in grade 5 might be less important for the choice of school type than the share of girls in other grades later on, e.g. grade 8. As described above, developmental psychologists have shown that starting with puberty, girls and boys conform to gender roles very strongly. This is called the ‘gender intensification phase’. Grade 5 students are about 10 years old, while students in grade 8 are about 14. According to this theory, gender composition in class may become more important in higher grades.

On the other hand, one might argue that the development of the self-concept of abilities starts at an early age and is a cumulative process. Since we do not know what grade is the most important one in shaping gender identity and the self-concept of abilities of the students, we also investigate grades 6–8. The first four rows of Table 11 show the estimated coefficients of both binary models for grades 5–8.²⁸

Table 11.

Effects of Girls – IV Estimates.

LPM (Coef)	Female weak		Female
	Unweighted	Weighted	Unweighted	Weighted
Grade 5	−0.339	−0.391	−0.459	−0.514
	(0.166)**	(0.168)**	(0.138)***	(0.140)***
Grade 6	−0.321	−0.365	−0.426	−0.480
	(0.174)*	(0.176)**	(0.144)***	(0.145)***
Grade 7	−0.287	−0.330	−0.388	−0.461
	(0.174)*	(0.174)*	(0.150)**	(0.152)***
Grade 8	−0.241	−0.325	−0.368	−0.465
	(0.166)	(0.167)*	(0.146)**	(0.150)***
2SLS	−0.408	−0.486	−0.549	−0.636
	(0.194)**	(0.197)**	(0.163)***	(0.168)***
First-Stage
Coefficients	0.836	0.829	0.836	0.829
	(0.031)***	(0.029)***	(0.031)***	(0.029)***
F-Statistics	717.38	808.26	717.38	808.26
Endogeneity of Grade 8
Test-Statistics	2.532	2.367	3.570	3.312
P-Value	0.112	0.124	0.059	0.069
Observations	2808	2808	2808	2808

Notes: Each coefficient represents a separate regression. School-fixed effects, school-specific cubic time trends, age, foreign, grade size, missing dummy for foreign included in all regressions. IV: gender composition in grade 8 is instrumented with gender composition in grade 5. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls.

^*Statistical significance at 10% level.

^**Statistical significance at 5% level.

^***Statistical significance at 1% level.

The estimates become smaller in magnitude and lose precision the higher the grade. This might indicate endogeneity problems in higher grades. To take care of this concern, we estimate an additional model, using gender composition in grade 5 as an instrument for gender composition in grade 8. The identifying assumption is that the gender composition in grade 5 is randomly assigned and related to the gender composition in grade 8 but has no separate effect on the choice of school type in grade 9. In this case, our main estimates for grade 5 are reduced form estimates or intention-to-treat effects and should therefore be regarded as lower bound estimates.

The lower panel of Table 11 presents the IV-estimates, the First-Stage results as well as the results of an endogeneity test. The Two Stage Least Squares estimates for Female range from −0.55 to −0.64, i.e. an increase in the share of girls in grade 8 by one standard deviation reduces the probability that girls attend a female dominated school type by 6–7 percentage points. These results can be interpreted as Local Average Treatment Effects, i.e. the causal effects for compliers. In our case, compliers are those students who experienced a relatively stable gender composition in grades 5 and 8.

The First-Stage is powerful, the estimates show that the fraction of girls in grade 5 is a strong instrument for the fraction of girls in grade 8. The F-Statistics of the excluded instrument in the First-Stage regressions are huge and largely exceed the critical values defined by Stock and Yogo (2002).²⁹

Furthermore, we performed a test of whether the share of girls in grade 8 is endogenous. This test is based on a Hausman Test that is robust to heteroscedasticity and clusters. The last two rows in Table 11 give the Test-Statistics as well as their P-Values. The Null of exogeneity of the share of girls in grade 8 is rejected at the 10% significance-level in the models for female school types. These results confirm our expectations of endogeneity problems in grades other than grade 5.

6. Conclusion

Studies in educational science show that girls are doing better in male dominated subjects like math and science, are more likely to choose these subjects and are more likely found in male dominated occupations, if they are educated in single-sex classes. Coeducational settings appear to reinforce gender-stereotypes, while single-sex schooling gives more freedom in exploring interests and abilities, especially for female students.

In this paper, we estimate the causal impact of gender composition in coeducational schools during the grades 5–8 on the choice of school type for female students in grade 9. The Austrian education system consists of a variety of intermediate and higher vocational school types with different orientations, some of which are preparing for traditional female and male occupations, like schools for domestic sciences or technical schools. We use register data of 19 cohorts of compulsory school students from Linz, the third largest city in Austria. Identification is based on population variation, i.e. the natural variation in the share of girls of adjacent cohorts within schools.

Our results show that female students choose the female dominated school types less likely and the technical school type more likely if they were exposed to a higher share of girls. The magnitudes of the effects are sizeable. An increase in the share of girls by one standard deviation (0.11), decreases the probability of choosing a female school type by about 4.8 percentage points, which is a reduction of 11%.

Occupational segregation of men and women in the labor market is an important determinant of gender wage differences. If policy is targeted at providing equal opportunities in the labor market, education policy and the question of coeducation versus single-sex schooling with its consequences for female occupational choices is important. This study has shown that the gender mix in schools (resulting from natural sources) is a crucial determinant of the choice of school type for female students and that this result is not driven by selection effects or unobserved achievement effects.

Our results are in line with other economic studies in this field and research in psychology and educational science. These studies suggest that female students establish a higher degree of self-confidence in male fields if they are in classes with a higher share of female students. However, we cannot identify the exact mechanism that underlies our estimated causal effect. Whether a more female environment benefits female students because they feel less constrained by gender stereotypes or because teachers behave differently cannot be inferred from our study. Nevertheless, we provide conclusive evidence that the gender mix in schools matters for females’ choice of secondary school type which can in our case be interpreted as “educational presorting” into typically male dominated and female dominated occupations.

Our results also corroborate the general finding from the literature that especially females react to their environment. As shown in experimental studies, females seem to be less bound by gender stereotypes and show different behavior (e.g. with respect to their reaction to competitive incentives) when they are in more female environments.

Although an extrapolation of our estimates to single-sex schooling may not be appropriate, they are very consistent with the existing evidence on the beneficial effects of single-sex schooling for female students. The question whether we should switch from coeducation to single-sex schooling is however, difficult to answer in light of the many open questions with respect to the overall effects of single-sex schooling: What are the effects on overall achievement for boys and for girls? And if separation is optimal, on what level should single-sex classes be introduced, at the school level, the class level or only in certain subjects? More economic research is needed in this field to find an optimal design of the education system with regard to coeducation and single-sex schooling.

Appendix A. Admission³⁰

Grades 5–8

While admission to a low track school in grade 5 only requires the successful completion of primary school, admission to a high track school depends on the marks in the last year of primary school. Students with marks ‘excellent’ or ‘good’ in the core subjects of the primary school (German writing, reading and mathematics) are admitted in any case, students with worse marks have to pass a school admission exam.³¹

Upgrading from a low track school to a high track school between grade 6 and grade 8 without an admission exam is possible if students were in the highest ability group in the main subjects (German, English and Mathematics) and had no mark worse than ‘satisfactory’ in all other subjects.³²

Grade 9

Students who want to attend a higher general school in grade 9 after completing a low track school are admitted without an admission exam if they were in the highest ability group and completed the low track school successfully, or if they were in the medium ability group and had marks ‘excellent’ or ‘good’ in the main subjects and no mark worse than ‘satisfactory’ in all other subjects.

Until 1996, all students who applied to a higher or intermediate vocational school had to pass an admission exam. Since then, for higher vocational schools, there is no admission exam for students coming from a high track school, for students who were in the highest ability group in the low track school and for students who were in the medium ability group in the low track school and had marks ‘excellent’ or ‘good’ in the main subjects. Students who apply for a higher vocational school that requires artistic skills have to pass a qualifying test. For intermediate vocational schools, only students who were in the lowest ability group in the low track school have to pass an admission exam. No entry requirements have to be fulfilled for the pre-vocational school.

Excess demand

In case of excess demand, the law prescribes the following decision rules for schools without a catchment area (higher general schools, higher and intermediate vocational schools): Students can be rejected if there is another school of the same type and orientation with a lower distance to the student's residence, and admission to this school is possible. This does not apply if the student has siblings that already attend the preferred school. If there is still excess demand, students are ranked by their previous educational attainment or by the result of an admission exam. Furthermore, the school committee can autonomously set additional rules for the ranking, e.g. establish a point system to make marks from the high track school and the low track school comparable.

Appendix B. Missing values

We do not observe the school choice in grade 9 for about 59% of low track students. For most of these cases, there is an explanation why the information is missing in the data. Part of the students drop out of fulltime education after grade 8 if they have already completed 9 years of schooling due to pre-school or grade repetition.

In the school year 2006/07, the percentage of drop outs after grade 8 was about 15% in Austria and 20% in Vienna (Statistik Austria, 2008). The figure for Linz should again be somewhere in-between. Even if the students do not drop out, the municipality of Linz may not report their school choice in grade 9 if the students have already completed 9 years of schooling. Reporting 9 years of compulsory schooling for each student is the single purpose of the data collection by the municipality.

In our data, the majority of students with missing values in grade 9 has attended preschool or repeated a grade. For about 29% of all students the information is missing due to unknown reasons. Furthermore, our data is incomplete concerning grade 9 due to unknown reasons in 3 years, the grade-5-cohorts in 1989–1991. When these years are ignored, the percentage of missings without any explanation drops to 22%.³³

Table B.1

Table B.1.

Summary statistics of Non-missing and Missing students in grade 9.

Variables	Summary statistics (Students in grade 5)
	Grade 9 Non-Missing		Grade 9 Missing
	Mean	Stdev	Mean	Stdev
Student-level variables
Female	0.450		0.434
Age in grade 5	10.671	0.406	11.132	0.670
Foreign language	0.111		0.169
Grade-level variables
Grade size	57.784	17.172	57.841	17.213
Fraction of girls	0.436	0.114	0.439	0.115
Preschool and grade repetition
Preschool	0.130		0.324
Grade repetition	0.049		0.301
Number of observations	6769		9847
Number of low track schools	18		18

shows summary statistics in grade 5, for both, those students who are observed in grade 9 and those who are not observed. The latter students are somewhat older because many of them attended pre-school or repeated a grade and the fraction of students with migration background is higher. While about 16% of our estimation sample attended a pre-school or repeated a grade, this percentage is about 51% for the students with missing values.

Most importantly, whether we observe a student in grade 9 is not related to the fraction of girls in grade 5. The mean share of females is 0.436 for the students we observe in grade 9 and 0.439 for the students we do not observe. To investigate this in more detail, we estimated our regression model with a dummy variable for “not observed in grade 9” as dependent variable and did not find any significant relationship with the share of females. Furthermore, we also looked at whether the probability of preschool or grade repetition is related to the fraction of female students. Again, there is no such relationship. Our results are also robust to controlling for preschool and grade repetition in our estimation model as well as to the exclusion of those students. We further investigated whether our missing data are coming from specific schools, this seems not to be the case. We did two further checks on that: we dropped 4/8 schools with the highest shares of missings (more than 65%/50%) from our analysis and the results are robust to that. Overall, we do not believe that the problem of missing data biases our results.

Appendix C. Time trends

Table C.1

Table C.1.

Sample Grade 5 – Various time trends.

Binary models	Unweighted		Weighted
	LPM (Coef)	Logit (ME)	LPM (Coef)	Logit (ME)
Female weak
Linear trends	−0.306	−0.343	−0.351	−0.397
	(0.155)**	(0.177)*	(0.158)**	(0.182)**
Quadratic trends	−0.357	−0.414	−0.408	−0.477
	(0.150)**	(0.174)**	(0.156)***	(0.183)***
Quartic polynomial	−0.341	−0.400	−0.415	−0.495
	(0.161)**	(0.188)**	(0.165)**	(0.196)**
Female
Linear trends	−0.343	−0.359	−0.385	−0.410
	(0.161)**	(0.176)**	(0.157)**	(0.174)**
Quadratic trends	−0.364	−0.401	−0.415	−0.462
	(0.151)**	(0.166)**	(0.154)***	(0.171)***
Quartic polynomial	−0.408	−0.394	−0.469	−0.473
	(0.131)***	(0.135)***	(0.133)***	(0.144)***

Ordered models	Unweighted	Weighted
	Ordered Logit (Coef)	Ordered Logit (Coef)
Ordered
Linear trends	−1.314	−1.539
	(0.711)*	(0.705)**
Quadratic trends	−1.436	−1.709
	(0.681)**	(0.697)**
Quartic polynomial	−1.688	−2.028
	(0.577)***	(0.594)***
Ordered detail
Linear trends	−1.111	−1.248
	(0.644)*	(0.635)**
Quadratic trends	−1.218	−1.395
	(0.618)**	(0.623)**
Quartic polynomial	−1.148	−1.411
	(0.586)**	(0.587)**

Notes: Each coefficient and marginal effect represents a separate regression. School-fixed effects, school-specific time trends as indicated, age, foreign, grade size, missing dummy for foreign included in all regressions. Heteroscedasticity and cluster-robust standard errors in parentheses (clusters are school-years). Weighted regressions: Weight = 1/Girls. N = 3046.

^*Statistical significance at 10% level.

^**Statistical significance at 5% level.

^***Statistical significance at 1% level.

.