Accurate method to estimate insulin resistance from multiple regression models using data of metabolic syndrome and oral glucose tolerance test

Abstract

Aims/Introduction

How to measure insulin resistance (IR) accurately and conveniently is a critical issue for both clinical practice and research. In the present study, we tried to modify the β‐cell function, insulin sensitivity, and glucose tolerance test (BIGTT) in patients with normal glucose tolerance (NGT) and abnormal glucose tolerance (AGT) by oral glucose tolerance test (OGTT) and metabolic syndrome (MetS) components.

Materials and Methods

There were 327 participants enrolled and divided into NGT or AGT. Data from 75% of the participants were used to build the models, and the remaining 25% were used for external validation. Steady‐state plasma glucose (SSPG) concentration derived from the insulin suppression test was regarded as the standard measurement for IR. Five models were built from multiple regression: model 1 (MetS model with sex, age and MetS components); model 2 (simple OGTT model with sex, age, plasma glucose, and insulin concentrations at 0 and 120 min during OGTT); model 3 (full OGTT model with sex, age, and plasma glucose and insulin concentrations at 0, 30, 60, 90, 120, and 180 min during OGTT); model 4 (simple combined model): model 1 and model 2; and model 5 (full model): model 1 and 3.

Results

In general, our models had higher r² compared with surrogates derived from OGTT, such as homeostasis model assessment‐insulin resistance and quantitative insulin sensitivity check index. Among them, model 5 had the highest r² (0.505 in NGT, 0.556 in AGT, respectively).

Conclusions

Our modified BIGTT models proved to be accurate and easy methods for estimating IR, and can be used in clinical practice and research.

Introduction

Insulin resistance (IR), first described by Himsworth1, is a synonym for impaired insulin action, which is now proved to be related to defects of insulin signaling in the cells. Other than being one of the most important pathophysiologies of type 2 diabetes, it is also considered to be the core of metabolic syndrome (MetS)2. Although IR is very important, it is still difficult to measure IR accurately in regular medical facilities.

Many methods, credible accurately to measure IR, have been published in the past. At present, the rule of thumb is that the more accurate the method, the more difficult and more expensive it will be. The hyperinsulinemic euglycemic clamp is widely accepted as the reference standard5. However, this method is time‐consuming, labor intensive and expensive. There are only a few medical centers and laboratories that can carry out this method. The steady‐state plasma glucose (SSPG) concentration obtained from the insulin suppression test (IST)6 is another accurate method for quantifying IR, but it requires infusion of somatostatin to suppress endogenous insulin secretion, and is thus expensive. Finally, the oral glucose tolerance test (OGTT) is simple, and widely used to diagnose glucose tolerance and type 2 diabetes. However, it does not measure IR directly, and the surrogates derived from OGTT are less accurate. So far, there is no satisfactory method that is both accurate and easily carried out for general researchers.

To solve the dilemma, Hansen et al.7 developed an algorithm (β‐cell function, insulin sensitivity and glucose tolerance test; BIGTT) to estimate both insulin sensitivity (IS; the reciprocal of IR conceptually) and acute insulin response accurately from OGTT. In short, they used both plasma glucose and insulin levels during OGTT to build a multiple regression equation that is used to estimate IS. The r² of the correlation between BIGTT and intravenous glucose tolerance test (IVGTT) is as high as 0.77 for IS. However, they did not put MetS components into their equations, which might be a drawback for the study as IR is the core of MetS, as aforementioned. Therefore, it would be reasonable to premise that by adding the MetS components into the equation, the predictive accuracy will be further improved. However, in Hansen's study7, the BIGTT was only evaluated in participants with normal glucose tolerance (NGT). Further evaluating patients with abnormal glucose tolerance (AGT) would perfect this test. In the present study, we modified the original BIGTT by adding the MetS components into the multiple regression equation (modified BIGTT; M‐BIGTT). The IR measured by IST (SSPG) was taken as the standard. To validate the M‐BIGTT, we compared the IR derived from the M‐BIGTT with SSPG in both NGT and AGT. Our purpose was to find a more practical and accurate method to measure IR.

Methods

Study Participants

The participants enrolled in the present study were from the clinics of Endocrinology and Metabolism of a local teaching hospital in Taiwan. The study was approved by the hospital ethics committee, and the nature, purpose and potential risks of the study were explained to subjects before obtaining their consent to participate. Subjects with major medical diseases, such as coronary heart disease, myocardial infarction, stroke, renal failure or type 1 diabetes, were excluded. If treated with medications for diabetes or other diseases, the types and doses of the medications were kept unchanged at least 3 weeks before the study. Three days before the study, the participants were asked to maintain a stable diet. On the day of study, study participants visited the clinic at 08.00 h after a 10‐h fast. After they had signed the consent form, a complete physical examination was carried out, and the body mass index (BMI) was calculated as weight/height² (kg/m²). Systolic blood pressure (SBP) and diastolic blood pressure (DBP) were measured by nursing stuff using standard mercury sphygmomanometers on the right arm of seated participants. Two visits for either the OGTT or IST were arranged randomly.

OGTT

On the study day, an intravenous catheter was placed in the antecubital vein. Fasting blood samples were drawn for biochemistry analysis. Participants orally consumed a standard 75‐g dose of glucose. Plasma glucose and insulin concentrations were measured before, and 30, 60, 90, 120 and 180 min after the glucose challenge. The participants were classified either NGT or AGT according to the results of the OGTT, which were categorized by the American Diabetes Association in 19978. The AGT included both prediabetic and diabetic participants9.

SSPG

On a separate day, IR was measured by the IST. An intravenous catheter was placed in each of the patient's arms as the OGTT. One arm was used for the administration of a 180‐min infusion of somatostatin (250 μg/h), insulin (25 mU/m²/min) and glucose (240 mg/m²/min). The other arm was used for collecting blood samples. Blood was sampled every 30 min initially, and then at 10‐min intervals from 150 to 180 min of the infusion to determine the SSPG concentrations for each individual. The SSPG concentration provided a direct measure of the ability of insulin to mediate disposal of an infused glucose load; the higher the SSPG, the more IR in the individual.

The IR surrogates, such as homeostasis model assessment‐insulin resistance (HOMA‐IR) and quantitative insulin sensitivity check index (QUICKI) derived from OGTT11, were also calculated and compared with SSPG.

Laboratory Measurement

On both days, determinations of glucose, insulin and lipid concentrations were made. Plasma was separated from blood within 1 h of blood collection and was frozen at −30°C until analysis.

Insulin was measured by the Coat‐A‐Count solid‐phase radioimmunoassay kit (Diagnostic Products, Los Angeles, CA, USA). Intra‐ and interassay coefficients of variance for insulin were 3.3 and 2.5%, respectively. Plasma glucose was measured using the YSI 203 glucose oxidase analyzer (Yellow Spring Instruments, Yellow Spring, OH, USA). Serum determinations of triglyceride (TG) were measured using the dry, multilayer analytical slide method in the Fuji Dri‐Chem 3000 analyzer (Fuji Photo Film, Tokyo, Japan). The serum level of high‐density lipoprotein cholesterol (HDL‐C) was determined by an enzymatic cholesterol assay method after dextran sulphate precipitation.

Statistical Analyses

spss version 13.0 statistical package for Windows (SPSS, Chicago, IL, USA) was used for data analysis. All data were evaluated for normal distribution by the Kolmogorov–Smirnov test, and for homogeneity of variances by Levene's test. The data of SSPG were logarithmically transformed and used as the dependent variables, as it is not normally distributed. A t‐test was used to compare data between two groups. Multiple regression was used to build models with details given later. All data were expressed as mean ± standard deviation.

Building the Models

To estimate IR, we used multiple regression analysis to build the models. We put sex, age, MetS components, plasma glucose and insulin concentrations obtained from OGTT as independent variables, and SSPG derived from IST as the independent variable in the enter method of multiple regression. From the simplest to the most complicated one, the variables put in the models were as follows:

• Model 1 (MetS model): sex, age and MetS components (BMI, SBP, DBP, TG, HDL‐C, fasting plasma glucose).

• Model 2 (simple OGTT model): sex, age, plasma glucose and insulin concentrations at 0 and 120 min during OGTT (G₀, G₁₂₀, I₀ and I₁₂₀, respectively).

• Model 3 (full OGTT model): sex, age, and plasma glucose and insulin concentrations at 0, 30, 60, 90, 120, and 180 min during OGTT.

• Model 4 (simple combined model): model 1 and model 2.

• Model 5 (full model): model 1 and 3.

In order to validate our models, 75% of participants were randomly selected. From these participants, each model generated its own optimal predictive equation for IR. To further increase the accuracy of the models, we built the equations separately in the NGT and AGT group. Then these equations were used to calculate IR in the remaining 25% of the study participants as external validation (NGT_EV, AGT_EV group, respectively). The correlation between the calculated IR and SSPG (the standard for IR) were evaluated with Pearson's correlation. The correlation coefficients (r²) obtained from each model were used for evaluations and comparisons between models. In general, the higher the r², the more accurate the model was.

Results

A total of 327 participants were enrolled in the present study. Among them, 167 participants were classified by OGTT as the NGT group and 160 as the AGT group. The demographic and biochemistry data are shown in Table 1. There were 18 participants (11.25%) with type 2 diabetes in the AGT group. The durations of type 2 diabetes were within 3 years. As participants in the external validation groups were randomly selected, there was no significant difference between the NGT and NGT_EV group or AGT and AGT_EV group. Because of the grouping criteria, it is not surprising that age, BMI, SBP, DBP, TG and SSPG were higher in the AGT group. The plasma glucose and insulin levels during the OGTT of each group are shown in Figure 1.

Table 1. General characteristics in different glucose tolerance.

	NGT	AGT	NGTEV	AGTEV
n	125	120	42	40
Sex (male/female)	45/80	62/58	17/25	21/19
Age (years)*	41.0 ± 11.6	47.8 ± 10.7	42.0 ± 11.9	47.4 ± 10.7
Body mass index (kg/m2)*	22.8 ± 3.0	24.9 ± 3.3	22.8 ± 2.8	25.1 ± 2.9
Systolic blood pressure (mmHg)*	114.3 ± 15.6	122.1 ± 14.9	114.4 ± 11.3	122.8 ± 17.8
Diastolic blood pressure (mmHg)*	75.2 ± 9.9	78.8 ± 9.0	73.2 ± 8.7	78.0 ± 9.4
Triglyceride (mmol/L)*	1.02 ± 0.54	1.37 ± 0.79	1.03 ± 0.43	1.23 ± 0.58
High density lipoprotein cholesterol (mmol/L)	1.09 ± 0.35	1.06 ± 0.34	1.03 ± 0.36	1.08 ± 0.40
Steady state plasma glucose (mmol/L)*	7.69 ± 3.42	10.45 ± 3.95	8.51 ± 3.87	10.42 ± 4.38

Data shown as means ± standard deviation. *P < 0.001 significant difference between normal glucose tolerance (NGT) and abnormal glucose tolerance (AGT) groups. NGT_EV, external validation group for normal glucose tolerance; AGT_EV, external validation group for abnormal glucose tolerance.

Figure 1.

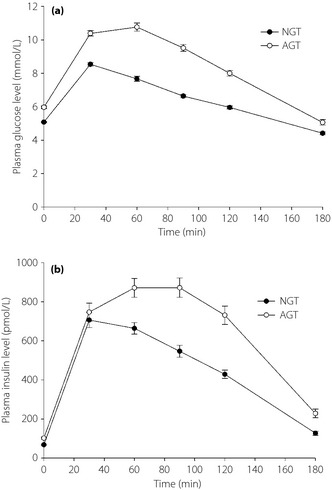
The (a) plasma glucose and (b) insulin concentrations during oral glucose tolerance test in normal glucose tolerance (NGT) and abnormal glucose tolerance test (AGT) groups.

The equations for either NGT or AGT in each model are shown in Table 2. The correlation (r² value) between the predicted IR derived from the equations, traditional surrogates derived from OGTT (HOMA‐IR and QUICKI) and SSPG are also shown. There are four important facts that could be noted from the table: (i) all estimated IRs were highly correlated with SSPG; (ii) model 5 had the highest r among the five models; and (iii) the r² values in AGT were all higher than those of NGT. Finally, the r² values of each model in both groups, except for NGT in model 1, were higher than those of HOMA‐IR and QUICKI.

Table 2. Predictive equation of each model and correlation between steady‐state plasma glucose, other traditional insulin resistance surrogates and models in different glucose tolerance.

Model – Group	Equation	r 2
Model 1
NGT	(1.439 + 0.018 × sex − 0.003 × age + 0.029 × BMI − 0.001 × SBP + 0.006 × DBP + 0.049 × TG − 0.046 × HDL − 0.116 × G0) × 103.333	0.238a
AGT	(1.345 + 0.07 × sex − 0.005 × age + 0.034 × BMI − 0.0001 × SBP + 0.0002 × DBP + 0.058 × TG − 0.049 × HDL − 0.005 × G0) × 103.333	0.341a
Model 2
NGT	(1.643 − 0.096 × sex − 0.002 × age − 0.027 × G0 + 0.027 × G120 + 0.00165 × I0 + 0.00037 × I120) × 103.333	0.325a
AGT	(1.783 + 0.036 × sex − 0.003 × age − 0.008 × G0 + 0.02 × G120 + 0.00122 × I0 + 0.00016 × I120) × 103.333	0.419a
Model 3
NGT	(1.228 − 0.074 × sex − 0.003 × age − 0.007 × G0 − 0.007 × G30 − 0.036 × G60 + 0.019 × G90 + 0.064 × G120 + 0.051 × G180 + 0.00123 × I0 + 0.00002 × I30 + 0.00035 × I60 + 0.00008 × I90 + 0.00009 × I120 − 0.00038 × I180) × 103.333	0.412a
AGT	(1.852 + 0.045 × sex − 0.005 × age − 0.027 × G0 − 0.017 × G30 + 0.01 × G60 + 0.029 × G90 − 0.0002 × G120 + 0.006 × G180 + 0.00087 × I0 + 0.00001 × I30 + 0.0001 × I60 + 0.00006 × I90 + 0.00003 × I120 + 0.000005 × I180) × 103.333	0.504a
Model 4
NGT	(1.373 − 0.054 × sex − 0.003 × age + 0.02 × BMI − 0.002 × SBP + 0.005 × DBP + 0.052 × TG − 0.047 × HDL − 0.085 × G0 + 0.025 × G120 + 0.00108 × I0 + 0.00039 × I120) × 103.333	0.453a
AGT	(1.381 − 0.053 × sex − 0.004 × age + 0.018 × BMI − 0.002 × SBP + 0.001 × DBP + 0.031 × TG − 0.024 × HDL − 0.009 × G0 + 0.017 × G120 + 0.00073 × I0 + 0.00013 × I120) × 103.333	0.489a
Model 5
NGT	(1.129 − 0.069 × sex − 0.003 × age + 0.018 × BMI − 0.003 × SBP + 0.005 × DBP + 0.051 × TG − 0.074 × HDL − 0.034 × G0 − 0.007 × G30 − 0.047 × G60 + 0.012 × G90 + 0.069 × G120 + 0.036 × G180 + 0.00075 × I0 − 0.00001 × I30 + 0.00026 × I60 + 0.00014 × I90 − 0.00012 × I120 − 0.00014 × I180) × 103.333	0.505a
AGT	(1.57 + 0.062 × sex − 0.005 × age + 0.014 × BMI − 0.001 × SBP + 0.002 × DBP + 0.045 × TG − 0.026 × HDL − 0.029 × G0 − 0.01 × G30 + 0.007 × G60 + 0.031 × G90 − 0.001 × G120 − 0.0002 × G180 + 0.00051 × I0 + 0.00003 × I30 + 0.00009 × I60 + 0.00003 × I90 − 0.00002 × I120 + 0.00003 × I180) × 103.333	0.556a
HOMA − IR
NGT	G0 × I0/22.5	0.245a
AGT	G0 × I0/22.5	0.234a
QUICKI
NGT	1/(logG0 + logI0)	0.179a
AGT	1/(logG0 + logI0)	0.143a

^aP < 0.001. Sex: male = 0, female = 1. AGT, abnormal glucose tolerance, BMI, body mass index; DBP, diastolic blood pressure; G_t, plasma glucose (mmol/L) at time t min; HDL‐C, high‐density lipoprotein‐cholesterol; HOMA‐IR, homeostasis model assessment‐insulin resistance; I_t, plasma insulin (pmol/L) at time t min; NGT, normal glucose tolerance; QUICKI, quantitative insulin sensitivity check index; SBP, systolic blood pressure; TG, triglyceride. Model 1 (metabolic syndrome model): sex, age, BMI, SBP, DBP, TG, HDL, G₀; model 2 (simple oral glucose tolerance test model): sex, age, G₀, G₁₂₀, I₀, I₁₂₀; model 3 (full oral glucose tolerance test model): sex, age, G₀, G₃₀, G₆₀, G₉₀, G₁₂₀, G₁₈₀, I₀, I₃₀, I₆₀, I₉₀, I₁₂₀, I₁₈₀; model 4 (simple combined model): sex, age, BMI, SBP, DBP, TG, HDL, G₀, G₁₂₀, I₀, I₁₂₀; model 5 (combined model): sex, age, BMI, SBP, DBP, TG, HDL, G₀, G₃₀, G₆₀, G₉₀, G₁₂₀, G₁₈₀, I₀, I₃₀, I₆₀, I₉₀, I₁₂₀, I_180.

To validate our most accurate model, we calculated the IR with the equation derived from model 5, and compared the values of IR to SSPG in the remaining 25% of participants (Figure 2). In both the NGT and AGT group, the correlation coefficients were all significant and relatively high (r² = 0.338 in NGT; r² = 0.376 in AGT; P < 0.001, respectively). Again, it could be noted that the r² in the AGT was still higher than that in NGT.

Figure 2.

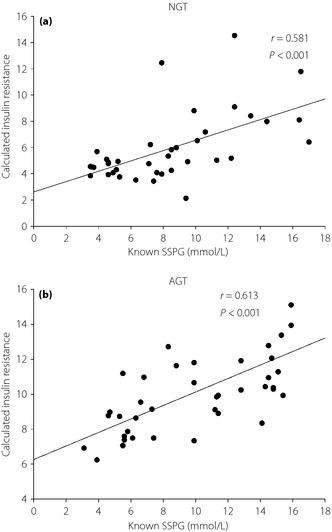
The linear relationship between calculated insulin resistance from model 5 and steady‐state plasma glucose (SSPG) in (a) the normal glucose tolerance group (NGT) and (b) the abnormal glucose tolerance group (AGT).

Discussion

Insulin resistance is one of the important defects in type 2 diabetes. If IR could be measured more extensively and accurately, it might help to solve many genetic and clinical dilemmas of diabetes. In the present study, we further modified Hansen's BIGTT in order to further increase its accuracy. Other than levels of plasma glucose and insulin from OGTT, we put MetS components into the model. The results of the present study have confirmed our assumption that the accuracy of our models could be improved. This is true for both NGT and AGT participants.

Generally speaking, the r² in the present study were all lower than those in Hansen's study. For instance, in the ‘full model’ of their study, which had all time‐points of the OGTT, sex and BMI had the r² equal to 0.77. Whereas in our study, model 5 was considered the most complete model, but it only had the r² value equal to 0.556. Other than the MetS components, the factors used in the models in both studies were similar. Thus, the r² value was expected to be higher. The possible explanation for our lower r² might come from the different ethnic group. It is known that diabetes in Asians does have different aspects than in Caucasians. For instance, the BMI of patients with type 2 diabetes is lower in Asians13. Furthermore, Seino et al.14 had reported that Japanese type 2 diabetes is characterized by a larger decrease in insulin secretion and, contrary to Caucasians, IR plays a less important role. However, this discrepancy should not decrease the importance of the present study, as our model was much better than other surrogates, such as HOMA‐IR and QUICKI (Table 2). In addition, our models could be easily implanted in computer software, such as Microsoft Excel, and then the IR could be estimated.

Revean4 suggested that IR is the core of MetS. A number of studies also showed that MetS components are strong predictors for the development of type 2 diabetes15, even since childhood19. Therefore, it is reasonable to use MetS components to predict the severity of IR. To date, there has been no other study exploring the measurement of IR by MetS components. Thus, it is also interesting to note that, from Table 2, model 1 (MetS model) had a lower r² than that of model 2 (simple OGTT model). This finding showed that the levels of plasma glucose and insulin during OGTT are better predictors for IR than the components of MetS. In other words, OGTT is more tightly related to the IR. Again, the present study is the first to explore the relative importance between the roles of MetS and OGTT in predicting IR. Another important finding worth further discussing is that when combining both OGTT and MetS models together (model 4 and model 5), the r² could still be increased. If both MetS and OGTT are related through a common pathway to IR, the combination of these two models would have little effect on the r². Obviously, this was not the case. The present study indirectly and further showed that both OGTT and MetS interact with IR through different pathways.

As glucose metabolism is assumed to be impaired in the AGT group, we built the models separately in the NGT and AGT group. However, in general, the r² values in AGT were higher than those in NGT. This might be due to the fact that the plasma glucose, insulin and levels of MetS components were significantly higher in the AGT group. As the increases of all these parameters are more or less related to IR, the high correlation coefficients in the models from AGT reflect their tighter relationships than the NGT. In other words, the more severe the impaired glucose tolerance, the more accurate the model is. This interesting finding further confirms the usefulness of our equations, especially in patients with AGT.

There were limitations to the present study. First, family history is one of the important determinates for predicting type 2 diabetes. However, we did not have this information in the model. We would expect a higher estimation power if it was included. Second, the number of external validations seemed to not be enough. That might be the reason for the decreased r² value in the remaining 25% of participants compared with the original r² value from the 75% of participants. However, we could not increase the number of the external validation, as this would have reduced the model accuracy. Third, type 2 diabetes was considered as chronic pro‐inflammatory status. Among the inflammation markers, C‐reactive protein (CRP) has been shown to be associated with IR in several studies20. Adding CRP could further increase accuracy in our models. However, the original goal of the present study was to build models with routine laboratory data. As CRP is not a necessary laboratory test for IR in daily practice, we did include CRP in the model. We must point out that this drawback might reduce the models' prediction ability. Fourth, it could be noted model 5 has the highest r² for estimating IR. However, this model is quite time‐consuming, which limits its use in daily practice. Thus, model 4 is probably the best model to be used. Fifth, in the models, we used BMI instead of waist circumference, which is one of the MetS components. We do agree that BMI might be less related to IR than waist circumference. However, Reaven et al.22 have shown that BMI and waist circumference are closely related. This might justify the use of BMI in the present study. Finally, it should be emphasized that there might be different underlying pathophysiologies in different ethnic groups; the extrapolation of our equations to other ethnic groups must be exercised with caution. The coefficients of the equations might need to be changed accordingly.

In conclusion, by using the MetS components and plasma glucose/insulin levels during the OGTT, IR could be estimated with high accuracy. The r² values were 0.505 and 0.556 for NGT and AGT, respectively. This is a relatively accurate and easy method to be used in primary care settings.

J Diabetes Invest 2014; 5: 290–296