Abstract
Capsid (CA) proteins from all retroviruses, including HIV-1, are structurally homologous dual-domain helical proteins. They form a capsid lattice composed of unitary symmetric CA hexamers. X-ray crystallography has shown that within each hexamer a monomeric CA adopts a single conformation where most helices are parallel to the symmetry axis. In solution large differences in averaged NMR spin relaxation rates for the two domains were observed, suggesting they are dynamically independent. One relevant question for the capsid assembly remains, whether the inter-domain conformer within a hexamer unit needs to be induced or pre-exists within the conformational space of a monomeric CA. The latter seems more consistent with the relaxation data. However, possible CA protein oligomerization and the structure of each domain will affect relaxation measurements and data interpretation. Here using CA proteins from Equine Infectious Anemia Virus (EIAV) as an example, we demonstrate a linear-extrapolation approach to obtain backbone 15N spin relaxation time ratios T1/T2 for a monomeric EIAV-CA in the presence of oligomerization equilibrium. The inter-domain motion turns out to be limited. The large difference in the domain averaged <T1/T2> for a CA monomer is a consequence of the orthogonal distributions of helices in the two domains. The new monomeric inter-domain conformation in solution is significantly different from that in CA hexamer. Therefore if capsid assembly follows a nucleation-propagation process, the inter-domain conformational change might be a key step during the nucleation, as the configuration in hexagonal assembly is never formed by diffusion of its two domains in solution.
Large proteins (> 20 kDa) may consist of multiple domains. Individual domains can function as a scaffold or catalytic unit so that the full-length protein is more efficient in serving as a structural component or performing an enzymatic reaction, or both.(1) A retroviral capsid (CA) protein, consisting of two helical domains, is a typical example of the utilization of both domains to assemble a dense core to protect the retroviral genomic RNA in complex with the nucleocapsid (NC) protein. CA and NC proteins, in addition to matrix (MA) protein, are the three major proteolytic products of the precursor Gag poly-protein formed during viral maturation. CA proteins from all species of retroviruses are 26-27 kDa in size and structurally homologous.(2) X-ray crystallography and cryo-Electron-Microscopy (EM) structures of CA proteins from N-tropic murine leukaemia virus (N-MLV),(3) HIV-1,(4-6) and Rous Sarcoma Virus (RSV)(7) have revealed that the outer-layer of the capsid core is composed of a hexagonal and pentagonal assembly of the 7-helix CA N-terminal domain (CAN) and the inner-layer is formed through dimerization of neighboring hexamers by the 4-helix C-terminal domain (CAC). The inter-domain conformation within all known CA assembly is unique and most helices, helices α1-3 and α7 of the CAN and helices α8-11 of the CAC, are parallel to the hexamer symmetric axis. Though the inter-domain structure of CA is available for the assembled lattice, the assembly process of CA itself is dynamic and less understood.(8) The proteolysis cleavage of Gag poly-protein, a process that has been targeted by HIV-1 drug, regulates the release of CA, but may or may not be directly related to the CA assembly.(9, 10) Structure and dynamics studies of CA in solution can perhaps address a relevant question whether the assemble ready conformer has to be induced from or is already pre-existing in its monomer state in solution. Analogous to helix-coil transition(11) or protein-ligand conformational switch,(12) if a retroviral capsid assembly has to be induced, other factors, e.g. pH or ligand or protein-protein interaction, must be involved to create an activated conformer of CA from its equilibrium state, corresponding to the initial process of nucleation-propagation; in contrary, pre-existing would suggest the assembly starts from a sub-population of assemble ready inter-domain conformer within an equilibrated ensemble of CA structures in solution.
Generally solution NMR can provide inter-domain structural information, i.e., inter-domain NOEs, residual dipolar coupling (RDC),(13-16) and relaxation time ratios T1/T2.(17-22) NOEs are measurable only if the inter-domain contacts involving protons are within a short distance and long lived. Even when these requirements are fulfilled, the NOEs may not be measureable in large proteins, since deuteration maybe required to obtain sharper resonance lines. RDCs are very useful in positioning domains relative to each other. If a multi-domain protein is within oligomerization equilibrium, RDCs are averaged results of all possible oligomers exchanging up to millisecond time scale and are strongly biased toward larger oligomers. RDC data interpretations quickly become difficult if the oligomerization is coupled to inter-domain structural change. The ratio of backbone 15N spin relaxation times T1/T2 is insensitive to fast local dynamics of the amide H-N bond,(23) and reflects the overall rotational diffusion of the domain.(24-27) The average T1/T2 values as well as their variation can be used to estimate a domain rotational correlation time and its geometrical shape, respectively. The average <T1/T2> of each domain can be directly used to indicate the presence of inter-domain motion.(28, 29)
The previous solution NMR studies on RSV-CA(28) have suggested that the motion of the two retroviral CA domains are independent of each other based on the lack of inter-domain NOEs and the difference in 15N T1/T2.(8) This observation is consistent with the pre-existing mechanism for CA assembly. However, CA proteins are likely to be in oligomerization equilibrium through domains CAN or CAC, and the measured T1/T2 might contain contributions from oligomers that can bias the relaxation values for each domain differently. For instance, the CA protein of Equine Infectious Anemia Virus (EIAV), belonging to the same lentivirus subfamily as HIV-1, weakly oligomerize and dimerize through its the CAN and CAC domains, respectively. And these two equilibriums appear to be independent processes as a result of the different motional time scales.(30) The assembled EIAV capsid is in the same conical shape as HIV-1 capsid.(31) The study here is to use NMR 15N relaxation and extrapolation data analysis to overcome oligomerization problem and at the same time to quantitatively reveal if the assemble-ready inter-domain conformer could be present in the conformational space of a monomeric EIAV-CA. Our results showed that the inter-domain structure of EIAV-CA monomer is relatively rigid and different from the assembled structure, and the CA assembly should be induced by other factors.
Materials and Methods
Backbone 15N T1 and T2 Measurements
The expression and purification of 15N/2H labeled EIAV-CA protein was described.(30) Four samples at protein concentrations of 0.426, 0.213, 0.106, and 0.053 mM were prepared in a buffer of 20 mM potassium phosphate at pH 6.7. All spin relaxation measurements were performed at 27 °C on a Bruker Avance 600 MHz spectrometer equipped with a cryogenic probe. Pulse sequences with TROSY detection scheme and minimal water saturation were applied.(32) For T1 measurements eight data points with relaxation delay of 80, 240, 420, 620, 840, 1140, 1460, and 1940 ms were collected. For T1ρ the 15N spin lock power was set at 2000 Hz and eight data points with relaxation delay of 2, 7.2, 12.8, 20, 28.8, 39.2, 50.4, and 67.2 ms were collected. Both T1 and T1ρ experiments were collected in an interleaved manner. NMRPipe was used to process all spectra.(33) Relaxation time constants and errors were obtained from exponential fitting on peak heights using Sparky (T.D. Goddard and D.G. Kneller, University of California, San Francisco). The calculation of T2 using T1 and T1ρ was previously described.(32)
Extrapolation and Extended Model Free Fitting of 15N T1/T2
The relaxation time ratios T1/T2 at four different protein concentrations were linearly extrapolated. The extrapolated value at the zero concentration was termed T1/T2 at “0 mM”. The error of the extrapolated T1/T2 was obtained from Monte-Carlo steps. The extended model free (EMF) fitting of T1/T2 was carried out as described previously.(34) A fully anisotropic tensor was adopted as the overall rotational diffusion tensor. The domain coordinates were obtained from the crystal structure (35) with the refined β-hairpin motif.(30) The EMF fitting parameters included three principal components of the overall rotational diffusion tensor (Dzz, Dyy and Dxx), two sets of Euler angles (α, β and γ) defining the orientation of the overall diffusion tensor within each of the domain coordinates, the domain motion order parameters S2domain and correlation time τdomain that describe the amplitude and time scale of the domain motion within the overall diffusion tensor frame (Table 1). The χ2 minimization was against the difference between the measured T1/T2 and the calculated values, i.e., Eq. (1), where N (N = 151) the total number of residues used for fitting and δ(T1/T2) is the experimental error. A simplex searching algorithm written in MATLAB (The Mathworks, MA) was used to locate the global minimal.
| (1) |
Table 1.
The extended model free fitting for 15N T1/T2 of EIAV-CA.
| Concentration (mM) | Domain | τm (ns)a | 2Dzz/(Dyy+Dxx) | Dyy/Dxx | S2 domain | τdomain (ns) | α | β | γ | χ2/N |
|---|---|---|---|---|---|---|---|---|---|---|
| “0” | CAN | 13.6 | 1.84 | 1.69 | 1.00 | n/a | 155° | 112° | 86.9° | 15.6 |
| CAC | 0.854 | 3.86 | 74.9° | 18.7° | 39.6° | |||||
| 0.4 | CAN | 18.6 | 1.70 | 1.51 | 1.00 | n/a | 158° | 112° | 82.2° | 60.9 |
| CAC | 0.900 | 1.87 | 61.4° | 18.2° | 50.5° |
τm was calculated from 1/(2Dzz+2Dyy+2Dxx).
Results
Simulation and Extrapolation on Concentration Dependent T1/T2
The observation of 15N T1/T2 ratios as a function of protein concentration originates from weak protein oligomerization.(36) When a protein “A” is in a monomer to oligomer (An) equilibrium as indicated by Eq. (2), two basic equations, Eq. (3-4), exist, where c is the total protein concentration, Kd is the dissociation constant, and n is the number of monomers within one oligomer. Solving Eq. (3-4) for [A] and [An] can be performed using Mathematica (Wolfram, IL) for various oligomeric states. For examples, the analytical solutions for [A] when n = 2 and 3 are given in Eq. 5 and 6, respectively. With the knowledge of [A], one can readily obtain the population fraction of monomer fA in the equilibrium using Eq. (7), and calculate the averaged value (T1/T2)ave according to Eq. (8), where (T1/T2)A and (T1/T2)An are relaxation times ratios for the monomer and the oligomer, respectively.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
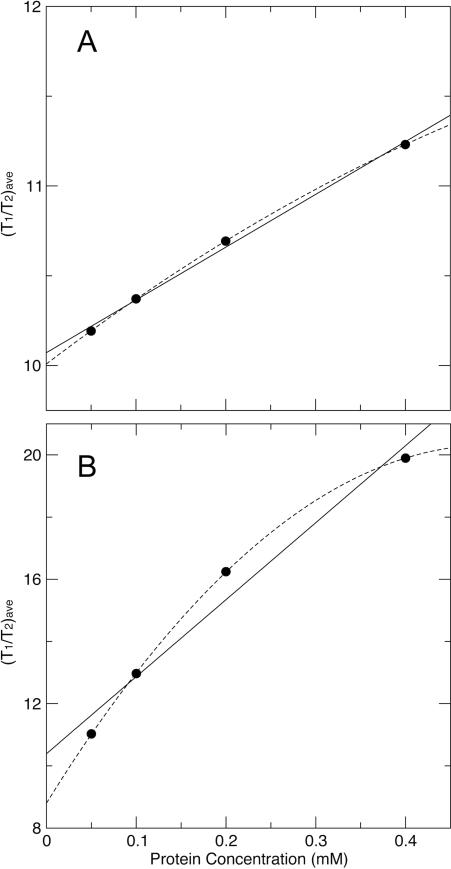
Now we consider simulating a system of monomer-dimer (n = 2) equilibrium with a weak dissociation constant Kd of 5 mM, and (T1/T2)mono and (T1/T2)dimer of 10 and 20, respectively. Using Eq. 5, 7, and 8, we calculated and plotted (T1/T2)ave at each concentrations of 0.05, 0.1, 0.2, and 0.4 mM (Fig. 1A), which were chosen to closely match the current experimental conditions. The linear and quadratic fittings yielded (T1/T2)ave-intercept values of 10.07 and 10.01, respectively. Such intercept values are taken as extrapolated data points, both of which are within 5%, roughly the experimental error range, of the target (T1/T2)mono value of 10. We then fit another system of monomer-trimer (n = 3) equilibrium with a weak dissociation constant Kd of 0.125 mM2, and (T1/T2)mono and (T1/T2)trimer of 10 and 30, respectively. Here we have assumed that there are one monomer-monomer interface within a dimer and three interfaces within a trimer, therefore the dissociation constant for the trimer is chosen to correspond to three times the free energy change of the dissociation of the dimer (-RTlnKd). Using Eq. 6, 7, and 8 we again calculated and plotted (T1/T2)ave at each concentrations of 0.05, 0.1, 0.2, and 0.4 mM (Fig. 1B). The linear and quadratic fittings yielded (T1/T2)ave-intercept values of 10.39 and 8.800, respectively. Only the linear fitting intercept value of 10.39 is within 5% of the targeted (T1/T2)mono value of 10.
Figure 1.
The linear (solid lines) and quadratic (dashed lines) fittings on simulated (T1/T2)ave data points (solid dots) under weak dimerization (A) and trimerization (B) equilibriums. The target (T1/T2)ave-intercept value is 10.
Of course our simulation is rudimentary and has a number assumptions. However, it does show that simpler linear fitting could be a more reliable method to obtain monomeric relaxation value when only data from a small number of concentrations are available. This constitutes one reason why we adopted the linear extrapolation for the study.
Concentration Dependent T1/T2 of EIAV-CA and its Extrapolation
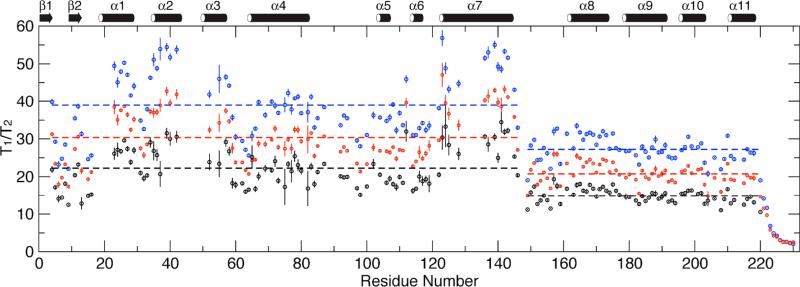
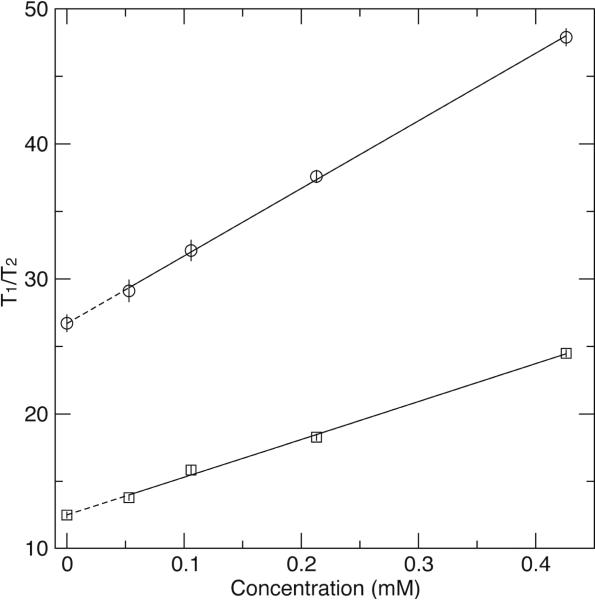
The 15N T1/T2 ratios were measured at four EIAV-CA concentrations, 0.4, 0.2, 0.1, and 0.05 mM, showing strong concentration dependent for residues in structured region of the protein (Fig. 2 and 3, Table S1). The full-length EIAV-CA protein has a total of 212 non-proline residues. Backbone 1H-15N resonances for 186 residues were assigned and missing residues are I2-M3, R18-T22, I43-E51, M53, N54, G65, Q127, and Y129-I134, which are located along the domain CAN oligomeric interfaces. The previous R2-CPMG dispersion results demonstrated residues with significant μs-ms exchange contributions are T16, D82, L87 and M102, where the last three are in the cyclophilin A (CypA) binding loop.(30) Those residues undergoing chemical exchange or missing have been removed from the analysis. Further, residues with significantly low signal to noise ratio, yielding large errors in their relaxation times, and the C-terminal flexible residues, displaying no concentration dependence, were removed. Finally 90 and 61 total residues for domains CAN and CAC, respectively, were left for T1/T2 analysis, which were tabulated in the supporting materials (Table S1). To obtain proper 15N T1/T2 for the monomeric EIAV-CA, we applied the linear as well as the quadratic extrapolations using all four sets of T1/T2. For all 151 data points the quadratic fitting did not yield statistically better fitting, judged by the F-test (data not shown), therefore, only the linear extrapolation was applied (examples of fitting shown in Fig. 3). The obtained new relaxation time ratios from the linear extrapolation were termed T1/T2 at “0 mM” and assumed to be the corresponding value in the monomeric state (Fig. 2).
Figure 2.
The measured (for clarity only the 0.4 mM and 0.2 mM datasets are shown in blue and red, respectively) and the extrapolated (“0” mM, black) backbone 15N spin relaxation time ratios T1/T2. The dashed lines mark the average <T1/T2> for each domain in each measurement and end at domain boundaries.
Figure 3.
Examples of linear extrapolation. The T1/T2 ratios are plotted as a function of protein concentration for N25 (circle) and M215 (square).
Empirical Estimation on <T1/T2> Yields Large Scale of Inter-Domain Motion
Similar to the previous observations on RSV-CA,(28) the domain averaged <T1/T2> values differ significantly for all measured and the extrapolated datasets (Fig. 2). The size ratio of the domain EIAVCAN (residue 1-146) and EIAV-CAC (residue 149-220) is 2:1. If the two domains are completely independent (S2domain = 0), under the assumptions of isotropic diffusion and isotropic distribution of H-N vectors, the <T1/T2> value of domain CAC should be 50% of the <T1/T2> value of domain CAN, roughly scaled with the relative domain sizes. For the “0 mM” dataset, the <T1/T2> value of domain CAC is 14.86, 66% of the <T1/T2> value of domain CAN of 22.26 (Fig. 2). The large difference in domain <T1/T2> suggests the presence of a large-scale inter-domain motion based on the assumption of the isotropic diffusion in each domain.
Numeric Fitting on T1/T2 Results in Limited Inter-Domain Motion
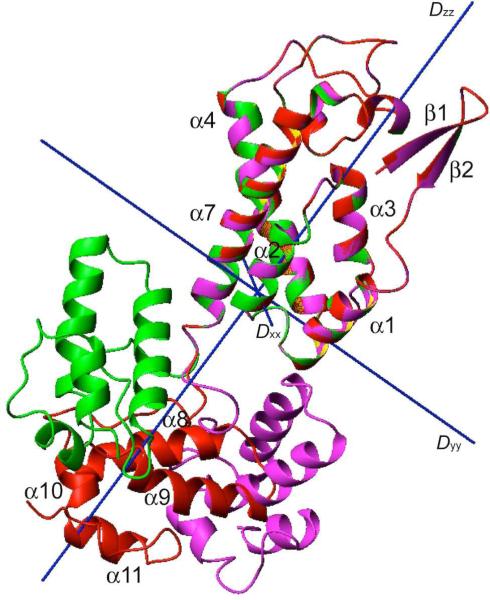
We fit the “0 mM” T1/T2 dataset using the EMF approach described previously (Table 1).(34) The resulting diffusion anisotropy (2Dzz/(Dxx+Dyy)) and asymmetry (Dyy/Dxx) are large, 1.84 and 1.69, respectively, indicating the “0 mM” T1/T2 values are very sensitive to structure coordinates. The S2domain for both domains are high, 1 and 0.854 for domain CAN and CAC, respectively, meaning inter-domain motion is limited and the empirically estimated large-scale of domain motion is not correct. The reason for the large difference in domain <T1/T2> is obvious once we rotated and positioned the two domains into the overall diffusion tensor (Fig. 4). It should be noted the simple domain rotation generated structure shown in Fig. 4 only represents a mean inter-domain conformation, not a structure ensemble from any simulated annealing calculations. The helices of domain CAC are all perpendicular to the long axis (Dzz) of the diffusion tensor, sampling the fastest components of the overall motion, in contrast, helices α1-3, and α7 of domain CAN run parallel to the long axis, experiencing slower tumbling from Dyy and Dxx. One cross-validation of the domain positioning result is to compare the T1/T2 values of the N-terminal β-hairpin residues, representing only 4% of the T1/T2 dataset, to the rest of the data. The N-terminal β-hairpin, though well ordered within the domain CAN,(37-39) is close in T1/T2 values to domain CAC. This could only be true if the two domains share the same diffusion tensor and the amide bond vectors of the β-hairpin are oriented similar to helices of domain CAC (Fig. 2 and 4).
Figure 4.
The alignment of domain CAN within the dual-domain EIAV-CA structure from the current T1/T2 analysis (red), monomeric crystal structure (magenta, 2EIA-B), and a monomer within the HIV-1-CA hexamer crystal structure (green, 3GV2).
In parallel the EMF fit for T1/T2 values of the 0.4 mM dataset was performed (Table 1). The nearly 4-fold higher χ2 value indicates the fitting quality is much worse than the extrapolated “0 mM” dataset. The overall correlation time of 18.6 ns is significantly higher than the monomer value of 13.6 ns. The lower diffusion anisotropy and asymmetry indicate less sensitivity of the 0.4 mM dataset to structural coordinates. The lower anisotropy/asymmetry also suggested a more compact conformer was formed upon oligomerization. The S2domain of CAC is higher, indicating even less inter-domain motion in oligomer. The Dzz axes of the fit overall diffusion tensors differ by 2.8° and 4.3° for domains CAN and CAC, respectively, from those of the monomeric tensor, indicating the oligomer (mostly dimer here) tensor direction is not significantly different from the monomer tensor.
Validation of T1/T2 Derived Inter-domain Structure
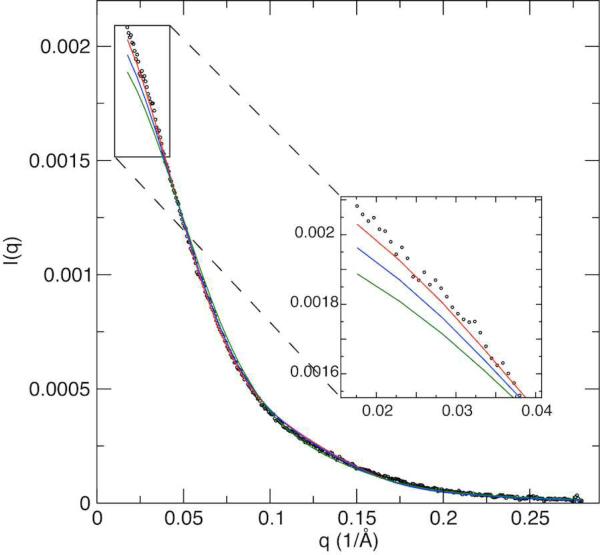
The new inter-domain conformation obtained using the extrapolated T1/T2 is different from that in the crystal structures of monomer EIAV-CA(35) or hexamer structure of HIV-1-CA (Fig. 4).(5) The hexamer is the unit for capsid-assembly of all retroviruses. This inconsistency in the inter-domain conformations prompted us to inspect if the T1/T2 derived inter-domain conformation in solution is a true representation. To further investigate this question, we performed a small angle X-ray scattering (SAXS) experiment at concentration of 0.05 mM. The SAXS profile showed the T1/T2 derived CA structure provides a better fit than the crystal structures of either monomer or a monomer unit within a hexamer (Fig. 5). As could be expected, the fit for the T1/T2 derived CA structure is not perfect at the long-range distance region, indicating the presence of a tiny population of oligomer even at this diluted concentration.
Figure 5.
Experimental (dots) and fitting curves (solid) of small angle X-ray scattering. The structural coordinates of the current T1/T2 determined (red), the monomeric EIAV-CA (2EIA, blue), and one monomer in hexameric HIV-1-CA (3GV2, green), were used for fittings. The EIAV-CA sample for SAXS measurement is 0.05 mM in the same buffer as NMR samples. Fitting of the structural coordinates were performed using XPLOR-NIH.(51)
Discussion
In summary we have presented a straightforward method to extract the mean inter-domain structure and dynamics information from backbone 15N T1/T2 data on a protein undergoing oligomerization. Based on simulations and statistical test we suggested the linear extrapolation, as opposed to a combination of linear and quadratic fittings,(36) should be applied to recover the monomer relaxation data at “0” concentration. If the contribution from protein oligomerization was not removed, the data fitting quality would be worse, meaning less agreement between structural coordinates and measured relaxation data. Worse fitting will also cause errors in the resulting parameters, i.e., the correlation time would be higher; the diffusion tensor anisotropy and asymmetry could be wrong; the inter-domain motion S2domain could be different, perhaps resulting in an inaccurate biological conclusion; the tensor direction might not be representative of the monomer if the oligomer tensor direction is significantly different. As has been shown previously, diffusion tensor anisotropy and asymmetry are a few long-range restraints for protein shape that can be used in NMR structure calculation.(25, 27, 40) Though not being tested here, any inaccuracy in the diffusion tensor can bring errors in refining a monomeric protein structure and domain positioning of a multi-domain protein. In theory we might be able to extend the usage of the precisely measured 15N T1/T2 to derive protein quaternary structure of oligomers. However, practical methods to take into account the exchange kinetics if it occurs in the ns timescale are not currently available though theoretical treatments do exist.(41, 42)
Though the inter-domain dynamics we identified on EIAV-CA using EMF method is relatively restricted with a higher order parameter S2domain of 0.85, it should not be deemed as the limit of the EMF method. Previous simulations and measurements suggested the EMF fitting approach could be valid for larger domain motions with S2domain as low as 0.4-0.5, corresponding to a semi-cone angle of 45° in the diffusion in the cone model.(43, 44)
Our structural data has an implication on the nucleation of a retroviral CA assembly. The CA assembly is not an isolated event, which results from the proteolytic processing of its precursor Gag, and rather complicated. The nucleation step in capsid assembly, though generally accepted,(45) has not been clearly demonstrated by any physical observations. In fact the in vitro assembly of a cone-shaped HIV-1 capsid using recombinant protein was only successful with a combination of its precursor CA-NC protein and RNA, not CA alone.(46, 47) Further, a close inspection of the recent 8Å cryo-EM structure of an immature Mason-Pfizer Monkey Virus (MPMV) CA-NC assembly (PDB id 4ARG) (47) revealed a similar inter-domain orientation to the one in a matured HIV-1-CA hexamer (PDB id 3GV2) (5). The difference lies in a translational movement of the CAC or the CAN domain. These results might suggest the capsid assembly proceed directly from its assembled proteolyitc fragment CA-NC proteins during maturation without major inter-domain re-orientation. Therefore the CA assembly probably does not require the diffusion and the nucleation-propagation in solution. A contrasting view can be made from the fact that only a small fraction of CA molecules processed from Gag were utilized for assembly (48) and the observations of the dual-core HIV-1 virion (49) suggest a CA release and re-assembly with several nucleation centers in solution have to take place. These observations argue against direct CA condensation from lattices of Gag or CA-NC. Our T1/T2 derived inter-domain structure suggested that the capsid assembly, if it is occurring in solution, does not start readily from a pre-existing assemble-ready conformer, rather a nucleation step involving at least significant inter-domain structure re-orientation appears to be necessary. This finding implies that factors other than the CA protein itself might play a role in promoting capsid assembly. This is inline with earlier observations where neutral pH and high salt concentration helped nucleation,(50) which had been shown to be important for in vitro assembly of tubular lattice using recombinant HIV-1-CA proteins.(45) The essential factors capable of inducing an authentic cone-shaped lattice are not known, but are potential for therapeutic targets.
Supplementary Material
ACKNOWLEDGMENT
We thank Alex Grishaev for measuring SAXS data and Charles Schwieters for help with XPLOR-NIH.
Funding Sources
No competing financial interests have been declared. The project was funded by the Intramural Research Programs of National Heart, Lung, and Blood Institute of the NIH.
ABBREVIATIONS
- CA
capsid
- EIAV
equine infectious anemia virus
- EMF
extended model free
- NC
nucleocapsid
REFERENCES
- 1.Petsko GA, Ringe D. Protein structure and function, New Science; Sinauer Associates. Blackwell Publishing; London Sunderland, MA Oxford: 2004. [Google Scholar]
- 2.Turner BG, Summers MF. Structural biology of HIV. J Mol Biol. 1999;285:1–32. doi: 10.1006/jmbi.1998.2354. [DOI] [PubMed] [Google Scholar]
- 3.Mortuza GB, Haire LF, Stevens A, Smerdon SJ, Stoye JP, Taylor IA. High-resolution structure of a retroviral capsid hexameric amino-terminal domain. Nature. 2004;431:481–485. doi: 10.1038/nature02915. [DOI] [PubMed] [Google Scholar]
- 4.Ganser-Pornillos BK, Cheng A, Yeager M. Structure of full-length HIV-1CA: a model for the mature capsid lattice. Cell. 2007;131:70–79. doi: 10.1016/j.cell.2007.08.018. [DOI] [PubMed] [Google Scholar]
- 5.Pornillos O, Ganser-Pornillos BK, Kelly BN, Hua YZ, Whitby FG, Stout CD, Sundquist WI, Hill CP, Yeager M. X-Ray Structures of the Hexameric Building Block of the HIV Capsid. Cell. 2009;137:1282–1292. doi: 10.1016/j.cell.2009.04.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Byeon IJL, Meng X, Jung JW, Zhao GP, Yang RF, Ahn JW, Shi J, Concel J, Aiken C, Zhang PJ, Gronenborn AM. Structural Convergence between Cryo-EM and NMR Reveals Intersubunit Interactions Critical for HIV-1 Capsid Function. Cell. 2009;139:780–790. doi: 10.1016/j.cell.2009.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cardone G, Purdy JG, Cheng NQ, Craven RC, Steven AC. Visualization of a missing link in retrovirus capsid assembly. Nature. 2009;457:694–698. doi: 10.1038/nature07724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Briggs JAG, Krausslich HG. The Molecular Architecture of HIV. J Mol Biol. 2011;410:491–500. doi: 10.1016/j.jmb.2011.04.021. [DOI] [PubMed] [Google Scholar]
- 9.Lanman J, Lam TT, Emmett MR, Marshall AG, Sakalian M, Prevelige PE. Key interactions in HIV-1 maturation identified by hydrogen-deuterium exchange. Nat Struct Mol Biol. 2004;11:676–677. doi: 10.1038/nsmb790. [DOI] [PubMed] [Google Scholar]
- 10.Ganser-Pornillos BK, Yeager M, Pornillos O. Assembly and Architecture of HIV. Adv Exp Med Biol. 2012;726:441–465. doi: 10.1007/978-1-4614-0980-9_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zimm BH, Bragg JK. Theory of the Phase Transition between Helix and Random Coil in Polypeptide Chains. J Chem Phys. 1959;31:526–535. [Google Scholar]
- 12.Frauenfelder H, Sligar SG, Wolynes PG. The Energy Landscapes and Motions of Proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 13.Yuwen T, Post CB, Skrynnikov NR. Domain cooperativity in multidomain proteins: what can we learn from molecular alignment in anisotropic media? J Biomol Nmr. 2011;51:131–150. doi: 10.1007/s10858-011-9548-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Prestegard JH, Al-Hashimi HM, Tolman JR. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Q Rev Biophys. 2000;33:371–424. doi: 10.1017/s0033583500003656. [DOI] [PubMed] [Google Scholar]
- 15.Dosset P, Hus JC, Marion D, Blackledge M. A novel interactive tool for rigid-body modeling of multi-domain macromolecules using residual dipolar couplings. J Biomol Nmr. 2001;20:223–231. doi: 10.1023/a:1011206132740. [DOI] [PubMed] [Google Scholar]
- 16.Ryabov Y, Fushman D. Analysis of interdomain dynamics in a two-domain protein using residual dipolar couplings together with N-15 relaxation data. Magn Reson Chem. 2006;44:S143–S151. doi: 10.1002/mrc.1822. [DOI] [PubMed] [Google Scholar]
- 17.Fushman D, Xu R, Cowburn D. Direct determination of changes of interdomain orientation on ligation: Use of the orientational dependence of N-15 NMR relaxation in Abl SH(32) Biochemistry-Us. 1999;38:10225–10230. doi: 10.1021/bi990897g. [DOI] [PubMed] [Google Scholar]
- 18.Ryabov YE, Fushman D. A model of interdomain mobility in a multidomain protein. J Am Chem Soc. 2007;129:3315–3327. doi: 10.1021/ja067667r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bruschweiler R, Liao XB, Wright PE. Long-Range Motional Restrictions in a Multidomain Zinc-Finger Protein from Anisotropic Tumbling. Science. 1995;268:886–889. doi: 10.1126/science.7754375. [DOI] [PubMed] [Google Scholar]
- 20.Ulmer TS, Werner JM, Campbell ID. SH3-SH2 domain orientation in Src kinases: NMR studies of Fyn. Structure. 2002;10:901–911. doi: 10.1016/s0969-2126(02)00781-5. [DOI] [PubMed] [Google Scholar]
- 21.Ryabov Y, Fushman D. Structural assembly of multidomain proteins and protein complexes guided by the overall rotational diffusion tensor. J Am Chem Soc. 2007;129:7894–7902. doi: 10.1021/ja071185d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ryabov Y, Fushman D. Interdomain mobility in Di-ubiquitin revealed by NMR. Proteins. 2006;63:787–796. doi: 10.1002/prot.20917. [DOI] [PubMed] [Google Scholar]
- 23.Kay LE, Torchia DA, Bax A. Backbone Dynamics of Proteins as Studied by N-15 Inverse Detected Heteronuclear Nmr-Spectroscopy - Application to Staphylococcal Nuclease. Biochemistry-Us. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 24.Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 25.Tjandra N, Garrett DS, Gronenborn AM, Bax A, Clore GM. Defining long range order in NMR structure determination from the dependence of heteronuclear relaxation times on rotational diffusion anisotropy. Nat Struct Biol. 1997;4:443–449. doi: 10.1038/nsb0697-443. [DOI] [PubMed] [Google Scholar]
- 26.Ryabov Y, Clore GM, Schwieters CD. Direct Use of N-15 Relaxation Rates as Experimental Restraints on Molecular Shape and Orientation for Docking of Protein-Protein Complexes. J Am Chem Soc. 2010;132:5987. doi: 10.1021/ja101842n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ryabov Y, Suh JY, Grishaev A, Clore GM, Schwieters CD. Using the Experimentally Determined Components of the Overall Rotational Diffusion Tensor To Restrain Molecular Shape and Size in NMR Structure Determination of Globular Proteins and Protein-Protein Complexes. J Am Chem Soc. 2009;131:9522–9531. doi: 10.1021/ja902336c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Campos-Olivas R, Newman JL, Summers MF. Solution structure and dynamics of the Rous sarcoma virus capsid protein and comparison with capsid proteins of other retroviruses. J Mol Biol. 2000;296:633–649. doi: 10.1006/jmbi.1999.3475. [DOI] [PubMed] [Google Scholar]
- 29.de Alba E. Structure and Interdomain Dynamics of Apoptosis-associated Speck-like Protein Containing a CARD (ASC) J Biol Chem. 2009;284:32932–32941. doi: 10.1074/jbc.M109.024273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen K, Piszczek G, Carter C, Tjandra N. The Maturational Refolding of the beta-Hairpin Motif of Equine Infectious Anemia Virus Capsid Protein Extends Its Helix alpha 1 at Capsid Assembly Locus. J Biol Chem. 2013;288:1511–1520. doi: 10.1074/jbc.M112.425140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Roberts MM, Oroszlan S. The Preparation and Biochemical-Characterization of Intact Capsids of Equine Infectious-Anemia Virus. Biochemical and Biophysical Research Communications. 1989;160:486–494. doi: 10.1016/0006-291x(89)92459-5. [DOI] [PubMed] [Google Scholar]
- 32.Chen K, Tjandra N. Water proton spin saturation affects measured protein backbone N-15 spin relaxation rates. J Magn Reson. 2011;213:151–157. doi: 10.1016/j.jmr.2011.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. Nmrpipe - a Multidimensional Spectral Processing System Based on Unix Pipes. Journal of Biomolecular Nmr. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 34.Baber JL, Szabo A, Tjandra N. Analysis of slow interdomain motion of macromolecules using NMR relaxation data. J Am Chem Soc. 2001;123:3953–3959. doi: 10.1021/ja0041876. [DOI] [PubMed] [Google Scholar]
- 35.Jin ZM, Jin L, Peterson DL, Lawson CL. Model for lentivirus capsid core assembly based on crystal dimers of EIAV p26. J Mol Biol. 1999;286:83–93. doi: 10.1006/jmbi.1998.2443. [DOI] [PubMed] [Google Scholar]
- 36.Jensen MR, Kristensen SM, Keeler C, Christensen HEM, Hodsdon ME, Led JJ. Weak self-association of human growth hormone investigated by nitrogen-15 NMR relaxation. Proteins. 2008;73:161–172. doi: 10.1002/prot.22039. [DOI] [PubMed] [Google Scholar]
- 37.Gitti RK, Lee BM, Walker J, Summers MF, Yoo S, Sundquist WI. Structure of the amino-terminal core domain of the HIV-1 capsid protein. Science. 1996;273:231–235. doi: 10.1126/science.273.5272.231. [DOI] [PubMed] [Google Scholar]
- 38.Macek P, Chmelik J, Krizova I, Kaderavek P, Padrta P, Zidek L, Wildova M, Hadravova R, Chaloupkova R, Pichova I, Ruml T, Rumlova M, Sklenar V. NMR Structure of the N-Terminal Domain of Capsid Protein from the Mason-Pfizer Monkey Virus. J Mol Biol. 2009;392:100–114. doi: 10.1016/j.jmb.2009.06.029. [DOI] [PubMed] [Google Scholar]
- 39.Cornilescu CC, Bouamr F, Carter C, Tjandra N. Backbone N-15 relaxation analysis of the N-terminal domain of the HTLV-I capsid protein and comparison with the capsid protein of HIV-1. Protein Sci. 2003;12:973–981. doi: 10.1110/ps.0235903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ryabov YE, Geraghty C, Varshney A, Fushman D. An efficient computational method for predicting rotational diffusion tensors of globular proteins using an ellipsoid representation. J Am Chem Soc. 2006;128:15432–15444. doi: 10.1021/ja062715t. [DOI] [PubMed] [Google Scholar]
- 41.Ryabov Y, Clore GM, Schwieters CD. Coupling between internal dynamics and rotational diffusion in the presence of exchange between discrete molecular conformations. J Chem Phys. 2012;136 doi: 10.1063/1.3675602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wong V, Case DA, Szabo A. Influence of the coupling of interdomain and overall motions on NMR relaxation. P Natl Acad Sci USA. 2009;106:11016–11021. doi: 10.1073/pnas.0809994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chang SL, Szabo A, Tjandra N. Temperature dependence of domain motions of calmodulin probed by NMR relaxation at multiple fields. J Am Chem Soc. 2003;125:11379–11384. doi: 10.1021/ja034064w. [DOI] [PubMed] [Google Scholar]
- 44.Chen K, Tjandra N. Extended model free approach to analyze correlation functions of multidomain proteins in the presence of motional coupling. J Am Chem Soc. 2008;130:12745–12751. doi: 10.1021/ja803557t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Barklis E, Alfadhli A, McQuaw C, Yalamuri S, Still A, Barklis RL, Kukull B, Lopez CS. Characterization of the In Vitro HIV-1 Capsid Assembly Pathway. J Mol Biol. 2009;387:376–389. doi: 10.1016/j.jmb.2009.01.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ganser BK, Li S, Klishko VY, Finch JT, Sundquist WI. Assembly and analysis of conical models for the HIV-1 core. Science. 1999;283:80–83. doi: 10.1126/science.283.5398.80. [DOI] [PubMed] [Google Scholar]
- 47.Bharat TAM, Davey NE, Ulbrich P, Riches JD, de Marco A, Rumlova M, Sachse C, Ruml T, Briggs JAG. Structure of the immature retroviral capsid at 8 angstrom resolution by cryo-electron microscopy. Nature. 2012;487:385–389. doi: 10.1038/nature11169. [DOI] [PubMed] [Google Scholar]
- 48.Briggs JAG, Simon MN, Gross I, Krausslich HG, Fuller SD, Vogt VM, Johnson MC. The stoichiometry of Gag protein in HIV-1. Nat Struct Mol Biol. 2004;11:672–675. doi: 10.1038/nsmb785. [DOI] [PubMed] [Google Scholar]
- 49.Briggs JAG, Wilk T, Welker R, Krausslich HG, Fuller SD. Structural organization of authentic, mature HIV-1 virions and cores. Embo J. 2003;22:1707–1715. doi: 10.1093/emboj/cdg143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ehrlich LS, Agresta BE, Carter CA. Assembly of Recombinant Human-Immunodeficiency-Virus Type-1 Capsid Protein Invitro. J Virol. 1992;66:4874–4883. doi: 10.1128/jvi.66.8.4874-4883.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schwieters CD, Kuszewski JJ, Tjandra N, Clore GM. The Xplor-NIH NMR molecular structure determination package. Journal of Magnetic Resonance. 2003;160:65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.