Abstract
In standard within-subject analyses of event-related fMRI data, two steps are usually performed separately: detection of brain activity and estimation of the hemodynamic response. Because these two steps are inherently linked, we adopt the so-called region-based Joint Detection-Estimation (JDE) framework that addresses this joint issue using a multivariate inference for detection and estimation. JDE is built by making use of a regional bilinear generative model of the BOLD response and constraining the parameter estimation by physiological priors using temporal and spatial information in a Markovian model. In contrast to previous works that use Markov Chain Monte Carlo (MCMC) techniques to sample the resulting intractable posterior distribution, we recast the JDE into a missing data framework and derive a Variational Expectation-Maximization (VEM) algorithm for its inference. A variational approximation is used to approximate the Markovian model in the unsupervised spatially adaptive JDE inference, which allows automatic fine-tuning of spatial regularization parameters. It provides a new algorithm that exhibits interesting properties in terms of estimation error and computational cost compared to the previously used MCMC-based approach. Experiments on artificial and real data show that VEM-JDE is robust to model mis-specification and provides computational gain while maintaining good performance in terms of activation detection and hemodynamic shape recovery.
I. Introduction
Functional Magnetic Resonance Imaging (fMRI) is a powerful tool to non-invasively study the relationship between a sensory or cognitive task and the ensuing evoked neural activity through the neurovascular coupling measured by the BOLD signal [1]. Since the 90’s, this neuroimaging modality has become widely used in brain mapping as well as in functional connectivity study in order to probe the specialization and integration processes in sensory, motor and cognitive brain regions [2–4]. In this work, we focus on the recovery of localization and dynamics of local evoked activity, thus on specialized cerebral processes. In this setting, the key issue is the modeling of the link between stimulation events and the induced BOLD effect throughout the brain. Physiological non-linear models [5–8] are the most specific approaches to properly describe this link but their computational cost and their identifiability issues limit their use to a restricted number of specific regions and to a few experimental conditions. In contrast, the common approach, being the focus of this paper, rather relies on linear systems which appear more robust and tractable [2, 9]. Here, the link between stimulation and BOLD effect is modelled through a convolutive system where each stimulus event induces a BOLD response, via the convolution of the binary stimulus sequence with the Hemodynamic Response Function (HRF1). There are two goals for such BOLD analysis: the detection of where cerebral activity occurs and the estimation of its dynamics through the HRF identification. Commonly, the estimation part is ignored and the HRF is fixed to a canonical shape which has been derived from human primary visual area BOLD response [10, 11]. The detection task is performed by a General Linear Model (GLM), where stimulus-induced components are assumed to be known and only their relative weighting are to be recovered in the form of effect maps [2]. However, spatial intra-subject and between-subject variability of the HRF has been highlighted [12–14], in addition to potential timing fluctuations induced by the paradigm (e.g. variations in delay [15]). To take this variability into account, more flexibility can be injected in the GLM framework by adding more regressors. In a parametric setting, this amounts to adding a function basis, such as canonical HRF derivatives, a set of gamma or logistic functions [15, 16]. In a non-parametric setting, all HRF coefficients are explicitly encoded as a Finite Impulse Response (FIR) [17]. The major drawback of these GLM extensions is the multiplicity of regressors for a given condition, so that the detection task becomes more difficult to perform and that statistical power is decreased. Moreover, the more coefficients to recover, the more ill-posed the problem becomes. The alternative approaches that aim at keeping a single regressor per condition and add also a temporal regularization constraint to fix the ill-posedness are the so-called regularized FIR methods [18–20]. Still, they do not overcome the low signal-to-noise ratio inherent to BOLD signals, and they lack robustness especially in non-activated regions. All the issues encountered in the previously mentioned approaches are linked to the sequential treatment of the detection and estimation tasks. Indeed, these two problems are strongly linked: on the one hand, a precise localization of brain activated areas strongly depends on a reliable HRF model; on the other hand, a robust estimation of the HRF is only possible in activated areas where enough relevant signal is measured [21]. This interdependence and retroactivity has motivated the idea to jointly perform these two tasks [22–24] (detection and estimation) in a Joint Detection-Estimation (JDE) framework [25] which is the basis of the approach developed in this paper. To improve the estimation robustness, a gain in HRF reproducibility is performed by spatially aggregating signals so that a constant HRF shape is locally considered across a small group of voxels, i.e. a region or a parcel. The procedure then implies a partitioning of the data into functionally homogeneous parcels, in the form of a cerebral parcellation [26].
As will be recalled in more detail in Section II, the JDE approach rests upon three main elements: i.) a non-parametric or FIR parcel-level modeling of the HRF shape; ii.) prior information about the temporal smoothness of the HRF to guarantee its physiologically plausible shape; and iii.) the modeling of spatial correlation between the response magnitudes of neighboring voxels within each parcel using condition-specific discrete hidden Markov fields. In [22, 23, 25], posterior inference is carried out in a Bayesian setting using a Markov Chain Monte Carlo (MCMC) method, which is computationally intensive and requires fine tuning of several parameters.
In this paper, we reformulate the complete JDE framework [25] as a missing data problem and propose a simplification of its estimation procedure. We resort to a variational approximation using a Variational Expectation Maximization (VEM) algorithm in order to derive estimates of the HRF and stimulus-related activity. Variational approximations have been widely and successfully employed in the context of fMRI data analysis: i.) to model auto-regressive noise in the context of a Bayesian GLM [27]; ii.) to characterize cerebral hierarchical dynamic models [28]; iii.) to model transient neuronal signals in a Bayesian dynamical system [29] or iv.) to perform inference of spatial mixture models for the segmentation of GLM effect maps [30]. As in our study, the primary goal of resorting to variational approximations is to alleviate the computational burden associated with stochastic MCMC approaches. Akin to [30], we aim at comparing the stochastic and variational-based inference schemes, but on the more complex matter of detecting activation and estimating the HRF whereas [30] treated only a detection (or segmentation) problem.
Compared to the JDE MCMC implementation, the proposed approach does not require priors on the model parameters for inference to be carried out. However, such priors may be injected in the adopted model for more robustness and to make the proposed approach fully auto-calibrated. Experiments on artificial and real data demonstrate the good performance of our VEM algorithm. Compared to the MCMC implementation, VEM is more computationally efficient, robust to mis-specification of the parameters, to deviations from the model, and adaptable to various experimental conditions. This increases considerably the potential impact of the JDE framework and makes its application to fMRI studies in cognitive and clinical neuroscience easier and more valuable. This new framework has also the advantage of providing straightforward criteria for model selection.
The rest of this paper is organized as follows. In Section II, we introduce the hierarchical Bayesian model for the JDE framework in the within-subject fMRI context. In Section III, the VEM algorithm based on variational approximations for inference is described. Evaluation on real and artificial fMRI datasets are reported in Section IV and the performance comparison between the MCMC and VEM implementations is carried out in Section V. Finally, Section VI discusses the pros and cons of the proposed approach and areas for further research.
II. Bayesian framework for the joint detection-estimation
Matrices and vectors are denoted with bold upper and lower case letters (e.g.
P and μ). A vector is by convention a column vector. The transpose is denoted by t. Unless stated otherwise, subscripts j, m, i and n are respectively indexes over voxels, stimulus types, mixture components and time points. The Gaussian distribution with mean μ and covariance matrix Σ is denoted by
 (μ, Σ). The main acronyms used in the paper are defined in Table I. Table II gathers definitions of the main variables and parameters. A graphical representation of the model is given in Fig. 1.
(μ, Σ). The main acronyms used in the paper are defined in Table I. Table II gathers definitions of the main variables and parameters. A graphical representation of the model is given in Fig. 1.
TABLE I.
Acronyms used in the JDE model presentation and inference.
| Acronym | Definition |
|---|---|
| JDE | Joint Detection-Estimation |
| HRF | Hemodynamic Response Function |
| FIR | Finite Impulse Response |
| NRL | Neural Response Level |
| PPM | Posterior Probability Map |
| PV | HRF Peak Value: max {hd Δ t}d =0: D |
| TTP | HRF Time-to-Peak: |
| FWHM | Full Width at Half Maximum: Δt × (d 2 − d 1) such that h d1Δt = h d2Δt = PV/2, d 1< d 2 |
| TTU | HRF Time-to-Undershoot: |
| ISI | Inter Stimuli Interval |
TABLE II.
Notations for variables and parameters used in the model for a given parcel
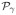 with Jγ voxels.
with Jγ voxels.
| Notation | Definition | Dimension | |
|---|---|---|---|
| Variables | y j ∈ ℝN | Observed BOLD signal at voxel j | N |
| b j ∈ ℝN | Acquisition noise vector at voxel j | N | |
| h γ = {hd Δ t, d = 0 … D} ∈ ℝD +1 | HRF sampled at Δt | D + 1 | |
|
|
NRL at voxel j for condition m | 1 | |
| n | NRLs for condition m | Jγ | |
|
|
Activation class for voxel j and condition m | 1 | |
|
|
Activation classes for condition m | Jγ | |
|
| |||
| Unknown Parameters | ℓ j ∈ ℝO | Low frequency drifts for voxel j | O |
| Γ j ∈ ℝN × N | Noise precision matrix for voxel j | N × N | |
| μ m = {μ 0 m, μ 1 m} ∈ ℝ2 | Mixture model means for NRLs in condition m | 2 | |
|
|
Mixture model variances for NRLs in condition m | 2 | |
| βm ∈ ℝ+ | Potts regularization parameter for condition m | 1 | |
| v h ∈ ℝ+ | HRF prior parameter | 1 | |
|
| |||
| Fixed | X m ∈ {0, 1}N × D +1 | Binary stimulus occurrence matrix for condition m | N × (D + 1) |
| P ∈ ℝN × O | Low frequency orthonormal function basis | N × O | |
Fig. 1.
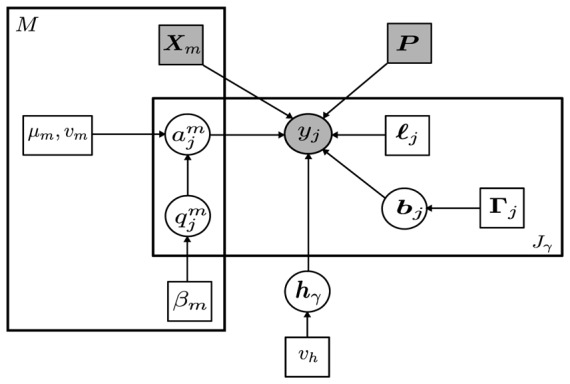
Graphical model describing dependencies between latent and observed variables involved in the JDE generative model for a given parcel
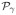 with Jγ voxels. Circles and squares indicate random variables and model parameters, respectively. Observed variables and fixed parameters are shaded. We used standard graphical notations where plates represent multiple similar nodes with their number given in the plate.
with Jγ voxels. Circles and squares indicate random variables and model parameters, respectively. Observed variables and fixed parameters are shaded. We used standard graphical notations where plates represent multiple similar nodes with their number given in the plate.
A. The parcel-based model
We first recast the parcel-based JDE model proposed in [23, 25] in a missing data framework. Let us assume that the brain is decomposed in
 = (
= (
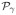 )γ
=1:
ϒ parcels, each of them containing Jγ voxels and having homogeneous hemodynamic properties. The fMRI time series y
j is measured in voxel j ∈
)γ
=1:
ϒ parcels, each of them containing Jγ voxels and having homogeneous hemodynamic properties. The fMRI time series y
j is measured in voxel j ∈
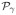 at times (tn)n
=1…
N, where tn = nTR, N being the number of scans and TR, the time of repetition. The number of different stimulus types or experimental conditions is M. For a given parcel
at times (tn)n
=1…
N, where tn = nTR, N being the number of scans and TR, the time of repetition. The number of different stimulus types or experimental conditions is M. For a given parcel
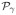 containing a group of connected voxels, a unique BOLD signal model is used in order to link the observed data Y = {y
j ∈ ℝN, j ∈
containing a group of connected voxels, a unique BOLD signal model is used in order to link the observed data Y = {y
j ∈ ℝN, j ∈
 } to the unknown HRF h
γ ∈ ℝD
+1 specific to
} to the unknown HRF h
γ ∈ ℝD
+1 specific to
 , and also to the unknown response amplitudes A = {a
m, m = 1 … M} with
being the magnitude at voxel j for condition m. More specifically, the observation model at each voxel j ∈
, and also to the unknown response amplitudes A = {a
m, m = 1 … M} with
being the magnitude at voxel j for condition m. More specifically, the observation model at each voxel j ∈
 is expressed as follows [23]:
is expressed as follows [23]:
| (1) |
where S
j
h
γ is the summation of the stimulus-induced components of the BOLD signal. The binary matrix
is of size N × (D + 1) and provides information on the stimulus occurrences for the m-th experimental condition, Δt < TR being the sampling period of the unknown HRF h
γ = {hd
Δ
t, d = 0 … D} in
 . This hemodynamic response is a consequence of the neuronal excitation which is commonly assumed to occur following stimulation. The scalars
’s are weights that model the response magnitude evoked by the stimuli, whose occurrences are informed by the X
m matrices (m = 0 … M). They model the transition between stimuli and the vascular response informed by the filter h
γ. It follows that the
’s are generally referred to as Neural Response Levels (NRL). The rest of the signal is made of matrix P, which corresponds to physiological artifacts accounted for via a low frequency orthonormal function basis of size N × O. With each voxel j is associated a vector of low frequency drifts ℓ
j ∈ ℝO which has to be estimated. Within parcel
. This hemodynamic response is a consequence of the neuronal excitation which is commonly assumed to occur following stimulation. The scalars
’s are weights that model the response magnitude evoked by the stimuli, whose occurrences are informed by the X
m matrices (m = 0 … M). They model the transition between stimuli and the vascular response informed by the filter h
γ. It follows that the
’s are generally referred to as Neural Response Levels (NRL). The rest of the signal is made of matrix P, which corresponds to physiological artifacts accounted for via a low frequency orthonormal function basis of size N × O. With each voxel j is associated a vector of low frequency drifts ℓ
j ∈ ℝO which has to be estimated. Within parcel
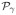 , these vectors may be grouped into the same matrix L = {ℓ
j, j ∈
, these vectors may be grouped into the same matrix L = {ℓ
j, j ∈
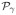 }. As regards observation noise, the b
j’s are assumed to be independent with
at voxel j (see Section II-B.1 for more details). The set of all unknown precision matrices (inverse of the covariance matrices) is denoted by Γ = {Γ
j, j ∈
}. As regards observation noise, the b
j’s are assumed to be independent with
at voxel j (see Section II-B.1 for more details). The set of all unknown precision matrices (inverse of the covariance matrices) is denoted by Γ = {Γ
j, j ∈
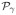 }. The forward BOLD model expressed in Eq. (1) relies on the classical assumption of a linear and time invariant system which is adopted in the GLM framework [2]. Indeed, it can easily be recast in the same formulation where the response magnitudes
’s and drift coefficient ℓ
j’s are equivalent to the effects associated with stimulus-induced and low frequency basis regressors, respectively. However, the JDE forward model generalizes the GLM model since the hemodynamics filter is unknown.
}. The forward BOLD model expressed in Eq. (1) relies on the classical assumption of a linear and time invariant system which is adopted in the GLM framework [2]. Indeed, it can easily be recast in the same formulation where the response magnitudes
’s and drift coefficient ℓ
j’s are equivalent to the effects associated with stimulus-induced and low frequency basis regressors, respectively. However, the JDE forward model generalizes the GLM model since the hemodynamics filter is unknown.
Finally, detection is handled through the introduction of activation class assignments Q = {q m, m = 1 … M} where and represents the activation class at voxel j for condition m. The NRL coefficients will therefore be expressed conditionally to these hidden variables. In other words, the NRL coefficients will depend on the activation status of the voxel j, which itself depends on the activation status of neighbouring voxels thanks to a Markov model used as a spatial prior on Q (cf Section II-B.2.c). Without loss of generality, we consider here two activation classes akin to [25] (activated and non-activated voxels). An additional deactivation class may be considered depending on the experiment as proposed within the JDE context in [31]. In the following developments, all provided formulas are general enough to cover this case.
B. A hierarchical Bayesian Model
In a Bayesian framework, we first need to define the likelihood and prior distributions for the model variables (Y, A, h γ, Q) and parameters (Θ). Using the hierarchical structure between Y, A, h γ, Q and Θ, the complete model is given by the joint distribution of both the observed and unobserved (or missing) data: p(Y, A, h γ, Q; Θ) = p(Y | A, h γ; Θ) p(h γ; Θ)p(A | Q; Θ) p(Q; Θ). To fully define the hierarchical model, we now specify each term in turn.
1. Likelihood
The definition of the likelihood depends on the noise model assumptions. In [23, 32], an autoregressive (AR) noise model has been adopted to account for serial correlations in fMRI time series. It has also been shown in [23] that a spatially-varying first-order AR noise model helps control the false positive rate. In the same context, we will assume such a noise model with where Λ j is a tridiagonal symmetric matrix which depends on the AR(1) parameter ρj [23]: (Λ j)1,1 = (Λ j)N,N = 1, for n = 2 : N − 1 and (Λ j)n +1 ,n = (Λ j)n,n +1 = −ρj for n = 1 : N − 1. These parameters are assumed voxel-specific due to their tissue-dependence [33, 34]. Denoting and ȳ j = y j − Pℓ j − S j h γ, the likelihood can be factorized over voxels as follows:
| (2) |
2. Model priors
a. Hemodynamic response function
Akin to [23, 25], we introduce constraints in the HRF prior that favor smooth variations in h
γ by controlling its second order derivative: h
γ~
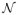 (0, v
hR) with
where D
2 is the second-order finite difference matrix and v
h is a parameter to be estimated. Moreover, boundary constraints have also been fixed on h
γ as in [23, 25] so that h
0 = hD
Δ
t = 0. The prior assumption expressed on the HRF amounts to a smooth FIR model introduced in [18] and is flexible enough to recover any HRF shape.
(0, v
hR) with
where D
2 is the second-order finite difference matrix and v
h is a parameter to be estimated. Moreover, boundary constraints have also been fixed on h
γ as in [23, 25] so that h
0 = hD
Δ
t = 0. The prior assumption expressed on the HRF amounts to a smooth FIR model introduced in [18] and is flexible enough to recover any HRF shape.
b. Neural response levels
Akin to [23, 25], the NRLs are assumed to be statistically independent across conditions: where θa = {θ m, m = 1 … M } and θ m gathers the parameters for the m-th condition. A mixture model is then adopted by using the assignment variables to segregate non-activated voxels from activated ones ( ). For the m-th condition, and conditionally to the assignment variables q m, the NRLs are assumed to be independent: . If then . It is worth noting that the Gaussianity assumed for a given NRL is similar to the assumption of Gaussian effects in the classical GLM context [10]. The Gaussian parameters θ m = {μim, vim, i = 0, 1} are unknown. For the sake of conciseness, we rewrite θa = (μ, v) where μ ={μ m, m = 1 … M} with μ m = {μ 0 m, μ 1 m} and v = {v m, m = 1 … M} with v m = {v 0 m, v 1 m}. More specifically, for non-activated voxels we set for all m, μ 0 m =0.
c. Activation classes
As in [25], we assume prior independence between the M experimental conditions regarding the activation class assignments. It follows that where we assume in addition that p(q m; βm) is a Markov random field prior, namely a Potts model. Such prior modeling assumption is consistent with the physiological properties of the fMRI signal where the activity is known to be correlated in space [33, 35]. Here, the prior Potts model with interaction parameter βm [25] is expressed as:
| (3) |
and where Z(βm) is the normalizing constant and for all (a, b) ∈ ℝ2, I(a = b) = 1 if a = b and 0 otherwise. The notation j ~ k means that the summation is over all neighboring voxels. Moreover, the neighboring system may cover a 3D scheme through the brain volume. The unknown parameters are denoted by β = {βm, m = 1 … M}. In what follows, we will consider a 6-connexity 3D neighboring system.
For the complete model, the whole set of parameters is denoted by Θ = {Γ, L, θa, v h, β} and belong to a set Θ.
III. Estimation by variational Expectation-Maximization
We propose to use an Expectation-Maximization (EM) framework to deal with the missing data namely, A ∈
 , h
γ ∈
, h
γ ∈
 , Q ∈
, Q ∈
 .
.
A. Variational Expectation-Maximization principle
Let
 be the set of all probability distributions on
be the set of all probability distributions on
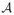 ×
×
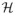 ×
×
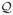 . EM can be viewed [36] as an alternating maximization procedure of a function
. EM can be viewed [36] as an alternating maximization procedure of a function
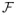 on
on
 , for all q ∈
, for all q ∈
 ,
,
| (4) |
where Eq[.] denotes the expectation with respect to q and
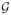 (q) = −Eq[log q(A, h
γ, Q)] is the entropy of q. This function is called the free energy functional. It can be equivalently expressed in terms of the log-likelihood as
(q) = −Eq[log q(A, h
γ, Q)] is the entropy of q. This function is called the free energy functional. It can be equivalently expressed in terms of the log-likelihood as
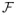 (q, Θ) = log p(Y |Θ)–KL(q ||p(A, h
γ, Q | Y, Θ)) where KL(q || p(A, h
γ, Q | Y, Θ)) is the Kullback-Leibler (KL) divergence between q and p(A, h
γ, Q | Y, Θ):
(q, Θ) = log p(Y |Θ)–KL(q ||p(A, h
γ, Q | Y, Θ)) where KL(q || p(A, h
γ, Q | Y, Θ)) is the Kullback-Leibler (KL) divergence between q and p(A, h
γ, Q | Y, Θ):
| (5) |
Hence maximizing the free energy with respect to q amounts to minimizing the Kullback-Leibler divergence between q and the posterior distribution of interest p(A, h
γ, Q | Y, Θ). Since the KL divergence is always non-negative, and because the KL divergence of the posterior distribution to itself is zero, it follows easily that the maximum free energy over all q ∈
 is the log-likelihood. The link to the EM algorithm follows straightforwardly. At iteration (r), denoting the current parameter values by Θ
(
r
−1), the alternating procedure proceeds as follows:
is the log-likelihood. The link to the EM algorithm follows straightforwardly. At iteration (r), denoting the current parameter values by Θ
(
r
−1), the alternating procedure proceeds as follows:
| (6) |
| (7) |
However, the optimization step in Eq. (6) leads to
, which is intractable for our model. Hence, we resort to a variational EM (VEM) variant in which the intractable posterior is approximated by constraining the space of possible q distributions in order to make the maximization procedure tractable. In that case, the free energy optimal value reached is only a lower bound on the log-likelihood. The most common variational approximation consists of optimizing over the distributions in
 that factorize as a product of three pdfs on
that factorize as a product of three pdfs on
 ,
,
 and
and
 respectively.
respectively.
Previous attempts to use variational inference [37, 38] and in particular in fMRI [27, 30] have been successful, with this type of approximations usually validated by assessing its fidelity to its MCMC counterpart. In Section IV, we will also provide such a comparison. The actual consequences of the factorization may vary with the models under study. Some couples of latent variables may capture more dependencies that would then need to be kept whereas others may induce only weak local correlation at the expense of a long-range correlation which to first order can be ignored (see [39] for more details on the consequences of the factorization for particular models). The way it may affect inference is that often variational approximations are shown to lead to underestimated variances and consequently to confidence intervals that are too narrow. Note that [38] suggested that nonparametric bootstrap intervals whenever possible may alleviate this issue. Also, when the concern is the computation of maximum a posteriori estimates, the required ingredients for designing an accurate variational approximation lie in the shape of the optimized free energy. All that is needed for our inference to work well is that the optimized free energy have a similar shape (mode and curvature) to the target log-likelihood whenever the likelihood is relatively large. As a matter of fact, there are cases, such as mixtures of distributions from the exponential family, where the variational estimator is asymptotically consistent. The experiments in [38] even report very accurate confidence intervals. Unfortunately no general theoretical results exist that would include our case to guarantee the accuracy of estimates based on the variational approximation. The other few cases for which the variational approach has shown good theoretical properties are to the best of our knowledge simpler than our current setting.
The fact that the HRF h γ can be equivalently considered as a missing variable or a random parameter induces some similarity between our Variational EM variant and the Variational Bayesian EM algorithm presented in [37]. Our framework varies slightly from the case of conjugate exponential models described in [37] and more importantly, our presentation offers the possibility to deal with extra parameters Θ for which prior information may not be available. This is done in a maximum likelihood manner and avoids the use of non-informative priors that could be problematic (difficulties with non informative priors are listed in [40, pp. 64–65]). As a consequence, the variational Bayesian M-step of [37] is transferred into our E-step while our M-step has no equivalent in the formulation of [37].
B. Variational Joint Detection-Estimation
We propose here to use a EM variant in which the intractable E-step is instead solved over
 , a restricted class of probability distributions chosen as the set of distributions that factorize as p̃
A,HγQ = p̃
A
p̃
Hγ
p̃Q where p̃A, p̃
Hγ and p̃Q are probability distributions on
, a restricted class of probability distributions chosen as the set of distributions that factorize as p̃
A,HγQ = p̃
A
p̃
Hγ
p̃Q where p̃A, p̃
Hγ and p̃Q are probability distributions on
 ,
,
 and
and
 , respectively. It follows then that our E-step becomes an approximate E-step, which can be further decomposed into three stages that consist of updating the three pdfs, p̃
Hγ, p̃A and p̃Q in turn using three equivalent expressions of
, respectively. It follows then that our E-step becomes an approximate E-step, which can be further decomposed into three stages that consist of updating the three pdfs, p̃
Hγ, p̃A and p̃Q in turn using three equivalent expressions of
 when p factorizes as in
when p factorizes as in
 . At iteration (r) with current estimates denoted by
and Θ
(
r
−1), the updating rules become:
. At iteration (r) with current estimates denoted by
and Θ
(
r
−1), the updating rules become:
In other words, the factorization is used to maximize the free energy by alternately maximizing it with respect to p Hγ, pA and pQ while keeping the other distributions fixed. The steps above can then be equivalently written in terms of minimizations of some Kullback-Leibler divergences. The properties of the latter lead to the following solutions (see Appendix A for details):
| (8) |
| (9) |
| (10) |
The corresponding M-step is (since Θ and are independent, see Eq. (4)):
| (11) |
These steps lead to explicit calculations for and the parameter set . Although the approximation by a factorized distribution may have seemed initially drastic, the equations it leads to are coupled. More specifically, the approximation consists of replacing stochastic dependencies between latent variables by deterministic dependencies between moments of these variables (see Appendices A to C as mentioned below).
VE-H step: From Eq. (8) standard algebra enables to derive that is a Gaussian distribution whose parameters are detailed in Appendix B. The expressions for and are similar to those derived in the MCMC case [23, Eq. (B.1)] with expressions involving the ’s replaced by their expectations with respect to (wrt) .
VE-A step : Using Eq. (9), standard algebra rules allow to identify the Gaussian distribution of which writes as with . More detail about the update of is given in Appendix C. The relationship with the MCMC update of A is not straightforward. In [23, 25], the ’s are sampled independently and conditionally on the ’s. This is not the case in the VEM framework but some similarity appears if we set the probabilities either to 0 or 1 and consider only the diagonal part of .
-
VE-Q step: Using the expressions of p(A|Q) and p(Q) in Section II, Eq. (10) yields which is intractable due to the Markov random field prior. To overcome this difficulty, a number of approximation techniques are available. To decrease the computational complexity of our VEM algorithm and to avoid introducing additional variables as done in [30], we use a mean-field like algorithm which consists of fixing the neighbours to their mean value. Following [41], can be approximated by a factorized density such that if ,
(12) where q̃ m is a particular configuration of q m updated at each iteration according to a specific scheme, ~ j denotes neighbouring voxels to j on the brain volume and . Hereabove, and denote the m and (m, m′) entries of the mean vector ( ) and covariance matrix ( ), respectively. The Gaussian distribution with mean μim and variance vim is denoted by
 ( . ; μim, vim), while
. More details are given in Appendix D.
( . ; μim, vim), while
. More details are given in Appendix D. -
M step: For this maximization step, we can first rewrite Eq. (11) as
(13) The M-step can therefore be decoupled into four sub-steps involving separately (L, Γ), (μ, v), v h and β. Some of these sub-steps admit closed-form expressions, while some other require resorting to iterative or alternate optimization. For more details about the related calculations, the interested reader can refer to Appendix E.
IV. Validation of the proposed approach
This section aims at validating the proposed variational approach. Synthetic and real contexts are considered respectively in sub-sections IV-A and IV-B. To corroborate the effectiveness of the proposed method, comparisons with its MCMC counterpart, as implemented in [25], will also be conducted throughout the present section. The two approaches have been tuned at best so as to make them as close as possible. This reduces essentially to moderate the effect of the MCMC priors. The hyper-priors have been parameterized by a set of hyper-parameters that have a limited impact on the priors themselves. For instance, for the mean and variance parameters involved in the mixture model (μ, v), conjugate Gaussian
 (0, wμ) and inverse-gamma
(0, wμ) and inverse-gamma
 (av, bv) hyper-prior distributions have been considered whose parameters have been tuned by hand so as to make them flat while proper (eg, wμ < +∞). For doing so, the relationship between the hyper-parameters (eg, av, bv) and the statistical moments of the distribution have been carefully studied to guarantee a large variance or a large entropy in the latter. Moreover, given the above mentioned flatness of the hyper-priors, the MCMC approach is fairly robust to hyper-parameter setting.
(av, bv) hyper-prior distributions have been considered whose parameters have been tuned by hand so as to make them flat while proper (eg, wμ < +∞). For doing so, the relationship between the hyper-parameters (eg, av, bv) and the statistical moments of the distribution have been carefully studied to guarantee a large variance or a large entropy in the latter. Moreover, given the above mentioned flatness of the hyper-priors, the MCMC approach is fairly robust to hyper-parameter setting.
A. Artificial fMRI datasets
In this section, experiments have been conducted on data simulated according to the observation model in Eq. (1) where P has been defined from a cosine transform basis as in [23]. The simulation process is illustrated in Fig. 2.
Fig. 2.
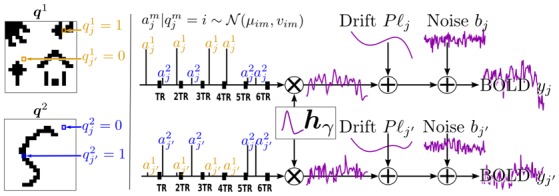
Single parcel (
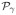 ) artificial data generation process using two experimental conditions (M = 2). From left to right: label maps q
m are hand-drawn. Conditionally on them, NRL values {
, j ∈
) artificial data generation process using two experimental conditions (M = 2). From left to right: label maps q
m are hand-drawn. Conditionally on them, NRL values {
, j ∈
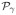 } are drawn from Gaussian distributions with means μim and variances vim whenever
. Then, for any given voxel j, the stimulus sequence of a given experimental condition m is multiplied by the corresponding NRL value
. The resulting sequence is convolved with a normalized HRF h
γ which is common to all conditions and voxels. Nuisance signals are finally added (drift Pℓ
j and noise b
j) to form the artificial BOLD signal y
j.
} are drawn from Gaussian distributions with means μim and variances vim whenever
. Then, for any given voxel j, the stimulus sequence of a given experimental condition m is multiplied by the corresponding NRL value
. The resulting sequence is convolved with a normalized HRF h
γ which is common to all conditions and voxels. Nuisance signals are finally added (drift Pℓ
j and noise b
j) to form the artificial BOLD signal y
j.
Different studies have then been conducted in order to validate the detection-estimation performance and robustness. For each of these studies, some simulation parameters have been changed such as the noise or the paradigm properties. Changing these parameters aims at providing for each simulation context a realistic BOLD signal while exploring various situations in terms of Signal-to-Noise Ratio (SNR).
1. Detection-Estimation performance
The first artificial data analysis was conducted on data simulated with a Gaussian white noise (I N is the N-dimensional identity matrix). Two experimental conditions have been considered (M = 2) while ensuring stimulus-varying Contrast-to-Noise Ratios (CNR)2 achieved by setting μ 11 = 2.8, μ 12 = 1.8, μ 01 = μ 02 = 0, and v 11 = v 12 = v 01 = v 02 = 0.5, so that a higher CNR is simulated for the first experimental condition (CNRm =1 = 15.68) compared to the second one (CNRm =2 = 6.48). For each of these conditions, the initial artificial paradigm comprised 30 stimulus events. The simulation process finally yielded time-series of 268 time-points. Condition-specific activated and non-activated voxels (Q values) were defined on a 20×20 2D slice as shown in Fig. 2[left]. No parcellation was performed. Simulated NRLs and BOLD signal were thus assumed to belong to a single parcel of size 20 × 20.
The Posterior Probability Maps (PPM) obtained using MCMC and VEM are shown in Fig. 3[middle] and Fig. 3[right]. PPMs here correspond to the activation class assignment probabilities . These figures clearly show the gain in robustness provided by the variational approximation. This gain consists of lower miss-classification error (a lower false positive rate) illustrated by higher PPM values, especially for the experimental condition with the lowest CNR (m = 2).
Fig. 3.
Detection results for the first artificial data analysis. Ground truth q m (left) and estimated Posterior Probability Maps (PPM) q̂ m using MCMC (middle) and VEM (right). Note that condition m = 2 (bottom row) is associated with a lower CNR than condition m = 1 (top row).
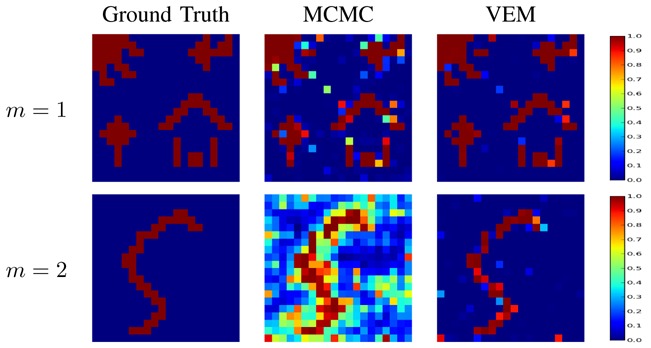
For a quantitative evaluation, the Receiver Operating Characteristic (ROC) curves corresponding to the estimated PPMs using both algorithms were computed. As shown in Fig. 4, they confirm that both algorithms perform well at high CNR (m = 1) and that the VEM scheme outperforms the MCMC implementation for the second experimental condition (m = 2).
Fig. 4.
Detection results for the first artificial data analysis. ROC curves associated with the label posteriors (q̂ m) using VEM and MCMC. Condition m = 1 is associated with a higher CNR than condition m = 2. Curves are plotted in solid and dashed line for VEM and MCMC, respectively.
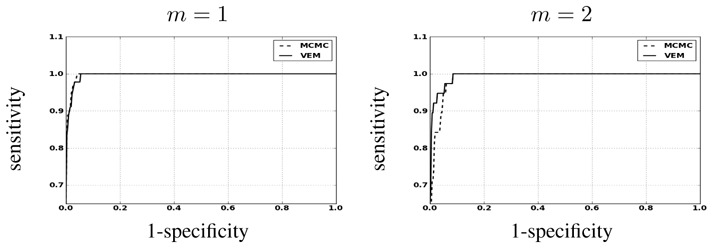
Fig. 5 shows the NRL estimates obtained by the two methods. Although some differences are exhibited on the PPMs, both algorithms report similar qualitative results wrt the NRLs. However, the difference between NRL estimates (VEM-MCMC) in Fig. 5[right] points out that regions corresponding to activated areas for the two conditions present positive intensity values, which means that VEM helps retrieving higher NRL values for activated area compared to MCMC.
Fig. 5.
Detection results for the first artificial data analysis. From left to right: Ground truth a m and NRL estimates â m by MCMC and VEM, and NRL image difference ( ) (right). Top row: m = 1; bottom row: m = 2.
Quantitatively speaking, the gain in robustness is confirmed by reporting the Sum of Squared Error (SSE)3 values on NRL estimates which are slightly lower using VEM compared to MCMC for the first experimental condition (m = 1: SSEMCMC = 0.012 vs. SSEVEM = 0.010), as well as for the second experimental condition (m = 2: SSEMCMC = 0.010 vs. SSEVEM = 0.009). These error values indicate that, even though the MCMC algorithm gives the most precise PPMs for the high CNR condition (Fig. 4, m = 1), the VEM approach is more robust than its MCMC alternative in terms of estimated NRLs. These values also indicate slightly lower SSE for the second experimental conditions (m = 2) compared to the first one (m = 1) with higher CNR. This difference is explained by the presence of larger non-activated areas for m = 2 where low NRL values are simulated, and for which the SSE is very low.
In addition, a test for equality of means has been conducted to test whether the quadratic errors means over voxels obtained with VEM and MCMC were significantly close. Very low p-values of 0.0377 and 0.0015 were obtained respectively for condition m = 1 and m = 2, which means that the null hypothesis (the two means are equal) is rejected for the usual 5% threshold. In other words, although the obtained error difference is small, it is significant from a statistical viewpoint. Interestingly, As m = 2 corresponds to a lower CNR, this highlights the significance of the gain in robustness we got with the VEM version in a degraded CNR context.
As regards HRF estimates, Fig. 6 shows both retrieved shapes using MCMC and VEM. Compared to the ground truth (solid line), the two approaches yield very similar results and preserve the most important features of the original HRF like the peak value (PV), time-to-peak (TTP) and time-to-undershoot (TTU).
Fig. 6.
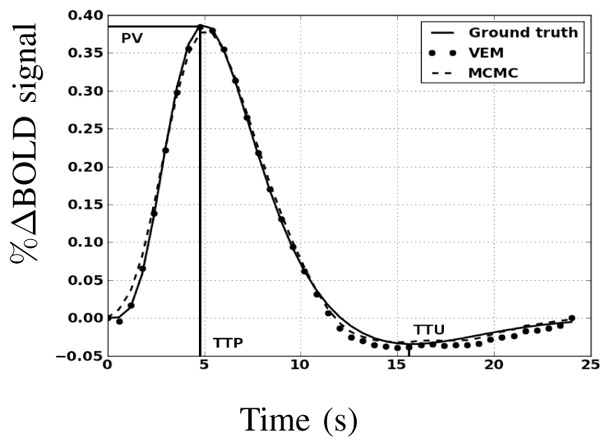
Estimation results for the first artificial data analysis. Ground truth HRF h and HRF estimates ĥ using the MCMC and VEM algorithms.
2. Estimation robustness
Since estimation errors may be caused by different perturbation sources, in the following, various Monte Carlo analyses have been conducted by varying one-at-a time several simulation parameters, namely the stimulus density, the noise parameters and the amount of spatial regularization. The differences in the obtained estimation errors have all been tested for statistical significance using tests for equality of means for the errors over 100 runs. For all reported comparisons, the obtained p-values were very low (p < 0.001) indicating that the performance differences, even when small, were statistically significant.
a. Varying the stimulus density
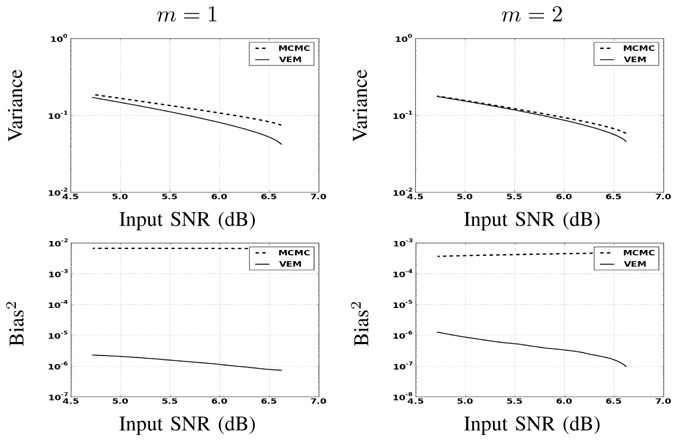
In this experiment, simulations have been conducted by varying the stimulus density from 5 to 30 stimuli in the artificial paradigm, which leads to decreasing Inter Stimuli Intervals (ISI) (from 47 s to 9 s, respectively). At each stimulus density, 100 realizations of the same artificial dataset have been generated so as to evaluate the estimation bias and variance of NRLs. Here, the stimuli are interleaved between the two conditions so that the above mentioned ISIs correspond to the time interval between two events irrespective of the condition they belong to. A second order autoregressive noise (AR(2)) has also been used for the simulation providing a more realistic BOLD signal [23]. The rest of the simulation process is specified as before. In order to quantitatively evaluate the robustness of the proposed VEM approach to varying input SNR4, results (assuming white noise in the model used for estimation for both algorithms) are compared while varying the stimulation rate during the BOLD signal acquisition. Fig. 7 illustrates the error evolution related to the NRL estimates for both experimental conditions wrt the ISI (or equivalently the stimulus density) in the experimental paradigm. Estimation error is illustrated in terms of Mean Squared Error (MSE)5, which splits into the sum of the variance (Fig. 7[top]) and squared bias (Fig. 7[bottom]). This figure shows that at low SNR (or high ISI), VEM is more robust in terms of estimation variance to model mis-specification irrespective of the experimental condition. At high SNR or low ISI, the two methods perform similarly and remain quite robust. As regards estimation bias, Fig. 7[bottom] shows less monotonous curves for m = 2, which may be linked to the lower CNR of the second experimental condition compared to the first one. However, the two methods still perform well since squared bias values are very low, meaning that the two estimators are not highly biased. As reported in Section IV-A.1, error values on NRL estimates remain comparable for both experimental conditions and all ISI values, although PPM results present some imprecisions for the low CNR condition (m = 2).
Fig. 7.
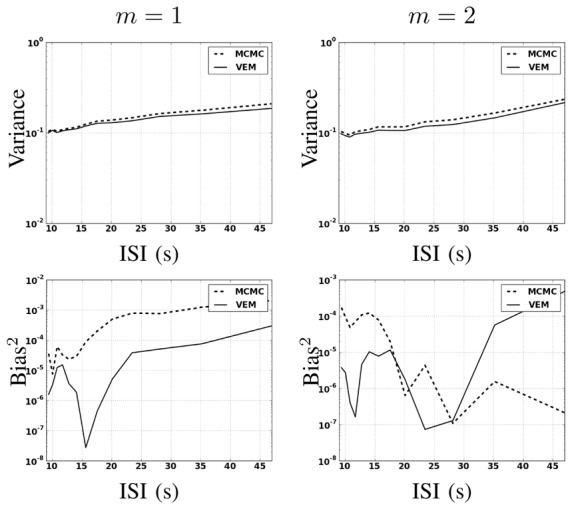
NRL estimation errors over 100 simulations in a semi-logarithmic scale in terms of variance (top) and squared bias (bottom) wrt ISIs for both experimental conditions m = 1 and m = 2.
As regards hemodynamic properties, Fig. 8[left] depicts errors on HRF estimates inferred by VEM and MCMC in terms of variance (Fig. 8[left-top]) and squared bias (Fig. 8[left-bottom]) wrt the ISI (or equivalently the stimulus density). The VEM approach outperforms the MCMC scheme over the whole range of ISI values, but the bias and variance remain very low for both methods. When evaluating the estimations of the key HRF features (PV, TTP and TTU), it turns out that the TTP and TTU estimates remain the same irrespective of the inference algorithm, which corroborates the robustness of the developed approach (results not shown). As regards PV estimates, Fig. 8[right] shows the error values wrt the ISIs. The VEM algorithm outperforms MCMC in terms of squared bias over all ISI values. However, the performance in terms of estimation variance remains similar with very low variance values over the explored ISIs range. For more complete comparisons, similar experiments have been conducted while changing the ground truth HRF properties (PV, TTP, TTU), and similar results have been obtained. In contrast to NRL estimations, variance and squared bias are here comparable. We can even note higher squared bias for PV estimates compared to the variance.
Fig. 8.
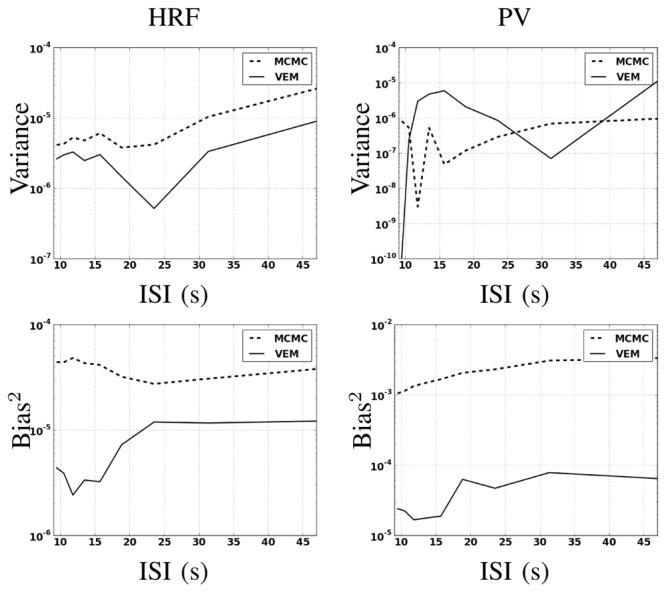
Estimation errors over 100 simulations in a semi-logarithmic scale in terms of variance (top) and squared bias (bottom) wrt ISIs for both the HRF and its PV.
b. Varying the noise parameters
In this experiment, several simulations have been conducted using an AR(2) noise with varying variance and correlation parameters in order to illustrate the robustness of the proposed VEM approach to noise parameter fluctuation. For each simulation, 100 realizations were generated so as to estimate the estimation bias and variance.
Performance of the two methods are evaluated in terms of MSE (splits into the sum of the variance and squared bias). Fig. 9 illustrates in a semi-logarithmic scale for NRLs the variance and squared bias of the two estimators plotted against the input SNR when varying the noise variance. This figure clearly shows that the bias introduced by both estimators is very low compared to the variance. Moreover, the bias introduced by VEM is very low compared to MCMC. As regards the variance, our results illustrate that VEM also slightly outperforms MCMC.
Fig. 9.
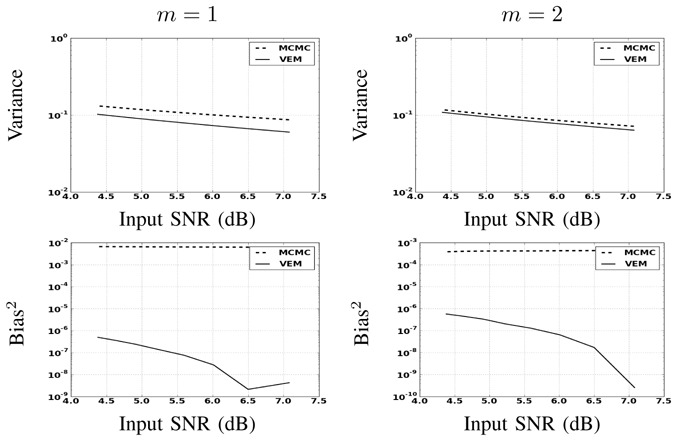
MSE on NRL estimates split into variance (top) and squared bias (bottom) wrt input SNR (AR(2) noise) by varying the AR(2) noise variance.
Fig. 10 depicts the variance and squared bias plotted in semi-logarithmic scale against input SNR when varying the noise autocorrelation. Overall, the same conclusions as for Fig. 9 hold. Moreover, as already observed in [42] at a fixed input SNR value, the impact of a large autocorrelation is stronger than that of a large noise variance irrespective of the inference scheme. Comparing Figs 9 and 10, this property is mainly visible at low input SNR (as usually observed on real BOLD signals).
Fig. 10.
MSE on NRL estimates split into variance (top) and squared bias (bottom) wrt input SNR (AR(2) noise) by varying the amount of AR(2) noise autocorrelation.
Although a slight advantage is observed for the VEM approach in terms of estimation error and for both experimental conditions, the two methods perform generally well with a relatively low error level. The slightly better performance of VEM compared to MCMC is likely due to a better fit under model mis-specification.
c. Varying the spatial regularization parameter
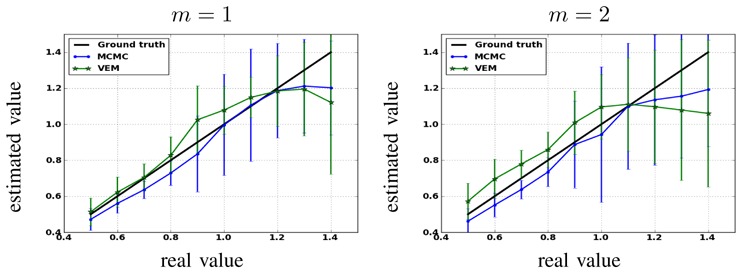
This section is dedicated to studying the robustness of the spatial regularization parameter estimation. For doing so, the synthetic activation maps of Fig. 2 are replaced with maps obtained as simulations of a 2-class Potts model with interaction parameter β that varies from 0.5 to 1.4. When positive, this parameter (β) favors spatial regularity across adjacent voxels, and hence smoother activation maps. Fig. 11 shows the estimated mean value β̂ and standard deviations for β = {βm, m = 1 … M} over 100 simulations using both algorithms and for the two experimental conditions. Three main regions can be distinguished for both experimental conditions. The first one corresponds to β ≤ 0.8, which approximatively matches the phase transition critical value for the 2-class Potts model. For this region, Fig. 11 shows that the VEM estimate (green curve) appears to be closer to the Ground truth (black line) than the MCMC one (blue curve). Also, the proposed VEM approach yields more accurate estimation, especially for the first experimental condition (m = 1) having relatively high CNR. The second region corresponds to β ∈ (0.8, 1.1), where MCMC inference becomes more robust than the VEM one. The third region is identified by β ≥ 1.1, where both methods give less robust estimation than for the first two regions. Based on these regions, we conclude that the variational approximation (mean-field) improves the estimation performance up to a given critical value. It turns out that such an approximation is more valid for low β values, which usually correspond to observed β values on real fMRI data.
Fig. 11.
Reference (black) and estimated mean values of β with VEM (green) MCMC (blue) for both experimental conditions (m = 1 and m = 2). Mean values and standard deviations (vertical bars) are computed based on 100 simulations.
When comparing estimates for the two conditions, the curves in Fig. 11 show that both methods generally estimate more precise β values for the first experimental condition (m = 1) having higher input CNR. For both cases, and across the three regions identified hereabove, the error bars show that the VEM approach generally gives less scattered estimates (lower standard deviations) than the MCMC one, which confirms the gain in robustness induced by the variational approximation.
Note here that estimated β values in the experiment of Section IV-A.1 lie in the first region for the first experimental condition ( and ). For the second condition (m = 2), and because input SNR is relatively low, no clear conclusion can be made since MCMC and VEM give relatively different values ( and ) and no ground truth is available since the activation maps have been drawn by hand and not simulated according to the Markov model.
B. Real fMRI datasets
This section is dedicated to the experimental validation of the proposed VEM approach in a real context. Experiments were conducted on real fMRI data collected on a single healthy adult subject who gave informed written consent. Data were collected with a 3-Tesla Siemens Trio scanner using a 3D Magnetization Prepared Rapid Acquisition GRadient Echo (MPRAGE) sequence for the anatomical MRI and a Gradient-Echo Echo Planar Imaging (GRE-EPI) sequence for the fMRI experiment. The acquisition parameters for the MPRAGE sequence were set as follows: Time of Echo: TE = 2.98 ms; Time of Repetition: TR = 2300 ms; sagittal orientation; spatial in-plane resolution: 1 × 1 mm2; Field of View: FOV = 256 mm2 and slice thickness: 1.1 mm. Regarding the EPI sequence, we used the following settings: the fMRI session consisted of N = 128 EPI scans, each of them being acquired using TR = 2400 ms, TE = 30 ms, slice thickness: 3 mm, transversal orientation, FOV = 192 mm2 and spatial in-plane resolution was set to 2 × 2 mm2. Data was collected using a 32 channel head coil to enable parallel imaging during the EPI acquisition. Parallel SENSE imaging was used to keep a reasonable Time of Repetition (TR) value in the context of high spatial resolution.
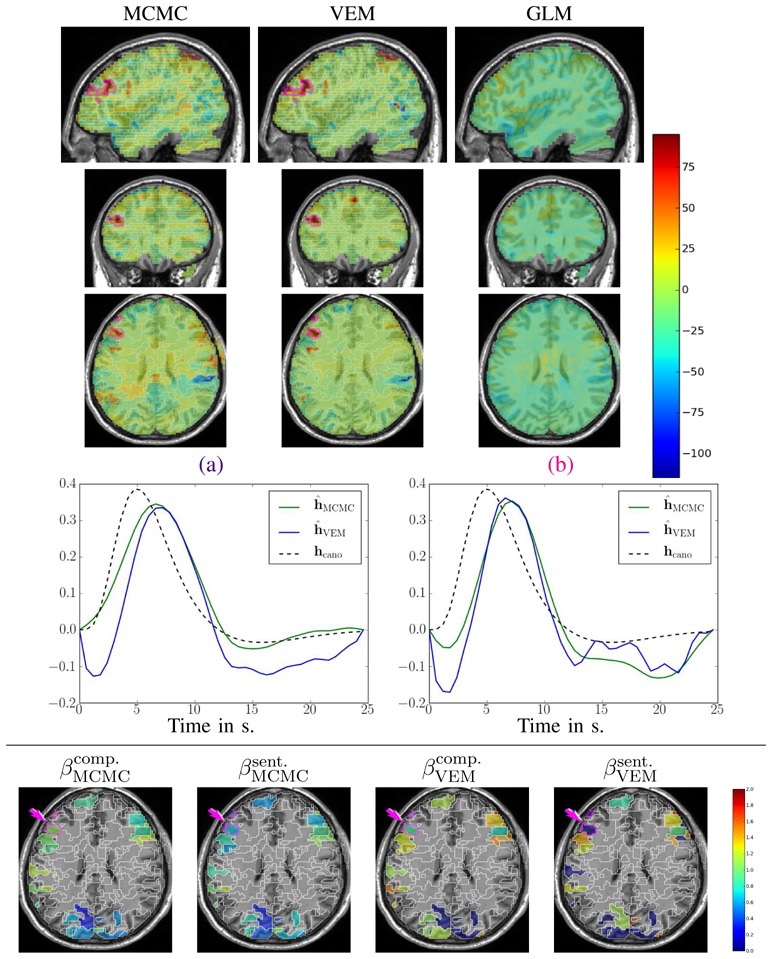
The design of the fMRI experiment was a functional localizer paradigm [43] that enables a quick mapping of cognitive brain functions such as reading, language comprehension and mental calculations as well as primary sensory-motor functions. It consists of a fast event-related design comprising sixty auditory, visual and motor stimuli, defined in ten experimental conditions and divided in two presentation modalities (auditory and visual sentences, auditory and visual calculations, left/right aurally and visually induced motor responses, horizontal and vertical checkerboards). The average ISI is 3.75 s including all experimental conditions. Such a paradigm is well suited for simultaneous detection and estimation, in contrast to slow event-related and block paradigms which are considered as optimal for estimation and detection, respectively [44]. After standard pre-processing steps (slice-timing, motion corrections and normalization to the MNI space), the whole brain fMRI data was first parcellated into ϒ = 600 functionally homogeneous parcels by resorting to the approach described in [26]. This parcellation method consisted of a hierarchical clustering (Euclidean distance, Ward’s linkage) of the experimental condition effects estimated by a GLM analysis. This GLM analysis comprised the temporal and dispersion HRF derivatives as regressors so that the clustering took some HRF variability into account. To enforce parcel connexity, the clustering process was spatially constrained to group only adjacent positions. This parcellation was used as an input of the JDE procedure, together with the fMRI time series. We stress the fact that the latter signals were not spatially smoothed prior to the analysis as opposed to the classical SPM-based fMRI processing. In what follows, we compare the MCMC and VEM versions of JDE with the classical GLM analysis as implemented in Nipy6 by focusing on two contrasts of interest: i) the Visual-Auditory (VA) contrast which evokes positive and negative activity in the primary occipital and temporal cortices, respectively, and ii) the Computation-Sentences (CS) contrast which aims at highlighting higher cognitive brain functions. Besides, results on HRF estimates are reported for the two JDE versions and compared to the canonical HRF, as well as maps of regularization factor estimates.
Fig. 12 shows results for the VA contrast. High positive values are bilaterally recovered in the occipital region and the overall cluster localizations are consistent for both MCMC and VEM algorithms. The only difference lies in the temporal auditory regions, especially on the right side, where VEM yields rather more negative values than MCMC. Thus VEM seems more sensitive than MCMC. The results obtained by the classical GLM (see Fig. 12[right]) are comparable to those of JDE in the occipital region with roughly the same level of recovered activations. However, in the central region, we observe activations in the white matter that can be interpreted as false positives and that were not exhibited using the JDE formalism. The bottom part of Fig. 12 compares the estimated values of the regularization factors β̂ between VEM and MCMC algorithms for two experimental conditions involved in the VA contrast. Since these estimates are only relevant in parcels which are activated by at least one condition, a mask was applied to hide non-activated parcels. We used the following criterion to classify a parcel as activated: max{(μ̂ 1 m)1≤ m ≤ M } ≥ 8 (and non-activated otherwise). These maps of β̂ estimates show that VEM yields more contrasted values between the visual and auditory conditions. Table III provides the estimated β̂ values in the highlighted parcels of interest. The auditory condition does not elicit evoked activity and yields lower β̂ values in both parcels whereas the visual condition is associated with higher values. The latter comment holds for both algorithms but VEM provides much lower values ( ) than MCMC ( ) for the non-activated condition. For the activated condition, the situation is comparable, with and . This illustrates a noteworthy difference between VEM and MCMC. Probably due to the mean field and variational approximations, the hidden field may not have the same behaviour (different regularization effect) between the two algorithms. Still, this discrepancy is not visible on the NRL maps.
Fig. 12.
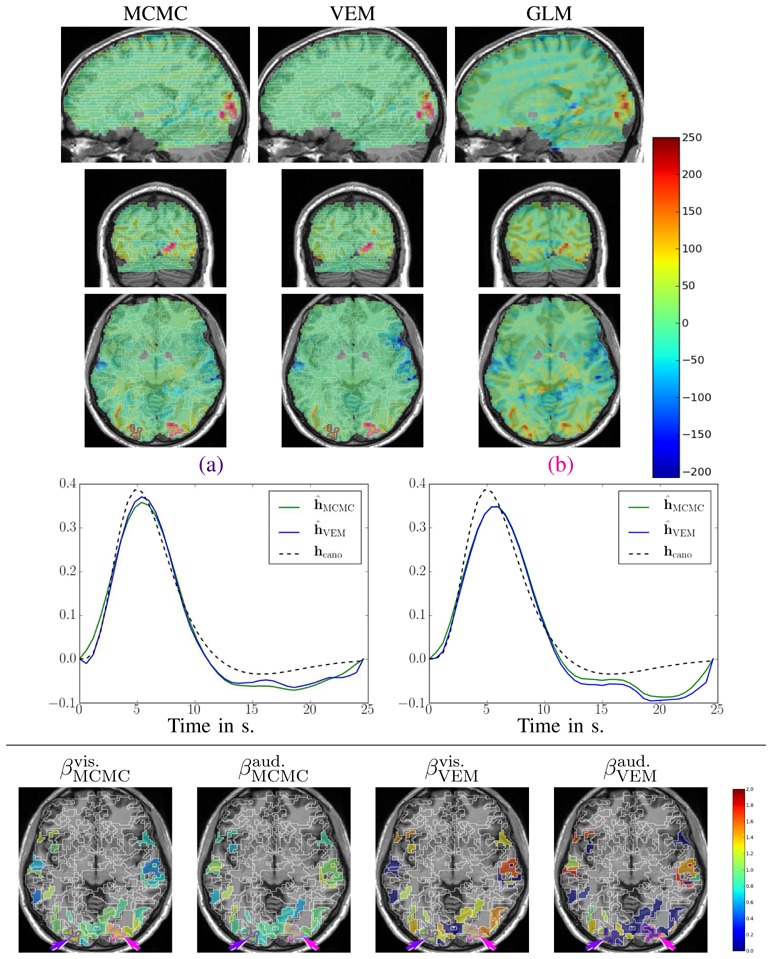
Results for the Visual-Auditory contrast obtained by the VEM and MCMC JDE versions, compared to a GLM analysis. Top part, from left to right: NRL contrast maps for MCMC, VEM and GLM with sagittal, coronal and axial views from top to bottom lines (neurological convention: left is left). Middle part: plots of HRF estimates for VEM and MCMC in the two parcels circled in indigo
 and
and
 on the maps: occipital
on the maps: occipital
 and
and
 , respectively. The canonical HRF shape is depicted in dashed line. Bottom part: axial maps of estimated regularization parameters β̂ for the two conditions, auditory (aud.) and visual (vis.), involved in the VA contrast. Parcels that are not activated by any condition are hidden. For all contrast maps, the input parcellation is superimposed in white contours.
, respectively. The canonical HRF shape is depicted in dashed line. Bottom part: axial maps of estimated regularization parameters β̂ for the two conditions, auditory (aud.) and visual (vis.), involved in the VA contrast. Parcels that are not activated by any condition are hidden. For all contrast maps, the input parcellation is superimposed in white contours.
TABLE III.
Comparison of the estimated regularization parameters β̂ obtained with VEM and MCMC JDE for the experimental conditions involved in the studied contrasts: Visual-Auditory (VA) and Computation-Sentences (CS). Results are provided for the two highlighted parcels for each contrast (see Figs. 12 and 13).
| VA contrast | CS contrast | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||
| β̂ for parcel γ 1 | β̂ for parcel γ 2 | β̂ for parcel γ 3 | β̂ for parcel γ 4 | ||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
| MCMC | 1.28 | 1.08 | 1.24 | 1.05 | 1.08 | 0.68 | 1.07 | 0.64 | |||||||
| VEM | 1.14 | 0.01 | 1.08 | 0.01 | 0.91 | 0.01 | 0.82 | 1.19 | |||||||
Fig. 12(a–b) depicts HRF estimation results which are rather close for both methods in the two regions under consideration. VEM and MCMC HRF estimates are also consistent with the canonical HRF shape. Indeed, the latter has been precisely calibrated on visual regions [10, 11]. These estimation results explain why JDE does not bring any gain in sensitivity compared to the classical GLM: the canonical HRF is the optimal choice for visual areas. We can note a higher variability in the undershoot part, which can be explained, first, by the fast event-related nature of the paradigm where successive evoked responses are likely to overlap in time so that it is more difficult to disentangle their ends; and second, by the lower signal strength and SNR in the tail of the response. To conclude on the VA contrast which focused on well-known sensory regions, VEM provides sensitive results consistent with the MCMC version, both wrt detection and estimation tasks. These results were also validated by a classical GLM analysis which yielded comparable sensitivity in a region where the canonical HRF is known to be valid (see Fig. 12[right]).
Results related to the Computation-Sentences (CS) contrast are depicted in Fig. 13. As for VA, NRL contrast maps ( ) are roughly equivalent for VEM and MCMC in terms of cluster localizations. Still, in Fig. 13[left-center], we observe that MCMC seems quite less specific than VEM as positive contrast values are exhibited in the white matter for MCMC, and not for VEM (compare especially the middle part of the axial slices). Here, GLM results clearly show lower sensitivity compared to the JDE results. For the estimates of the regularization parameters, the situation is globally almost the same as for the VA contrast, with VEM yielding more contrasted β̂ maps than MCMC. However, these values are slightly lower than the ones reported for the VA contrast.
Fig. 13.
Results for the Computation-Sentences contrast obtained by the VEM and MCMC JDE versions compared to a GLM analysis. Top part, from left to right: NRL contrast maps for MCMC, VEM, and GLM, with sagittal, coronal and axial views from top to bottom lines (neurological convention: left is left). Middle part: plots of HRF estimates for VEM and MCMC in the two parcels circled in
 and
and
 on the maps:
on the maps:
 and
and
 , respectively. The canonical HRF shape is depicted in dashed line. Bottom part: axial maps of estimated regularization parameters β̂ for the two conditions, computation (comp.) and sentence (sent.), involved in the CS contrast. Parcels that are not activated by any condition are hidden. For all contrast maps, the input parcellation is superimposed in white contours.
, respectively. The canonical HRF shape is depicted in dashed line. Bottom part: axial maps of estimated regularization parameters β̂ for the two conditions, computation (comp.) and sentence (sent.), involved in the CS contrast. Parcels that are not activated by any condition are hidden. For all contrast maps, the input parcellation is superimposed in white contours.
We first focus on the left frontal cluster, located in the middle frontal gyrus which has consistently been exhibited as involved in mental calculation [45]. HRF estimates in this region are shown in Fig. 13(b) and strongly depart from the canonical version, which explains the weaker sensitivity in the GLM results as the canonical HRF model is not optimal in this region. Especially, the TTP value is much more delayed with JDE (7.5 s), compared to the canonical situation (5 s). The VEM and MCMC shapes are close to each other, except at the beginning of the curves where VEM presents an initial dip. This might be interpreted as a higher temporal regularization introduced in the MCMC scheme. Still, the most meaningful HRF features such as the TTP and the Full Width at Half Maximum (FWHM) are very similar.
The second region of interest for the CS contrast is located in the inferior parietal lobule and is also consistent with the computation task [45]. Note that the contrast value is lower than the one estimated in the frontal region, whatever the inference scheme. Interestingly, this activation is lost by the GLM fitting procedure. HRF estimates are shown in Fig. 13(a). The statement relative to the previous region holds again: they strongly differ from the canonical version, which explains the discrepancy between the different detection activation results each method retrieved. When comparing MCMC and VEM, even if the global shape and the TTP position are similar, the initial dip in the HRF estimate is still stronger with VEM and the corresponding FWHM is also smaller than for the MCMC version. As previously mentioned, this suggests that MCMC may tend to over-smooth the HRF shape. Results for the regularization parameters, as shown in Table III [4th col.], indicate that β̂ for VEM and the Sentence condition is not as low as it is for the other parcels and the non-activated conditions ( against ). This is explained by the fact that both Computation and the Sentence conditions yield activations in this parcel as confirmed by the low contrast value.
The studied contrasts represent decreasing CNR situations, with the VA contrast being the stronger and CS the weaker. From the detection point of view, the contrast maps are very similar for both JDE versions and are only dimly affected by the CNR fluctuation. In contrast, HRF estimation results are much more sensitive to this CNR variation, with stronger discrepancies between the VEM and MCMC versions, especially for the HRF estimates associated with the CS parietal cluster. The latter shows the weaker contrast magnitude. Still, both versions provide results in agreement on the TTP and FHWM values. Indeed, the differences mainly concern the heading and tailing parts of the HRF curves.
V. Algorithmic efficiency
In this section, the computational performance of the two approaches are compared on both artificial and real fMRI datasets. Both algorithms were implemented in Python and fully optimized by resorting to the efficient array operations of the Numpy library7 as well as C-extensions for the computationally intensive parts (e.g. NRL sampling in MCMC or the VE-Q step for VEM). Moreover, our implementation handled distributed computing resources as the JDE analysis consists of parcel-wise independent processings which can thus be performed in parallel. This code is available in the PyHRF package8.
For both the VEM and MCMC algorithms, the same stopping criterion was used. This criterion consists of simultaneously evaluating the online relative variation of each estimate. In other words, for instance for the estimated ĥ γ, one has to check whether . By evaluating a similar criterion cA for the NRLs estimates, the algorithm is finally stopped once cH ≤ 10−5 and cA ≤ 10−5. For the MCMC algorithm, this criterion is only computed after the burn-in period, when the samples are assumed to be drawn from the target distribution. The burn-in period has been fixed manually based on several a posteriori controls of simulated chains relative to different runs (here 1000 iterations). More sophisticated convergence monitoring techniques [46] should be used to stop the MCMC algorithm, but we chose the same criterion as for the VEM to carry out a more direct comparison.
Considering the artificial dataset presented in Section IV-A.1, Fig. 14 illustrates the evolution of cH and cA with respect to the computational time for both algorithms. Only about 18 seconds are enough to reach convergence for the VEM algorithm, while the MCMC alternative needs about 1 minute to converge on the same Intel Core 4 - 3.20 GHz - 4 Gb RAM architecture. The horizontal line in the blue curve relative to the MCMC algorithm corresponds to the burn-in period (1000 iterations). It can also be observed that the gain in computational efficiency the VEM scheme brings is independent of the unknown variables (e.g. NRLs or HRF) we look at.
Fig. 14.
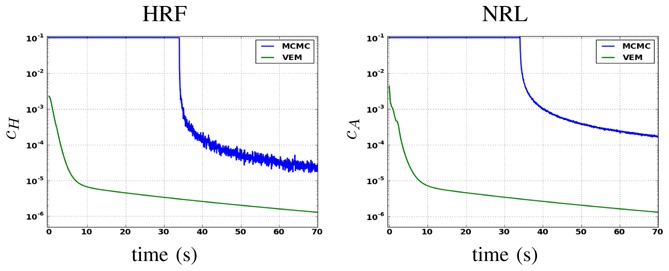
Convergence curves in semi-logarithmic scale of HRF (left) and NRL (right) estimates using MCMC (blue lines) and VEM (green lines).
To illustrate the impact of the problem dimensions on the computational cost of both methods, Fig. 15 shows the evolution of the computational time of one iteration when varying the number of voxels (left), the number of experimental conditions (center) and the number of scans (right). The three curves show that the computational time increases almost linearly (see the blue and red curves) for both algorithms, but with different slopes. Blue curves (VEM) have steeper slopes than red ones (MCMC) in the three plots showing that the computational time of one iteration increases faster with VEM than with MCMC wrt the problem dimensions.
Fig. 15.
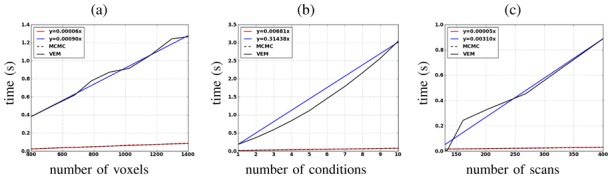
Evolution of the computational time per iteration using the MCMC and VEM algorithms when varying the problem dimension according to: (a): number of voxels; (b): number of conditions; (c): number of scans.
As regards computational performance on the real fMRI data set presented in Section IV-B and comprising 600 parcels, the VEM also appeared faster as it took 1.5 hours to perform a whole brain analysis whereas the MCMC version took 12 hours. These analysis timings were obtained by a serial processing of all parcels for both approaches. When resorting to the distributed implementation, the analysis durations boiled down to 7 mins for VEM and 20 mins for MCMC (on a 128-core cluster). To go further, we illustrate the computational time difference (Δt = t MCMC −t VEM) between both algorithms in terms of parcel size which ranged from 50 to 580 voxels. As VEM vs. MCMC efficiency appears to be influenced by the level of activity within the parcel, we resorted to the same criterion as in Section IV-B to distinguish non-activated from activated parcels and tag the analysis durations accordingly in Fig. 16.
Fig. 16.
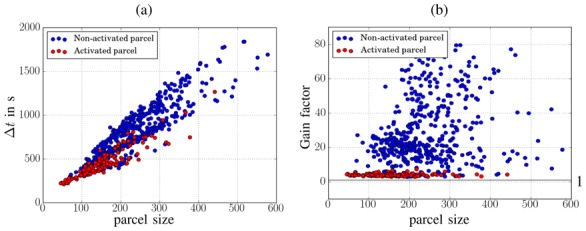
Comparison of durations for MCMC and VEM analyses in terms of parcel size, each dot coding for a different parcel. (a): differential timing Δt = t
MCMC −t
VEM. (b): gain factor Gf = t
MCMC
/t
VEM of VEM compared to MCMC, the horizontal line indicates a gain factor of one (Gf = 1). Circles are
 -colored for parcels estimated as activated, ie max{(μ̂
1
m)1≤
m
≤
M} ≥ 8 and
-colored for parcels estimated as activated, ie max{(μ̂
1
m)1≤
m
≤
M} ≥ 8 and
 -colored otherwise.
-colored otherwise.
Fig. 16(a) clearly shows that the differential timing Δt between the two algorithms is higher for non-activated parcels (blue dots) and increases with the parcel size, which confirms the utility of the proposed VEM approach especially in low CNR/SNR circumstances. To further investigate the gain in terms of computational time induced by VEM, Fig. 16(b) illustrates the gain factor (Gf = t MCMC /t VEM) for activated and non-activated parcels. This figure shows that the VEM algorithm always outperforms the MCMC alternative since Gf ≥ 1 in all parcels (see horizontal line in Fig. 16[b]). Moreover, the gain factor Gf is clearly higher for non-activated parcels for which the input SNRs and CNRs are relatively low, and we found Gf ∈ [2.7, 80].
VI. Discussion and conclusion
In this paper, we have proposed a new intra-subject method for parcel-based joint detection-estimation of brain activity from fMRI time series. The proposed method relies on a Variational EM algorithm as an alternative solution to intensive stochastic sampling used in previous work [23, 25]. Compared to the latter formulation, the proposed VEM approach does not require priors on the model parameters for inference to be carried out. However, to achieve gain in robustness and make the proposed approach completely auto-calibrated, the adopted model can be extended by injecting additional priors on some of its parameters as detailed in Appendix E for β and v h estimation.
Illustrations on simulated and real datasets have been deeply conducted in order to assess the robustness of the proposed method compared to its MCMC counterpart in different experimental contexts. Simulations have shown that the proposed VEM algorithm retrieved more accurate activation labels and NRLs especially at low input CNR, while yielding similar performance for HRF estimation. VEM superiority in terms of NRLs and labels estimation has been confirmed by mean equality statistical tests over estimation errors obtained through 100 Monte Carlo runs. Conducted tests showed very low p-values, which means that differences in terms of obtained error means were statistically significant. Simulations have also shown that our approach was more robust to any decrease of stimulus density (or equivalently to any increase of ISI value). Similar conclusions have been drawn wrt noise level and autocorrelation structure. In addition, our VEM approach provided more robust estimation of the spatial regularization parameter and more compact activation maps that are likely to better account for functional homogeneity. These good properties of the VEM approach are obtained faster than using the MCMC implementation. Simulations have also been conducted to study the computational time variation wrt the problem dimensions, which may significantly vary from one experimental context to another.
As a general comment, this performance of VEM compared to MCMC may be counterintuitive. The sampled chain in MCMC is supposed to converge to the true target distribution after the burn-in period. However, since non-informative priors are used in the MCMC model such as the uniform prior for Potts parameters β, imprecisions in the target distribution may occur. In this case, VEM may outperform MCMC as observed in our simulations. Also, in some of the experiments, the model assumes a 2-class Potts model for the activation classes while we used more realistic synthetic images instead. The images we used (e.g. the house shape) are more regular and realistic than would be a typical realization of a Potts model. Then, our results show lower MSE (variance and squared bias) for VEM when the noise model is mis-specified and we suspect that VEM is less sensitive to model mis-specification. In a mis-specification context, the variational approach may be favored by the fact that the factorization assumption acts as an extra regularizing term that smoothes out the solutions in a more appropriate manner. There exists a number of other studies in which the variational approach is compared to its MCMC counterpart and provides surprisingly accurate results [30, 38, 47, 48]. It is true that results showing the superior performance of VEM over MCMC are more seldom. For instance, the results reported in [38] show that their variational approach is highly accurate in approximating the posterior distribution. These authors show like us, smaller MSE for the variational approach vs MCMC on simulations and point out a MCMC sensitivity to initialization conditions. On a computational efficiency point of view, most works on variational methods lead to EM-like algorithms in which one iteration consists of updating sufficient statistics (e.g. means and variances) that characterize the distribution approximating the target posterior. In our setting the approximating distribution is made of Gaussian parts fully specified by their mean and variance. In contrast, sampling-based methods like MCMC are not focused on sufficient statistics computation, but rather simulate realizations from the full posterior. Approximating a limited number of moments is less complex than approximating a full distribution, which may also be an ingredient that explains improved VEM efficiency and performance.
Regarding real data experiments, VEM and MCMC showed similar results with a higher specificity for the former. Compared to the classical GLM approach, the JDE methodology yields similar results in the visual areas where the canonical HRF is well recovered, whereas in the areas involved in the CS contrast, the estimation of more adapted HRFs that strongly differ from the canonical version enables higher sensitivity in the activation maps. These results further emphasize the interest of using VEM for saving a large amount of computational time. From a practical viewpoint, another advantage of the proposed algorithm lies in its simplicity to track convergence even if the latter is local: the VEM algorithm only requires a simple stopping criterion to achieve a local minimizer in contrast to the MCMC implementation [25]. It is also more flexible to account for more complex situations such as those involving higher AR noise order, habituation modeling [49] or considering three instead of two activation classes with an additional deactivation class.
To confirm the impact of the proposed inference, comparisons between the MCMC and VEM approaches should also take place at the group level. The most straightforward way would be to compare the results of random effect analyses (RFX) based on group-level Student t-test on averaged effects, the latter being computed either by a standard individual SPM analysis or by the two VEM and MCMC JDE approaches. In this direction, a preliminary study has been performed in [14] where group results based on JDE MCMC intra-subject analyses provide higher sensitivity than results based on GLM based intra-subject analyses. Ideally, the JDE framework could be extended to perform group-level analysis and yield group-level NRL maps as well as group-level HRFs. To break down the complexity, this extension could operate parcel-wisely by grouping subject-dependent data into group-level functionally homogeneous parcels. This procedure would result in a hierarchical mixed effect model and encode mean group-level values of NRLs and HRFs so that subject-specific NRL and HRF quantities would be modeled as fluctuations around theses means.
Such group-level validations would also shed the light on the impact of the used variational approximation in VEM. In fact, no preliminary spatial smoothing is used in the JDE approach in contrast to standard fMRI analyses where this smoothing helps retrieving clearer activation clusters. In this context, the used mean field approximation especially in the VE-Q step should help getting less noisy activation clusters compared to the MCMC approach. Eventually, akin to [23], the model used in our approach accounts for functional homogeneity at the parcel scale. These parcels are assumed to be an input of the proposed JDE procedure and can be a priori provided independently by any parcellation technique [26, 50]. In the present work, parcels have been extracted from functional features we obtained via a classical GLM processing assuming a canonical HRF for the entire brain. This assumption does not bias our HRF local model estimation since a large number of parcels is considered (600 parcels) with an average parcel size of 250 voxels.
However, on real dataset, results may depend on the reliability of the used parcellation technique. A sensitivity analysis has been performed in [51] on real data and for MCMC JDE version, that assesses the reliability of this parcellation against a computationally heavier approach which tends, by randomly sampling the seed positions of the parcels, to identify the parcellation that retrieved the most significant activation maps. Still, it would be of interest to investigate the effect of the parcellation choice in the VEM context, and more generally to extend the present framework to incorporate an automatic online parcellation strategy to better fit the fMRI data while accounting for the HRF variability across regions, subjects, populations and experimental contexts. The current variational framework has the advantage to be easily augmented with parcel identification at the subject-level as an additional layer in the hierarchical model. Automatically identifying parcels raises a model selection problem in the sense of getting sparse parcellation (reduced number of parcels) which guarantees spatial variability in hemodynamic territories while enabling the reproducibility of parcel identification across fMRI datasets. More generally, a model selection approach can be easily carried out within the VEM implementation as variational approximations of standard information criteria based on penalised log-evidence can be efficiently used [52].
Appendix
A. Derivation of the VEM formula
We show here how to obtain the Variational E-steps using the properties of the Kullback-Leibler divergence without resorting to calculus of variation as usually done. We illustrate the approach for the derivation of the VE-H step (Eq. (8)). The following VE-steps can be derived similarly. Dropping the (r) and (r − 1) superscripts, the VE-H step is defined as
The definition (4) of function
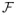 leads to
leads to
from which it follows that:
In the last equality above, we artificially introduced the exponential by taking the logarithm. We then denote by p̃ Hγ the distribution on h γ proportional to exp(Ep̃Ap̃Q[log p(Y, A, h γ, Q; Θ)]). The normalizing constant of the latter quantity is by definition independent of h γ so that
where KL(p Hγ || p̃ Hγ) is the Kullback-Leibler divergence between p Hγ and p̃ Hγ. From the KL divergence properties, it follows that the optimal p Hγ is p̃ Hγ which provides Eq. (8) as desired.
B. VE-H step
For the VE-H step, the expressions for and are:
| (14) |
| (15) |
with and denoting respectively the m and (m, m′) entries of the mean vector ( ) and covariance matrix ( ) of the current .
C. VE-A step
The VE-A step also leads to a Gaussian pdf for . The parameters are updated as follows:
| (16) |
where a number of intermediate quantities need to be specified. First, and where G is the matrix G = [g 1| … |g M] made of columns g m = X m h γ. The m-th column of G̃ is then also denoted by . Then, and is an M × M matrix whose element (m, m′) is given by:
D. VE-Q step
From p(A|Q) and p(Q) in Section II, it follows that the (a m, q m) couples correspond to independent hidden Potts models with Gaussian class distributions. It follows an approximation that factorizes over conditions: where is the posterior of q m in a modified hidden Potts model f, in which the observations ’s are replaced by their mean values and an external field { } is added to the prior Potts model . It follows that the defined Potts reads:
| (17) |
Since the expression in Eq. (17) is intractable, and using the mean-field approximation [41], is approximated by a factorized density such that if ,
| (18) |
where q̃ m is a particular configuration of q m updated at each iteration according to a specific scheme and .
E. M step
1. M-(μ, v) step
By maximizing with respect to (μ, v), Eq. (13) reads:
| (19) |
By denoting , and after deriving wrt μim and vim for every i ∈ {0, 1} and m ∈ {1 … M}, we get and .
2. M-vh step
By maximizing with respect to v h, Eq. (13) reads:
| (20) |
It follows the closed-form expression given by
| (21) |
For a more accurate estimation of v h, one may take advantage of the flexibility of the VEM inference and inject some prior knowledge about this parameter in the model. Being positive, a suitable prior can be an exponential distribution with mean :
| (22) |
Taking this prior into account, the new expression of the current estimate is: with
3. M-β step
By maximizing with respect to β, Eq. (13) reads:
| (23) |
Updating β consists of making further use of a mean field-like approximation [41], which leads to a function that can be optimized using a gradient algorithm. To avoid over-estimation of this key parameter for the spatial regularization, one can introduce for each βm, some prior knowledge p(βm; λ βm) that penalises high values. As in Eq. (22), an exponential prior with mean can be used. The expression to optimize is then given by:
| (24) |
After calculating the derivative wrt βm, we retrieve the standard equation detailed in [41] in which is replaced by . It can be easily seen that, as expected, subtracting the constant λ βm helps penalizing high βm values.
4. M-(L, Γ) step
This maximization problem factorizes over voxels so that for each j ∈
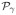 , we need to compute:
, we need to compute:
| (25) |
where . Finding the maximizer wrt ℓ j leads to (G̃ is defined in the VE-A step):
| (26) |
After calculating the derivative wrt ℓ j, we get . In the AR(1) case, with , we can then derive the following relationship:
| (27) |
where F 1 is a function linking the estimates and . The above formula is similar to that in [23, p.965, B.2], when replacing h γ by and a by .
Denoting and considering the maximization wrt , similar calculations lead to:
| (28) |
where F 2 is a function linking the estimates with and . Matrix is a M × M matrix similar to the matrix H̃ j introduced in the VE-A step. Its (m, m′) entry is given by .
Eventually, the maximization wrt ρj leads to , with and where has the same expression as without the (r) superscript. Matrices U 1 and U 2 are respectively M × M and N × N matrices defined as and . The derivative, denoted by Λj of Λj wrt ρj writes , where the entries of B and C are zero except (B)n , n which is 1 for n = 2 : (N − 1) and for (C)n , n +1 and (C)n +1, n which are −1 for n = 1 : (N − 1). The derivative, denoted by , of Λ̃j wrt ρj can be written as: where B̃ and C̃ are M × M matrices whose entries (m, m′) are respectively and . Eventually, the derivative wrt ρj leads to:
Then can be estimated as a solution of the fixed point equation .
Note that in the Gaussian noise case, the updating of the noise parameters reduces to the estimation of which simplifies into .
Footnotes
This acronym and other non standard ones used in the paper are also defined in Table I.
In the present context, for any condition m, .
.
The SNR is given by: .
MSEa∘m = E[||a∘ m − a m||2] = bias2(a∘ m) + var(a∘ m).
References
- 1.Ogawa S, Lee T, Kay A, Tank D. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci USA. 1990;87(24):9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Friston KJ, Holmes AP, Poline JB, Grasby PJ, Williams SCR, Frackowiak RSJ, Turner R. Analysis of fMRI time-series revisited. Neuroimage. 1995 Mar;2(2):45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- 3.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995 Oct;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 4.Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005 Jul;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Buxton RB, Frank L. A model for the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J Cereb Blood Flow Metab. 1997 Jan;17(1):64–72. doi: 10.1097/00004647-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 6.Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: the balloon model, Volterra kernels, and other hemodynamics. Neuroimage. 2000 Jun;12:466–477. doi: 10.1006/nimg.2000.0630. [DOI] [PubMed] [Google Scholar]
- 7.Buxton RB, Uludag K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. Neuroimage. 2004;23(Suppl 1):S220–S233. doi: 10.1016/j.neuroimage.2004.07.013. [DOI] [PubMed] [Google Scholar]
- 8.Riera JJ, Watanabe J, Kazuki I, Naoki M, Aubert E, Ozaki T, Kawashima R. A state-space model of the hemodynamic approach: nonlinear filtering of BOLD signal. Neuroimage. 2004;21:547–567. doi: 10.1016/j.neuroimage.2003.09.052. [DOI] [PubMed] [Google Scholar]
- 9.Lashkari D, Sridharan R, Vul E, Hsieh PJ, Kanwisher N, Golland P. Search for patterns of functional specificity in the brain: a nonparametric hierarchical Bayesian model for group fMRI data. Neuroimage. 2012 Jan;59(2):1348–1368. doi: 10.1016/j.neuroimage.2011.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time-series. Hum Brain Mapp. 1994;1:153–171. [Google Scholar]
- 11.Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci. 1996 Jul;16(13):4207–4221. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Handwerker DA, Ollinger JM, D’Esposito M. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage. 2004 Apr;21:1639–1651. doi: 10.1016/j.neuroimage.2003.11.029. [DOI] [PubMed] [Google Scholar]
- 13.Ciuciu P, Vincent T, Fouque A-L, Roche A. Improved fMRI group studies based on spatially varying non-parametric BOLD signal modeling. 5th Proc. IEEE ISBI; Paris, France. May 2008; pp. 1263–1266. [Google Scholar]
- 14.Badillo S, Vincent T, Ciuciu P. Impact of the joint detection-estimation approach on random effects group studies in fMRI. 8th Proc. IEEE ISBI; Chicago, IL. Apr. 2011; pp. 376–380. [Google Scholar]
- 15.Lindquist MA, Meng Loh J, Atlas LY, Wager TD. Modeling the hemodynamic response function in fMRI: efficiency, bias and mis-modeling. Neuroimage. 2009 Mar;45(1 Suppl):S187–S198. doi: 10.1016/j.neuroimage.2008.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Glover GH. Deconvolution of impulse response in event-related BOLD fMRI. Neuroimage. 1999 Apr;9(4):416–429. doi: 10.1006/nimg.1998.0419. [DOI] [PubMed] [Google Scholar]
- 17.Henson R, Rugg M, Friston K. The choice of basis function in event-related fMRI. Neuroimage (HBM’01) 2001 Jun;13(6):149. [Google Scholar]
- 18.Goutte C, Nielsen FA, Hansen LK. Modeling the haemodynamic response in fMRI using smooth filters. IEEE Trans Med Imag. 2000 Dec;19(12):1188–1201. doi: 10.1109/42.897811. [DOI] [PubMed] [Google Scholar]
- 19.Ciuciu P, Poline J-B, Marrelec G, Idier J, Pallier Ch, Benali H. Unsupervised robust non-parametric estimation of the hemodynamic response function for any fMRI experiment. IEEE Trans Med Imag. 2003 Oct;22(10):1235–1251. doi: 10.1109/TMI.2003.817759. [DOI] [PubMed] [Google Scholar]
- 20.Marrelec G, Ciuciu P, Pélégrini-Issac M, Benali H. Estimation of the hemodynamic response function in event-related functional MRI: Bayesian networks as a framework for efficient Bayesian modeling and inference. IEEE Trans Med Imag. 2004 Aug;23(8):959–967. doi: 10.1109/TMI.2004.831221. [DOI] [PubMed] [Google Scholar]
- 21.Kershaw J, Ardekani BA, Kanno I. Application of Bayesian inference to fMRI data analysis. IEEE Trans Med Imag. 1999 Dec;18(12):1138–1152. doi: 10.1109/42.819324. [DOI] [PubMed] [Google Scholar]
- 22.Makni S, Ciuciu P, Idier J, Poline JB. Joint detection-estimation of brain activity in functional MRI: a multichannel deconvolution solution. IEEE Trans Signal Processing. 2005 Sep;53(9):3488–3502. [Google Scholar]
- 23.Makni S, Idier J, Vincent T, Thirion B, Dehaene-Lambertz G, Ciuciu P. A fully Bayesian approach to the parcel-based detection-estimation of brain activity in fMRI. Neuroimage. 2008 Jul;41(3):941–969. doi: 10.1016/j.neuroimage.2008.02.017. [DOI] [PubMed] [Google Scholar]
- 24.de Pasquale F, Del Gratta C, Romani GL. Empirical Markov Chain Monte Carlo Bayesian analysis of MRI data. Neuroimage. 2008 Aug;42(1):99–111. doi: 10.1016/j.neuroimage.2008.04.235. [DOI] [PubMed] [Google Scholar]
- 25.Vincent T, Risser L, Ciuciu P. Spatially adaptive mixture modeling for analysis of within-subject fMRI time series. IEEE Trans Med Imag. 2010 Apr;29(4):1059–1074. doi: 10.1109/TMI.2010.2042064. [DOI] [PubMed] [Google Scholar]
- 26.Thirion B, Flandin G, Pinel P, Roche A, Ciuciu P, Poline JB. Dealing with the shortcomings of spatial normalization: Multi-subject parcellation of fMRI datasets. Hum Brain Mapp. 2006 Aug;27(8):678–693. doi: 10.1002/hbm.20210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Penny WD, Kiebel S, Friston KJ. Variational Bayesian inference for fMRI time series. Neuroimage. 2003 Jul;19(3):727–741. doi: 10.1016/s1053-8119(03)00071-5. [DOI] [PubMed] [Google Scholar]
- 28.Friston KJ, Mattout J, Trullijo-Barreto N, Ashburner J, Penny W. Variational free energy and the Laplace approximation. Neuroimage. 2007 Jan;34(1):220–234. doi: 10.1016/j.neuroimage.2006.08.035. [DOI] [PubMed] [Google Scholar]
- 29.Makni S, Beckmann Ch, Smith S, Woolrich M. Bayesian deconvolution fMRI data using bilinear dynamical systems. Neuroimage. 2008 Oct;42(4):1381–1396. doi: 10.1016/j.neuroimage.2008.05.052. [DOI] [PubMed] [Google Scholar]
- 30.Woolrich M, Behrens T. Variational Bayes inference of spatial mixture models for segmentation. IEEE Trans Med Imag. 2006 Oct;25(10):1380–1391. doi: 10.1109/tmi.2006.880682. [DOI] [PubMed] [Google Scholar]
- 31.Risser L, Vincent T, Forbes F, Idier J, Ciuciu P. Min-max extrapolation scheme for fast estimation of 3D Potts field partition functions. application to the joint detection-estimation of brain activity in fMRI. 2011 Dec;65(3):325–338. [Google Scholar]
- 32.Woolrich M, Ripley B, Brady M, Smith S. Temporal autocorrelation in univariate linear modelling of fMRI data. Neuroimage. 2001 Dec;14(6):1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- 33.Woolrich M, Jenkinson M, Brady J, Smith S. Fully Bayesian spatio-temporal modelling of fMRI data. IEEE Trans Med Imag. 2004 Feb;23(2):213–231. doi: 10.1109/TMI.2003.823065. [DOI] [PubMed] [Google Scholar]
- 34.Penny WD, Flandin G, Trujillo-Bareto N. Bayesian comparison of spatially regularised general linear models. Hum Brain Mapp. 2007 Apr;28(4):275–293. doi: 10.1002/hbm.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Penny WD, Trujillo-Barreto N, Friston KJ. Bayesian fMRI time series analysis with spatial priors. Neuroimage. 2005;23(2):350–362. doi: 10.1016/j.neuroimage.2004.08.034. [DOI] [PubMed] [Google Scholar]
- 36.Neal RM, Hinton GE. A view of the EM algorithm that justifies incremental, sparse and other variants. In: Jordan MI, editor. Learning in Graphical Models. Kluwer Academic Publishers; Dordrecht, Netherlands: 1998. pp. 355–368. [Google Scholar]
- 37.Beal MJ, Ghahramani Z. The variational Bayesian EM Algorithm for incomplete data: with application to scoring graphical model structures. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, West M, editors. Bayesian Statistics. Oxford University Press; 2003. pp. 453–464. [Google Scholar]
- 38.Goldsmith J, Wand MP, Crainiceanu C. Functional regression via variational Bayes. Electronic Journal of Statistics. 2011 Jan;5:572–602. doi: 10.1214/11-ejs619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Beal MJ. PhD thesis. Gatsby Computational Neuroscience Unit, University College; London: 2003. Variational Algorithms for Approximate Bayesian Inference. [Google Scholar]
- 40.Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. 2. Chapmann & Hall; London, UK: 2004. [Google Scholar]
- 41.Celeux G, Forbes F, Peyrard N. EM procedures using mean field-like approximations for Markov model-based image segmentation. Pattern Recognition. 2003 Jan;36(1):131–144. [Google Scholar]
- 42.Casanova R, Ryali S, Serences J, Yang L, Kraft R, Laurienti PJ, Maldjian JA. The impact of temporal regularization on estimates of the BOLD hemodynamic response function: a comparative analysis. Neuroimage. 2008 May;40(4):1606–1618. doi: 10.1016/j.neuroimage.2008.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pinel P, Thirion B, Mériaux S, Jobert A, Serres J, Le Bihan D, Poline JB, Dehaene S. Fast reproducible identification and large-scale databasing of individual functional cognitive networks. BMC Neurosci. 2007 Oct;8(1):91. doi: 10.1186/1471-2202-8-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Liu TT, Frank LR, Wong EC, Buxton RB. Detection power, estimation efficiency, and predictability in event-related fMRI. Neuroimage. 2001 Apr;13(4):759–773. doi: 10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- 45.Gruber O, Indefrey P, Steinmetz H, Kleinschmidt A. Dissociating neural correlates of cognitive components in mental calculation. Cereb Cortex. 2001 Apr;11(4):350–359. doi: 10.1093/cercor/11.4.350. [DOI] [PubMed] [Google Scholar]
- 46.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Stat Science. 1992;7(4):457–472. [Google Scholar]
- 47.Carbonetto P, Stephens M. Scalable Variational Inference for Bayesian Variable Selection in Regression, and its Accuracy in Genetic Association Studies. Bayesian Analysis. 2012;7:73–108. [Google Scholar]
- 48.Nummenmaa A, Auranen T, Hämäläinen MS, Jääskeläinen IP, Lampinen J, Sams M, Vehtari A. Hierarchical Bayesian estimates of distributed MEG sources: theoretical aspects and comparison of variational and MCMC methods. Neuroimage. 2007 Apr;35(2):669–685. doi: 10.1016/j.neuroimage.2006.05.001. [DOI] [PubMed] [Google Scholar]
- 49.Ciuciu P, Sockeel S, Vincent T, Idier J. Modelling the neurovascular habituation effect on fMRI time series. 34th Proc. IEEE ICASSP; Taipei, Taiwan. Apr. 2009; pp. 433–436. [Google Scholar]
- 50.Tucholka A, Thirion B, Perrot M, Pinel P, Mangin J-F, Poline J-B. Probabilistic anatomo-functional parcellation of the cortex: how many regions?. 11thProc. MICCAI, LNCS Springer Verlag; New-York, USA. 2008. [DOI] [PubMed] [Google Scholar]
- 51.Vincent T, Ciuciu P, Thirion B. Sensitivity analysis of parcellation in the joint detection-estimation of brain activity in fMRI. 5th Proc. IEEE ISBI; Paris, France. May 2008; pp. 568–571. [Google Scholar]
- 52.Forbes F, Peyrard N. Hidden Markov Random Field model selection criteria based on mean field-like approximations. IEEE Trans Pattern Anal Mach Intell. 2003 Sep;25(9):1089–1101. [Google Scholar]


