Electrocorticographic amplitude predicts finger positions during slow grasping motions of the hand

Abstract

Four human subjects undergoing subdural electrocorticography for epilepsy surgery engaged in a range of finger and hand movements. We observed that the amplitudes of the low-pass filtered electrocorticogram (ECoG), also known as the local motor potential (LMP), over specific peri-Rolandic electrodes were correlated (p < 0.001) with the position of individual fingers as the subjects engaged in slow and deliberate grasping motions. A generalized linear model (GLM) of the LMP amplitudes from those electrodes yielded predictions for positions of the fingers that had a strong congruence with the actual finger positions (correlation coefficient, r; median = 0.51, maximum = 0.91), during displacements of up to 10 cm at the fingertips. For all the subjects, decoding filters trained on data from any given session were remarkably robust in their prediction performance across multiple sessions and days, and were invariant with respect to changes in wrist angle, elbow flexion and hand placement across these sessions (median r = 0.52, maximum r = 0.86). Furthermore, a reasonable prediction accuracy for grasp aperture was achievable with as few as three electrodes in all subjects (median r = 0.49; maximum r = 0.90). These results provide further evidence for the feasibility of robust and practical ECoG-based control of finger movements in upper extremity prosthetics.

1. Introduction

It has been demonstrated recently that individuated finger and wrist movements, wrist rotations and grasp patterns of the hand can be deciphered from the recorded activity of multiple neurons in the motor cortex [1–5]. Similarly, neural decoding has been demonstrated using multiunit neuronal activity in monkeys and humans to control a cursor and a robotic arm [6–8] and to replicate the movements of individuated finger flexions and extensions [9]. While this augers well for the development of high throughput neuroprosthetics for the control of fully dexterous prosthetic and robotic devices, the suboptimal long-term stability and highly invasive nature of these recordings raise concerns about their practical use, at least in the near future. On the other hand, completely non-invasive neural signals such as the electroencephalogram (EEG) have been used to generate control signals of up to three degrees of freedom [10–18]. However, given its low bandwidth [19], it seems unlikely that the EEG contains relevant information that can be used to decipher the full plethora of dexterous hand movements. An alternative ‘middle ground’ may be the electrocorticogram (ECoG), consisting of cortical activity recorded at the surface of the brain (i.e. subdural or epidural) [20]. Compared to the EEG, the ECoG has higher spatial resolution on the order of millimeters, greater sensitivity for activity at higher frequencies and a higher signal-to-noise ratio [20]. While implantation of subdural ECoG electrode arrays for neuroprosthetics would require invasive surgery, the procedure does not necessitate penetration of the cortex as do microelectrode arrays. This less invasive ECoG approach could arguably reduce the risk associated with the surgical implantation, as well as the rate of long-term complications, both in terms of damage to the cortical tissue as well as signal stability and decoding stationarity.

Previous studies have shown that various features of the ECoG power spectrum are modulated in part by movement-related activity. For example, the power of oscillatory activity in the mu band (8–12 Hz) and the beta band (13–26 Hz) is suppressed (i.e., event-related desynchronization, or ERD), in association with movement onset [21–23] and maintenance [23]. Concurrently, there may be an event-related increase in power at higher frequencies, namely the gamma band (35–70 Hz) and ‘high gamma’ band (>70 Hz) [23, 24]. These higher frequency changes are spatially well localized over the areas of the sensorimotor cortex that are associated with the performed movements [23]. Activity in particular frequency bands have often been conceptualized to arise from changes in neural synchrony at different spatiotemporal scales [25, 26]. In addition to their use for functional brain mapping [23, 27–30], the aforementioned ECoG indices of motor cortex activation have been used to generate control signals of one [31, 32] or two degrees of freedom [33] during actual or imagined movements. ECoG signals have also been used to decode multiple classes of motor tasks such as tongue movements, lip protrusion and finger extension [34–36], hand and face movements [37, 38], and verbalization [38]. Brain–machine interfaces for the control of cursors on computer screens using ECoG activity have subsequently been developed by utilizing these principles [30, 39–42].

One disadvantage of most of these control schemes is that they rely principally on user training or ‘operant conditioning’, whereby the subject learns to modulate a control signal (e.g., the power in a specific frequency band), by engaging in a repeatable mental task that is often quite different from the outcome of that control. For control of prosthetic arms and robotic devices with multiple degrees of freedom, purely operant conditioned schemes might not be desirable. A more intuitive and scalable approach requires deciphering a subject’s native motor intent from observed neural signals. With rapid advancements in the field of upper extremity prosthetics, there is a need to develop methods to decipher the movements of individual fingers as well as dexterous hand movements (e.g., grasps and prehension modes). Decoding such a plethora of grasping and individual finger movements from the ECoG could form a basis for an intuitive closed loop BMI, which would minimize the burden of operant conditioning for control of biomimetic prosthetic limbs with higher degrees of freedom. However, until recently, there was limited evidence to suggest that ECoG signals contain information relevant to deciphering the kinematics of a complex and dexterous motor task.

In numerous studies in non-human primates engaged in individuated finger movements, neuronal firing rate modulation has been shown to occur in widespread spatial patterns [43, 44]. Functional magnetic resonance imaging (fMRI) studies in humans have confirmed the broad spatial representation of hand movements [45, 46], suggesting that the temporal modulation of ‘mesoscopic’ neural signals such as the ECoG, as well as the EEG and magnetoencephalogram (MEG), could also carry information related to these movements. Although there is some evidence that the EEG and MEG contain information related to finger movements [47–50], these are unlikely control signals for long-term and high throughput neuroprosthetics because of their low signal-to-noise ratio and, in the case of the MEG, the lack of portability.

Characteristic ECoG spectral changes have been reported during individual finger and hand movements [51]. In a recent report, repetitive finger tapping movements were classified successfully from the activity of the ECoG [52]. It has also been shown that there is a temporal correlation between repetitive tapping of individuated finger movements and the principal spectral components of a subset of ECoG electrodes over the motor cortex [53]. More recently, flexions of individual fingers have been decoded from the ECoG [54]. In these studies, spectral and temporal features of the ECoG served as the input signals to decoding algorithms that tracked the position of the arm [33], or fingers during repetitive tapping motions [54]. These aforementioned studies also reported that the amplitude modulation of the smoothed (i.e. low-pass filtered) ECoG signal, also referred to as the local motor potential (LMP) [33], correlated strongly with the time course of arm movements [33] and contributed significantly to the neural decoding of finger [54] and arm kinematics [33, 39]. Similar slow waves have been previously reported in the EEG [12].

In this study, we investigated the ECoG correlates f finger positions during slow and deliberate grasping movements of the hand in four human subjects with previously implanted ECoG grids with peri-Rolandic coverage. Firstly, we hypothesized that the LMP contained information relevant to finger positions during these grasping movements. Next, we developed generalized linear models (GLMs) using these LMPs, from selected ECoG electrodes, for decoding of the time course of finger positions during these slow movements. We also tested the robustness of these decoding models to variations in wrist angle, arm position and natural changes in attention and cognitive states across multiple sessions and days. Additionally, we investigated the effect of the number of ECoG electrodes on the decoding accuracy achievable by the GLMs. The results of this study provide further evidence that the human ECoG can be used to control bio-mimetic upper extremity prosthetics.

2. Experimental methods

2.1. Experimental subjects and data collection

The participants in this study were four subjects (two males, two females, aged 15–58 years) who had received a temporary implantation of an ECoG grid to help with the planning of the surgical treatment for intractable epilepsy. The size and location of the ECoG grid placement was driven solely by the subjects’ clinical need without any influence from this study. Only subjects who had some coverage over their motor cortex were considered as potential participants. All subjects gave informed consent and the study was approved by the Johns Hopkins Institutional Review Board (IRB). The ECoG grid arrays consisted of 88–114 platinum electrodes (Adtech Medical Instrument Corp., Racine, WI), 4 mm in diameter, placed 10 mm apart (center to center), embedded in a Silastic sheet and implanted on the cortical epipial surface. The study was conducted over one or two days over multiple experimental sessions lasting 1–2 hours, approximately 4–6 days after surgical implantation of the grids. The ECoG grids were typically removed within 7–8 days of implantation, at the time of resection surgery. ECoG activity was recorded using a 128-channel EEG amplifier (Stellate Systems Inc., Montreal). The ECoG was referenced to an inactive intracranial electrode, low-pass filtered at 300 Hz and digitized at 1000 Hz per channel. The DC offset was also removed from the signal. The kinematics of hand movement were digitized at 25 Hz by an 18-sensor data glove as depicted in figure 1 (CyberGlove, Immersion Corp.). Temporal synchronization between the CyberGlove (CG) and the ECoG data was maintained by simultaneously writing event markers, as well as time stamps, to the event channels of both data files (ECoG and CyberGlove). Patients A, B and D had electrode grids placed over the right hemisphere. Patient C had grids over the left hemisphere. The electrode locations were determined by co-registration of high-resolution pre-implantation MRI and post implantation CT using anatomical fiducials (subjects A–C) with Curry software (Neuroscan Inc.) or using volumetric co-registration (subject D) with Bioimage (Yale University) [55]. Electrode locations were also verified using surgical photographs, post-implantation x-rays (antero–posterior and lateral projections) and data from stimulation mapping. The placement of the grids in the four subjects is shown in figure 2. Routine clinical electrocortical stimulation mapping (ESM) data are also overlaid in figure 2, indicating the spatial locations of the electrodes that elicited motor and/or sensory responses during ESM. Table 1 summarizes the additional clinical information about the study participants. In all cases, the hand contralateral to the ECoG grid was used for recording kinematic data for the experiment.

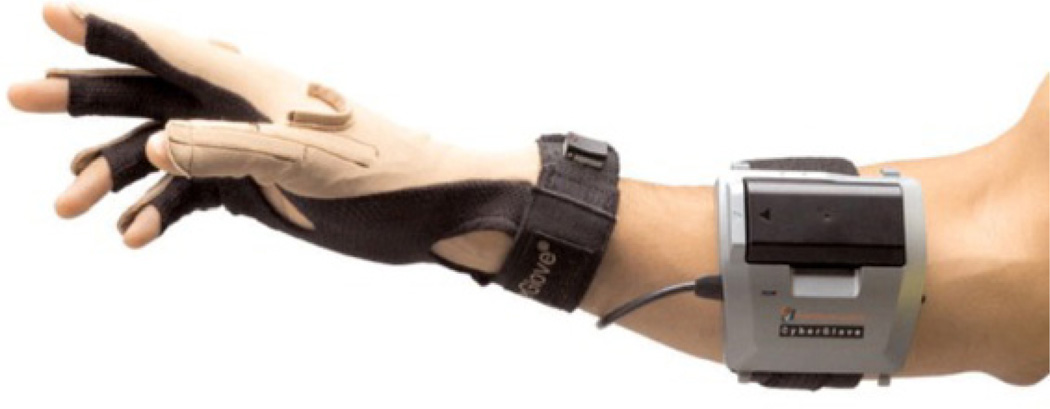
Figure 1.

Wireless CyberGlove (Immersion Corp.) for tracking finger and wrist motion. The 18-sensor track flexions and extensions of the distal and proximal interphalangeal joints, metacarpophalangeal joints as well as abductions and adductions of the fingers.

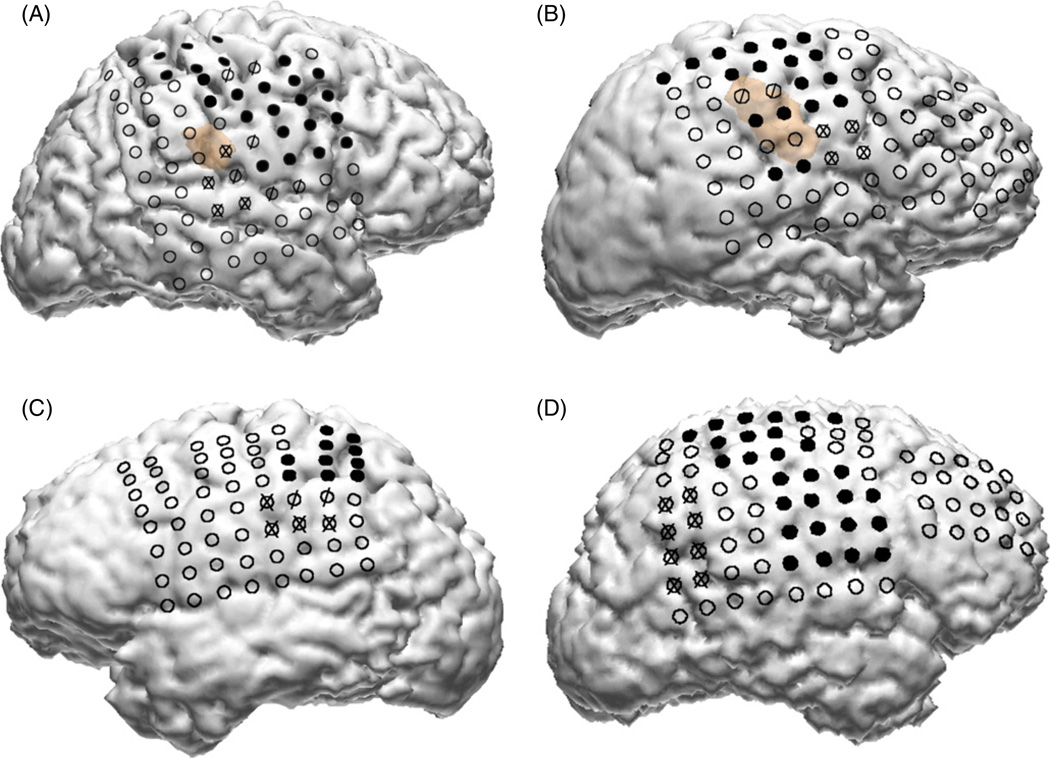
Figure 2.

Locations of ECoG grids in the four subjects. In all subjects some portion of the primary motor, supplementary motor and premotor cortices were covered by the grids. Electrodes depicted in solid black are those for which electrical stimulation mapping (ESM) elicited a primary motor response. Electrodes marked with an ‘X’ are those for which ESM elicited a sensory response. Electrodes marked with a ‘/’ had both motor and sensory responses during ESM. The brown background in subjects A and B depicts the location of cortical dysplasias in these subjects.

Table 1.

Summary and additional clinical information of study subjects.

Subject	Gender	Age	Handedness	ECoG coverage	Seizure focus/pathology	CyberGlove hand
A	Male	55	Right	Right frontal-parietal-temporal grid	Right parietal operculum/cortical dysplasia	Left
B	Female	20	Right	Right frontal-parietal-temporal grid	Right frontal-parietal operculum/cortical dysplasia	Left
C	Male	48	Right	Left frontal-parietal grids, left temporal strips	Left posterior superior frontal gyrus/post-traumatic encephalomalacia	Right
D	Female	15	Right	Right frontal-parietal grid	Right superior frontal sulcus/cortical dysplasia	Left

2.2. Experimental protocol

Subjects were seated comfortably on their hospital bed, with their forearm resting on a pillow placed on their side or lap. The elbow joint was typically semi-flexed in this configuration. The hand was held in a comfortable position, typically semi-prone. Care was taken that the hand did not touch the pillow or any other object during the movements. Subjects wore the data glove for the entire duration of the experiment and engaged in a variety of self-paced and verbally-cued hand movements. The data used for this study were a subset of the experimental sessions, and consisted of the movements to open or close the hand in a slow grasping motion. The range of excursion of the fingertips was as much as 10 cm across its entire range (from full flexion to extension). Although subjects were instructed to repeat an open–close movement, there were variations in the correlation between the individual fingers, the time spent in any given state (open–close or rest) as well as the speed of transition. Each session of data recording lasted between 60–180 s, and varied, depending on the investigators’ assessment of the subject’s attentiveness and ability to continue performing the task with a degree of repeatability. Each session typically consisted of 30–40 trials of verbally-cued open–close movements. Subjects were given breaks lasting 1–5 min between sessions. For subject A, data were recorded on two separate days.

2.3. Data exclusion criteria

Each session of kinematic data was first examined to exclude any segments that corresponded to non-compliance with the experiment. The segments were excluded if they fell into any of the following categories.

1. If the patient had an ictal episode (as indicated by the attending clinician).

2. If the patient stopped performing the designated hand movement for more than 10 s.

3. If the patient moved the hand away from its resting position on the pillow. This was noted during the experimental session and later confirmed by reviewing the video recording of the session. However, changes in wrist angle (such as moving from a semi-prone to a prone hand position) did not result in removing the data from analysis.

Only the segments of the data that qualified in the above categories were removed, and the remainder of a session was included in the analysis.

2.4. Correlation with the ECoG amplitude

The ECoG signal was re-referenced using a common average reference (CAR) filter [56]:

$$X{(t)}_n^{\mathrm{C}\mathrm{A}\mathrm{R}}=X{(t)}_n-\frac{1}{N}\sum _{k=1}^{N}X{(t)}_k,$$ (1)

where X(t)_n and $X{(t)}_n^{\text{CAR}}$ are the ECoG and CAR referenced ECoG amplitudes on the nth channel out of a total of N recorded channels.

We observed that the CAR filtered ECoG amplitude of some electrodes in all subjects correlated weakly with the time course of instantaneous finger joint angles (as digitized by the CyberGlove sensors). By low-pass filtering these signals using themoving average filter described in equation (2) we observed that these correlations became large and significant. In this study, we chose the size of the moving average window to be 2 s, which is analogous, albeit lower in frequency content, to the LMP described in two recently published studies [33, 54] which used moving average window sizes of 100 ms and 166 ms respectively:

$$\mathrm{L}\mathrm{M}\mathrm{P}{(t)}_n=\frac{1}{T}{\int }_{t-\frac{T}{2}}^{t+\frac{T}{2}}X{(\tau )}_n^{\mathrm{C}\mathrm{A}\mathrm{R}}.$$ (2)

We tested the hypothesis that individual LMPs, extracted from each ECoG electrode, were significantly correlated with the kinematics of the metacarpophalangeal and interphalangeal joints, as recorded by the respective CyberGlove sensors. We first calculated the pairwise correlations (Pearson’s r) between the instantaneous finger joint angles (as digitized by the CyberGlove) and each LMP. Features demonstrating large (r > 0.1) and significant correlation [57] (t-test for significance of Pearson’s r; p < 0.01, Bonferroni corrected for multiple pairwise comparisons) were considered tuned to the respective finger position. To account for neuromuscular transmission delays, this process was repeated at multiple ‘brain-to-hand’ time lags. An optimal time lag was chosen by maximizing the cumulative strength of the significant correlations between the LMPs and the CG sensor kinematics. The selection of the optimal LMP channels, time lag parameters, τ, and the decoding filter parameters (described in section 2.5 below) were consistently done by a five-fold cross validation in all sessions in all subjects whereby 80% of the data were used for training and 20% for testing the filters.

2.5. A generalized linear model for decoding finger kinematics

The kinematic data were de-correlated using principal component analysis (PCA). Each PC of hand movement was modeled as a linear combination of the LMPs:

$$Y_k(t)={\beta }_0+\sum _{n=1}^N{\beta }_n\mathrm{L}\mathrm{M}\mathrm{P}{(t+\tau )}_n,$$ (3)

where Y_k denotes the kth PC, β₀ through β_n denote the parameters of the model, and τ denotes the time delay between the LMP and hand kinematics. These parameters were estimated using the GLM framework [58] under the Gaussian distribution using a linear link function. The parameters of the model were calculated using the standard GLM functions in MATLAB (MathWorks Inc., Natick, MA). The LMPs, thus extracted from the respective ECoG channels, were rank ordered in terms of their correlations with the respective PCs. In order to assess the effect of the number of input electrodes on the prediction accuracy of the model, multiple GLMs were built using an increasing number of LMPs as inputs.

2.6. Robustness of the prediction filters across multiple sessions with variations in wrist angle and hand position

Unlike previous studies, in our experimental protocol there were no rigorous constraints on the arm position with respect to the subject. Typically, during the resting periods between experimental sessions, subjects re-adjusted their posture, hand position and elbow placement on the pillow, etc. Although there was no recording system to digitize these motions, the video recording of the session was carefully reviewed by at least two investigators. For every session, a gross assessment of wrist supination/pronation angle was made (e.g., semiprone, prone, etc), in addition to the hand position with respect to the first trial. In order to assess the robustness and stationarity of the decoding models across these variations, GLMs built on data from one session were tested on different sessions conducted on the same day as well as the following day, where applicable.

2.7. Evaluation statistics

All the GLMs were tested using a five-fold cross validation (with 80% of a session used for selecting the optimal LMP channels and GLM training, and 20% for testing). The correlation coefficient between the actual and model predicted kinematics was calculated. The significance of each correlation coefficient was tested using methods described in [57] (p < 0.01, Bonferroni corrected for multiple pairwise comparisons). We also tested the hypothesis that the error in prediction was zero (Wilcoxon signed rank test; p < 0.05). These hypothesis tests were repeated for each cross validation and with models built with different numbers of LMPs as inputs.

3. Results

3.1. Correlation between fingers

As a first step toward analyzing the kinematic data, we de-correlated the individual finger motions using PCA. In all the subjects, the first PC accounted for greater than 90% of the variability of finger positions. This first PC corresponded, in all subjects, to the slow opening and closing movements of the hand. The next five PCs each had almost exclusive contributions from individual finger position variations over and above the correlated open–close movement of the hand.

3.2. Correlation and tuning at multiple time lags

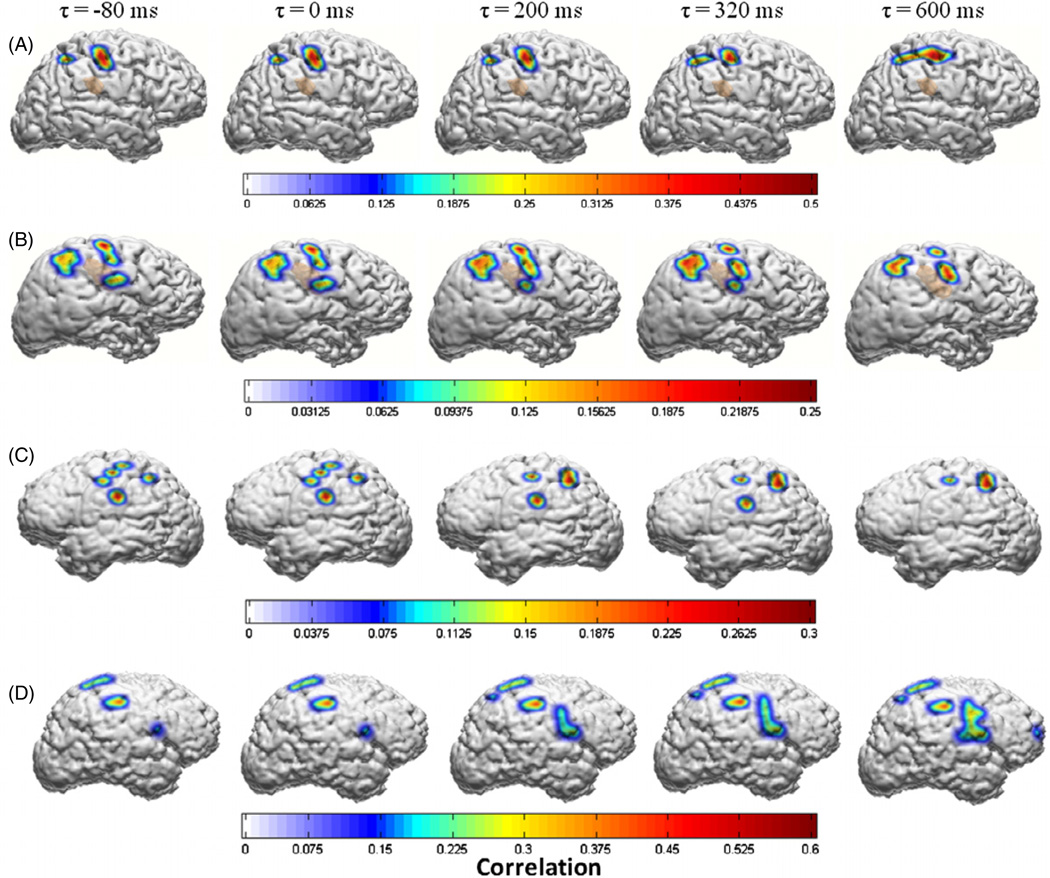
Figure 3 depicts the correlations between the LMP and the first PC of hand movements at different brain-to-hand time lags. Only significant correlation coefficients (p < 0.01, Bonferroni corrected) at multiple brain-to-hand lags (τ) are depicted. These figures were generated from a single session of kinematic data (2–3 min) for each subject. For building GLM decoders, subject specific optimal values of ‘τ’ were selected based on the maximal cumulative correlation across all LMPs for a given cross validation. The variations in the optimal brain-to-hand time lag across multiple cross validations in any given subject were negligible across multiple sessions, and in the interest of simplicity of the linear model, we chose a single delay parameter across all ECoG channels for each subject. This suggests that for the purposes of a closed loop BMI, an optimal time-lag parameter calculated on the basis of initial training data is likely to remain consistent.

Figure 3.

Spatial distribution of the correlations between the LMPs and the first principal component of finger movements as a function of temporal shift (τ) between the LMPs and the kinematic variable in subjects A, B, C and D, respectively. Only significant values of r (p < 0.01, Bonferroni corrected for multiple pairwise comparisons) are displayed. These figures were generated from a single session of kinematic data (2–3 min) for each subject. For building GLM decoders, subject specific optimal values of ‘τ’ were selected based on the maximal cumulative correlation across all LMPs.

3.3. Decoding accuracy within sessions

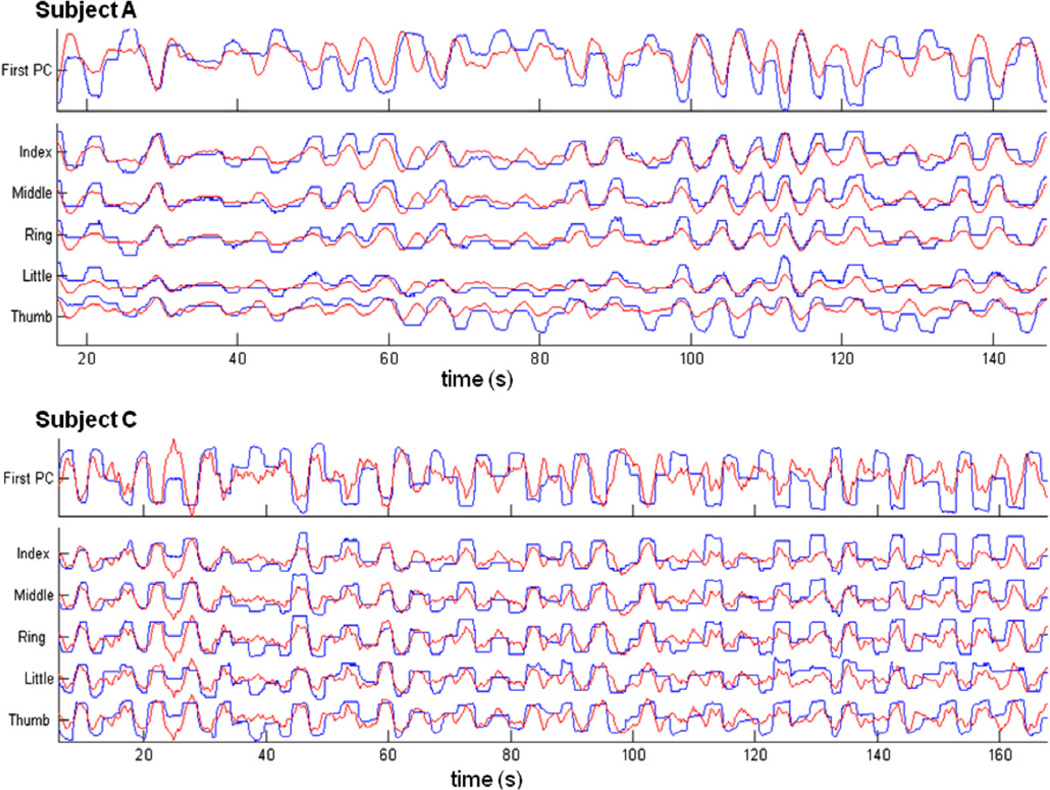
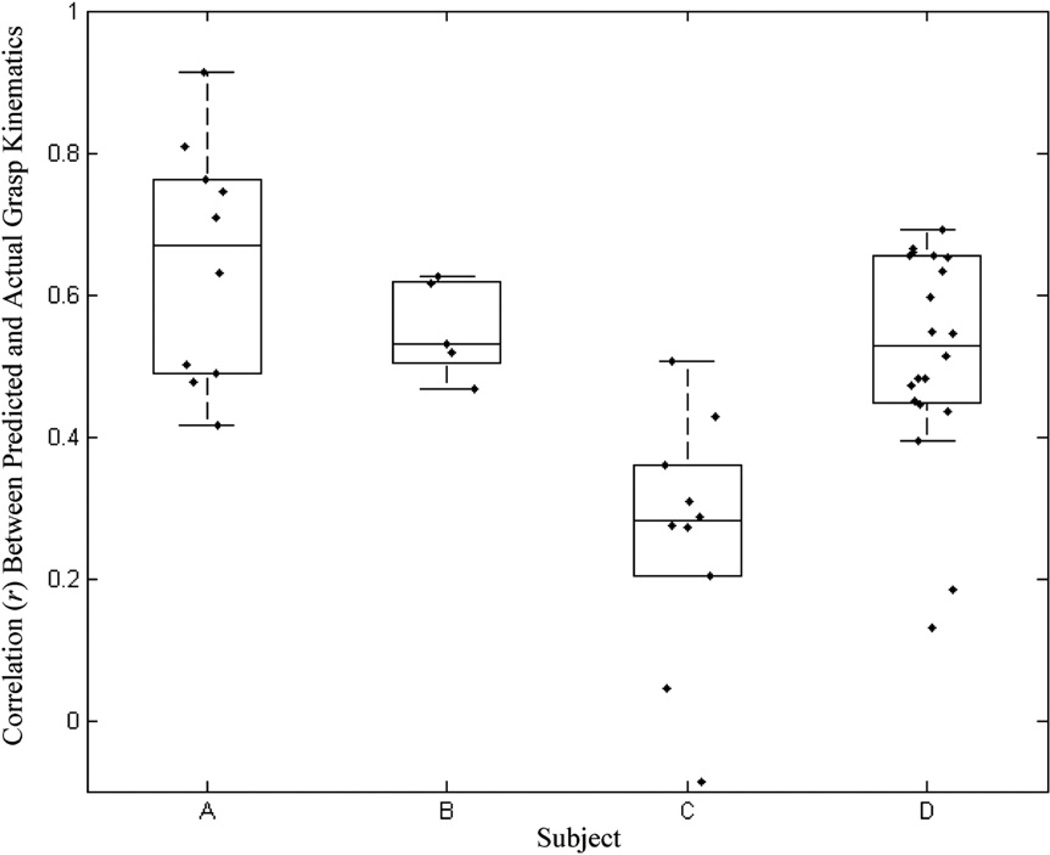
We trained and tested the decoding filters on individual sessions using a five-fold cross validation. Figure 4 shows some examples of the performance of the decoding filter in tracking the first PC of hand movements and the respective individual finger positions on segments of data that were not used for training the models. Figure 5 summarizes the decoding performances on all four subjects achieved by five-fold cross validations on all sessions. The median and maximum decoding correlations in each subject were (subject, median r, maximum r): (subject A, 0.67, 0.92); (subject B, 0.53, 0.69); (subject C, 0.20, 0.61); (subject D, 0.53, 0.74). All the prediction correlations were significant (p < 0.01, Bonferroni corrected for multiple comparisons). The error in prediction was not statistically significant in greater than 78% of sessions across all subjects (Wilcoxon signed rank test; p < 0.05).

Figure 4.

Examples of actual (blue) and predicted (red) finger trajectories in one session each for two high-performing subjects (A and C). The top trace in each plot shows the tracking performance of a linear decoding model to the first PC of finger movement. Subsequent traces show the tracking performance of linear decoding models of the individual fingers. In both these examples, models were trained on the first half of the data and tested on the second half.

Figure 5.

Summary of decoding performance in four subjects—A, B, C and D—with GLMs trained on data segments from the same session. Each data point represents the correlation (r) between the actual and predicted kinematics of the first principal component of finger movements. The boxplots surrounding the actual data points depict the median decoding correlation. The whiskers represent 1.5 inter-quartile ranges above and below the median.

3.4. Decoding accuracy across sessions and days

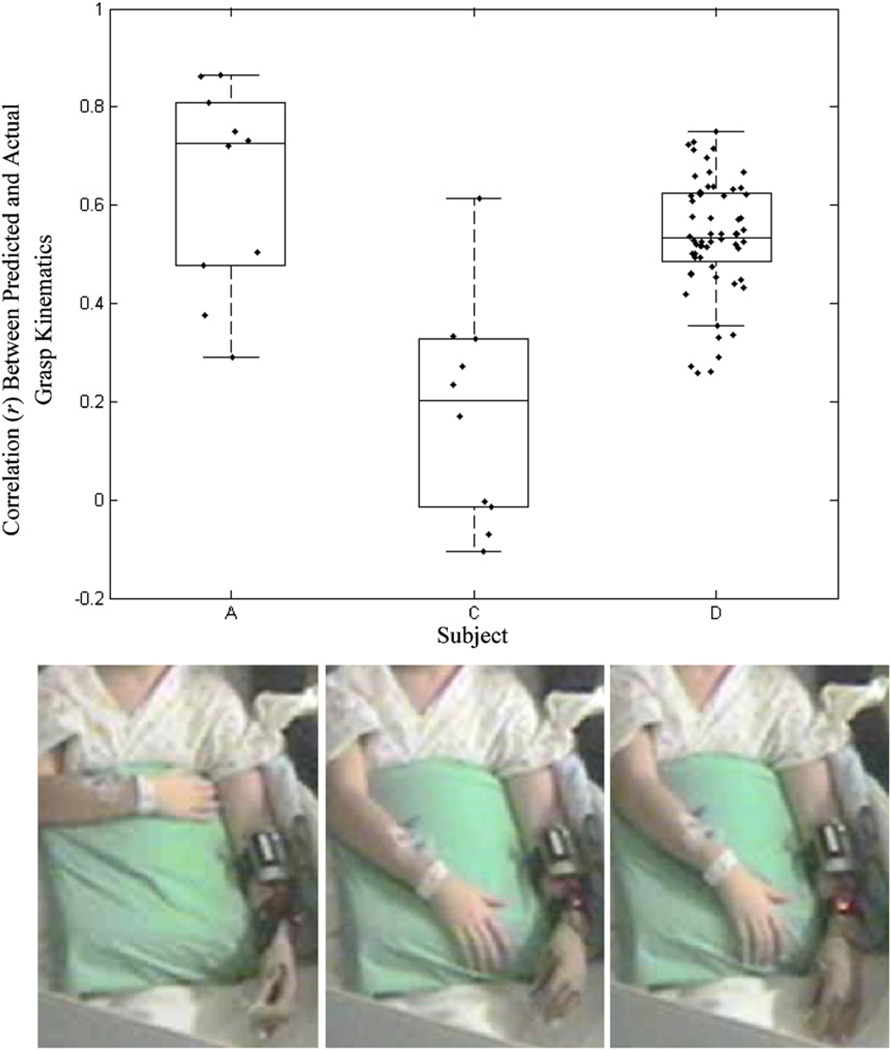
To test the robustness of the decoding filters across variations in the hand position, wrist orientation and natural variations in the level of arousal or attention, we trained the GLMs on a given session of data and tested their performance on data from different sessions (across days, where applicable). This was repeated for all permutations of available data trials in all subjects. Figure 7 summarizes the prediction correlations achieved in all subjects under these varying conditions. The insets show an example of variations in wrist angle between sessions. Although the prediction correlations were lower than those achieved by a decoder trained on a segment of the same session, they were large and significant (p < 0.01).

Figure 7.

(a) Decoding performance of GLMs trained and tested on different sessions with marked variations in wrist rotation, elbow flexion, forearm orientation and across multiple days. The inset pictures (b) depict an example of three separate sessions in subjects C. Note the change in the angle of wrist pronation. GLM decoders were trained on data from one trial and tested on a different trial. The boxplots show the median correlation between the actual and predicted kinematics of the first principal component of finger movements across all cross-trial permutations.

3.5. Minimum number of electrodes

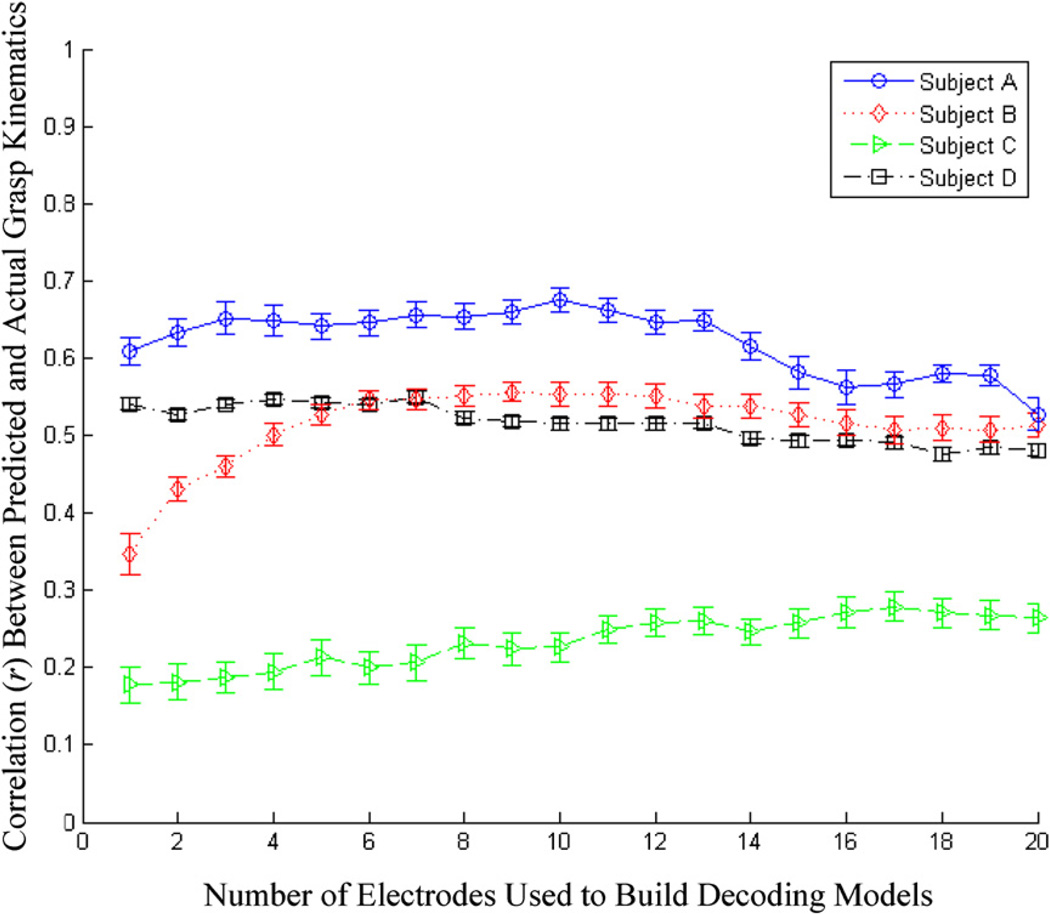
The available ECoG channels were rank ordered by correlation of the LMP to the kinematic variable. GLMs were built with increasing number of LMPs from this rank ordered list as input variables. Figure 6 summarizes the mean prediction accuracy achieved in all four subjects as a function of the number of ECoG channels used to build the models. It can be seen that decoding accuracies reached a maximum at around three to six electrodes, after which there was a saturation, or even degradation in performance of the filters. This could have been a result of the adding unrelated neural background activity.

Figure 6.

Decoding performance in all four subjects as a function the number of ECoG channels used in the respective decoding model. The LMPs were rank ordered in terms of their correlation with the finger movements and GLMs were built by dropping LMP channels from this list. The traces depict the mean decoding correlations between the actual and predicted kinematics with testing data, along with the standard error of the mean (error bars).

3.6. Electrodes chosen from specific cortical regions

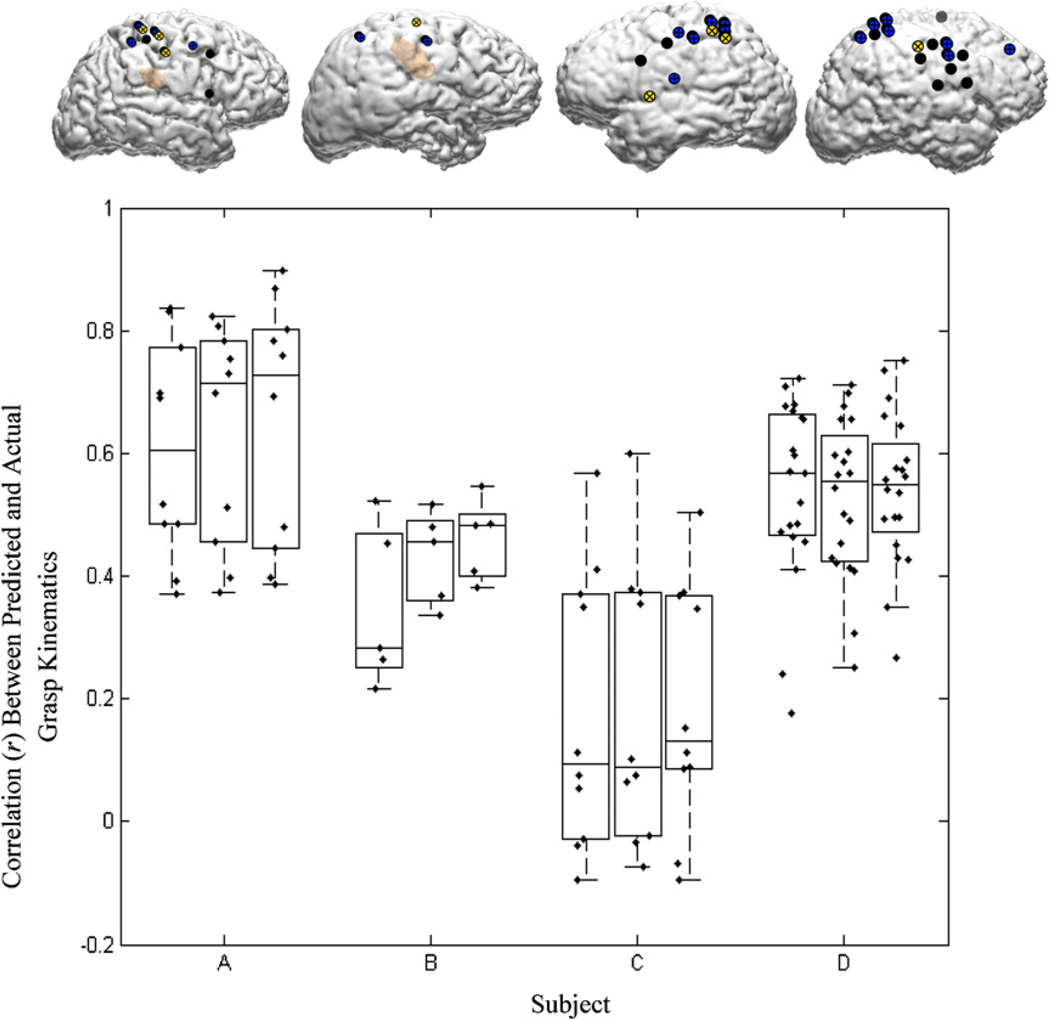
Figure 8 summarizes the decoding accuracies achieved by training GLMs on LMPs derived from one, two and three electrodes, respectively, over the motor cortex. The insets show the locations of the chosen electrodes. These decoding results are based on training and testing within each session (five-fold cross validation) for all the subjects. The error in prediction is non-significant in greater than 77% of the trials (Wilcoxon signed rank test; p < 0.05).

Figure 8.

Decoding accuracies achieved with one, two and three ECoG channels (left to right) for each subject. The first, second and third rank-ordered electrodes are depicted on the brain images (yellow = first rank-ordered electrode, blue = second rank-ordered electrode, black = third rank-ordered electrode). The boxplots show the distribution of decoding performances on individual segments of the data from five-fold cross validation, using increasing number of channels (plotted from left to right).

4. Discussion

In this study, we showed that the amplitude of the low-pass filtered ECoG signal (the local motor potential, LMP) correlates strongly with slow grasping motions of the hand and can be used to decode hand grasping movements under relatively unconstrained experimental conditions. The LMPs from a subset of ECoG electrodes demonstrated a large and significant correlation with finger kinematics. The LMP is a recently reported phenomenon that has been observed during two-dimensional movement trajectories of the arm [33], and has been shown to contain information related to finger flexions [54]. Our findings are consistent with these reports and expand them by showing that the LMP alone is sufficient for robust decoding of finger positions during slow grasping movements of the hand. The spatial distributions of the LMPs and their correlations with the kinematics of grasping motions of the hand were remarkably stationary across multiple sessions involving variations in wrist angle, elbow flexion and arm location. This enabled the development of robust linear decoding models that had good prediction accuracies (median r = 0.51, maximum r = 0.92), which are consistent across multiple sessions and days (median r = 0.52, maximum r = 0.86). Furthermore, we found that reasonable decoding accuracies for these movements could be achieved with as few as one to three ECoG electrodes over the peri-Rolandic cortex (median r with three electrodes = 0.49, maximum r = 0.90). It should be noted that subject C, who had a poor coverage of the motor cortex, as evidenced in figure 2, had a weaker decoding performance compared to the other three subjects. The robustness of the decoding models with even a limited number of electrodes, combined with the stationarity of the filters across variations in the position of the upper extremity, suggests the possibility of a practical ECoG-based brain–machine interface for control of upper extremity prosthetics.

The neural generators for the LMP are not known and further investigation is needed with concurrent measurements of neuronal spikes, local field potentials and the ECoG. Given the spatial distributions of the hand-movement relevant LMPs and their strong correlations with hand motions, it can be speculated that they are the direct result of the increase in population firing rates of cortical neurons in those locations. This is consistent with reports in primates [43, 44] and in fMRI studies in humans [45, 46] that show spatiotemporally distinct but focal increases in neuronal activation during movements related to the hand. It has also been reported previously that this phenomenon is distinctly different in its spatiotemporal tuning distribution from that of the traditional spectral power bands (i.e., mu, beta, gamma bands) [39]. These LMPs are slower changes that occur at modulation rates less than 1 Hz. It is therefore not surprising that the tuning of this phenomenon to faster hand movements including rapid finger motions is minimal. In our own data, collected from the same subjects, the LMP was not tuned to higher frequency movements beyond 0.5 Hz. Preliminary results from our group confirm [54] the tuning of high-frequency spectral components to the more dexterous and highly individuated finger movements, similar to the ones reported in [53].

It can be argued that the observed amplitude modulation evident in the LMP is an artifact resulting from induced noise in the ECoG channels, i.e. as a direct result of the hand movements. However, multiple factors suggest otherwise. Firstly, the ECoG was re-referenced using a common average reference filter, which tends to cancel out noise at low spatial frequencies. Secondly, the spatial distribution of the channels in which the LMP correlated well with hand movements is over motor cortical regions, which is an unlikely coincidence in all four subjects. Furthermore, the observed correlation between the LMP and movement was consistent only at frequencies of hand kinematics below 0.5 Hz, which would not be expected if it were an artifactually induced phenomenon.

4.1. Relevance to neuroprosthetics/brain–machine interfaces

Most previously reported BMIs based on ECoG or EEG signals utilize the modulation of sensorimotor rhythms such as the mu, beta and gamma rhythms [10–18]. Subjects gain volitional control over the spatiotemporal patterns of these rhythms based on extensive user training, often involving largely counterintuitive schemes that have no direct link with the end effector (such as the position of a cursor or the grasp aperture of a prosthetic device). There is little evidence to suggest that the temporal modulation of these higher-frequency components are directly correlated with a motor end effector. These purely operant-conditioned BMI control schemes might therefore involve a long training time and a counter intuitive mode of operation, especially when they involve control of prosthetics. Additionally, for control of motor prosthetics with high degrees of freedom, the decoding of the neural signatures of native motor intent is a desirable starting point. This study shows that it is possible to decode the continuous kinematics of slow grasping motions of the hand using the neural correlates of natural hand movements. This would arguably reduce the training time for control of a prosthetic device, and would enable an intuitive neural control scheme for prosthetics.

One surprising result of this study is the relative stationarity of the ‘brain-to-hand’ tuning, in the presence of variations in positioning of the upper limb, including wrist rotation, elbow flexion and arm abduction/adduction. Linear models trained on the kinematics of one session of data were able to predict the finger positions across different days and sessions (involving variations in the limb position and orientation). Additionally, there were arguably differences in the cognitive state as well as head orientation, eye gaze direction, etc. The fact that the decoding filters were robust to such variability has positive implications for the stability and specificity of the LMP toward hand and finger motions, especially toward the need for decoding finger movements independent of the state of the rest of the upper limb.

We were able to achieve reasonable correlations in predicting an important kinematic variable using only the signals from one or two electrodes located over the motor cortex. These decoding correlations were comparable to those that have been reported in other studies related to one- and two-dimensional movement trajectories [59]. Again, this bodes well for a practical neural interface that has a limited cortical footprint, similar to microelectrode arrays. Most ECoG studies have utilized signals from a large grid of electrodes. While this has understandably been driven by the availability of neural data in any given subject, it is clear that such an extensive grid of electrodes may not be feasible for long-term implantation, for driving a communication or a control device. While there are promising prospects of being able to decode the full plethora of dexterous hand movements from multiunit activity [1] or possibly from ECoG [53], one may envision a neural prosthetic that leverages penetrating electrodes for ‘finer decoding’, combined with a smaller number of larger ECoG electrodes for the decoding of ‘coarser’ movements. The advantage of the ECoG is its low impedance (compared to intra-cortical microelectrode arrays) and relative signal stability over a longer duration, even in the face of fibrosis and tissue reaction [60]. Additionally, for practical purposes, a low-frequency signal such as the LMP would be associated with a very low data bandwidth and computational complexity. Although our implementation was not based on a causal filter, it is clear that such a modification to this scheme for real-time implementation is trivial. A linear filter such as the one used here allows for an intuitive understanding of the contributions of various input space parameters and is easy to train and operate (a mere matrix multiplication in both cases, under the GLM). Such an algorithm is particularly well suited for full implementation in embedded electronics.

4.2. Limitations and future directions

One major limitation of current ECoG-based experimental studies is the fact that the electrode placement is often suboptimal, being driven solely by the clinical circumstances of the patient. The grids in our subjects had only partial peri-Rolandic coverage and were not consistent between subjects. Additionally, ictal episodes, either during or before the experimental sessions, can potentially compromise the quality of the ECoG data as well as the ability of the subject to concentrate on the given task. This could lead to marked non-stationarity in the pattern and rhythm of hand movements performed during the motor tasks. Although, theoretically, the neural signature of such atypical hand movements could have been captured by the decoder, they were few and sparse and in our opinion, contributed only to the degradation of decoding performance. This was especially true in subject C, where (in addition to sparse motor cortical coverage) the frequency and duration of self-cued hand movements were varied and non-stereotypical. Compared to similar experiments in non-human primates, there was poor control over the experimental constraints such as positioning of the subject, relative placement of the hand, and compliance to the instructions. Although this did elucidate the robustness of the filter to these variations, it is likely that we lost repeatable and highly controlled neural signatures corresponding to highly decorrelated finger motions. Another factor to recognize when interpreting this study is that, unlike the intended beneficiaries of BMIs, the subjects of this study had intact upper limbs and no known motor deficits. In individuals with severe paralysis or amputation, it might be argued that the signal patterns might differ from the sample population studied here. While we do agree that there might be important differences in the topography and reactivity of ECoG signals between the two populations, e.g. due to reorganization and plasticity, it has been shown in numerous studies in humans that subjects with amputations or limb weakness are able to achieve BMI control by modulating neural populations that would otherwise participate in natural limb movements [6, 61, 62].

The goal of offline decoding is to ultimately enable subjects to achieve closed loop control of a BMI. In this case, the ability to decode the kinematics of continuous hand and finger motions using a GLM makes this a promising first step toward closed loop control of individual fingers of a neurally controlled upper extremity prosthetic device. In this study, we have been able to decode the time course of finger positions during slow, unconstrained grasp movements. This was achieved using a linear weighted sum of the ECoG LMP alone, showing that the LMP alone contains sufficient information for the same. Furthermore, this decoding was surprisingly robust to variations in the position and orientation of the wrist and forearm across multiple sessions, and a reasonable decoding accuracy could be achieved with as few as one to three electrodes over the peri-Rolandic areas. This combination of factors, such as the minimal number of electrodes required, robustness across sessions, computational simplicity and ease of potential implementation in embedded electronics, auger well for a practical EcoG-based neuroprosthetic for control of biomimetic and dexterous upper extremity prosthetic.