Temperature of the Magnetic Nanoparticle Microenvironment: Estimation from Relaxation Times

Abstract

Accurate temperature measurements are essential to safe and effective thermal therapies for cancer and other diseases. However, conventional thermometry is challenging so using the heating agents themselves as probes allows for ideal local measurements. Here, we present a new noninvasive method for measuring the temperature of the microenvironment surrounding magnetic nanoparticles from the Brownian relaxation time of nanoparticles. Experimentally, the relaxation time can be determined from the nanoparticle magnetization induced by an alternating magnetic field at various applied frequencies. A previously described method for nanoparticle temperature estimation used a low frequency Langevin function description of magnetic dipoles and varied the excitation field amplitude to estimate the energy state distribution and the corresponding temperature. We show that the new method is more accurate than the previous method at higher applied field frequencies that push the system farther from equilibrium.

1. Introduction to temperature measurements using magnetic spectroscopy of Brownian motion

Magnetic nanoparticles (MNPs) are used as drug delivery carriers (Berry, C.C., 2009, Fay, F. and Scott, C.J., 2011, Shenoi, M.M. et al., 2011) and thermal therapy agents (magnetohypertermia, ablation) in the treatment of cancer (Thiesen, B. and Jordan, A., 2008, Jordan, A., 2009, Mithun M Shenoi, M.M. et al., 2011, Shenoi, M.M. et al., 2011, Weaver, J.B., 2012, Johannsen, M. et al., 2010). Thermal therapies require accurate monitoring of the temperature of the MNPs for optimal and consistent results.

Temperature measurements of the microenvironment surrounding the MNPs are challenging. There are few noninvasive methods and even fewer capable of measuring temperature in vivo. A number of MRI related temperature measurement methods (Rieke, V. and Butts Pauly, K., 2008) have been developed but in practice, therapies that use magnetic fields to heat the MNPs cannot function in the strong static field required by the MRI.

Temperature measurements of the MNPs themselves can be achieved through magnetic spectroscopy of nanoparticle Brownian motion (MSB) (Weaver, J.B. et al., 2008, Rauwerdink, A.M. and Weaver, J.B., 2010). MSB should be possible for in vivo application with nanogram amounts of MNPs because it measures the same signals as the already well validated method of magnetic particle imaging (MPI) (Gleich, B. andWeizenecker, J., 2005, Weizenecker, J. et al., 2007, Weizenecker, J. et al., 2009, Ferguson, R.M. et al., 2012, Ferguson, R.M. et al., 2011, Ferguson, R.M. et al., 2009). However, the primary advantage of MSB measurements of temperature is that it should be possible to measure the temperature during heating using the same alternating field used to heat the MNPs. The previously reported method (Rauwerdink, A.M. et al., 2009, Weaver, J.B. et al., 2009) varies the amplitude of the applied magnetic field to produce calibration data for all subsequent MSB measurements during heating. We describe an alternative method of producing calibration data that is more accurate at high frequencies in this paper. The alternative method varies the frequency of the applied field to generate calibration data used to produce temperature estimates from subsequent MSB measurements during heating. We show that the accuracy of the two methods is determined by the relevance of the models used to describe the magnetization in the two methods. The previously described method uses a steady-state model appropriate when the MNPs magnetizations move much more quickly than the magnetic field changes. The new method uses a dynamic model appropriate when MNPs magnetizations move more slowly than the field changes. We have compared the methods quantitatively and present their relative strengths and weaknesses for monitoring the temperature during thermal therapies.

The previously reported MSB temperature measurement method (Weaver et al. 2009, Rauwerdink et al. 2009) relies on the dependence of the average MNP magnetization on the ratio of the field strength to the temperature. This functionality derives from the Langevin function which approximates the magnetization under Maxwell-Boltzmann statistics

$$\langle M\rangle \approx \text{coth}(\frac{\mu B}{k_{B}T})-\frac{K_{B}T}{\mu B}$$ (1)

with μ the magnetic moment of the particles, B the applied magnetic field, T the absolute temperature and k_B Boltzmann’s constant. Maxwell-Boltzmann statistics assume the magnetizations of the MNPs are in equilibrium all the time. The nanoparticles are driven to oscillate by a sinusoidally varying applied field. For a given temperature, magnetization data are recorded for a set of excitation field amplitudes of order 10mT. Subsequent changes in temperature can be estimated from changes in the data. When the temperature is different, the magnetization retains the same value if the field strength is adjusted accordingly. We refer to this as ‘scaling’ the amplitude, and call the method the MSB ‘amplitude sweep method’. If the temperature change is unknown, the scaling factor can be found to make two data sets equal, and thus the temperature change can be inferred. Temperature estimates using the amplitude sweep method have shown good accuracy, 0.3°C, over temperatures ranging from 20–50°C (Weaver, J.B. et al., 2009). The method is independent of particle concentrations and sizes in this biologically relevant regime. However, the approach assumes there is time for the MNPs to reach equilibrium at each point during the sinusoidal applied field. That is only true when the relaxation is very fast compared to the period of the applied field (Kubo, R., 1966). The relaxation time characterizes the rotational mobility of the MNP magnetizations and quantifies the retention of the MNP alignment after an applied field is removed. Relaxation is accomplished by two mechanisms: physical rotation (Brownian) or internal magnetic realignment (Néel). Relaxation effects dominate equilibrium mechanics as the frequency increases (Martens, M.A. et al., 2013, Reeves, D.B. and Weaver, J.B., 2012, Weaver, J.B. and Kuehlert, E., 2012, Weizenecker, J. et al., 2010).

At higher frequencies, it should still be possible to estimate temperature through the relaxation time because it also depends on temperature. Both Brownian and Néel mechanisms are affected by the temperature but by selecting large particles (100nm diameters), we can ensure Brownian relaxation is dominant. Reducing the complexity to Brownian relaxation makes it simpler but a similar method is possible for the Néel mechanism. The Brownian relaxation time was defined by Einstein (Einstein, A., 1905):

$$\tau =\frac{3\eta V_H}{K_{B}T},$$ (2)

where μ is the solution viscosity, and V_H is the hydrodynamic volume of the particles. In the present work, a different MSB approach to measuring temperature is proposed that is based on the Brownian relaxation time. The relaxation time has been measured quantitatively using MSB (Weaver, J.B. and Kuehlert, E., 2012). The relaxation time can be simulated and experimentally determined, and creates a direct connection between the magnetization dynamics and the parameters of the particles’ environment, namely: temperature, and viscosity.

The relaxation time is found as well from another scaling relationship as the magnetization depends on a product of the frequency of oscillation and the relaxation time. If the relaxation time changes, one only has to adjust the frequency by the correct amount to realign data with the data of previous relaxation times. Accordingly, in these experiments, a set of frequencies is used so we call the method the `frequency sweep method’. The advantage of the frequency sweep method is that its accuracy improves with increasing frequency compared to the accuracy of the amplitude sweep method that degrades with increasing frequency, as the equilibrium approximation weakens with the increase in frequency. In this paper, we concentrate on a range of temperatures related to clinical applications, from 21.5–50°C, including landmarks such as normal body temperature range (37°C, 39.89°C) and thermal therapy temperatures (hyperthermia 42–45°C, thermoablation >50°C), and we show that the new relaxation time measurements can determine the temperature of MNPs with an accuracy of 0.42°C.

2. Methods

When an oscillating field is applied to a sample of MNPs, the field works to align the MNPs against thermal fluctuations. The magnetization of the MNPs is thus not a perfect sinusoid, but rather a distorted one, due to these thermal effects. MSB measures the harmonics of the magnetization produced by the MNPs (traditionally the ratio of the 5^th over the 3^rd harmonics as it is concentration independent), and quantifies the balance between the magnetic forces that try align the MNPs and their rotational Brownian motion that tend to randomize their directions. For short relaxation times, the MNPs saturate quickly, and a sharp corner in the magnetization is produced. For longer relaxation times, the approach to saturation is smoother and thus higher harmonics are reduced, so the ratio decreases.

2.1. Experimental determination of the MNPs relaxation time

The MSB method used to estimate MNP relaxation time (Weaver, J.B. and Kuehlert, E., 2012) rests on the form of the magnetization; it depends monotonically on the product of frequency and relaxation time. The MSB harmonics, which express the magnetization in the frequency domain, also depend on this product. That means the harmonics remain the same if the relaxation time increases and the frequency decreases by that same factor. First, the harmonics are recorded over a set of frequencies from MNPs in a reference state with a known relaxation time to generate a calibration curve. Then, when the state is altered, the corresponding change back onto the calibration curve determines the change in the state. If only a single variable, i.e. temperature, is adjusted, the data are shifted by a single `scaling factor’—the amount the relaxation time changed. In a realistic measurement, the new state is unknown, so a least squares map between the initial and final curves determines the scaling factor, and thus the change in the relaxation time.

2.2. Experimental Apparatus

The data are taken with a spectrometer similar to the one previously described by Weaver et al. (Weaver, J.B. et al., 2008), (Weaver, J.B. and Kuehlert, E., 2012). A sinusoidal voltage generated by a phase-locked amplifier (Stanford Research Systems, Sunnyvale, CA) was amplified (QSC PL 236, QSC Audio Products, Costa Mesa, CA) and placed across a resonant coil to produce the applied field. The resonant frequency of the coil was varied by adding different capacitors in series with the coil; the switching was done using a relay interface device (USB-ERB24, Measurement Computing, Norton, MA). The capacitors led to seven resonant frequencies: 290, 510, 755, 1050, 1270, 1890, and 2110 Hz. An in depth description of the apparatus, as well as its diagram can be found in (Weaver, J.B. and Kuehlert, E., 2012).

For the frequency sweep data collection, the amplitude of the applied magnetic field was set at 10 mT/μ₀. To compare the accuracy of the present temperature measurements with data obtained using the previously reported amplitude based measurements method (Weaver, J.B. et al., 2009) amplitude sweeps were conducted at 5,7.5,10,12.5 and 15 mT/μ₀, respectively.

The time derivative of the MNP magnetization was measured using a solenoid pickup coil. The background current generated in the pickup coil by the drive field was canceled by a balancing coil wound oppositely and placed in series with the pickup coil. The induced voltage in the pickup coil determines changes in the particle magnetization and the 3^rd and 5^th harmonics of this signal can be measured using the lock-in amplifier. The iron detectability limit of the current setup was ~20µg Fe.

2.3. Simulations

Simulations of rotating magnetic nanoparticles have been achieved previously using several schemes. The Langevin equation approach uses a stochastic differential equation in order to model classical rotating dynamics with the addition of thermal fluctuations introduced by Brownian motion (Reeves, D.B. and Weaver, J.B., 2012). The Langevin equation for a single particle magnetization is given by

$$\frac{d\stackrel{\rightharpoonup }{\mu }}{dt}=\frac{1}{6\eta V_H}(\stackrel{\rightharpoonup }{\mu }\times \stackrel{\rightharpoonup }{B}+\stackrel{\rightharpoonup }{N}(t))\times \stackrel{\rightharpoonup }{\mu }.$$ (3)

where μ is the magnetic moment of the particles, V_H is the hydrodynamic volume of a particle, η is the dynamic viscosity of the media and B is the applied magnetic field. The fluctuations are modeled by N(t) as a perfectly time and space uncorrelated Markovian white noise force. This is a Gaussian distribution with zero mean and standard deviation determined by the temperature T, k_B the Boltzmann constant, the volume and the viscosity as,

$$\langle \stackrel{\rightharpoonup }{N}(t)\rangle =0,\langle \stackrel{\rightharpoonup }{N}(t)\stackrel{\rightharpoonup }{N}(t\text{'})\rangle =12K_{B}T\eta V_H\delta (t-t\text{'}).$$ (4)

We assume the particles have a spherical shape, hence V_H can be calculated based on the measured hydrodynamic diameter of the nanoparticles. The values for the dynamic viscosity at temperature for PBS were taken from published tabulated data for water (Kestin, J. et al., 1978). Using the Stratanovich interpretation of a stochastic integral, an Euler-Marayuma numerical scheme is employed (Gard, T.C., 1998). By simulating many trajectories, the average magnetization can be developed. The harmonics of the magnetization are found from a discrete Fourier transform, and numerical simulations can be used for comparison to experiments. Eventually, using harmonic ratios, the relaxation time of the MNPs can be simulated in analogy to the experiments.

2.4. Nanoparticle samples

The MNPs used in this study are Hydroxyethyl starch (HES) coated (100nm) iron oxide nanoparticles manufactured by Micromod Partikeltechnologie (GmbH, Germany). They consist of a magnetic core approximately 50nm in diameter formed of a conglomerate of magnetite crystals coated with starch that is bound electrostatically to the magnetic core. Their properties, including transmission electron microscope images, can be found in (Bordelon, D.E. et al., 2011). The particles measured hydrodynamic diameter size is approximately 113nm (Malvern ZetaSizer Nano ZS, Malvern Instruments Ltd, UK) and their manufactured iron concentration is 27mg/ml.

The samples used in the study consist of 20µl of MNPs, suspended in 200µl phosphate buffered saline (PBS) media containing 0.05% Tween 20 as surfactant. The suspensions were placed in silicone coated 2ml Eppendorf tubes. The surfactant and silicone coating of the tubes prevented the adherence of the MNPs to the tube walls that degrades the signal.

3. Results and discussion

3.1. Experimental data

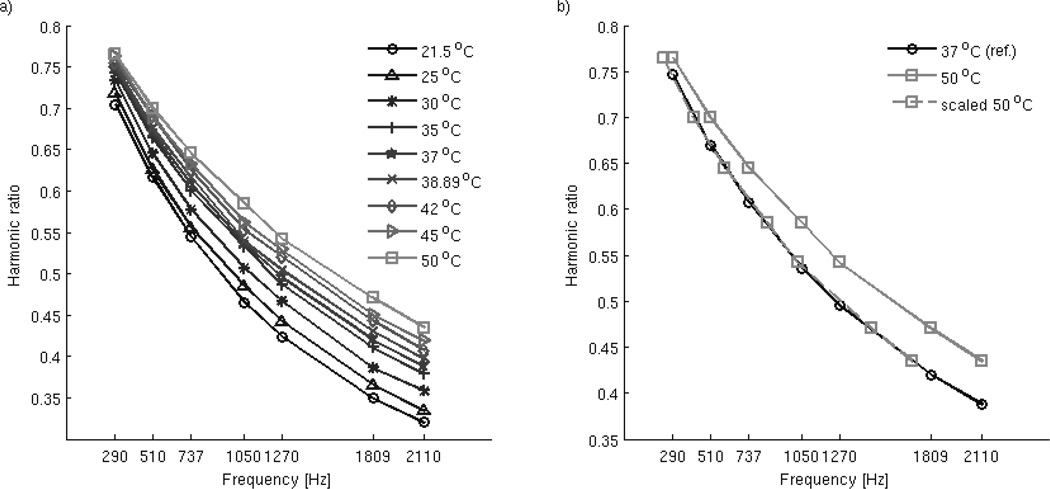
The MNP spectra, shown in Figure 1a), were measured at a range of temperatures, from 21–50°C in 5°C increments, including landmarks such as normal body temperature range (37°C, 39.89°C) and common hyperthermia treatment temperatures (42, 45°C). Before measurements, the pick-up coil was warmed up to a temperature of 25°C and maintained during data collection by water cooling (water temperature was maintained at 20±.5°C. The sample was placed in the coil and a single harmonic at a single frequency was measured, amounting to ~2s, with slight variations due to the time required to remove the sample from the coil. Then the sample is returned to the dry bath for 2 minutes before the next measurement to minimize heat exchange between sample and the coil and allow for temperature equalization of both sample and coil.

Figure 1.

Dependency of the harmonic ratios of the MNP sample with temperature (a), and example of the goodness of fit of scaling the harmonic ratio with the relaxation time for two temperature values (b).

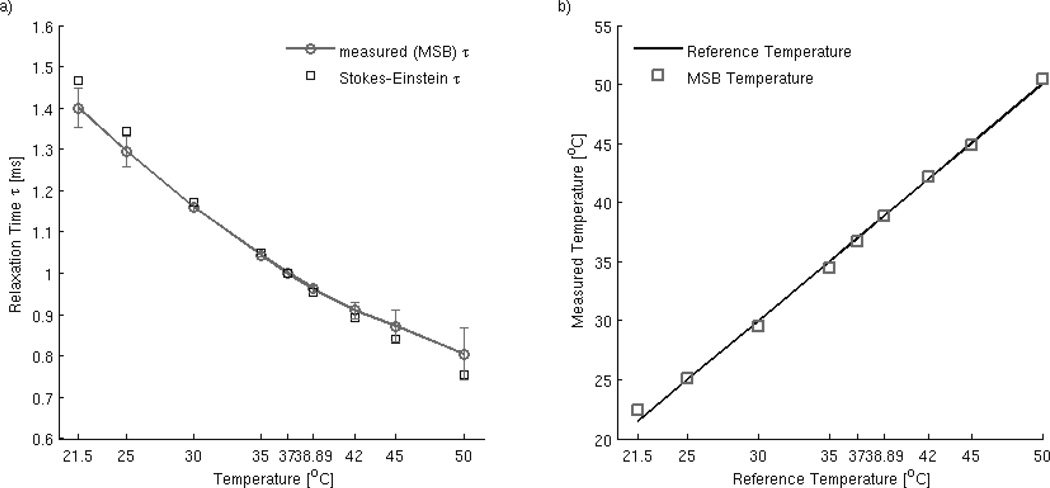
As mentioned previously, we used normal body temperature as the reference state of the MNPs. Knowledge of the harmonic ratio values at different temperatures (termed altered states) lets us compute the corresponding shift in the frequency range that allows us to scale the altered values back to the reference state by numerical interpolation (Figure 1b). The corresponding calculated frequency shift is the relaxation time relating the current temperature state to the reference temperature values. The relaxation time values calculated from the measured MSB harmonic ratios are listed in Table 1. The reference temperature was 37°C for the simulated data.

Table 1.

Relaxation time values comparison: Brownian relaxation time predicted values and MSB measurement calculated values.

Temperature (°C)	Brownian Relaxation Time	Relaxation Time from MSB measurements	Error (%)
21.50	1.4664	1.4005	4.4940
25	1.3428	1.2949	3.5672
30	1.1713	1.1610	0.8794
35	1.0481	1.0436	0.4293
37*	1.0000	1.0000	0.0000
38.89	0.9551	0.9625	0.7748
42	0.8931	0.9105	1.9483
45	0.8401	0.8727	3.8805
50	0.7539	0.8051	6.7914
		Error Std. (%)	2.2878
		Error Mean (%)	2.5294

^*reference temperature

A direct comparison between relaxation times computed from Einstein’s theoretical formulation given by eq. (2) and the MSB measured data is pictured in Figure 2a). The mean error between the experimental values and the theoretical values is 2.53% (standard deviation of error 2.29%). We used the relaxation time calculated from measured data and listed in Table 1 to estimate the temperature using eq. (2). The MSB estimate of temperature and the reference temperature of the sample is shown in Figure 2b). This reference temperature was the thermometer readout of the dry bath at a time approximately 2–3s prior to the MSB data collection. The mean error value and the standard deviation of the error between the temperatures are 1.15% and 1.25% respectively. This corresponds to an accuracy of 0.42°C, for the chosen range of frequency. The value is greater than the accuracy reported for the amplitude method (0.3°C), but as discussed below the current method shows a decrease in error with higher frequency values.

Figure 2.

a) Comparison between the relaxation time calculated from MSB measured harmonic ratios and the values predicted by Einstein’s formulation. The mean error value is 2.5%; b) Accuracy of the frequency sweep method by comparison with reference temperature values (thermometer readouts of the sample) set in the dry bath approximately 2–3s before the MSB measurements take place).

3.2. Comparison of MSB temperature measurement methods: frequency sweep and amplitude sweep method

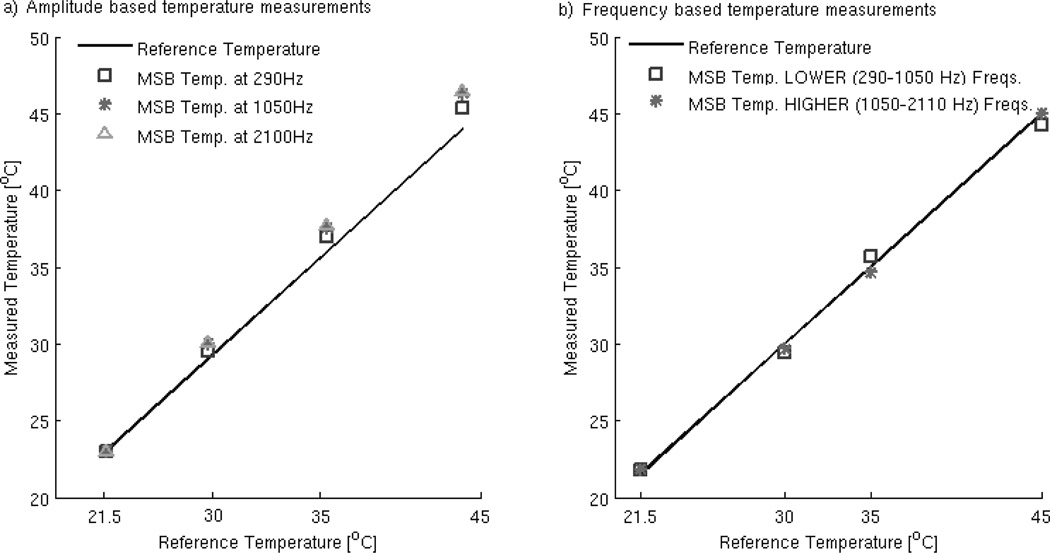
The MSB frequency sweep temperature measurement method was experimentally validated in the previous section. It can also be compared to the MSB amplitude sweep method of measuring temperature. A study of the experimental accuracy of the two methods comparing measured temperatures and reference values is illustrated in Figure 3. Amplitude sweeps (5–15mT, with 2.5mT increments) were measured at three frequencies: 290 Hz, 1050 Hz and 2110 Hz. These amplitude and frequency values included the highest and lowest implemented on the apparatus. The temperatures used were 21.5, 30, 35 and 45°C, and 21.5°C is the reference for computing the scaling factors. The lowest value was chosen as the reference in particular to monitor the behavior of errors with temperature increase. As illustrated in Figure 3a), the results display an increase in error values with increasing frequency as well as increasing temperature. The mean and standard deviations of the temperature errors, listed in Table 2, show the mean error at the highest frequency range is almost double that of the amplitude sweep at the lowest frequency.

Figure 3.

Accuracy comparison between the amplitude sweep (a) and the frequency sweep (b) temperature measurement methods for MSB measured data.

Table 2.

Comparison of error values for the two MSB temperature measurement methods, experimental data.

	At frequency:	Error Std. (%)	Error mean (%)
Amplitude sweep method	290 Hz	1.339	1.847
	1050 Hz	2.258	3.234
	2100 Hz	2.454	3.501
	Frequency ranges:	Error Std. (%)	Error mean (%)
Frequency sweep method	290–1050 Hz	0.306	1.721
	1050–2110 Hz	0.582	0.876

The values of temperature obtained for an field of 10mT from frequency sweeps are divided into two sets of values: a ‘Lower’ frequency range 290–1050 Hz and a ‘Higher’ frequency range 1050–2110 Hz, showing a decrease in error for the ‘Higher’ range of frequencies (Figure 3b). In contrast with the amplitude sweep based method results, the mean error value for the ‘Higher’ frequency range is about half than the one corresponding to the ‘Lower’ range.

To assess the validity of the two methods in regimes beyond the experimental capabilities, we employed simulated data, obtained from solving Eq. 2 numerically, for 10⁵ particles and determining their average magnetization at a given field amplitude, frequency and temperature. We considered the magnetic dipole moment m₀=7.96×10⁻¹⁸Am² (Martens, M.A. et al., 2013). Knowing the magnetization, we calculated the harmonic ratios of the signal and the corresponding relaxation times. The computations were carried out in Matlab, and depending on the number of iterations and convergence parameters, the wall time varied between a few minutes and a few hours, per data set. The same temperatures as the experimental study were considered (i.e. room temperature reference 21.5, as well as 30, 35 and 45 °C).

To illustrate the loss of accuracy for the amplitude based method we considered a low range of field values (1–2mT) and increasing frequency values, over a few orders of magnitude, respectively 20, 100, 200, and 1000Hz. The mean and standard deviation values of the errors, listed in Table 3, confirm a significant increase in error values with increasing frequency: more than 100% increase in error for two orders of magnitude variation in frequency values. This is to be expected as the amplitude sweep method makes use of the quasi-static Langevin function, hence will exhibit good accuracy only for low frequency values.

Table 3.

Comparison of error values for the two temperature measurement methods, simulated data.

	At frequency:	Error Std. (%)	Error mean (%)
Amplitude sweep based method (amplitude range 1–2mT)	20 Hz	0.139	0.128
	100 Hz	1.543	1.740
	200 Hz	2.180	2.216
	1000 Hz	715.702	434.720
	Frequency ranges:	Error Std. (%)	Error mean (%)
Frequency sweep based method (amplitude 50mT)	290–2100 Hz	0.364	0.093
	2110–3000 Hz	0.011	0.050
	3000–4000 Hz	0.019	0.026
	4000–5000 Hz	0.014	0.016

For the frequency based method, a larger frequency range was needed in order to show the increase in accuracy with the increase in frequency. Values between 290Hz and 5000Hz were chosen, divided into four frequency intervals (290–2100Hz, 2100–3000Hz, 3000–4000Hz, 4000–5000Hz), and the applied field amplitude was set at 50mT. The temperature errors, listed in Table 3, show that the method gains accuracy with an increase in frequency range.

In thermal therapy applications where these methods might be most immediately applicable, it is probably technically easiest to vary the amplitude rather than the frequency although both are quite feasible. It should be fairly simple to integrate either of the two methods into an MPI system assuming the gradient required by the MPI system can be turned off to allow heating. It might also be possible to integrate temperature sensitivity into the MPI image; it is possible to vary the frequency of the field inversion used to create the image which might mimic the frequency variation method. However, MPI scanning would have to be performed separately from the heating because the large fields used to heat would interfere with the imaging fields. The fields used to heat would also distort the particle dynamics by introducing more complex relaxation mechanisms.

There should be little difference in the physiologic effects of the two methods but this deserves a good deal more study.

Both the experimental and the simulated results suggest that the dominant effect of temperature at low frequencies is the change in the distribution of MNP energy states determined by the angle the magnetization makes with the applied magnetic field. This is understood from the fact that the nanoparticle relaxation time is much shorter than the oscillation period and equilibrium can be maintained. At higher frequencies, the equilibrium approximation weakens and the impact of temperature must be seen through the change in the relaxation time. The fact that the shift occurs at such low frequencies suggests that at high frequencies like those used for thermal therapies, the temperature will have to be accessed through the relaxation time, and thus the new method will be necessary.

4. Conclusions

The work presented here demonstrates a new, noninvasive method for measuring the temperature of the microenvironment surrounding magnetic nanoparticles (MNPs). The new measurement method, called MSB frequency sweep method in order to distinguish it from a previously established MSB amplitude sweep method, measures the relaxation time and then takes advantage of the direct temperature dependence in the Brownian formulation. For the range of temperatures that is of interest to the most likely clinical applications—drug delivery and thermal therapies—the method estimates the MNP temperature with excellent accuracy. The apparatus is inexpensive, yet has the potential for in vivo use in a clinical setting: a clinical apparatus would mimic the MPI designs of concentric cylindrical coils around the patient (Weizenecker, J. et al., 2009) or a set of coils placed on the surface of the patient (Sattel, T.F. et al., 2009). Over the frequency range studied experimentally, the new frequency sweep method leads to lower errors than the previously reported amplitude sweep method. Furthermore, the stochastic simulations show that the errors of the amplitude sweep method increase with frequency while the frequency method only improves. This is important for systems like MNP hyperthermia that use kilohertz frequencies. The failure of the old amplitude method at high frequencies is a direct consequence of the fact that it is based Maxwell-Boltzmann statistics and therefore requires a quasi-static approximation. In conclusion, the frequency sweep method, based on the relaxation time of MNPs, is shown to be a superior technique for measuring MNP temperature.