Development of a regional-scale pollen emission and transport modeling framework for investigating the impact of climate change on allergic airway disease

Abstract

Exposure to bioaerosol allergens such as pollen can cause exacerbations of allergenic airway disease (AAD) in sensitive populations, and thus cause serious public health problems. Assessing these health impacts by linking the airborne pollen levels, concentrations of respirable allergenic material, and human allergenic response under current and future climate conditions is a key step toward developing preventive and adaptive actions. To that end, a regional-scale pollen emission and transport modeling framework was developed that treats allergenic pollens as non-reactive tracers within the WRF/CMAQ air-quality modeling system. The Simulator of the Timing and Magnitude of Pollen Season (STaMPS) model was used to generate a daily pollen pool that can then be emitted into the atmosphere by wind. The STaMPS is driven by species-specific meteorological (temperature and/or precipitation) threshold conditions and is designed to be flexible with respect to its representation of vegetation species and plant functional types (PFTs). The hourly pollen emission flux was parameterized by considering the pollen pool, friction velocity, and wind threshold values. The dry deposition velocity of each species of pollen was estimated based on pollen grain size and density. An evaluation of the pollen modeling framework was conducted for southern California for the period from March to June 2010. This period coincided with observations by the University of Southern California's Children's Health Study (CHS), which included O₃, PM_2.5, and pollen count, as well as measurements of exhaled nitric oxide in study participants. Two nesting domains with horizontal resolutions of 12 km and 4 km were constructed, and six representative allergenic pollen genera were included: birch tree, walnut tree, mulberry tree, olive tree, oak tree, and brome grasses. Under the current parameterization scheme, the modeling framework tends to underestimate walnut and peak oak pollen concentrations, and tends to overestimate grass pollen concentrations. The model shows reasonable agreement with observed birch, olive, and mulberry tree pollen concentrations. Sensitivity studies suggest that the estimation of the pollen pool is a major source of uncertainty for simulated pollen concentrations. Achieving agreement between emission modeling and observed pattern of pollen releases is the key for successful pollen concentration simulations.

1. Introduction

Exposure to respirable allergenic materials from ruptured pollen grains can stimulate the production of antibodies in the human body and trigger allergic airway diseases (AAD), such as asthma, sinusitis, and allergic rhinitis (Taylor et al., 2002; Adhikari et al., 2006). AAD is a serious public health concern worldwide with the most prevalent impacts among children and adolescents (Nathan et al., 1997; WHO 2003; Miguel et al., 2006; Taylor et al., 2007). The burden from AAD may increase further in the future due to intensive human activities that perturb the environment and change land management practices, which could shift the pollen amount, pollen allergenicity, duration of pollen season, and pollen spatial distributions (Beggs 2004; D'Amato et al., 2007; Reid and Gamble, 2009). Evidence also suggests that sensitization to pollen allergens can be enhanced with co-stressors such as gaseous and/or particle-phase of air pollutants including nitrogen dioxide, ozone, and diesel exhaust particles (e.g. Knox et al., 1997; Motta et al., 2006; Després et al., 2012). Hence, building a quantitative model to link airborne pollen levels, concentrations of respirable allergenic material, and human allergenic response under current and future climate conditions is needed to assess the health impacts on AAD and develop corresponding preventive actions (Hugg and Rantio-Lehtimäki, 2007; Efstathiou et al., 2011). Simulating the spatial-temporal variation of pollen occurrence is the central task toward this goal.

The dispersal of pollen grains and their fragments in the atmosphere is controlled by meteorological factors as well as the pollen physical characteristics such as shape, density, size, and vitality (Helbig et al., 2004; Pfender et al., 2007; Veriankaite et al., 2010; Despés et al., 2012). Even though pollen dispersal is normally treated as a local scale transport phenomenon, long distance dispersal (LDD) through mechanically- and thermally-induced updraft turbulent eddies and regional transport is also possible (Kuparinen, 2006). These additional dispersal mechanisms have been confirmed both by observations (Cecchi et al., 2006; Ranta et al., 2006; Skjøth et al., 2007; Mahura et al., 2007) and by modeling using back trajectory analysis (Smith et al., 2008; Markra et al., 2010) and source apportionment (Veriankaitė et al., 2010; Zink et al., 2012). The regional transport of pollen is especially important from a health impact perspective since non-local pollen sources from LDD will change the local pollen load and shift the exposure potential for pollen allergens (Sofiev et al., 2006; Zink et al., 2012). Long-term pollen observations from networks such as the European Aeroallergen Network Pollen Database (EAN, http://ean.polleninfo.eu/Ean/) and US National Allergy Bureau pollen counts database (NAB, http://www.aaaai.org/global/nab-pollen-counts.aspx) would provide a platform to evaluate regional pollen dispersion simulation results if these data could be made available.

Several numerical models have been used to simulate regional pollen transport for the purpose of evaluating the impact of pollen dispersal to AAD or cross pollination (e.g., Hunt et al., 2001; Tackenberg et al., 2003; Helbig et al., 2004; Schuler and Schlünzen, 2006; Verinakaite et al., 2010, Siljamo et al., 2012). Even though the details of the schemes vary, two core parts are central to all models, namely pollen emission and pollen transport. For the pollen emission component, the start, end, and duration of the pollen season as well as the diurnal emission profiles are typically generated via a regression analysis between observed pollen counts and key meteorological factors such as temperature, relative humidity, and wind speed (Jones and Harrison 2004; Schuler and Schlünzen, 2006; Laursen et al., 2007; Marceau et al., 2011). The spatial patterns of the pollen sources are based on vegetation distribution maps, which are subject to large uncertainties (Sofiev et al., 2006; Skjøth et al., 2010; Pauling et al., 2011; Sofiev et al., 2013). For pollen transport modeling, the pollen dispersion is either modeled by Lagrangian trajectory models such as PAPPUS (Tackenberg et al., 2003), SMOP-2D (Jarosz et al., 2004), CALPUFF (Pfender et al., 2006), and HYSPLIT (Pasken and Pietrowicz, 2005; Verinakaite et al., 2010), or by Gaussian advection-diffusion models such as ADMS (Hunt et al., 2001), DRAIS/MADEsoot (Helbig et al., 2004), Aquilon (Dupont et al., 2006), and METRAS (Schuler and Schlünzen, 2006). Some key physical modules such as dry deposition due to gravity, washout by precipitation, and re-suspension by updrafts can be parameterized explicitly into a model (Helbig et al., 2004; Kuparinen, 2006; Siljamo et al., 2012).

In recent years, there has been a growing effort to simulate regional pollen dispersal within the framework of sophisticated regional air-quality models, which has multiple benefits compared to the traditional approach. First, it can be used in forecast mode to predict the pollen concentrations on a daily basis (Zink et al., 2012). Second, the predicted air pollutant concentrations already included in air quality models are also important for AAD assessment, thus allowing the adjuvant effects of pollution and pollen exposure on AAD to be evaluated under the same modeling framework. Third, pollen grains can serve as cloud condensation nuclei (CCN) or ice nuclei (IN) for cloud formation and thereby change precipitation patterns, which can have important impacts on aerosols and related pollutants (Möhler et al., 2007). Thus simulating pollen within this type of modeling framework is a step towards being able to quantify the feedbacks between pollen concentration and radiative forcing. In Europe, the air quality models SILAM (System for Integrated modeLling of Atmospheric coMposition; Sofiev et al., 2013, 2006) and COSMO-ART (COnortium for Small-scale MOdeling – Aerosols and Reactive Trace gases; Vogel et al., 2008) have been used to forecast regional birch pollen dispersion by adding a pollen emission prediction module. In North America, a combined MM5-CMAQ-Pollen model merges the Mesoscale Meteorological Model (MM5; Grell et al., 1994), components of the Biogenic Emissions Inventory System (BEIS) and major elements of SILAM and COSMO-ART for pollen emissions, and the Community Multiscale Air Quality (CMAQ, Byun and Schere, 2006) modeling system for pollen transport; the combined model was used to simulate birch and ragweed pollen dispersion behaviors during their peak pollination periods in 2002 for the northeastern US (Efstathiou et al., 2011).

In this study, using a new model for predicting the daily pollen pool in terrestrial, temperate vegetation, a new hourly pollen emission flux parameterization scheme has been developed and incorporated into the state-of-the-art mesoscale Weather Research and Forecasting Model (WRF; Skamarock et al., 2008) and CMAQ air-quality modeling framework to simulate regional pollen dispersion behaviors. This simulation platform has the flexibility to predict the temporal-spatial variations of different pollen species under current and future climate conditions. The model results can be linked with AAD clinical data to assess and forecast pollen impacts on target sensitive groups. Model evaluation has been carried out by simulating representative allergenic pollen species during the Mar–Jun 2010 flowering season over southern California where the Children Health Study (CHS) campaign had collected pollen count and measured exhaled nitric oxide in study participants. The uncertainties of the emission and transport modules of this modeling framework are also discussed through sensitivity studies. The framework can also be applied to estimate the changes in the timing of pollen seasons and the magnitude of pollen production for selected allergenic species over California under current and future climate scenarios; description and results are available in the companion paper (Duhl et al., 2013).

2. Methodology

2.1 STaMPS model

The Simulator of the Timing and Magnitude of Pollen Season (STaMPS) is a model that generates daily pools of pollen available for release (emission potentials) into the atmosphere. It is a module within the Model of Emissions of Gases and Aerosols from Nature (MEGAN; Guenther et al., 2006, 2012) and is driven by meteorological conditions such as temperature and precipitation. It is designed to be sensitive to potential climate shifts and flexible with respect to its representation of pollen species and plant functional types (PFTs). A detailed description of the STaMPS model is provided in a companion paper by Duhl et al. (2013); only a brief description is given here.

The magnitude of daily pollen emission potential P_a (grains m⁻²) at each simulation grid cell for a given pollen species is determined as:

$$P_a={\epsilon }_{sp}\cdot {\alpha }_{P,TP}\cdot \gamma$$ (1)

where ε_sp is the pollen pool size (grains m⁻²), which was directly derived from literature values or the associated average values for the PFT to which a given species belongs; α_P,TP is a coefficient with values between 0 and 1 that modifies the pool size according to either to precipitation (α_P) or both temperature and precipitation (α_TP); and γ is the total area occupied by the species in a grid cell. The total area occupied by the species in a grid cell, γ, was determined using fractional vegetation and land cover datasets such as the National Land Cover Database (NLCD; http://www.epa.gov/mrlc/nlcd-2001.html) and species inventories from different sources, including Forest Inventory & Analysis datasets (FIA; http://www.fia.fs.fed.us/tools-data/default.asp), Natural Resources Conservation Service datasets (NRCS; http://soildatamart.nrcs.usda.gov/), and the Cropland Data Layer from National Agricultural Statistic Service (CDL/NASS; http://www.nass.usda.gov/research/Cropland/SARS1a.htm). The homogenization process for combining these different datasets is documented in detail in the companion paper (Duhl et al., 2013).

The onset and duration of pollen season for each species was based on the thermal time approach, modeled after García-Mozo et al. (2002). Pollen is available to be released into the atmosphere after a prescribed species-specific threshold of heat-accumulation units (i.e., Growing Degree Days, GDD) for flowering is achieved. Different species have different associated pollen production response curves, sensitive to either precipitation or both ambient temperature and precipitation. For some species with dual heating and vernalization requirements (e.g., birch, olive, and walnut), chilling units must also be accumulated until a species-specific chilling threshold has been achieved before GDD accumulation is initiated. The chilling module for birch, olive, and walnut was based on the chill-heating model of De Melo-Abreu et al. (2004), in which the accumulation of chilling units is determined via a piecewise approximation using the ratio of the actual hourly temperature data for a location to an optimal chilling temperature for a given species. After initiation, the distribution of the potential pollen pool is assumed to be lognormal over two-week duration. Hence, the peak value of daily pollen emission potential will appear at day eight with normally distributed emissions seven days before and after the peak day.

2.2 Pollen emission flux parameterization

The MEGAN/STaMPS model determines the onset and duration of the pollen season and the potential amount of pollen, P_a, that can be emitted into the atmosphere for each day during the pollen season. The actual amount of pollen emitted into the atmosphere depends on dispersion conditions and is a fraction of P_a. There are very few comprehensive parameterizations of pollen emission that can be applied at a regional scale, especially with respect to the diurnal variation in pollen release and changing ambient meteorological conditions. The parameterization scheme proposed by Helbig et al. (2004) based on friction velocity, u_*, has been widely used in other regional modeling studies (Sofiev et al., 2006; Vogel et al., 2008, Efstathiou et al., 2010; Zink et al., 2012). A recent paper by Sofiev et al. (2013) reported a new birch pollen emission scheme based on a temperature-dependent parameterization (Linkosalo et al., 2010) and used the convective velocity scale (w_*) together with the 10-m wind speed to represent the influence of both mean wind and convection on pollen emission. The authors suggested that this was a more realistic approach for free convection and low mean wind conditions.

Since the MEGAN/STaMPS pollen emission potential module already explicitly accounts for P_a with different species based on species-specific temperature-precipitation regression mechanisms, only the wind effect in scaling the pollen potential P_a is considered to calculate the rate of emission into the atmosphere. Hence, the hourly average vertical emission rate, E_P (grains s⁻¹ m⁻²), at each grid cell is proportional to P_a, u_* (m s⁻¹), and a wind effect scale factor, K_e:

$$E_P=\frac{P_a}{H_s\cdot C}\cdot K_e\cdot u_{\ast }$$ (2)

where the constant, C, is the conversion constant from day to seconds, and H_s (m) is the average canopy height for species within each genus. Values of H_s used in this study are listed in Table 1. In Equation (2), P_a|H_s represents the characteristic concentrations (grains m⁻³) of pollens within the canopy. The wind effect scale factor, K_e, is a non-dimensional factor between 0 and 1 and is parameterized following Helbig et al. (2004) using a threshold friction velocity, u_*te, which is the product of a resistance factor, α and a standard threshold friction velocity, u_*t (m s⁻¹):

$$K_e=\{\begin{array}{cc}1-\frac{u_{\ast te}}{u_{\ast }},\hfill & u_{\ast }>u_{\ast te}\hfill \\ 0,\hfill & u_{\ast }\le u_{\ast te}\hfill \end{array}\phantom{\}}$$ (3)

$$u_{\ast te}=\alpha \cdot u_{\ast t}=\alpha \cdot {(0.0123\times [\frac{{\rho }_P}{\rho }\cdot g\cdot d_p+\frac{0.0003}{\rho \cdot d_P}\left]\right)}^{1∕2}$$ (4)

Equation (4) for u_*t is the regression formula based on wind tunnel data for sand erosion (Greeley & Iversen, 1985) and is related to the pollen density, ρ_P (kg m⁻³), and aerodynamic diameter, d_P (m); ρ is the air density (kg m⁻³); and g is the gravitational acceleration (9.8 m s⁻²). Equations (2) and (3) indicate that the amount of pollen released each hour depends on the ratio of the threshold friction velocity and the friction velocity. For a given 10-m wind speed, higher canopy height means higher emissions because of higher friction velocity as a result of higher surface roughness and zero-plane displacement height. The resistance factor, α, is introduced here to distinguish the different natures of sand erosion on the ground and the pollen release above the canopy height. It is a ratio of an empirical threshold wind speed, U_10,e, and the modeled 10-meter wind speed, U₁₀:

$$\alpha =U_{10e}∕U_{10}$$ (5)

For the base case, the value of U_10e was set at 2.9 m s⁻¹ for all pollen genera following Helbig et al. (2004). As discussed below and listed in Table 2, we also performed sensitivity simulations using different values of U_10e. Equations (3) – (5) indicate that the greater the ambient wind speed, the smaller the threshold friction velocity (u_*te), which means that a higher proportion of P_a can be released into the atmosphere.

Table 1.

Pollen genera considered in this study and their physical properties.

Genus	Pollen Species Included	Density ρP (kg·m−3)	Diameter DP (μm)	Settling (Velocity Vdp (m·s−1)	CalculatedaVdp (m·s−1)	Canopy Height Hs (m)	Threshold Friction Velocitybu*te (m·s−1)
Betula (birch trees)	Betula pedula	800c	24c	0.013d	0.014	6c	0.37
Bromus (grass)	B. diandrus and B. mollis	900d	24c	N.A.	0.0158	0.1	0.37
Juglans (walnut trees)	J. regia and J. californica	940d	35	0.029–0.044d	0.035	9.2	0.31
Morus (mulberry trees)	M. alba, M. rubra, and unspciated Morus trees	1140e	19	N.A.	0.0126	7.6	0.41
Olea (olive trees)	O. europaea	1000	25	N.A.	0.019	7.2	0.36
Platanus (plane trees)	P. acerifolia	920d	19	0.0104d.	0.0096	6.8	0.42
Quercus (oak trees)	Early-blooming oak species: Q. agrifolia, Q. douglasii, Q. dumosa, Q. engelmannii,Q. laurifolia, Q. lobata, Q. turblinella, Q. velutina, Q. virginiana, Q. wislizeni Late-blooming oak species: Q. alba, Q. chrysolepis, Q. coccinea, Q. gambelii, Q. garryana,Q.grisea, Q. Ilex, Q. kelloggii, Q. macrocarpa, Q. palustris, Q. rubra, and misc. Quercus species	1058f	31	0.029d	0.0309	9.6f	0.33

^aCalculated using Equation (6) and the listed density and diameter.

^bAssume air density ρ of 1.161 kg/m³, 10-m wind speed U₁₀ of 3 m s⁻¹ and empirical threshold wind speed U_10e of 2.9 m s⁻¹ in Eq. (5).

^cEfstathiou et al. (2010).

^dJackson & Lyford (1999).

^eMartonen and O'Rourke (1993);

^fSchuler and Schlunzen (2006).

Table 2.

List of WRF-MEGAN-CMAQ simulations.

Case ID	Description	Purpose
BASE	Base case simulation
BCON	Use dynamic boundary conditions extracted from D1 of CMAQ pollen transport simulation	Case study with simulated pollen concentration influenced by outside domain
PAHI	Use the upper bound estimates of pollen emission pollen emission pool size εsp in Eq. (1). Compared with case BASE, +74% for birch and walnut, +113% for grass, +53% for walnuts, +43% for olive and +93% for oak	Sensitivity study of the uncertainties for pollen emission pool size εsp estimates to their simulated concentration
PALO	Use the lower bound estimates of εsp. Compared with case BASE, −74% for birch and walnut, −113% for grass,−53% for walnuts, −43% for olive and −93% for oak
UTHI	Set empirical threshold wind speed U10e in Eq. (4) as 4.0m/s compared with case BASE 2.9m/s	Sensitivity study of empirical threshold wind speed U10e setting to simulated pollen concentration
UTLO	Set empirical threshold wind speed U10e in Eq. (4) as 2.0m/s compared with case BASE 2.9m/s
DVHI	Increase the mean diameter of each pollen genera in Table 1 by 10% compared to case BASE	Sensitivity study of dry deposition velocity Vdp calculation for pollen genera to their simulated concentration
DVLO	Decrease the mean diameter of each pollen genera in Table 1 by 10% compared to case BASE

The emission flux parameterization scheme used in this study differs significantly from the earlier parameterization of Helbig et al. (2004) in that their bloom probability function, which was based on an assumed timing and duration of the flowering season, is replaced here by more explicit modeling of pollen emission potential, driven by temperature and/or precipitation. Equation (1) does not include a leaf area index (LAI) factor because biomass and fractional vegetation cover are already considered in the pollen emission potential calculation.

The dry deposition process during pollen dispersion is modeled using the settling velocity, V_dp (m s⁻¹), which is calculated according to Equation (6) (Seinfeld and Pandis, 1998):

$$V_{dp}=\frac{{\rho }_p\cdot g\cdot C_c\cdot d_p^2}{18\mu }$$ (6)

where C_c is the slip correlation coefficient and μ is the viscosity of air as a function of temperature. For each genus modeled here, we assume monodisperse spherical particles, with particle diameters and densities based on values reported in the literature; the assumed particle diameter d_P, densityρ_P, and settling velocities V_dp as calculated by Equation (6) are provided in Table 1. Table 1 also lists the measured settling velocity reported by Jackson and Lyford (1999). Uncertainty in model results associated with deposition velocities is addressed with sensitivity simulations (see Section 2.5) and discussed in Section 3.3. Due to the relatively large diameter of pollen grains, the contribution of canopy resistance to bulk dry deposition rate is small. The hourly dry deposition flux of simulated pollen can be calculated using as V_dp dry deposition rate following the Regional Particulate Model (RPM) approach (Binkowski and Shankar, 1995). Pollen dispersion is also subject to wet deposition via cloud scavenging and precipitation. The algorithms for wet deposition processes in our framework are taken from the Regional Acid Deposition Model (RADM) (Change et al., 1987).

2.3 WRF-MEGAN-CMAQ modeling framework

The STaMPS model for daily pollen emission potentials and the pollen emission flux parameterization scheme described above were incorporated into the WRF-MEGAN-CMAQ regional air-quality modeling system to simulate the variation of temporal-spatial patterns for different species. This WRF-MEGAN-CMAQ modeling framework has been applied to provide daily air-quality forecasts (e.g., Herron-Thorpe et al., 2012), to study present-day air quality issues (e.g., Appel et al., 2012), and to investigate the impact of climate change on regional air quality (e.g., Avise et al., 2012). Similarly, the modeling framework can be applied for retrospective analyses and daily forecasts of pollen concentrations, and to project the impact of pollen on AAD under future climate conditions by using downscaled meteorological fields from global climate models and the corresponding estimation of pollen emission fluxes. In addition, the modeled pollen concentrations can be used to derive the concentration response function (CRF) for overall and species-specific allergen concentrations for key respiratory health outcomes.

The schematic flowchart of this modeling framework is given in Fig. 1, with the core modules relevant for pollen highlighted in grey. The key meteorological variables for pollen emission and dispersion – wind speed and direction, temperature, relative humidity (RH), radiation, and dew point temperature – are predicted by WRF. WRF's dynamical core includes multiple physical schemes for radiation, cumulus, microphysics, planetary boundary layer (PBL) meteorology, and land-surface process representation (Skamarock et al., 2008). Hourly temperature and precipitation needed for the STaMPS model are provided by WRF through the Meteorology-Chemistry Interface Processor (MCIP) utility (Otte and Pleim, 2010). The Models-3 Community Multiscale Air Quality (CMAQ) modeling system from US EPA (Byun and Schere, 2006) is applied as the host model to simulate pollen transport. CMAQ is a highly modular Eulerian model with state-of-art chemical and physical process schemes to solve the mass and energy conversation equations. Selected pollen species were added into CMAQ by treating them as non-reactive tracers. The emission flux of different pollen species are released into the first model layer. Once released, the pollen tracers were subjected to the standard CMAQ transport process modules of advection, diffusion, dry deposition and cloud washout. This approach required hourly gridded emission fluxes and dry deposition velocities for each species of pollen as inputs for CMAQ.

Fig. 1.

Flowchart of a regional WRF-MEGAN-CMAQ air-quality modeling framework with pollen emission and transport modeling highlighted.

2.4 Simulation Domain and Model configurations

During March–June 2010, pollen counts and the fractional exhaled nitric oxide (FeNO) level of 950 children participants were measured at eight sites across southern California as part of the University of Southern California's Children's Health Study (CHS, McConnell et al., 2006). These sites were selected to detect the spatial variability in air pollution and pollen exposures, and their health impacts across the target communities (see Fig. 2). Pollen samples were collected using Burkard Sporewatch samplers and were subsequently analyzed using standard protocols by a pollen counter who has been certified by the NAB. Results were reported as daily mean number concentration (grains m⁻³). In addition to the CHS community sites, long-term pollen counts were collected at the campus of California Institute of Technology in Pasadena, CA (data available at http://pollen.caltech.edu/DataFrameset.html). As in most communities, the availability of long-term pollen count data over southern California is limited. Therefore, the observational data acquired during the CHS study provide a unique opportunity to evaluate a pollen dispersion model on a regional scale. This is also the first modeling study on pollen regional dispersion to include the western U.S.

Fig. 2.

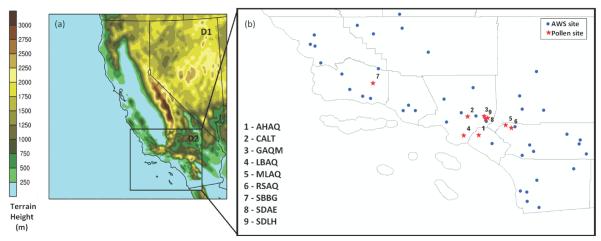
(a) Domain coverage of the 12-km California (D1) and 4-km Southern California (D2) grids with terrain height; and (b) the location of pollen sampling sites (red) and the AWS sites (blue).

Six tree pollen genera and one grass pollen genus are included in the STaMPS model for this study, representing important allergenic species that typically bloom in southern California during the period covered in our simulations (Hjelmroos-Koski et al., 2006). These genera are: Betula (birch tree), Bromus (brome grass), Juglans (walnut tree), Morus (mulberry tree), Olea (olive tree), Platanus (plane tree) and Quercus (oak tree). Each pollen genus contains a number of species, with varied abundance over the study domain. For instance, there is only one species considered in birch tree pollen genus (Betula pedula), while 19 species are included in the oak tree pollen genus over Southern California. For genera that include more than one species, P_a is calculated from the STaMPS model for the lumped results, which are sensitive to the grouping of blooming categories (based on GDD threshold, Duhl et al., 2013) for included species. The important physical properties of each genus such as pollen density and aerodynamic diameter, canopy height, and threshold friction velocity are summarized in Table 1 and are taken from previous studies (Martonen & O'Rourke, 1993; Jackson & Lyford, 1999; Schueler and Schlünzen, 2006; Efstathiou et al., 2011). All data for each genus are the representative mean of their included pollen species. Platanus pollen is not included in the CMAQ simulations because no observational data were available for model evaluation.

Two nesting domains with horizontal grid cell sizes of 12 km × 12 km (D1) and 4 km × 4 km (D2) with 105 × 95 (D1) and 126 × 93 (D2) cells were set up for the WRF and CMAQ models; domain coverage is shown in Fig. 2. CMAQ simulations for pollen dispersion were initially conducted for the inner domain (D2) with boundary conditions of zero. The WRF version 3.2.1 meteorological simulations were driven by initial and boundary conditions from the North American Regional Reanalysis results (NARR; Mesinger et al., 2006). Twenty-nine vertical layers were constructed from the ground to the 50 mb level, with 11 vertical layers in the lowest 1 km above the surface and first layer height at around 40 m. The physical options chosen for the WRF simulations were: Yonsei University scheme (YSU) for PBL simulation; Thompson scheme for microphysics; thermal diffusion methods for land-surface model; and Monin-Obukhov profile for surface scheme (Skamarock et al., 2008). In order to capture the wind pattern over complex topography in southern California, an analytical nudging technique (Otte et al., 2008) was applied to the outer domain above the PBL top height using NARR temperature, wind, and moisture fields. Observational nudging was applied to the inner domain at the surface layer using wind and temperature data that were obtained from the California Air Resources Board (CARB) from 46 meteorological stations throughout the region. The CMAQ version 4.7.1 was compiled with the option to run only for dispersion of pollen tracers or with full chemical reactions of other air pollutants. The global mass-conserving Yamartino scheme was chosen to calculate the horizontal and vertical advection terms, while the horizontal diffusion term was calculated based on local wind deformation (Byun and Schere, 2006). Vertical diffusion was calculated using the Asymmetric Convective Model version2 (ACM2) in CMAQ (Byun and Schere, 2006). The off-line calculated average settling velocities (Eq. 6) of each pollen genus in Table 1 were written into MCIP METCRO2D files to drive the CMAQ dry deposition module.

The STaMPS model was run over the 4-km southern California domain (D2) for all cases and over the 12-km larger domain (D1) for the BCON sensitivity case (see Section 2.5 below). Even though the focus this study is March–June 2010, to simulate pollen potential P_a daily temperatures starting from six months prior and monthly precipitation starting from 15 months prior were used by STaMPS to model vernalization and chilling (vernalization) requirements and to model the effect of prior-year wet season precipitation on pollen potential (see Duhl et al., 2013 for details). For the October 2009–June 2010 period, daily temperature and precipitation fields from the WRF model were used to drive the STaMPS model. For computational efficiency, for the October 2008–September 2009 period 30-arcsecond PRISM monthly precipitation data (PRISM Climate Group, 2010) were used.

2.5 Case study design

Before running CMAQ for the pollen dispersion simulation, the overall performance of predicted pollen emission potentials P_a by the STaMPS model was compared with observed pollen count data to assess the general observed day-by-day temporal trend. This comparison resulted in an adjustment made to the lumping scheme for the Quercus genus by separating the included oak species into two categories, one early-blooming and one late-blooming (Table 1), according to the phenological observations and qualitative time-of-flowering data from the NRCS dataset (Duhl et al., 2013). For the base case (`BASE'), the validated P_a go through the emission flux parameterization process and the WRF-MEGAN-CMAQ modeling framework as described in Sections 2.2 and 2.3 to simulate the ambient pollen level.

In order to test the impact of uncertainties from important model parameters on the simulated pollen concentrations, four sets of sensitivity simulations were also conducted with the descriptions documented in Table 2. The first set of sensitivity simulations (`BCON') was designed to test the impact of boundary conditions on the simulated pollen concentrations. In this case, the pollen concentrations from the outer domain were also simulated by CMAQ to provide dynamic conditions for the inner domain instead of using zero values. The second set of sensitivity simulations (`PAHI' and `PALO') were designed to test the impact of pollen emission potential estimates on simulated pollen concentrations. The uncertainties in P<sub>a</sub> mainly come from the variation in pollen pool size ε<sub>sp</sub> estimates, species composition, and the fractional vegetation cover datasets used in the model (Eq. 1). Pollen production can vary by at least an order of magnitude between species within a given genus (Duhl et al., 2013). In this study, only the uncertainties in the pollen pool size estimates were quantified, based on the work of Molina et al. (1996). The estimated standard deviations of the six pollen genera ε<sub>sp</sub> are ±74% for birch and walnut, ±113% for grass, ±53% for walnuts, ±43% for olive, and ±93% for oak. Case PAHI used the upper bound estimates of ε<sub>sp</sub> while case PALO used the lower bound estimates of ε<sub>sp</sub>. The third set of sensitivity simulations (`UTHI' and `UTLO') were designed to test the impact of the empirical threshold wind speed settings on simulated pollen concentration. Smaller U<sub>10e</sub> results in increased pollen release into atmosphere under the same wind conditions (Eq. 5). The lower and upper settings of U<sub>10e</sub> in the UTHI and UTLO simulations were 2.0 m·s<sup>−1</sup> and 4.0 m·s<sup>−1</sup>, respectively, compared with the base case setting 2.9 m·s<sup>−1</sup>. The last set of sensitivity simulations (`DVHI' and `DVLO') were designed to test the uncertainties in deposition velocity calculation to simulated pollen concentration. Higher deposition rates are associated with faster dry deposition processing and thus lower ambient pollen concentrations. The estimated mean diameters in Table 1 for each pollen genus were varied by ±10% for the two sensitivity simulations, corresponding to approximately ±20% changes in deposition velocity V_dp based on Equation (6); note that this ±20% in V_dp is greater than the difference between the base case V_dp and the measured V_dp (Table 1).

3. Results and Discussion

3.1 Meteorological simulation

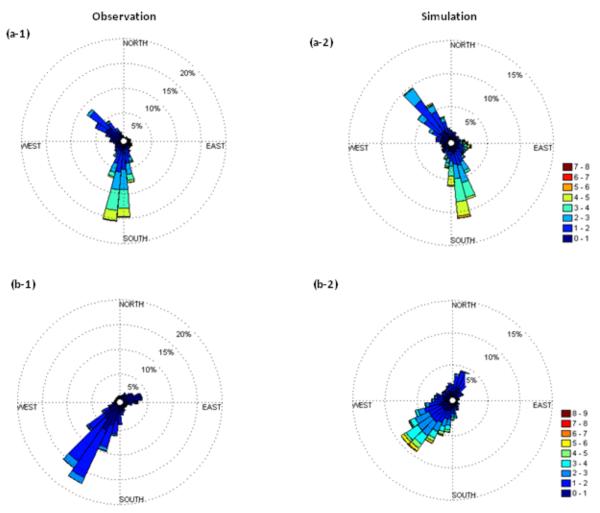
Meteorological variables predicted by WRF and processed through MCIP are used by the MEGAN and CMAQ models to model the pollen potential, emissions, and regional dispersion. A key step in accurately simulating ambient pollen concentrations is being able to accurately simulate meteorological fields, especially the spatial distribution of winds given the complex terrain in southern California (Fig. 2), which leads to diurnal land-sea breezes and mountain-valley circulations. The comparison of observed and simulated surface winds during March – June 2010 at two sites is shown in Fig. 3. At the UC Riverside site (Fig. 3a), the observed and modeled wind patterns are quite similar with nearly 50% occurrence of southerly and 50% northwesterly winds and average wind speeds of 3–4 m s⁻¹ during the four-month simulation period. The WRF model with the data assimilation performed well for wind speed as well as wind direction at this site. For the Pomona site (Fig. 3b), which is several kilometers away from the Caltech sampling site (CALT, Fig. 2), the model performed less well. Southwesterly winds were dominant both in the observations and simulations (more than 90% occurrence), but the model had the tendency to overestimate wind speeds under mild wind conditions.

Fig. 3.

Wind rose plots comparing observed (left column) and simulated (right column) winds during March – June 2010 at UC Riverside (33.96°N, 117.33°W) (top) and Pomona (34.05°N, 117.81°W) (bottom).

Table 3 summarizes the month-by-month WRF-MCIP model performance at 46 sites inside the 4-km southern California domain (D1). Simulated surface wind speeds, 2-m temperatures, relative humidities (RH), downward solar radiation at the ground, and dew points are evaluated with corresponding observations using standard statistical metrics such as mean, index of agreement (Willmott et al., 1981), correlation coefficient (r), root mean square error (RMSE), mean bias (MB), and normalized mean bias (NMB) and error (NME). The patterns of temporal variation for temperature and radiation were simulated well by the WRF model with r near 0.9 or higher for all four months. Since only temperature and wind observational data were nudged in the inside simulation domain, the model tends to underestimate the daily radiation peaks but shows decent agreement with ground temperature. The model performed less well for wind fields; it overestimated surface wind speeds by 30% on average, and the simulated wind direction was more divergent as indicated by the MNB index. Except for wind, the model performance for June 2010 is better than the other three months in terms of r and NMB. In general, the WRF configuration used in the study generated good meteorological fields, judging from the fact that almost all NMB are less than ± 30%.

Table 3.

Performance statistics of monthly averages for 4-km southern California WRF simulation.

	Obs Mean	Model Mean	IOAa	r b	RMSEc	MBd	MNB(%)e	NMB(%)f	NME(%)g
	March 2010
Wind Speed (m·s−1)	1.7	2.3	0.76	0.68	1.2	0.5	75	33	53
Wind Direction (deg)	190	191	0.76	0.57	97	0.3	294	1	30
Temperature (°C)	13.0	13.0	0.94	0.92	2.3	−0.1	6	−1	15.0
RH (%)	62	47	0.75	0.72	21.2	−14	−19	−23	28
Radiation (W m2)	389	510	0.93	0.88	161	44	31	12	31
Dew Point (°C)	5.7	4.4	0.54	0.46	4.5	−2.9	−98	−76	90
	April 2010
Wind Speed (m·s−1)	1.8	2.5	0.76	0.68	1.3	0.5	70	32	52
Wind Direction (deg)	206	208	0.74	0.54	95	12	282	2	27
Temperature (°C)	13.8	13.5	0.93	0.90	2.4	−0.2	1	−2	14
RH (%)	64	52	0.78	0.75	18	−12	−16	−18	24
Radiation (W·m2)	425	529	0.89	0.82	206	40	78	10	36
Dew Point (°C)	6.6	5.4	0.61	0.47	3.9	−2.2	−49	−39	54
	May 2010
Wind Speed (m·s−1)	1.9	2.4	0.76	0.68	1.2	0.5	71	33	53
Wind Direction (deg)	213	219	0.73	0.53	91	6	216	4	27
Temperature (°C)	16.5	16.5	0.91	0.90	2.7	0.2	5	2	14
RH (%)	59	46	0.76	0.76	19	−13	−20	−21	27
Radiation (W·m2)	472	619	0.91	0.86	195	64	62	14	32
Dew Point (°C)	7.6	6.0	0.59	0.49	4.3	−2.6	−42	−39	52
	June 2010
Wind Speed (m·s−1)	1.7	2.3	0.67	0.58	1.4	0.6	86	43	65
Wind Direction (deg)	212	214	0.65	0.42	96	0.5	212	2	30
Temperature (°C)	20.1	20.1	0.89	0.91	3.0	0.2	3	3	13
RH (%)	61	51	0.74	0.78	17	−11	−11	−13	23
Radiation (W·m2)	463	619	0.95	0.93	162	71	61	17	28
Dew Point (°C)	10.9	10.1	0.63	0.53	3.2	−0.9	8	−7	24

^aIOA: index of agreement (Willmott et al., 1981);

^br: correlation coefficient;

^cRMSE: root mean square error;

^dMB: mean bias;

^eMNB: mean normalized bias;

^fNMB: normalized mean bias;

^gNME: normalized mean error.

3.2 Pollen emission potential and emission rate

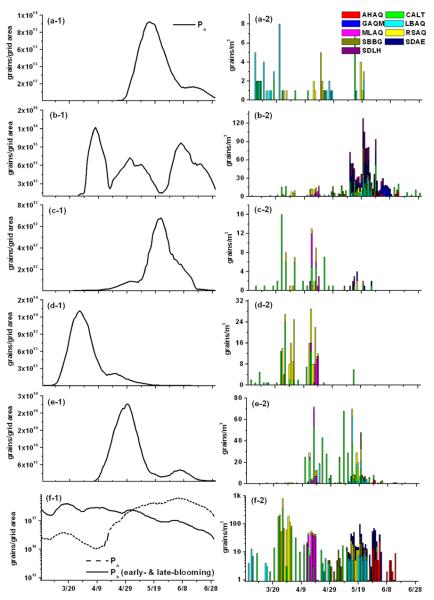
Accurate geographical distributions of relevant vegetation species, predictions of the timing of the pollen season, and pollen emission potentials (P_a) are also important factors for simulating ambient pollen concentrations. The prediction of the onset and duration of flowering season can be evaluated with the concurrent ambient observation of pollen concentrations. Even though LDD behavior affects the spatial distribution and magnitude of pollen concentrations at the local scale (Zink et al., 2012), there should be a correlation between the timing of pollen emission and that of concentration on the regional scale. Fig. 4 provides an illustrative comparison between the day-by-day, domain-averaged simulated P_a and the observed pollen counts. For birch trees, the predicted flowering season started on April 27^th, 2010; P_a peaked on May 16^th, 2010 (P_a = 9×10¹³ grains m⁻²) and the birch pollen season lasted for the rest of the simulation period (Fig. 4 a-1). The observed birch peak concentration in mid-May (7 grains m⁻³) corresponds to the timing of emission peak. However, the appearance of birch pollen in earlier March at sites CALT and LBAQ is not represented by the current STaMPS simulation (Fig. 4a-2). This could be due to the fact that birch pollen cannot be differentiated at the species level, and there may be other Betula species present in the domain other than just B. pendula with unique flowering seasons. For grass pollen, the P_a predicted by STaMPS started on March 19^th, 2010 and presented a tri-modal temporal distribution pattern (Fig. 4b-1), which correlates with the observed regional high concentrations over the simulation domain especially during May 2010 (136 grains m⁻³, Fig. 4b-2). For walnut trees, the simulated temporal pattern of P_a is slightly offset with pollen count observations. Even though the high concentrations at a single site, CALT, (green in Fig. 4c-2) on March and earlier April 2010 are not represented in the STaMPS predictions, the later observed pollen concentrations at multiple sites do match with concurrent emission prediction. For mulberry (Fig. 4d) and olive trees (Fig. 4e), both the predicted onset and duration of flowering season from STaMPS closely match the corresponding pollen count temporal pattern at the nine stations for which data are available. For the oak tree pollen emission potential simulation (Fig. 4f-1), the day-by-day variation of predicted emission using an old species lumping scheme (blue) did not match with that of the observations (Fig. 4f-2), with the simulations predicting higher pollen levels in June while the observed concentrations peaked in March. The temporal trend of P_a with the updated lumping scheme that separates oak species into early-blooming and late-blooming groups results in a much better agreement with the observed data (solid lines in Fig. 4f-1), compared to the results when all oak species are lumped into one group (dashed lines in Fig. 4f-1). This is consistent with the fact that the oak genus in the model contains several species with different thermal requirements for flowering (Table 1) (Duhl et al., 2013).

Fig. 4.

Temporally-aligned pollen emission potentials P_a (left) and observed pollen counts (right) for (a) birch, (b) grass, (c) walnut, (d) mulberry, (e) olive, and (f) oak.

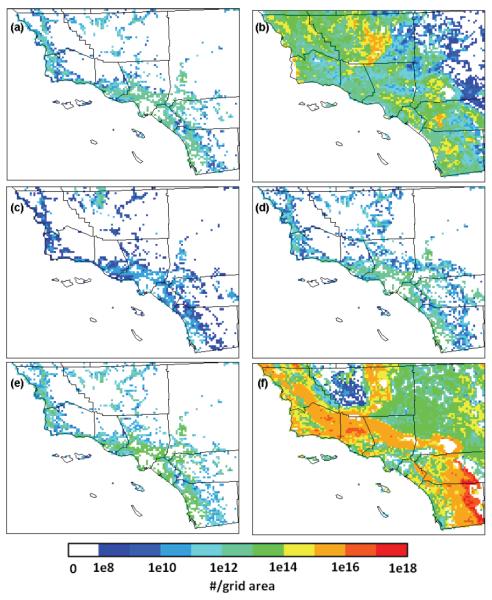
Fig. 5 provides the spatial distribution of simulated total emission potential of six pollen genera during Mar–Jun 2010 over the 4-km domain (D2). The spatial patterns of the different pollen genera vary, with birch (Fig. 5a), walnut (Fig. 5c), mulberry (Fig. 5d) and olive (Fig. 5e) mostly occurring along the coast, and grasses (Fig. 5b) and oak (Fig. 5f) more evenly distributed across the simulation domain. Notice that the color bar in Fig. 3 is on a logarithmic scale; the variation in estimated P_a for different grid cells for different grid cells is high. For instance, the variation of oak tree P_a for different grid cells is greater than ten orders of magnitude, with a maximum value of 1.0×10¹⁸ grains per grid area along southeast border and a minimum value of 1.0×10⁸ grains per grid area near northwest corner of the domain. In terms of absolute value, comparing the total P_a between different pollen genera indicates that oak tree pollen has the greatest potential, with nearly half of the grid cells more than 1.0×10¹⁵ grains per grid area. In contrast, the typical value for walnut trees pollen is only 1.0×10⁹ ~ 1.0×10¹⁰ grains per grid area. The representativeness of the estimated P_a and locations of each pollen genus will strongly impact model performance with respect to final simulated pollen concentrations.

Fig. 5.

Simulated spatial patterns of total pollen emission potential during Mar–Jun 2010 for (a) birch, (b) grass, (c) walnut, (d) mulberry, (e) olive, and (f) oak.

By using the emission flux parameterization scheme described in section 2.2, the hourly gridded emission rates, E_P, of the six pollen genera were calculated for input into the CMAQ model. Only a portion of the pollen potential amount can be emitted into the atmosphere, constrained by the wind conditions. For the different pollen genera, the average fraction of P_a actually emitted varied from 35% for oak to 85% for birch under the base case model configuration. Fig. 6 shows the average diurnal profile of threshold friction velocity (Fig. 6a) and the average normalized hourly emission flux (Fig. 6b) for oak pollen emission during the simulation period for the grid cell that includes Pasadena, CA. By introducing the resistance factor α into Eq. (4), u_*te has a diurnal profile rather than the constant value, which is only determined by pollen physical properties such as diameter and density. At the Pasadena cell location, the daily pattern of average u_*te for oak tree pollen emission (Fig. 6a) peaks in early morning and starts to decline after sunrise with the lowest value around 4 pm local time. This means that there is a higher chance of pollen release to the atmosphere under convective conditions. The average normalized hourly oak pollen emission flux (with standard deviation) at Pasadena shows a dominant peak during afternoon with around 20% of daily total emission release at 4 pm local time and a small peak during evening hours. The calculated typical E_P diurnal profile has a unimodal distribution with the peak in the afternoon, which is consistent with other observational and modeling studies (Jones and Harrison, 2004; Laursen et al., 2007; Marceau et al., 2011).

Fig. 6.

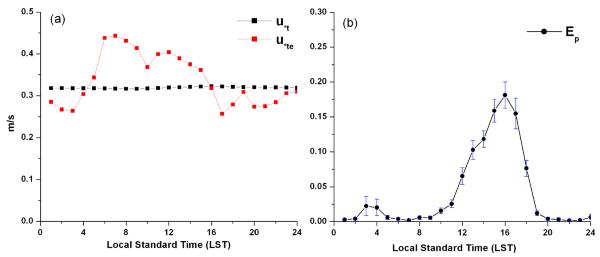
Average diurnal profile of (a) threshold friction velocity and (b) average normalized hourly emission flux with standard deviation (shown as error bars) for oak pollen emission during flowering season at Pasadena CA.

3.3 Pollen Concentrations

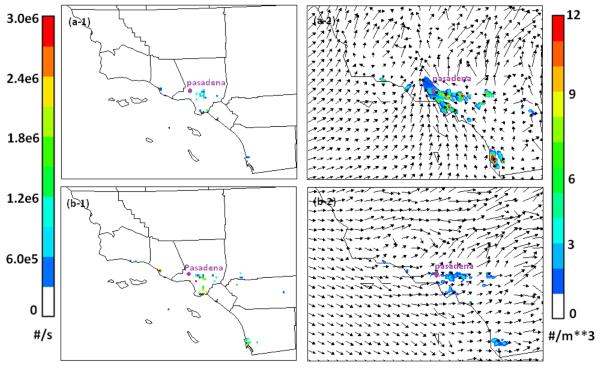
Due to the relatively short lifetime of simulated pollen grains in the atmosphere- half lives of roughly a few hours to a day (Sofiev et al., 2006), the impact of pollen emission on a receptor is highly dependent on the PBL structure and meteorological conditions. Fig. 7 demonstrates how olive pollen emission near Pasadena could impact or not impact the cell containing the city within the course of a single day (April 12, 2010). It can be seen that within 24 hours, the predicted pollen concentration for the receptor site in Pasadena (purple dot in the figure) can vary greatly as the wind pattern changes. During daytime (3 pm Pacific Standard Time (PST)), even though the hourly emission flux is stronger (Fig. 7b-1), the strong sea breeze penetrated several miles inland and diluted the pollen concentration at Pasadena. In contrast, at night (midnight PST), a dominant southerly synoptic flow coupled with the valley (downhill) wind formed a surface convergence zone and caused the local pollen sources to more significantly impact Pasadena. This situation can strengthen with the reduction of PBL height at night. The diurnal variation of simulated olive concentration varied from 0 to 9 grains m⁻³.

Fig. 7.

Simulated olive emissions (left panel) and pollen plumes with wind vector overlays (right panel) on April 12, 2010 (a) at midnight PST when Pasadena was affected; and (b) at 3:00 pm PST when Pasadena, CA was not affected.

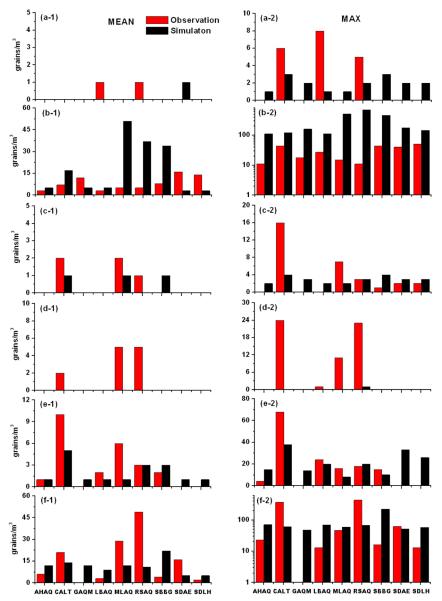
The method for evaluating pollen concentration simulation performance differs from the usual statistical metrics for assessing standard air-quality models. Sofiev et al. (2013) applied threshold-based statistics such as model accuracy, probability of detection, false alarm ratio etc., to assess the SILAM model's ability to predict certain birch pollen concentration thresholds. However, this method requires a large volume of observational data - thousands of samples. Ambient pollen count data are very sparse in the western U.S. Furthermore, the NAB has not allowed access to its historical dataset, which makes it hard to get pollen count data besides the CHS campaign and long-term Caltech data for the simulation period. For this study, daily mean pollen count data are only available from nine sites for the four-month simulation time window. At some sites, the sampling frequency is longer than daily, resulting in an even more limited dataset. Hence, we evaluate the overall model agreement in terms of daily mean and maximum for each site as well as the spatial distribution of pollen concentrations. For clarity in evaluating the spatial representativeness of the model, the nine pollen monitoring sites were grouped into three regions of the simulation domain: 1) Santa Barbara County (SBC), containing pollen site SBBG; 2) Los Angeles Metropolitan Area (LAM), containing pollen sites CALT, LBAQ, GAQM, SDAE, and SDLH; and 3) Riverside & Orange Counties (ROC), containing pollen sites AHAQ, MLAQ, and RSAQ.

3.3.1 Birch tree pollen concentration

Fig. 8a compares the time series of observed pollen count concentration (red dots) and simulated concentration (black line) for case BASE during the four-month simulation window at the Caltech site (CALT). The model can reproduce the observed peak in early May (observed concentration 6 grains m⁻³ versus simulated concentrations 3 grains m⁻³) but misses the earlier observed peaks during March. This is presumed to be due to either a temporal non-alignment between modeled pollen seasons and observed concentrations at large scale during that time (Fig. 4a) or to the presences additional birch species in the domain with unique flowering requirements which were not included in the simulation. Fig. 9a provides the overall performance of WRF/MEGAN/CMAQ modeling system in reproducing the spatial birch concentrations in terms of mean (Fig. 9a-1) and maximum (Fig. 9a-2) at the nine available sites. The mean concentration level for birch during the flowering season is very low (less than 1 grains m⁻³); hence the receptor points in the model can easily miss the pollen plume given the distortion of simulated wind field relative to the observations or the mismatch of emission representation from the STaMPS model. In terms of the maximum concentration prediction, the case simulation BASE tends to underestimate in the SBC and LAM regions but overestimate at ROC region. The results of multiple sensitivity simulations (Table 2) to test the impact of boundary conditions, emission pool size, empirical wind threshold setting, and deposition velocity calculation of birch pollen are summarized in Table 4. The reported values are the average concentration of sites within each of the three grouped regions and are rounded to the nearest integer number. Compared with the case simulation BASE, the case simulations BCON with the dynamic boundary condition did not improve the birch simulation result much. However, by varying the emission pool size estimation, case simulations PAHI and PALO for birch could impact the final simulation results by 30% or more for the maximum concentration. For instance, the simulated maximum at LAM region increases from 2 grains m⁻³ for case BASE to 4 grains m⁻³ for case PAHI compared with the corresponding observed concentration 7 grains m⁻³. No significant model improvement was found with case UTHI and UTLO for birch simulation. The sensitivity simulation that decreased the birch pollen grain mean diameter estimates (DVLO) showed a decreased underestimation of maximum concentration of ~33% over the middle and southern regions of the simulation domain.

Fig. 8.

Time series of simulated pollen concentrations at the Caltech site (CALT) during Mar–Jun 2010 for (a) birch, (b) grass, (c) walnut, (d) mulberry, (e) olive, and (f) oak.

Fig. 9.

Modeled vs. observed mean (left panel) and maximum (right panel) pollen concentrations at nine observation sites for (a) birch, (b) grass, (c) walnut, (d) mulberry, (e) olive, and (f) oak.

Table 4.

Evaluation of simulated daily mean and daily maximum pollen concentrations (grains·m⁻³) for different cases over three grouped regions in southern California.

		Mean (grains·m−3)									Maximum (grains·m−3)
	OBSa	BASE	BCON	PAHI	PALO	UTHI	UTLO	DVHI	DVLO	OBS	BASE	BCON	PAHI	PALO	UTHI	UTLO	DVHI	DVLO
Santa Barbara (SBC) b
Birch	0	0	0	0	0	0	0	0	0	0	3	4	7	3	3	3	3	5
Grass	8	34	36	42	27	32	35	28	39	44	457	479	605	297	451	465	332	547
Walnut	0	1	1	2	1	1	1	1	1	1	4	4	8	4	4	4	3	6
Mulberry	0	0	0	1	0	0	0	0	0	0	1	1	7	1	1	1	1	4
Olive	2	3	3	4	2	3	3	3	3	15	10	11	19	8	10	12	7	16
Oak	4	22	27	32	13	23	25	16	28	16	223	264	289	171	217	250	199	254
LA Metropolitan Area (LAM) c
Birch	1	0	0	0	0	0	0	0	0	7	2	2	4	2	2	2	2	3
Grass	10	6	7	19	4	6	6	4	9	36	141	143	178	92	120	159	110	151
Walnut	1	0	0	1	0	0	0	0	0	7	3	3	10	3	3	3	3	7
Mulberry	3	2	2	2	2	2	2	2	2	13	8	8	11	7	8	10	7	10
Olive	6	3	3	5	2	3	3	4	3	46	20	21	37	16	20	27	15	31
Oak	11	7	8	13	4	6	8	9	6	114	58	69	89	49	51	63	50	77
Riverside & Orange (ROC) d
Birch	1	1	1	1	1	1	1	1	1	5	2	2	3	2	2	2	2	3
Grass	5	31	31	43	19	28	34	27	36	13	181	183	262	127	150	201	154	222
Walnut	2	0	0	1	0	0	0	0	0	9	2	2	7	2	2	2	2	4
Mulberry	4	1	1	2	1	1	1	1	1	17	9	9	13	7	9	10	8	12
Olive	3	2	2	3	2	2	2	2	3	10	7	7	12	7	7	9	7	8
Oak	29	10	10	16	8	9	10	8	12	159	64	64	82	50	60	69	55	72

^aThe description of each simulation cases refer to Table 3.

^bSanta Barbara: includes pollen count sites `SBBG' (Fig. 2);

^cLA Metropolitan Area: includes pollen count sites `CALT', `LBAQ', `GAQM', `SDAE' and `SDLH';

^dRiverside & Orange: includes pollen count sites `AHAQ',`MLAQ' and `RSAQ'.

3.3.2 Grass pollen concentration

For case BASE, the model has poor performance for grass at the CALT site in terms of both the mean value and daily variation trend (Fig. 8b). In terms of the model spatial variation representation performance, the case BASE tends to overestimate the mean grass pollen concentration by 4–6 times over SBC and ROM regions, but exhibits comparable level at LAM region (simulated 6 grains m⁻³ versus observed 10 grains m⁻³). In terms of maximum concentration, the BASE case heavily overestimates by a factor of 10 or more over the whole simulation domain. A possible reason for the overestimation is that the geographic locations of most receptor sites are very close to locations of the peak emission potentials (see Fig. 2b and Fig. 5b). Since the spatial gradient of grass P_a predicted by the STaMPS model is quite large and the magnitude can vary by three orders within a few kilometers (Fig. 5b), the pollen plume from the nearby source will easily impact the receptor sites and cause high spikes in CMAQ simulation under certain wind conditions. For sensitivity simulations, even though decreasing the emission pool size (case PALO) and increasing the grass pollen mean diameter (case DVHI) will improve the overestimation situation from 20% to 38% and 15% to 27% respectively, depending on the region, the current model still has systematic overestimations for grass, which suggests the possible deficits for geographic representation of gridded emission in the STaMPS model.

3.3.3 Walnut trees pollen concentration

For walnut, the simulated concentrations at CALT site is very sparse and systematically low (1 grain m⁻³) compared to observed mean value (5 grains m⁻³ in Fig. 8c), which suggests that the pollen potential or species abundance may be underestimated. The vegetation datasets used in this study could have significantly underestimated walnut distribution if the tree inventory datasets used to determine urban tree species distribution are not representative of the actual urban canopy (Duhl et al., 2013). In terms of spatial distribution, the case BASE also tends to underestimate walnut pollen concentrations both in mean and maximum (Fig. 9c). The total walnut emission potential was 2–3 orders of magnitude smaller during the simulation window compared with other pollen genera (Fig. 5), hence the simulated ground concentration is also low. Sensitivity simulations suggest increasing emission pool size (case PAHI) will result in much better agreement with the observed mean and maximum in all three regions (Table 4), which again implies a tendency for emission underestimation in STaMPS over most of the domain. Varying the settling velocity estimates (case DVHI and DVLO) will impact the simulated maximum concentration by 33% to 133% but has little impact on simulated mean concentration.

3.3.4 Mulberry tree pollen concentration

The case BASE simulation for mulberry compares reasonably well with observations at CALT, following the daily variation trend and keeping the ratio between simulated and observed mean within a factor of two (Fig. 8d). In terms of spatial pattern, the model performance is also reasonably good, with biases for mean and maximum concentrations within ±100% (Fig. 9d). By varying the emission potential estimates, the model performance both for mean and maximum, improved for most regions. For instance, at ROC region the simulated mean concentration for case PAHI increased from 1 grains m⁻³ to 2 grains m⁻³ compared with observation of 4 grains m⁻³ while the simulated maximum concentration increased from 9 grains m⁻³ to 13 grains m⁻³ compared with observation of 17 grains m⁻³. Using lower empirical wind threshold setting (case UTHI) and deposition velocity (case DVLO) will improve the model performance on mulberry maximum value simulation but have little impact on mean value simulation.

3.3.5 Olive tree pollen concentration

For olive the time series comparison for case BASE at site CALT is also in reasonably good agreement with the observed peak during the end of April (Fig. 8e). The model was able to predict the olive spatial distribution pattern, with the predicted mean and maximum values quite similar to observations at several sites, such as SBBG site at the northwestern corner of D2, LBAQ site at the center of D2, and RSAQ site in the southeastern corner of D2 (Fig. 9e). For sensitivity simulations, the case PAHI simulation (Table 4) shows better predictive capability for the maximum concentration at some regions (e.g., from 20 grains m⁻³ to 37 grains m⁻³ compared with observed value of 46 grains m⁻³ at LAM region). Like the model performance for mulberry tree pollen, decreasing pollen diameter estimates (case DVLO) and U_10e setting (case UTHI) will also significantly improve the underestimation of observed maximum value with comparable percentage (20% to 35% for DVLO and 14% to 50% for UTHI) but have nearly no improvement on the mean concentration simulation.

3.3.6 Oak tree pollen concentration

The case BASE configuration for oak performs less well at site CALT (Fig. 7f), missing completely a large observed peak in late March, where the observed peak concentration was ~400 grains m⁻³ but the simulated value was only 150 grains m⁻³ (Fig. 8f). Spatially, no obvious relationship exists between observation and simulation. The observed mean oak pollen concentration peaks at site RSAQ and has the lowest value at site SBBG, which is consistent with the spatial pattern of its emission potential (Fig. 5f). However, the corresponding simulated mean oak pollen concentration at site RSAQ underestimates the observation by nearly a factor of five (11 grains m⁻³ versus 50 grains m⁻³), while at site SBBG there is a factor of five overestimation (25 grains m⁻³ versus 5 grains m⁻³). As discussed in section 3.2, the variation of oak pollen emission potential across the domain is ten orders of magnitude and has high uncertainties. Oak pollen emission in some areas, especially in the highly heterogeneous areas near urban locations, appears to be based on a dataset that is not representative of the actual species distribution. Significant additional work is needed to better constrain this estimate using novel techniques with emphasis on improving species distribution datasets and our knowledge of the timing of phonological events (Duhl et al., 2012). Back trajectory analysis using the NOAA HYSPLIT model (Draxler and Rolph, 2003) shows that air masses reaching the site for three days before the observed peak (May 27) were coming predominantly from the north (Fig. 10a). The sensitivity case simulation BCON only increases pollen concentration by ~10% (from 150 to 177 grains m⁻³), which is still lower by a factor of two relative to the observations. The calculated average settling velocity for oak is quite high (0.0309 m s⁻¹, see Table 1), which means that the atmospheric lifetime is relatively short and that the concentrations of oak pollen are dominated by local dispersion. Thus, the model underestimation of oak pollen at the site CALT may suggest that pollen emission is underestimated near the site. The sensitivity simulations by varying U_10e and velocity V_dp still exhibited systematic underestimations for oak pollen over different regions (Table 4). Instead of the threshold friction velocity method used in this paper, Schueler and Schlünzen (2006) parameterized oak pollen release as the function of water vapor pressure deficit, which was derived by regression analysis from measured temperature, RH, and wind speed with a synchronous record of pollen count. Hence, the universal feasibility of the parameterization scheme described in section 2.2 for oak tree pollen may need to be revised in future simulations.

Fig. 10.

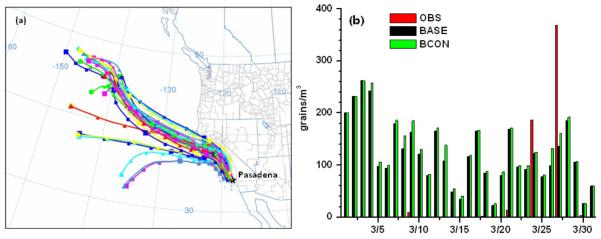
Sensitivity study for oak pollen simulation during the episode around March 27^th, 2010 at Pasadena CA, with (a) three-day back trajectories from HYSPLIT; and (b) model evaluation with pollen concentration boundary conditions from outer domain (BCON) and without (BASE).

4. Summary

In this paper, a regional-scale pollen release and transport modeling framework was developed to simulate pollen concentrations. The regional model includes WRF for meteorological field simulation, MEGAN/STaMPS for pollen emission potential estimates, and CMAQ for pollen tracer transport. The new model STaMPS under the framework of MEGAN was designed to predict daily pollen emission potential based on species-specific pollen pool size, vegetation cover data sets and meteorological conditions. Temperature and precipitation are the major drivers in STaMPS and determine the onset, duration and magnitude of pollen emission potential during the flowering season. The hourly emission flux of pollen was parameterized using friction velocity and a wind effect scale factor. Pollen grains were treated as passive tracers in CMAQ, emitted above the canopy height under favorable wind conditions. Dry deposition and precipitation wash-out are considered the only removal pathways from the atmosphere. Compared with previous regional pollen modeling approaches, this framework has two advantages. First, the MEGAN/STaMPS pollen emission potential model allows a sophisticated dynamic response of pollen potential and release to the key meteorological drivers: temperature, precipitation, and wind speed. This results in a more realistic treatment of the pollen emission temporal variation, with explicit modeling of the onset and duration of the pollen season and explicit treatment of hourly pollen release due to local wind conditions. Second, the new framework can include multiple pollen genera with varying physical properties (e.g. density, diameter, release canopy height) in a single simulation, and can be used not only for retrospective case studies but also for future-climate projection scenarios.

The WRF/MEGAN/CMAQ framework for regional pollen release and transport modeling was evaluated for southern California using four months of simulation, Mar–Jun 2010, which coincided with an extensive set of pollen observations collected as part of the University of Southern California's Children's Health Study. Five allergenic tree pollen genera (birch, walnut, mulberry, olive, and oak) and one grass pollen genus were included in the dispersion and transport model for these simulations. When comparing the means and maxima of pollen observations with the simulation results, the framework exhibited relatively good performance for birch, mulberry and olive, but generally overestimated grass pollen and underestimated the mean concentrations for walnut and the maximum concentrations for oak pollen.

Seven sensitivity simulations were carried out to investigate the impact of the boundary conditions, pollen pool size, empirical wind threshold value, and deposition velocity on the model results. Adding outer domain simulations to provide dynamic boundary conditions slightly improved the model performance under favorable wind conditions. Simulation results are very sensitive to the estimated pollen emission potential, both in terms of magnitude and spatial distribution. With respect to uncertainty in the pollen emission potential, here we have only addressed the uncertainty associated with pollen pool size. As discussed in the companion paper (Duhl et al., 2013), the errors in speciation composition and in applying tree inventories for urban areas are potentially large but have not been quantified, nor can they be quantified until there are relevant species-composition ground-truth datasets available to do so. Thus, the uncertainty associated with pollen emission potential is potentially greater than those addressed in the sensitivity simulations performed here. The time alignment between predicted emission potential by the MEGAN/STaMPS model and regional-scale pollen observations is a key factor for successful CMAQ simulation. For walnut, mulberry and olive tree pollen, adjusting the empirical wind threshold value or deposition velocity setting in CMAQ or MCIP can significantly improve the model performance on maximum concentration, which is important for epidemic exposure study. However, the current pollen release parameterization scheme still was unable to reproduce the observed pattern for grass and oak pollen even taking all above sensitivities into account. More concurrent observations linking the meteorological factors to the pollen count data are needed to refine the parameterization scheme to achieve improved model performance.

The accuracy of simulated wind fields in WRF is one of the key factors for accurate pollen transport simulation. Data assimilation (both analysis nudging at the outer domain and observational nudging at the inner domain) was used in WRF to improve model performance. However, the model tends to overestimate wind speed, especially during the calm wind conditions. This leads to overestimation of hourly emission flux. On the other hand, higher wind speeds tend to distribute the pollen grains over longer distances and thus can lead to underestimation of ambient pollen concentrations.

Pollen resuspension processes including the rebound and re-entrainment of pollen after deposition to the ground or plant surface could contribute to increased airborne pollen concentrations (Jarosz et al., 2004; Helbig et al., 2004). These impacts are more pronounced during gusty winds over relatively dry terrain (Sofiev et al., 2013). Our current modeling framework does not include this phenomenon due to lack of understanding of the behaviors of pollen grains after they contact the surface (Helbig et al., 2004). Dupont et al. (2006) introduced a simple resuspension rate as a fraction of deposited pollen amount to calculate the resuspension flux. The underestimation of oak pollen especially may be improved by incorporating this physical process into the modeling framework. The uncertainly in pollen size distribution and its impact on bulk dry deposition rate is not fully addressed in this study. Pollen grains are not ideal spheres. Many have very distinctive shapes, some of which are adapted to the function of increasing the probability of lofting or the time aloft. A single average value for the diameter and density for all the lumping species under each genus may not be representative. Another limitation of current modeling efforts is to treat pollen only as intact grains without considering the behavior of their respirable fragments. Compared with whole pollen grains with relatively large diameters (see Table 1), the smaller pollen fragments are capable of depositing in the lower respiratory tract and triggering asthma (Miguel et al., 2006). A parameterization of the pollen rupture process and estimation of released pollen number size distribution is a key future direction to improve regional pollen transport models. The uncertainties in rainfall prediction are another potentially liming factor. The location and timing of rainfall is difficult to predict especially over the complex terrain of southern California; a single rain event could effectively wash out most pollen from the air. For future work, additional important allergenic pollen species over the study area such as sagebrush should also be added into the model framework to quantify their concentration variation and associated health impacts. Also for future work, public release of the historical ambient data from the National Allergy Bureau would allow for a far more extensive evaluation of the modeling framework, should that data ever become more widely available. Finally, direct wind tunnel laboratory measurements on pollen emission under different wind conditions are also needed to better quantify the different threshold friction velocity for different pollen species.

In terms of the application of this regional pollen release and transport modeling platform on predicting the pollen exposure due to climate change, the companion paper Duhl et al. (2013) demonstrated its capacity by estimating the pollen production potential difference under current (1995–2004) and projected future (2045–2054) meteorological conditions. The future climate simulation is the WRF downscaling results of the ECHAM5 global climate model under the IPCC A1B scenarios. With the projected warmer temperature and less precipitation in spring and summer over California by climate model, pollen seasons will occur an average of 5–8 days earlier with 0.1–10% less pollen production amount than the current scenario, depending on the species considered. The ambient pollen exposure level will also subject to noticeable change due to the change of pollen production potential, and will bring challenges for mitigating allergenic airway disease in the future.