Abstract
Although noise has a proven beneficial role in brain functions, there have not been any attempts on the dedication of stochastic resonance effect in neural engineering applications, especially in researches of brain-computer interfaces (BCIs). In our study, a steady-state motion visual evoked potential (SSMVEP)-based BCI with periodic visual stimulation plus moderate spatiotemporal noise can achieve better offline and online performance due to enhancement of periodic components in brain responses, which was accompanied by suppression of high harmonics. Offline results behaved with a bell-shaped resonance-like functionality and 7–36% online performance improvements can be achieved when identical visual noise was adopted for different stimulation frequencies. Using neural encoding modeling, these phenomena can be explained as noise-induced input-output synchronization in human sensory systems which commonly possess a low-pass property. Our work demonstrated that noise could boost BCIs in addressing human needs.
Noise, as a ubiquitous random or unpredictable fluctuation or perturbation, commonly exists in neural systems of humans and other mammals. The concept of stochastic resonance (SR), which was introduced in the early 1980s by Benzi1, describes the phenomenon whereby random fluctuations or noise can enhance the detectability and/or synchronization of a weak signal in certain non-linear dynamic systems, i.e., noise paradoxically does not worsen but improves system performance. The “beneficial” effects of noise have widely existed in excitable neural systems, and both experimental studies and theoretical investigations have shown particular circumstances in which synchronization of neuronal firing was enhanced by the presence of random fluctuations2,3,4,5. At the level of neural ensembles, synchronized firing patterns would give rise to large-scale macroscopic oscillations, which can be observed in electroencephalography (EEG). Srebro and Malladi6 have successfully observed the enhancement of steady-state visual evoked potential (SSVEP) with presentation of alternating visual noise and gratings. However, as some researchers like Farquhar J. et al.7,8,9 have used noise-tagged stimulation for its spread spectrum advantage in BCI applications, there have not been any reports on noise-benefited brain-computer interfaces (BCIs) under SR mechanism. Moreover, the extent of performance improvements in SR-manipulated BCIs has not yet been demonstrated.
In this work, we showed that presenting visual noise to subjects can reliably enhance oscillatory EEG activities for BCI applications. We proposed a novel steady-state motion visual evoked potential (SSMVEP, i.e., one kind of SSVEP) based BCI (SSMVEP-BCI) paradigm10 with motion stimulation plus three-dimensional (3D) spatial-temporal visual noise to investigate the influence of external noise on promotion of SSMVEP that would eventually enhance BCI performance. In this paper, visual noise under different intensity levels was used to mask steady-state motion stimulation for the evoking of SSMVEP, while a multivariate objective detection method evaluated the optimal noise level that would maximize SSMVEP responses and thus BCI accuracy and efficiency. Finally numerical simulation analysis to qualitatively mimic encoding of periodic stimulation into spike trains in the presence of visual noise was used to elucidate how such irregularity affected spiking and synchronization of neuron ensembles. Our work demonstrates that SR effect would enable a new generation of BCIs to provide superior performance and additional flexibility.
Results
SR effect was observed in offline experimental analysis
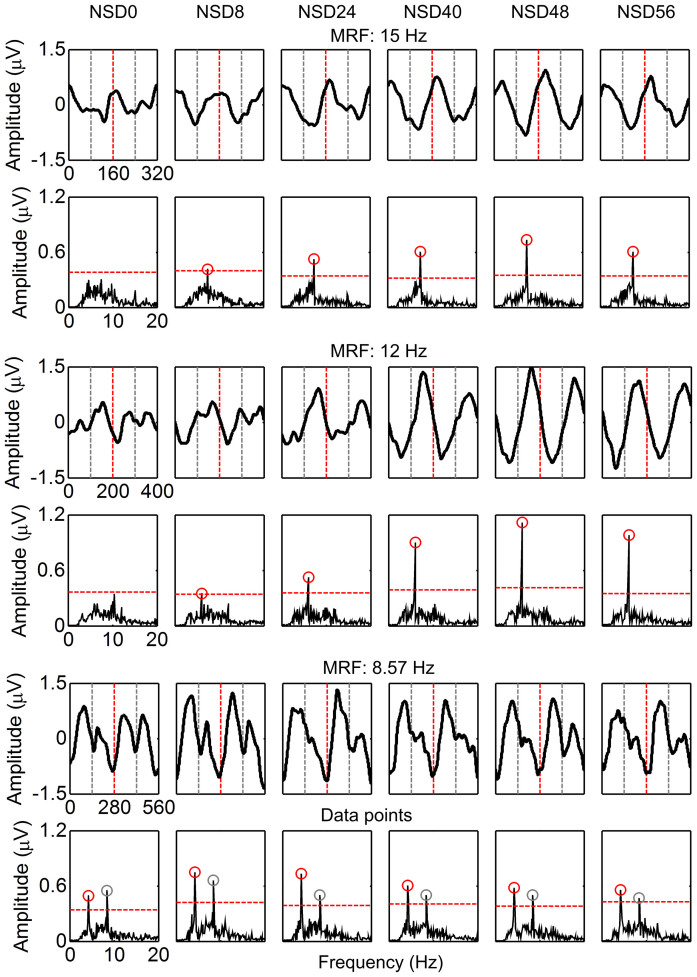
Of the twenty subjects that participated in this study, seven male subjects (Subjects 1–7) were first studied in offline experiments to examine brain responses under SR mechanism. Here 3D spatial-temporal visual noise, which referred to as dynamic changes of two-dimensional (2D) spatial noise speckles in one-dimensional (1D) timeline, was used to mask stimulators and updated in 1/60 second. Noise speckles obeyed 2D Gaussian intensity distributions with gray mean (gray level = 128), and noise intensity level was graded by noise standard deviation (NSD) of 0, 8, 24, 40, 48, or 56 (see Supplementary Figure S1 online). For each subject, 30 epochs were recursively implemented as the subject attending on a specific stimulator under a certain visual noise level. Among the seven subjects, the magnitudes of grand-averaged SSMVEP evoked by motion reversal frequencies (MRFs) of 15 and 12 Hz were progressively increased to maxima under NSD of 48 and then decreased, showing a bell-shaped resonance-like form as a function of noise strength (i.e., a fingerprint of SR phenomenon; Figure 1). The maxima were about two and three times higher than that under NSD of 0. Corresponding SSMVEP spectra at sub-harmonics (i.e., motion stimulus harmonics, MSHs) of 7.5 and 6 Hz increased about three and six times under NSD of 48 compared to that under NSD of 0 (Figure 1). Specifically, motion reversal harmonics (MRHs) and MSHs did not reach their maxima concurrently. As forcing frequency decreased, a noise-induced suppression of MRHs occurred along with the resonance enhancement at the MSHs, which can be clearly observed in SSMVEP spectra evoked by MRF of 8.57 Hz (Figure 1) till the NSD increased up to 8. More specific phenomena can be found in individual subjects (see Supplementary Figure S2 online), where averaged SSMVEP on some subjects (e.g., MRF of 12 Hz in Subject 1 and 6 and MRF of 8.57 Hz in Subject 7) consisted of two nearly identical waves corresponding to each motion reversal when no noise masked, and merged to a single wave when noise increased.
Figure 1. Grand-averaged offline SSMVEP magnitudes and spectra as a function of NSD for seven subjects.
For grand-averaged SSMVEP, each panel shows averaged SSMVEP within two cycles of motion-reversal stimulation (i.e., four motion reversals) with the NSD marked above it. In panels, two cycles are separated by vertical dotted lines in red and two motion reversals within one cycle are separated by dotted lines in gray. For amplitude spectra of averaged SSMVEP, each panel shows SSMVEP spectrum at the MRH and MSH with the NSD marked above it. Horizontal dotted lines in red indicate the threshold to visualize the significance of SSMVEP spectra under different NSDs, which was empirically chosen as six times the mean of the amplitude spectra between 3 and 30 Hz. Gray circles indicate the MRHs of SSMVEP spectra above the threshold. Red circles indicate the MSHs above the threshold.
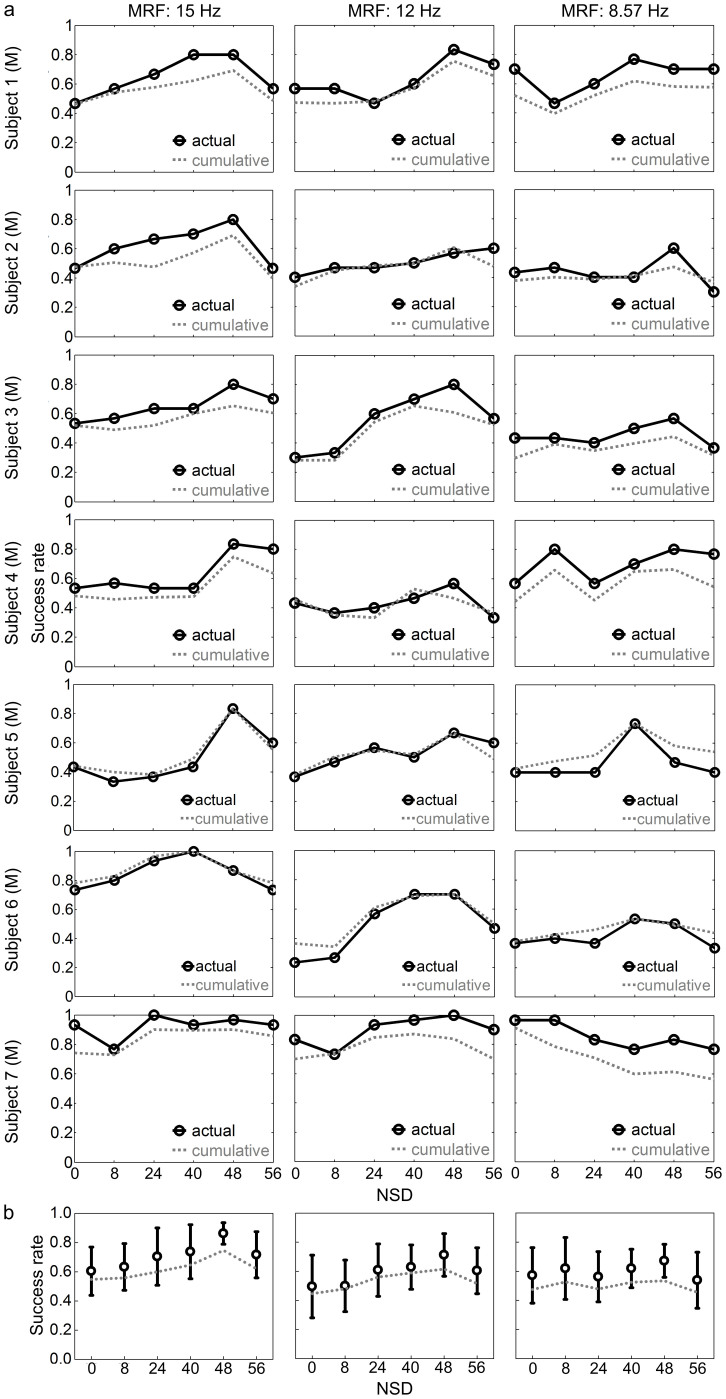
For the simultaneous suppression of MRH and enhancement of MSH when noise increased, SSMVEP spectra on the two components were concurrently introduced into multi-harmonic-generalized Circular Hotelling's T2 test (GT2circ)11 to quantify whether SSMVEP magnitudes boost at a certain noise level would quantitatively benefit SSMVEP-BCI performance. Across all three MRFs, offline success rates (Figure 2a) over 5-s epochs exhibited bell-shaped correlation with noise for most subjects, and also peaked at NSD of 48, similar to SSMVEP spectra distributions (Figure 1). The mean success rate across all seven subjects significantly increased from 60.42% ± 17.68 (range: 43.33–93.33% correct epochs) under NSD of 0 to a maximum of 86.25% ± 7.86 (range: 80.00–100.00% correct epochs) under NSD of 48 at MRF of 15 Hz (one-way ANOVA: F(1,12) = 14.27, P = 0.002, Cohen's d = 1.888), and from 49.58% ± 22.99 (range: 23.33–83.33% correct epochs) to a maximum of 71.25% ± 15.63 (range: 56.67–100.00% correct epochs) at 12 Hz (F(1,12) = 4.86, P = 0.045, Cohen's d = 1.102). The same trend of increase can be seen at 8.57 Hz, from 57.14% ± 20.59 (range: 36.67–96.67% correct epochs) under NSD of 0 to a maximum of 67.14% ± 12.24 (range: 50.00–83.33% correct epochs) under NSD of 48; however, this effect does not reach statistical significance (F(1,12) = 1.22, P = 0.291, Cohen's d = 0.590; Figure 2b). More specific success rates over six different time-window lengths from 2.5 to 5 second per epoch can be found in Supplementary Figure S3 online. Corresponding cumulative mean accuracy, which statistically approximates expected SR correlation, is represented in Figure 2a. Exceptions can also be found at MRF of 8.57 Hz whose resonance points shifted to lower noise values (e.g., in Subject 4) or even vanished (e.g., in Subject 7), which was consistent with SSMVEP magnitudes and spectra distributions (see Supplementary Figure S2 online). This resulted in multiple peaks in the cumulative mean-accuracy curve averaged across subjects (Figure 2b).
Figure 2. Offline success rates as a function of NSD.
(a) Success rates for individual subjects. Each circle on the solid black curve indicates actual success rate over the 5-s epochs with the NSD marked below it. The actual success rates under different NSDs were calculated as the percentage of correctly judged epochs within 30 epochs. Dotted gray curves indicate the cumulative average of accuracies, which was calculated as the mean of the success rates over six different time-window lengths from 2.5 to 5 second per epoch in steps of 0.5 second. (b) Success rates across seven subjects. Error bars in black indicate mean and SD of accuracies over 5-s epochs across subjects. Dotted gray curves indicate the cumulative average of accuracies across subjects. The character ‘M' in brackets indicates male subjects.
SR promoted accuracy and efficiency in online brain-control tasks
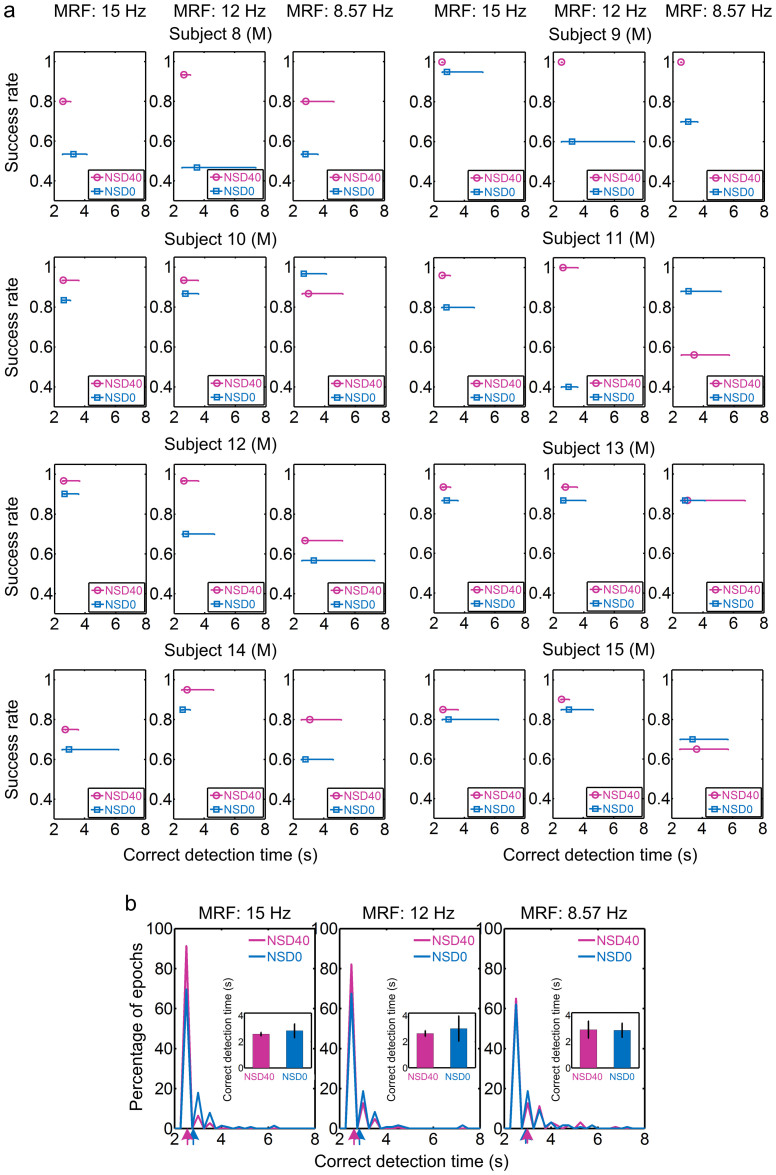
Motivated by the performance promotion of offline experimental tasks under visual noise masking, we developed an online SSMVEP-BCI under non-noise and NSD of 40 conditions to quantify whether practical BCIs could benefit from SR. Eight male subjects (Subjects 8–15) participated in online brain-control tasks performed using a cathode-ray tube (CRT) monitor. The task was implemented in a semi-synchronous way, wherein the duration of stimulation varied from 2 to 10 second until the target was successively identified twice as being the same. Thus, online success rate and correct detection time, which characterized BCI accuracy and efficiency, were assessed to benchmark system performance under different noise levels. Since the concurrence of high success rate and the preference of correct detection time to predefined minimal values implied superior performance, it can be seen that tasks at MRFs of 15 and 12 Hz under NSD of 40 performed better than that without visual noise, especially in Subjects 8–9 and 11 (Figure 3a). Exceptions also occurred at MRF of 8.57 Hz in Subjects 10 and 11, where both accuracy and efficiency prevailed under NSD of 0 rather than 40. This was analogous to offline results in Subjects 4 and 7 (Figure 2).
Figure 3. Online success rate and correct detection time under NSD of 40 versus 0 in semi-synchronous online brain-control tasks performed using a CRT monitor.
(a) Online success rate and correct detection time for individual subjects. Results under NSD of 40 are shown in magenta and those under NSD of 0 are in blue. Each error bar characterizes the distribution of correct detection time upon a certain success rate that was calculated as the percentage of correctly judged epochs. The upper and lower bounds of each error bar were set with maxima and minima of the time distribution, and the central point (circle and square) represents the mean. For convenience, the upper end of the ordinate was set above 1. (b) Histograms of detection time of correctly detected epochs across eight subjects. Insets show grand-averaged correct detection time. Arrows below plots mark the mean value for each histogram.
Across subjects, grand-averaged online success rates under NSD of 40 significantly increased 36% (one-way ANOVA: F(1,14) = 13.50, P = 0.003, Cohen's d = 1.837) at MRF of 12 Hz (NSD40, 95.21% ± 3.50 vs. NSD0, 70.00% ± 19.09), while the same trend of variation of 14% (F(1,14) = 3.47, P = 0.084, Cohen's d = 0.931) can be found at 15 Hz (NSD40, 89.92% ± 8.89 vs. NSD0, 79.17% ± 13.69). But only 7% difference (F(1,14) = 0.43, P = 0.525, Cohen's d = 0.326) existed at 8.57 Hz (NSD40, 77.63% ± 14.26 vs. NSD0, 72.67% ± 16.09). Whereas grand-averaged correct detection time under NSD of 40 was significantly less than that under NSD of 0 at 15 Hz (NSD40, 2.60 ± 0.20 seconds vs. NSD0, 2.83 ± 0.61 seconds; unbalanced one-way ANOVA: F(1,298) = 20.33, P = 9.390 × 10−6, Cohen's d = −0.519) and at 12 Hz (NSD40, 2.67 ± 0.31 seconds vs. NSD0, 2.88 ± 0.74 seconds; F(1,288) = 10.74, P = 0.001, Cohen's d = −0.392; Figure 3b). The smaller fluctuation of correct detection time under NSD of 40 also signified greater identification consistency and fewer potentially frustratingly long epochs. This was largely due to the higher percentage of successfully detected epochs (91% at 15 Hz and 82% at 12 Hz) around 2.5 second (minimal time to identify targets) under NSD of 40 versus 0 (70% at 15 Hz and 67% at 12 Hz; Figure 3b). Small variation of correct detection time was observed under NSD of 40 versus 0 at 8.57 Hz (NSD40, 2.98 ± 0.79 seconds vs. NSD0, 2.96 ± 0.76 seconds; F(1,261) = 0.04, P = 0.845, Cohen's d = 0.026), where visual noise wielded little beneficial influence on this frequency. These results suggested that certain noise level can effectively promote both accuracy and efficiency of SSMVEP-BCI on most forcing frequencies, while little inconsistency on lower frequencies would not substantially affect BCI performance across subjects. Some tasks above showed nearly perfect performance in 100% success rates when optimal visual noise was applied, that is, a ceiling effect (see Figure 3a). Thus, to evaluate the explicit difference between conditions with and without visual noise, we tested an additional group of nine subjects on LCD monitor. Results in Supplementary results and Supplementary Figure S4a online showed that tasks on LCD monitor prevented the ceiling effect and uncovered some import phenomena, such as the similar, but more prominent, exceptions at MRF of 8.57 Hz. The difference between CRT and LCD tasks may due to the fact that the stimulation brightness of LCD monitor is lower than that of CRT monitor12.
SR and low-pass behavior can be explained by neural encoding simulation
Considering the addition of visual noise on the promotion of SSMVEP-BCI performance and its different impacts on higher and lower forcing frequencies, we investigated the ensemble properties of 10,000 perfect-integrate-and-fire (PIF) neurons in response to motion stimulation with spatial-temporal noise, while the SR effect was characterized by interspike intervals (ISIs) at MSH periods13. This selection was consistent with experimental results that the SSMVEP boost came from resonance enhancement at the MSHs.
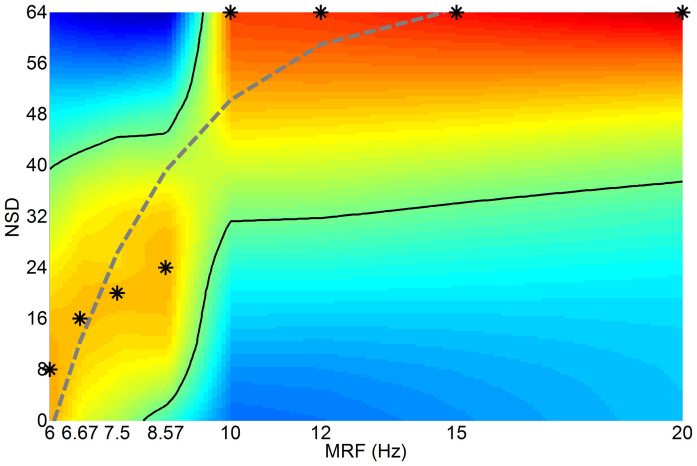
In Figure 4, it can be seen that the normalized ISIs at each forcing frequency increased to a maximum and then decreased with increasing noise. This is because low noise levels were associated with random cycle skippings between any two successive firings, which led to aperiodic firings and multimodal distribution of ISIs. As noise increased, the ISIs drew closer to the MSH period, indicating that spikes fired more regularly with less skipping. This is referred to as noise-induced synchronization, or SR. Further increase of noise would result in an increased proportion of firings within a single cycle, tending towards noise-induced bursts regardless of forcing frequency.
Figure 4. Simulation of SR evolutions among different forcing frequencies.
For eight MRFs of 6, 6.67, 7.5, 8.57, 10, 12, 15, and 20 Hz (i.e., with MSHs of 3, 3.33, 3.75, 4.29, 5, 6, 7.5, and 10 Hz) and seventeen NSDs of 0–64 in increments of 4, normalized ISIs at the period of each MSH was assigned to the surface plot using linear interpolation, and the positions of larger values are depicted by warmer colors. Asterisk (*) indicates maximal ISIs at each MSH period. Solid black curves indicate the contour of the effective region of large ISIs, while dotted gray curve indicates the exponential approximation of relationship between optimal NSDs and forcing frequencies.
It also can be seen in Figure 4 that the effective region of normalized large ISIs extended to larger noise levels when the forcing frequencies became higher; low forcing frequencies tended to be optimized at low noise levels, while stronger noise was required to maximize high-frequency responses regardless of where PIF threshold boundaries were drawn. Distinct dispersion between responses at MRFs of 8.57 Hz and at 12, 15 Hz was also observed. This may be due to the low-pass phenomenon, wherein membrane voltage was progressively dampened below threshold with increasing forcing frequency. So, large noise was required to push the membrane voltage across threshold when forcing frequency was high. The slope of the “optimal NSD – forcing frequency” curve (Figure 4) varied as a function of forcing frequency, which approximately obeyed NSDOPT ~ e−μf with μ > 0. This function demonstrated that the growth rate of optimal noise level NSDOPT would slow down when forcing frequency f increased, which qualitatively confirmed the dispersion between responses at MRFs of 8.57 Hz and at 12, 15 Hz and the almost identical optimal noise levels needed by MRFs of 12 and 15 Hz in the experimental results.
Discussion
Up to the present, SR terminology was used frequently in a broad sense, referring to any kind of noise-constructive phenomena in non-linear systems14. The beneficial role of noise in the nervous system was supposed to enhance the transmission of neural signaling15,16,17 and was evidenced in photo- and mechanoreceptors of crayfish2,18, sensory cells of sharks19, and visual perception tasks of humans20. Since nerve cells in sensory organs are described as thresholding devices without assuming particular mechanisms, the subject of SR has evoked excitement in the field of computational neuroscience, especially in visual21 and auditory22 processing, and cognition23. The purpose of the present study was to gain a general understanding of noise-enhanced neural encoding in the human visual system using a SSMVEP-BCI approach and provide a model that bridged the complexity of biophysical observations with the simplicity of noise-induced synchronization and linearization in neural firings. This work helps clarify the conditions under which such SR phenomena could occur, as well as their underlying mechanisms.
In our study, offline and online tasks with periodic visual stimulation plus moderate spatiotemporal noise can achieve better performance, implying that human visual systems may exploit the power of randomness to enhance neural signal transmission. Noticeable exceptions were that the tasks at MRF of 8.57 Hz manifested low performance under a certain noise level which seemed to optimize performance of the other two stimulations (i.e., 12 and 15 Hz). This was likely caused by the low-pass property of sensory neurons. Therefore, it would be more feasible to utilize each individual optimal noise level for each stimulation frequency separately to promote BCI performance. However, in the current study, a fixed noise level would be adequate to promote SSMVEP-BCI performance on almost all stimulation frequencies and a little inconsistency would not substantially affect BCI performance across subjects. In addition, individual optimal noise levels were needed for different subjects even at the same stimulation frequency. This may be due to the high variability of sensory thresholds and internal noise sources which would result in different selectivity of cells in the visual cortex such that some subjects may have already been optimized intrinsically6. Applying the right amount of noise to each specific subject would reduce the inter-subject variability.
It is important to note that sensory neurons frequently interact with periodic stimulations. When a subject is presented with a visual stimulation, light information will arrive at the photoreceptors of the retina and propagate through the optic nerves to the visual cortex and other higher-order sensory or cortical regions. The relation between visual modulations and sensory neuronal input is monotonically proportional, so modulation strength which is not large enough to push the neuronal membrane voltage across the intrinsic threshold non-linearity alone would be properly assisted with visual noise at a moderate intensity to accomplish threshold-crossings. Therefore, the appearance of SR can be roughly explained by that addition of visual noise effectively turn neurons from sub- to supra-threshold. This procedure was illustrated by the simultaneous stimulation of PIF neurons with periodic drive and noise. The model qualitatively predicted some of salient features which can be observed in experimental recordings; the fits from PIF simulation to experimental results are surprisingly good, which indicates that the model has theoretical and practical significance.
It is also known that neural responses to sinusoidal visual modulations often show considerable harmonic distortions which can be attributed to threshold non-linearity; the amplitudes of Fourier components at the harmonics will be modified and the responses distorted in comparison to the input. With addition of visual noise, the input shifts from the threshold so regularly that the synchronization between periodic drive and crossing events increases, while the contribution of threshold non-linearity decreases. The output becomes more sinusoidal to the input than it would have been. This enlarges the spectral coherence that measures the periodicity and removes other harmonic distortions (i.e., addition of noise linearizes the responses). This so-called noise-induced linearization (NIL) can be categorized within the framework of SR24,25,26. The NIL phenomena can be observed in Figure 1, where the spectra quantifying the input-output synchronization exhibited a strong increase of peak height at each MSH (i.e., SR) and a steady reduction of peak height at each MRH when noise increased. Growing noise would bring linear susceptibility at high frequencies (Figure 4), and with the further increase of noise, the Fourier peak which closed to the MSH would finally disappear due to the variability of firings is increased so as to cause the responses to be noisy and even destroyed.
Results display an abundance of low-pass behaviors (Figures 1,2,3,4), wherein an increase in forcing frequency would be optimized by an increasing noise level. This may originate from the low-pass phenomenon existing in visual pathways27; attenuation of the average high-cutoff frequency can be observed from spike responses of lateral geniculate nucleus (LGN) cells to responses in input layers of the V1 region when multiple LGN cells converged into a single V1 cell. A major attenuation from V1 input layers to the second- and higher-order neurons in V1 and even to extrastriatal area V2 also exists. The occurrence of this low-pass phenomenon in real visual systems may result from membrane resistive and capacitive characteristics of sensory neurons and associate with the fact that an increased input frequency would weaken the modulation of noise-free membrane voltage28. Therefore, the higher the forcing frequency, the more noise is required to make real neuron fire. The capacitive low-pass membrane modeling in the neuron-like model is directly related to cellular biophysics29 so simulation results were in line with experimental observations among different forcing frequencies. The exceptional deviation between the position of optimal noise levels in experiments and that of normalized maximal ISIs in theoretical simulations may be due to the presence of internal noise in living neurons30,31, which was not taken account into neuron-like modeling. Therefore, more external noise was needed in the theoretical model to mimic the same total amount of noise.
Our simulation study of parallel arrays differs from other types of neural networks in that elements are not actually coupled. The motivation primarily stems from a number of neurophysiological studies showing that sensory neurons tend to be arranged in a highly parallel structure and possess all features necessary for exhibiting SR32. Note that, the numerical parameters in our study are at a physiologically relevant range and tuning neural signal transmission independent of specific parameter values does not remove the beneficial role of noise.
Taken together, our work suggests that it may be possible to artificially introduce noise into sensory neurons in order to improve neural signal transmission. With “optimal” transduction, noise-induced neuronal synchronization at the single neuron level may lead to a similar effect in large-scale synchronization of certain sensory organs33, or even brain waves34, as improving SSMVEP-BCI performance in our study. Given evidence of SR in various functional levels of biological systems, our results may provide insight on how resonance promotes perceptual and behavioral functions in neural engineering applications; it is not surprising that SR holds potential for the future design of neural prostheses controlled by BCIs in health rehabilitations, by suggesting that rehabilitation paradigms, which take advantage of cortical neuronal plasticity, will likely benefited from the excitability of neurons with SR mechanism35.
Methods
Subjects
All subjects, aged 23–29 years old, were graduate students from Xi'an Jiaotong University (Shaanxi, China). All had normal or corrected-to-normal eyesight and experienced SSVEP-BCIs before. All subjects were studied after giving informed written consent in compliance with the guidelines approved by the institutional review board of Xi'an Jiaotong University. Of the total twenty subjects, seven male subjects were first tested in offline experiments, which were performed using cathode-ray tube (CRT) monitor, to assess whether SR existed in SSMVEP or not. The other thirteen subjects only participated in online brain-control tasks, in which eight males were tested using CRT and liquid crystal display (LCD) monitors, and six males and three females were tested with LCD monitor.
Stimulation design
Motion-reversal visual stimulations were introduced into the spatial selective attention-based steady-state BCI paradigm. Three motion-reversal stimulators were simultaneously presented to subjects through a gamma-corrected 21″ EIZO CRT or a 22″ Dell LCD monitor at a resolution of 1024 × 768 pixels and refresh rate of 60 Hz. Each subject was situated 70 cm from the screen with the center at eye level. Three stimulators were uniformly arranged in an equilateral triangle with the eccentricity from the center of the monitor to that of each stimulator at a visual angle of 7.2° (Supplementary Figure S5 online). Each stimulator was a motion ring whose width was kept constant at half the radius of the circular region (Michelson contrast of 98.8%) throughout the motion reversal procedure. The circular area was 4.8° in diameter, in accordance with previous studies showing that a stimulus size beyond 3.8° would saturate VEP responses36. Each stimulator was distinct at mutually irrational MRF, and MRFs of 15, 12, and 8.57 Hz were assigned to the lower right, lower left, and upper stimulators, respectively, in accordance with the integer division of 60 Hz refresh rate. The motion reversal procedure was scheduled according to our earlier study10. Here 3D spatial-temporal noise, which referred to as dynamic changes of 2D spatial noise speckles in 1D timeline, was used to mask stimulators and screen background, and updated in 1/60 second. Each noise speckle subtended a square area of 5 min of visual angle and obeyed 2D Gaussian intensity distributions with gray mean (gray level = 128). Noise level was graded by NSD of 0, 8, 24, 40, 48, or 56 (see Supplementary Figure S1 online). It should be noted that for avoidance of truncation beyond the gray level range of [0, 255], where grayscale noise becomes black and white, the strongest NSD is restricted to within 64. Presentation of the stimulation was controlled by Psychophysics Toolbox (http://psychtoolbox.org/)37,38.
Offline experimental tasks
Subjects were requested to sit on an armchair in a dimly lit room without electromagnetic shielding. Just as traditional SSVEP-BCIs, subjects were asked to binocularly fixate on the center of the target stimulator and were instructed not to track stimulator movement or the varying of noise with their eyes. The three stimulators were simultaneously presented and visual noise level was constant throughout the 5-s epoch. Two adjacent epochs were isolated by a gray screen, and the interval time was fixed to 1.5 second. An experimental run involved 15 such epochs and lasted 1.6 min. For each subject, six experimental tasks were performed, and each task (Tasks 1–6) was implemented under each of six NSDs, respectively. Tasks 1–6 were performed randomly to avoid adaptation of long-term stimulation that could potentially affect assessment of SR effect39. Each task contained six runs, where every two runs were implemented on an identical stimulator. Subjects were allowed to blink or rest their bodies as long as they wished between runs. Therefore, horizontal or vertical electrooculography signals were not recorded and epochs contaminated by few artifacts were also not excluded.
Target identification
For each epoch, a GT2circ test, which is a multi-harmonic version of the famous Circular Hotelling's T2 (T2circ) test40, was used to check the presence of SSMVEP on the statistics of responses at each MRH and its MSH sub-harmonic. Each rectangular sliding window corresponding to three cycles of each MRF stimulation (i.e., 840 data points for MRF of 8.57 Hz, 600 data points for 12 Hz, and 480 data points for 15 Hz) was sequentially slid over the epoch with one-cycle overlap (i.e., 280 data points for 8.57 Hz, 200 data points for 12 Hz, and 160 data points for 15 Hz) and then submitted to fast Fourier transform (FFT) operation individually. If the epoch was not evenly divisible into integer cycles, the end of the epoch was truncated. The resulting sets of complex Fourier components corresponding to each MRH and its MSH sub-harmonic were converted to a four-variable matrix and passed to each GT2circ test. GT2circ provides a probability to determine whether sets of Fourier components are consistent with random fluctuations alone or imply the presence of periodic components beyond a given confidence level. If the Fourier components at each MRH and its MSH sub-harmonic were sufficiently strong to exceed the confidence level, the presence of SSMVEP at this MRF was statistically identified. In our study, the confidence level was set as 0.95 in offline analyses and 0.99 in online brain-control tasks. The stimulation with the maximal confidence probability exceeding the confidence level would be classified as attended stimulation.
Online brain-control tasks
Similar to offline experiments, two sessions (i.e., each under NSD of 0 and 40) of online brain-control tasks were implemented on each subject to compare online brain-control performance under different noise levels. Each session contained 6–12 runs and each run consisted of 15 epochs. Experimental runs under NSD of 0 and 40 were also performed randomly to avoid adaptation of long-term stimulation. The main difference from offline experiments was that online brain-control tasks were implemented in a semi-synchronous way wherein the duration of stimulation varied from 2 to 10 second rather than fixed to 5 second. In each epoch, 1 second of red cue above the target stimulator instructed subjects to pay attention to that stimulation. Then two seconds of stimulations were presented and EEG signals were recorded and delivered to GT2circ test. The duration of stimulation increased in steps of 0.5 second such that the window sliding, FFT processing, and GT2circ evaluation would repeat until the target was twice identified as the same stimulator in succession (either correct or not). This means that the minimal time to identify a target was around 2.5 second. Once the target was identified, another 1 second of green cue appeared in the center of the screen to mark the result and the epoch ended. If brain responses failed to meet the detection criteria for any of the three stimulations beyond 10 second, this epoch would end with no cue.
To benchmark brain-control performance under different noise levels, we analyzed online success rate and correct detection time. The online success rate was assessed as the percentage of correctly judged epochs. The correct detection time encompassed the stimulation duration and corresponding detection time when the target was correctly judged.
Statistical analysis
Data are expressed as mean ± SD. The statistics significance was evaluated using one-way ANOVA. The criterion for statistical significance was p < 0.05.
Numerical simulation
To study the information transmission of SR behavior in SSMVEP of different frequencies, a straightforward neural encoding scheme was designed to mimic the relationship between sensory stimulation and brain responses characterized by macroscopic properties of neural populations. Rather than modeling a specific region of the human visual system, this simulation only considered general encoding of an array of biophysically uncoupled PIF neurons to capture the diverse nature of neuronal circuits41.
The procedure was divided into two steps, i.e., a bank of spatiotemporal filters that modeled receptive fields in cascade with PIF neurons capable of firing spikes time-locked to the stimulus42. Here, the transmission of stimulation along the visual pathway was approximated using a 3D spatiotemporal receptive field (STRF) to describe a neuron's preference to spatiotemporal patterns of stimulation43. A family of such filters mapped different stimulation specificities from 3D spatiotemporal space into 1D feature space. The receptive-field outputs were then encoded by PIF neural circuits into spike trains. SR measures can be characterized by ISIs, which indicate the timing difference between two successive spikes13. In our study, STRF was estimated by the response-triggered average method from the STRFlab Toolbox (http://www.strflab.berkeley.edu/), and the PIF model was implemented with the TED Toolbox44.
To minimize computational burden, all stimulation frames were first cropped to a square of 151 × 151 pixels and then spatially down-sampled to 37 × 37 pixels (Supplementary Figure S1 online). To allow computations to be repeated, 2D noise masking was generated by Matlab (Mathworks, Natick, MA) ‘randn' function with random number generator set as Mersenne Twister. A 300-frame (60 frames/s × 5 second) stimulation movie was passed through a bank of 1369 STRF filters, and the receptive-field outputs were summed with uniformly random weights after mean removal to form inputs of a group of 10,000 PIF neurons, each sharing common periodic features but entirely independent fluctuating input parts, as in real situations when a periodic signal was applied to a heterogeneous population. Here, we also considered encoding of neuron ensembles with random thresholds to mimic the underlying diversity of sensory neurons45,46. Thresholds in PIF ensembles were uniformly distributed within a certain range and each neuron possessed a unique threshold throughout the simulation. Because the critical threshold for firing increased as forcing frequency decreased, the upper bound of the threshold range was selected corresponding to the value where the firing of neuronal ensembles emerged at least one ISIs at MRF of 20 Hz under NSD of 64, while the lower bound was chosen to be slightly greater than the grand average of receptive-field outputs.
To eliminate transients caused by stimulation onset, simulation results collected during the initial 1 second were excluded from data analysis. Thus, within the stimulation time of 1–5 seconds, the strength of ISIs at the period of forcing, which roughly represented the number of spikes triggered at every cycle over 10,000 neuron realizations, was used to measure synchronization of the spike timing with periodic forcing47,48,49. It was a direct way to quantify the degree of input-output synchronization and the “resonance” of the model against different noise levels. Such ensemble property eliminated statistical fluctuations on the output of individual neurons and loosely mimicked the behavior of large-scale neural populations. To facilitate the comparison of SR evolution among different forcing frequencies, for every forcing frequency, all ISIs under NSD of 0–64 in increments of 4 were normalized to mean of 0 and SD of 1 by Z-scoring. Please see Supplementary methods for more specific description of the simulation model.
Author Contributions
J.X. designed and performed experiments and theoretical simulation, analyzed data, and wrote the paper; G.X. designed and performed experiments and theoretical simulation; J.W. designed experiments; S.Z. developed analytical tools; and F.Z., Y.L., C.H. and L.L. analyzed data. All authors reviewed the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
This research was supported by National Natural Science Foundation of China (NSFC) Grant 51175412 and Research Fund for the Doctoral Program of Higher Education of China (RFDP) Grant 20110201110022 (to G.X.).
References
- Benzi R., Sutera A. & Vulpiani A. The mechanism of stochastic resonance. J. Phys. A: Math. Gen. 14, L453–L457 (1981). [Google Scholar]
- Douglass J. K., Wilkens L., Pantazelou E. & Moss F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 365, 337–340 (1993). [DOI] [PubMed] [Google Scholar]
- Wiesenfeld K., Pierson D., Pantazelou E., Dames C. & Moss F. Stochastic resonance on a circle. Phys. Rev. Lett. 72, 2125–2129 (1994). [DOI] [PubMed] [Google Scholar]
- Jung P. & Mayer-Kress G. Spatiotemporal stochastic resonance in excitable media. Phys. Rev. Lett. 74, 2130–2133 (1995). [DOI] [PubMed] [Google Scholar]
- Levin J. & Miller J. P. Broadband neural encoding in the cricket cereal sensory system enhanced by stochastic resonance. Nature 380, 165–168 (1996). [DOI] [PubMed] [Google Scholar]
- Srebro R. & Malladi P. Stochastic resonance of the visually evoked potential. Phys. Rev. E 59, 2566–2570 (1999). [Google Scholar]
- Farquhar J., Blankespoor J., Vlek R. & Desain P. Towards a noise-tagging auditory BCI-paradigm. In Proc. of the 4th Int. Brain-Computer Interface Workshop and Training Course 50–55 (2008). [Google Scholar]
- Desain P., Farquhar J., Blankespoor J. & Gielen S. Detecting spread spectrum pseudo random noise tags in EEG/MEG using a structure based decomposition. In Proc. of the 4th Int. Brain-Computer Interface Workshop and Training Course 80–85 (2008). [Google Scholar]
- Desain P. & Farquhar J. Method for processing a brain wave signal and brain computer interface. U.S. Patent WO2010008276A1 (2010). [Google Scholar]
- Xie J., Xu G., Wang J., Zhang F. & Zhang Y. Steady-state motion visual evoked potentials produced by oscillating newton's rings: implications for brain-computer interfaces. PLoS ONE 7, e39707 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaleb I., Davila C. E. & Srebro R. A new multi-harmonic statistic for the detection of steady-state evoked potentials. Conf. Proc. 16th Southern Biomedical Engineering 441–444 (1997). [Google Scholar]
- Menozzi M., Napflin U. & Krueger H. CRT versus LCD: A pilot study on visual performance and suitability of two display technologies for use in office work. Displays 20, 3–10 (1999). [Google Scholar]
- Longtin A. Stochastic resonance in neuron models. J. Stat. Phys. 70, 309–327 (1993). [Google Scholar]
- McDonnell M. D. & Abbott D. What is stochastic resonance? definitions, misconceptions, debates, and its relevance to biology. PLoS Comput. Biol. 5, e1000348 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau D. & Chapeau-blondeau F. Neuronal signal transduction aided by noise at threshold and at saturation. Neural Process. Lett. 20, 71–83 (2004). [Google Scholar]
- Blanchard S., Rousseau D. & Chapeau-blondeau F. Noise enhancement of signal transduction by parallel arrays of nonlinear neurons with threshold and saturation. Neurocomputing 71, 333–341 (2007). [Google Scholar]
- Chapeau-Blondeau F., Duan F. & Abbott D. Synaptic signal transduction aided by noise in a dynamical saturating model. Phys. Rev. E 81, 021124 (2010). [DOI] [PubMed] [Google Scholar]
- Pei X., Wilkens L. A. & Moss F. Light enhances hydrodynamic signaling in the multimodal caudal photoreceptor interneurons of the crayfish. J. Neurophysiol. 76, 3002–3011 (1996). [DOI] [PubMed] [Google Scholar]
- Braun H. A., Wissing H., Schafer K. & Hirsch M. C. Oscillation and noise determine signal-transduction in shark multimodal sensory cells. Nature 367, 270–273 (1994). [DOI] [PubMed] [Google Scholar]
- Simonotto E. et al. Visual perception of stochastic resonance. Phys. Rev. Lett. 78, 1186–1189 (1997). [Google Scholar]
- Stemmler M., Usher M. & Niebur E. Lateral interactions in primary visual cortex: a model bridging physiology and psychophysics. Science 269, 1877–1880 (1995). [DOI] [PubMed] [Google Scholar]
- Longtin A., Bulsara A. & Moss F. Time-interval sequences in bistable systems and the noise-induced transmission of information by sensory neurons. Phys. Rev. Lett. 67, 656–659 (1991). [DOI] [PubMed] [Google Scholar]
- Riani M. & Simonotto E. Stochastic resonance in the perceptual interpretation of ambiguous figures: a neural network model. Phys. Rev. Lett. 72, 3120–3123 (1994). [DOI] [PubMed] [Google Scholar]
- Stocks N. G. et al. in Fluctuations and Order: The New Synthesis (ed. Millonas, M.) 53–67 (Springer, Berlin, 1993). [Google Scholar]
- Dykman M. I. et al. Noise-induced linearisation. Phys. Lett. A 193, 61–66 (1994). [Google Scholar]
- Gammaitoni L., Hanggi P. & Marchesoni F. Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998). [Google Scholar]
- Nowak L. G., Sanchez-Vives M. V. & McCormick D. A. Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb. Cortex 7, 487–501 (1997). [DOI] [PubMed] [Google Scholar]
- Anderson J. S., Carandini M. & Ferster D. Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. J. Neurophysiol. 84, 909–926 (2000). [DOI] [PubMed] [Google Scholar]
- Carandini M. & Mechler F. Spike train encoding by regular-spiking cells of the visual cortex. J. Neurophysiol. 76, 3425–3441 (1996). [DOI] [PubMed] [Google Scholar]
- Mainen Z. F. & Sejnowski T. J. Reliability of spike timing in neocortical neurons. Science 268, 1503–1506 (1995). [DOI] [PubMed] [Google Scholar]
- van Steveninck R. R. R., Lewen G. D., Strong S. P., Koberle R. & Bialek W. Reproducibility and variability in neural spike trains. Science 275, 1805–1808 (1997). [DOI] [PubMed] [Google Scholar]
- Luchinsky D. G., Mannella R., Mcclintock P. V. E. & Stocks N. G. Stochastic resonance in electrical circuits–II: nonconventional stochastic resonance. IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process. 46, 1215–1224 (1999). [Google Scholar]
- Kitajo K., Nozaki D., Ward L. M. & Yamamoto Y. Behavioral stochastic resonance within the human brain. Phys. Rev. lett. 90, 218103 (2003). [DOI] [PubMed] [Google Scholar]
- Mori T. & Kai S. Noise-induced entrainment and stochastic resonance in human brain waves. Phys. Rev. Lett. 88, 218101 (2002). [DOI] [PubMed] [Google Scholar]
- Destexhe A. & Marder E. Plasticity in single neuron and circuit computations. Nature 431, 789–795 (2004). [DOI] [PubMed] [Google Scholar]
- Ng K. B., Bradley A. P. & Cunnington R. Stimulus specificity of a steady-state visual-evoked potential-based brain–computer interface. J. Neural Eng. 9, 036008 (2012). [DOI] [PubMed] [Google Scholar]
- Brainard D. H. The psychophysics toolbox. Spat. Vis. 10, 433–436 (1997). [PubMed] [Google Scholar]
- Pelli D. G. The video toolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis. 10, 437–442 (1997). [PubMed] [Google Scholar]
- Bergholz R., Lehmann T. N., Fritz G. & Rüther K. Fourier transformed steady-state flash evoked potentials for continuous monitoring of visual pathway function. Doc. Ophthalmol. 116, 217–229 (2008). [DOI] [PubMed] [Google Scholar]
- Victor J. D. & Mast J. A new statistic for steady-state evoked potentials. Electroencephalogr. Clin. Neurophysiol. 78, 378–388 (1991). [DOI] [PubMed] [Google Scholar]
- Knight B. W. Dynamics of encoding in a population of neurons. J. Gen. Physiol. 59, 734–766 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar A. A. & Pnevmatikakis E. A. Faithful representation of stimuli with a population of integrate-and-fire neurons. Neural Comput. 20, 2715–2744 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen F. E. et al. Estimating spatio-temporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Network: Comput. Neural Syst. 12, 289–316 (2001). [PubMed] [Google Scholar]
- Lazar A. A. & Pnevmatikakis E. A. Video time encoding machines. Neural Networks, IEEE Transactions on. 22, 461–473 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D. S., Victor J. D., Knight B. W., Ozaki T. & Kaplan E. Response variability and timing precision of neuronal spike trains in vivo. J. Neurophysiol. 77, 2836–2841 (1997). [DOI] [PubMed] [Google Scholar]
- Lazar A. A., Pnevmatikakis E. A. & Zhou Y. Y. Encoding natural scenes with neural circuits with random thresholds. Vision Res. 50, 2200–2212 (2010). [DOI] [PubMed] [Google Scholar]
- Bulsara A. R., Lowen S. B. & Rees C. D. Cooperative behavior in the periodically modulated Wiener process: noise-induced complexity in a model neutron. Phys. Rev. E 49, 4989–5000 (1994). [DOI] [PubMed] [Google Scholar]
- Bulsara A. R., Elston T. C., Doering C. R., Lowen S. B. & Lindenberg K. Cooperative behavior in periodically driven noisy integrate-fire models of neuronal dynamics. Phys. Rev. E 53, 3958–3969 (1996). [DOI] [PubMed] [Google Scholar]
- Shimokawa T., Pakdaman K. & Sato S. Time-scale matching in the response of a leaky integrate-and-fire neuron model to periodic stimulus with additive noise. Phys. Rev. E 59, 3427–3443 (1999). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information