A Comparison of Multiple Imputation and Fully Augmented Weighted Estimators for Cox Regression with Missing Covariates

Abstract

Several approaches exist for handling missing covariates in the Cox proportional hazards model. The multiple imputation (MI) is relatively easy to implement with various software available and results in consistent estimates if the imputation model is correct. On the other hand, the fully augmented weighted estimators (FAWEs) recover a substantial proportion of the efficiency and have the doubly robust property. In this paper, we compare the FAWEs and the MI through a comprehensive simulation study. For the MI, we consider the multiple imputation by chained equation (MICE) and focus on two imputation methods: Bayesian linear regression imputation and predictive mean matching. Simulation results show that the imputation methods can be rather sensitive to model misspecification and may have large bias when the censoring time depends on the missing covariates. In contrast, the FAWEs allow the censoring time to depend on the missing covariates and are remarkably robust as long as getting either the conditional expectations or the selection probability correct due to the doubly robust property. The comparison suggests that the FAWEs show the potential for being a competitive and attractive tool for tackling the analysis of survival data with missing covariates.

1. Introduction

Missing covariate problems are very common in epidemiologic studies and clinical trials with survival outcomes, where the Cox proportional hazards (PH) model [1] is usually used for analysis. In many situations, some covariates are always observed while others are only available for a subset of the study subjects by design or happenstance. Using only complete data, known as the complete-case (CC) analysis, may not only lose efficiency but also yield biased estimates when the missing mechanism depends on the outcome [2]. When the missing covariates are missing at random (MAR), i.e. the probability of missingness depends only on the observed data [3], several methods have been developed to handle the missing data problem in the Cox PH model. In this paper, we review and compare two approaches: the augmented inverse probability weighted (AIPW) and multiple imputation methods.

The AIPW estimation of the Cox PH model with missing covariates was first proposed by Robins, Rotnitzky and Zhao [4], also described by Nan, Emond and Wellner [5] and further developed by Wang and Chen [6]. The AIPW estimation improves the efficiency of the non-augmented inverse probability weighted (IPW) method by adding an augmented term to the original IPW estimating functions. And the resulting estimators are doubly robust: they are consistent if either the selection probability model or the conditional distribution of the missing covariates given the observed data is correctly specified. Recently, Qi et al. [7] proposed the FAWEs in which the selection probability and the conditional expectations are estimated by the nonparametric Nadaraya-Watson kernel method. The FAWEs are more efficient than the IPW estimators with true selection probability, and they require neither a parametric model for the selection probability nor parametric specification of the conditional distribution of the missing covariates given the observed data [7].

On the other hand, multiple imputation (MI) [3] is widely used to handle missing data in practice because the concept is relatively simple and various software including SAS and R are available for implementation [8]. The main idea of this approach is to first generate multiply complete data sets by imputing missing values, then analyze these imputed data sets with standard complete-data analysis procedures and combine the multiple analysis results to yield a single inference using the “Rubin's rules” [3]. From a Bayesian perspective, the imputed values are generated from an imputation model which characterizes the posterior predictive distribution of the missing values given observed data [3]. The choice of variables in the imputation model is critical. When missing covariates are to be imputed, it is essential to include the outcome variable of the data analysis in the imputation models [9]. Otherwise, the outcome-covariate association might be biased towards null using the imputed data [10]. Little [11] has discussed general strategies for dealing with missing covariates. Applications of MI for the Cox PH model with missing covariates can be found in Paik [12], van Buuren et al. [13], Barzi and Woodward [14] and White and Royston [15].

The comparison of the AIPW and the MI methods with missing covariates has been conducted for linear models [16] and generalized linear models [17]. Results suggest that the AIPW estimators generally are more robust than the MI method when the covariate distributions are mis-specified. However, there is a lack of relevant literature in survival analysis. In this paper, we compare the two approaches for the Cox PH model with missing covariates through an extensive simulation study. We assume throughout that the data are MAR, and that censoring is non-informative. For the AIPW approach, we adopt the FAWEs by Qi et al. [7]. For MI, there are two widely available methods of model-based imputation, multiple imputation based on the multivariate normal distribution (MVNI), originally implemented by Schafer [18], and the multiple imputation by chained equation (MICE) [13, 19]. We consider MICE in the simulation study since the Cox PH model is semiparametric while implementing MVNI through a fully Bayesian modeling approach requires specification of the baseline hazard function [12]. With MICE, we focus on two imputation models for continuous missing covariates: Bayesian linear regression imputation [3] and predictive mean matching [20], and the Bayesian logistic regression imputation for binary data [3, 13, 21], supported by the MICE package in R. We intend to assess the performance of the FAWEs and the MI methods in the following scenarios:

1. when the missing and the observed covariates are correlated and mis-specification exists on models for either selection probability or covariate distributions,

2. when the censoring time depends on missing covariates,

3. when the correlation between missing and observed covariates and the amount of missing data vary over a range of values,

4. when the PH assumption does not hold, motivated by the fact that it is not uncommon applying the Cox PH model to data from other distributions in practice [22].

The rest of the paper is organized as follows: in Section 2, we review the FAWEs and the MI methods used for comparison. Section 3 describes the simulation study and presents the results. In Section 4, we will present a data example from the on-going Childhood Autism Risk from Genetics and the Environment (CHARGE) study. And discussion follows in Section 5.

2. Methods

2.1. Notation

We consider the Cox PH model [1] specified by the hazard function λ (t ∣Z) = λ₀ (t) exp(β^TZ), where λ₀ (t) is an arbitrary and unspecified baseline function and Z denotes a set of time-independent covariates. Let T, C and X = min(T, C) be the failure, censoring and observed time for a subject, respectively. The failure indicator δ = I(T ≤ C) is 1 if the subject experiences an event and δ = 0 if censored. We assume that given Z, T and C are independent. Suppose some elements of Z are missing, and write Z = (Z^m, Z^o), where Z^o denotes the covariates that are always observed (the observed covariates), and Z^m denotes the covariates that are sometimes missing (the missing covariates). Let the selection indicator V equal 1 if Z^m is available, and V = 0 if Z^m is missing. Under MAR, the missing-data mechanism is determined by the conditional distribution of V given (X, δ, Z^o), which is Bernoulli with selection probability π = Pr(V = 1 ∣X, δ, Z^o). Let $\left(X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o,{\mathbf{\text{Z}}}_i^m,V_i\right)$, i = 1, …, n be i.i.d copies of (X, δ, Z^o, Z^m, V), then the observed data available for analysis are $\left(X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o,{\mathbf{\text{Z}}}_i^m\right)$ if V_i = 1 and $\left(X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o\right)$ if V_i = 0.

2.2. Fully Augmented Weighted Estimators

The FAWEs are doubly robust AIPW estimators, which generalized the non-augmented IPW estimators. The fully augmented weighted estimating function include two terms. The first term is an IPW estimating function based on the idea of Horvitz and Thompson [23] and the second term is a mean zero augmentation term including incomplete observations. Specifically, the fully augmented weighted estimating function by Qi et al. has the form [7]:

$$U_{f\mathit{\text{aw}}}(\beta ,\pi )=\sum _{i=1}^n\frac{V_i}{{\pi }_i}{\int }_0^{\tau }\left\{{\mathbf{\text{Z}}}_i-\frac{{\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(1)}\left(\beta ,\pi ,t\right)}{S_{\mathit{\text{aw}}}^{(0)}\left(\beta ,\pi ,t\right)}\right\}d{N}_i(t)+\sum _{i=1}^n{A}_i^F(\beta ,\pi ),$$ (1)

where

$$A_i^F(\beta ,\pi )=(1-\frac{V_i}{{\pi }_i}){\int }_0^{\tau }\left\{E\left\{{\mathbf{\text{Z}}}_{i}d{N}_i(t)\mid X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o\right\}-\frac{{\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(1)}(\beta ,\pi ,t)}{S_{\mathit{\text{aw}}}^{(0)}(\beta ,\pi ,t)}E\{d{N}_i(t)\mid X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o\}\right\},$$

and for k = 0, 1,

$${\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(k)}(\beta ,\pi ,t)=\frac{1}{n}\sum _{j=1}^n\left[\frac{V_j}{{\pi }_j}{Y}_j(t){\text{Z}}_j^{\otimes k}exp({\beta }^T{\mathbf{\text{Z}}}_j)+(1-\frac{V_j}{{\pi }_j})Y_j(t)E\{{\mathbf{\text{Z}}}_j^{\otimes k}exp({\beta }^T{\mathbf{\text{Z}}}_j)\mid X_j,{\delta }_j,{\mathbf{\text{Z}}}_j^o\}\right],$$ (2)

where N(t) = δI(X ≤ t) and Y(t) = I(X ≥ t) are the counting process and the at-risk process, respectively, corresponding to (X, δ), and a^⊗0 = 1, a^⊗1 = a. This fully augmented weighted estimating function uses inverse probability weighting in both the augmentation term $A_i^F(\beta ,\pi )$ and the augmented averages ${\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(k)}(\beta ,\pi ,t)$ (k = 0, 1). The augmentation term $A_i^F(\beta ,\pi )$ is essentially the weighted (by 1 − V_i/π_i) conditional expectation of the summand in the first term, i.e. ${\int }_0^{\tau }\{{\mathbf{\text{Z}}}_i-{\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(1)}(\beta ,\pi ,t)/S_{\mathit{\text{aw}}}^{(0)}(\beta ,\pi ,t)\}d{N}_i(t)$, given the observed data. This term makes use of both complete and incomplete data, allowing incomplete observations to contribute to parameter estimation directly. Similarly, the augmented averages ${\mathbf{\text{S}}}_{\mathit{\text{aw}}}^{(k)}(\beta ,\pi ,t)$ (k = 0, 1) also include contributions from the incomplete observations.

The conditional expectations $E\{{\mathbf{\text{Z}}}_{i}d{N}_i(t)\mid X_i,{\delta }_i,{\mathbf{\text{Z}}}_i^o\}$ and $E\{{\mathbf{\text{Z}}}_j^{\otimes k}exp({\beta }^T{\mathbf{\text{Z}}}_j)\mid X_j,{\delta }_j,{\mathbf{\text{Z}}}_j^o\}$ (k = 0, 1) in (1) and (2) depend on the unknown cumulative baseline hazard function and the conditional distribution of Z^m given Z^o. To estimate these conditional expectations, Qi et al. [7] implemented nonparametric kernel smoothing techniques, specifically, the Nadaraya-Watson estimator [24, 25]. When π is unknown, the Nadaraya-Watson estimator can also be used to estimate it based on all available data. Details of these estimations can be found in Appendix I. The advantage of adopting nonparametric estimations is that it does not impose parametric assumptions on π or the association between Z^m and Z^o. To obtain estimates, the Newton-Raphson algorithm can be used to solve the fully augmented weighted estimating equations. And the resultant FAWEs have the doubly robust property: they are consistent if either the selection probability or the conditional expectations are correctly estimated.

Under certain conditions (refer to [7]), the FAWEs are asymptotically consistent for the true parameter β and normally distributed with mean 0 and variance matrix which consists of two terms: the variance pertaining to the Cox partial likelihood estimator based on full cohort data and a term quantifying the efficiency loss due to missing covariates. This asymptotic variance is smaller than that of the non-augmented IPW estimator (termed simple weighted estimator in [7]) with true selection probability, indicating improved efficiency of the FAWEs over the IPW estimator [7]. More over, when Z^m can be exactly specified by (X, δ, Z^o), the FAWEs achieve the efficiency of the Cox partial likelihood estimator based on the full cohort data [7]. Detailed expression of the asymptotic variance and its consistent estimator can be found in Appendix II.

2.3. Multiple Imputation

MI is a simulation based approach to deal with incomplete data, developed from a Bayesian perspective. The main idea is to replace each missing value with several imputed values and produce multiply imputed data sets. Generally for a univariate Z^m under MAR, and given the observed data (X, δ, Z^o), several sets of plausible values for Z^m can be drawn from an appropriate imputation model p(Z^m ∣X, δ, Z^o). When there are multiple missing covariates, multiple imputation by chained equations (MICE) [13, 19] can be used. MICE starts by filling in missing values arbitrarily, then the aforementioned univariate method can be applied to each missing covariate Z^m in turn, using the current imputed values of the other missing covariates when drawing new values of Z^m. This procedure is iterated until convergence, often achieved in less than 10 cycles [26].

After obtaining imputed data sets, a complete data method (Cox regression in our case) is performed on each data set separately. Then analysis results from the multiply imputed data sets are combined to yield an overall inference that incorporates the within- and between-imputation variation using “Rubin's rules” [3]. Let β̂_k be the coefficient estimate obtained from the imputed data set k (for k = 1, …, M) and V_k be the estimated variance of β̂_k. Then the combined estimate equals $\overline{\beta }={\sum }_{k=1}^M{\widehat{\beta }}_k/M$, and the overall variance is given by Var(β̄) = W̄ + (1 + M⁻¹)B, where $\overline{W}={\sum }_{k=1}^M{V}_k/M$, and $B={\sum }_{k=1}^M({\widehat{\beta }}_k-{\overline{\beta }}_k){({\widehat{\beta }}_k-{\overline{\beta }}_k)}^T/(M-1)$ [18].

An appropriate imputation model for missing covariates hinges on a valid characterization of the conditional distribution of the missing covariates given the observed data. Under the Cox PH regression model, however, such conditional distribution does not have standard and closed forms [15]. A practical strategy is to use some common regression models to approximate the covariate distribution. Following an influential paper on the practical use of MI [13] and a recent paper of MI for the Cox PH model [15], linear regression and logistic regression models can be used to impute continuous and binary missing covariates, respectively. For example, results from these studies suggested the following model can be an appropriate imputation model for a continuous $Z^m:Z^m\sim {\theta }_0+{\theta }_{1}X+{\theta }_2\delta +{\ominus }_3^T{\mathbf{\text{Z}}}^o$. This model includes all available variables, the survival outcome X, δ, and the observed covariates Z^o, as predictors, and is referred as “full imputation model” in our simulation study (Section 3). To investigate the robustness of the MI under model misspecification, we also consider the imputation model excluding some or all elements of Z^o, eg. Z^m ∼ θ₀ + θ₁X + θ₂δ, called the “reduced imputation model”.

The MI methods is supported by many software packages such as SAS [27] (www.sas.com), STATA [28] (www.stata.com) and R [21] (www.r-project.org). A good summary of software packages for the MI can be found in Harel and Zhou [8]. The MICE packge in R supplies a number of built-in elementary imputation models [29], and we primarily use the impute.norm and impute.pmm methods for continuous missing covariates and impute.logreg for binary missing covariates from this package to carry out our simulation study. Below we briefly describe these methods for a univariate Z^m:

• impute.norm uses Bayesian linear regression imputation [3], assuming that Z^m given the observed data follows a normal distribution and noninformative priors for the parameters.

• impute.pmm implements predictive mean matching [20], a general purpose semi-parametric imputation method. It is a modification to impute.norm that may help to preserve subtle deviations from normality of the residuals. The method uses the predictive mean to define a match between $Z_{\mathit{\text{mis}}}^m$ (the missing components of Z^m) and $Z_{\mathit{\text{obs}}}^m$ (the observed components of Z^m). And the imputed value of each $Z_{\mathit{\text{mis}}}^m$ will be the $Z_{\mathit{\text{obs}}}^m$ whose predicted value is closest to that of the $Z_{\mathit{\text{mis}}}^m$ [30].

• impute.logreg imputes binary data by the Bayesian logistic regression model [3, 13, 21].

3. Simulation

3.1. General Description

A comprehensive simulation study was conducted to examine and compare the moderate sample size (n = 250) performance of the FAWEs and MI methods, as well as to compare their performance with that of the full-cohort (Cox regression based on full cohort data) and the CC analyses. The simulation study focused on the case for a single missing covariate, but the comparison would be similar for situations with multiple missing covariates. We designed four simulation settings to assess the performance of the FAWEs and the MI methods respectively corresponding to the four scenarios discussed in the Introduction. The first three settings considered survival outcomes generated by the Cox PH model and the fourth setting used survival outcomes generated by a lognormal accelerated failure time (AFT) model. The Cox PH model was used as the analytic model in all settings, and one thousand data sets were generated in each simulation setting. For implementation of the imputation methods, five imputed data sets were generated and five iterations were employed to impute each data set.

The performances of the FAWEs and the MI estimators were evaluated based on the following quantities [31]:

• Percentage bias (PB): the relative magnitude of the raw bias to the true value of the parameter, calculated by (E(β̂) − β)/β. A bias is considered large if the percentage bias exceeds 5% in either direction.

• Coverage rate (CR): percentage of times that the true parameter value is covered in the 95% confidence interval. It is calculated based on the theoretical standard errors (SEs) of the point estimates.

• Average length of confidence interval (AL): the average of the 1000 lengths of the 95% confidence intervals (CIs). It is used as a measure of precision of the estimates for comparison between the FAWEs and the MI estimators. We compare the length of CIs, not SEs because the former takes into account that inference is based on a t-distribution for MI while the FAWEs are asymptotically normal. A high coverage rate together with narrow, calibrated CIs suggests greater accuracy and higher power.

We present the four simulation settings and simulation results one by one below. We use MI norm, MI pmm and MI logreg to denote impute.norm, impute.pmm and impute.logreg methods respectively when describing results.

3.2. Simulation Scenario 1

Simulation setting 1 was designed to compare the robustness of the FAWEs and the MI methods with either selection probability or covariate distributions specified wrong when the missing and the observed covariates are correlated. The hazard function was specified by λ(t ∣Z) = exp(β^TZ), where β = (−ln(2), ln(2), ln(2)) and Z contained one missing covariate Z^m and two observed covariates $Z_1^o$ and $Z_2^o$ with pairwise correlation coefficient of 0.3. The missing covariate Z^m followed a standard normal distribution, and $Z_1^o$ and $Z_2^o$ were both binary variables taking values 0 and 1 with probability 0.5. A uniform censoring time was used with the upper limit selected to give 40% cases (uncensored observations). The selection probability was associated with X, δ, $Z_1^o$ and $Z_2^o$, causing 40% of cohort members to have missing Z^m.

We assess the robustness of the FAWEs by considering four situations: (a) both π and E's (the conditional expectations in Equations (1) and (2)) were correctly estimated, i.e. their Nadaraya-Watson estimators used X, δ, $Z_1^o$ and $Z_2^o$; (b) π was estimated wrong because its Nadaraya-Watson estimator used X, δ and $Z_1^o$ or only X and δ, but E's were correctly estimated; (c) π was estimated correctly, but E's were wrongly estimated because their Nadaraya-Watson estimators used X, δ and $Z_1^o$ or only X and δ; (d) both π and E's were wrongly estimated because their Nadaraya-Watson estimators used X, δ and $Z_1^o$ or only X and δ.

We assess the robustness of MI norm and MI pmm by considering both the “full imputation model” (the imputation model with X, δ, $Z_1^o$ and $Z_2^o$), and the “reduced imputation model” (the imputation model with X, δ and $Z_1^o$ or only X and δ).

Simulation results are presented at the top of Table 1. The CC analysis produced large bias because the selection probability depended on the outcome variables. The biases and coverages for the FAWEs were within reasonable limits as long as either the conditional expectations or the selection probability was correctly estimated, confirming the double-robustness property. When both π̂ and the estimated conditional expectations Ê were wrong, the FAWEs yielded slightly large bias for the parameter estimates of $Z_1^o$ and $Z_2^o$. For the FAWE with π̂ and Ê based on (X, δ), both ${\widehat{\beta }}_1^o$ and ${\widehat{\beta }}_2^o$ had negative biases, indicating that the estimates might be biased towards null when $Z_1^o$ and $Z_2^o$ were not used in estimating π̂ and Ê. Similarly, for the FAWE with π̂ and Ê based on (X, δ, $Z_1^o$) without $Z_2^o,{\widehat{\beta }}_2^o$ had negative bias, which implies that the estimate for ${\beta }_2^o$ might attenuate to 0 and tend to be smaller than its true parameter value when $Z_2^o$ was not used in obtaining π̂ and Ê. On the other hand, since $Z_1^o$ was correlated with Z^m and $Z_2^o$, the estimate of ${\beta }_1^o$ might tend to be larger than its true parameter value when including $Z_1^o$ in the estimation of π and E besides (X, δ), resulting in positive bias for ${\widehat{\beta }}_1^o$. The same pattern remained when including $Z_2^o$ in and excluding $Z_1^o$ from the estimation of π and E in that ${\widehat{\beta }}_2^o$ had positive bias while ${\widehat{\beta }}_1^o$ had negative bias. The FAWEs with wrong Ê also had larger AL than those with correct Ê, implying that the precision of FAWEs may be suffered by not including all the variables in estimating the conditional expectations.

Table 1.

Simulation comparison of the FAWEs and MI estimators of the Cox model parameter β = (−ln(2), ln(2), ln(2)), where $Z_1^o$ and $Z_2^o$ ∼ Bernoulli(0.5) and Z^m, $Z_1^o$, and $Z_2^o$ are correlated with pairwise correlation coefficient = 0.3; uniform censoring time, censoring rate 60%; and selection probability $\pi (X,\delta ,Z_1^o,Z_2^o)={(1+\text{exp}(1.2-\delta -2X-Z_1^o-Z_2^o))}^{-1}$.

Approach	Details	PB %			AL			95% CR
		βm	${\beta }_1^o$	${\beta }_2^o$	βm	${\beta }_1^o$	${\beta }_2^o$	βm	${\beta }_1^o$	${\beta }_2^o$
Zm ∼ N(0, 1), 70% cases and 53% controls selected
Full cohort		-0.40	1.28	1.52	0.46	0.87	0.87	0.95	0.96	0.96
Complete-case		-2.23	-12.57	-11.05	0.55	1.07	1.08	0.94	0.92	0.93
FAWE
	correct π̂, correct Ê(1)	1.43	1.45	2.44	0.56	0.91	0.91	0.92	0.96	0.94
	wrong π̂, correct Ê(2)
	π̂(X, δ, $Z_1^o$)	1.48	1.47	2.66	0.55	0.92	0.92	0.91	0.95	0.95
	π̂(X, δ)	1.62	1.86	2.79	0.53	0.92	0.92	0.91	0.95	0.95
	correct π̂, wrong Ê(3)
	Ê(X, δ, $Z_1^o$)	1.65	1.41	1.58	0.58	0.96	1.22	0.93	0.96	0.98
	Ê(X, δ)	1.64	-0.21	1.66	0.60	1.21	1.21	0.94	0.98	0.98
	wrong π̂, wrong Ê(4)
	π̂, Ê(X, δ, $Z_1^o$)	2.45	6.00	-7.42	0.57	0.94	1.13	0.93	0.95	0.93
	π̂, Ê(X, δ)	3.83	-8.58	-6.74	0.58	1.13	1.14	0.95	0.94	0.94
MI
	Full imputation model(5)
	MI norm	-2.04	-0.93	0.22	0.61	0.95	0.96	0.96	0.97	0.97
	MI pmm	0.69	-0.65	0.89	0.54	0.92	0.92	0.91	0.96	0.95
	Reduced imputation model(6)
	MI norm(X, δ, $Z_1^o$)	-7.25	1.31	-21.30	0.60	0.96	0.91	0.95	0.97	0.93
	MI pmm(X, δ, $Z_1^o$)	-4.44	1.50	-20.83	0.50	0.90	0.87	0.86	0.95	0.92
	MI norm(X, δ)	-14.39	-24.27	-23.55	0.59	0.90	0.90	0.91	0.91	0.92
	MI pmm(X, δ)	-12.41	-24.31	-23.52	0.46	0.85	0.86	0.79	0.89	0.89
Zm ∼ Bernoulli(0.5), 71% cases and 52% controls were selected
Full cohort		1.97	1.36	-0.07	0.87	0.89	0.88	0.95	0.96	0.97
Complete-case		0.32	-7.04	-9.25	1.03	1.09	1.09	0.95	0.94	0.94
FAWE
	correct π̂, correct Ê(1)	2.60	1.58	-0.26	1.02	0.91	0.91	0.93	0.96	0.96
	wrong π̂, correct Ê(2)
	π̂(X, δ, $Z_1^o$)	2.66	1.59	-0.19	1.00	0.90	0.93	0.92	0.96	0.96
	π̂(X, δ)	2.91	1.78	-0.09	0.98	0.93	0.93	0.91	0.96	0.96
	correct π̂, wrong Ê(3)
	Ê(X, δ, $Z_1^o$)	2.87	0.48	2.83	1.07	0.96	1.22	0.95	0.97	0.98
	Ê(X, δ)	2.85	3.64	2.24	1.10	1.22	1.21	0.95	0.99	0.98
	wrong π̂, wrong Ê(4)
	π̂, Ê(X, δ, $Z_1^o$)	3.74	6.12	-6.16	1.06	0.93	1.13	0.94	0.96	0.93
	π̂, Ê(X, δ)	6.50	-3.04	-4.94	1.08	1.15	1.15	0.94	0.94	0.94
MI
	Full imputation model(5)
	MI logreg	2.71	0.91	-0.96	1.12	0.92	0.92	0.95	0.97	0.97
	Reduced imputation model(6)
	MI logreg(X, δ, $Z_1^o$)	-5.28	1.03	-11.41	1.12	0.92	0.88	0.95	0.97	0.96
	MI logreg(X, δ)	-17.62	-11.55	-13.37	1.10	0.88	0.88	0.94	0.96	0.96

Notes: Cohort size is 250 and the expected number of complete observations is 150.

The numbers in bold are those with |PB| > 5% or CR < 0.90.

Both π and E were estimated using the Nadaraya-Watson estimator with normal kernel and bandwidth $h=4{\sigma }_{\text{W}}{n}_{\text{W}}^{-1/3}$.

⁽¹⁾Both π̂ and Ê were obtained correctly using (X, δ, $Z_1^o$, $Z_2^o$).

⁽²⁾Ê was obtained correctly using (X, δ, $Z_1^o$, $Z_2^o$) and π̂ based on the variables in the brackets.

⁽³⁾π̂ was obtained correctly using (X, δ, $Z_1^o$, $Z_2^o$) and Ê based on the variables in the brackets.

⁽⁴⁾π̂ and Ê were obtained based on the variables in the brackets.

⁽⁵⁾Imputation models contained (X, δ, $Z_1^o$, $Z_2^o$).

⁽⁶⁾Imputation models contained the corresponding variables in the brackets.

For the MI estimators, both biases and coverages were within reasonable limits when using the full imputation model. MI pmm had similar AL to those of the FAWEs with correct Ê while MI norm had larger AL than the FAWEs with correct Ê, suggesting these FAWEs may have better efficiency than MI norm. When using the reduced imputation models, i.e. excluding $Z_1^o$ or both $Z_1^o$ and $Z_2^o$ from the imputation models, both MI norm and MI pmm generated large biases and low coverage rates. This indicates that the MI estimators may be rather sensitive to exclusion of certain relevant variables from the imputation models.

In the same setting, we also replicated the simulation using Z^m as a binary variable taking values 0 and 1 with probability 0.5. Logistic regression models were used to impute Z^m in the MI method. Simulation results are presented at the bottom of Table 1. In general, the results show similar patterns as those in the case where Z^m was continuous. The FAWEs were doubly robust and had smaller AL for β̂^m than MI logreg. When both π̂ and Ê were wrong, the FAWEs yielded slightly large bias for the parameter estimate of Z^m, and MI logreg had large bias for most of the parameter estimates when using the reduced imputation models.

In Simulation Scenarios 2 - 4, the FAWE with both π and E's correctly estimated and the MI using the full imputation model were considered.

3.3. Simulation Scenario 2

The focus of the second setting was to investigate how association between the censoring time and the missing covariate would affect the performance of the FAWE and the MI methods. The hazard function was specified by λ(t ∣Z) = λ₀(t) exp(β^TZ), with a Weibull baseline hazard λ₀(t) = 0.8(0.6)^0.8t^−0.2, β = (−ln(2), ln(2)) and Z = (Z^m, Z^o). The missing covariate Z^m followed N(1/2, 1/12), and Z^o was a binary variable taking values 0 and 1 with probability 0.5. Censoring times were generated using exponential distributions depending on Z^o only and on both Z^m and Z^o, respectively, both yielding about 70% censoring rate. The selection probability was associated with X, δ and Z^o, allowing about 35% of cohort members to have missing Z^m.

Results are presented in Table 2. When the censoring time depended on Z^o but not on Z^m, the FAWE and both imputation methods performed well. When the censoring time depended on both Z^m and Z^o, the performance of the FAWE changed little. However, both MI estimators, especially MI norm had large bias for β^m. This suggests that the FAWE may outperform both imputation methods when censoring times depend on missing covariates.

Table 2.

Simulation comparison of the FAWE and MI estimators of the Cox model parameter β = (−ln(2), ln(2)), where Z^m∼ N(1/2, 1/12), Z^o ∼ Bernoulli(0.5) and Z^m and Z^o are independent; Weibull baseline hazard λ₀(t) = 0.8(0.6)^0.8t^−0.2, exponential censoring time, censoring rate 70%; and selection probability π(X, δ, Z^o) = (1 + exp(0.35 − 2δ − X − Z^o))⁻¹.

Approach	PB %		AL		95% CR
	βm	βo	βm	βo	βm	βo
Exponential censoring time with mean (0.25 + 0.5Zo)/2.2
Full cohort	0.89	0.00	1.58	1.07	0.95	0.95
Complete-case	-5.48	-50.66	1.66	1.16	0.95	0.73
FAWE	1.03	-1.43	1.78	1.08	0.95	0.94
MI norm	-0.96	-0.37	1.85	1.08	0.95	0.95
MI pmm	0.06	-0.43	1.72	1.08	0.93	0.95
Exponential censoring time with mean (0.5Zm + 0.5Zo)/2.1
Full cohort	2.67	-0.46	1.67	1.11	0.95	0.95
Complete-case	6.32	-49.95	1.75	1.22	0.94	0.75
FAWE	1.25	-1.71	1.87	1.13	0.93	0.95
MI norm	-14.76	4.24	1.91	1.12	0.95	0.95
MI pmm	-6.76	2.84	1.86	1.12	0.93	0.95

Notes: Cohort size is 250 and the expected number of complete observations is 163 with 91% cases and 54% controls selected.

The numbers in bold are those with |PB| > 5% or CR < 0.90.

For FAWE, both π and E were obtained based on (X, δ, Z^o) using the Nadaraya-Watson estimator with normal kernel and bandwidth $h=4{\sigma }_{\text{W}}{n}_{\text{W}}^{-1/3}$.

For MI, imputation models contained (X, δ, Z^o).

3.4. Simulation Scenario 3

The third simulation setting was designed to study the effect of the strength of correlations between the missing and the observed covariates, and the amount of missing data on the performance of the two approaches. The hazard function was specified by λ(t ∣Z) = exp(β^TZ), with β = (−ln(2), ln(2)) and Z = (Z^m, Z^o). The covariates Z^m and Z^o followed bivariate normal distributions with the correlation coefficient varying from 0 to 0.7. A uniform censoring time was used with the upper limit selected to give 35% cases. The selection probability was determined by X, δ, and Z^o, resulting in 30% to 80% missing data.

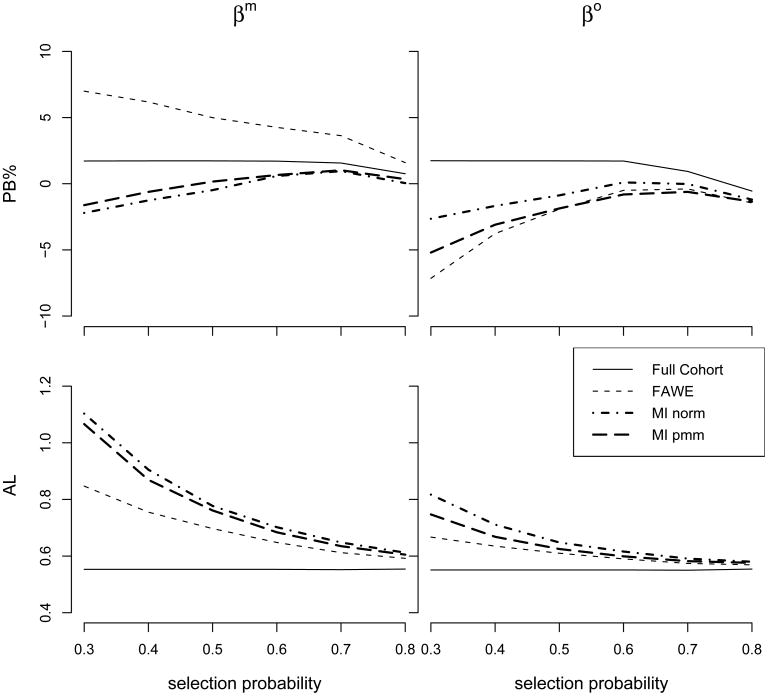
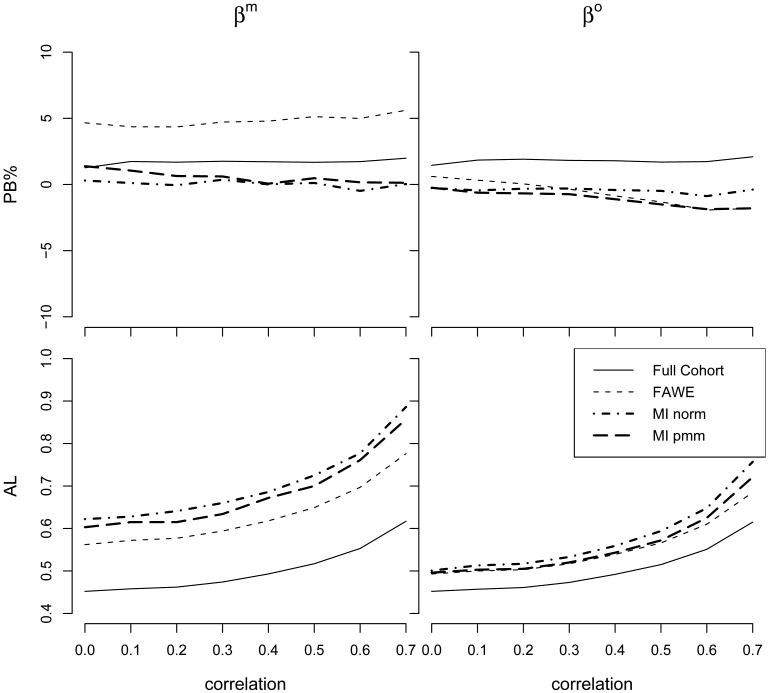
Simulation results show the general trend of decreasing bias and increasing precision for all estimators over increasing selection probability (e.g. Figure 1.), and slightly increasing bias and decreasing precision over increasing correlation coefficients (e.g. Figure 2.). Figure 1 displays the plots of PB and AL versus selection probability when the correlation coefficient was 0.6. For β^m, the FAWE showed slightly larger bias (PB was still close to 5%) than the MI estimators when the selection probability was below 50%; all estimators performed similarly when the selection probability was above 50%. For β^o, the bias was similar among the FAWE and the MI estimators. The plots of AL vs the selection probability (Figure 1) show that for both β^m and β^o the FAWE had noticeable smaller AL than the MI estimators, especially when the selection probability was below 50%. This suggests that the FAWE may have better efficiency than the two imputation methods under large amount of missing data.

Figure 1.

Percentage bias (PB) and average length (AL) vs. selection probability for the FAWE and the MI methods of the Cox Model. Baseline hazard function is 1, β = (−ln(2), ln(2)), where Z^m, Z^o ∼ N(0, 1), with correlation coefficient of 0.6; uniform censoring time with censoring rate 65%; and selection probability π(X, δ, Z^o) = (1 + exp(a + bδ + cX + dZ^o))⁻¹, where a,b,c,d were selected to generate 30% to 80% of cohort members to have missing Z^m; the cohort size is 250. For FAWE, both π and E were obtained based on (X, δ, Z^o) using the Nadaraya-Watson estimator with normal kernel and bandwidth h = 4σ_Wn^−1/3. For MI, imputation models contained (X, δ, Z^o).

Figure 2.

Percentage bias (PB) and average length (AL) vs. correlation for the FAWE and the MI methods of the Cox Model. Baseline hazard function is 1, β = (−ln(2), ln(2)), where Z^m, Z^o ∼ N(0, 1), with correlation coefficients ranging from 0 to 0.7; uniform censoring time with censoring rate 65%; and selection probability π(X, δ, Z^o) = (1 + exp(a + bδ + cX + dZ^o))⁻¹, where a,b,c,d are selected to generate 50% of cohort members to have missing Z^m; the cohort size is 250. For FAWE, both π and E were obtained based on (X, δ, Z^o) using the Nadaraya-Watson estimator with normal kernel and bandwidth h = 4σ_Wn^−1/3. For MI, imputation models contained (X, δ, Z^o).

Figure 2 presents the plots of PB and AL versus the correlation coefficient between Z^m and Z^o when the selection probability was 50%. For β^m, the FAWE showed slightly larger bias (PB was still close to 5%) and smaller AL than the MI estimators across the range of various correlations, while they performed similarly for β^o.

3.5. Simulation Scenario 4

In this scenario, we explored the performance of the FAWE and the MI methods when the PH assumption was violated. Specifically, the failure time was generated from a lognormal AFT model: log(T) = β^TZ + σε, where β = (−ln(2), ln(2)), Z = (Z^m, Z^o), σ = 1 and ε ∼ normal(0,1). Both Z^m and Z^o followed a standard normal distribution and they were independent. Exponential censoring time was considered with rate selected to generate 60% cases. The selection probability depended on X, δ, and Z^o, resulting in 20% missing data.

Table 3 presents the results. Since the Cox PH model and the AFT model are on different scales, describe different quantities and there is not direct transformation between the two models in general, it is not proper to calculate the bias and precision quantities based on the parameter values used in generating the survival data [32]. Instead, we used the average parameter estimates from the full-cohort analysis as the “true” parameter values in simulation assessment. Comparing to estimates from the full-cohort analysis, the FAWE had reasonable bias and close to reasonable coverage. But the MI estimators had larger biases, especially for β^m. This implies that the FAWEs can yield results close to those of the full-cohort data analysis even when the PH regression assumption is violated, while the MI estimators may not.

Table 3.

Simulation comparison of the FAWE and MI estimators of the Lognormal AFT Model parameter β = (−ln(2), ln(2)), where σ² = 1; Z^m, Z^o ∼ N(0, 1) and Z^m and Z^o are independent; exponential censoring time with mean |0.75Z^o|/0.12, causing censoring rate 40%; and selection probability π(X, δ, Z^o) = (1 + exp((−0.4 − δ − X − Z^o))⁻¹.

Approach	PB %		AL		95% CR
	βm	βo	βm	βo	βm	βo
Full cohort	0.00	0.00	0.40	0.37	0.93	0.93
Complete-case	0.99	-6.24	0.43	0.41	0.93	0.89
FAWE	1.16	-0.94	0.41	0.36	0.89	0.88
MI norm	-12.84	-5.66	0.45	0.38	0.88	0.89
MI pmm	-11.14	-4.14	0.45	0.38	0.89	0.91

Notes: Cohort size is 250 and the expected number of complete observations is 200 with 81% cases and 78% controls selected.

The numbers in bold are those with |PB| > 5% or CR < 0.90.

For FAWE, both π and E were obtained based on (X, δ, Z^o) using the Nadaraya-Watson estimator with normal kernel and bandwidth h = 4σ_Wn^−1/3.

For MI, imputation models contained (X, δ, Z^o).

3.6. Result Summary

In summary, the results from the simulation study suggest the following:

1. The FAWEs are consistent as long as either the selection probability or the conditional expectations are estimated correctly while the MI estimators can be biased when the imputation models exclude some relevant variables.

2. The performance of the FAWEs are not affected when the censoring time depends on the missing covariates while the MI estimators may have large bias in such situations.

3. The FAWEs may have better precision than the MI estimators in some situations, eg. under large amount of missing data.

4. When the PH assumption is violated, the FAWEs produce results closer to those of the full-cohort analysis than the MI methods.

4. Data Example: the CHARGE Study

The research reported here was partially motivated by a particular missing data problem in the Childhood Autism Risk from Genetics and the Environment (CHARGE) study. The CHARGE study is an ongoing population-based case-control study being conducted in the M.I.N.D. (Medical Investigation of Neurodevelopmental Disorders) Institute of University of California Davis [33]. The overall goal of the study is to uncover environmental and genetic factors that increase the risk and severity of autism, a complex developmental disorder with symptoms encompassing a range of deficits in social interaction, language and repetitive or stereotyped behaviors manifested by the age of three.

In this specific analysis, we attempt to study the association between language development (characterized by verbal or non-verbal and time to first real words) and polybrominated diphenyl ether 85 (PBDE-85) using 440 boys from the CHARGE study. PBDE-85 is a flame retardent with potential neurodevelopmental toxicity used widely in homes such as construction materials, foam seats and furniture. To save cost, the concentrations of PBDE-85 in serum was measured only for a random sample of 43 cases (autistic children) and 19 controls (typically developing children). So about 86% of the boys had missing PBDE-85 (378/440). The missing data mechanism is related to children's diagnosis status (case or control) by design and hence it is reasonable to assume MAR in the data analysis.

For data analysis, we used a Cox PH regression model. The survival outcomes were verbal status and time to first real words, and the covariates included PBDE-85 (log-transformed) and two fully observed covariates: diagnosis status and child's age. About 9% boys had a censored outcome (402 verbal boys). We applied the CC analysis, the FAWE, MI norm, and MI pmm to the CHARGE data. Child's age, diagnosis status, time to first real words and verbal status were used in the imputation models for the MI estimators and the Nadaraya-Watson estimators of the selection probability and the conditional expectations for the FAWE. Due to the high missing rate, 1000 imputed data sets were generated and 1000 iterations were employed to impute each data set in the MI methods.

The analysis results in Table 4 showed that PBDE-85 was not significantly associated with language development after adjusting for diagnosis status and child's age. The CC analysis usually had the largest coefficient estimate and length of CI for all three covariates probably due to excluding all the incomplete data. The FAWE had slightly larger coefficient estimate for PBDE-85 and smaller coefficient estimate for diagnosis than the MI estimators while all the FAWE and MI estimators had similar estimates for child's age. Estimate from the FAWE had the smallest length of CI for PBDE-85, and the lengths of CI were similar for diagnosis status and child's age among all the FAWE and MI estimators, consistent with the pattern seen in our simulation study.

Table 4.

Analysis of the CHARGE data using a Cox regression model and various methods.

Approach	Coefficient Estimate			Length of CI			P-value
	PBDE	DS	Age	PBDE	DS	Age	PBDE	DS	Age
Complete-case	0.15	1.23	-0.03	0.50	1.19	0.06	0.25	0.00	0.07
FAWE	0.13	1.04	-0.01	0.32	0.47	0.02	0.12	0.00	0.09
MI norm	0.12	1.15	-0.01	0.47	0.50	0.02	0.33	0.00	0.07
MI pmm	0.11	1.16	-0.01	0.34	0.47	0.02	0.22	0.00	0.08

Notes: PBDE is log-transformed PBDE-85 and DS is diagnosis status.

For FAWE, both π and E were obtained based on verbal status, time to first words, DS and age.

using the Nadaraya-Watson estimator with normal kernel and bandwidth h = 4σ_Wn^−1/3.

For MI, imputation models contained verbal status, time to first real words, DS and age.

5. Discussion

In this article, we have compared the FAWE and the MI methods for the Cox PH model when the primary covariates of interest are only observed for a subset of the study sample. Both methods make use of incomplete observations as well as complete observations to obtain estimates, but in different ways. The FAWEs directly use the incomplete data nonparametrically in the estimating equations, and have the doubly robust property. Their bias and coverages are within reasonable limits as long as either the selection probability or the conditional expectations are estimated correctly. The efficiency of the FAWEs estimates appear relatively insensitive to misspecification of the selection probability in the simulation study, though more sensitive to misspecification of the conditional expectations. When the true selection probability is known, it can be used directly in the FAWEs to produce similar estimates [7]. On the other hand, the MI methods use the incomplete data when generating imputed data sets. It is crucial that the imputation model include all relevant variables to yield valid results. Omitting one or more relevant observed covariates may result in poor estimates with severe bias and low coverage rate. In addition, simulation results show the general trend of increasing bias and decreasing precision for both methods over increasing level of missingness. When the amount of missing data is greater than 75 - 80%, the FAWEs and the MI may have large bias or worse precision, especially for the parameter estimates of the missing covariates. However, the performance of these methods may also depend on other factors such as sample size, effect size and the correlation among covariates and outcome variables. So these methods might still yield useful results in certain situations with high missingness rates.

In our simulation study, we find that MI methods yield estimates with large bias when the censoring time depends on missing covariates (see Table 2). This indicates that the MI estimators may require independence between censoring times and missing covariates to produce consistent estimates, like the nonparametric maximum likelihood (NPML) method [34]. But the FAWEs perform well when the censoring time depends on the missing covariates, and similarly to the case when the censoring time and the missing covariates are independent. Thus, compared to the MI methods, the FAWEs have the advantage of allowing censoring times to depend on missing covariates.

Using the Cox PH model to analyze data appears to be a common practice even when the PH assumption is violated. Our simulation study shows that the FAWE performs much more similarly to the full-cohort analysis than the MI methods when fitting a Cox model to data generated by a lognormal AFT model. Hence the former approach might be more desirable if treating the full-cohort analysis results as the “gold standard”. On the other hand, to obtain more reasonable results, it needs to extend both approaches to missing covariate problems under other survival models such as AFT models including the lognormal AFT model and the parametric Weibull PH model. In addition, we focused on comparing the two approaches for time-independent covariates in this paper since the FAWEs have not been developed for time-dependent covariates yet. It will be interesting and important to extend the FAWEs to time-dependent covariates and compare it with the MI. We plan to further investigate these topics in the future.

In practice, when handling survival data with missing covariates, it is important to examine the data closely before conducting analysis, and try to understand the reasons for missing observations. Variables related to the missing data mechanism need to be included in the analysis, in one way or another, whichever method is used. Multiple imputations are relatively easy to implement with various software available but they can be sensitive to model misspecification. In contrast, the FAWEs recover a substantial proportion of the efficiency and are also remarkably robust as long as getting either the conditional expectations or the selection probability correct. They also require less restrictive assumptions on censoring mechanism. Hence, we believe that the FAWEs show the potential for being a competitive and attractive tool for tackling the analysis of survival data with missing covariates. Further computational and software development is needed for this method to be available to many practitioners.

Appendix I: Nadaraya-Watson estimators for the conditional expectations and the selection probability

Let W = (X, δ, Z^o), and let φ(w) = E{f ∣w} denote the conditional expectation of f given W. Assuming φ(w) is a smooth function with r continuous and bounded partial derivatives with respect to the continuous components of W a.e., then a Nadaraya-Watson estimator of φ(w) in (1) is given by

$$\widehat{\varphi }(\mathbf{\text{w}})=\frac{{\sum }_{i=1}^n{V}_i{\mathit{\text{f}}}_i{K}_h(\mathbf{\text{w}}-{\mathbf{\text{W}}}_i)}{{\sum }_{j=1}^n{V}_j{K}_h(\mathbf{\text{w}}-{\mathbf{\text{W}}}_j)},$$ (3)

where K is an rth-order kernel function and h is a smoothing parameter. The Nadaraya-Watson [24, 25] estimator can be also used to estimate the selection probability π based on all available data:

$$\widehat{\pi }(w)=\frac{{\sum }_{i=1}^n{V}_i{K}_h(\mathbf{\text{w}}-{\mathbf{\text{W}}}_i)}{{\sum }_{j=1}^n{K}_h(\mathbf{\text{w}}-{\mathbf{\text{W}}}_j)}.$$ (4)

When both selection probabilities and conditional expectations are estimated nonparametrically, different kernel functions could be employed in the two places. For simplicity we used the same kernel function in our simulations. To obtain these Nadaraya-Watson estimators, the R function ksmooth was employed with normal kernel and smoothing parameter h = 4σ_Wn^−1/3 when W contained one continuous element; the sm.regression in the sm library of A.W.Bowman and A.Azzalini was used when W contained two continuous elements.

Appendix II: Asymptotic distribution of the FAWEs and the consistent estimator of Σ_{f aw}(π)

Under certain conditions (refer to [7]), the FAWEs are asymptotically consistent for the true parameter β and normally distributed with mean 0 and variance matrix Σ⁻¹Σ_{f aw}(π)Σ⁻¹ with ${\sum }_{f\mathit{\text{aw}}}(\pi )=\sum +{\sum }_{f\mathit{\text{aw}}}^{\ast }(\pi )$, where $\sum =E\{{\mathbf{\text{M}}}_{\stackrel{\sim }{\text{Z}}}{\mathbf{\text{M}}}_{\stackrel{\sim }{\text{Z}}}^T\},{\sum }_{f\mathit{\text{aw}}}^{\ast }(\pi )=E\{({\pi }^{-1}-1)\text{var}({\mathbf{\text{M}}}_{\stackrel{\sim }{\text{Z}}}\mid X,\delta ,{\mathbf{\text{Z}}}^o)\}$, and ${\mathbf{\text{M}}}_{\stackrel{\sim }{\text{Z}}}={\int }_0^{\tau }[\mathbf{\text{Z}}-E\{Y(t)\mathbf{\text{Z}}exp({\beta }^T\mathbf{\text{Z}})\}/E\{Y(t)exp({\beta }^T\mathbf{\text{Z}})\}]\mathit{\text{dM}}(t)$ is the martingale transformation with mean E{M_Z̃} = 0 and variance Σ [7].

Consistent estimators of the variances for the FAWEs can be obtained as shown in Qi et al. [7]. Specifically, to estimate the variance Σ_{f aw}(π) for β̂_{f aw}(π̂, Ê), let

$$d{\widehat{\mathrm{\Lambda }}}_0^{f\mathit{\text{aw}}}(t,\widehat{\pi })=\frac{1}{n}\frac{{\sum }_{i=1}^{n}d{N}_i(t)}{S_{\mathit{\text{aw}}}^{(0)}({\widehat{\beta }}_{f\mathit{\text{aw}}}(\widehat{\pi },\widehat{E}),\widehat{\pi },t)},$$

$${\widehat{\mathbf{\text{M}}}}_{\stackrel{\sim }{\text{Z}}}={\int }_0^{\tau }\left[\mathbf{\text{Z}}-\frac{{\widehat{\mathbf{\text{S}}}}_{\mathit{\text{aw}}}^{(1)}({\widehat{\beta }}_{f\mathit{\text{aw}}}(\widehat{\pi },\widehat{E}),\widehat{\pi },t)}{{\widehat{S}}_{\mathit{\text{aw}}}^{(0)}({\widehat{\beta }}_{f\mathit{\text{aw}}}(\widehat{\pi },\widehat{E}),\widehat{\pi },t)}\right][\mathit{\text{dN}}(t)-Y(t)exp({\widehat{\beta }}_{f\mathit{\text{aw}}}^T(\widehat{\pi },\widehat{E})\mathbf{\text{Z}})d{\widehat{\mathrm{\Lambda }}}_0^{f\mathit{\text{aw}}}(t,\widehat{\pi })],$$

to be the estimators of dΛ₀(t) and M_Z̃, respectively. Then Σ and ${\sum }_{f\mathit{\text{aw}}}^{\ast }(\pi )$ are estimated respectively by

$$\widehat{\sum }=-\frac{1}{n}\frac{\partial }{\partial \beta }{\widehat{\text{U}}}_{f\mathit{\text{aw}}}({\widehat{\beta }}_{f\mathit{\text{aw}}}(\widehat{\pi },\widehat{E}),\widehat{\pi }),$$

and

$${\widehat{\sum }}_{f\mathit{\text{aw}}}^{\ast }(\pi )=\frac{1}{n}\sum _{i=1}\frac{V_i(1-{\widehat{\pi }}_i)}{{\widehat{\pi }}_i^2}{\left({\widehat{\mathbf{\text{M}}}}_{\stackrel{\sim }{\text{Z}},i}-{\widehat{\mathbf{\text{M}}}}_{\stackrel{\sim }{\text{Z}},i}^0\right)}^{\otimes 2},$$

where ${\widehat{\mathbf{\text{M}}}}_{\stackrel{\sim }{\text{Z}}}^0$ is obtained using the Nadaraya-Watson estimator given in (3).