Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells

Abstract

The performance of organometallic perovskite solar cells has rapidly surpassed that of both conventional dye-sensitized and organic photovoltaics. High-power conversion efficiency can be realized in both mesoporous and thin-film device architectures. We address the origin of this success in the context of the materials chemistry and physics of the bulk perovskite as described by electronic structure calculations. In addition to the basic optoelectronic properties essential for an efficient photovoltaic device (spectrally suitable band gap, high optical absorption, low carrier effective masses), the materials are structurally and compositionally flexible. As we show, hybrid perovskites exhibit spontaneous electric polarization; we also suggest ways in which this can be tuned through judicious choice of the organic cation. The presence of ferroelectric domains will result in internal junctions that may aid separation of photoexcited electron and hole pairs, and reduction of recombination through segregation of charge carriers. The combination of high dielectric constant and low effective mass promotes both Wannier-Mott exciton separation and effective ionization of donor and acceptor defects. The photoferroic effect could be exploited in nanostructured films to generate a higher open circuit voltage and may contribute to the current–voltage hysteresis observed in perovskite solar cells.

The development of halide pervoskite solar cells is as rapid as the technology is proving successful.¹⁻⁶ Research on these compounds dates to the 1920s.⁷ The most widely used hybrid perovskite solar cell material is methylammonium lead iodide (CH₃NH₃PbI₃ or MAPbI₃), where MA is a positively charged organic cation at the center of a lead iodide cage structure (Figure 1). Initially employed as a light sensitizer in mesoporous dye cells, these materials also function as an absorber and transport layer in a solid-state dye cell architecture, and most recently as the bulk material in a standard planar thin-film solar cell.⁸

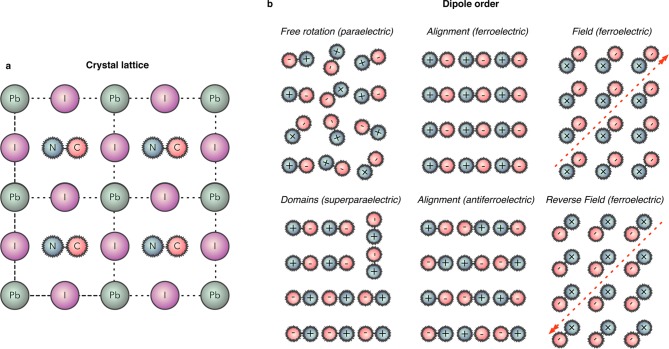
Figure 1.

Schematic perovskite crystal structure of MAPbI₃ (a), and the possible orientations of molecular dipoles within the lattice (b). Note that MA has an associated molecular dipole of 2.3 D, a fundamental difference compared to the spherical cation symmetry in inorganic perovskites such as CsSnI₃.

Here we build upon recent computational studies⁹⁻¹⁶ and calculate the electrostatic cohesion energy, the electronic band energies, optical transitions, cation molecular polarization tensors, and energetic barriers for rotation in hybrid lead iodide perovskites. We show how lattice polarization is affected by the polar organic cation, and how this gives rise to ferroelectric behavior, which could enhance photovoltaic performance.

Perovskite Structure

The crystal structure adopted by CaTiO₃ (the mineral perovskite) is also found for a wide range of materials with ABX₃ stoichiometry with two well-studied cases being SrTiO₃ and BaTiO₃. Examples of insulating, semiconducting, and superconducting perovskite structured materials are known; they represent a unique system class across solid-state chemistry and condensed matter physics. In particular, they are the archetypal systems for phase transitions with accessible cubic, tetragonal, orthorhombic, trigonal, and monoclinic polymorphs depending on the tilting and rotation of the BX₆ polyhedra in the lattice.¹⁷ Reversible phase changes can be induced by a range of stimuli including electric field, temperature, and pressure.

There have been several reports of structural characterization for single crystals of MAPbI₃ and related compounds.^18,19 Orthorhombic, tetragonal, and cubic polymorphs have been identified, analogous to the inorganic perovskites. Indeed it has been suggested that for MAPbI₃ an orthorhombic to tetragonal transition occurs at ∼160 K with a cubic phase being stable from around 330 K.¹⁹ Disagreement between X-ray and electron diffraction has been noted, which suggests the presence of nanoscale structural domains.¹⁹ This local disorder is also present in thin-film samples. The structure of thin-films within mesoporous titania has been investigated using X-ray scattering,²⁰ which showed that the majority of the MAPbI₃ exists in a disordered state with a structural coherence length of only 14 Å, that is, the length of just two PbI₃ cages. This behavior will be explained below in the context of feedback between molecular and lattice polarization, which is a ferroelectric effect.

Perovskite Composition

Within the formal stoichiometry of ABX₃, charge balancing can be achieved in a variety of ways. For metal oxide perovskites (ABO₃), the valence of the two metals must sum to six, that is, I–V–O₃, II–IV–O₃, and III–III–O₃ perovskites are known with common examples being KTaO₃, SrTiO₃, and GdFeO₃. The range of accessible materials can be extended by partial substitution on the anion sublattice, for example, in the formation of oxynitride and oxyhalide perovskites.²¹ With substitution on the metal sublattice, the so-called double, triple, and quadruple perovskites are formed,²² which may offer a route for property optimization of hybrid compounds.

For halide perovskites, the valence of the two cations must sum to three, so the only viable ternary combination is I–II-X₃, for example, CsSnI₃. In hybrid halide perovskites such as MAPbI₃, a divalent inorganic cation is present with the monovalent metal replaced by an organic cation of equal charge. In principle, any singly charged molecular cation could be used, once there is sufficient space to fit it within the inorganic cage. If the size is too large, then the 3D perovskite structure is broken, as demonstrated in the series of hybrid structures with lower dimensionality in the inorganic networks.^15,23−25 For layered structures, the crystal properties become highly anisotropic.

The stability of ionic and heteropolar crystals, such as perovskites, is influenced by the Madelung electrostatic potential. The lattice energy and site electrostatic potentials is explored for each perovskite stoichiometry (Table 1). These are calculated with an Ewald summation (in three dimensions) of the formal ion charges within the code GULP.²⁶ For group VI anions, the lattice energy decreases as the charge imbalance between the A and B sites is removed; a lower charge on the A site is favored. However, for group VII anions (i.e., halides) the electrostatic stabilization is notably reduced with a lattice energy of just −29.71 eV/cell and an electrostatic potential on the anion site ca. 50% of the group VI anions. Because of this weaker, less-confining, potential, lower ionization potentials (workfunctions) are expected for halide perovskites compared to, for example, metal oxides.^27,28

Table 1. Electrostatic Lattice Energy and Site Madelung Potentials for a Range of ABX₃ Perovskite Structures (Cubic Lattice, a = 6.00 Å) Assuming the Formal Oxidation State of Each Species^a.

stoichiometry	Elattice (eV/cell)	VA (V)	VB (V)	VX (V)
I–V–VI3	–140.48	–8.04	–34.59	16.66
II–IV–VI3	–118.82	–12.93	–29.71	15.49
III–III–VI3	–106.92	–17.81	–24.82	14.33
I–II–VII3	–29.71	–6.46	–14.85	7.75

^aThe hybrid halide perovskites are of type I–II–VII₃. Calculations are performed using the code GULP.

From Inorganic to Hybrid Compounds

An important distinction between inorganic and hybrid perovskites is the change from a spherically symmetric A site (inorganic) to one of reduced symmetry (hybrid). The characteristic space groups of perovskite compounds are formally reduced. For example, the MA cation has the C_3v point group and the associated highest-symmetry perovskite structure will be pseudocubic and not possess the inversion symmetry of its inorganic analogue. Thus, uncertainty in assigned average diffraction patterns is not surprising.

The presence of a polar molecule at the center of the perovskite cage also introduces the possibility of orientational disorder and polarization as drawn in Figure 1. A typical solid-state dielectric will exhibit a combination of fast electronic (ε_∞) and slow ionic (ε_ionic) polarization, which both contribute to the macroscopic static dielectric response (ε₀ = ε_∞ + ε_ionic + ε_other). A molecular response (ε_molecular) can occur for materials containing molecules with a permanent dipole, which will likely occur more slowly (due to the moment of inertia of the molecules, and kinetically limited reordering of domains). This orientational effect is usually reserved for polar liquids.²⁹

We have investigated the following energetics of rotation of three organic cations within the lead iodide perovskite structure: (i) ammonium, NH₄⁺ (A); (ii) methylammonium, CH₃NH₃ (MA); and (iii) formamidinium, NH₂CHNH₂⁺ (FA). These were performed using density functional theory (DFT), using the PBEsol³⁰ exchange-correlation functional and the VASP code^31,32 with the setup details previously reported.¹³ Here, we kept the cell lattice parameters fixed and rotated the cell over the long axis of the molecule, an equivalent rotation to tumbling the molecule end over end. This gives us an upper, unrelaxed, limit of the rotation barrier. The resulting barriers for rotation in the cage are 0.3, 1.3, and 13.9 kJ/mol, respectively. The value for MA is consistent with observed high rates of rotation at room temperature from ²H and ¹⁴N spectra.³³

The organic cations MA and FA have a large built-in polarization, most obviously in the case of methylammonium. To investigate this we calculate the polarization tensor in vacuum with the GAUSSIAN³⁴ package on singly charged cations. We find that the molecular polarization tensor is dominated by a dipole contribution. The dipoles, in Debye, for B3LYP/6-31G* (CCSD/cc-pVQZ) calculations are (i) A, 0.0 (0.0); (ii) MA, 2.29 (2.18); and (iii) FA, 0.21 (0.16). An obvious route to increasing the strength of this dipole is successive fluorination of the methyl in methylammonium. We calculate the dipole increase from methylammonium (2.29 D) to mono-, bi- and trifluorination to be 5.35, 6.08, and 6.58 D, respectively (B3LYP/6-31G*). These permanent dipoles will interact with an external electric field and with each other.

In the hybrid perovskite, the cations are surrounded by a polarizable medium (the perovskite cage), whereas our dipole calculations are in the gas phase. As a first approximation, we therefore repeat these calculations with the polarizable continuum model (PCM) with a choice of solvent (ethanol, ε₀ = 24.852) that matches our calculated dielectric constant for the bulk material and is a suitably bulky solvent that it should have a comparable cavity volume to the pore in the perovskite cage. We use the gas phase geometries. The dipoles in Debye for B3LYP/6-31G* PCM calculations with ethanol are (i) A, 0.0; (ii) MA, 2.65; (iii) FA, 0.24; (iv) MA-F3, 7.19. A more careful calculation would require a better model for the cavity; however these data do show that only a small deviation from the gas phase values occur, which suggests that the permanent dipole moment of these molecules is robust to the local polarization environment.

Hybrid halide perovskite solar cells have a typical active region thickness of 1 μm and a built in voltage of 1 V, resulting in an electric field of ca. 1 × 10⁶ Vm^–1. The dipole potential energy is U = −pE, and so the energy change in going from aligned to antialigned with the electric field is 2pE or 4 × 10^–5 eV D^–1. The interaction energy of 9 × 10^–2 meV for MA is small compared to the thermal energy, and so weak macroscopic ordering of the cations as a result of the internal field of the solar cell is expected, but more careful quantification is required to understand the field interactions with domains.

The interaction energy of two point dipoles, going from parallel ferroelectric to antiferroelectric alignment, is

1

In applying this to nearest-neighbor cation dipoles within the perovskite structure, we are making two approximations. The first is the point dipole approximation. Our molecules are too close for this to be correct and the origin of the molecular dipole is likely to move within the perovskite cage as the cation rotates. The second is in assuming the vacuum dielectric constant. There will be electron density shielding the region of space between these two cations, but the cations face each other through a relatively open face of the perovskite structure; the upper limit of the screening is the macroscopic static dielectric constant (ε₀ = 25.7 for MAPbI₃)¹³ that should be valid over longer distances.

Due to the many unknowns in the location and dynamic behavior of the cation and the difficulty in fully treating the interaction of the molecular charge density with the periodic electronic structure of the perovskite, we present these energies as a first approximation. These energies can be used to parametrize a classical Hamiltonian for the interaction of the rotating dipoles and as activation energies for use in looking for order–disorder transitions experimentally.

Considering a cubic perovskite structure with 6.29 Å between nearest neighbors, the parallel ferroelectric alignment energy of methylammonium is 48 meV. Because of the p² dependence on the dipole moment while keeping methylammonium lattice parameters, this energy is much smaller than thermal energy for FA, 0.3 meV; zero for A; and much greater for fluorinated MA, 436 meV.

Systematic variation of the organic cation (such as by fluorination) and studying the electrical properties of the resulting devices would offer direct evidence of the molecular dipole derived contribution to the operation of hybrid halide perovskite solar cells. Polarization of the inorganic perovskite cage will be discussed separately below.

Electronic Structure

For MAPbI₃ and related materials, the upper valence band is predominately composed of I 5p orbitals, while the conduction band is formed of Pb 6p.^13,14 There is hybridization between the filled Pb 6s band with I 5p that result in antibonding states at the top of the valence band (analogous to p–d coupling in II–VI semiconductors). Electron and hole conduction therefore occurs along distinct pathways at the R point of the first Brillouin zone.¹⁴ Both Pb and I are heavy ions, and as such both the valence and conduction bands contain considerable relativistic effects, that is, for a quantitative treatment of the electronic band structure spin–orbit coupling must be included.¹⁴ The band gap predicted by a relativistic self-consistent quasiparticle GW method is 1.67 eV, which is in good agreement with the measured value of 1.61 eV from room temperature photoluminescence (PL).³⁵

Lead is commonly used in ferroelectric and multiferroic materials as its lone pair of electrons is a driving force for structural distortions.^36,37 Note that the multivalency of Pb (and Sn for stannous halides) will also be important for the defect chemistry. While present as divalent cations in these structures (s²p⁰), a higher tetravalent oxidation state is also accessible (s⁰p⁰). Self-oxidation could facilitate the generation of electrons (n-type doping; Pb^II → Pb^IV + 2e^–) or in the trapping of holes (p-type compensation; Pb^II + 2h⁺ → Pb^IV). The thermodynamics of these processes merit further investigation.

For all cases investigated, the organic cation acts as a charge compensating center but does not participate in the frontier electronic band structure.^13,15 Occupied molecular states are found well below the top of the valence band and empty molecular states found well above the bottom of the conduction band. The choice of organic moiety does influence the lattice constant and, therefore, will change the electronic structure indirectly, in a similar manner to the application of hydrostatic pressure.

Unusually, the band gaps of hybrid perovskites have been reported to increase with increasing cell volume (decreasing pressure),¹⁵ which is opposite to the behavior of most semiconductors.³⁸ Indeed the calculated band gap deformation potential

2

for MAPbI₃ is positive (α_V^R = 2.45 eV). As the fundamental band gap is determined at the boundary of the Brillouin zone (R), the out-of-phase band-edge states are stabilized as the lattice expands. Similar behavior is observed for Pb chalcogenides.³⁹ The deformation of the gap at the Γ point is negative (α_V = −1.08 eV), following standard expectation. Measurements of temperature dependent PL indicate a decrease in band gap with decreasing temperature (lattice contraction) to ∼1.55 eV at 150 K, which is at the onset of a phase change.³⁵

The implication of the deformation potential is that for smaller molecular cations, lower band gaps should be observed. Indeed, the smallest possible counterion is a proton (H⁺) to form HPbI₃, which results in a calculated lattice parameter of 6.05 Å and an associated band gap of less than 0.3 eV. In contrast, the band gap changes on halide substitution are influenced more by the electronic states of the anion, that is, from Cl to Br to I the valence band composition changes from 3p to 4p to 5p with a monotonic decrease in electron binding energy (lower ionization potential). The substitution of Br by I in FAPbX₃ has been shown to decrease the band gap from 2.23 to 1.48 eV.⁴⁰

The effective masses of both carriers are k-dependent, as the result of nonparabolic energy bands near the extremal points, as confirmed by self-consistent GW calculations.¹⁴ These calculations have also shown that relativistic renormalization of the band gap is of a similar magnitude to the band gap itself; these materials are far removed from conventional semiconductors such as Si. Close to the band extrema the carriers are light with m_h^* and m_e of approximately 0.12 m₀ and 0.15 m₀, respectively.⁴¹

As a result of the high dielectric constant, the associated Wannier-Mott exciton radius (within effective mass theory, that is, a₀ = ε₀/m_e in au)⁴² is large (204 Å) with a binding energy (E_b = 1/(2ε₀a₀)) of 0.7 meV. It is clear that excitons will not play a significant role in the photovoltaic device physics. Indeed, magnetoabsorption measurements at 4.2 K suggested an exciton radius of 28 Å and a binding energy of 37 meV in the low-temperature low-symmetry phase of single-crystal MAPbI3.⁴³

The valence band energy (ionization potential) of MAPbI₃ is 5.7 eV below the vacuum level (Figure 3). The computed bulk ionization potential and electron affinity of 5.7 and 4.1 eV are consistent with the use of TiO₂ (electron acceptor) and Au (gold acceptor) in photovoltaic devices.⁸ This ionization potential is comparable to thin-film solar cell absorbers such as Cu₂ZnSnS₄,⁴⁴ which implies that other device configurations, for example, a Mo back-contact (to replace Au) and a CdS buffer layer (to replace TiO₂), are possible. In contrast, the valence band of Si is significantly higher in energy.

Figure 3.

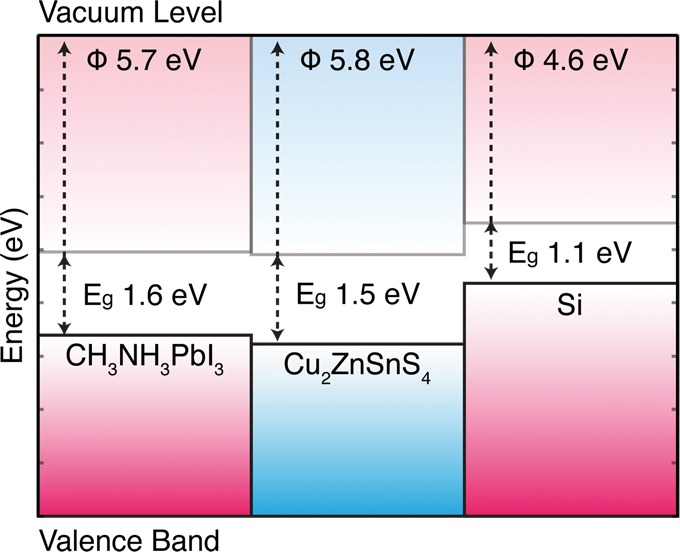
Valence band ionization potentials of MAPbI₃ with respect to the vacuum level. Calculations were performed on the nonpolar (110) surface with slab thickness of 25 Å and a vacuum thickness of 15 Å. The Kohn–Sham eigenvalues (PBEsol) are corrected by the bulk quasi-particle energies (ΔE = 0.2 eV). Values for the energetically similar inorganic thin-film absorber Cu₂ZnSnS₄⁴⁵ and Si⁴⁶ are shown for comparison.

Carriers, Defects and Decomposition

The bulk electronic structure also has implications for carrier concentrations. These materials are intrinsic semiconductors with initial reports of relatively high doping densities, for example, above 10¹⁹ cm^–3 in MASnI₃.⁴⁷ Unlike traditional inorganic absorber materials where defect formation can be controlled thermodynamically, the solution processing of these materials at low temperatures is more likely to be kinetically controlled with defects in the lattice (e.g., cages with missing MA cations) being a product of the crystallization process. Initial computations suggest that the low energy defects all exhibit resonant or shallow impurity bands.¹⁶

The Mott criterion (n_ca₀ = 0.26)⁴⁸ based on the calculated band structure parameters, predicts a transition to a degenerate semiconductor could happen from carrier concentrations (n_c) as low as 10¹⁶cm^–3. Note that this is a lower estimate that will be increased by both the nonparabolic nature of the band edges and fluctuations in the local elecrostatic potentials due to structural inhomogeneity.

There are a number of potential routes for the control of carrier concentrations (doping). First, a mixture of charged and neutral counter-cations (e.g., NH₄⁺ and NH₃) would result in an electron deficiency and hence p-type doping. Conversely, the inorganic cage could be altered by partial substitution of Pb by a trivalent cation would result in an electron excess and hence n-type doping. Tl and Bi are two obvious candidates due to their similar size.

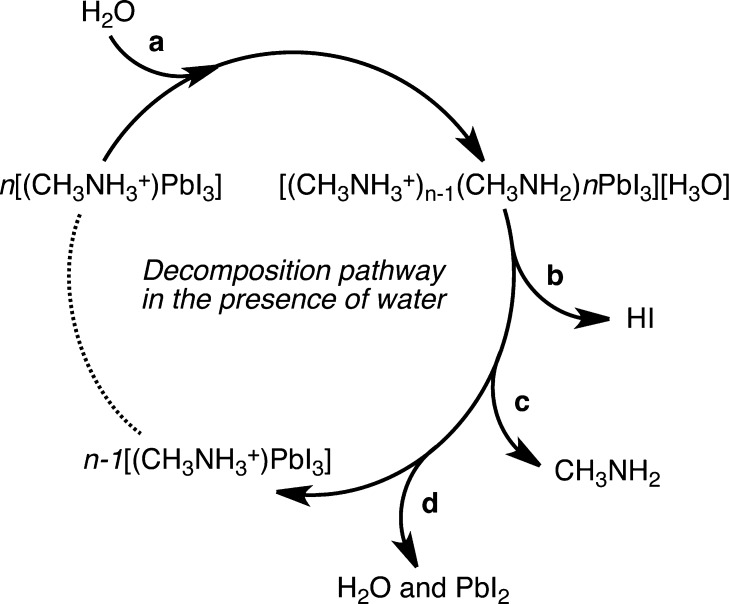
There are reports of hybrid perovskites reacting with Lewis bases with the most notable being irreversible degradation in the presence of H₂O and temporary bleaching in the presence of ammonia.⁴⁹ There are several plausible mechanisms by which this decomposition may occur. We propose the simple acid–base reaction shown in Figure 4. In the case of water exposure, a single water molecule is sufficient to degrade the material; however, an excess of water is required to dissolve the HI and CH₃NH₂ byproducts. As a result, a closed system with trace amounts of H₂O will result in partial decomposition of the hybrid perovskite until either (i) the HI has saturated the H₂O or (ii) the vapor pressure of CH₃NH₂ has reached equilibrium. In the presence of sufficient water the material degrades entirely to form PbI₂.

Figure 4.

Possible decomposition pathway of hybrid halide perovskites in the presence of water. A water molecule, a, is required to initiate the process with the decomposition being driven by the phase changes of both hydrogen iodide, (b, soluble in water) and the methylammonia (c, volatile and soluble in water). This pathway results in the formation of a yellow solid, which corresponds the experimentally observed PbI₂, d.

The proposed mechanism for reversible perovskite bleaching is similar to that of water decomposition, where a reaction analogous to Figure 4 may occur. In this case, the ionic salt (and strong acid) HI, would form a separate ionic salt with NH₃. This Grotthuss mechanism⁵⁰ should cause a concerted proton transfer throughout the material resulting in three thermally reversible outcomes: (i) the methylammonia evaporates, resulting in the inclusion of NH₄ as the organic ion in the perovskite, with the simultaneous production of HI; (ii) the system degrades to form HI, PbI₂, and volatile organics; and (iii) the CH₃NH₃⁺/CH₃NH₂–NH₃/NH₄⁺ reaction occurs on the surface causing the material to form the neutral CH₃NH₂. This acid–base reaction is reversible and ammonia is more volatile than the heavier methylammonia (which may be trapped within the material), resulting in transient bleaching.

To our knowledge, there has been no reports of hybrid perovskites incorporating aprotic organic ions (such as tetramethylammonium, (CH₃)₄N⁺). Such a material would not be capable of the reaction mechanism depicted in Figure 4 and so may be more chemically stable. The built-in molecular dipole, which could be important for the performance of these materials in a solar cell, could be achieved by selective flourination.

We speculate that decomposition or reversible bleaching should be observed in the presence of any small Lewis acid with a protic hybrid perovskite, and such an experimental study would help understanding the degradation pathways of hybrid perovskite solar cells.

Spontaneous Electric Polarization

Most inorganic perovskites display spontaneous electric polarization, arising from the breaking of crystal centro-symmetry, as a result of the B cation moving away from the center of the BX₆ octahedron.¹⁷ The phenomenon is particularly pronounced in hybrid halide perovskites, where the asymmetry of the organic cation ensures the absence of an inversion center in the structure.

The magnitude of the bulk polarization has been probed using Berry phase calculations within the modern theory of polarization.^51,52 The calculated values (PBEsol functional) are presented in Table 2. For MAPbI₃, the electronic polarization of 38 μC/cm² is comparable to ferroelectric oxide perovskites (e.g., ca. 30 μC/cm² in KNbO₃⁵³). Indeed, the application of ferroelectric oxides to photovoltaics has been recently demonstrated.⁵⁴

Table 2. Calculated Properties of Four Hybrid Lead Halide Perovskites from Density Functional Theory^a.

Cation	D	a	ΔP	Erot	Edip
NH4	0.00	6.21	8	0.3	0.00
CH3NH3	2.29	6.29	38	1.3	4.60
CF3NH3	6.58	6.35	48	21.4	42.00
NH2CHNH2	0.21	6.34	63	13.9	0.03

^aThe molecular dipole (D) is given in Debye, calculated by vacuum B3LYP/6-31G* in GAUSSIAN. The pseudo-cubic lattice constant (a = (V)^1/3) in Å; the lattice electronic polarisation (ΔP) in μC/cm²; and the rotation barrier (E_rot) in kJ/mol, calculated by PBESol in VASP. The nearest-neighbour dipole interaction (E_dip) in kJ/mol is estimated from a point dipole calculation.

The strong polarization of the lattice has two potential advantages for photovoltaic operation: (i) enhanced charge separation and concomitant improved carrier lifetimes;⁵⁵ (ii) open circuit voltages above the band gap of the material.⁵⁴ Both effects are linked to the internal electric field, which results as a consequence of lattice polarization. The mechanisms are shown schematically in Figure 5.

Figure 5.

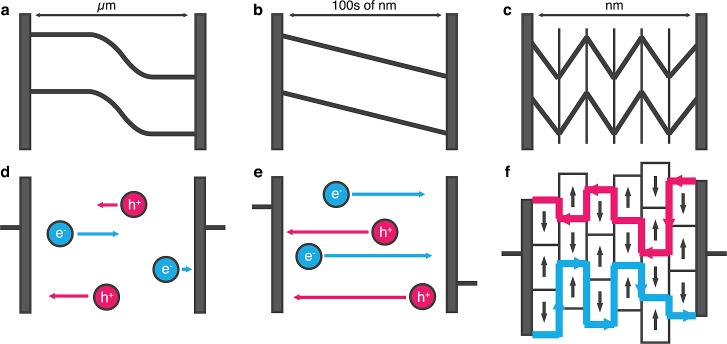
Schematic of the 1D built-in potential (upper panels) and associated 2D electron and hole separation pathways (lower panels) in (a,d) a macroscopic p–n junction; (b,e) a single domain ferroelectric thin-film; (c,f) a multidomain ferroelectric thin-film. In the multidomain ferroelectric, which we propose for hybrid perovskites, electrons will move along minima in the potential, while holes will move along maxima (i.e., antiphase boundaries).

Traditional semiconductor photovoltaic devices separate charge carriers at p–n junctions (Figure 5a). A ferroelectric domain with its built-in electric field (Figure 5b) acts to separate the exciton generated by photoabsorption in effect acting as a p–n junction. A standard planar p–n junction is on the order of micrometers and separated charge carriers must diffuse through the junction to reach their respective electrodes; during this diffusion process carriers may encounter one another and recombine. The size of ferroelectric domains is smaller on the nanometer scale (several cages for the hybrid perovskites). The probability of carrier recombination within a domain is therefore reduced with respect to a traditional heterojunction.

The carriers in the ferroelectric material can diffuse to domain boundaries, where there is a buildup of carriers of a given type (Figure 5c) along peaks and troughs in the electric potential generated by local dipole order. The carriers may then diffuse along these “ferroelectric highways” toward the electrodes, unimpeded by carriers of the opposite charge; essentially we have an intrinsic semiconductor region where local hole and electron segregation reduces recombination. We propose this as the origin of exceptionally long carrier diffusion lengths^56,57 despite local structural disorder. The carrier density of these ferroelectric boundaries as well as the domain orientation will be influenced by the applied voltage and hence give rise to hysteresis, or spurious fluctations, in electrical measurements.

The contribution of these photoferroic effects could be assessed and controlled by modification of the counterion. The molecular dipole can be tuned with the simple example discussed earlier being the incorporation of more electronegative species on one side of the MA cation (Figure 2). Even for APbI₃, where there is no molecular dipole, the lattice is weakly polarized (8 μC/cm²) and this effect would likely be enhanced toward lower symmetry interfaces and grain boundaries. Notably, the largest degree of polarization is observed for FAPbI₃ (63 μC/cm²), which is not the most polar cation, but its larger size induces a polar deformation of the PbI₃ cage.

Figure 2.

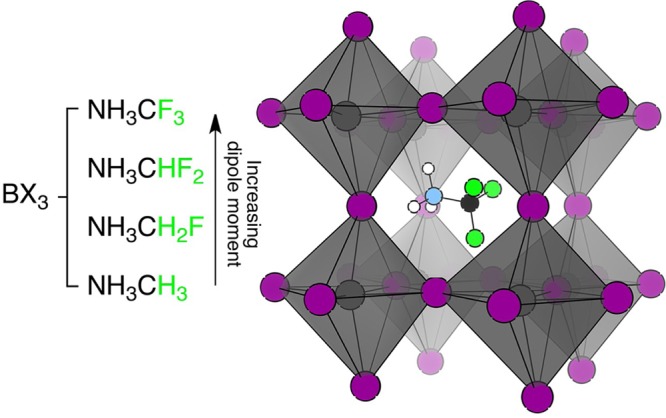
A significant increase in dipole moment (from 2.3 to 6.6 D, by a vacuum calculation with B3LYP/6-31G*) is achieved through increasing the degree of methyl-fluorination.

It is interesting to note that the “ferroelectric highways” are distinct but similar to the proposed mechanism for carrier separation in thin-film CuInSe₂ solar cells, where Cu-rich and Cu-poor domains (ordered defect complexes) have been linked to internal homojunctions that facilitate efficient charge carrier separation and reduced carrier recombination.^58,59

In summary, we have provided insights into the key materials properties of organometallic perovskites that contribute to their photovoltaic performance. Further investigations are required to assess the mechanisms proposed including the role of ferroelectric domains and the small exciton binding energies. Opportunities have been discussed for rational modification of material characteristics through modifying the organic cation. In particular, we suggest manipulating the dipole moment (to affect ferroelectric behavior and dielectric constant), cation size (to manipulate band gap and ferroelectric behavior) and to move to an aprotic cation (to avoid a degradation pathway). A lead free material with high performance and reduced degradation would represent a major step forward for this technology. We hope that the description of the atomistic origin of favorable material characteristics exhibited by MAPI₃ may offer some guidance for the design of improved organometallic perovskites.

Supporting Information Available

GAUSSIAN input and output files used in this work are electronically available in a Figshare data set.⁶⁰ This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.